RBSE Solutions for Class 11 Chemistry Chapter 7 Equilibrium

Rajasthan Board RBSE Solutions for Class 11 Chemistry Chapter 7 Equilibrium Textbook Exercise Questions and Answers.

RBSE Class 11 Chemistry Solutions Chapter 7 Equilibrium

RBSE Class 11 Chemistry Equilibrium InText Questions and Answers

Question 7.1 
The following concentrations were obtained for the formation of NH₃ from N₂ and H₂ a eqilibrium at 500K. [N₂] = 1.5 × 10⁻² M, [H₂]  = 3.0 × 10^-2 M and [NH₃] = 1.2 × 10^-2 M  Calculate equilibrium constant. 
Answer:
Given, 
[N₂] = 1.5 × 10⁻² M 
[H₂] = 3.0 × 10^-2 M 
[NH₃] = 1.2 × 10^-2 M 
Reaction is given as below 

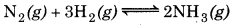
Equilibrium constant 
\(\begin{aligned} K_c & =\frac{\left[\mathrm{NH}_3(\mathrm{~g})\right]^2}{\left[\mathrm{~N}_2(\mathrm{~g})\right]\left[\mathrm{H}_2(\mathrm{~g})\right]^3} \\ & =\frac{\left[1.2 \times 10^{-2}\right]^2}{\left[1.5 \times 10^{-2}\right]\left[3.0 \times 10^{-2}\right]^3} \end{aligned}\)
= 1.06 x 10³ mol^-1 L^-2

 

Question 7.2.
At equilibrium, the concentration of N₂ = 3.0 × 10^-3 M, O₂ = 4.2× 10^-3 M and NO = 2.8 × 10^-3 M in a sealed vessel at 800K.  What will be Kc for the reaction 

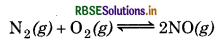
Answer:
Given [N₂] = 3.0 × 10^-3 M 
[O₂] = 42 × 10⁻³ M 
[NO] = 28 × 10^-3 M 
For the reaction, 

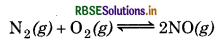
Equilibrium constant 

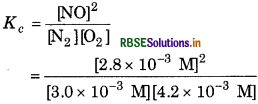
= 0.622 

Question 7.3. 
PCl₅, PCl₃ and Cl₂ are at equilibrium at  500K and having concentration 1.59 M PCI, 1.59 M Cl₂ and 1.41 M PCl₅. Calculate the K, for the reaction: 
Answer:

Given, 
[PCl₃] = 1.59 M 
[Cl₂] = 1.59 M 
[PCl₅] = 1.41 M 
For the reaction 

Equilibrium constant 

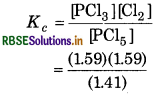
= 1.79 M 

Question 7.4. 
The value of Kc =  4.24 at 800 K for the reaction, 

Calculate equilibrium concentrations of CO₂, H₂, CO and H₂O at 800K, if only CO  and  H₂O are present initially concentrations of 0.10 M each. 
Answer:
The given reaction is 

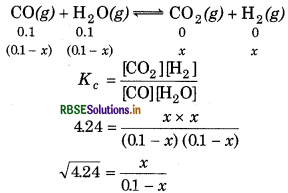
2.06(0.1 − x) = x 
x = 0.067 
[CO₂] = [H₂] = 0.067 M 
[CO] = [H₂O] = 0.1 - 0.067 
 = 0.033 M. 

 

 Question 7.5.
For the equilibrium, 

The value of the equilibrium constant, Kc is 3.75 x 10^-6 at 1069 K. Calculate the Kp for the reaction at this temperature. 
Answer:
Given, 
 Kc = 3.75 × 10^-6 
T = 1069 K 
Kp = ? 
∴ We know that, 
Kp = Kc(RT) ∆n 
For the reaction, 

∆n = np - nr 
= 3 - 2 = 1 
Kp = 3.75 × 10-6 (0.0831 × 1.069)1 
= 0.033 atm. 

Question 7.6.
The value of K, for the reaction, 

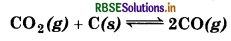
is 3.0 at 1000 K. If initially PCO₂ = 0.48 bar and PCO₂ bar and pure graphite is present, calculate the equilibrium partial pressures of CO and CO₂. 
Answer:
Given, 
Kp = 3 
Initial pressure PCO₂ = 0.48 bar 
PCO = 0 bar
Suppose 'x' be the pressure of CO₂, then for the reaction, 

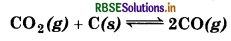
4 x 2 = 3 (0.48 - x) 
4 x 2  = 1.44 - 3x 
4 x 2 + 3 x - 1.44 = 0 
From quadratic equation, ax² + bx + c = 0 
a = 4, b = 3, c = 1.44 

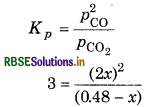
4x² = 3(0.48 - x)
4x² = 1.44 - 3x
4x² + 3x - 1,44 = 0
From quarditic equation ax² + bx + c = 0
a = 3 b = 3 c = -1.44

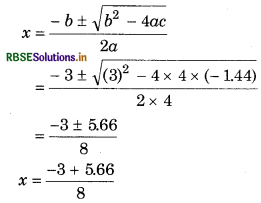
[The value of x can not be negative so we neglect that value] 
= \(\frac{2.66}{8}\)
= 0.33 
Hence, the equilibrium partial pressures are 
PCO = 2x = 2 × 0.33 = 0.66 bar 
PCO² = 0.48 x = 0.48 - 0.33

Question 7.7.
The value of Kc for the reaction 
\(2 \mathbf{A} \rightleftharpoons \mathbf{B}+\mathbf{C}\) is 2 × 10^-3. 
At a given time, the composition of reaction mixture is [A] = [B] = [C] = 3 × 10^-4 M. In which direction, the reaction will proceed? 
Answer: 
Given, [A] = [B] = [C] = 3 × 10^-4 M 
Kc = 2 × 10^-3 
For the reaction, 
\(2 \mathrm{~A} \rightleftharpoons \mathrm{B}+\mathrm{C}\)
Reaction Quotient is given by, 
\(\begin{aligned} Q_c & =\frac{[B][C]}{[A]^2} \\ & =\frac{\left(3 \times 10^{-4}\right) \times\left(3 \times 10^{-4}\right)}{\left(3 \times 10^{-4}\right)^2} \end{aligned}\)
= 1 
∴ The reaction will proceed in the backward direction. 

Question 7.8. 
13.8 g of N₂O₄ was placed in a 1L reaction  vessel at 400K and allowed to attain equilibrium. 
\(\mathrm{N}_2 \mathrm{O}_4(g) \rightleftharpoons 2 \mathrm{NO}_2(g)\)
The total pressure at equilibrium was found to be 9.15 bar. Calculate K, and partial pressure at equilibrium. 
Answer:
Given, Mass of N₂O₄ = 13.8 g 
Total volume = 1 L 
T = 400.K 
Molar mass of N₂O₄ = 14 (2) + 16 (4) = 92 g 
Number of moles  =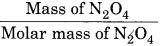
R  = 0.083 bar L mol^-1 K^-1 
∵ pV = nRT 
P× 1L = 0.15 mol × 0.083 bar L mol-1K-1 × 400 K 
P = 4.98 bar 
For the reaction, 
Intial pressure 
\(\mathrm{N}_2 \mathrm{O}_4(g) \rightleftharpoons 2 \mathrm{NO}_2(g)\)
Ptotal at equilibrium = PN₂O₄ + PNO₂ 
9.15(4.98x) + 2x 
9.15 = 4.98 + x 
X 9.15 - 4.98 = 4.17 bar 
Partial pressures at equilibrium are : 
PN₂O₄  = 4.98 - 4.17 = 0.81 bar 
PNO₂  = 2x =  2 × 4.17 = 8.34 bar 
\(K_p=\frac{\left(p_{\mathrm{NO}_2}\right)^2}{p_{\mathrm{N}_2 \mathrm{O}_4}}\) =  85.87 
Kp = KcRT)∆n 
∆n = 2 - 1 
\(K_c=\frac{K_p}{(R T)^{\Delta n}}=\frac{85.87}{(0.083 \times 400)^1}\) = 2.586 

Question 7.9. 
3.00 mol of PCl₅ kept in 1L closed reaction vessel was allowed to attain equilibrium at 380 K. Calculate composition of the mixture at equilibrium. K₂ = 180. 
Answer:
Given, Kc = 1.80 
T = 380 K 
For the reaction, 
\(\mathrm{PCl}_5 \rightleftharpoons \mathrm{PCl}_3+\mathrm{Cl}_2\)
Suppose x mol/litre of PCl₅ be dissociated. 
At equilibrium (3 - x) 
Equilibrium constant, 

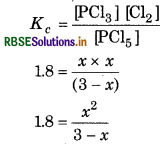
x² = 1.8 (3x) = 5.4 - 1.8x 
x² + 1.8x - 5.4 = 0 
From quadratic equation, ax² + bx + c = 0 
a = 1, b = 1.8, c = -54

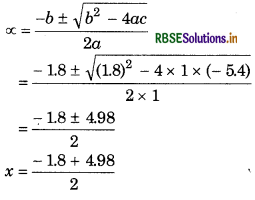
(∵The value of x can not be negative so we neglect this value) 
\(=\frac{3.18}{2}\)
= 1.59 
Hence
[PCl₅] = 3 - x = 31.59 = 1.41M 
[PCl₃] = [Cl₂] = x = 1.59 M 

Question 7.10. 
The value of ∆G^θ for the phosphorylation  of glucose in glycolysis is 13.8 kJ/mol. Find the value of K ̧ at 298 K. 
Answer:
Given, ∆G^θ = 13.8 kJ mol^-1 = 13.8 × 10³ J mol^-1 
T = 298 K 
R = 8.314J mol^-1 K^-1 
As we know that, 
∆G^θ = RT In Kc 

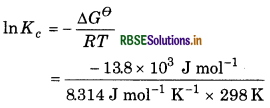
= - 5.569 
Kc = e 5.569   
= 3.81× 10^-3 

Question 7.11. 
Hydrolysis of sucrose gives, 

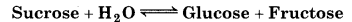
Equilibrium constant K, for the reaction is 2 × 10¹³ at 300 K. Calculate AG at 300K. 
Answer:
Given, K. = 2 × 10¹³ K, 
T = 300 K 
R = 8.314J mol^-1 K^-1 
We know that, 
∆Gθ = -RT In Kc  
= -8.314J mol^-1  K^-1  × 300 K × ln (2 × 10¹³) 
= 7.64 × 10⁴ J molTM 

Question 7.12. 
What will be the conjugate bases for the  following Bronsted acids: 
HF, H₂SO4 and HCO₃. 
Answer: 

Bronsted acid	Conjugate base
HF	F-
H2SO4	HSO4-
HCO3-	CO2-3

Question 7.13. 
Write the conjugate acids for the following Bronsted bases: NH₂^- NH₃ and HCOO^- 
Answer:

Bronsted base	Conjugate acid
NH2-	NH3
NH3	NH4+
HCOO-	HCOOH

Question 7.14. 
The species: H₂O, HCO₃, HSO₄^- and NH₃ can act both as Bronsted acids and bases. For each case, give the corresponding conjugate acid and conjugate base. 
Answer:

Species	Conjugate acid	Conjugate base
H2O	H3O+	OH-
HCO3-	H2CO3	CO2-3
HSO4-	H2SO4	SO42-
NH3	NH4+	NH2-

 

Question 7.15. 
Classify the following species into Lewis acids and Lewis bases and show how these act as such: 
(a) OH^- (b) F^-  (c) H⁺ (d) BCl₃  
Answer:
(a) OH^-: It is a Lewis base because it can donate electron pair. 
(b): F: It is a Lewis base because it can donate electron pair. 
(c) H⁺: It is electron deficient species and it can accept electron pair so it acts as Lewis acid. 
(d) BCl₃: It is an electron deficient species and it can accept electron pair so it acts as Lewis acid. 

Question 7.16. 
The concentration of hydrogen ion in a sample of soft drink is 3.8 × 10^-3 M. What is its pH? 
Answer:
[H⁺] = 3.8 × 10^-3 M 
 pH = -log [H⁺] = log [3.8 × 10^-3] 
= -log 3.8 + log 10^-3 
= - log 3.8 + (-3 log10) 
= -(0.58) + (- 3.0) 
= -(-2.42) = 2.42 
So, the pH of the soft drink is 2.42 and it is acidic in  nature. 

Question 7.17. 
Calculate pH of a 1.0 × 10^-8 M solution of HCl. 
Answer:

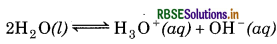
Kw = [H₃O⁺] [OH^-] 
= 10^-14 
Suppose, x = [H₃O⁺] = [OH ^-] from H₂O [H₃O⁺] is generated.
(i) From the ionization of HCl dissolved 

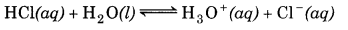
and (ii) From ionization of H₂O 
In these very dilute solutions, both sources of H₃O⁺ 
must be considered, 
[H₃O⁺] = 10 − 8 + x 
Kw = [H₃O⁺] [OH^-] 
10^-14 = (10^-8 + x) (x) 
10^-14 = 10^-8 x + x² 
or x² + 10^-8 x 10^-14 
∴ [OH^-] = x = 9.5 × 10^-8 
pOH = -log[OH^-] 
- log[9.5 × 10^-3] = 7.02 
pH = 14 - pOH = 14 - 7.02 = 6.98 

Question 7.18. 
The ionization constant of HF is 3.2 × 10^-4  Calculate the degree of dissociation of HF in its 0.02 M solution. Calculate the concentration of all species present (H₃O⁺ F and HF) in the solution and its pH. 
Answer:
Given, K = 3.2 × 10^-4 Ka 
Intial concentration of HF = 0.02 M 
For the reactions, 

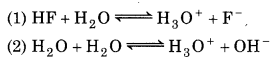
Since Ka > Kw
So, Reaction (1) is the main reaction. 

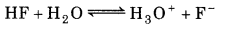
Substituting equilibrium  concentrations  in  the  equilibrium reaction for main reaction gives :
Ionization constant 

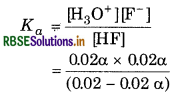
We get the following quadratic equation, 
a²  + 1.6 × 10^-2α- 1.6 × 10^-2 
= 0 
From quadratic equation, ax² + bx + c = 0
a = 1 b = 1.6 x 10^-2 c = -1.6 x 10^-2

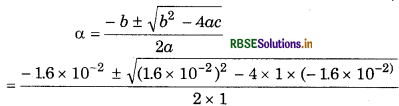
= 0.12 and - 0.12 
The negative root is not acceptable and therefore, 
α = 0.12 
This me that the degree of ionization, a = 0.12, then equilibrium concentration of other species viz. 
HF, F^- and H₃O⁺ are given by : 
[H₃O⁺] = [F^-] = Cα 
= 0.02 × 0.12 
= 24 × 10^-3 M 
[HF] = C (1 - α) 
= 0.02 (1 - 0.12) 
=  17.6 × 10^-3 M 
pH = -log[H⁺] 
= -log (2.4 × 10^-3)= 262 

Question 7.19.
The pH of 0.1 M monobasic acid is 4.50. Calculate the concentration of species H+ A ̄ and HA at equilibrium. Also, determine the value of Ka and pKɑ of the monobasic acid. 
Answer:
Given, pH = 4.50 
 ∵pH = -log[H⁺] 
∴[H⁺] = 10-pH 
= 10 - 4.50 - 316 × 10^-5 
[H⁺] = [A^-] = 3.16 × 10^-5  
[HA] = 0.1 (3.16 × 10^-5 ) ≈ 0.1 
For the reaction, 

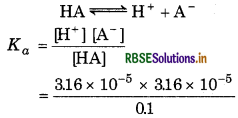
= 1.0 × 10^-8 
pKa = -log Ka 
= - log (10⁸) = 8 log 10 = 8 

Question 7.20.
Calculate the pH of 0.08 M solution of hypochlorous acid, HOCl. The ionization constant of the acid is 2.5 × 10^-5  Determine the percent dissociation of HOCl. 
Answer:
Initial conc. of HOCl = 0.08 M 
Ka = 2.5 × 10^-5 
For the reaction, 

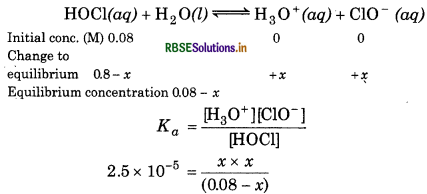
x² = 2.0 × 10^-6 
∴ x = 1.41 × 10^-3 
[H⁺] = 1.41 × 10^-3 M 
∴ % dissociation = {[HOCl] dissociated/[HOC]] initial} × 100 
\(=\frac{1.41 \times 10^{-3}}{0.8} \times 100\)
= 1.76% 
pH = -log[H⁺] 
= -log (1.41 × 10^-3) 
=  2.85 

Question 7.21. 
The pH of 0.004 M hydrazine solution is 9.7. Calculate its ionization constant K, and pKь. 
Answer:
Given, 
pH = 9.7 
[NH₂NH₂] = 0.004 
pH = -log[H⁺] 
or [H⁺] = 10-pH = 10-9.7
= antilog (-9.7) 
= 167 x 10^-10
∴ Kw = [H⁺] [OH^-]
[OH^-] = \(\frac{K_w}{\left[\mathrm{H}^{+}\right]}\)
\(=\frac{1 \times 10^{-14}}{1.67 \times 10^{-10}}\)
= 5.98 x 10^-5
[NH₂NH₃⁺ ] = [OH^-] = 598 × 10^-5
For the rection,

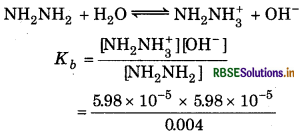
= 8.96 x 10^-7
PKb = log K-log (896 x 10^-7)
= 6.04

Question 7.22. 
Calculate the pH of the solution in which 0.2 M NH₃Cl and 0.1 M NH₃ are present. The pK of ammonia solution is 4.75.
Answer:
Given, Intial concentration of [NH⁺]= 0.2 M
Initial concentration of NH = 0.1 M
PKb = 4.75
 ∵ PKb = -log Kb
or
kb = antilog (-pkb)
= antilog (-4.75)
= 1.77 x 10^-5 M
Kantilog (- pK) = antilog (- 4.75) = 177 x 10^-5 M
For the reaction,

 ∵ Kb is small, so, we can neglect x in comparison to 0.1 M and 0.2 M. Hence,
∴ 1.77 x 10^-5 = \(=\frac{0.20 \times x}{0.10}\) = 2x
[OH^-] = x = 0.88 x 10^-5
\(x=\frac{1.77 \times 10^{-5}}{2}\) = 0.88 x 10^-5
∵ Kw = [H⁺][OH^-]
or
\(\begin{aligned} {\left[\mathrm{H}^{+}\right] } & =\frac{K_w}{\left[\mathrm{OH}^{-}\right]} \\ & =\frac{1.0 \times 10^{-14}}{0.88 \times 10^{-5}} \end{aligned}\)
= 1.12 × 10^-9 
pH = -log[H⁺]
= -log(1.12 x 10^-9)
= & 9.5

Question 7.23. 
Determine the degree of ionization and pH of a 0.05 M of ammonia solution. The ionization constant of ammonia is 1.77 x 10. Also calculate the ionization constant of the conjugate acid of ammonia.
Answer:
Given, Kb = 1.77 x 10^-5
[NH₃ ] = 0.05 M
For the reaction,

[OH^-] = Cα = 0.05α
\(K_b=\frac{0.05 \alpha^2}{1-\alpha}\)
The value of a is small so it is neglected in comparison to 1.
or Kb = 0.05α²

= 0.018
[OH^-] = Cα = 0.05 x 0.01894 x 10 M
 ∵ Kw = [H⁺] [OH^-]
or
\(\begin{aligned} {\left[\mathrm{H}^{+}\right] } & =\frac{K_w}{\left[\mathrm{OH}^{-}\right]} \\ & =\frac{1.0 \times 10^{-14}}{9.4 \times 10^{-4}} \end{aligned}\)
= 1.06 x 10^-11
 ∵ pH = -log [H⁺]
-log (1.06 x 10^-11) = 1.097
 ∵ Kw = Ka x Kb

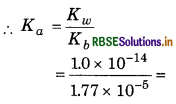
= 5.64 × 10^-10

Question 7.24. 
Calculate the pH of a 0.10 M ammonia solution. Calculate the pH after 50.0 mL of this solution is treated with 25.0 mL of 0.10 M HCl. The dissociation constant of ammonia, K_b = 1.77 x 10^-5.
Answer:
For the reaction,

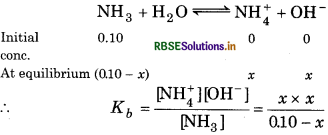
0.10 - x = 0.1
\(K_b=\frac{x^2}{0.1}\)
1.77 × 10^-5 = \(\frac{x^2}{0.1}\)
x² = 1.77 × 10^-6 
or x = 1.33 x 10^-3
∴ [OH^-] = x = 1.33 x 10^-3
Now,
Kw = [H⁺][OH^-]
∴ [H⁺] = \(\frac{K_w}{\left[\mathrm{OH}^{-}\right]}\)

\(=\frac{1.0 \times 10^{-14}}{1.33 \times 10^{-3}}\)
= 7.51 x 10^-12
∵ pH = -log [H⁺]
= -log (7.5 x 10^-12) = 1.112

When we added 25 mL of 0.1 M HCl solution (i.e., 2.5 m mol of HCl) to 50 mL of 0.1 M ammonia solution (i.e.,5 m mol of NH₃), 2.5 m mol of ammonia molecules are neutralized. The resulting 75 mL solution contains the remaining unneutralized 2.5 m mol of NH₃ molecules (0.033 M) and 2.5 m mol of NH₄⁺ (0.033 M).

the NH₃ exists in the following equilibrium:

Where
y = [OH^-] = [NH⁺₄]
Since, 75 mL solution after neutralization already has 2.5 m mol NH₄⁺ ions (i. e., 0.033 M), so, total concentration of NH₄⁺ is given as:
∴ [NH₄⁺] = 0033 + y
As if is small,
∴ [NH₄OH] = 0.033 M and [NH₄⁺] = 0.033 M

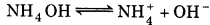
pH = -log[H⁺]
= 0.56 x 10^-9
= -log (0.56 x 10^-9)
= 9.24

Question 7.25. 
The pK_a of acetic acid and pK_b of ammonium hydroxide are 4.76 and 4.75 respectively. Calculate ammonium acetate solution.
Answer:
Given, pKa = 4.76
PK_b = 4.75
pH = 7 + 1/2[pK_a - pK_b]
= 7 + 1/2[4.76 - 4.75]
= 7 + 1/2[0.01]
= 7.005

Question 7.26. 
Calculate the solubility of A₂X₃ in pure water, assuming that neither kind of ion reacts with water. The solubility product of A₂X₃. Ksp = 1.1× 10^-23.
Answer:
Given, Ksp = 1.1 × 10^-23
For the reaction,

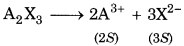
K sp = [A³⁺]² [x^2-]³
If S = solubility of A₂X₃, then, 
[A³⁺] = 2S, 
[X^2-] = 3S 
∴ Kp =(2S)² (3s)³ = 108 S⁵
\(S^5=\frac{1.1 \times 10^{-23}}{108}\)
= 1× 10^-25
∴ S = 1 x 10⁵ mol L^-1

Question 7.27. 
The values of Kp of two sparingly soluble salts Ni(OH)₂ and AgCN are 2.0 × 10^-15 and 6 x 10^-17 respectively, which salt is more soluble? Explain.
Answer:
Given, Ksp of Ni(OH)₂ = 2.0 x 10^-15
Ksp of AgCN = 6.0 x 10^-17
For the reaction,

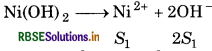
Ksp = [Ni][OH^-]₂
2.0 × 10^-15 S₁ x (25)²
= 2.0 × 10^-15 = 4s²
\(S_1^3=\frac{2.0 \times 10^{-15}}{4}\)
= 0.5 x 10^-15
∴ S₁ = 0.58 × 10^-4
For the reaction,
AgCN → Ag^- + CN^-
S₂ S₂
Ksp =[Ag⁺][CN^-]
6.0 × 10^-17 = S₂ x S₂ 
S = 60 × 10^-17
∴ S₂ = 7.8 x 10^-9
∵ The solubility of Ni(OH)₂ is higher than AgCN, so, Ni(OH) ₂ is more soluble than AgCN.

Question 7.28. 
Calculate the molar solubility of Ni(OH)₂ in 0.10M NaOH. The ionic product of Ni(OH) is 2.0 × 10^-15.
Answer:
For the reaction,

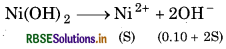
As Ksp is small 28 << 0.10
∴ (0.10 + 2s) = 0.10
∴ Ksp = S x (0.10)²
2.0 × 10^-15 = S x 0.01
S = 20 x 10^-13 
M = [Ni²⁺]

RBSE Class 11 Chemistry Equilibrium Textbook Questions and Answers

Question 7.1. 
A liquid is in equilibrium with its vapour in a sealed container at a fixed temperature. The volume of the container is suddenly increased.
(a) What is the initial effect of the change on vapour pressure?
(b) How do rates of evaporation and condensation change initially?
(c) What happens when equilibrium is restored finally and what will be the final vapour pressure?
Answer:
(a) Since same amount of vapour is distributed in larger space so, initially, the vapour pressure will decrease.
(b) As the temperature is fixed, the rate of evaporation remains constant in a closed vessel. However, the rate of condensation will be low initially because there are fewer molecules per unit volume in the vapour phase and hence the number of collisions per unit time with the liquid surface decreases.
(c) When equilibrium is restored finally, rate of evaporation is equal to rate of condensation. The final vapour pressure will be same as it was originally, it is due to the fact that vapour pressure of a liquid depends only on temperature but not on volume.

Question 7.2.
What is K, for the equilibrium when the equilibrium substance is concentration for each
[SO₂] = 0.60 M, [O₂] = 0.82 M and [SO₃] = 1.90 M,

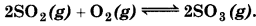
Answer:
Given,
[SO₂] = 0.60 M
[O₂] = 0.82 M
[SO₃] = 1.90 M
For the reaction,

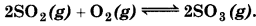
Equilibrium constant

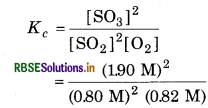
= 12.229 M^-1 
= 12.229 LMW^-1

Question 7.3.
 At a certain temperature and total pressure of 10 Pa, iodine vapour contains 40% by volume of I atoms. Ią (g) 21(g). Calculate K, for the equilibrium. 21(g)
Answer:
\(\mathrm{I}_2(g) \rightleftharpoons 2 \mathrm{I}(g)\)
Total pressure = 105 Pa
Since out of total volume, 40% by volume are I atoms
∴ 60% are I2 molecules (gaseous)
∴ Partial pressure of 1(g) = \(\frac{40}{100}\) x 10⁵ pa = 4 x 10⁴ pa
Partial pressure of 12(g) \(=\frac{60}{100}\) x 10⁵ pa = 6 x 10⁴ pa
∴ \(K_p=\frac{\left(p_{\mathrm{I}}\right)^2}{\left(p_{\mathrm{I}_2}\right)}=\frac{\left(4 \times 10^4\right)^2}{6 \times 10^4}\)
= 2.67 x 10⁴ Pa

Question 7.4.
Write the expression for the equilibrium constant, Kc for each of the following reactions:

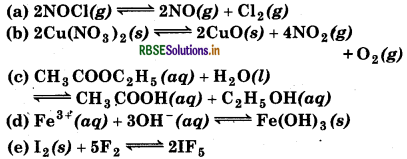
Answer:

Question 7.5. 
Find out the value of K, for each of the following equilibria from the value of Kp. 

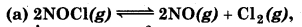
Kp = 1.8 x 10^-2 at 500K

Kp = 167 at 1073 K.
Answer:
(a) For the reaction,

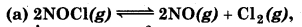
∆ng = np - nr
= 3 - 2 = 1
∴ Kp = Kc(RT)∆ng
or

(b) For the reaction, 

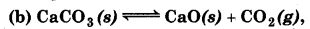
∆ng = np - nr = 1 - 0 = 1
∵ Kp = Kc (RT)∆ng
= 1.87

Question 7.6. 
For the following equilibrium
Kc = 6.3 x 10¹⁴ at 1000 K:

Both the forward and reverse reactions in the equilibrium are elementary bimolecular reactions. What is Kc for the reverse reaction?
Answer:
Given, Kc =  63 x 1014
Reaction is given as,

For the reverse reaction,
\(\begin{aligned} K_c^{\prime} & =\frac{1}{K_c} \\ & =\frac{1}{6.3 \times 10^{14}} \end{aligned}\)
= 1.59 x 10^-15

Question 7.7.
Explain why pure liquids and solids can be ignored while writing the equilibrium constant expression.
Answer:
Concentration of pure solid and liquids remain constant as their densities are constant. Therefore, concentration terms of pure solids and pure liquids can be ignored while writing the equilibrium constant expression.

Question 7.8. 
Reaction between Ng and Og takes place as follows: 

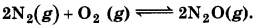
If a mixture of 0.482 mol N₂ and 0.933 mol of O₂ is placed in a 10 L reaction vessel and allowed to form N₂O at a temperature for which Kc =  2.0 × 10^-37, determine the composition of equilibrium mixture.
Answer:
Let the concentration of N₂O at equilibrium be x.

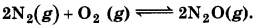
The given reaction is: 
2N₂(g) + O₂(g) → 2N₂O(g) 
Initial concentration : 0.482 mol 0.933 mol 
At equilibrium : (0.482 - x) mol (1933 - x) mol x mol 
Therefore, at equilibrium in the 10 L vessel : 
[N₂] = 0.482 - x/10 
[O₂] = 0.933 - x / 10 
[N₂O] = x/10 
The value of equilibrium constant i.e., 
Kc = 2.0 × 10^-37  is very small. Therefore, the amount of  N₂ and O₂ reacted is also very small. Thus, x can be neglected from the expressions of molar concentrations of N₂ and O₂. 
Then, 
[N₂] = 0.482 / 10 = 0.0482 mol L^-1 
or 
[O₂] = 0.933 / 10 = 0.0933 mol L^-1 
Ķc = [N₂O(g)]²/(N₂(g)]²[O₂(g)] 
⇒ 2.0 × 10^-37 × (0.0482)²(0.0933) 
⇒ (x²/100) = 2.0 x 10^-37 x (0.0482)²(0.0933)
⇒ x² = 43.35 × 10^-40 
⇒ x = 6.6 × 10^-20 
[N₂O] = x/ 10 = 6.6 × 10^-20/10 = 6.6 × 10^-21 
The composition of equilibrium mixture = 6.6 × 10^-21. 

Question 7.9. 
Nitric oxide reacts with Br₂ and gives nitrosyl bromide as per reaction given below: 

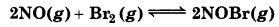
When 0.087 mol of NO and 0.0437 mol of Br₂ are mixed in a closed container at constant temperature, 0.0518 mol of NOBr is obtained at equilibrium. Calculate equilibrium amount of NO and Br₂. 
Answer:
The given reaction is: 
2NO(g) + Br₂ (g) → 2NOBr(g) 
2 mol  1 mol  2 mol 
Now, 2 mol of NOBr are formed from 2 mol of NO.  Therefore, 0.0518 mol of NOBr are formed from 0.0518 mol of NO.  Again, 2 mol of NOBr are formed from 1 mol of Br₂. Therefore, 0.0518 mol of NOBr are formed from (0.0518 / 2) mol of Br₂, or 0.0259 mol of NO. 
The amount of NO and Br₂ present initially are as follows: 
[NO] = 0.087 mol 
[Br₂] = 0.0437 mol 
Therefore, the amount of NO present at equilibrium are: 
[NO] = 0.087 - 0.0518 = 0.0352 mol 
And, the amount of Br 2 present at equilibrium is : 
[Br₂] = 0.0437 - 0.0259 = 0.0178 mol 

Question 7.10. 
At 450 K, Kp = 2 × 10¹⁰/bar for the given  reaction at equilibrium 

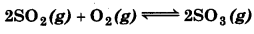
What is K, at this temperature ? Kp = 2 × 10¹⁰ bar^-1 
Answer:
Given, 
Kp = 2 × 10¹⁰ bar^-1 
For the reaction, 

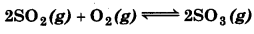
∆ng = np - nr 
= 2 - 3 = -1 
Kp = Kc (RT)∆ng 

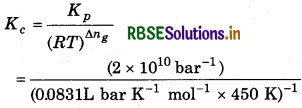
= 7.48 × 10¹¹ L mol^-1 

Question 7.11. 
A sample of HI(g) is placed in flask at a pressure of 0.2 atm. At equilibrium, the partial pressure of HI(g) is 0.04 atm. What is K, for the given equilibrium? 

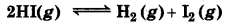
Answer:
The initial concentration of HI is 0.2 atm. 
At equilibrium, it has a partial pressure of 0.04 atm. Therefore, a decrease in the pressure of HI is 
0.2 - 0.04 = 0.16 
The given reaction is: 

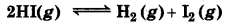
Therefore, K 
\(K_p=\frac{P_{H_2} \times P_{I_2}^{=0}}{P_{H I^2}^2}\)
= 0.08 x 0.8 /(0.04)² 
= 0.0064 /0.0016 = 4.0 
So, the value of K, for the given equilibrium is 4.0. 

Question 7.12. 
A mixture of 1.57 mol of N₂, 1.92 mol of H₂ and 8.13 mol of NH, is introduced into a 20 L reaction vessel at 500 K. At this temperature, the equilibrium constant, Ke for the reaction \(\mathrm{N}_2(g)+3 \mathrm{H}_2(g) \rightleftharpoons 2 \mathrm{NH}_3(g)\) is 1.7 × 10². Is the reaction  the reaction mixture at equilibrium? If not, what is the direction of the net reaction ? 
Answer:
The given reaction is : 
\(\mathrm{N}_2(g)+3 \mathrm{H}_2(g) \rightleftharpoons 2 \mathrm{NH}_3(g)\)
The given concentrations of various species are 
[N₂] = 1.57/ 20 mol L^-1 
[H₂] = 1.92/20 mol L ^-1 
[NH₃] = 8.13/20 mol L^-1 
Now, reaction quotient Qc is: 
Qc = [NH₃]² /[N₂][H₂]³ 
= (8.13/ 20)²/(1.57/20) (1.92/20)³ = 2.4 × 10³ 
Since, Qc ≠ Kc (1.7 × 10²), the reaction mixture is not at equilibrium. 
Again, Qc (2.4 × 10³) > Kc (1.7 × 10²) 
Hence, the reaction will proceed in the backward direction. 

Question 7.13. 
The equilibrium constant expression for a  gas reaction is, 
K = [NH₃]⁴ [O₂]⁵/ [NO]⁴ [H₂O]⁶ Write the balanced chemical equation corresponding to this expression. 
Answer:
The balanced chemical equation corresponding to the given expression can be written as: 

Question 7.14. 
One mole of H₂O and one mole of CO are taken in 10 L vessel and heated to 725 K. At equilibrium, 40% of water (by mass) reacts with CO according to the equation, 
H₂O(g) + CO(g) → H₂(g) + CO₂(g) 
Calculate the equilibrium constant for the reaction. 
Answer:
At equilibrium, H₂O = 0.6 (since 40% reacts) [CO] = 0.6 
and [H₂] = 0.4 and [CO₂] = 0.4 

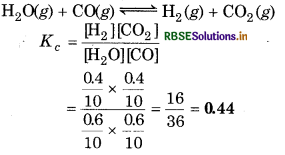
=  0.44 

Question 7.15. 
At 700 K, equilibrium constant for the reaction H₂(g) + I₂ (g) → 2HI (g) is 54.8. If 0.5 mol L^-1  of HI(g) is present at equilibrium at 700 K, what are the concentrations of H₂(g) and I₂(g) assuming that we initially started with HI (g) and allowed it to reach equilibrium at 700 K. 
Answer:
For the reaction, 
H₂(g) + I₂(g) → 2HI (g) 
K₂ = 54.8 
For the reverse reaction, 
\(K_c^{\prime}=\frac{1}{K_c}=\frac{1}{54.8}\)
At equilibrium, 
[HI] = 0.5 mol L^-1 
[H₂] = [1₂] = x mol L 

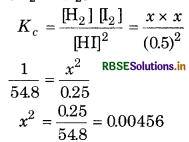
or  = 0.00456 
∴ x = 0.068 
∴ [H₂] = [I₂] = x = 0.068 mol L ^-1 

Question 7.16. 
What is the equilibrium concentration of each of the substances in the equilibrium when the initial concentration of ICl was 0.78 M ? 
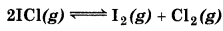Kc = 0.14
Answer: 

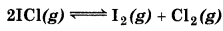
Kc = 0.14
Suppose at equilibrium, 
[I₂] = [Cl] = x mol L^-1, 
then 

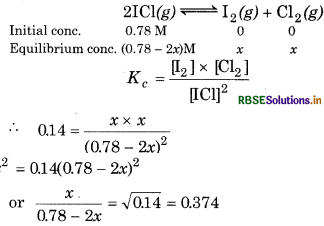
= 0.374 
or 
x = 0.292 - 0.748x 
1.748x = 0.292 or x = 0.167 
Hence, at equilibrium, 
[I₂] = [Cl₂] = 0.167 M, 
[ICI] = 0.78 - 2 × 0.167 M = 0.446 M 

Question 7.17. 
Kp = 0.04 atm at 899 K for the equilibrium  shown below. What is the equilibrium concentration of C₂H₆ when it is placed in a flask at 4.0 atm pressure and allowed to come to equilibrium? 

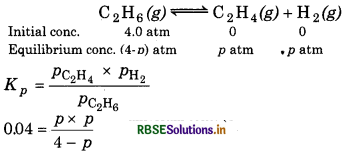
Answer: 
The given reaction is 
Initial conc. 
p₂  + 0.04 p − 0.16 = 0 
From quadratic equation ax² + bx + c = 0 
a = 1, b = 0.04, c = -0.16 

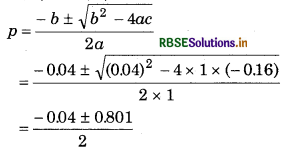
∵ The negative value of p is not acceptable, so 
\(p=\frac{-0.04+0.801}{2}\)
= 0.38 atm 
∴ Equilibrium concentration of C₂H₆ (g) = 4 − p 
= 4 - 0.38 
= 3.62 atm. 

Question 7.18. 
Ethyl acetate is formed by the reaction between ethanol and acetic acid and the equilibrium is represented as : 

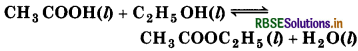
(a) Write the concentration ratio (reaction quotient) Q for this reaction (Note : water C  is not in excess and is not a solvent in this reaction). 
(b) At 293 K, if one starts with 1.00 mol of acetic  acid and 0.18 mol of ethanol, there is 0.171 mol of ethyl acetate in the final equilibrium mixture. Calculate the equilibrium constant. 
(c) Starting with 0.5 mol of ethanol and 1.0 mol of acetic acid and maintaining it at 293 K, 0:214 mol of ethyl acetate is found after sometime. Has equilibrium been reached? 
Answer: 
The given reaction is 

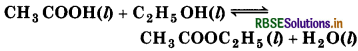
H₂O is not in excess and is not a solvent. 
\(\text { (a) } Q_c=\frac{\left[\mathrm{CH}_3 \mathrm{COOC}_2 \mathrm{H}_5(l) \times\left[\mathrm{H}_2 \mathrm{O}(l)\right]\right.}{\left[\mathrm{CH}_3 \mathrm{COOH}(l)\right] \times\left[\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}(l)\right]}\)

(b) [CH₃COOH (l)] = 1.00 mol 
[C₂H₅OH(l)] = 0.18 mol 
[CH₃COOC₂H₅ (l)] = 0.171 mol 
From the reaction, 

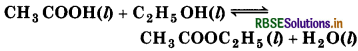
where V = Volume of container (in L) 
Equilibrium constant 

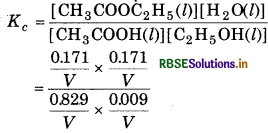
= 3.92 

(c) For the reaction, 

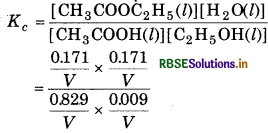
= 0.214 
As Qc = Kc, equilibrium has not been attained. 

Question 7.19.
A sample of pure PCl₅ was introduced into an evacuated vessel at 473K. After equilibrium was attained, concentration of PCl5 was found to be 0.5 x 10^-1 mol L^-1. If value of K, is 83 × 10^-3, what are the concentrations of PCl₃ and Cl₂ at equilibrium? 

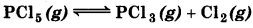
Answer: 
Suppose equilibrium conc. [PCl₃] = [Cl₂ ] = x 

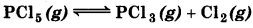
At equilibrium 0.05 mol L^-1 
As PCl5 dissociates to give PCl₃ and Cl₂. 
\(K_c=\frac{\left[\mathrm{PCl}_3\right] \times\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}=\frac{x \times x}{0.5 \times 10^{-1}}\)
8.3 × 10^-3 × 0.5 × 10^-1 = x² 
or 
x²  = 4 × 10^-4 
x = 2 × 10^-2 mol L^-1 
Hence the conc. of PCl₃ and Cl₂ at equilibrium 
= 0.02 mol L^-1. 

Question 7.20. 
One of the reaction that takes place in producing steel from iron ore is the reduction of iron (II) oxide by carbon monoxide to give iron metal and CO₂. 

Kp = 0.265 atm at 1050 K  What are the equilibrium partial pressures of CO and CO₂ at 1050 K if the initial partial pressures are: PCO = 14 atm and PCO₂ = 0.80 atm? 
Answer: 
Given, Kp = 0.265 atm at 1050 K 
PCO = 1.4 atm 
PCO₂ = 0.80 atm PCO₂ 
For the reaction, 

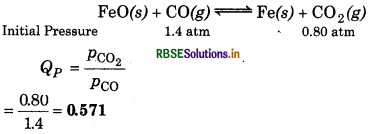
∴Qp > Ke, so the reaction will proceed in reverse direction. Due to this reason, pressure of CO₂ will decrease and that of CO will increase to attain equilibrium. 
Hence, 
 PCO₂ = (0.80 - p) 
 PCO = (1.4 + p) 
∴ \(\begin{aligned} K_p & =\frac{p_{\mathrm{CO}_2}}{p_{\mathrm{CO}}} \\ 0.265 & =\frac{0.80-p}{1.4+p} \end{aligned}\)
Or1.265 p = 0.80 - 0.429 
∴ \(p=\frac{0.429}{1.265}\)
= 0.339 atm 
Hence, at equilibrium, 
PCO₂  =  0.80 - p 
= 0.80 - 0.339 
= 0.461 atm 
1.4 + p= 1.4 + 0.339 
= 1.739 atm 

Question 7.21. 
Equilibrium constant, Kc for the reaction, 

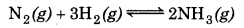
 at 500 K is 0.061. At a particular time, the analysis shows that composition of the reaction mixture is 3.0 mol L^-1 N₂, 2.0 mol L^-1 H₂  and 0.5 mol L^-1 NH₃. Is the reaction at equilibrium? If not, in which direction does the reaction tend to proceed to reach equilibrium? 
Answer: 
Given, K = 0.061 
[N₂] = 3.0 mol L^-1 
[H₂] = 2.0 mol L^-1 
[NH₃] = 0.5 mol L^-1 
For the given reaction, 

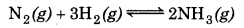
Reaction quotient 
\(Q_c=\frac{\left[\mathrm{NH}_3\right]^2}{\left[\mathrm{~N}_2\right]\left[\mathrm{H}_2\right]^3}=\frac{(0.5)^2}{3.0 \times(2.0)^3}\)
= 0.0104 
∵Qc ≠ Kc, so, the reaction is not in equilibrium. As 
Qc < Kc, reaction will proceed in the forward direction. 

Question 7.22. 
Bromine monochloride (BrCl) decomposes into bromine and chlorine and reaches the equilibrium 

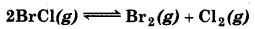
for which Kc = 32 at 500 K. If initially pure BrCl is present at a concentration of 3.30 × 10^-3 mol L^-1, what is its molar concentration equilibrium? 
Answer: 
For the reaction, 

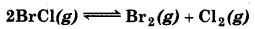
Equilibrium constant 

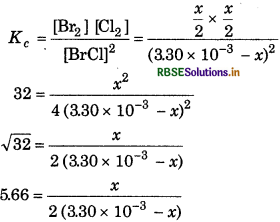
x = 11.32 × 3.30 × 10^-3 - 11.32x 
x + 11.32x = 11.32 × 3.30 × 10^-3 
12.32x = 11.32 × 3.30 × 10⁻³ 
or 
\(x=\frac{11.32 \times 3.30 \times 10^{-3}}{12.32}\)
At equilibrium, 
[BrCl] = 3.30 × 10^-3 
= 3.30 × 10^-3 - 3.0 × 10^-3 
= 0.30 × 10 3.0 × 10^-4 mol L 

 Question 7.23. 
At 1127 K and 1 atm pressure, a gaseous mixture of CO and CO₂ in equilibrium with solid carbon has 90.55% CO by mass 

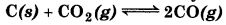
Calculate Ke for this reaction at the above temperature. 
Answer: 
Let the total mass of the gasesous mixture = 100 g. 
Mass of CO = 90.55 g 
And, mass of CO₂ = (100 - 90.55) = 9.45 g 
Now, number of moles of CO₂ nCO₂ = 90.55/28 
 = 3.234 mol 
Number of moles of CO₂, nCO₂ = 9.45/440215 mol Partial pressure of CO, pCO = [nCO/nCO + nCO₂] 
× P total  
= [3234/3.234 + 0.215] × 1 = 0.938 atm 
Partial pressure of CO₂, pCO₂ 
= [nCO₂/nCO + nCO₂] × P total 
= [0.215,/3234 + 0215] × 1 
= 0.062 atm 
Therefore
Kp = [CO]²/ [CO] 
= (0.938)2/0.062 = 1419 atm 
For the given reaction, 
We know that, 
∆n = 2 -1 = 1 
Kp = K(RT) ∆n 
14.19 = Kc (0.082 × 1127)1. 
= 0.154 mol/L 

Question 7.24. 
Calculate 
(A) ∆G° and 
(B) the equilibrium constant for the formation  of NO₂ from NO and O₂ at 298 K 

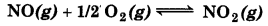
where ∆fG° (NO₂) = 52.0 kJ/mol 
∆fG° (NO) = 87.0 kJ/mol 
∆fG° (O₂) = 0 kJ/mol 
Answer: 
(A) For the given reaction, ∆fG° = ∆G° (Products) - ∆G° = 52.0 (87 + 0) 
∆G (Reactants) 
 ∆fG° = - 35.0 kJ mol^-1 
 
(B) We know that,  ∆fG° = RT log K с 
∆G° = 2.303 RT log Ke 
log Kc = -35.0 × 10³/-2.303 x 8.314 × 298 
= 6.134 
Kc antilog (6.134) = 1.36 × 10⁶ = 1.36 × 10⁶ 

Question 7.25. 
Does the number of moles of reaction products increase, decrease or remain same when each of the following equilibria is subjected to a decrease in pressure by increasing the volume? 

Answer: 
According to Le-Chatelier's lecreasing pressure, equilibrium will shift in that lirection where volume (i. e., number of moles in gaseous tate) increases. 

(a)
∆ng = np - nr 
= 2 - 1 =1 
The number of moles of reaction products increases in his reaction. 

(b)
∆ng = np - nr
= 0 - 1 = -1
The number of moles of reaction products decreases in his reaction.
 
(c)
∆ng = np - nr 
= 4 - 4 = 0 
The number of moles of reaction products remains ame in this reaction. 

Question 7.26. 
Which of the following reactions will get affected by increase the pressure? Also, mention whether change will cause the reaction to go into forward or backward direction? 

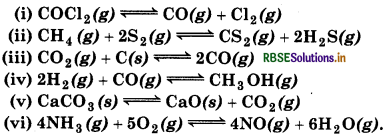
Answer:
According to Le-Chatelier's principle, ncreasing pressure, equilibrium will shift in that on direction where volume (i. e., number of moles in gaseous state) decreases. 

(i)
np = 2
nr = 3
np = nr
∵ np > nr
∴ Equilibrium will shift to the backward direction or increase in pressure. 


np = 3
nr = 3
∵ np = nr
∴ The reaction will not be affected by increase in pressure. 

 
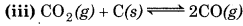
np = 2
nr = 1
∵ np > nr 
∴ Equilibrium will shift to the backward direction or increasing pressure. 

 
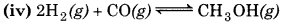
np = 1
nr = 3
np < nr
∴ Equilibrium will shift to the forward direction or incerase in pressure. 

np = 1
nr = 0
np > nr 
∴ Equilibrium will shift to the backward direction or increase in pressure. 

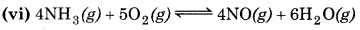
np = 10
nr = 9
np > nr 
∴ Equilibrium will shift to the backward direction or increase in pressure. 

Question 7.27. 
The equilibrium constant for the following  reaction is 1.6 × 10⁵ at 10²⁴ K. 

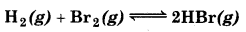
Find the equilibrium pressure of all gases if 10.0 bar of HBr is introduced into a  sealed container at 10²⁴ K ? 
Answer: 
Kc = 1.6 × 10⁵ 

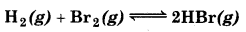
Taking square root of both sides 
\(\begin{aligned} K_p & =\frac{P_{\mathrm{HBr}}^2}{P_{\mathrm{H}_2} \times P_{\mathrm{Br}_2}} \\ 1.6 \times 10^5 & =\frac{(10-P)^2}{(P / 2)(P / 2)} \end{aligned}\)
200P = 10 - P 
\(4 \times 10^2=\frac{10-P}{P / 2}\)
= 2.5 × 10² bar 
= P/2 = 2.5 × 10² bar 
PHBr = 10 - P ≈ 10 bar 

Question 7.28. 
Dihydrogen gas is obtained from natural gas by partial oxidation with steam as per endothermic reaction: 

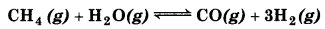
(a) Write an expression for Kp for the above reaction. 
(b) How will the values of Kp and composition of the equilibrium mixture be affected by 
(i) increasing the pressure? 
(ii) increasing the temperature? 
(iii) using a catalyst? 
Answer: 
(a) For the reaction, 

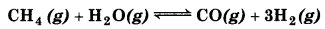
\(K_p=\frac{p_{\mathrm{CO}} \times p_{\mathrm{H}_2}^3}{p_{\mathrm{CH}_4} \times p_{\mathrm{H}_2 \mathrm{O}}}\)

(b) (i) In above reaction, 
np = 4
nr = 2 
np > nr
∴ Equilibrium will shift in the backward direction on increase in pressure. 

(ii) Since the reaction is endothermic i.e., heat is absorbed, so, according to Le-Chatelier's principle, equilibrium will shift to the forward direction on increase in temperature. 
(iii) Equilibrium composition will not be disturbed by using a catalyst but equilibrium will be attained quickly. 

Question 7.29. 
Describe the effect of: 
(a) addition of H₂ 
(b) addition of CH₃OH 
(c) removal of CO 
(d) removal of CH₃OH on the equilibrium of the reaction 

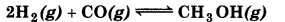
Answer: 
(a) On addition of H₂, equilibrium will shift in the  forward direction. 
(b) On additon of CH₃OH, equilibrium will shift in backward direction. 
(c) On removal of CO, equilibrium will shift in the backward direction. 
(d) On removal of CH₃OH, equilibrium will shift in the forward direction. 

Question 7.30. 
At 473K, equilibrium constant K. for decomposition of phosphorus pentachloride, PCl₅ is 8.3 × 10³. If decomposition is depicted as: 

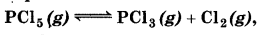
∆,He = 124.0 kJ mol^-1 
(a) Write an expression for Kp for the reaction. 
(b) What is the value of Kp for the reverse reaction at the same temperature? 
(c) What would be the effect on Kc if (i) more PCl₅ is added (ii) pressure is increased (iii) the temperature is increased? 
Answer: 
(a) For the reaction, 

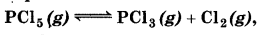
Kc = 8.3 × 10^-3 

(b) Given, 
 ∴ For the reverse reaction, 
\(K_c^{\prime}=\frac{1}{K_c}=\frac{1}{8.3 \times 10^{-3}}\)
= 120.48 

(c) (i) If more PCl₅ is added, then Q, becomes less than Ke, so the reaction will proceed in the forward direction. 
(ii) If the pressure is incerased, the reaction will proceed towards backward direction as it contains less number of reacting gaseous species. 
(iii) If the temperature is incresed, the reaction will proceed in the forward direction as the reaction is endothermic in nature.

Question 7.31. 
Dihydrogen gas used in Haber's process is produced by reacting methane from natural gas with high temperature steam. The first stage of two stage reaction involves the formation of CO and H₂. In second stage, CO formed in first stage is reacted with more steam in water gas shift reaction. 

If a reaction vessel at 400°C is charged with an equimolar mixture of CO and steam such that PCO = PH₂O = 40 bar, what will be the partial pressure of H₂ at equilibrium ? Kp = 10.1 at 400°C. 
Answer:
Given, KP = 10.1 
For the reaction, 

or p = 12.71 - 3.17p 
or p + 3.17p = 12.71 
or 4.17p = 12.71 
or \(p=\frac{12.71}{4.17}\)
or 3.04 br 
PH₂ = 3.04 bar 

Question 7.32. 
Predict which of the following reactions  will have appreciable concentration of reactants and products 
(a)   Kc = 5 × 10^-39 
(b) 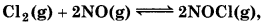Kc = 3.7 × 10⁸ 
(c) 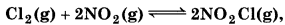 Kc = 1.8 
Answer: 
(a) Kc = 5 x 10^-39 
Since, the value of Kc is very small, so, there will be appreciable concentration of reactants only. 
(b) 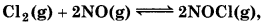Kc = 3.7 × 10⁸ 
Since, the value of Kc is very large, so, there will be appreciable concentration of products only. 
(c)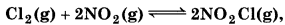
Since, Kc =  1.8 which is neither very small nor very large, so, there will be appreciable concentrations of both reactants and products. 

Question 7.33. 
The value of Kc for the reaction 3O₂ → 2O₃
(g) is 2.0 × 10^-50 at 25°C. If the equilibrium concentration of O₂ in air at 25°C is 1.6 × 10², what is the concentration of O₃? 
Answer: 
Given, 
Kc = 2.0 × 10^-50
[O₂] = 1.6 × 10^-2 
For the reaction, 
3O₂ → 2O₃
Equilibrium constant, 
\(\begin{aligned} K_c & =\frac{\left[\mathrm{O}_3\right]^2}{\left[\mathrm{O}_2\right]^3} \\ 2.0 \times 10^{-50} & =\frac{\left[\mathrm{O}_3\right]^2}{\left[1.6 \times 10^{-2}\right]^3} \end{aligned}\)
[O₃]² = 2.0 × 10^-50 × (1.6 × 10⁻²)³ 
= 8.192 × 10^-56 
 [O₃] = 286 × 10^-28 mol L^-1

 

 Question 7.34.
The reaction, imm is at equilibrium at 1300 K in a 1 L flask. It also contains 0.30 mol of CO, 0.10 mol of H₂ and 0.02 mol of H₂O and an unknown amount of CH₄ in the flask. Determine the concentration of CH₄ in the mixture. The equilibrium constant, Kp for the reaction at the given temperature is 3.90. 
Answer: 
Given, 
Kc = 3.90 
[CO] = 0.30 
[H₂] = 0.10 
[H₂O] = 0.02 
[CH₄] = ? 
For the reaction 
\(\mathrm{CO}(\mathrm{g})+3 \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons \mathrm{CH}_4(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{g})\)
Equilibrium constant 

= 0.0585 M 
[CH₄] eq. = 5.85 × 10^-2 M 

Question 7.35.
What is meant by the conjugate acid-base pair? Find the conjugate acid base for the following species: 
HNO₂, CN^-, HClO₄, F^- OH^-, CO₃^2- and S^2- 
Answer: 
The acid-base pair which differs only by one proton (H⁺) is known as conjugate acid-base pair. 

Species	Conjugate acid	Conjugate base
HNO2	-	NO2-
CN-	HCN	-
HClO4	-	ClO4-
F-	HF	-
OH-	H2O	-
CO32	HCO3-	-
S2-	HS-	-

 

Question 7.36. 
Which of the following are Lewis acids? 
H₂O, BF₃, H⁺ and NH⁺₄
Answer: 
Lewis acids are electron pair acceptor. So, BF₃, H⁺ and NH⁺₄ are Lewis acids. 

Question 7.37. 
What will be the conjugate bases for the Bronsted acids: HF, H₂SO₄ and HCO^-₃ ? 
Answer: 

Bronsted acid	Conjugate base
HF	F-
H2SO4	HSO4-
HCO3-	CO32-

 
Question 7.38. 
Write the conjuate acids for the following Bronsted bases: NH^-2, NH₃ and HCOO^- 
Answer: 

Bronsted base	Conjugate acid
NH-2	NH3
NH3	NH4+
HCOO-	HCOOH

Question 7.39. 
The species H₂O, HCO₃, HSO₄^- and NH₃ can act both as Bronsted acid and bases. For each case given the corresponding conjugate acid and base. 
Answer: 

Question 7.40. 
Classify the following species into Lewis  acids and Lewis bases and show how these act as Lewis acid/base : 
(a) OH^- 
(c) H⁺ 
(b) F^- 
(d) BCl₃. 
Answer: 
(a) OH^-Lewis base, as it can donate electron pair because of electron rich. 
(b) F^-Lewis base, as it can donate electron pair because of electron rich. 
(c) H^-Lewis acid, as it can accept electron pair because of electron deficiency. 
(d) BCl₃^-Lewis acid, as it can accept electron pair because of electron deficiency. 

Question 7.41. 
Answer: 
The concentration of hydrogen ion in a sample of soft drink is 3.8 × 10⁻³ M, what is its pH? 
pH = -log[H₃O⁺] 
= -log 3.8 × 10^-3 
= -(-3) log 10 - log 3.8 
= 3.0 - 0.5798 
[ log 10 = 1] 
 pH = 2.42 
 
 Question 7.42.
The pH of a sample of vinegar is 3.76. Calculate the concentration of hydrogen ion in it. 
Answer: 
Given, 
pH = 3.76 
pH = -log[H⁺] 
3.76 = - log [H⁺] 
[H⁺] = antilog (- 3.76) 
= 1738 × 10^-4 M 
 
Question 7.43. 
The ionization constant of HF, HCOOH and HCN at 298 K are 6.8 × 10^-1.8 × 10^-4 and 4.8 × 10^-9 respectively. Calculate the ionization constants of the corresponding conjugate base. 
Answer: 
Let Ka = dissociation ionization constant of a weak acid. 
kb = Ionization constant of its conjugate base 
kw = Ionic product of water 
= 1.0 × 10^-14 at 298 K 
Ka Kb = Kw 
HF/F^-2 
KHF / KF^-  = 1.0 × 10⁻¹⁴ 
6.8 × 10^-4 × KF^- = 1.0 × 10^-14 
\(K_{\mathrm{F}^{-}}=\frac{1.0 \times 10^{-14}}{6.8 \times 10^{-14}}\)
= 1.5 × 10 ^-11 

HCOOH/HCOO^- 
KHCOOH x KHCOO^- = 1.0 × 10^-14 
1.8 × 10^-4 × KHCOO^- = 1.0 × 10^-14 
\(K_{\mathrm{HCOO}^{-}}=\frac{1.0 \times 10^{-14}}{1.8 \times 10^{-14}}\)
= 5.6 × 10^-11 

HCN/CN^- 
KHCN × KCN^- = 1.0 × 10^-14 
4.8 × 10^-9 × KCN^- = 1.0 × 10^-14 
\(K_{\mathrm{CN}^{-}}=\frac{1.0 \times 10^{-14}}{4.8 \times 10^{-9}}\)
= 2.08 × 10^-6 

Question 7.44. 
The ionization constant of phenol is 1.0 × 10 What is the concentration of phenolate ion in 0.05 M solution of phenol? What will be its degree of ionization if the solution is also 0.01 M in sodium phenolate? 
Ka = 1.0 x 10^-10
Answer: 
For the reaction, 

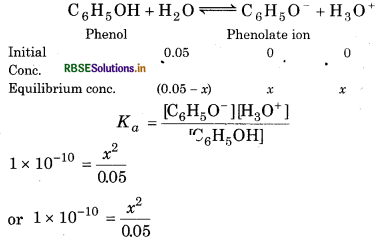
x² = 5 × 10^-12 
[ ∴  0.05 - x = 0.05] 
X = 2.23 × 10^-6 M 
Or 
In the presence of 0.01 M C₆H₅ONa, suppose y is the amount of phenol dissociated, then at equilibrium, 
[C₆H₅OH] = 0.05 - y = 0.05 M 
[C₆H₅O] = 0.01 + y = 0.01 M 
\(K_a=\frac{\left[\mathrm{C}_6 \mathrm{H}_5 \mathrm{O}^{-}\right]\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{\left[\mathrm{C}_6 \mathrm{H}_5 \mathrm{OH}\right]}\)
or \(\frac{0.01 \times y}{0.05}\)
y = 5 x 10^-10 
Degree of ionization 
\(\alpha=\frac{y}{c}=\frac{5 \times 10^{-10}}{0.05}\)
= 1× 10^-8C.

Question 7.45. 
The first ionization constant of H₂S is 9.1× 10^-8. Calculate the concentration of HS^- ions in its 0.1 M solution. How will this concentration be affected if the solution is 0.1 M in HCl also? If the second 'dissociation constant of H₂S is 12× 10^-13 Calculate the concentration of S₂^- under both conditions. 
Answer: 
To calculate the concentration of HS ion. 
Case I: In case of absence of HCl 

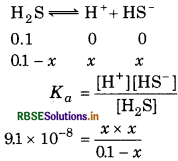
or (9.1 × 10^-8)(0.1 - x) = x² 
Taking (0.1 - x) M = 0.1 M 
∴ (9.1 × 10^-3)(0.1) = x² 
9.1 × 10^-9 = x² 
x = \(\sqrt{9.1 \times 10^{-9}}\)
[HS^-] = 9.54 × 10^-5 M 

Case II: In case of presence of HCl 
In the presence of 0.1 M of HCl, [HS^-] = yM 

∴ 0.1 + y = 0.1 and 0.1 -  y ⇒ 0.1 
∴ 9.1 × 10^-8 = \(\frac{y \times 0.1}{0.1}\)
∴ y = 9.1 x 10^-8 
[HS^-] = 9.1× 10^-8 M 

(ii) To calculate the concentration of [S₂^-] 
Case I: In the absence of HCl 

[HS^-] = 9.54 × 10^-5M
[From I ionization, Case I]  
Let 
[S₂^-] = x 
[H⁺] = 9.54 × 10^-5M 
[From I ionization, Case I] 
\(\begin{aligned} K_{a_2} & =\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{S}^{2-}\right]}{\left[\mathrm{HS}^{-}\right]} \\ & =\frac{\left(9.54 \times 10^{-5}\right) \times x}{9.54 \times 10^{-5}} \end{aligned}\)
1.2 × 10^-13 = x ⇒ [S₂^-] 

Case II: In the presence of 0.1 M HCl 
Let the concentration of HS^- be x2 M 
[HS] = 9.1 × 10^-8M 
[From I case II] 
[H⁺] = 0.1 M 
[From HCl, case II] 
[S₂^-]  = - x
then 
\(K_{a_2}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{S}^{2-}\right]}{\left[\mathrm{HS}^{-}\right]}\)
= 1.092 × 10^-19 M

Question 7.46. 
The ionization constant of acetic acid is 1.74 × 10^-5. Calculate the degree of dissociation of acetic acid in its 0.05 M solution. Calculate the concentration of acetate in the solution and its pH. 
Answer: 
∴ Ka = 1.74 × 10^-5, a = ?, c = 0.05 M 

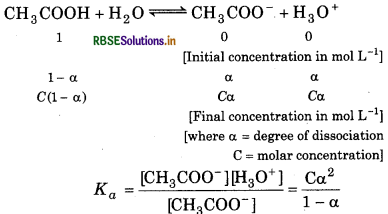
a < 1, ∴ a can be ignored from the denominator 
∴ Kα = Cα² 
or 

= 18.6 x 10^-2
[CH₃COO^-] = Cα = 
\(\begin{aligned} & =\sqrt{1.74 \times 10^{-5} \times 0.05} \\ & =\sqrt{0.87 \times 10^{-6}} \end{aligned}\)

[CH₃COO^-] = 0.933 × 10^-3 
= 9.33 × 10^-4 M 
pH = -log[H⁺] 
= -log 9.33 × 10^-4 
= -(-4) - log 9.3 
= 4 - 0.9 
= 3.03 

Question 7.47.
It has been found that the pH of a 0.01 M solution of an organic acid is 4.15. Calculate the concentration of anion, the ionization constant of the acid and its pKa· 
Answer:

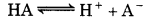
pH = -log[H⁺] 
[H⁺] = antilog (- 4.15) 
= 5.85 
= 7.08 × 10^-5 M 
[A -] = [H⁺] = 7.08 × 10^-5 M 
\(\begin{aligned} K_a & =\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]} \\ & =\frac{\left(7.08 \times 10^{-5}\right)\left(7.08 \times 10^{-5}\right)}{10^{-2}} \end{aligned}\)
= 5.01 × 10^-7 
pKa = log Ka 
= -log(5.01 × 10^-7) 
= 7 - 0.699 = 6.301 

Question 7.48
Assuming complete dissociation, calculate pH for the following solutions : 
(a) 0.003 M HCI 
(b) 0,005 M NaOH 
(c) 0.002 M HBr 
(d) 0.002 M KOH 
Answer: 
(a) HCl (aq) → H⁺(aq) + Cl^-(aq) 
[HCI] = 0.003 M 
As HCl is completely dissociated into H+ ions 
[H⁺] = [HCl] = 0.003 M 
pH = -log [H⁺] = -log 3 × 10^-3 
= -(-3) log 3 = 3 - log 3 
= 3 - 0.477 = 2.523 

(b) NaOH(aq) → Na⁺(aq) + OH^-(aq) 
[NaOH] = 0.005 = 5 x 10^-3 M 
[OH^-] = [NaOH] = 5 × 10^-3 M 
\(\left[\mathrm{H}^{+}\right]=\frac{K_w}{\left[\mathrm{OH}^{-}\right]}=\frac{1.0 \times 10^{-14}}{5.0 \times 10^{-3}}\)
[H⁺] = 20 × 10^-12 
pH  = -log 2 × 10^-12 
= - (-12) - log 2 
= 120.30 

(c) HBr → H+ + Br ^̄ 
[HBr] = 0.002 M 
As HBr is completely dissociated 
[H⁺] = [HBr] = 0.002 M 
= 2.0 × 10^-3 M 
pH = -log [H⁺] 
= -log 2 × 10^-3 
= -(-3) - log 2 
= 3 -  log 2 = 3 - 0.3 = 2.70 

(d) KOH → K⁺ + OH^-, 
completely dissociated, 
0.002 M 
0.002 M 
[OH^-] = 0.002 M 
\(\left[\mathrm{H}^{+}\right]=\frac{K_w}{\left[\mathrm{OH}^{-}\right]}=\frac{1.0 \times 10^{-14}}{5.0 \times 10^{-3}}\)
= 5 × 10^-12 
pH = -log (H⁺) = - (- 12) - log 5 
= 12 - 0.70 = 11.30 

Question 7.49.
Calculate the pH of the following solutions: 
(a) 2 g of TIOH dissolved in water to give 2 litre  of soluition. 
(b) 0.3 g of Ca(OH)₂ dissolved in water to give  500 ml of solution. 
(c) 0.3 g of NaOH dissolved in water to give 200  ml of solution. 
(d) 1 ml of 13.6 M HCl is diluted with water to give 1 litre of solution. 
Answer: 
(a) Given, 
Mass of TIOH = 2 g 
Volume of solution = 2 litre 
Molecular mass of TIOH = 204 + 16 + 1 = 221 g mol^-1 
∴ Concentration of TIOH in mol/L (molarity) 

= 0.00452 = 4.52 × 10^-3 M 
∵ pOH = -log [OH] 
= -log [4.52 × 10^-3] 
= - 0.6551 +3 
2.3449 = 2.34 
∵ pH + pOH = 14 
or 
pH = 14 - pOH = 14 - 2.34 = 11.66

(b) Given, 
Mass of Ca(OH)₂ = 0.3 g 
Volume of Solution = 500 mL = 0.5 L 
Molar mass of Ca(OH)₂ = 40 + [(16 + 1) × 2] 
= 74 g mol -1 
Concentration of Ca(OH)₂ in mol/L (molarity) 
 
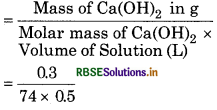
= 0.0081 = 8.1 × 10^-3 
1 mole of Ca(OH)₂ given 2 moles of OH ̄. So, 
[OH^-] = 2 × 8.1 × 10^-3 = 16.2 × 10^-3 
= 1.62 × 10⁻² 
Now, 
pOH = -log[OH^-] 
= - log [1.62 × 10^-2] 
= - log 1.62 + 2 log 10 
= - 0.2095 + 2 
= 1.7905 = 1.79 
pH + pOH = 14 
or pH = 14 - pOH = 14-1.79 = 12.21 

(c) Given, 
Mass of NaOH = 0.3 g 
Volume of Solution = 200 ml - 0.2 L 
Molar mass of NaOH = 23 + 16 + 1 
= 40 g mol^-1 
∴ Concentration of NaOH in mol/L (molarity) 

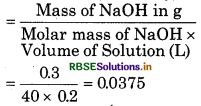
= 3.75 × 10² 
Now, 
pOH = log [OH^-] 
= -log [3.75 × 10^-2] 
= -log 3.75 + 2 log 10 
= - 0.5740 + 2 
= 1.426 = 1.43 
∵ pH + pOH = 14 
pH = 14 - pOH = 14 - 1.43 = 1257 
or 

(d) Given, 
Volume of HCl(V₁) = 1 mL 
Molarity of HCl (M₁) = 13.6 M 
Volume of Solution (V₂) = 1 litre = 1000 mL 
In case of dilution, 
 M₁V₁ = M₂V₂ 
13.6 × 1 = M₂ × 1000 
\(M_2=\frac{13.6 \times 1}{1000}\)
= 0.0136 
= 1.36 x 10^-2 M 
∵ pH = -log [H⁺] 
= -log [1.36 × 10^-2] 
= -log 1.36 + 2 log 10 
= -0.1335 + 2 
= - 1.8665 

Question 7.50. 
The degree of ionization of a 0.1M  bromoacetic acid solution is 0.132. Calculate the pH of the solution and the PK of bromoacetic acid. 
Answer: 
Given that, 
Degree of ionization, a = 0.132 
Concentration, C = 0.1 M 
Thus, the concentration of H₂O⁺ = C· α 
= 0.1 × 0.132 = 0.0132 
Now, 
pH = -log[H⁺] 
= -log(0.132) 
= 1.879 or 1.88 
Also, 
Ka = Cα² 
= 0.1 × (0.132)² 
= 0.0017 
pKα = 275 

Question 7.51. 
The pH of 0.005 M codeine (C₁₈H₂₁NO₃ ) 9.95. Calculate ionization  solution is 9.95. constant and pkb. 
Answer: 
Codeine is a base 

pH = 9.95 
∵ pOH = 149.95 - 4.05 
- log[OH^-] = 4.05 
OH = antilog (-4.05) 
= 5.95 = 8.91 × 10^-5 
\(\begin{aligned} K_b & =\frac{\left(\mathrm{BH}^{+}\right)\left(\mathrm{OH}^{-}\right)}{(\mathrm{B})} \\ & =\frac{\left(\mathrm{OH}^{-}\right)^2}{(\mathrm{~B})}=\frac{\left(8.91 \times 10^{-5}\right)^2}{5 \times 10^{-3}} \end{aligned}\)
= 1588 × 10^-6 
pK = -log (1.588 × 10^-6) 
6 - 0.1987 = 5.8 

Question 7.52. 
What is the pH of 0.001 M aniline solution? The ionization constant of aniline is 4.27 × 10^-10. Calculate the degree of ionization of aniline in the solution. Also calculate the ionization constant of the conjugate acid of aniline. 
Answer: 

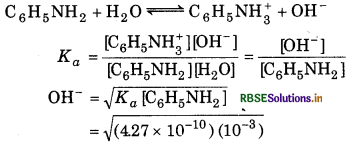
= 6.534 × 10^-7 M 
pOH = -log (OH) 
= -log (6.534 × 10^-7) 
= - 7 - 0.8152 
= 6.18 
pH + РОН = 14 
pH = 14 - pOH = 14 - 6.18 = 7.82 


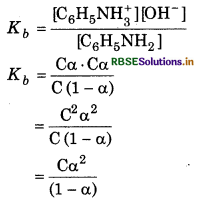
For weak base 1 - α = 1 
So, 
Kb = Cα² 
or Degree of ionization 
\(\begin{aligned} & \alpha=\sqrt{\frac{K_b}{\mathrm{C}}} \\ & =\sqrt{\frac{4.27 \times 10^{-10}}{0.001}} \end{aligned}\)
= 6.53 × 10^-4 
Ionization constant (K) of [C₆H₅NH₃⁺] 
\(\begin{aligned} K_a & =\frac{K_w}{K_b} \\ & =\frac{10^{-14}}{4.27 \times 10^{-10}} \end{aligned}\)
= 234 × 10^-5

Question 7.53.
Calculate the degree of ionization of 0.05 M acetic acid if its pKa value is 4.74. How is the degree of dissociation affected when its solution also contains 
(a) 0.01 M 
(b) 0.1 M in HCl ? 
Answer: 
Given, 
Concentration of acetic acid (C) = 0.05 M 
pKa = 4.74 
pKa = -log Ka 
or 
4.74 = -log Ka 
log Ka = -4.74 = 5.26 
Ka = antilog 5.26 
= 1.82 × 10^-5 
Degree of ionization α = 
\(\begin{aligned} \alpha & =\sqrt{\frac{K_a}{\mathrm{C}}} \\ & =\sqrt{\frac{1.82 \times 10^{-5}}{0.05}}=\sqrt{3.64 \times 10^{-4}} \end{aligned}\)
= 1908 × 10^-2 

(a) When solution contains 0.01 M HCl 
immm
∵ CH₃COOH is a weak acid and HCI is a strong acid, so we can assume that, Ca + 0.01 ≈ 0.01 

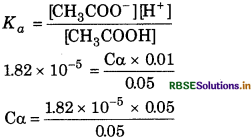
Ca = 91 × 10^-5 
\(\alpha=\frac{9.1 \times 10^{-5}}{C}=\frac{9.1 \times 10^{-5}}{0.05}\)
= 182 × 10^-3

(b) When solution contains 0.1 M HCl Similarly, for the reaction

 

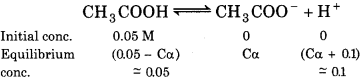
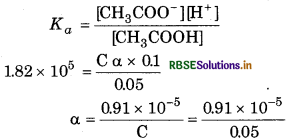
= 1.82 x 10^-4

Question 7.54. 
The ionization constant of dimethylamine is 5.4 × 10^-4. Calculate its degree of ionisation in its 0.02 M solution. What percentage of dimethylamine is ionized if the solution is also 0.1 M in NaOH ? 
Answer: 
Given, 
Kb  = 5.4 × 10^-4 
C = 0.02 M 
Degree of ionization α = 
\(\begin{aligned} \alpha & =\sqrt{\frac{K_b}{C}} \\ & =\sqrt{\frac{5.4 \times 10^{-4}}{0.02}} \end{aligned}\)
= 1.64 × 10^-1 = 0.164 
In the presence of 0.1 M NaOH, 

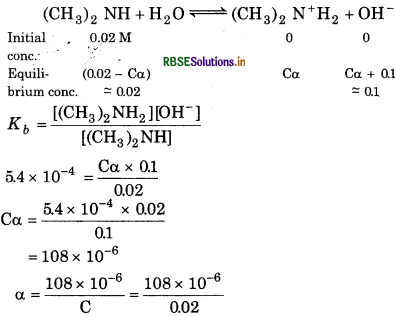
= 5.4 × 10^-4 
= 5.4 × 10^-3 × 0.02 
% degree of ionization = 5.4 × 10^-3 
= 0.54% 

Question 7.55
Calculate the hydrogen ion concentration in the following biological fluids whose pH are given below: 
(a) Human muscle-fluid, 6.83. 
(b) Human stomach fluid, 1.2. 
(c) Human blood, 7.38. 
(d) Human saliva, 6.4. 
Answer: 
(a) pH of human muscle fluid = 6.83 
pH = -log [H⁺] 
6.83 = log [H⁺] 
log [H⁺] = 6.83 
[H⁺] = antilog (-6.83) 
∴ [H⁺] = antilog (- 6.4) 
∴ [H⁺] = antilog 7.17 
 = 1.48 × 10^-7 M 
 
(b) pH of human stomach-fluid = 1.2 
or  - log[H⁺] = 1.2 
[H⁺] = antilog (-1.2) 
∴ [H⁺] = antilog 2.8 = 6.3 × 10^-2 
= 0.063 M 

(c) pH of human blood = 7.38 
or - log[H⁺] = 7.38 
[H⁺] = antilog (-7.38) 
∴ [H⁺] = antilog 8.62 
= 417 × 10^-8 M 

(d) pH of human saliva = 6.4 
 = - log[H⁺] = 6.4 
[H⁺] = antilog (- 6.4) 
∴ [H⁺] = antilog 7.6 
= 3.98 × 10^-7 M 

Question 7.56. 
The pH of milk, black coffee, tomato juice, lemon juice and egg white are 6.8, 5.0, 4.2, 2.2 and 7.8 respectively. Calculate corresponding hydrogen ion concentration in each. 
Answer: 
For milk : 
or 
pH = 6.8 
pH = -log[H⁺] 
6.8 = - log [H⁺] 
log [H⁺] = 6.8 = 7.20 
[H⁺] = antilog 7.20 
= 1.585 × 10^-7 M 
For black coffee : 
pH = 5.0 
∴ pH = -log[H⁺] 
5.0 = -log[H⁺] 
log[H⁺] = 5.0 

For lemon juice : 
pH = 2.2 
[H⁺] = 10^-5 M 
2.2 = -log[H⁺]
log[H⁺] = 2.2 = 3.80 
[H⁺] = antilog 3.80 
= 6310 × 10^-3 M 

For egg white: 
pH = 7.8 
pH = -log [H⁺] 
7.8 = -log [H⁺] 
log [H⁺] = 7.8 = 8.20 
[H⁺] = antilog 8.20 
= 1585 × 10 M 

Question 7.57.
If 0.561 g of KOH is dissolved in water to give 200 mL of solution at 298 K, Calculate the concentrations of potassium, hydrogen and hydroxyl ions. What is its pH? 
Answer: 
Given, Mass of KOH = 0.561 g 
Volume of solution = 200 mL = 0.2L 
Molar mass of KOH = 39.1 + 16 + 1 
= 56.1 

[K⁺] = 0.05 M 
[OH^-] = 0.05 M 
[H⁺] [OH^-] = Kw 
[H⁺] [OH^-] = Kw
[ ∵ Kw = 1.0 × 10^-14] 
0.05 
= 20 × 10^-14 M 
= 2.0 × 10^-13 M 
Now, 
pH = -log [H⁺] 
= - log [2.0 × 10^-13] 
= - log 2 + 13 log 10 
= - 0.3010 + 13 
= 12.699 

Question 7.58. 
The solubility of Sr(OH)₂ at 298 K is 19.23 g/L of solution. Calculate the concentrations of strontium and hydroxyl ions and the pH of the solution. 
Answer: 
Given that, 
Solubility of Sr(OH)₂ = 19.23 g/L 
Then, concentration of Sr(OH)₂ = 19.2/121.63 M 
= 0.158 M 
Now, 
Sr(OH)₂(aq) → Sr²⁺(aq) + 2(OH ^-)(aq) 
[Sr²⁺] = 0.1581M 
[OH] = 2 × 0.1581 M = 0.3126 M 
And, [H⁺] [OH] = Kw 
[H⁺] = K12/[OH^-] 
= 10-14/0.312 
= 3.2 × 10^-14 
pH = -log[H⁺] 
- log(3.2 × 10⁻¹⁴ ) = 13.49 

Question 7.59. 
The ionization constant of propanoic acid  is 1.32 × 10^-5. Calcualte the degree of ionization of the acid in its 0.05 M solution and also its pH. What will be its degree of ionzation if the solution is 0.01 M HCl also? 
Answer: 
Ka = 1.32 × 10^-5, α = ?, c = 0.05, pH = ? 

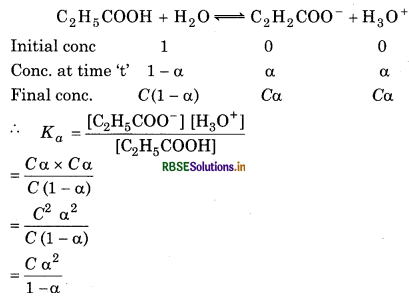
∵a << 1 ∵ a can be neglected from the denominator 
Ka = Ca² 
∴ \(K_a=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}\)
[H₃O⁺] = C α = 0.05 × 1.63 × 10^-2 
= 0.0815 × 10^-2 
= 8.15 × 10^-4 
pH = -log[H₃O⁺] 
= -log[8.15 × 10^-4] 
= -(4) - log 8.15 
= 4 - 3.09 
= 0.91 
In the presence of 0.01 M of HCl. 
Let a' be the degree of ionization. 
[H₃O⁺] = 0.01 
[A^-] = 0.05 α 
[HA] = 0.05 
\(K_a=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}\)
α  = 1.32 x 10^-3
[A-] = [C₂H₅COO^-] 
[HA] = [C₂H₅COOH] 

Question 7.60. 
The pH of 0.1 M solution of cyanic acid (HCNO) is 2.34. Calculate the ionization constant of the acid and its degree of ionization in the solution. 
Answer: 

pH = -log [H⁺] 
= 2.34 
or log[H⁺] = 2.34 = 3.66 
or [H⁺] = Antilog 3.66 
= 457 × 10^-3 M 
[CNO^-] = [H⁺] = 457 × 10^-33 M 
Ka = (4.57 × 10^-3) (4.57 × 10^-3) 
= 2.09 × 10^-4 
\(K_a=\frac{\left(4.57 \times 10^{-3}\right)\left(4.57 \times 10^{-3}\right)}{0.1}\)
= 0.0457 

Question 7.61.
The ionization constant of nitrous acid is 45 × 10⁴. Calculate the pH of 0.04 M sodium nitrite solution and also its degree of hydrolysis. 
Answer:
Kh = Kw/Ka 
= 10^-14/(45 × 10^-4) 
= 2.22 × 10^-11 
\(\begin{aligned} h & =\sqrt{K_h / \mathrm{C}} \\ & =\sqrt{2.22 \times 10^{-11} / 0.04} \\ & =\sqrt{5.5 \times 10^{-10}} \end{aligned}\)
= 2.36 × 10^-5 

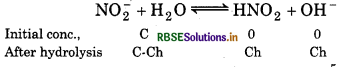
[OH^-] = Ch = 0.04 × 2.36 × 10^-5 
= 9.44 × 10^-7 
pOH = -log (9.44 × 10^-7) 
7 - 0.9750 = 6.03 
pH = 14 - pOH 
= 14 - 6.03 = 7.97 

Question 7.62.
A 0.02 M solution of  pyridinium hydrochloride has pH = 3.44. Calculate the ionization constant of pyridine. 
Answer: 
Pyridinium hydrochloride is the salt of a weak base pyridine and a strong acid HCl. 
Hence pH = - [log Kulog K + log c] 
∵ 3.44 = 1/2 -14 - log Kb + log 2.0 × 10^-2] 2 
6.88 = 14 + log Kb + 1.70 
or log kb = 8.82 - 9.18 
Kantilog 9.18 = 15 × 10^-9 

Question 7.63. 
Predict if the solutions of the following salts are neutral, acidic or basic: 
NaCl, KBr, NaCN, NH₄ NO₃, NaNO₂ and KF 
Answer: 
NaCl: It is a salt of strong acid (HCl) and strong base (NaOH), so, its aqueous solution is neutral. 
KBr: It is a salt of strong acid (HBr) and strong base (KOH), so, its aqueous solution is neutral. 
NaCN: It is a salt of weak acid (HCN) and strong base (NaOH), so, its aqueous solution is basic. 
NH4NO₃: It is a salt of strong acid (HNO₃) and weak base (NH₄OH), so, its aqueous solution is acidic. 
NaNO₂: It is a salt of weak acid (HNO₂) and strong base (NaOH), so its aqueous solution is basic. 
KF: It is a salt of weak acid (HF) and strong base (KOH), so, its aqueous solution is basic. 

Question 7.64. 
The ionization constant of chloroacetic  acid is 1.35 × 10^-3. What will be the pH of 0.1 M acid and its 0.1 M sodium salt solution? 
Answer: 
The given reaction is
 
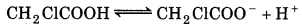
\(\left[\mathrm{H}^{+}\right]=\sqrt{K_a C}=\sqrt{1.35 \times 10^{-3} \times 0.1}\)
= 1.16 × 10^-2 
∴ pH = -log [H] = -log 1.16 x 10^-2  
= 2 - 0.06 = 1.94 
Sodium salt of chloroacetic acid is salt of strong base NaOH and weak acid chloroacetic acid (ClCH₂COOH) 
Hence, 
pH  = 1/2[log Ku + log Ka - log c] 
pH = 1/2[log K₂+ log Ka - log c] 
PH = 1/2[-log K₂ - log Ka + log c] 
= [+ 14 - log 1.35 × 10^-3 + log 10^-1]/2 
\(=\frac{14+2.87-1}{2}\)
= 7.94 
Hence, pH = 7.94. 

Question 7.65. 
Ionic product of water at 310 K is 2.7 × 10^-14 What is the pH of neutral water at this temperature? 
Answer: 
For pure water 
7.66. 
Kw = [H₃O⁺] [OH ̄] 
Κω 
[H₃O⁺] = [OH^-] 
Kw = [H₃O⁺]₂ 
[H₃O⁺] = √Kw = √27 × 10^-14 
pH 
= 1.643 × 10⁻⁷ mol L^-1 
= -log [H₃O⁺]
= -log (1.643 × 10^-7) 
= 7 - log 1.643 
= 7 0.2156 = 678 

Question 7.66.
Calculate pH of following mixtures: 
(i) 10 mL of 0.2 M Ca(OH)₂ + 25 mL of 0.1 M HCl 
(ii) 10 mL of 0.01 m H₂SO₄ + 10 mL of 0.01 m Ca(OH)₂ 
(iii) 10 mL of 0.1 m H₂SO₄ + 10 mL of 0.1 M KOH 
Answer: 
(i) 10 mL of 0.2 m Ca(OH)₂ + 25 mL of 0.1 m HCl 
Moles of H₃O⁺ = \(\frac{25 \times 0.1}{1000}\) = 0.0025 mol 
Moles of  OH^- = \(\frac{10 \times 0.2 \times 2}{1000}\) = 0.0040 mol
Excess of OH^-  = 0.0040 - 0.0025 = 0.0015 mol 
\(\mathrm{OH}^{-}=\frac{0.0015}{35 \times 10^{-3}} \mathrm{~mol} / \mathrm{L}\)
= 0.0428 mol/L 
pOH = -log [OH ̄] 
= -log [0.0428] 
= 1.36 
pH = 14 - pOH = 14 - 1.36 = 1263 

(ii) 10 mL of 0.01 M H₂SO₄ + 10 mL of 0.01 M Ca (OH) 
Moles of H₃O⁺ = \(\frac{2 \times 10 \times 0.01}{1000}\) = 0.0002 mol 
Moles of OH^- = \(\frac{2 \times 10 \times 0.01}{1000}\) = 0.0002 mol 
Since there is neither an excess of H₃O⁺ nor OH ̄, So solution is neutral and hence, pH = 7 

(iii) 10 mL of 0.1 M H₂SO₄ + 10 ml of 0.1 M KOH 
Moles of H₃O⁺ = \(\frac{2 \times 10 \times 0.1}{100}\) = 0.002 mol 
Moles of OH^- = \(\frac{10 \times 0.1}{1000}\)  = 0.001 mol 
Excess of H₃O⁺ = 0.002 - 0.001 = 0.001 mol 
∴ [H₃O⁺] =  \(\frac{0.001}{20 \times 10^{-3}}\) = 0.05 
pH = -log [H₃O⁺] = log(0.05) 
= 1.3 

Question 7.67. 
Determine  the  solubilities of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercurous iodide at 298 K from their solubility product constants given below: 
Ksp (Ag₂CrO₄ ) = 1.1× 10^-12 
Ksp (BaCrO₄ ) = 1.2 × 10^-10 
Ksp [Fe(OH)₃ ] = 1.0 × 10^-38 
Ksp (PbCl₂) = 1.6 × 10^-5 
Ksp (Hg₂I₂) = 4.5 × 10^-29 
Determine also the  individual ions. 
Answer: 
For silver chromate : 

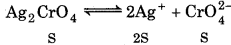
Ksp = [Ag⁺]²[CrO₂^-] 
Ksp = [2s]² · [S] = 4S³ 
\(\begin{aligned} & S^3=\frac{K_{\mathrm{sp}}}{4} \\ & S^3=\frac{1.1 \times 10^{-12}}{4} \end{aligned}\)
= 0.275 × 10^-12 
3 log S = log 2.75 × 10^-23 
13 + 0.4393 = -12.5607 
log S = \(\frac{-12.5607}{3}\)
- 4.1869 = 5.8131 
S antilog 5.8131 = 6.503 × 10⁻⁵ M 
[Ag⁺] = 28 = 2 × 6.503 × 10^-5 
= 13.006 × 10 = 1.3 × 10^-4 M 
[CrO₄^2-] = S = 6503 × 10^-5 M 

For barium chromate : 

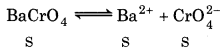
K sp = 1.2 × 10^-10 
(Solubility of BaCrO₄ is S and mol L^-1) 
Ksp = 1.2 × 10^-10 = [Ba²⁺][CrO₂ ̄] = S₂ 
S =  \(\frac{1.0 \times 10^{-38}}{27}\) = 1.1 × 10^-5 M 
[Ba²⁺] = [CrO₂] = 1.1× 10^-5 M 

For ferric hydroxide: 

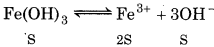
(Solubility of Fe(OH)₃ is S mol L^-1) 
K sp = S.(3S)³ = 2781 
\(S^4=\frac{1.0 \times 10^{-38}}{27}\)
= 0.037 × 10^-38 
4 log S = log 3.7 × 10^-40 

4 log S = -40 + 0.5682 = - 39.4318 
\(\log S=\frac{-39.4218}{4}\) = 9.8579 = 10.1421 
S = antilog 10.1421 = 1.387 x 10^-10 
S = 1.39 × 10^-10 
[Fe³⁺] = 139 × 10^-10 M 
[OH^-] = 3S = 3 x 1.39 × 10^-10 
= 4.17 x 10 ^-10 M

For lead chloride : 

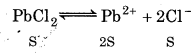
(Solubility of PbCl is S mol L^-1) 
Ksp = [Pb²⁺][Cl^-]₂ 
K sp = S (2S)² = 4s³  
K = 1.6 × 10^-5 
\(S^3=\frac{K_{s p}}{4}=\frac{1.6 \times 10^{-5}}{4}\)
= 0.4 × 10^-5 
3 log S = log 0.4 × 10^-5 = log 4.0 × 10^-5 
3 log S  = - 6 + 0.6021 = 5.3979 
log S = \(\frac{-5.3979}{3}\)
= - 1.7993 = -2.2007 
S = antilog 2.2007 = 1.585 × 10^-2 
= 1.59 × 10^-2 M 
Solubility of 
PbCl₂ = 1.59 × 10⁻² M 
[Pb²⁺] = 159 x 10^-2 M 
[Cl^-] = 2 × 1.59 × 10^-2 M = 3.18 × 10^-2 M 

For mercurous iodide : 

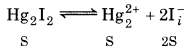
= 4.5 × 10^-29 
(Solubility of Hg₂I₂ is S mol L^-1) 
K sp = [Hg²⁺] [I^-]² 
K sp =S.(2S)² = 4S³ 
\(S^3=\frac{K_{s p}}{4}=\frac{4.5 \times 10^{-29}}{4}\)
= 1.125 × 10^-29 
3 log S = log (1.125 × 10^-29)
3 log S = - 29 + 0.0512 
log S = \(\frac{-28.9488}{3}\) = -  9.6496 
log S = \(\frac{-28.9488}{3}\) = - 9.6496 
log S = 9.6496 = 10.3504 
log S = antilog 10.3504 = 2.241 × 10^-10 M 
Solubility of Hg₂I₂ = 2.241 × 10^-10 M 
[Hg²⁺] = 2241× 10^-10 M 
[I] = 2 × 2.241 x 10^-10 M = 4.482 × 10^-10 M 

Question 7.68. 
The solubility product constant of Ag₂CrO₄  and AgBr are 1.1× 10 and 5.0 × 10^-13 respectively. Calculate the ratio of the molarities of their saturated solutions. 
Answer: 
Let solubility of Ag₂CrO₄ = S 

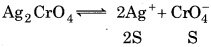
K sp = (25)² (S) 
1.1 × 10⁻² = 4S³ 
S = 6.5 x 10^-5M 
Let S' be the solubility of AgBr 

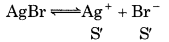
K sp = s² 
5 × 10^-13 = s² 
S' = 7.07 × 10^-7 
∴ Ratio of the molarities of their saturated solutions 
\(=\frac{S}{S^{\prime}}=\frac{6.5 \times 10^{-5}}{7.07 \times 10^{-7}}\)
= 919 

Question 7.69. 
Equal volumes of 0.002 M solutions of  sodium iodate and cupric chlorate are mixed together. Will it lead to precipitation of copper iodate. For cupric iodate, Kp = (7.4 × 10^-8) 
Answer: 
Given, 
K sp of cupric iodate [C₄ (IO₃)₂] = 7.4 × 10^-8 
As equal volumes of sodium iodate and copper chlorate solutions are mixed, so, the molar concentrations of both the solutions would be reduced to half i. e., 0.001 M. 
For the reaction, 

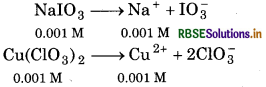
After mixing [IO₃^-] = [NaIO₃] = 0.001 M 
[Cu²⁺] = [Cu(IO₃)₂] 
= 0.001 M 

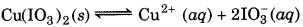
Ionic Product = [Cu²⁺] [IO₃^-]₂ 
= (0.001) (0.001)₂ 
= 1 × 10^-9 
Since ionic product is less than Ksp, therefore no precipitation takes place. 

Question 7.70. 
The ionization constant of benzoic acid is 6.46 × 10^-5 and Ksp for silver benzoate is 2.5 × 10^-13. How many times is silver benzoate more soluble in a buffer of pH 3.19 compared to its solubility in pure water? 
Answer: 
Since pH = 3.19 
∴ [H₃O⁺] = 6.46 × 10^-4M 

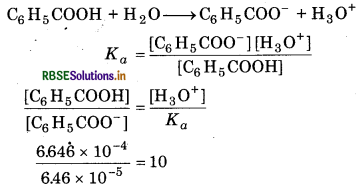
Let the solubility of [C₆H₅COO^-] = x 
10 [C₆H₅COO^-] + [C₆H₅COO^- ]=x 
[C₆H₅COO^-] = \(\frac{x}{11}\)
Ksp =[Ag⁺][C₆H₅COO^-] 
2.5 × 10^-13 = \(x \times \frac{x}{11}\)
x = 1.66 × 10^-6 mol/littre 
 ∴The solubility of silver benzoate in pH 3.19 solution is 1.66 × 10^-6 mol /L. Now, Let the solubility of C₆H₅COO Ag be x mol/L 
Then 
[Ag⁺] = xM and [C₆H₅COO^-] = x M 
= [Ag⁺] [C₆H₅COO^-] 
= (x) × (x′ ) 
= (x)2 
\(x^{\prime}=\sqrt{K_{s p}}=\sqrt{2.5 \times 10^{-13}}\)
= 5 × 10^-7 mol/L 
Hence, silver benzoate in 3.32 times more soluble in low pH solution. 

Question 7.71. 
What is the maximum concentration of equimolar solutions of ferrous sulphate and sodium sulphide so that when mixed 
in eqaul volumes, there is no precipitation of iron sulphide ? (For iron sulphide Kgp = 6.3 × 10^-18). 
Answer:
Given, K sp = 6.3 × 10^-18 
Let, the concentration of each of FeSO₄ and Na₂S is x mol L^-1. Then after mixing equal volumes : 

K sp = [Fe²⁺ ][S₂] 
6.3 × 10^-18 = \(\frac{x}{2} \times \frac{x}{2}\)
x² = 6.3 × 10^-18 × 4 
= 25.2 × 10^-18 × 4 
x = 5.02 × 10^-9 mol L ^-1 
∴Hence, maximum concentration of FeSO₄ and Na₂S which will not precipitate FeS = 5.02 × 10^-9 mol L^-1. 

Question 7.72. 
What is the minimum volume of water required to to dissolve 1g of calcuium sulphate at 298 K ? (For calcium sulphate, K, is 9.1× 10^-6) 
 Answer: 

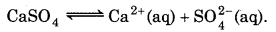
K sp = [Ca²⁺] [SO₂^-4]
= S × S = S² 
K sp for CaSO₄ = 9.1 × 10^-6 
∴ S² = 9.1 × 10^-6 
\(S=\sqrt{9.1 \times 10^{-6}}\)
= 3.02 × 10^-3 mol L^-1 
Now, molar mass of CaSO₄
= 40 + 32 + 4 × 16 
= 136 g 
\(S=\frac{n}{V}=\frac{w}{\text { M.V }}\)
∴= 3.02 × 10^-3 × 136 gL^-1 
= 0.411 gL^-1 
Thus for dissolving 0.411 g water required = 1 L^-1
∴ For dissolving 1 gm CaSO₄ 
Water required  = \(\frac{1}{0.411}\)
= 243 L. 

Question 7.73. 
The concentration of sulphide ion in 0.1M HCl solution saturated with hydrogen sulphide is 1.0 × 10^-19 M. If 10 mL of this is added to 5 mL of 0.04 M solution of the following FeSO₄, MnCl₂, ZnCl₂ and CdCl₂. In which of which of these solutions. precipitation will take place? 
Answer: 
For precipitation to take place, it is required that the calculated ionic product exceeds the KSD value. 
Before mixing: 
 [S^2-] = 1.0 × 10^-19 M [M²⁺ ] = 0.04 M 
After Mixing 
volume = 10 mL 
[S^2-] = ? 
Volume = (10 + 5) = 15 mL 
volume = 5 mL 
[M²⁺] = ? 
Volume = 15 mL 
[S^2-]  = \(\frac{1.0 \times 10^{-19} \times 10}{15}\) = 6.67 × 10^-20 M 
[M²⁺] = \(\frac{0.04 \times 5}{15}\) = = 1.33 × 10^-2 M 
Ionic product = [M²⁺ ][S^{2 ̄} ] 
= (1.33 × 10^-2) (6.67 × 10^-20) 
= 8.87 × 10^-2 
This ionic product exceeds the K sp of ZnS and Cds. Therefore, precipitation will occur in CdCl₂ and ZnCl₂ solution.