RBSE Solutions for Class 11 Chemistry Chapter 5 States of Matter

Rajasthan Board RBSE Solutions for Class 11 Chemistry Chapter 5 States of Matter Textbook Exercise Questions and Answers.

RBSE Class 11 Chemistry Solutions Chapter 5 States of Matter

RBSE Class 11 Chemistry States of Matter InText Questions and Answers

Question 5.1.
A balloon is filled with hydrogen at room temperature. it will burst, if pressure exceed 0.2 bar. If at 1 bar pressure, the gas occupies 2.27 L volume, upto what volume can the balloon be expanded?
Answer:
According to Boyle's law, P₁V₁ = P₂V₂ 
P₁ = 1 bar, V₁ = 2.27 L
If P₂ = 0.2 bar then V₂ = \(\frac{P_1 V_1}{P_2}\)
If  \(=\frac{1 \times 2.27}{0.2}\)
V₂ = 1135 L

Question 5.2.
A ship sailing in pacific ocean consists of a balloon which is filled with 2L air, where temperature is 23.4°C; Now, what will be the value of the balloon when the ship reaches Indian ocean, where temperature is 26.1°C ?
Answer:
Given that
V₁ = 2L
T₂ = 26.1 + 273 = 299.1 K
T (234 + 273) K  = 2964 K
From Charles' law,

= 2L x 1.0092018 L

 

Question 5.3
At 25°C and 760 mm of Hg pressure a gas occupies 600 mL volume. What will be its pressure at a height where temperature is 10°C and volume of the gas is 640 mL?
Answer:
Given,
P₁ = 760 mm of Hg 
V₁ = 600 mL
T₁ = 25 + 273  = 298 K
P₂ =?
V₂ = 640 mL
T₂ = 10 + 273 = 283 K
According to combined gas Law,

= 6766 mm Hg

Question 5.4.
A neon-dioxygen mixture contains 70.6 g dioxygen and 167.5 g neon. If the pressure of the mixture of gases in the cylinder is 25 bar, what is the partial pressure of dioxygen and neon in the mixture ? (Atomic mass of Ne = 20u)
Answer:
Mass of dioxygen = 70.6 g
Molecular mass of dioxygen = 32 g mol^-1
Number of moles of dioxygen = \(\frac{70.6 \mathrm{~g}}{32 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 2.21 mol
Mass of neon = 167.5g
Molecular mass of neon= 20 g mol^-1
Number of moles of neon = \(\frac{167.5 \mathrm{~g}}{20 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 8375 mol
Mole fraction of dioxygen = \(\frac{n_1}{n_1+n_2}\)
\(=\frac{2.21}{2.21+8.375}\)
\(=\frac{2.21}{10.585}\)
= 0.21
Mole fraction of neon = \(\frac{n_2}{n_1+n_2}\)
\(\begin{aligned} & =\frac{8.375}{2.21+8.375} \\ & =\frac{8.375}{10.585}=0.79 \end{aligned}\)
∵ Partial pressure of gas = mole fraction x total pressure
∴ Partial pressure of dioxygen = 0.21 × (25 bar)
= 5.25 bar
Partial pressure of neon = 0.79 × (25 bar) = 19.75 bar

RBSE Class 11 Chemistry States of Matter Textbook Questions and Answers

Question 5.1. 
What will be the minimum pressure required to compress 500 dm3 of air at 1 bar to 200 dm3 at 30°C?
Answer:
Given,
P₁ = 1 bar
V₁ = 500 dm³
V₂ = 200 dm³
P₂ =?
From Boyle's law,
P₁V₁ = P₂V₂
(1 bar) x (500 dm³) = P₂ × (200 dm3)

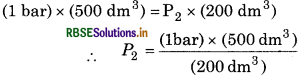
= 2.5 bar

Question 5.2.
A vessel of 120 mL capacity contains a certain amount of gas at 35°C and 1.2 bar pressure. The gas is transferred to another vessel of volume 180 mL at 35°C. What would be its pressure?
Answer:
Given,
V₁ = 120 mL
P₁ = 12 bar
V₂ = 180 mL
P₂ =?
From Boyle's Law,
P₁V₁ = P₂V₂
(1.2 bar) x (120 mL) = P₂ x (180 mL)

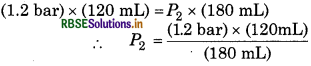
= 0.8 bar

Question 5.3. 
Using the equation of state PV = nRT; show that at a given temperature, density of a gas is proportional to gas pressure P.
Answer:
Given,
PV = nRT

This equation shows that density of a gas is proportional to gas pressure P (d x P).

Question 5.4. 
At 0°C, the density of a certain oxide of a gas'at 2 bar is same as that of dinitrogen at 5 bar. What is the molecular mass of the oxide ?
Answer:
Given,
P₁ = 2 bar
P₁ = 5 bar 
M₁ =?
M₂ =28 (Molecular mass of dinitrogen = 28)
∵  \(d=\frac{P M}{R T}\)

For oxide of gas \(d_1=\frac{P_1 M_1}{R T}\)
For dinitrogen \(d_2=\frac{P_2 M_2}{R T}\)
∵ Density of both gases are same.

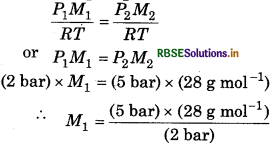
= 70 g mol^-1

Question 5.5.
Pressure of 1g of an ideal gas A at 27°C is found to be 2 bar. When 2 g of another ideal gas B is introduced in the same flask at same temperature, the pressure becomes 3 bar. Find the relationship between their molecular masses.
Answer:
At 27°C,
Pressure of 1 g of an ideal gas A = 2 bar 
Pressure of 2 g of another ideal gas B = 3 bar 
∴Pressure due to gas B = 3 - 2 = 1 bar
From ideal gas equation,

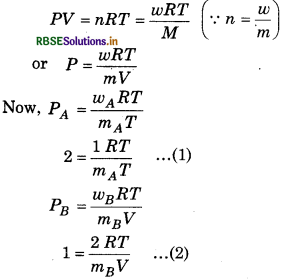
From equation (1) and (2)
\(\frac{2}{1}=\frac{m_B}{2 m_A}\)
MB = 4m A

Question 5.6.
The drain cleaner, Drainex contains small bits of aluminium which react with caustic soda to produce dihydrogen. What volume of dihydrogen at 20°C and one bar will be released when 0.15 g of aluminium reacts?
Answer:
The reaction is written as,
2Al + 2NaOH + 2H₂O₂ → NaAlO₂ + 3H₂↑
(27 x 2 = 54) (224 L x 3 at STP = 67.2 L)
∵ 54 g of aluminium gives 67.2 L of H₂ at STP 
∴ 0.15 g of aluminium will give (V₁) = \(\frac{67.2 \times 0.15}{54}\)
= 0.187 L of H₂
Given,
P₁ =1atm
P₁ bar = 0.987 atm
T₁ = 273 K
T₂ = 273 + 20 = 293 K
V₂ =?

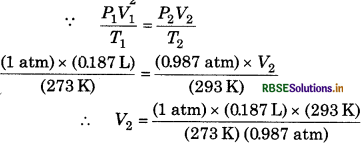
= 0.2033 L
= 2033 mL

Question 5.7.
What will be the pressure exerted by a mixture of 3.2 g of methane and 4.4 g of carbon dioxide contained in a 9 dm3 flask at 27°C ?
Answer:
Mass of methane = 3.2 g 
Molecular mass of methane (CH₄)
= 12 + 4 = 16
∴ Number of moles of CH₄

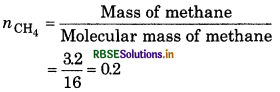
Mass of Carbon dioxide = 4.4g
Molecular mass of CO₂ = 12 + (2 x 16) = 44
∴Number of moles of CO₂

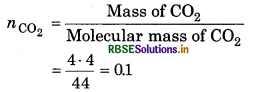
Volume of flask (V) = 9 dm³ = 9 x 10 m³
T = 27 + 273 = 300 K
For Methane PCH₄ = \(\frac{n R T}{V}\)

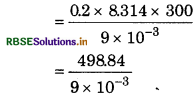
= 5.54 x 10⁴ Pa
For CO₂

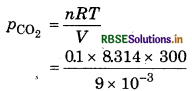
= 2.77 x 10⁴ Pa
Total pressure exerted by mixture
= PCH₄ + PCO₂
= 5.54 x 10 + 277 × 10⁴
= (5.54 + 2.77) × 10⁴
= &31× 10⁴ Pa

Question 5.8.
What will be the pressure of the gaseous mixture when 0.5 L of Hg at 0.8 bar and 2.0 L of dioxygen at 0.7 bar are introduced in a 1 L vessel at 27°C?
Answer:
Given, For H₂,
V₁ = 0.5L 
V₂ = 1L
P₁ = 0.8 bar
P2 =?
From Boyle's law,
P₁V₁ = P₂V₂
(0.8 bar) x (0.5 L) = P₂ × (1 L)

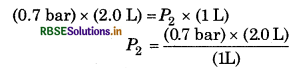
= 0.4 bar
For O₂,
V₁ = 20L 
V₂ = 1L
P₁ = 0.7 bar
P₂ =?
From Boyle's law,
P₁V₁ = P₂V₂
(0.7 bar) x (2.0 L) = \(P_2=\frac{(0.7 \mathrm{bar}) \times(2.0 \mathrm{~L})}{(1 \mathrm{~L})}\) = 1.4 bar
∴ Total pressure of gaseous mixture
= PH₂ + PO₂ = 0.4 + 14
= 18 bar

Question 5.9.
Density of a gas is found to be 5.46 g/dm3 at 27°C and 2 bar pressure. What will be its density at STP?
Answer:
Given,
∴ We know that,
d₁ = 5.46 g dm^-3
T₁ = 27 + 273 = 300 K
P₁ = 2 bar
T₂ = 273 K
P₂ = 1 bar 
d₂ =?

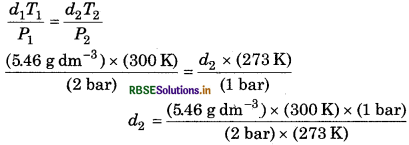
= 3.0 gdm^-3

Question 5.10.
34.05 mL of phosphorus vapour weighs 0.0625 g at 546°C and 0.1 bar pressure. What is the molar mass of phosphorus ? 
Answer:
R = 0.083 bar dm³ k^-1 mol^-1
PV = nRT i.e.,n = \(\frac{P V}{R T}\)
\(=\frac{1.0 \mathrm{bar} \times\left(34.05 \times 10^{-3} \mathrm{dm}^3\right)}{0.083 \text { bar } \mathrm{dm}^3 \mathrm{k}^{-1} \times 819 \mathrm{k}}\)
= 5 × 10^-4 mol.
∴ Mass of 1 mole = \(\frac{0.0625}{5 \times 10^{-4}}\)
g = 125g
∴ Molar mass = 125 g mol^-1.

Question 5.11.
A student forgot to add the reaction mixture to the round bottom flask at 27°C but instead he/she placed the flask on the flame. After a lapse of time, he realized his mistake, and using a pyrometer he found the temperature of the flask to be 477°C. What fraction of air would have been expelled out?
Answer:
Given, T₁ = 27 + 273 = 300 K
T₂ = 477 + 273 = 750K
From Charles' law,

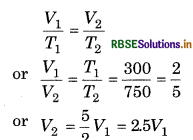
∴ Volume of air expelled out
= 25 V₁ - V₁
= 1.5 V₁
∴ Fraction of air expelled out
\(=\frac{1.5 V_1}{2.5 V_1}=\frac{3}{5}\)

Question 5.12. 
Calculate the temperature of 4.0 mol of a gas occupying 5 dm3 at 3.32 bar. (R = 0.083 bar dm³ K^-1mol^-1).
Answer:
Given
P = 332 bar
V = 5 dm³
R = 0.083 bar dm³ K^-1mol^-1
n  = 4.0
T = ?
From ideal gas equation,
PV = nRT

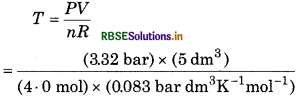
= 50 K

Question 5.13.
Calculate the total number of electrons present in 1.4 g of dinitrogen gas.
Answer:
Mass of dinitrogen (N) = 1.4g
Molar mass of dinitrogen (N₂) = 28
∴ Number of moles of dinitrogen

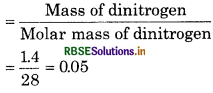
Total number of electrons present in 0.05 moles of dinitrogen = 0.05 x  6022 × 10²³ x 14
= 4.2154 x 10²³ electrons

Question 5.14. 
How much time would it take to distribute one Avogadro's number of wheat grains, if 1010 grains are distributed each second?
Answer:
∵10¹⁰ grains of wheat are distributed in 1 s. 
∴ 6.022 × 10²³ grains of wheat will be distributed in

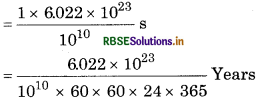
= 190956 x 10⁶ years

Question 5.15. 
Calculate the total pressure in a mixture of 8 g of dioxygen and 4 g of dihydrogen confined in a vessel of 1 dm3 at 27° C. R = 0.083 bar dm³ K₁ mol^-1.
Answer:
For dioxygen,
mass of dioxygen = 8g
molar mass of dioxygen = 32
∴ Number of moles of dioxygen

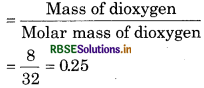
= 0.25
For dioxygen,
mass of dihydrogen = 4 g
molar mass of dihydrogen = 2
∴ Number of moles of dihydrogen

Total number of moles (n) = 2 + 0.25 = 2.25 moles
V = 1 dm3
T = 27+ 273 = 300 K
R = 0.083 bar dm³ K^-1 mol^-1
From ideal gas equation,
PV = nRT
∴ \(P=\frac{n R T}{V}\)
\(=\frac{(2.25 \mathrm{moles}) \times\left(0.083 \mathrm{bar} \mathrm{dm}^3 \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right) \times(300 \mathrm{~K})}{\left(1 \mathrm{dm}^3\right)}\)
= 56.025 bar

Question 5.16. 
Pay load is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the pay load when a balloon of radius 10 m, mass 100 kg is filled with helium at 1.66 bar at 27°C. (Density of air = 12kg m and R = 0.083bar LK^-1 mol^-1).
Answer:
Given
Radius of balloon (r) = 10 m
P = 1.66 bar
T = 27 + 273 = 300 K
density of air (d) = 1.2 kg m
R = 0.083 bar LK^-1 mol^-1
Volume of balloon \((V)=\frac{4}{3} \pi r^3\)
\(=\frac{4}{3} \times \frac{22}{7} \times(10)^3\)
= 4190.48 m
Mass of displaced air = density x volume
= 1.2 × 4190.48
= 5028,6 kg
From ideal gas equation,
PV = nRT
\(\begin{aligned} & n=\frac{P V}{R T} \\ = & \frac{(1.66 \mathrm{bar}) \times\left(4190.48 \mathrm{~m}^3\right)}{\left(0.083 \mathrm{bar} \mathrm{L}^{-1} \mathrm{~mol}^{-1}\right) \times(300 \mathrm{~K})} \end{aligned}\)
= 279.36 x 10³ moles
Mass of Helium = 279.36 × 10³ x 4
= 1117.44 kg 
Mass of filled balloon = 100 + 1117.44
= 1217.44 kg
Pay load = 50286 - 1217.44
= 381116 kg

Question 5.17. 
Calculate the volume occupied by &8 g of CO₂ at 31.1°C and 1 bar pressure. R = 0.083 bar L K¹ mol^-1.
Answer:
Given, mass of CO₂ (W) = 88 g
T = 31.1 + 273 = 3041 K
p = 1 bar
Molar mass of CO₂ (M) = 12 + (2 x 16) = 44
R = 0.083 bar LK^-1 mol^-1
V = ?
Number of moles of CO₂,

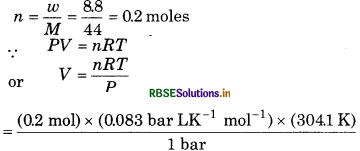
= 5.05 L

Question 5.18. 
2.9 g of a gas at 95°C occupied the same volume as 0.184 g of dihydrogen at 17°C, at the same pressure. What is the molar mass of the gas?
Answer:
For a gas,
Mass of gas = 29 g
Let molar mass of gas = M g mol^-1
T = 95 + 273 = 368 K
Number of moles of gas \(\frac{2.9}{M}\)
∵ PV = nRT
\(P V=\frac{2.9}{M} \times R \times(368 \mathrm{~K})\) ........... (i)
For dihydrogen, 
Mass of dihydrogen = 0.184 g
Molar mass of dihydrogen = 2
T = 17 + 273 =  290 K
Number of moles of dihydrogen = \(\frac{0.184}{2}\)
∵ PV = nRT
\(P V=\frac{0.184}{2} \times R \times(290 \mathrm{~K})\) ...... (ii)
Fromn equation (i) and (ii),

= 40 g mol-1

Question 5.19. 
A mixture of dihydrogen and dioxygen at one bar pressure contains 20% by weight of dihydrogen. Calculate the partial pressure of dihydrogen.
Answer:
∵ Mass of dihydrogen in 20% of dioxygen.
So,
Mass of dihydrogen = 20 g
Molar mass of dihydrogen = 2
∴ Number of moles of dihydrogen
\( n_{\mathrm{H}_2}=\frac{20}{2}\)
= 10 moles.
Mass of dioxygen = 80 g
Molar mass of dioxygen = 32
∴ Number of moles of dioxygen
\(n_{\mathrm{O}_2}=\frac{80}{32}\)
= 2.5 moles
Partial pressure of dihydrogen

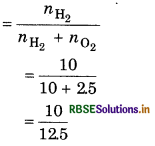
= 0.8 bar

Question 5.20. 
What would be the SI unit for the quantity PV₂T/n? PV₂T₂ Nm 2 x (m³)2 × (K)₂ mol
Answer:
SI unit of

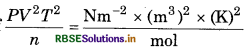
= Nm⁴ k₂mol^-1

Question 5.21. 
In terms of Charles' law explain why - 273°C is the lowest possible temperature?
Answer:
From Charles' law,

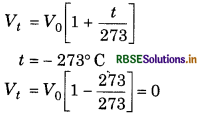
Hence, -273° C is the lowest temperature because below this temperature, the volume will become negative. This is meaningless.

Question 5.22. 
Critical temperature for carbon dioxide and methane are 311°C and -819°C respectively. Which of these has stronger intermolecular forces and why?
Answer:
Carbon dioxide has high critical temperature than methane it means that CO₂ can be liquified at higher temperature more easily. So, CO has stronger intermolecular forces than methane.

Question 5.23. 
Explain the physical significance of van der waals parameters.
Answer:
From van der waals equation,
\(\left(P+\frac{n^2 a}{V^2}\right)(V-n b)\) = nRT
where 'd' and 'b' = van der Waals parameters These parameters depend upon nature of gas. 

Significance of 'd':
It gives the magnitude of attractive forces between the gaseous molecules. Its unit is L²mol^-2. Greater the value of 'a', greater will be the intermolecular force of attraction between molecules of gas.

Significance of 'b':
It is excluded volume per mol of a gas. Its unit is L¹ mol^-1. The volume of 'b' is four times the actual volume of the gas molecules.