RBSE Solutions for Class 11 Chemistry Chapter 6 ऊष्मागतिकी

Rajasthan Board RBSE Solutions for Class 11 Chemistry Chapter 6 ऊष्मागतिकी Textbook Exercise Questions and Answers.

RBSE Class 11 Chemistry Solutions Chapter 6 ऊष्मागतिकी

RBSE Class 11 Chemistry ऊष्मागतिकी Textbook Questions and Answers

प्रश्न 6.1. 
सही उत्तर चुनिए:
ऊष्मागतिकी अवस्था फलन एक राशि है,
(i) जो ऊष्मा परिवर्तनों के लिए प्रयुक्त होती है। 
(ii) जिसका मान पथ पर निर्भर नहीं करता है। 
(iii) जो दाब आयतन कार्य की गणना करने में प्रयुक्त होती है। 
(iv) जिसका मान केवल ताप पर निर्भर करता है।
उत्तर:
(ii) जिसका मान पथ पर निर्भर नहीं करता है। 

प्रश्न 6.2. 
एक प्रक्रम के रुद्धोष्म परिस्थितियों में होने के लिए:
(i) ∆T = 0
(ii) ∆p = 0
(iii) ∆g = 0
(iv) w = 0
उत्तर:
(iii) क्योंकि रुद्धोष्म प्रक्रम में ऊष्मा का विनिमय नहीं होती है। 

प्रश्न 6.3. 
सभी तत्त्वों की एन्थल्पी उनकी संदर्भ-अवस्था में होती है। 
(i) इकाई
(ii) शून्य
(iii) < 0
(iv) सभी तत्त्वों के लिए भिन्न होती है।
उत्तर:
(ii)

प्रश्न 6.4. 
मेथेन के दहन के लिए ∆U° का मान -X kJ mol^-1 है। इसके लिए ∆H° का मान होगा:
(i) = ∆U
(ii) > ∆U
(iii) < ∆U
(iv) = 0
उत्तर:
(iii) मेथेन के दहन का समीकरण निम्न है:
CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O(l)
इसके लिए ∆H (g) = 1 - 3 = -2
चूँकि ∆H = ∆U® + ∆n(g) RT
अतः ∆H < ∆U

प्रश्न 6.5. 
मेथेन, ग्रेफाइट एवं डाइहाइड्रोजन के लिए 298 K पर दहन एन्थैल्पी के मान क्रमशः - 890.3kJ mol^-1 - 393.5kJ mol^-1 एवं - 285.8kJmol^-1 हैं। CH₄(g) की विरचन एन्थैल्पी क्या होगी?
(i) - 74.8 kJ mol^-1
(ii) - 52.27 kJ mol^-1
(iii) + 74.8 kJ mol^-1
(iv) + 52.26kJ mol^-1
उत्तर:
(i) ∆fH° (CH) = 2∆cH (H₂) - ∆cHO - ∆cH(CH₄)
= 2(-285.8) + (-393.5) - (-890.3)
= -74.8 kJ mol^-1

प्रश्न 6.6. 
एक अभिक्रिया A + B → C + D + q के लिए
एन्ट्रॉपी परिवर्तन धनात्मक पाया गया। यह अभिक्रिया संभव होगी:
(i) उच्च ताप पर
(ii) केवल निम्न ताप पर
(iii) किसी भी ताप पर नहीं 
(iv) किसी भी ताप पर 
उत्तर:
(iv) क्योंकि अभिक्रिया ऊष्माक्षेपी है (∆H < 0) तथा एन्ट्रॉपी बढ़ रही है (∆S (0)) अत: यह अभिक्रिया सभी तापों पर सम्भव होगी।

प्रश्न 6.7. 
एक प्रक्रम में निकाय द्वारा 701 J ऊष्मा अवशोषित होती है एवं 394 J कार्य किया जाता है। इस प्रक्रम में आंतरिक ऊर्जा में कितना परिवर्तन होगा?
उत्तर:
निकाय द्वारा अवशोषित ऊष्मा (q) = + 701 J
निकाय द्वारा किया गया कार्य (w) = 394 J
(ऋणात्मक चिह्न इसलिए प्रयुक्त किया गया है क्योंकि निकाय द्वारा कार्य किया गया है।)
अतः आन्तरिक ऊर्जा में परिवर्तन (∆U)
∆U = q + w
= 701 - 394 = 307 J

प्रश्न 6.8. 
एक बम कैलोरीमीटर में NH₂CN (s) की अभिक्रिया डाइऑक्सीजन के साथ की गई एवं ∆U का मान -742.7 kJ mol पाया गया (298 K पर )। इस अभिक्रिया के लिए 298 K पर एन्थल्पी परिवर्तन ज्ञात कीजिए:
NH₂CN(s) + O₂(g) → N₂(g) + CO₂ (g) + H₂O(l) 
उत्तर:
∆U = 742.7 kJ mol^-1
R = 8.314 × 10^-3 kJ k^-1 mol^-1 T = 298 K
∆n(e) = 2-3/2 = 0.5
(संतुलित समीकरण के अनुसार)
अतः एचैल्पी परिवर्तन, ∆H = ∆U + ∆n(g)RT
∆H = - 742.7 (kJ) + 0.5 (mol) × 8.314 × 10³ (kJ k^-1 mol^-1) × 298 K
∆H = - 742.7 + 1.238.7
∆H = 742.7 + 1.239  = 741.46 = 741.5
∆H = - 741.5 kJ

प्रश्न 6.9. 
60.0g ऐलुमिनियम का ताप 35°C से 55°C करने के लिए कितने किलो जूल ऊष्मा की आवश्यकता होगी? AI की मोलर ऊष्माधारिता 24 J mol^-1 K ' है ।
उत्तर:
AI के मोल (77) =
\(=\frac{\mathrm{m}}{\mathrm{M}}=\frac{60(\mathrm{~g})}{27 \mathrm{~g} \mathrm{~mol}^{-1}}=2.22 \mathrm{~mol}\)
(AI का परमाणु द्रव्यमान = 27 )
Al की मोलर ऊष्माधारिता (Cm) = 24.0J mol^-1 K^-1
∆T = 55 - 35 = 20° या 20K
अत: 9 = Cm x n x ∆T
= 24.0 (J mol^-1 k^-1) × 2.22 (mol) x 20 (k)
q = 1065.6 J ≈ 1.0656kJ
q = 1.066kJ.

प्रश्न 6.10 
10.0°C पर 1 मोल जल की बर्फ - 10°C पर जमाने पर एन्थैल्पी परिवर्तन की गणना कीजिए।
∆jsH = 6.03 kJ mol^-1 0°C पर,
Cp [H₂O(l)] = 75.3J mol^-1 K^-1
C [H₂O)] = 36.8J mol^-1 K^-1
उत्तर:

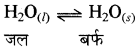
T = - 10°C = - 10° + 273.15  = 263.15 K
T2 = 0°C = 0°C + 273.15 K
∆T = T2 - T1 = 10K
माना T1 ताप पर हिमीकरण (Freezing) की एन्थैल्पी ∆H₁ है। 
तथा T2 ताप पर हिमीकरण की एन्थैल्पी ∆H₂ = - ∆Has
= - 6.03 kJ mol^-1
= - 6030 J mol^-1
( गलन की एन्थैल्पी)
किरचॉफ समीकरण के अनुसार
\(\frac{\Delta \mathrm{H}_2-\Delta \mathrm{H}_1}{\mathrm{~T}_2-\mathrm{T}_1}\) =  Cp(बर्फ) - Cp (जल)
या
\(\frac{-6030-\Delta \mathrm{H}_1\left(\mathrm{~J} \mathrm{~mol}^{-1}\right)}{10(\mathrm{k})}\)
= 36.8 (J mol^-1 k^-1) - 75.3 (Jmol^-1 k^-1)
या -6030 - ∆H = 10 - 38.5
∆H = 385 - 6030 = - 5645Jmol^-1
∆H = - 5.645 kJ mol^-1

प्रश्न 6.11. 
CO₂ की दहन एन्यैल्पी -393.5kJ molt है। कार्बन एवं ऑक्सीजन से 35.2g CO₂ बनने पर उत्सर्जित ऊष्मा की गणना कीजिए।
उत्तर: 
C के दहन की अभिक्रिया निम्न प्रकार होगी:
C(s) + O₂(g) → CO₂(g), ∆CH = -393.5 kJ mol^-1
1 मोल CO₂ = 44g CO₂
अतः 44g CO₂ के बनने पर उत्सर्जित ऊष्मा = 393.5kJ
अतः 35.2 g CO2 के बनने पर उत्सर्जित ऊष्मा = \(\frac{393.5 \times 35.2}{44}\)
= 314.8 kJ
= - 314.8 kJ (ऋणात्मक चिह्न इसलिए प्रयुक्त किया गया है क्योंकि ऊष्मा उत्सर्जित हो रही है।)

प्रश्न 6.12. 
CO (g), CO₂ (g), N₂O(g) एवं N₂O₄(g) की विरचन एन्थल्पी क्रमशः 110, 393, 81 एवं 9.7kJ mol^-1 है। अभिक्रिया N₂O (g) + 3CO (g) → NO (g) + 3CO₂ (g) के लिए ∆H का मान ज्ञात कीजिए।
उत्तर:
प्रश्न में दी गयी अभिक्रिया के अनुसार
∆rH° = ∑∆fH° (उत्पाद) – ∑∆fH° (अभिकारक)
= 3∆fH°(CO₂) + ∆fH°(N₂O) - 3∆fH°(CO) - ∆fH°(N₂O₄)
= 3(393) + 81.0 - 3(-110) - 9.7
= 1179 + 81.0 + 330 - 9.7
= - 777.7 kJ mol^-1
= 778 kJ mol-¹

प्रश्न 6.13. 
N₂ (g) + 3H₂ (g) → 2NH (g); 4,H° = - 92.4 kaJ mol^-1 NH₃ गैस की मानक विरचन एन्थैल्पी क्या है? 
उत्तर: 
अभिक्रिया में 2 मोल NH बन रही है तथा हमें एक मोल NH3 बनने की मानक विरचन एन्थैल्पी ज्ञात करनी है। अतः ∆f H° (NH₃)(g) = ∆rH°/2 = \(\frac{(-92.4)}{2}\)
= - 46.2 kJ mol^-1
= - 46.2 kJ mol^-1

प्रश्न 6.14. 
निम्नलिखित आँकड़ों से CH₃OH(l) की मानक - विरचन एन्थैल्पी ज्ञात कीजिए:
(i) CH₃OH (l) + 3/2O₂(g) → CO₂(g) + 2H₂O(l); ∆rH° =-726 kJ mol^-1
(ii) C(ग्रेफाइट) + O₂(g) → CO₂(g); ∆cH = -393 kJ mol^-1
(iii) H₂(g) + O₂(g) → H₂O(l); ∆fH°= -286 kJ mol^-1
उत्तर:
CH₃OH के बनने की अभिक्रिया निम्न है:
C(s) + 2H₂(g) + 1/2O₂(g) → CH₃OH ∆fH° = ±?
समीकरण (iii) को 2 से गुणा करने पर
2H₂(g) + O₂(g) → 2H₂O(l); ∆fH° = - 572 kJ mol^-1
इसमें समीकरण (ii) जोड़ने पर

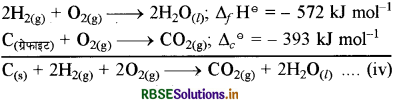
∆H = (-393572) = - 965 kJ mol^-1 
समीकरण (iv) में समीकरण (i) घटाने पर आवश्यक अभिक्रिया प्राप्त होगी।

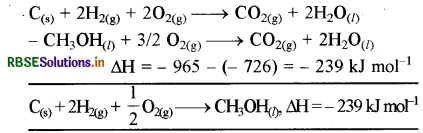
 ∆H = 239 kJ mol^-1

 

प्रश्न 6.15. 
CCl₄ (g) C(g) + 4Cl(g) लिए एन्यैल्पी - परिवर्तन ज्ञात कीजिए एवं CCl₄ आबंध एन्यैल्पी की गणना कीजिए:
∆vapH°(CCl₄) = 30.5 kJ mol^-1
∆H (CCl₄) = -135.5 kJ mol^-1
∆H° (C) = 715.0 kJ mol^-1  ∆aH  कणन एन्थैल्पी है:
∆H° (Cl₂) = 242 kJ mol^-1
उत्तर:
प्रश्न में दिए गए मानों के अनुसार ऊष्मा रासायनिक अभिक्रियाएँ निम्न प्रकार होंगी:
(i) CCl₄ → CCl₄(g) ∆H =  30.5 kJ mol^-1
(ii) C(s) + 2Cl₂(g) → CCl₄(l) ∆H₂ = -135.5 kJ mol^-1
(iii) C(s) → Cg ∆H₃ = 715.0 kJ mol^-1
(iv) Cl₂(g) → 2Cl(g) ∆H₁ = 242 kJ mol^-1
प्रश्नानुसार आवश्यक अभिक्रिया है:
CCl₄(g) → C(g) + 4Cl(g) ∆H = ?
समीकरण (iv) को 2 से गुणा करके समीकरण (iii) में जोड़कर तथा इनमें से समीकरण (i) तथा (ii) को घटाने पर आवश्यक अभिक्रिया प्राप्त होगी

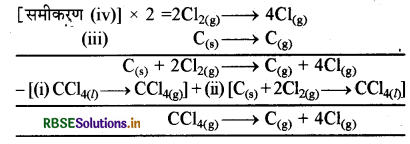
∆H = ∆H3 + 2∆H4 – (∆H1 + ∆H2)
∆H = 715.0 + 2(242) - 30.5 - (-135.5)
∆H = 715.0 + 484 + 105 = 1304kJ mol
∆H = 1304kJ mol^-1
अत: CCl₄ में C-Cl आबन्ध की एन्थैल्पी

प्रश्न 6.16. 
एक विलगित निकाय के लिए ∆U = इसके लिए ∆S क्या होगा?
उत्तर:
∆U = 0 वाले विलगित निकाय के लिए, ∆S > 0 होगा अतः अभिक्रिया स्वतः प्रवर्तित होगी। उदाहरण - गैसों का मिश्रण बनना, ∆U = 0 लेकिन ∆S > 0(+ve) क्योंकि गैसों का मिश्रण बनने पर अव्यवस्था (एन्ट्रॉपी) बढ़ती है।

प्रश्न 6.17. 
298 K पर अभिक्रिया 2A + B → C के लिए ∆H = 400kJmol एवं ∆S = 0.2kJK mol^-1 ∆H एवं ∆S को ताप विस्तार में स्थिर मानते हुए बताइए कि किस ताप पर अभिक्रिया स्वतः होगी?
उत्तर:
गिब्स हेल्महोल्ट्ज समीकरण के अनुसार
∆G = ∆H - T∆S
साम्यावस्था पर ∆G = 0 अतः ∆H = T∆S
\(\mathrm{T}=\frac{\Delta \mathrm{H}}{\Delta \mathrm{S}}=\frac{400 \mathrm{~kJ} \mathrm{~mol}^{-1}}{0.2 \mathrm{~kJ} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}}\)
अतः अभिक्रिया 2000 K पर साम्य में होगी तथा 2000 K से अधिक ताप पर अभिक्रिया स्वतः प्रवर्तित होगी।

प्रश्न 6.18. 
अभिक्रिया 2Cl(g) → Cl(g) के लिए ∆H एवं ∆S के चिह्न क्या होंगे?
उत्तर:
इस अभिक्रिया के लिए ∆H = (-ve) क्योंकि बन्ध बनने पर ऊर्जा उत्सर्जित होती है। (ऋणात्मक) ∆S = (-ve) क्योंकि एन्ट्रॉपी का मान कम हो रहा है। (ऋणात्मक) क्योंकि परमाणु मिलकर अणु बना रहे हैं तथा अणुओं में अव्यवस्था परमाणुओं की तुलना में कम होती है।

प्रश्न 6.19. 
अभिक्रिया 2A (g) + B (g) → 2D(g) के लिए ∆U° = - 10.5 kJ एवं ∆S° = 44.1 JK^-1 अभिक्रिया के लिए ∆G की गणना कीजिए और बताइए कि क्या अभिक्रिया स्वतः प्रवर्तित हो सकती है?
उत्तर:
∆H° = ∆U° + ∆n(g)RT
∆U° = -10.5 kJ, T = 298 K ( मानक परिस्थिति)
∆n(g) = 2 - 3 = - 1 mol
R = 8.314 × 10^-3 kJ K^-1 mol^-1
अत: ∆H° = 10.5 (kJ) + (- 1) mol 8.314 × 10-3 (kJ k^-1 mol^-1 ) x 298 ( k )
∆H° = -12.978 kJ
गिब्स हेल्महोल्ट्ज समीकरण के अनुसार
∆G° = ∆H° - T∆S (∆S = 44.1 kJ k^-1)
∆G° = - 12.978 (kJ) - (298 (k) - 44.1 x 10³) (kJ k^-1)
∆G = 12.978 + 13.141
∆G° = 0.163 kJ
∆C = 0.163 kJ चूंकि 4G° धनात्मक है अतः अभिक्रिया स्वतः प्रवर्तित नहीं होगी।

प्रश्न 6.20. 
300K पर एक अभिक्रिया के लिए साम्य स्थिरांक 10 है| ∆G° का मान क्या होगा? R = 8.314 JK mol^-1
उत्तर:
∆G° = 2.303RT log K^-1
∆G° = - 2,303 × 8.314 Jk^-1 mol^-1 x 300 (k) log 10 (log 10 = 1)
∆G° = - 5744 J mol^-1 = 5.744 kJ mol^-1
∆G° = - 5.744kJ mol^-1

प्रश्न 6.21. 
निम्नलिखित अभिक्रियाओं के आधार पर NO (g) तथा NO₂ (g) के ऊष्मागतिकी स्थायित्व पर टिप्पणी कीजिए-
1/2N₂(g) + 1/2O₂(g) → NO(g); ∆rH° = 90kJ mol^-1
NO(g) + 1/2 O₂ (g) → NO₂(g); ∆rH° = 74kJ mol^-1
उत्तर:
NO (g) के लिए ∆fH° = +ve अत: NO (g) अस्थायी है। लेकिन NO₂ (g) के लिए ∆fH° = -ve अत: NO₂ (g) स्थायी है। अतः NO₂(g) बनेगा।

प्रश्न 6.22. 
जब 1.00 मोल H₂O(l) को मानक परिस्थितियों में विरचित किया जाता है, तब परिवेश के एन्ट्रॉपी परिवर्तन की गणना कीजिए: ∆fH° = - 286 kJ mol^-1
उत्तर:
∆fH° (H₂O) = - 286.0kJ mol^-1
अर्थात् परिवेश को ऊष्मा दी जा रही है अर्थात् अभिक्रिया से ऊष्मा उत्सर्जित हो रही है। मानक परिस्थिति में T = 298K
∴ 9(sure) = (H₂O(1) के लिए) T = 298 K
= - (- 286 kJ mol^-1) = + 286 kJ mol
\(\Delta \mathrm{S}_{\text {(surr) }}=\frac{\mathrm{q}_{\text {(surr) }}}{\mathrm{T}}=\frac{286 \times 10^3 \mathrm{~J} \mathrm{~mol}^{-1}}{298.00 \mathrm{~K}}\)
∆S (surr) = 959.73 JK mol^-1