RBSE Solutions for Class 11 Chemistry Chapter 6 Thermodynamics

Rajasthan Board RBSE Solutions for Class 11 Chemistry Chapter 6 Thermodynamics Textbook Exercise Questions and Answers.

RBSE Class 11 Chemistry Solutions Chapter 6 Thermodynamics

RBSE Class 11 Chemistry Thermodynamics InText Questions and Answers

Question 6.1. 
Express the change in internal energy of a system, when
1. No heat is absorbed by the system from the surroundings, but work (w) is done on the system. What type of wall does the system have?
2. No work is done on the system, but q amount of heat is taken out from the system and given to the surroundings. What type of wall does the system have?
3. We amout of work is done by the system and q amount of heat is supplied to the system. What type of system would it be?
Answer:

1. ∆U = Wad, the system has adiabatic wall. 
2. ∆U = -q, the system has thermally conducting wall. 
3. ∆U = q - W, the system will be closed system.

Question 6.2.
Two litres of an ideal gas at a pressure of 10 atm expands isothermally at 25°C into a vaccum until its total volume is 10 litres. How much heat is absorbed and how much work is done in the expansion?
Answer: 
Given, V₁ = 2L
V₂ = 10L
For isothermal irreversible change,
q = -W = Pex (V₂ - V₁)
For isothermal expansion (i.e., at temperature) of an ideal gas into vacuum,
Pex, = 0
q = -W = Pe x [(10 - 2)]
= 0(8)
= 0
∴ No heat is absorbed and no work is done in the isothermal expansion.

 

Question 6.3.
Answer:
q = -W = Pex (V₂ - V₁)
= 1 (10 - 2)
= 1(8)
= 8L atm.

Question 6.4.
Consider the same expansion in problem 6.2, but this time against a constant external pressure of 1 atm.
Answer: 
For isothermal reversible change,
q = -W = 2.303 nRT log \(\frac{V_2}{V_1}\)
=2.303 pV log \(\frac{V_2}{V_1}\)
= 2303 x 10 atm x 2 L log = 32.2 Latm
= 32.2 × 10¹³J = 3261.86J.

Question 6.5.
If water vapour is assumed to be a perfect gas, molar enthalpy change for vaporisation of 1 mol of water at 1 bar and 100°C is 41 kJ mol1. Calculate the internal energy change, when (i) 1 mol of water is vaporised at 1 bar pressure and 100°C. (ii) 1 mol of water is converted into ice. 
Answer: 
(i) For the reaction,
Given,
H₂O(l) → H₂O(g)
 T = 100 + 273 = 373 K
∆H = 41 kJ mol^-1
∆U =?
∆HAU + ∆nRT
∆U = ∆H - ∆nRT
= 41 kJmol^-1 -1 x 83J mol^-1 K^-1 x 373K
= 41.00 kJ mol^-1 3096 kJ mol^-1
= 37.904 kJ mol^-1

(ii) For conversion of water in to ice, the change is
H₂O(l) → H₂O(g)
In this change the volume change is negaugible.
Hence
∆H = ∆U = 41.00 kJ mol^-1

Question 6.6. 
1 g of graphite is burnt in a bomb calorimeter in excess of oxygen at 298 K and 1 atm pressure according to equation: 
C(graphite) + O₂(g) → CO₂(g)
During the reaction, temperature rises from 298 to 299 K. If the heat capacity of bomb calorimeter is 20.7 kJ/K, what is the enthalpy change for the above reaction at 298 K and 1 atm?
Answer: 
Suppose q is the quantity of heat from the reaction mixture and C, is the heat capacity of the calorimeter then the quantity of heat absorbed by the calorimeter
q = Cv x ∆T
Quantity of heat from the reaction will have the same magnitude but opposite sign because the heat lost by the system (reaction mixture) is equal to the heat absorbed by the calorimeter.
q = -C, x ∆T
= -20.7 kJ/K x (299 - 298) 
K = -20.7 kJ
Thus, AU for the combustion of the 1 g of graphite = -20.7 kJ.
For combustion of 1 mol of graphite 
\(=\frac{12.0 \mathrm{~g} \mathrm{~mol}^{-1} \times(-20.7 \mathrm{~kJ})}{1 \mathrm{~g}}\)
= -248 x 10^-2 kJ mol^-1. 
since ∆n = 0 ∆HAU = -2.48 × 10² kJ mol^-1

Question 6.7.
A swimmer coming out from a pool is covered with a film of water weighing about 18 g. How much heat must be supplied to evaporate this water at 298 K ? Calculate the internal energy vaporisation at 298 K.
of(∆vap H- for water at 298 K = 44.01kJ mol^-1)
Answer: 
The process of evaporation is
18gH₂O(l) → 18gH₂O(g)
Number of moles in 18g H₂O = \(\frac{18 g}{18 g \mathrm{~mol}^{-1}}\) = 1 mol
∆ng = 1 - 0 = 1 mol
∆vapU = ∆vapH - ∆ng RT
= 4401 kJ mol^-1 - (1 mol)
(8314 × 10^-3 kJK^-1 mol^-1) (298 K)
= 4401 kJ mol^-1 - 248 kJ mol^-1
= 4153 kJ mol^-1

Question 6.8.
The combustion of 1 mole of benzene takes place at 298 K and 1 atm. After combustion, CO₂(g) and (H₂O) are produced and 3267.0kJ of heat is liberated. Calculate the standard enthalpy of formation -A,H® of benzene. Standard enthalpy of formation of CO₂(g) and (H₂O) are 393.5 kJ mol^-1 and - 285.83 kJ mol^-1respectively.
Answer: 
The formation reaction of benzene is given by 
6C (s) + 3H₂(g) C(a) + O₂(g) + C₆H₆; ∆fHθ =? ...... (i)
C(s) + O₂(g) → CO₂(g) ........ (ii)
∆fHe =-3935 kJ
H₂(g) + 1/2 O₂(g) → H₂O(l)  ∆fH° = -285.83 kJ mol^-1 ......... (iii)
The enthalpy of combustion of 1 mol of Benzene is
C₆H₆(l) + 15/2O₂(g) → 6CO₂(g) + 3H₂O(l)
∆fH° =-3267 kJ mol^-1 ...(iv)
On multiplying equation (ii) by 6 and equation (iii) by 3
we get
6C (graphite) + 6O₂(g) → 6CO₂(g)
∆fH° =-2361 kJ mol^-1
3H₂(g) + 3/2O₂(g) → 3H₂O(7)
∆fH° =-857.49 kJ mol^-1
Adding the above two equations
6CO₂(g) + 3H₂O(l) → C₆H₆(l) + 15/2O₂(g) 
∆fH = -321849 kJ mol^-1 ......... (v)

Question 6.9. 
Predict in which of the following, entropy increases/decreases:
(i) A liquid crystallizes into a solid.
(ii) Temperature of a crystalline solid is raised from 0 K to 115 K.
(iii) 2NaHCO₃ (s) → Na₂CO₃ (s) + CO₂(g) + H₂O(g)
(iv) H₂(g) → 2H₂(g)
Answer: 
(i) A liquid crystallizes into a solid. Here, entropy decreases because after freezing, the molecules attain an ordered state.
 
 (ii) Temperature of a crystalline solid is raised from 0 K to 115 K. At 0 K, the constituent particles are static and entropy is minimum. If temperature is raised to 115 K, these begin to move and oscillate about their equilibrium positions in the lattice and system becomes more disordered. So, entropy increases.

(iii) In the reaction, 2NaHCO₃(g) → Na₂CO₃(g)  + CO₂(g) + H₂O(g) the number of gaseous component are increasing hence the entropy of system will increase.

(iv) H₂(g) → 2H₂(g)
In this reaction, one molecule of dihydrogen gives two atoms of hydrogen i.e., number of particles increases leading to more disordered state. Hence, two moles of H-atoms have higher entropy than one mole of dihydrogen molecule.

Question 6.10. 
For oxidation of iron,
4Fe(S) + 3O₂(g) → 2FeO₃(e)
entropy change is -549.4 JK mol^-1 at 298 K. Inspite of negative entropy change of this reaction, why is the reaction spontaneous? (∆,H for this reaction is 1648 x 10³ J mol^-1).
Answer: 
As the reaction is exothermic, heat given out by the reaction is absorbed by the surroundings at room temperature (25°C). Hence the entropy of surroundings increases.
\(\Delta \mathrm{S}_{\text {surroundings }}=\frac{1648 \times 10^3 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}}{298 \mathrm{~K}}\)
= 5530 JK 1mol^-1

∆S total = ∆System + ∆Ssurroundings
= -549.4 + 5530 Jk^-1 mol^-1
= -4980.6 Jk^-1 mol^-1
As ∆Stotal is positive, the reaction is spontanesus.

Question 6.11.
Calculate A, G for conversion of Oxygen to Ozone.
\(\frac{3}{2} \mathrm{O}_{2(g)} \longrightarrow \mathrm{O}_{3(g)}\) at 298 K. If k, for this conversion is 247 x 10^-29.
Answer: 
We know that ∆r G® = -2.303 RT log kp
and R = 8.314 JK^-1 mol^-1
Therefore, ∆rGR = -2.303 RT log k
= -2.303 x 8314 JK^-1 mol^-1 × 298 K x log 2.47 × 10^-29
= 163000 J mol^-1
= 163 kJ mol^-1

Question 6.12. 
Find out the value of equilibrium constant for the following reaction at 298 K.
\(2 \mathrm{NH}_3(g)+\mathrm{CO}_2(g) \rightleftharpoons \mathrm{NH}_2 \mathrm{CONH}_2(a q)+\mathrm{H}_2 \mathrm{O}(l)\)
Standard Gibbs energy change, ∆rGR at the given temperature is 13.6 kJ mol^-1.
Answer:
Given,
∆rG- = -2303 RT log K
∆rGe = -136 kJ mol^-1
= -136 x 103 J mol^-1
T = 298 K
\(\log K=\frac{-\Delta_r G^{\Theta}}{2303 R T}\)
\(=\frac{-\left(-13.6 \times 10^3 \mathrm{~J} \mathrm{~mol}^{-1}\right)}{2.303 \times\left(8.314 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right) \times(298 \mathrm{~K})}\)
= 2.38
K = antilog 2.38 
= 2.4 × 10²

Question 6.13.
At 60C dinitrogen tetroxide is fifty percent dissociated. Calculate the standard free energy change at this temperature and at one atmosphere.
Answer: 

If N₂O is 50% dissociated, the mole fraction of both the substances is given by,

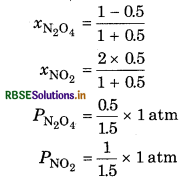
The equilibrium constant Kp is given by,

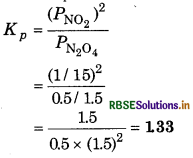
∴  ∆rGθ = -RT In Kp
= - 2.303 RT log Kp
= - 2.303 x (8.314J K^-1 mol^-1) x (333K) log 1.33
= - 790 K J mol^-1

RBSE Class 11 Chemistry Thermodynamics Textbook Questions and Answers

 Question 6.1.
A thermodynamic state function is a quantity.
(i) used to determine heat changes.
(ii) whose value is independent of path. 
(iii) used to determine pressure volume work. 
(iv) whose value depends on temperature only. 
Answer:wer:
(ii) Whose value is independent of path

Question 6.2.
For the process to occur under adiabatic conditions, the correct condition is:
(i) ∆T = 0
(ii) ∆p = 0
(iv) w = 0
(iii) q = 0
Answer:
(iii) q = 0

Question 6.3.
The enthalpies of all elements in their standard states are:
(i) Unity
(ii) Zero
(iii) ∆ < 0
(iv) different for each element
Answer:
(ii) Zero.

Question 6.4. 
∆U of combustion of methane is -X kJ mol^-1. The value of ∆HR is:
(i) = ∆U
(iil) < ∆U
(ii) > ∆U
(iv) = 0
Answer:
(iii) < ∆U
Reason: CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O(l)
∆ng = np - nr
=1 - 3 = -2
∆HAU + ∆nRT
= -∆U°- 2RT
Thus ∆H° < ∆U
Hence (iii) is the correct Answer.

Question 6.5. 
The enthalpy of combustion of methane, graphite and dihydrogen at 298 K are -890.3 kJ mol^-1, -393.5 kJ mol^-1 and -285.8 kJ mol^-1 respectively. Enthalpy of
 formation of CH₄(g) will be:
(i) -74.8 kJ mol^-1
(ii) - 52.27 kJ mol^-1
(iii) +74.8kJ mol^-1
Answer:
(i) -748 kJ mol^-1.
Reason: CH₄(g) + 2O₂(g) → CO₂ (g) + 2H₂O(l); ∆H = -890.3 kJmol^-1 ....... (i)
C(s) + O₂(g) → CO₂(g); ∆H = -393.5 kJ mol^-1 ....... (ii)
H₂(g) + 1/2O₂(g) →  H₂O (l) ∆H = -2858 kJ mol^-1 ......... (iii)
For the reaction, C(s) + 2H₂(g) → CH₄(g); ∆H =? 
Eq. (ii) + 2 x Eq. (iii) - Eq. (i)
∆H = -395.5 + 2 x (-2858)-(-890.3)
= -74.8 kJ mol^-1

Question 6.6.
A reaction, A + B → C + D + q is found to have a positive entropy change. The reaction will be.
(i) possible at high temperature
(ii) possible only at low temperature 
(iii) not possible at any temperature 
(iv) possible at any temperature
Answer:
(iv) possible at any temperature.

Question 6.7.
In a process, 701 J of heat is absorbed by a system and 394 J of work is done by the system? What is the change in internal energy for the process?
Answer:
∆U = q + W, 
where ∆U is the change in internal energy
Given
q = +701 J
Since the work is done by the system; W is -ve.
∴ ∆U = q - W (701 - 394) J = 307 J
∴ Change in internal energy = 307 J

Question 6.8. 
The reaction of cyanamide NH₂CN(s) with O2 was affected in a bomb calorimeter and AU was found to be - 742.7 kJ/mol at 298 K. Calculate enthalpy change for the reaction at 298 K.
NH₂CN(8) + 3/2O₂(g) → N₂ (g) + CO₂ (g) + H₂O(l)
Answer:
The given reaction is
NH₂CN(s)  + 3/2O₂(g) → N₂(g) + CO₂(g) + H₂O(l) 
∆U = -742.7 kJ mol^-1
Enthalpy change ∆H = ∆U +  ∆nRT
where ∆ng = change in the no. of moles (gaseous)
= np - nr
= 2- 3/2 = 1/2
[T = 298 K, R = 0.0083 kJ mol^-1 K^-1]
∆H = -7427 + 1/2(0.0083)  x 298
= (-742.7 +1.24) kJ 
= -7415 kJ mol^-1
∴ Enthalpy change for the reaction is - 741.5 kJ mol^-1.

Question 6.9. 
Calculate the number of kJ necessary to raise the temperature of 60 g of aluminium from 35°C to 55°C. Molar heat capacity of Al is 24 J mol^-1 K^-1.
Answer:
Mass of Al given is 60 g
∆T = 55 - 3520°C
No. of moles of aluminium = \(\frac{\text { Mass of Al }}{\text { Atomic mass of Al }}=\frac{60}{27}\)
Molar heat capacity = 24 J/mol K
= Moles x  ∆T x Molar heat capacity
Total heat required i.e., T  = 60/27 x 20 x 24 J
= 1067 J = 1067 kJ

Quesyion 6.10. 
Calculate the enthalpy change on freezing of 1.0 mol of water at 10.0°C to ice at - 10.0°C.
∆fus H = 6.03 kJ mol^-1 at 0°
Cp[H₂O(l)] = 75.3J mol^-1 K^-1
Cp[H₂O(l)] = 36.8J mol^-1 K^-1
Answer:
Enthalpy change for the conversion of 1 mole liquid water at 10°C into 1 mole liquid water at 0°C.
∆H1 = Cp [H₂O (l)] × ∆T
= -75.3J mol^-1 K^-1 x 10 K
= -753J mol^-1
= -0.753 kJ mol^-1
Enthalpy of fusion
∆H₂ = ∆H freezing 
= -∆H fusion
= -603 kJ mol^-1
Now, enthalpy change for the conversion of 1 mole of ice at 0°C to 1 mole of ice at 10°C,
∆H₂ = Cp [H₂O(s)] x ∆T
= -368J mol^-1 K^-1 x 10 K
= -368 J mol^-1 = -0.368 kJ mol^-1
∴ According to Hess's law of constant heat summation, 
∆H total = ∆H₁ + ∆H₂ + ∆H₃ = -(0.753 + 603 + 0.368) kJ mol^-1 
= -7.151kJ mol^-1

Question 6.11. 
Enthalpy of combustion of carbon to CO is 393.5 kJ/mol. Calculate the heat released upon formation of 35.2 g of CO₂ from carbon and dioxygen gas?
Answer:

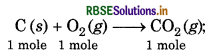
∆H = -393.5 kJ/mol^-1
For the formation of 44 g of CO₂, heat released is = 393.5 kJ mol^-1
For the formation of 35.2 g of CO₂ heat released is
\(=\frac{-393.5}{44} \times 35.2\)
= -3148 kJ mol^-1

Question 6.12. 
Enthalpies of formation of CO(g), CO₂(g), N₂O(g) and N₂O, (g) are - 110,- 393.81 and 9.7 kJ mol^-1. Find the value of ∆rH for the reaction.
N₂O₄(g) + 3CO(g) → N₂O(g) + 3CO₂ (g) 
Answer:
N₂O₄(g) + 3CO(g) → N₂O(g) + 3CO₂(g) 
∆rH^θ = ?
∆rH^θ = ∑∆H (Product) - ∆H(reactants) = [∆/H(N₂O) + 3 x ∆/H(CO₂)]
= [∆fH(N₂O) + 3 x ∆f(CO₂)]
= [81 + 3 x (393)] - [9.7 + 3 (-110)] = -777.8 kJ

Question 6.13. 
Given: N₂(g) + 3H₂(g) → 2NH₃ (g);
∆rH^θ = -92.4 kJ mol^-1
What is the standard enthalpy of formation of NH₃ gas?
Answer:
Given: N₂(g) + 3H₂(g) → 2NH₃(g);
∆fH^θ = -92.4 kJ mol^-1
This is the heat evolved for 2 moles of NH₃(g).
∴ Heat evolved for 1 mole of NH₃(g)
\(=\frac{-92.4}{2}\)
= -462 kJ
Hence, ∆fH^θ of NH3 gas = - 46.2 kJ mol^-1

Question 6.14. 
Calculate the standard enthalpy of formation of CH₃OH(l) from the following data:
(i) CH₃OH(l) + 3/2O₂(g) → CO₂(g) + 2H₂O(l) ∆rH^θ = -726 kJ mol^-1 ........ (i)
(ii) C (graphite) + O₂(g) → CO₂(g); ∆cH^θ = -726 kJ mol^-1 ........... (ii)
(iii) H₂(g) + 1/2 O₂(g) → H₂O(l); ∆fH^θ = -286kJ mol^-1 ........... (iii)
Answer:
The required equation is
C (graphite) + 2H₂(g) + 1/2O₂(g) → CH₃OH(l);
∆fH® = ?
Multiply eq. (iii) by 2 and add to eq.  (ii) 
C (graphite) + 2H₂(g) + 1/2O₂ (g) → CO₂(g) + 2H₂O(l)
∆fH = (2 x -286) + (-393)
= -572 - 393
= -965 kJ mol^-1
Subtract eq. (i) from eq. (iv)
C (graphite) + 2 H₂(g) + 1/2O₂(g) → CH₃OH(l);
∆H = 965 - (-726) 
=-239 kJ mol^-1
∆fH = -239 kJ mol^-1

Question 6.15. 
Calculate the enthalpy change for the process.
CCI₄(g) → C(g) + 4 Cl(g)
and calculate bond enthalpy of C-Cl in CCl₄ (g).
∆vapH (CCl₄) = 30.5 kJ mol^-1
∆H (CCl₄)= -135.5 kJ mol^-1
∆H (C) = 715.0 kJ mol^-1
where ∆H is enthalpy of atomisation.
∆H (Cl₂) = 242 kJ mol^-1
Answer:
(i) CCl₄ (l) → CCl₄(g); ∆H = 30.5 kJ mol^-1
(ii) C(s) + 2Cl₂(g) → CCl₄ (l); ∆H2 =-135.5 kJ mol^-1
(iii) C(s) → C(g);  ∆H₃ = 7150 kJ mol^-1
(iv) Cl₂ (g) → 2Cl(g)    ∆H₁ = 242 kJ mol^-1
Required equation is
CCl₄ (g) → C(g) + 4 Cl(g), ∆H =?
Now carry out the following operation to get the required equation is
Eq. (iii) + 2  x Eq. (iv) -Eq. (i) - Eq. (ii)
∴ ΔΗ = ΔΗ₃ + 2ΔΗ₄ - ΔΗ₁ - ΔΗ₂
ΔH = 715 + 2 x 242 - 30.5 - (-135.50)kJ mol^-1
= 1304 kJ mol^-1
Since during this reaction, 4 C-Cl bonds are broken, bond enthalpy of C-Cl in CCl₄  (average value)
\(=\frac{\Delta H}{4}=\frac{1304}{4}\)
= 326 kJ mol^-1

Question 6.16. 
For an isolated system, ∆U = 0, what will be ∆S?
Answer:
For an isolated system.
∆U = 0
So, the spontaneous change will occur if
∆S > 0

Question 6.17.
For the reaction at 298 K. 2A + B → C, ∆H = 400 kJ mol^-1 and ∆S = 0.2 kJ K1 mol^-1. At what temperature, will the reaction become spontaneous considering ∆H and ∆S to be constant over the temperature range?
Answer:
For the reaction, 2A + B →  C;
and
∆H = 400 kJ K 1mol^-1
∆S = 0.2 kJ K 1mol^-1
∆G = ∆H - T∆S
For a spontaneous reaction, ∆G has to be negative value, ∆H is 400 kJ mol^-1 (positive).
∴T∆S has to be > ∆H
or
\(T>\frac{\Delta H}{\Delta S}>\frac{400}{0.2}\)
T > 2000 K
For the reaction to be spontaneous T > 2000 K.

Question 6.18. 
For the reaction,
2Cl(g) → Cl₂(g), What are the signs of ∆H and ∆S?
Answer:
2Cl(g) → Cl₂(g),
In this reaction, a molecule of chlorine (Cl₂) is formed from its two gaseous atoms and the energy is released with the formation of bond.
So, ∆H is negative.
Moreover, in this reaction, randomness decreases with the formation of Cl₂ molecule so entropy also decreases. Thus, ∆S is negative.

Question 6.19. 
For the reaction,
2A(g) + B(g) → 2 D(g)
∆U = -10.5 kJ and ∆S = -44.1Jk^-1
Calculate ∆G for the reaction, and predict whether the reaction may occur spontaneously.
Answer:
For the given reaction,
2A(g) + B(g) → 2 D(g)
∆ng = 2 - 3 = -1 mol
Substituting the value of ∆U in the expression of ∆H:
∆H* = ∆U® + ∆n ̧RT
= (-10.5 kJ) + (-1) (8314 x 103 kJ K^-1)
= -10.5 kJ - 248 kJ
= -1298 kJ
When we substitute the value of ∆H and ∆S in the expression of ∆GR, then according to Gibbs' Helmholtz equation;
∆G = ∆H - T∆S®
= -1298 kJ -  (298 K) (-44.1 JK^-1)
= - 12.98 kJ -(-13.14 kJ)
∆GR = 0.164 kJ
Since ∆G for the reaction is positive, the reaction will not occur spontaneously.

Question 6.20. 
The equilibrium constant for a reaction is 10. What will be the value of ∆G? R = 8.314 JK^-1 mol^-1, T 300 K.
Answer:
The equilibrium constant given for a reaction is 10.
i.e.,
K = 10
∆G = -2303 RT log K
= -2303 x 8.314 x 300 log 10 
= -2.303 × 8,314 x 300 x 1
[as log 10 = 1]
= -5744.142 J mol^-1
= -5.744 kJ mol^-1

Question 6.21. 
Comment on the thermodynamic stability of NO (g), given
1/2N₂(g) + 1/2O₂(g) → NO(g); ∆r Hθ = 90 kJ mol^-1
NO(g) + 1/2O₂(g) → NO₂(g); ∆rHθ = -74 kJ mol^-1
Answer:
For the reaction,
1/2N₂(g) + 1/2O₂(g) → NO(g); ∆r Hθ = 90 kJ mol^-1
The formation of NO is an endothermic process since heat is absorbed in this process.
NO(g) + 1/2O₂(g) → NO₂(g); ∆rHθ = -74 kJ mol^-1
This equation shows that the oxidation of NO into NO₂ is an exothermic process since heat is liberated and it is energetically more feasible. Hence, NO(g) is thermodynamically unstable and it would get converted into NO₂ (g) spontaneonsly.

Question 6.22. 
Calculate the entropy change in surroundings when 1.00 mol of H₂O(l) is formed under standard conditions. ∆fHθ = -286 kJ mol^-1.
Answer:. Reaction for the formation of H₂O(n) is given below:
H₂(g) + 1/2O₂(g)  → H₂O(l)  ∆fHθ = -286 kJmol^-1
∆fHθ = -286 kJ mol^-1
This reaction is exothermic because heat is evolved in this reaction. So, it is absorbed by the surroundings. 
q surr = +286 kJ mol^-1
Now,
\(\Delta S_{\text {surr }}=\frac{q_{\text {surr }}}{T}\) 
\(=\frac{286 \times 10^3 \mathrm{Jmol}^{-1}}{298 \mathrm{~K}}\) 
= 959.73 J k^-1 mol^-1