RBSE Solutions for Class 11 Chemistry Chapter 2 परमाणु की संरचना

Rajasthan Board RBSE Solutions for Class 11 Chemistry Chapter 2 परमाणु की संरचना Textbook Exercise Questions and Answers.

RBSE Class 11 Chemistry Solutions Chapter 2 परमाणु की संरचना

RBSE Class 11 Chemistry परमाणु की संरचना Textbook Questions and Answers

प्रश्न 2.1. 
(i) एक ग्राम भार में इलेक्ट्रॉनों की संख्या का परिकलन कीजिए।
(ii) एक मोल इलेक्ट्रॉनों के द्रव्यमान और आवेश का परिकलन कीजिए।
उत्तर:
(i) एक इलेक्ट्रॉन का द्रव्यमान = 9.1 x 10^-28 g
= 9.1 × 10^-31 kg
(1 g = 10³ kg)
अतः 10^-3 kg भार में इलेक्ट्रॉनों की संख्या
$=\frac{10^{-3} \mathrm{~kg}}{9.1 \times 10^{-31} \mathrm{~kg}}$
= 1.0989 × 10²⁷ इलेक्ट्रॉन
= 1.099 × 10²⁷ इलेक्ट्रॉन

 (ii) एक इलेक्ट्रॉन का द्रव्यमान = 9.1 × 10^-31 kg
अतः 1 मोल इलेक्ट्रॉनों का द्रव्यमान = एक इलेक्ट्रॉन का द्रव्यमान × आवोगाद्रो संख्या
= 9.1 × 10^-31 × 6.022 × 10²³
= 5.480 × 10^-7 kg
एक इलेक्ट्रॉन पर आवेश = 1.60219 x 10^-19 C

अतः एक मोल इलेक्ट्रॉनों पर आवेश
= 1.60219 × 10^-19 × 6.022 × 10²³
9.648 × 10⁴C = 9.65 × 10⁴ C

प्रश्न 2.2. 
(i) मेथेन के एक मोल में उपस्थित इलेक्ट्रॉनों की संख्या का परिकलन कीजिए।
(ii) 7 mg 14C में न्यूट्रॉनों की (क) कुल संख्या तथा (ख) कुल द्रव्यमान ज्ञात कीजिए। (न्यूट्रॉन का द्रव्यमान = 1.675 x 10^-27 kg मान लीजिए )
(iii) मानक ताप और दाब (STP) पर 34mg NH₃ में प्रोटॉनों की (क) कुल संख्या और (ख) कुल द्रव्यमान बताइए। दाब और ताप में परिवर्तन से क्या उत्तर परिवर्तित हो जाएगा?
उत्तर:
(i) मेथेन (CH₄ ) के एक अणु में इलेक्ट्रॉनों की संख्या = 6 + 4 = 10
अत: CH के एक मोल में इलेक्ट्रॉनों की संख्या = एक मोल में अणुओं की संख्या एक अणु में
= 6.022 × 10²³ x 10
= 6.022 × 10²⁴

इलेक्ट्रॉनों की संख्या

(ii) 7 mg 14C = 7 × 10³ g  14C
14C का मोलर द्रव्यमान = 14 g
(क) 14C के मोल = 
$=\frac{7 \times 10^{-3} \mathrm{~g}}{14}$
अतः 14C के परमाणुओं की संख्या
= मोल × आवोगाद्रो संख्या
= 7/14 × 10 × 6.022 × 10²³
14C के एक परमाणु में न्यूट्रॉनों की संख्या 14 - 6 = 8
अतः 14C के = 7/14 × 10^-3 × 6.022 × 10²³
परमाणुओं में न्यूट्रॉनों की संख्या
= 7/14 × 10³ × 6.022 × 10²³ x 8
= 2.4088 × 10²¹ न्यूट्रॉन

(ख) एक न्यूट्रॉन का द्रव्यमान 1.675 x 10^-27 kg 
न्यूट्रॉनों का कुल द्रव्यमान = न्यूट्रॉनों की कुल संख्या x एक न्यूट्रॉन का द्रव्यमान
= 2,4088 × 10²⁴ x 1.675 × 10^-27kg
= 4.0347 × 10 kg

(iii) 34mg NH = 0.034 g NH₃ = 34 × 10g NH₃
(क) 17 g NH₃ = 1 मोल NH₃ = 10 मोल प्रोटॉन
(NH₃ के एक अणु में प्रोटॉनों की संख्या 7 + 3 = 10)
= 10 × 6.022 × 10²³ प्रोटॉन = 6.022 × 10²⁴ प्रोटॉन
अतः 34 × 10₃g NH के मोल
$=\frac{34 \times 10^{-3} \mathrm{~g}}{17}$
अतः प्रोटॉनों की कुल संख्या = मोल × आवोगाद्रो
संख्या = $\frac{6.022 \times 10^{24} \times 34 \times 10^{-3}}{17}$
= 1.2044 x 10²² प्रोटॉन

(ख) प्रोटॉनों का कुल द्रव्यमान = प्रोटॉनों की संख्या x एक प्रोटॉन का द्रव्यमान
= 1.2044 × 10²² × 1.6726 × 10^-27 kg
= 2.01447 × 10⁵ kg
= 2.015 × 10⁵ kg
नोट : ताप व दाब में परिवर्तन से उत्तर पर कोई प्रभाव नहीं

प्रश्न 2.3. 
निम्नलिखित नाभिकों में उपस्थित न्यूट्रॉनों और प्रोटॉनों की संख्या बताइए।
¹³₆C, ¹⁶₈O, ²⁴₁₂Mg, ⁵⁶₂₆Fe, ⁸⁸₃₈Sr
उत्तर:
न्यूट्रॉनों की संख्या (n) = द्रव्यमान संख्या (A) -  परमाणु क्रमांक (Z)
प्रोटॉनों की संख्या = परमाणु क्रमांक (Z)

नाभिक	द्रव्यमान संख्या (A)	परमाणु क्रमांक (प्रोटॉनों की संख्या) (Z)	न्यूट्रॉनों की संख्या = ( द्रव्यमान संख्या - परमाणु क्रमांक) [n= A - Z]
136C	13	6	(13 – 6) = 7
168O	16	8	(16 – 8) = 8
2412Mg	24	12	(24 – 12) = 12
5626Fe	56	26	(56 – 26) = 30
8838Sr	88	38	(88 – 38) = 50

 

प्रश्न 2.4. 
नीचे दिए गए परमाणु द्रव्यमान (A) और परमाणु संख्या (Z) वाले परमाणुओं का पूर्ण प्रतीक लिखिए:
(i) Z = 17, A = 35 
(ii) Z = 92, A = 233 
(iii) Z = 4, A = 9
उत्तर:
(i) ³⁵₁₇Cl (क्लोरीन) 
(ii) ²²³₉₂U (यूरेनियम)
(iii) ⁹₄Be (बेरिलियम)

प्रश्न 2.5. 
सोडियम लैम्प द्वारा उत्सर्जित पीले प्रकाश की तरंगदैर्घ्य (A) 580 nm है। इसकी आवृत्ति (v) और तरंग संख्या (V) का परिकलन कीजिए।
उत्तर:
उत्सर्जित प्रकाश की तरंगदैर्घ्य (A) = 580nm
= 580 × 10^-9m, c = 3 x 10⁸ ms^-1
आवृत्ति (v) = $\frac{c}{\lambda}=\frac{3 \times 10^8}{580 \times 10^{-9}}$
= 5.17 × 10¹⁴ s^-1
तरंग संख्या = $\bar{v}=\frac{1}{\lambda}=\frac{1}{580 \times 10^{-9}}$ = 1.72 x 10⁶ m^-1

प्रश्न 2.6. 
प्रत्येक ऐसे फोटॉन की ऊर्जा ज्ञात कीजिए:
(i) जो 3 x 10⁵ Hz आवृत्ति वाले प्रकाश के संगत हो।
(ii) जिसकी तरंगदैर्घ्य 0.50 A हो।
उत्तर:
(i) फोटॉन की ऊर्जा (E) = hv
h = प्लांक स्थिरांक
= 6.626 × 10^-34 Js
अतः E = 6.626 × 10^-34Js × 3 × 10¹⁵ s^-1
E = 1.9878 × 10¹⁸ J
E = 1.988 × 10^-18 J

(ii) ऊर्जा (E) = hv
c = 3 × 10⁸ ms^-1
λ = 0.5 A
= 0.5 x 10^-10 m
$\mathrm{E}=\frac{6.626 \times 10^{-34} \mathrm{JS} \times 3 \times 10^8 \mathrm{~ms}^{-1}}{0.5 \times 10^{-10} \mathrm{~m}}$
= 3.9756 × 10^-15 J
ऊर्जा = 3.98 × 10^-15 J

प्रश्न 2.7.
2 × 10^-10 काल (Time) वाली प्रकाश तरंग की तरंगदैर्घ्य, आवृत्ति और तरंग संख्या की गणना कीजिए।
उत्तर:
प्रकाश तरंग का काल =(T) = 2 × 10^-10 s

(i) आवृत्ति v = 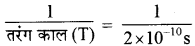= 5 × 10⁹ s^-1

(ii) तरंगदैर्घ्य λ = $\frac{c}{v}=\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{5 \times 10^9 \mathrm{~s}^{-1}}$
λ = 6.0 × 10^-2 m

(iii) तरंग संख्या = 1/λ = $\frac{1}{6.0 \times 10^{-2} \mathrm{~m}}$
= 16.66 m^-1

प्रश्न 2.8. 
ऐसा प्रकाश, जिसकी तरंगदैर्घ्य, 4000 Pm हो और जो 1 J ऊर्जा दे, के फोटॉनों की संख्या बताइए। 
उत्तर:
ऊर्जा, (E) = hv
N फोटॉनों की ऊर्जा, E = Nhv = Nh c/λ
अतः
N = Ελ/hc
E = IJ, 2 = 4000 Pm = 4000 x 10^-12 m 
h = 6.626 × 10^-34J तथा c = 3 x 10⁸ ms^-1 
अतः फोटॉनों की संख्या (N)
$=\frac{1 \mathrm{~J} \times 4000 \times 10^{-12} \mathrm{~m}}{6.626 \times 10^{-34} \mathrm{Js} \times 3 \times 10^8 \mathrm{~ms}^{-1}}$
= 2.012 × 10¹⁶ फोटॉन

प्रश्न 2.9. 
यदि 4 x 10⁷ m तरंगदैर्घ्यं वाला एक फोटॉन 2.13 eV कार्यफलन वाली धातु की सतह से टकराता है तो 
(i) फोटॉन की ऊर्जा (eV में ) 
(ii) उत्सर्जन की गतिज ऊर्जा और 
(iii) प्रकाशीय इलेक्ट्रॉन के वेग का परिकलन कीजिए। (1eV 1.6020 x 10^-19 J)
उत्तर:
(i) फोटॉन की ऊर्जा E = hv = hc/λ
$=\frac{6.626 \times 10^{-34} \mathrm{Js} \times 3 \times 10^8 \mathrm{~ms}^{-1}}{4 \times 10^{-7} \mathrm{~m}}$
= 4.969 × 10^-19 J
= 4.97 × 10^-19 J
$E=\frac{4.97 \times 10^{-19}}{1.6020 \times 10^{-19}}$
= 3.10 ev

(ii) ऊर्जा (E) = K. E. ( गतिज ऊर्जा ) + कार्यफलन
K. E. = E - कार्यफलन
= 3.10 - 2.13 = 0.97 ev

(iii) गतिज ऊर्जा KE. = 1/2 mv²
प्रकाशीय इलेक्ट्रॉन का वेग (v) = $\sqrt{\frac{2 . K E}{m}}$
KE. = 0.97eV = 0.97 × 1,602 x 10^-19 J 
= 0.97 × 1.602 × 10^-19 kg m^-2 s^-2
$\mathrm{v}=\sqrt{\frac{2 \times 0.97 \times 1.602 \times 10^{-19} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-2}}{9.1 \times 10^{-31} \mathrm{~kg}}}$
v = 5.84 × 10⁵ ms^-1

प्रश्न 2.10. 
सोडियम परमाणु के आयनन के लिए 242nm तरंगदैर्घ्य की विद्युत चुम्बकीय विकिरण पर्याप्त होती है। सोडियम की आयनन ऊर्जा kJ mol^-1 में ज्ञात कीजिए।
उत्तर:
242 mm तरंगदैर्घ्य (2) की विद्युत चुम्बकीय विकिरण सोडियम परमाणु के आयनन के लिए पर्याप्त है। अतः आयनन ऊर्जा विकिरण की ऊर्जा
λ  = 242nm = 242 x 10^-9 m
आयनन ऊर्जा (E) = hv
$=\frac{h c}{\lambda}=\frac{6.626 \times 10^{-34} \mathrm{Js} \times 3 \times 10^8 \mathrm{~ms}^{-1}}{242 \times 10^{-9} \mathrm{~m}}$
= 8.21 × 10^-19 J / फोटॉन
= 8.21 × 10^-22 kJ/फोटॉन
एक मोल सोडियम की आयनन ऊर्जा = आयनन ऊर्जा × आवोगाद्रो संख्या
= 8.21 × 10^-22 kJ x 6.022 × 10²³
= 494kJ mol^-1

प्रश्न 2.11. 
25 वॉट का एक बल्ब 0.57 pm तरंगदैर्घ्यं वाले पीले रंग का एकवर्णी प्रकाश उत्पन्न करता है। प्रति सेकण्ड क्वांटा के उत्सर्जन की दर ज्ञात कीजिए।
उत्तर:
तरंगदैर्ध्य (A) = 0.57 pm = 0.57 x 10^-6 m
बल्ब की क्षमता 25 वॉट = 25 Js^-1
फोटॉन की ऊर्जा (E) = hv = hc/λ
$=\frac{6.626 \times 10^{-34} \mathrm{Js} \times 3 \times 10^8 \mathrm{~ms}^{-1}}{0.57 \times 10^{-6} \mathrm{~m}}$
= 3.48 × 10^-19 J
प्रति सेकण्ड क्वान्टा के उत्सर्जन की दर = 
$=\frac{25 \mathrm{Js}^{-1}}{3.48 \times 10^{-19}}$
= 7.18 × 10¹⁹ g^-1

प्रश्न 2.12. 
किसी धातु की सतह पर 6800 A तरंगदैर्घ्यं वाली विकिरण डालने से शून्य वेग वाले इलेक्ट्रॉन उत्सर्जित होते हैं। धातु की देहली आवृत्ति (g) और कार्यफलन (Wo) ज्ञात कीजिए। 
उत्तर:
तरंगदैर्घ्य A = 6800 A = 6800 × 10^-10 m
देहली आवृत्ति = $\frac{c}{\lambda_0}=\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{6800 \times 10^{-10} \mathrm{~m}}$
= 4.41 × 10¹⁴ g^-1
कार्यफलन = hvo
क्योंकि वेग शून्य होने से गतिज ऊर्जा (K.E.) भी शून्य होगी। 
अतः कार्यफलन Wo = 6.626 × 10³⁴ x 4.41 x 10⁴ = 2.92 × 10^-19 J

प्रश्न 2.13. 
जब हाइड्रोजन परमाणु के n = 4 ऊर्जा स्तर से = 2 ऊर्जा स्तर में इलेक्ट्रॉन जाता है, तो किस तरंगदैर्घ्य का प्रकाश उत्सर्जित होगा?
उत्तर:
हाइड्रोजन के लिए - तरंग संख्या ( v ) = $\mathbf{R}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)$
प्रश्नानुसार, R = 109677 cm^-1,
n₂ = 4,
n₁ = 2
$\begin{aligned} & \bar{v}=109677\left(\frac{1}{2^2}-\frac{1}{4^2}\right) \\ & \bar{v}=109677 \times \frac{3}{16} \end{aligned}$
v = 20564.4 cm^-1
तरंगदैर्ध्य  =
λ = $\frac{1}{\bar{v}}=\frac{1}{20564.4} \mathrm{~cm}$
λ  = 486 × 10^-7 cm
λ = 486 × 10^-9 m
λ  = 486 nm

प्रश्न 2.14. 
यदि इलेक्ट्रॉन n = 5 कक्ष में उपस्थित हो, तो H परमाणु के आयनन के लिए कितनी ऊर्जा की आवश्यकता होगी ? अपने उत्तर की तुलना हाइड्रोजन परमाणु की आयनन एन्थैल्पी से कीजिए। (आयनन एन्थैल्पी 1 कक्षक से इलेक्ट्रॉन को निकालने के लिए आवश्यक ऊर्जा होती है।)
उत्तर:
हाइड्रोजन के प्रथम कक्ष में इलेक्ट्रॉन की ऊर्जा
E1 = -2.18 × 10^-18 J/परमाणु
$\mathrm{E}_n=-\frac{2.18 \times 10^{-18}}{n^2} \mathrm{~J}$
n = 5
अत: E5 = $=-\frac{2.18 \times 10^{-18}}{(5)^2} \mathrm{~J}$/परमाणु
= 8.72 × 10^-20 J/परमाणु
अतः 5वें कक्ष से इलेक्ट्रॉन को निकालने के लिए आवश्यक ऊर्जा
IE5 = E∞ – E5, (E∞ = 0) 
IE5 = 0 (-8.72 × 10^-20 J)
IE5 = 8.72 × 10^-20 J
अतः = 1 कक्ष से इलेक्ट्रॉन को निकालने के लिए आवश्यक
IE1 = E∞ - E1 
= 0 - (-2.18 × 10^-18 J)
= 2.18 × 10^-18 J
दोनों आयननएन्थैल्पी की तुलना, = $\frac{\mathrm{IE}_5}{\mathrm{IE}_1}=\frac{8.72 \times 10^{-20} \mathrm{~J}}{2.18 \times 10^{-18} \mathrm{~J}}$
= 4 x 10^-2

प्रश्न 2.15. 
जब हाइड्रोजन परमाणु में उत्तेजित इलेक्ट्रॉन n = 6 से मूल अवस्था में जाता है, तो प्राप्त उत्सर्जित रेखाओं की अधिकतम संख्या क्या होगी?
उत्तर:
जब इलेक्ट्रॉन वें कोश से मूल अवस्था में आता है तो प्राप्त उत्सर्जन रेखाओं की संख्या
$=\frac{n(n-1)}{2}$
यहाँ 1 = 6
$=\frac{6(6-1)}{2}=15$
= 15
अतः प्राप्त उत्सर्जन रेखाएँ 15

प्रश्न 2.16. 
(i) हाइड्रोजन के प्रथम कक्ष से सम्बन्धित ऊर्जा -2.18 × 10^-18 J atom^-1 है। पाँचवें कक्ष से सम्बन्धित ऊर्जा बताइए। 
(ii) हाइड्रोजन परमाणु के पाँचवें बोर कक्ष की त्रिज्या की गणना कीजिए।
उत्तर:
(i) हाइड्रोजन में वें कक्ष की ऊर्जा = $\frac{-2.18 \times 10^{-18}}{n^2} \mathrm{~J}$
n = 5
अत: $\mathrm{E}_5=\frac{-2.18 \times 10^{-18}}{5^2}$
= 8.72 × 10^-20 J

(ii) हाइड्रोजन परमाणु के वें बोर कक्ष की त्रिज्या 
rn = 0.529 x n² A
n = 5
rs = 0.529 × 5² = 13.225 A
= 1.3225 nm

प्रश्न 2.17. 
हाइड्रोजन परमाणु की बामर श्रेणी में अधिकतम तरंगदैर्घ्य वाले संक्रमण की तरंग संख्या की गणना कीजिए।
उत्तर:
तरंग संख्या v = 1/λ
अतः अधिकतम होने पर
तथा ऊर्जा न्यूनतम होगी, क्योंकि
E = hv
बामर श्रेणी के लिए n1 = 2, n2 = 3 (न्यूनतम v)

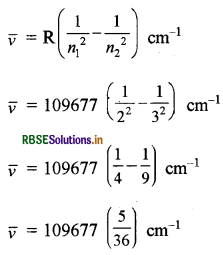
v = 1.52329 × 10⁴ cm^-1
= 1.5233 × 10⁶ m^-1

प्रश्न 2.18. 
हाइड्रोजन परमाणु में इलेक्ट्रॉन को पहली कक्ष से पाँचवीं कक्ष तक ले जाने के लिए आवश्यक ऊर्जा की जूल गणना कीजिए। जब यह इलेक्ट्रॉन तलस्थ (मूल) अवस्था में लौटता है, तो किस तरंगदैर्घ्य का प्रकाश उत्सर्जित होगा ? (इलेक्ट्रॉन की तलस्थ अवस्था ऊर्जा = 2.18 x10^-11 ergs है। )
उत्तर:
हाइड्रोजन परमाणु के लिए - मूल अवस्था की ऊर्जा,
E1 = 2.18 × 10^-11 ergs.
पाँचवीं कक्ष की ऊर्जा, 
$\begin{aligned} \mathrm{E}_5= & \frac{E_1}{n^2}=\frac{-2.18 \times 10^{-11}}{5^2} \\ & =\frac{-2.18 \times 10^{-11}}{25} \text { ergs. } \end{aligned}$
ऊर्जा में अन्तर, ∆ E = E5 - E1

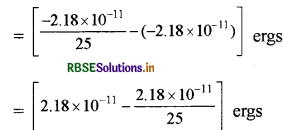
∆E = 2.09 × 10^-11 ergs.

इलेक्ट्रॉन के मूल अवस्था में लौटने पर उत्सर्जित प्रकाश की तरंगदैर्ध्य:
λ = 9.51  × 10^-18J
2 = 9.51 × 10^-8  x 10¹⁰ A = 951 A

प्रश्न 2.19. 
हाइड्रोजन परमाणु में इलेक्ट्रॉन की ऊर्जा En = (2.18 x 10^-18)/n 2 J द्वारा दी जाती है। 2 कक्ष से इलेक्ट्रॉन को पूरी तरह निकालने के लिए आवश्यक ऊर्जा की गणना कीजिए। प्रकाश की सबसे लम्बी तरंगदैर्घ्य ( cm में ) क्या होगी, जिसका उपयोग इस संक्रमण में किया जा सके?
उत्तर:
इलेक्ट्रॉन को 1 = 2 कक्ष से निकालने अर्थात् इसे अनन्त
तक ले जाने के लिए आवश्यक ऊर्जा
∆E = E∞  - E2
E∞  = 0, E2 = $\frac{-2.18 \times 10^{-18}}{2^2}$ J = 5.45 × 10^-19 J
अतः
∆E = 0 - (-5.45 × 10^-29) J 
= 5.45 × 10^-19 J
अतः तरंगदैर्घ्य $\lambda=\frac{h c}{\Delta E}=\frac{6.626 \times 10^{-34} \mathrm{Js} \times 3 \times 10^8 \mathrm{~ms}^{-1}}{5.45 \times 10^{-19} \mathrm{~J}}$

λ = 3.647 × 10^-7 m
λ = 3647 × 10^-10 m = 3647 A
λ = 3647 A

प्रश्न 2.20 
2.05 × 10⁷ mst वेग से गति कर रहे किसी इलेक्ट्रॉन का तरंगदैर्घ्यं क्या होगा?
उत्तर:
इलेक्ट्रॉन का तरंगदैर्घ्य 
$=\frac{6.626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1}}{9.1 \times 10^{-31} \mathrm{~kg} \times 2.05 \times 10^7 \mathrm{~ms}^{-1}}$
λ = 3.55 × 10^-11m

प्रश्न 2.21. 
इलेक्ट्रॉन का द्रव्यमान 9.1 x 10 kg है। यदि इसकी गतिज ऊर्जा 3.0 x 10⁵ J हो, तो इसकी तरंगदैर्घ्य की गणना कीजिए।
उत्तर:
गतिज ऊर्जा (K.E.) = 1/2 mv²
K.E. = 3 × 10^-25 J, इलेक्ट्रॉन का द्रव्यमान
m = 9.1 x 10^-31 kg
अतः इलेक्ट्रॉन का वेग  $(v)=\left[\frac{2 \times K . E .}{m}\right]^{\frac{1}{2}}$
$v=\left(\frac{2 \times 3.0 \times 10^{-25}}{9.1 \times 10^{-31}}\right)^{\frac{1}{2}}$
= 0.8119 × 10³ ms^-1
= 0.812 × 10³ ms^-1
तरंगदैर्घ्य, $\lambda=\frac{h}{m \mathrm{v}}=\frac{6.626 \times 10^{-34}}{9.1 \times 10^{-31} \times 0.812 \times 10^3}$
λ = 0.8967 × 10^-6 m
λ = 0.8967 x 10^-6 x 10¹⁰ A
λ = 8967 A

प्रश्न 2.22. 
निम्नलिखित में से कौन सम- इलेक्ट्रॉनीय स्पीशीज है, अर्थात् किनमें इलेक्ट्रॉनों की समान संख्या है? Na⁺ K⁺ Mg²⁺, Ca²⁺, S^-2, Ar
उत्तर:
(i) Na⁺ में इलेक्ट्रॉन = 111 = 10
(ii) K⁺ = 19 - 1 = 18 इलेक्ट्रॉन
(iii) Mg²⁺ = 12 - 2 = 10 इलेक्ट्रॉन
(iv) Ca²⁺ = 20 - 2 = 18 इलेक्ट्रॉन
(v) Ar = 18 इलेक्ट्रॉन
(vi) S^-2 = 16 + 2 = 18 इलेक्ट्रॉन
अतः Na' तथा Mg²⁺ समइलेक्ट्रॉनीय हैं, एवं K⁺ Ca²⁺, Ar तथा S^2- समइलेक्ट्रॉनीय हैं।

प्रश्न 2.23. 
(i) निम्नलिखित आयनों का इलेक्ट्रानिक विन्यास लिखिए-
(क) H
(ख) Na⁺
(ग) O₂^-
(घ) F^-
(ii) उन तत्वों की परमाणु संख्या बताइए, जिनके सबसे बाहरी इलेक्ट्रॉनों को निम्नलिखित रूप में दर्शाया जाता है:
(क) 3s¹
(ख) 2p³
(ग) 3p⁵
(iii) निम्नलिखित विन्यासों वाले परमाणुओं के नाम बताइए-
(क ) [He] 2s¹
(ख) [Ne] 3s² 3p³
(ग) [Ar] 4s² 3d¹
उत्तर:
(i) (क) H^- (1 + 1 = 2 इलेक्ट्रॉन) = 1S²

(ख) Na⁺(11 - 1 = 10 इलेक्ट्रॉन)
= 1s² 2S² 2p6

(ग) O₂^- (8+ 2 = 10 इलेक्ट्रॉन)
= 1s² 2s² 2p⁶

(घ) F^- (9 + 1 = 10 इलेक्ट्रॉन) = 1s² 2s² 2p⁶

(ii) (क) 1s² 2s² 2p⁶ 3s¹ = 11 इलेक्ट्रॉन अतः
परमाणु संख्या = 11

(ख) 1s² 2s² 2p³ = 7 इलेक्ट्रॉन अतः परमाणु संख्या = 7

(ग) 1s² 2s² 2p⁶ 3s² 3p⁵ = 17 इलेक्ट्रॉन अतः परमाणु संख्या = 17

(iii) (क) [He] 2s¹ = 3 इलेक्ट्रॉन Li ( लीथियम)
(ख) (Ne) 3s² 3p³ = 15 इलेक्ट्रॉन = P (फॉस्फोरस)
(ग) [Ar] 4s² 3d¹ = 21 इलेक्ट्रॉन = Sc (स्केण्डियम)

प्रश्न 2.24. 
किस निम्नतम मान द्वारा g कक्षक का अस्तित्व अनुमत (सम्भव) होगा?
उत्तर:
g उपकोश के लिए l = 4
l = 4 के लिए " का न्यूनतम मान 5 होगा क्योंकि l = 0 से (n-1) होता है।

प्रश्न 2.25. 
एक इलेक्ट्रॉन किसी 3d कक्षक में है। इसके लिए n, 1 और my के सम्भव मान दीजिए।
उत्तर:
3d कक्षक के लिए n = 3, l = 2 और m1 = -2, -1, 0, +1, +2 में से कोई एक मान होगा।

प्रश्न 2.26. 
किसी तत्व के परमाणु में 29 इलेक्ट्रॉन और 35 न्यूट्रॉन हैं। 
(i) इसमें प्रोटॉनों की संख्या बताइए।
(ii) तत्व का इलेक्ट्रॉनिक विन्यास बताइए। 
उत्तर:
(i) किसी तत्व में प्रोटॉनों की संख्या
इलेक्ट्रॉनों की संख्या = 29

(ii) तत्व का इलेक्ट्रॉनिक विन्यास 1s², 2s², 2p⁶, 3s², 3p⁶, 3d⁶, 4s¹

प्रश्न 2.27. 
H²⁺, H₂ और O₂⁺ स्पीशीज में उपस्थित इलेक्ट्रॉनों की संख्या बताइए।
उत्तर:
H²⁺ = 2 - 1 = 1 इलेक्ट्रॉन
H₂ = 2 इलेक्ट्रॉन
O⁺₂ = 16 - 1 = 15 इलेक्ट्रॉन

प्रश्न 2.28. 
(i) किसी परमाणु कक्षक का 3 है। उसके लिए l और m1  के सम्भव मान क्या होंगे?
(ii) 3d कक्षक के इलेक्ट्रॉनों के लिए m1 और l क्वांटम संख्याओं के मान बताइए।
(iii) निम्नलिखित में से कौनसे कक्षक सम्भव हैं: 1p, 25, 2p और 3f
उत्तर:
(i) जब 1 = 3 तो l = 0, 1, 2, क्योंकि = 0 से (n - 1)
l = 0 के लिए m1 = 0
l = 1 के लिए m1 = -1, 0, + 1
l = 2 के लिए m1 = -2, -1, 0, +1, +2
( क्योंकि m1 = - 1 से 0 से + 1)

(ii) 3d कक्षक के लिए l = 2 और m1 = -2, -1, 0, +1, +2

(iii) 2s तथा 2p सम्भव हैं क्योंकि 2s के लिए n = 2, l = 0 (सम्भव ) तथा 2p के लिए = 2, 1 = 1 ( सम्भव ) लेकिन 1p तथा 3f  सम्भव नहीं हैं क्योंकि 1p के लिए n = 1 तथा l = 1 होना चाहिए जो कि सम्भव नहीं है। इसी प्रकार 3f के लिए n = 3 तथा l = 3 होना चाहिए जो कि संभव नहीं है क्योंकि l का मान n के बराबर नहीं होता।

प्रश्न 2.29
s, p, d संकेतन द्वारा निम्नलिखित क्वान्टम संख्याओं वाले कक्षकों को बताइए।
(क)  n = 1, l = 0
(ख) n = 3, l = 1
(ग) n = 4, l = 2
(घ) n = 4, l = 3
उत्तर:
(क) Is (ख) 3p (ग) 4d (ष) 4f

प्रश्न 2.30 
कारण देते हुए बताइए कि निम्नलिखित क्वान्टम संख्या के कौनसे मान सम्भव नहीं हैं:
उत्तर:
(क), (ग) तथा (ङ) सम्भव नहीं हैं। शेष सम्भव हैं क्योंकि ( क ) में n = 0 है जबकि ” का मान 1 से प्रारम्भ होता है। 
(ग) में l का मान n के समान है जो कि सम्भव नहीं है क्योंकि l = 0 से n - 1 तक होता है।
(ङ) में l का मान n के समान है जो कि सम्भव नहीं है।

प्रश्न 2.31. 
किसी परमाणु में निम्नलिखित क्वान्टम संख्याओं वाले कितने इलेक्ट्रॉन होंगे:
(क) n  = 4, ms = -1/2
(ख) n = 3, l = 0
उत्तर:
(क) n = 4 अर्थात् चतुर्थ कोश में इलेक्ट्रॉनों की कुल
संख्या = 2n² = 2 x 4² = 32
इनमें से 16 इलेक्ट्रॉनों के लिए, ms = 1/2 होगा तथा शेष 16 के लिए Ms = +1/2 होगा अतः n = 4 तथा ms = 1/2 वाले 16 इलेक्ट्रॉन होंगे।

(ख) n = 3 तथा l = 0 के लिए 3s कक्षक होगा, जिसमें दो इलेक्ट्रॉन आ सकते हैं क्योंकि किसी भी कक्षक की अधिकतम इलेक्ट्रॉन
क्षमता = 2

प्रश्न 2.32. 
यह दर्शाइए कि हाइड्रोजन परमाणु की बोर कक्षा की परिधि उस कक्षा में गतिमान इलेक्ट्रॉन की दे ब्रॉग्ली तरंगदैर्घ्य का पूर्ण गुणक होती है।
उत्तर:
बोर मॉडल के अनुसार:
$\begin{aligned} & m \mathrm{v} r=\frac{n h}{2 \pi} \\ & 2 \pi r=\frac{n h}{m \mathrm{~V}} \end{aligned}$
अत: 2πr = nλ
अतः परिधि (2πr) = nλ अर्थात् बोर कक्षा की परिधि उस कक्षा में गतिमान इलेक्ट्रॉन की दे ब्रॉग्ली तरंगदैर्घ्य का पूर्ण गुणक होती है।

प्रश्न 2.33. 
He से प्राप्त तरंग दैर्ध्य के स्पेक्ट्रम के n = 4 से n = 2 बामर संक्रमण बराबर वाला संक्रमण हाइड्रोजन स्पेक्ट्रम में क्या होगा?
उत्तर:
किसी परमाणु के लिए - तरंग संख्या
$=\mathbf{R}_H Z^2\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)$
He⁺ स्पेक्ट्रम के लिए = 1/λ = RH × 22
$\left(\frac{1}{2^2}-\frac{1}{4^2}\right)$  (Z = 2, 11 = 2, 12 = 4)
$\begin{aligned} & \frac{1}{\lambda}=\mathrm{R}_{\mathrm{H}} \times 4\left(\frac{1}{4}-\frac{1}{16}\right) \\ & \frac{1}{\lambda}=4 \mathrm{R}_{\mathrm{H}}\left(\frac{3}{16}\right)=\frac{3 \mathrm{R}_{\mathrm{H}}}{4} \end{aligned}$
हाइड्रोजन स्पेक्ट्रम के लिए

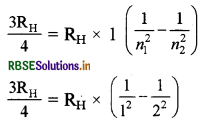
अतः n1 = 1 और n2 = 2
इसलिए हाइड्रोजन स्पेक्ट्रम में यह संक्रमण = 2 से n = 1 के समान होगा।

प्रश्न 2.34. 
He⁺(g) → He + e^- प्रक्रिया के लिए आवश्यक ऊर्जा की गणना कीजिए। हाइड्रोजन परमाणु की तलस्थ अवस्था (मूल अवस्था) में आयनन ऊर्जा 2.18 x 10^-18 J atom है।
उत्तर:
हाइड्रोजन परमाणु के लिए हो रहा है।
E1 = I.E. (आयनन ऊर्जा) = - 2.18 x 10^-18 J
He+ के लिए E1 = E1(H) x Z2
= - 2.18 × 10^-18 x 22 J
= - 8.72 × 10^-18 J
He⁺(g) ( 1s1 ) → He²⁺ + e^-  में He का आयनन
अतः आवश्यक ऊर्जा
= E1(He^-) = ( 8.72 x 10^-18) J
= 8.72 x 10^-18 J प्रति परमाणु

प्रश्न 2.35. 
यदि कार्बन परमाणु का व्यास 0.15 nm है, तो उन कार्बन परमाणुओं की संख्या की गणना कीजिए, जिन्हें 20 cm स्केल की लम्बाई में एक-एक करके व्यवस्थित किया जा सकता है। 
उत्तर:
कार्बन परमाणु का व्यास (d) = 0.15 nm
= 0.15 × 10^-9 m
स्केल की लम्बाई (l) = 20 cm = 20 x 10^-2 m
कार्बन परमाणुओं (n) की संख्या = $\frac{l}{d}=\frac{20 \times 10^{-2} \mathrm{~m}}{0.15 \times 10^{-9} \mathrm{~m}}$
= 1.33 x 10⁹m

प्रश्न 2.36. 
कार्बन के 2 x 10⁸ परमाणु एक कतार में व्यवस्थित हैं। यदि इस व्यवस्था की लम्बाई 2.4 cm है, तो कार्बन परमाणु की त्रिज्या की गणना कीजिए।
उत्तर:
कार्बन परमाणुओं की संख्या (n) = 2 × 10⁸
व्यवस्था की लम्बाई (l) = 2.4 cm
= 2.4 x 10^-2 m
= 2.4 × 10⁷ nm
अत: कार्बन परमाणु का व्यास (d) = l/n
$=\frac{2.4 \times 10^7 \mathrm{~nm}}{2 \times 10^8}$
= 0.12 nm
तथा कार्बन परमाणु की त्रिज्या r = d/2 = $\frac{0.12}{2}$
= 0.06nm

प्रश्न 2.37. 
जिंक परमाणु का व्यास 2.6 A है:
(क) जिंक परमाणु की त्रिज्या Pm में तथा 
(ख) 1.6 cm की लम्बाई में कतार में लगातार उपस्थित परमाणुओं की संख्या की गणना कीजिए। 
उत्तर:
(क ) Zn परमाणु का व्यास = 2.6 A
अतः त्रिज्या = 2.6/1
= 1.3 A
= 1.3 × 10^-10 m
= 1.3 × 10^-10 x 10¹² Pm
= 130 Pm
= 1.3 × 10^-2 Pm

(ख) लम्बाई (l) = 1.6 cm = 1.6 × 10² m
Zn के एक परमाणु का व्यास (d) = 2.6 A = 2.6 × 10^-10 m
अतः Zn परमाणुओं की संख्या n = l/d
$=\frac{1.6 \times 10^{-2} \mathrm{~m}}{2.6 \times 10^{-10} \mathrm{~m}}$
= 6.15 × 10⁷

प्रश्न 2.38. 
किसी कण का स्थिर विद्युत आवेश 2.5 x 10^-16 C है। इसमें उपस्थित इलेक्ट्रॉनों की संख्या की गणना कीजिए। 
उत्तर:
कण पर स्थिर विद्युत आवेश = 2.5 x 10^-16 C
एक इलेक्ट्रॉन पर आवेश = 1.6022 x 10^-19 C
अतः कण में उपस्थित इलेक्ट्रॉनों की संख्या
$=\frac{2.5 \times 10^{-16}}{1.6022 \times 10^{-19}}$
= 1560

प्रश्न 2.39. 
मिलिकन के प्रयोग में तेल की बूँद पर चमकती X-किरणों द्वारा प्राप्त स्थैतिक विद्युत आवेश प्राप्त किया जाता है। तेल की बूँद पर यदि स्थैतिक विद्युत आवेश -1.282 x 10^-18 C है तो इसमें उपस्थित इलेक्ट्रॉनों की संख्या की गणना कीजिए।
उत्तर:
एक इलेक्ट्रॉन पर आवेश = -1.6022 × 10^-19 C
तेल की बूँद पर आवेश = 1.282 x 10^-18 C
अतः तेल की बूंद में उपस्थित इलेक्ट्रॉनों की संख्या
$=\frac{-1.282 \times 10^{-18} \mathrm{C}}{-1.6022 \times 10^{-19} \mathrm{C}}$ = 8

प्रश्न 2.40. 
रदरफोर्ड के प्रयोग में सोने, प्लैटिनम आदि भारी परमाणुओं की पतली पन्नी पर कणों द्वारा बमबारी की जाती है। यदि ऐलुमिनियम जैसे हल्के परमाणु की पतली पन्नी ली जाए, तो उपर्युक्त परिणामों में क्या अन्तर होगा?
उत्तर:
ऐलुमिनियम जैसे हल्के परमाणु का नाभिक छोटा होने के कारण (कम आयतन) अधिक कण पार होंगे तथा धनावेश कम होने के कारण थोड़े से a कण ही कम कोण पर विक्षेपित होंगे।

प्रश्न 2.41. 
Br तथा " Br प्रतीक मान्य हैं, जबकि 35 Br तथा 35 Br मान्य नहीं हैं। संक्षेप में कारण बताइए।
उत्तर:
किसी दिए गए तत्व के लिए समस्थानिकों में प्रोटॉनों की समान संख्या तथा समान परमाणु क्रमांक के लिए द्रव्यमान संख्या भिन्न- भिन्न हो सकती है। अतः प्रतीक में द्रव्यमान संख्या दर्शाना आवश्यक है तथा परमाणु क्रमांक को तत्व के संकेत के बायीं ओर नीचे एवं द्रव्यमान संख्या को ऊपर की तरफ लिखा जाता है। अतः 35 Br तथा 35 Br मान्य नहीं हैं।

प्रश्न 2.42. 
एक 81 द्रव्यमान संख्या वाले तत्व में प्रोटॉनों की तुलना में 31.7% न्यूट्रॉन अधिक हैं। इसका परमाणु प्रतीक लिखिए। 
उत्तर:
द्रव्यमान संख्या (81) = प्रोटॉनों की संख्या + न्यूट्रॉनों
की संख्या
माना प्रोटॉनों की संख्या = x
अतः प्रश्नानुसार न्यूट्रॉनों की संख्या = $\frac{x+31.7 x}{100}$
= 1.317 x
द्रव्यमान संख्या (81) = x + 1.317x
2.317x = 81
= $\frac{81}{2.317}$
= 34.958 = 35
प्रोटॉनों की संख्या 35, अतः तत्व ब्रोमीन होगा तथा परमाणु
प्रतीक = 8135Br

प्रश्न 2.43 
37 द्रव्यमान संख्या वाले एक आयन पर ऋणावेश की एक इकाई है। यदि आयन में इलेक्ट्रॉन की तुलना में न्यूट्रॉन 11. 1% अधिक हैं, तो आयन का प्रतीक लिखिए।
उत्तर:
आयन पर एक इकाई ऋणावेश है अर्थात् आयन में इलेक्ट्रॉनों की संख्या प्रोटॉनों की संख्या से एक अधिक है। अतः इलेक्ट्रॉनों तथा न्यूट्रॉनों की कुल संख्या 37 + 1 = 38
माना इस आयन में इलेक्ट्रॉनों की संख्या = x
अतः आयन में न्यूट्रॉनों की संख्या = $\frac{x+11.1 x}{100}$
आयन में इलेक्ट्रॉनों तथा न्यूट्रॉनों = 1.11 x
( 38 ) = x + 1.11x 
2.111 = 38
$x=\frac{38}{2.111}$
x = 18
अतः आयन में इलेक्ट्रॉनों की संख्या = 18
प्रोटॉनों की संख्या = 18 - 1 = 17
अतः तत्व का परमाणु क्रमांक = 17 तथा यह तत्व क्लोरीन (Cl) है।
अतः आयन का प्रतीक = Cr

प्रश्न 2.44. 
56 द्रव्यमान संख्या वाले एक आयन पर धनावेश की 3 इकाई है और इसमें इलेक्ट्रॉन की तुलना में 30.4% न्यूट्रॉन अधिक है। इस आयन का प्रतीक लिखिए।
उत्तर:
आयन पर तीन इकाई धनावेश है। इसलिए इसमें इलेक्ट्रॉनों की संख्या प्रोटॉनों की संख्या से तीन कम है।
अतः द्रव्यमान संख्या (56) प्रोटॉनों की संख्या + न्यूट्रॉनों की
संख्या
(56 - 3) इलेक्ट्रॉनों की संख्या + न्यूट्रॉनों की संख्या माना आयन में इलेक्ट्रॉनों की संख्या = x
अतः न्यूट्रॉनों की संख्या = $\frac{x+30.4 x}{100}$
= 1.304x
किन्तु आयन में इलेक्ट्रॉनों की संख्या तथा न्यूट्रॉनों की संख्या का
योग = 53
अत: x + 1.304x = 53
2.304x = 53
$x=\frac{53}{2.304}$
x = 23 = इलेक्ट्रॉनों की संख्या
प्रोटॉनों की संख्या = 23 + 3 = 26 अतः यह तत्व (Fe) आयरन
है तथा आयन का प्रतीक, 5626Fe³⁺ है।

प्रश्न 2.45. 
निम्नलिखित विकिरणों के प्रकारों को आवृत्ति के बढ़ते हुए क्रम में व्यवस्थित कीजिए:
(क) माइक्रोवेव ओवन ( oven) से विकिरण
(ख) यातायात संकेत से त्रणमणि (amber) प्रकाश 
(ग) एफ.एम. रेडियो से प्राप्त विकिरण
(घ) बाहरी दिक् से कॉस्मिक किरणें
(च) X - किरणें
उत्तर:
(घ) > (च) > (ख) > (क) > (ग)
कॉस्मिक किरणें X - किरणें त्रणमणि (amber) प्रकाश > माइक्रो ओवन विकिरण एफ.एम. रेडियो विकिरण।

प्रश्न 2.46. 
नाइट्रोजन लेजर 337.1 nm की तरंग दैर्ध्य पर एक विकिरण उत्पन्न करती है। यदि उत्सर्जित फोटॉनों की संख्या 5.6 x 10²⁴ हो, तो लेजर की क्षमता की गणना कीजिए।
उत्तर:
लेजर की शक्ति (क्षमता) E = Nhv = Nh c/λ
तथा
λ = 337.1 nm = 337.1 x 10^-9 m
N = फोटॉनों की संख्या 5.6 x 10²⁴,
अतः
C = 3.0 × 10⁸ ms^-1
$\mathrm{E}=\frac{\left(5.6 \times 10^{24}\right)\left(6.626 \times 10^{-34} \mathrm{Js}\right)\left(3.0 \times 10^8 \mathrm{~ms}^{-1}\right)}{337.1 \times 10^{-9} \mathrm{~m}}$
E = 3.3 × 10⁶ J

प्रश्न 2.47. 
निऑन गैस को सामान्यतः संकेत बोर्डों में प्रयुक्त किया जाता है। यदि यह 616 nm पर प्रबलता से विकिरण उत्सर्जित करती है, तो
(क) उत्सर्जन की आवृत्ति, (ख) 30 सेकण्ड में इस विकिरण द्वारा तय की गई दूरी, (ग) क्वान्टम की ऊर्जा तथा (घ) उपस्थित क्वान्टम की संख्या की गणना कीजिए। (यदि यह 2 J की ऊर्जा उत्पन्न करती है।)
उत्तर:
(क) तरंगदैर्ध्य (λ) = 616 nm = 616 × 10^-9 m
प्रकाश का वेग c = 3 x 10⁸ ms^-1
अतः आवृत्ति (v) = $\frac{\mathrm{c}}{\lambda}=\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{616 \times 10^{-9} \mathrm{~m}}$
= 4.87 × 10¹⁴ s^-1

(ख) विकिरण द्वारा तय की गई दूरी = वेग x समय
c = 3 x 10⁸ ms^-1, t = 30s
= c x t
= 3 × 10⁸ ms^-1 × 30 s
= 9 × 10⁹ m

(ग) क्वान्टम की ऊर्जा E = hv
h = 6.626 × 10^-34 Js v = 4.87 × 10¹⁴s^-1
E = 6.626 × 10^-34 Js × 4.87 × 10⁴ g^-1 32.268 x 10^-20 J
= 32.27 × 10^-20 J
(घ) क्वान्टम की संख्या 

= 6.19 × 10¹⁸ J

प्रश्न 2.48. 
खगोलीय प्रेक्षणों में कुल ऊर्जा एक क्वान्टम की ऊर्जा दूरस्थ तारों से मिलने वाले संकेत बहुत कमजोर होते हैं। यदि फोटॉन संसूचक 600 nm के विकिरण से कुल 3.15 x 10^-18 J प्राप्त करता है, तो संसूचक द्वारा प्राप्त फोटॉनों की संख्या की गणना कीजिए।
उत्तर:
तरंगदैर्घ्य 1 = 600nm = 600 × 10^-9 m, फोटॉन की
ऊर्जा = 3.15 × 10^-18 J
एक फोटॉन की ऊर्जा, E = hv = hc/λ
n फोटॉनों की ऊर्जा, E = nhc/λ
फोटॉन की संख्या, n = Eλ/hc
$=\frac{3.15 \times 10^{-18} \mathrm{~J} \times 600 \times 10^{-9} \mathrm{~m}}{6.626 \times 10^{-34} \mathrm{Js} \times 3 \times 10^8 \mathrm{~ms}^{-1}}$
अतः फोटॉनों की संख्या = 9.5 = 10

प्रश्न 2.49. 
उत्तेजित अवस्थाओं में अणुओं के जीवनकाल का माप प्राय: लगभग नेनो सेकण्ड परास वाले विकिरण स्त्रोत का उपयोग करके किया जाता है। यदि विकिरण स्रोत का काल 2 ns और स्पंदित (pulsed) विकिरण स्रोत के दौरान उत्सर्जित फोटॉनों की संख्या 2.5 x 10¹⁵ है, तो स्रोत की ऊर्जा की गणना कीजिए। 
उत्तर:
स्रोत में विकिरण का काल, T = 2 ns
= 2 × 10^-9 S
आवृत्ति (v) =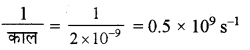
ऊर्जा (E) = nhv
उत्सर्जित फोटॉनों की संख्या = 2.5 x 10¹⁵
अतः E = 2.5 × 10¹⁵ x 6.626 × 10³⁴ Js
= 8.282 × 10^-10 J

प्रश्न 2.50. 
सबसे लम्बी द्विगुणित तरंगदैर्घ्य जिंक अवशोषण संक्रमण 589 और 589.6 nm पर देखा जाता है। प्रत्येक संक्रमण की आवृत्ति और दो उत्तेजित अवस्थाओं के बीच ऊर्जा के अन्तर की गणना कीजिए।
उत्तर:
λ1 = 589 nm = 589 × 10^-9m,
λ2 = 589.6 nm = 589.6 × 10^-9 m

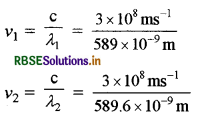
V1 = 5.0933 × 10¹⁴ s^-1
V2 = 5.0881 × 10¹⁴ s^-1
ऊर्जा अन्तर AE = E2 - E1 
∆E = hv2 - IVA
∆E = h ( V2 - V1)
= 6.626 x 10^-34 Js (5.09335.0881) x 10¹⁴ s^-1
= 6.626 × 10^-34 × 0.0523 × 10¹⁴
= 3.46 × 10^-22 J

प्रश्न 2.51. 
सीजियम परमाणु का कार्यफलन 1.9 eV है तो (क) उत्सर्जित विकिरण की देहली तरंगदैर्घ्यं (ख) देहली आवृत्ति की गणना कीजिए। (ग) यदि सीजियम तत्व को 500 nm की तरंगदैर्घ्य के साथ विकीर्णित किया जाए, तो निकले हुए फोटो इलेक्ट्रॉन की गतिज ऊर्जा और वेग की गणना कीजिए।
उत्तर:
सीजियम परमाणु का कार्यफलन (ऊर्जा) Wo = 1.9eV
= 1.9 × 1.6 × 10^-19 J
[l eV = 1.6 × 10^-19 J]
= 3.04 × 10^-19 J

(क)
$\begin{aligned} & \mathbf{W}_0=\frac{h c}{\lambda_0} \\ & \lambda_0=\frac{h c}{W_0}=\frac{6.626 \times 10^{-34} \mathrm{Js} \times 3 \times 10^8 \mathrm{~ms}^{-1}}{3.04 \times 10^{-19} \mathrm{~J}} \end{aligned}$
λ = 6.538 × 10⁷ m = 6.54 x 10⁷ m
= 654 nm
अतः उत्सर्जित विकिरण की देहली तरंगदैर्घ्य = 654 nm
(ख) $v_0=\frac{c}{\lambda_0}=\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{6.538 \times 10^{-7} \mathrm{~m}}$

= 4.588 × 10¹⁴ s^-1
= 4.59 × 10¹⁴ s^-1

(ग) 500nm ( 500 x 10 m) तरंगदैर्घ्य के विकिरण
वाले फोटॉन की ऊर्जा
$\mathrm{E}=\frac{h c}{\lambda}=\frac{6.626 \times 10^{-34} \mathrm{JS} \times 3 \times 10^8 \mathrm{~ms}^{-1}}{500 \times 10^{-9} \mathrm{~m}}$
E = 3.97 × 10^-19
निकले हुए फोटो इलेक्ट्रॉन की गतिज ऊर्जा (KE.) = hv - hvo
=(3.97 - 3.04) 10^-19 J
K.E. = 0.93 x 10^-19 J = 9.30 × 10^-20 J
K.E. = 1/2 mv²
अतः फोटो इलेक्ट्रॉन का वेग 
$\begin{aligned} (\mathrm{v}) & =\sqrt{\frac{2 \times \mathrm{K.E} .}{\mathrm{m}}} \\ & =\sqrt{\frac{2 \times 9.30 \times 10^{-20} \mathrm{~J}}{9.1 \times 10^{-31} \mathrm{~kg}}} \end{aligned}$
v = 4.52 x 10 ms^-1

प्रश्न 2.52. 
जब सोडियम धातु को विभिन्न तरंगदैयों के साथ विकीर्णित किया जाता है, तो निम्नलिखित परिणाम प्राप्त होते हैं:

Λ(nm)	500	450	400
V x 105 m s-1	2.55	4.35	5.20

देहली तरंगदैर्ध्य और प्लांक स्थिरांक की गणना कीजिए।
उत्तर:
माना देहली तरंगदैर्घ्य = 2g nm = 2 x 10⁹ m
h (v - Vo) = 1/2 mv²
hc $\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)$ = 1/2 mv²
मान रखने पर

समीकरण ( 2 ) में समीकरण (1) का भाग देने पर

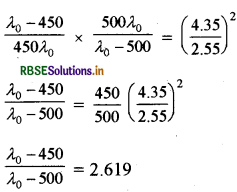
λ0 - λ450 = 2.619 λ0 - 1309.5
1.619 λ0 = 859.5.
λ0 = 530.88 = 530.9 nm
λ0 का मान समीकरण (3) में रखने पर
$\frac{h\left(3 \times 10^8\right)}{10^{-9}}\left(\frac{1}{400}-\frac{1}{530.9}\right)$ = 1/2(9.1 × 10^-31) (5.20 x 10⁵ )²
h (3 × 10¹⁷) $\left(\frac{530.9-400}{212360}\right)$ = 1/2(9.1 × 10^-31) × 27.04 × 10¹⁰.
h × 10³ × 18.4921 = 1⁄2(246.064 x 10^-21)
$h=\frac{123.032 \times 10^{-21}}{18.4921 \times 10^{13}}$
= 6.6532 × 10^-34 Js

प्रश्न 2.53. 
प्रकाश विद्युत प्रभाव प्रयोग में सिल्वर धातु फोटो इलेक्ट्रॉन का उत्सर्जन 0.35 V की वोल्टता द्वारा रोका जा सकता है। जब 256.7 nm के विकिरण का उपयोग किया जाता है, तो सिल्वर धातु के लिए कार्यफलन की गणना कीजिए।
उत्तर:
0.35 V की वोल्टता द्वारा फोटो इलेक्ट्रॉन के उत्सर्जन को रोका जा सकता है। अतः फोटो इलेक्ट्रॉन की गतिज ऊर्जा 0.35 V के बराबर होगी
K.E. = 0.35 V = 0.35 x 1.6 x 10^-19 J = 0.56 × 10^-19 J
E = hv = hc/λ
λ = 256.7 nm = 256.7 x 10 m
$=\frac{6.626 \times 10^{-34} \mathrm{Js} \times 3 \times 10^8 \mathrm{~ms}^{-1}}{256.7 \times 10^{-9} \mathrm{~m}}$
= 7.74 × 10^-19 J
विकिरण की ऊर्जा = कार्यफलन + फोटो इलेक्ट्रॉन की गतिज ऊर्जा
hv = Wo + K.E.
कार्यफलन Wo = hvKE.
कार्यफलन = 7.74 x 10^-19 J - 0.56 x 10^-19 J
= 7.74 - 0.56 (10^-19) J
=7.18 × 10^-19 J
कार्यफलन
$\frac{7.18 \times 10^{-19}}{1.6 \times 10^{-19}} \mathrm{ev}$
= 4.48 ev

प्रश्न 2.54. 
यदि 150 Pm तरंगदैर्घ्य का फोटॉन एक परमाणु से टकराता है और इसके अन्दर बँधा हुआ इलेक्ट्रॉन 1.5 x 10 ms^-1 वेग से बाहर निकलता है तो उस ऊर्जा की गणना कीजिए, जिससे यह नाभिक बँधा हुआ है।
उत्तर:
तरंगदैर्ध्य 2. = 150 Pm = 150 x 10^-12 m
फोटॉन की ऊर्जा (E) = hc/λ

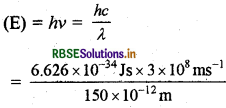
= 1.32 × 10^-15 J

उत्सर्जित इलेक्ट्रॉन की गतिज ऊर्जा (K.E.) = 1/2mv²
= 1/2 × 9.11 × 10^-31 × (1.5 x 10⁷ )²
= 1.025 x 10^-16 J 
= 0.1025 x 10^-15 J 
बन्धन ऊर्जा = आपतित फोटॉन की ऊर्जा - गतिज ऊर्जा (K.E.)
= 1.32 × 10^-15 J - 0.1025 x 10^-15 J
बन्धन ऊर्जा = 1.217 × 10^-15 J
$=\frac{1.217 \times 10^{-15}}{1.6 \times 10^{-19}}$
= 7.6 × 10³ eV.

प्रश्न 2.55. 
पाशन आरम्भ होता है। कक्ष 10¹⁵ (Hz) श्रेणी का उत्सर्जन संक्रमण " कक्ष से = 3 में खत्म होता है तथा इसे 3.29 x 10¹⁵(HZ) से दर्शाया जा सकता है। यदि संक्रमण 1285 nm पर प्रेक्षित होता है, तो " के मान की गणना कीजिए तथा स्पेक्ट्रम का क्षेत्र भी बताइए।
उत्तर:
आवृत्ति (v) = C/λ (A = 1285 nm = 1285 × 10^-9m)

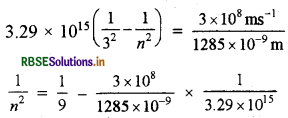
1/n2 = 0.111 - 0.071
1/n2 = 0.04 = 1/25
n2 = 25, n = 5
थे विकिरण अवरक्त क्षेत्र में होते हैं।

प्रश्न 2.56. 
उस उत्सर्जन संक्रमण के तरंगदैर्ध्य की गणना कीजिए, जो 1.3225 nm त्रिज्या वाले कक्ष से आरम्भ और 211.6 Pm पर समाप्त होता है। इस संक्रमण की श्रेणी का नाम और स्पेक्ट्रम का क्षेत्र भी बताइए।
उत्तर:
वें कक्ष की त्रिज्या = $\frac{0.529 n^2}{Z}$
r2 = 1.3225 nm = 1322.5 Pm = 52.9 n₂² Pm
$\mathrm{n}_2^2=\frac{1322.5}{52.9}=25$
n2 = 5
r1 = 211.5 Pm = 52.9 n₁² Pm.
$\mathrm{n}_1^2=\frac{211.6}{52.9}=4$
n1 = 2
चूँकि n1 = 2, 12 = 5 अतः यह संक्रमण बामर श्रेणी से सम्बन्धित है तथा यह दृश्य क्षेत्र में होता है।
v = 1.097 × 10⁷ m^-1 $\left(\frac{1}{n_1{ }^2}-\frac{1}{n_2^2}\right)$
v = 1.097 × 10⁷ $\left(\frac{1}{2^2}-\frac{1}{5^2}\right)$
V = 1.097 × 21/100 × 10⁷ m^-1
$\lambda=\frac{1}{\bar{v}}=\frac{100}{1.097 \times 10^7 \times 21} \mathrm{~m}$
= 434 × 10^-9 m = 434nm

प्रश्न 2.57. 
दे ब्रॉग्ली द्वारा प्रतिपादित द्रव्य के दोहरे व्यवहार से इलेक्ट्रॉन सूक्ष्मदर्शी की खोज हुई, जिसे जैव अणुओं और अन्य प्रकार के पदार्थों के अति आवर्धित प्रतिबिम्ब के लिए उपयोग में लाया जाता है। इस सूक्ष्मदर्शी में यदि इलेक्ट्रॉन का वेग 1.6 x 10⁶ ms^-1 है, तो इस इलेक्ट्रॉन से सम्बन्धित दे ब्रॉग्ली तरंगदैर्घ्य की गणना कीजिए।
उत्तर:
वेग, v = 1.6 x 10⁶ms^-1 इलेक्ट्रॉन का द्रव्यमान
m = 9.1 × 10^-31 kg
अतः तरंगदैर्ध्य
$=\frac{6.626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1}}{9.1 \times 10^{-31} \mathrm{~kg} \times 1.6 \times 10^6 \mathrm{~ms}^{-1}}$
λ = 4.55 × 10^-10 m
λ = 455Pm.

प्रश्न 2.58. 
इलेक्ट्रॉन विवर्तन के समान न्यूट्रॉन विवर्तन सूक्ष्मदर्शी को अणुओं की संरचना के निर्धारण में प्रयुक्त किया जाता है। यदि यहाँ 800 Pm की तरंगदैर्घ्य ली जाए तो न्यूट्रॉन से सम्बन्धित अभिलाक्षणिक वेग की गणना कीजिए।
उत्तर:
तरंगदैर्घ्य (A) = 800 Pm = 800 x 10^-12 m
= 8 x 10^-10 m
न्यूट्रॉन का द्रव्यमान
= 1.675 × 10^-27 kg
$=\frac{6.626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1}}{9.1 \times 10^{-31} \mathrm{~kg} \times 1.6 \times 10^6 \mathrm{~ms}^{-1}}$
λ = 494.47 ms^-1
λ = 494.5ms^-1

प्रश्न 2.59. 
यदि बोर के प्रथम कक्ष में इलेक्ट्रॉन का वेग है, तो इससे सम्बन्धित दे ब्रॉग्ली तरंगदैर्घ्य की 2.19 × 10^-6 ms^-1 गणना कीजिए।
उत्तर:
वेग v = 2.19 × 10⁶ms^-1
द्रव्यमान m = 9.1 x 10^-31 kg
तरंगदैर्घ्य 
$\lambda=\frac{h}{m \mathrm{v}}=\frac{6.626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1}}{9.1 \times 10^{-31} \mathrm{~kg} \times 2.19 \times 10^6 \mathrm{~ms}^{-1}}$
λ = 3.32 × 10^-10m = 332Pm

प्रश्न 2.60. 
एक प्रोटॉन, जो 1000 V के विभवान्तर से गति कर रहा है, से सम्बन्धित वेग 4.37 10⁵ms है। यदि 0.1 kg द्रव्यमान की हॉकी की गेंद इस वेग से गतिमान है तो इससे सम्बन्धित तरंगदैर्घ्य की गणना कीजिए।
उत्तर:
गेंद का वेग v 4.37 10⁵ ms^-1 तथा द्रव्यमान,
m = 0.1 kg
तरंगदैर्ध्य (A) =
$\frac{h}{m \mathrm{v}}=\frac{6.626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1}}{0.1 \mathrm{~kg} \times 4.37 \times 10^5 \mathrm{~ms}^{-1}}$
λ = 1.516 × 10³⁸ m

प्रश्न 2.61. 
यदि एक इलेक्ट्रॉन की स्थिति को ± 0.002nm की शुद्धता से मापा जाता है, तो इलेक्ट्रॉन के संवेग में अनिश्चितता की गणना कीजिए। यदि इलेक्ट्रॉन का संवेग $\frac{h}{4 \pi_m \times 0.05 n m}$ तो क्या इस मान को निकालने में कोई कठिनाई होगी?
उत्तर:
स्थिति में अनिश्चितता, ∆x = 0.002nm = 2 × 10^-3 = 2 x 10^-12 m तथा 
h = 6.626 × 10^-34 kgm² s^-1  
हाइजेनबर्ग के अनिश्चितता के सिद्धान्त के अनुसार
संवेग की अनिश्चितता = $\frac{h}{4 \pi \Delta x}$ 
$=\frac{6.626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1}}{4 \times 3.14 \times 2 \times 10^{-12} \mathrm{~m}}$
= 2.6377 × 10^-23 kg ms^-1
= 2.638 × 10^-23 kg ms^-1
वास्तविक संवेग
$\begin{aligned} & =\frac{h}{4 \pi \times 0.05 \mathrm{~nm}} \\ & =\frac{6.626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1}}{4 \times 3.14 \times 5 \times 10^{-11} \mathrm{~m}} \end{aligned}$
(0.05 nm = 5 × 10^-11m) = 1.055 × 10^-24 kg ms^-1
यह वास्तविक संवेग नहीं होगा अतः इसे परिभाषित नहीं किया जा सकता क्योंकि संवेग का सही मान संवेग की अनिश्चितता से भी कम है।

प्रश्न 2.62. 
छ: इलेक्ट्रॉनों की क्वान्टम संख्याएँ नीचे दी गई हैं। इन्हें ऊर्जा के बढ़ते क्रम में व्यवस्थित कीजिए। क्या इनमें से किसी की ऊर्जा समान है?

n  = 4	l = 2	m1 = -2	ms = -1/2
n = 3	l = 2	m1 = 1	ms = + 1/2
n = 4	l = 1	m1 = 0	ms = + 1/2
n = 3	l = 2	m1 = -2	ms = -1/2
n = 3	l = 1	m1 = -1	ms = + 1/2
n = 4	l = 1	m1 = 0	ms = -1/2

उत्तर:
बोर बरी नियम ( + / नियम) के अनुसार इन इलेक्ट्रॉनों की ऊर्जा का बढ़ता क्रम निम्न प्रकार होगा - 5 < 2 = 4 < 6 = 3 < 1 तथा इनमें से इलेक्ट्रॉन 2, 4 एवं 3, 6 की ऊर्जा समान है क्योंकि इनसे सम्बन्धित उपकोश निम्न प्रकार हैं-
(1) 4d
(2) 3d
(3) 4p
(4) 3d
(5) 3p
(6) 4p

प्रश्न 2.63. 
ब्रोमीन परमाणु में 35 इलेक्ट्रॉन होते हैं। इसके 2p कक्षक में छ: इलेक्ट्रॉन, 3p कक्षक में छ: इलेक्ट्रॉन तथा 4p कक्षक में पाँच इलेक्ट्रॉन होते हैं। इनमें से कौनसा इलेक्ट्रॉन न्यूनतम प्रभावी नाभिकीय आवेश अनुभव करता है?
उत्तर:
किसी परमाणु में जैसे-जैसे नाभिक से दूर जाते हैं, प्रभावी नाभिकीय आवेश कम होता जाता है। 4p कक्षक नाभिक से अधिकतम दूरी पर स्थित है क्योंकि का मान उच्चतम है अतः 4p कक्षक के इलेक्ट्रॉन न्यूनतम प्रभावी नाभिकीय आवेश का अनुभव करेंगे।

प्रश्न 2.64. 
निम्नलिखित में से कौनसा कक्षक उच्च प्रभावी नाभिकीय आवेश अनुभव करेगा?
(i) 2s और 3s (ii) 4d और 4f तथा (iii) 3d और 3p 
उत्तर:
(i) 2s (ii) 4d (iii) 3p
क्योंकि ( n + 1) नियम के अनुसार जिस कक्षक का n + l का मान कम है वह नाभिक के अधिक समीप होगा अतः उच्च प्रभावी नाभिकीय आवेश का अनुभव करेगा।

प्रश्न 2.65. 
Al तथा Si में 3p कक्षक में अयुग्मित इलेक्ट्रॉन होते हैं। कौनसा इलेक्ट्रॉन नाभिक से अधिक प्रभावी नाभिकीय आवेश अनुभव करेगा?
उत्तर:

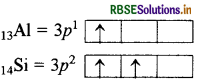
Si में नाभिकीय आवेश (14) Al (13) से अधिक होता है अतः इसके अयुग्मित इलेक्ट्रॉन अधिक प्रभावी नाभिकीय आवेश अनुभव करेंगे। 

प्रश्न 2.66. 
इनमें अयुग्मित इलेक्ट्रॉनों की संख्या बताइए।
(क) P
(घ) Fe
(ख) Si
(ङ) Kr
(ग) Cr
उत्तर:
(क) 15 P = 1s², 2s², 2p⁶, 3s², 3px¹,  3py¹,
3pz¹ (अयुग्मित इलेक्ट्रॉन = 3)

(ख) 14Si = 1s², 2s², 2p⁶, 3s², 3px¹,
3py¹ (अयुग्मित इलेक्ट्रॉन = 2)

(ग) 24 Cr = 1s², 2s², 2p⁶, 3s², 3p⁶, 3d⁵, 4s¹

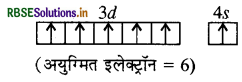
(घ) 26Fe = 1s², 2s², 2p¹, 3s², 3p⁶, 3d⁶, 4s²

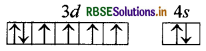
(अयुग्मित इलेक्ट्रॉन = 4)

(ङ) 36Kr = 1s², 2s², 2p⁶, 3s², 3p⁶, 3d¹⁰, 4s², 4p⁶
(अयुग्मित इलेक्ट्रॉन शून्य )

प्रश्न 2.67. 
(क)  n = 4 से संबंधित कितने उपकोश हैं? 
(ख) उन उपकोशों में कितने इलेक्ट्रॉन उपस्थित होंगे, जिनके
लिए m = - 1/2 एवं n 4 है।
उत्तर:
(क) n = 4 के लिए, 1 = 0, 1, 2, 3

1 = 0	उपकोश
1	4s
2	4p
3	4d

अतः n = 4 के लिए चार उपकोश (4s, 4p, 4d तथा 4f) होंगे।
(ख) n = 4 के लिए कक्षकों की संख्या = 4s² = 16 तथा प्रत्येक कक्षक में उपस्थित एक इलेक्ट्रॉन के लिए m, = -1⁄2 होगा। अतः = 4 वाले उपकोशों में ms = -1/2 वाले 16 इलेक्ट्रॉन होंगे।