RBSE Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry

Rajasthan Board RBSE Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry Textbook Exercise Questions and Answers.

RBSE Class 11 Chemistry Solutions Chapter 1 Some Basic Concepts of Chemistry

RBSE Class 11 Chemistry Some Basic Concepts of Chemistry InText Questions and Answers

Question 1.1. 
Calculate the molecular mass of glucose (C₆H₁₂O₆) molecule.
SolutIon: 
Atomic mass of C = 12.011 u
Atomic mass of H = 1.008 u
Atomic mass’of O = 16.00 u
Molecular mass of C₆H₁₂O₆
= 6 x (12.011 u) + 12 x (1.008 u) + 6 x (1600 u)
= 72.066 u + 12.096 u + 9600 u
= 180.162 u

Question 1.2. 
A compound contains 4.07% hydrogen, 24.27% carbon and 71.65% chlorine. Its molar mass is 98.96 g. What are its empirical and molecular fomula?
Solution: 

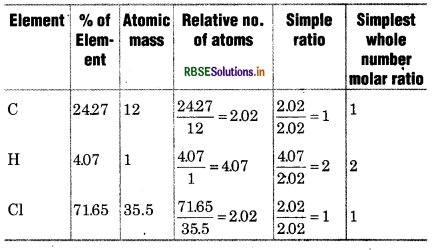
∴ Empirical formula of compound = C₁H₂Cl₁
= CH₂ Cl
Empirical formula mass = 12 x 2 (1) + 35.5
= 49.5
Moleular mass = 98.96

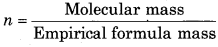
= \(\frac{98.96}{49.5}\) = 2

Molecular formula = n x Empirical formula
= 2 x CH₂Cl
= C₂H₄Cl₂

 

Question 1.3. 
Calculate the amount of water (g) produced by the combustion of 16 g of methane.
Solution: 
The balanced equation for the combustion of
methane (CH₄) is 
CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O(g)
16g of CH₄ = lmole of CH₄
∵1 mol of CH₄(g) gives 2 mol of H₂O(g).
2 mol of water(H₂O) = 2 x (+16)
= 2 x 18 = 36g
1 mol of H₂O 18g H₂Os =  \(\frac{18 \mathrm{~g} \mathrm{H}_2 \mathrm{O}}{1 \mathrm{~mol} \mathrm{H}_2 \mathrm{O}}\) = 1
∴ 2 moles H₂O x \(\frac{18 \mathrm{~g} \mathrm{H}_2 \mathrm{O}}{1 \mathrm{~mol} \mathrm{H}_2 \mathrm{O}}\) = 2 x 18gH₂O = 36gH₂O

Question 14. 
How many moles of methane are required to produce 22 g CO₂ after combustion?
Solution:
The chemical reection for combustion of methane is:

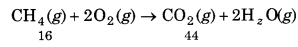
∵ 44g CO₂ (g) is obtained from 16g CH₄(g)
[1 mol CO₂(g) is obtained from 1 mol of CH₄(g)]
Number of moles of CO₂(g)
= 22gCO₂(g) x \(\frac{1 \mathrm{molCO}_2(g)}{44 \mathrm{~g} \mathrm{CO}_2(g)}\)
= 0.5 mol CO₂(g)
∴ 0.5 mol CO₂ (g) would be obtained from 0.5 mol CH₄(g)
Hence, 0.5 moI of meihane is required to porduce 22g of CO₂(g) after combustion.

Question 1.5. 
50.0 kg of N₂(g) and 10.0 kg of H₂(g) are mixed to produce NH₃(g). Celculate the amount of NH₃ formed. Identify the limiting reagent in the production of NH₃ in this reaction.
Solution: 
A balanced equetion is 

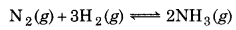
Number of moles of N₂
= 5OkgN₂ x \(\frac{1000 \mathrm{~g} \mathrm{~N}_2}{1 \mathrm{~kg} \mathrm{~N} \mathrm{~N}_2} \times \frac{1 \mathrm{~mol} \mathrm{~N} \mathrm{~N}_2}{28 \mathrm{~g} \mathrm{~N}_2}\)
= 1786 x 10² mol

Number of moles of H₂
= 10kgH₂ x \(\frac{1000 \mathrm{~g} \mathrm{H}_2}{1 \mathrm{~kg} \mathrm{H}_2} \times \frac{1 \mathrm{~mol} \mathrm{H}_2}{2.016 \mathrm{~g} \mathrm{H}_2}\)
= 496 x 10³ mol
∵1 mol N₂(g) requires 3 moles H₂(g) for the reaction
∴ For 17.86 x 10² mol of N₂,
No. of moles of H₂(g)
= 1786 x 10²molN₂ x im
= 536 x  10³ molH₂
But we have only 4.96 x 10³ mol H₂. Therefore. dihydrogen is the limiting reagent in this case. Therefore, NH₃(g) would be obtained only from that
amount of available dihydrogen i.e. 4.6 x  10³ mol
∵ 3 mol H₂ (g) gives 2 mol NH₃ (g)
∴ 4.96 x 10³ mol H₂(g) will give
= 4.96 x 10³ mol H₂(g) x \(\frac{3 \mathrm{~mol} \mathrm{H}_2(g)}{1 \mathrm{~mol} \mathrm{~N}_2(g)}\)
= 3.30 x 10³ mol NH₃(g)
lmolNH₃(g) = 17.OgNH₃(g)
3.30 x 10 mol NH₃(g) x \(\frac{17.0 \mathrm{~g} \mathrm{NH}_3(g)}{1 \mathrm{molNH}_3(g)}\)
= 3.30 x 10³ x 17g NH₃(g)
= 56.1 x 10³g NH₃(.g)
= 56.1 kg NH₃(g)

Question 1.6. 
A solution is prepared by adding 2 g of a substance ‘A’ to 18 g of water, calculate the mass percent of the solute.
SolutIon: 
Mass of substance ‘A’ =2 g
Mass of water = 18g

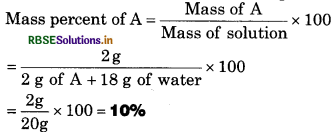
Question 1.7. 
Calculate the molarity of NaOH in the solution prepared by dissolving its 4g in enough water to form 250 mL of the solution.
SolutIon: 
Mass of NaOH = 4g
Molar mass of NaOH = 23 + 16 +1 =40
Volume of solution = 250 mL
Molarity = ?

Question 1.8. 
The density of 3 M solution of NaCl is 1.25 g mL¹. Calculete the molality of the solution.
Solution: 
M = 3 mol L’
Molar mass of NaCI = 23 + 35.5 = 58.5
Mas8 of NaC1 in iL solution = 3 x 58.5 = 175.5 g
Mass of 1 L solution = 1000 x 125 =  1250 g
(∵Mass = volume x density)
Mass of water in solution = 1250 - 175.5
= 10745 g

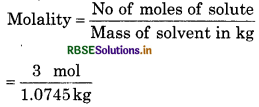
= 279 m

RBSE Class 11 Chemistry Some Basic Concepts of Chemistry Textbook Questions and Answers

Question 1.1. 
Calculate the molar mass of the following:
(i) H₂O 
(ii) CO₂ 
(iii) CH₄
SolutIon: 
(i) Molar mass of H₂O
= 2 x (1.008u) + 16.00 u
= 2.016 u + 16.00 u
= 18.02 u

(ii) Molar mass of CO₂
= 12.011 u + 2 x (16.00 u)
= 12.011 u + 32.00 u
= 44.O1u

(iii) Molar mass of CH₄
=12.011 u + 4 x (1.008 u)
= 12.011 u + 4.032 u
= 16.0434 u

Question 1.2. 
Calculate the mass percent of different elements present n sodium sulphate (Na₂SO₄).
Solution: 
Molar mass of Na₂SO₄
= 2 x (23.00 u) + 32.066 u + 4 x (16.00 u)
= 46.00 u + 32.066 u + 6400u
= 142.066 u

Question 1.3. 
Determine the empirical formula of an oxide of iron, vhich has 96.9% iron and 30.1% dioxygen mass.
Solution: 

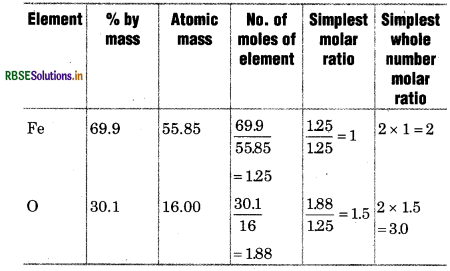
∴ Empirical formula of oxide of iron.
= Fe₂O₃.

Question 1.4. 
Calculate the amount of carbon dioxide that could be produced when:
(1) 1 mole of carbon is burnt in air.
(ii) 1 mole of carbon is burnt in 16g of dioxygen.
(iii) 2 molar of carbon are burnt in 16 g of dioxygen.
SolutIon: 
Balanced equation is:

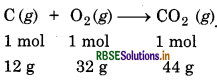
(i) From the above reaction
1 mol of carbon on burning in air produces
1 mol of CO₂ i.e. 44g of CO₂

(ii) When 1 mo1 of carbon is burnt in 16 g of dioxygen then 22g of CO will be produced. In this case, dioxygen
is a limiting reagent. 
∵32 g of O₂ gives 44 g of CO₂
∵ 16 g of O₂ will give = \(\frac{44}{32} \times 16\)
= 22 g of CO₂

(iii) As dioxygen is a limiting reagent, therefore, 16 g of dioxygen can react only with 0.5 mol of carbon to produce
22 of CO₂.

Question 1.5. 
Calculete the mass of sodium acetate (CH₃COONa) required to make 500 mL of 0.375 molar aqueous solution. Molar mass of sodium acetate is 82.0245 g mo1^-1.
Solution: 
Volume of solution 500 mL
Molarity = 0.375 M
Molar mass of sodium acetate (M) = 82.0245 g mol^-1

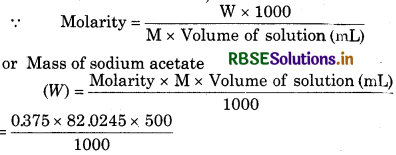
= 15.379 g

Question 1.6. 
Calculate the concentration of nitric acid in moles per litre in a sample which has a density l.41g mU’ and the mass percent of nitric acid in it being 69%.
Solution: 
Density of solution = 1.41 g mL^-1
Mass % of HNO₃ = 69%
69% of HNO₃ means loo g of its solution contains 69 g HNO₃
∴ Mass of solution =100 g
Mass (w) of HNO₃ = 69 g
Moler mass (M) of HNO₃ = L008 + 14.007 + 3 x 16.00
= 63.015g mol^-1

= 15.439 M

Question 1.7. 
How much copper can be obtained from loo g of copper sulphate (CuSO₄)?
Solution: 
Mass of CuSO₄ 100 g
Molar mass of CuSO₄ = 63.5 + 32 + 4 x 16
= 159.5g mol^-1
1 mol of CuSO₄ contains 1 mol of Cu.
∵159.5 g of CuSO₄ forms = 63.5 g of Cu.
∵ 100 g of CuSO₄ will form = \(\frac{63.5 \mathrm{~g}}{159.5 \mathrm{~g}}\)
= 39.81 g of Cu.

Question 1.8. 
Determine the molecular formula of an oxide of iron, in which the mass percent of iron and oxygen are 69.9 and 30.1 respectively.
Solution: 
∴ Empirical formula of oxide of iron = Fe₂O₃
Empirical formula mass = 2 x 55.85 + 3 x 16.00
= 159.1 g mol^-1
\(=\frac{159.8}{159.7}=1\)
Molecular formula = n x Empirical formula
= n x Fe₂O₃
= 1 x Fe₂O₃
= Fe₂O₃

Question 1.9. 
Calculate the atomið mass (average) of chlorine using the following data:

%Natural	Abundence	Molar mass
35Cl	75.77	34.9689
35Cl	24.33	36.9659

Solution:
Fractional abundance òf ³⁵Cl  
\(=\frac{75.77}{100}\) = 0.7577
Molar mass of ³⁵Cl = 34.9689
Molar mass  Cl = 36.9659
∵ Average atomic mass of chlorine
= Fractional abundance òf ³⁵Cl x Molar mass of ³⁵C1 +
Fracttonal abundance of  Cl x Molar mass  Cl
= 0.7 577 x 34.9689 + 02423 x 36.9659
= 26.4959 + 8.9568
= 35.4527 amu

Question 1.10. 
In three moles of ethane (C₂H₆), calculate the following:
(i) Number of moles of carbon atoms
(ii) Number of moles of hydrogen atoms
(iii) Number of molecules of ethane
Solution: 
(i) ∵ 1 mol of ethane (C₂ H₆ )contain 2 mol of carbon atoms.
∴ 3 mol of C₂H₆ will contain = 2 x 3 = 6 mol of carbon atoms

(ii) ∵ 1 mol of ethane (C₂ H₆ )contains 6 mol of hydrogen atoms.
∴ 3 mol of C₂H₆ will contain = 6 x 3 = 18 mol of hydrogen atons.

(iii) ∵ 1 mol of ethane (C₂ H₆) contains 6.022 x 10²³ molecules of ethane.
∴3 moles of C₂H₆ will contain
= 3 x 6.022 x 10²³
= 18.066 x 10²³ molecules
= 1.8066 x 10 molecules

Question 1.11. 
What is the concentration of sugar (C₁₂H₂₂O₁₁) in mol L^-1 if its 20 g are dissolved in enough water to make a final volume up to 2L?
Solution: 
Mass of C₁₂H₂₂O₁₁(w) = 20 g
Volume of solution = 2L
Molar mass ofC₁₂H₂₂O₁₁
M = 12 x 12.01 + 22 x 1.008 x 11 x 16.0O
= 34229

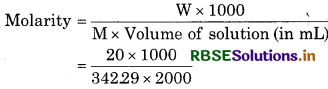
= 0.029 M

Question 1.12. 
f the density of methanol is 0.793 kg L’, what is its volume needed for making 2.5 L
of its 0.25 M solution?
Solution: Denstiy of methanol = 0.793 kg L’
= 0.793 X 10³g L^-1
Molar mass of methanol (CH₃OH)
= 1 x 12.01 + 4 x 1.008 + 16.00
= 32.042 

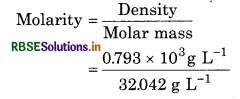
= 24.749 molL¹
∴ Initial molarity (M₁) = 24.749 M
Initial volume (V₁) = ?
Final molarity (M₂) = 025 M
Final volume (V₂) = 2.5 L
∵ M₁V₁ = M₂V₂
24.749 x V₁ = 0.25 x 2.5
\(V_1=\frac{0.25 \times 2.5}{24.749}\)
= 25.25 ML

Question 1.13. 
Pressure is determined as force per unit area of the surface. The SI unit of pressure, pascal is as shown below:
1Pa = lNm^_-2
If mass of air at sea level is 1034 g cm², calculate the pressure in pascal.
Solution: 
Mass of air at sea level =1034 g cm^-2
As we know that,
Acceleration due to gravity
g = 9.8 ms^-2
Pressure of air = \(\frac{1034}{1000}\) x 9.8 x 100 x 100
= 1.012322 x 10⁵ pa

Question 1.14. 
What is the SI unit of mass? How is it defined?
Solution: 
The S.J unit of mass is kilogram (kg). It is defined as the amount of matter present in a substance.

Question 1.15. 
Match the following prefixes with their multiples:

Prefixes	Multiples
Micro	106
deca	109
mega	10-6
giga	10-15
femio	10

Solution: 

Prefixes	Multiples
Micro	106
deca	109
mega	10-6
giga	10-15
femio	10

Question 1.16
What do you mean by significant figures?
Solution: 
The total number of digits in a number, which are meaningful with certainty are called significant figures. e.g 3.016 has four significant figures.

Question 1.17. 
A sample of drinking water was found to be severely contaminated with chloroform, CHCl₃, supposed to be carcinogenic in nature.The level of contamination was 15 ppm (by mass).
(i) Express this in percent by mass.
(ii) Determine the molality of chloroform in the water sample.
Solution: 
(i) 15 ppm means 15 parts in 10⁶ parts
Mass % = \(\frac{15 \times 100}{10^6}\) = 1.5 x 10³%

(ii) Molar mass of CHCl₃ (M)
= 12.01 + 1.008 + 3 x 35.5
= 119.36gmol^-1
1.5 x 10% means 1.5 x 10³g CHCl₃ is found in loo g sample.

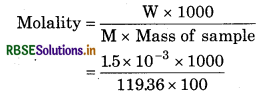
= 1.26 x 10⁴m

Question 1.18. 
Express the following in the scientific notation:
1. 0.0048
2. 234,000
3. 80088
4. 500.0
5. 6.0012
Solution: 

1. 0.0048 = 48 × 10^-3
2. 234,000 = 234 x 10⁵
3. 80088 = 008 x 10³
4. 5000 = 500 x 10²
5. 6.0012 = 6.0012

Question 1.19. 
How many significant figures are present in the following?

(i) 0.0025

(ii) 208

(iii) 5005

(iv) 126,000

(v) 500.0

(vi) 2.0034

Solution: 

Number	Significant figures
(i) 0.0025	2
(ii) 208	3
(iii) 5005	4
(iv) 126,000	3
(v) 500.0	4
(vi) 2.0034	5

Question 1.20. 
Round up the following upto three significant figures:
1. 34.216
2. 10.4107
3. 0.04597
4. 2808
Solution: 

1. 34.216 = 34.2
2. 10.4107 = 10.4
3. 0.04597 0.0460
4. 2808 = 2810 or 2810 x 10³

Question 1.21. 
The following data are obtained when dinitrogen and dioxygen react together to form different compounds:

Mass of dioxygen	Mass of dinitrogen
(i) 14 g	16g
(ii) 14 g	32g
(iii) 28 g	32g
(iv) 28 g	80g

(a) Which law of chemical combination is obeyed by the above experimental data?
(b) Fill in the blanks in the following conversions:
(i) 1 km = ................ mm = ............... pm
(ii) 1mg = ................ kg ............... ng
(iii) 1 mL.=................ L = ................ dm3
Solution: 

Mass of dioxygen	Mass of dinitrogen
(i) 14 g	16g
(ii) 14 g	32g
(iii) 28 g	32g
(iv) 28 g	80g

The above experimental data obey law of multiple proprotions.
According to this law," when two elements combine to form more than one compound, then the masses of one of the elements which combine with fixed mass of other element are in the simple whole number ratio,"
(b) (i) 1 km = 10 mm = 10¹⁵ pm
(ii) 1 mg = 10 kg = 10⁶ ng
(iii) 1 ml = 10^-3L= 10^-3 dm³

Question 1.22. 
If the speed of light is 3.0 x 10 ms1, calculate the distance covered by light in 2.00 ns.
Solution: 
Speed of light = 3.0 x 10 ms^-1
Time = 2.00 ns
= 2 × 10 9 8
∵ Distance = speed x time
= 30 x 10 ms 1 x 2 x 10^-9 s
= 60 × 10^-1 m
= 0.60 m

Question 1.23. 
In a reaction,
A + B₂ → AB₂
Identify the limiting reagent, if any, in the following reaction mixtures:
(i) 300 atoms of A + 200 molecules of B
(ii) 2 mol A + 3 mol B
(iii) 100 atoms of A + 100 molecules of B
(iv) 5 mol A + 2.5 mol B
(v) 2.5 mol A + 5 mol B
Solution: 
A + B₂ → AB₂
(i) In above rection,
∵1 atom of A reacts with 1 molecule of B.
 ∴200 atoms of A will react with 200 moleculers of B. Hence, in this case, 'B' is the limiting reagent, as 'A' is in excess.
 
(ii) In above reaction,
∵1 mol of A reacts with 1 mol of B
 ∴2 mol of A will react with 2 mol of B.
Hence, in this case, 'A' is the limiting reagent, as 'B' is in. excess.

(iii) In above reaction,
∵1 atom of A reacts with 1 molecule of B.
 ∴100 atoms of A will react with 100 molecules of B. Hence, in this case there is no limiting reagent.

(iv) In above reaction,
∵1 mol of 'A' reacts with 1 mol of B
 ∴2.5 mol of 'A' will react with 2.5 mol of B.
Hence, in this case, 'B' is limiting reagent, as 'A' is in excess.

(v) In above reaction,
∵1 mol of 'A' reacts with 1 mol of 'B'.
 ∴2.5 mol of 'A' will reacts with 2.5 mol of 'B'.
Hence, In this case, 'A' is limiting reagent, as, 'B' is in excess.

Question 1.24. 
Dinitrogen and dihydrogen react with each other to produce ammonia according to the following chemical equation:
Ng (g) + H₂(g) → 2 NH₃ (g)
(i) Calculate the mass of ammonia produced if 2.00 10 g dinitrogen reacts with 1.00 x 10³ g of dihydrogen.
(ii) Will any of the two reactants remain unreacted?
(iii) If yes, which one and what would be its mass?
Solution: 

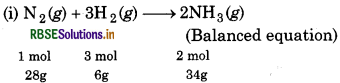
∵ 28g of N₂ react with 6g of Hg
∴ 1g of N reacts with g of H ₂
∴ 2000g of Ng will react with = \(\frac{6}{28} \times 2000\)
= 428.57 g of H ₂
Since H₂ is in excess, so, N₂ is the limiting reagent. N₂ limits the amount of ammonia produced.
∵ 28g of N₂ produces 34g of NH₃.
∴ 2000g of N₂ will produce = \(\frac{34}{28}\) x 2000
= 2428.57 g of NH₃

(ii) Hydrogen (H₂) will remain unreacted because it is in excess.

(iii) Amount of H₂ remain unreacted
= 1000 - 428.57 = 571.43 g

Question 1.25. 
How are 0.50 mol Na₂CO₃ and 0.50 M Na₂CO₃ different?
Solution: 
Molar mass of Na₂CO₃ = 2 x 23 + 12 × 3 × 16 = 10⁶ g mol^-1
1 mol of Na₂CO₃ means 10⁶ g of Na₂CO₃ 
0.50 mol of Na₂CO₃ means = 0.50 x 10⁶ g
= 53 g of Na₂CO₃ 
0.50 M Na₂CO₃ means 0.50 mol i.e., 53g of Na₂CO₃ are present in 1 litre of the solution.

Question 1.26. 
If 10 volumes of dihydrogen gas reacts with five volumes of dioxygen gas, how many volumes of water vapour would be produced?
Solution:
The balanced equation is,
2H₂(g) + O₂(g) → 2H₂O(g)
Hence, the above equation shows that 10 volumes of water vapour[ (H₂O(g)] will be produced.

Question 1.27. 
Convert the following into basic units:
(i) 28.7 pm 
(ii) 15.15 pm 
(iii) 25365 mg 1pm = 10^-12 m
Solution: 
(i) ∵ 1 pm  = 10^-12 m
∴ 28.7 pm = 287 x 10^-12 m

(ii) 15.15 pm = 15.15 x 10^-12 m
= 15.15 x 10^-11 m

(iii) ∵ 1mg = 10^-6 Kg
∴ 25365 mg = 253265 x 10^-6 kg
= 2.5365 x 10^-2 kg

Question 1.28. 
Which one of the following will have the largest number of atoms?
(i) 1g Au(s)
(ii) 1g Na(s)
(iii) 1g Li(s)
(iv) 1g of Cl₂(g)
Solution: 
(i) Atomic mass of Au = 197
 ∴ Number of atoms in 1 g Au(s) = \(\frac{1}{197}\) x 6.022 × 10²⁸
= 3.057 x 10²¹ atoms

(ii) Atomic mass of Na = 23 
 ∴ Number of atoms in 1g Na(s) = \(\frac{1}{23}\) x 6.022 x 10²³
= 2.618 x 10²² atoms

(iii) Atomic mass of Li = 7
 ∴ Number of atoms in 1 g Li(s)
= \(\frac{1}{7}\) x 6022 × 10²³
= 8.6042 × 10²² atoms

(iv) Molar mass of Cl2 = 2 x 35.5 = 71 Number of atoms in 1g of Cl₂ (g)
= \(\frac{1}{71}\) × 6022 × 10²³
= 8.48 x 10²¹ atoms
Therefore, 1g of Li(s) will have the largest number of atoms.

Question 1.29. 
Calculate the molarity of a solution of ethanol in water, in which the mole fraction of ethanol is 0.040 (assume the density of water to be one).
Solution: 
Molarity means number of moles of solute in one litre of solution.
1L of ethanol = 1 L of water
Number of moles of H₂O in 1 litre water
= \(\frac{1000 \mathrm{~g}}{18}\)
= 55.55 mol

For a binary solution
X1 + X2 = 1
Хн₂о + Хс₂н₅он = 1
 ∴Хн₂O = 1 - Хс₂н₅он
= 1 - 0.040
= 0.96
\(\begin{aligned} X_{\mathrm{H}_2 \mathrm{O}} & =\frac{n_{\mathrm{H}_2 \mathrm{O}}}{n_{\mathrm{H}_2 \mathrm{O}}+n_{\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}}} \\ 0.96 & =\frac{55.55}{55.55+n_{\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}}} \end{aligned}\)

or 53.328 + 0.96 nc₂H₂OH = 55.55
or
0.96 nc₂H₂OH = 55.55 - 53.328
= 2.222
\(n_{\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}}=\frac{2.222}{0.96}\)
= 2.3145
Molarity = 2.3145 mol L^-1

Question 1.30. 
What will be the mass of one 12C atom in g? 
Solution : 
1 mole of 12 C atoms = 6.022 x 10²³
= 12 g of carbon
∵ 6022 x 10²³ atoms of 12 C have mass = 12 g
 ∴ 1 atom of 12 C will have mass
= \(\frac{12}{6.022 \times 10^{23}} g\)
= 1.9927 x 10^-23 g atoms

Question 1.31. 
How many significant figures should be present in the answer of the following calculation?
\(\text { (i) } \frac{0.02856 \times 298.15 \times 0.112}{0.5785}\)
(ii) 5 x 5.364
(iii) 0.0125 + 0.7864 + 0.0215
Solution: 

= 1648511
= 1.65
It is due to the fact that 0.112 has only three significant figures, so, final result should have three significant figures.

(ii) 5 × 5364 = 26.82
26.82 should have 4 significant figures.

(iii) 0.0125 + 0.7864 + 00215
= 0.8204
= 0.820
It is due to the fact that 0.0215 or 0.0125 has three significant figures, so, final result should have only three significant figures.

Question 1.32. 
Use the data given in the following table to calculate the molar mass of naturally occurring argon isotopes:

Istope	Isotopic Molar mass	Abudance
36Ar	35.96755 g mol-1	0.377%
38Ar	37.96272 g mol-1	0.063%
40Ar	39.9642 g mol-1	99.600%

Solution: 
Average molar mass of argon
= (0,00337 x 3596755) + (0.00063)
= 37.96272) + (0.9960 × 39.9624)
= 0.121 + 0.024 + 39.803
= 39.948 g mol^-1

Question 1.33. 
Calculate the number of atoms in each of the following:
(i) 52 moles of Ar
(ii) 52 u of He
(iii) 52 g of He
Solution: 
(i) ∵ 1 mol of Ar contains 6.022 x 10²³ atoms 
∴ 52 mol of Ar will contain = 52 x 6.022 × 10²³ atoms
= 313.144 x 10²³ atoms
= 3.1314 x 10²⁵ atoms

(ii) 4 u of He contains 1 atom of He
∴52 u of He will contain = x 52 atoms = 13 atoms

(iii) 1 mol of He = 4 g of He = 6.022 x 10²³ atoms
= \(\frac{6.022 \times 10^{23}}{4} \times 52 \text { atoms }\)
= 7.8286 x 10²⁴ atoms

Question 1.34. 
A welding fuel gas contains carbon and hydrogen only. Burning a small sample of it in oxygen gives 3.38 g carbon dioxide, 0.690 g of water and no other products. A volume of 10.0 L (measured at STP) of this welding gas is found to weigh 11.6 g. Calculate. (i) empirical formula, (ii) molar mass of the gas and (iii) molecular formula. C + O₂ → CO₂
Solution:

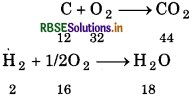
(i) ∵44g of CO₂ contains 12g of carbon:
∴ 3.38 g of CO₂ will contain
= \(\frac{12}{44}\) x 3.38 g
= 0.9218 g of Carbon

∵ 18g of H₂O contains 2g of hydrogen
∴ 0.690 g of H₂O will contain
= \(\frac{2}{18}\) x 0.690 g
= 0.0767 g of hydrogen
Total mass of compound = 0.9218 + 0.0767
= 0.9985 g
% of C = \(\frac{0.9218}{0.9985}\) x 100 
= 92.318 
= 92.32%
% of H = \(\frac{0.0767}{0.9985}\) x 100 = 7.68%
∴ Empirical formula of compound = CH

(ii) ∵ 10.0 L of the given gas weigh 11.6 g at STP 
∴ 22.4 L of the given gas will weigh
\(=\frac{11.6 \times 22.4}{10}\)
= 25984 g at STP

∴ Molar mass = 25984 g mol^-1 =  26 g mol^-1

(iii) Empirical formula mass of CH = 12 + 1 = 13

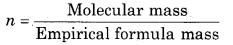
= \(\frac{26}{13}\) = 2
∴ Molecular formula = n x Empirical formula
= 2 × CH
= C₂H₂

Question 1.35. 
Calcium carbonate reacts with aqueous HCl to give CaCl, and CO₂ according to the reaction,
CaCO₃(s) + 2HCl(aq) → CaCl₂(aq) + CO₂(g) + H₂O(l)
What mass of CaCO₃ is required to react completely with 25 mL of 0.75 M HCl?
Solution: 
Volume of HCl = 25 mL
Molarity of HCl = 0.75 M
Molecular mass of HCl (m) = 1 + 35.5 = 36.5 g mol¹

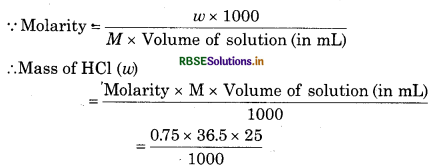
= 0.6844 g
For the reaction,
CaCO₃(s) + 2HCl (aq) → CaCl₂ (aq) + CO2(g) + H₂O(l)
100 g 2 x 36.5 = 73 g
According to balanced chemical equation,
∵ 73 g HCl reacts completely with 100 g of CaCO₃
∴ 0.6844 g HCl will react with
= \(\frac{100}{73}\) x 0.6844 = 0.9375 g

Question  1.36. 
Chlorine is prepared in the laboratory by treating manganese dioxide (MnO₂) with aqueous hydrochloric acid according to the reaction
4HCl(aq) + MnO₂ (s) → 2H₂O(l) + MnCl₂ (aq) + Cl₂(g) 
How many grams of HCl reacts with 5.0 g of manganese dioxide ?
Solution: 
For the reaction,
4HCl(aq) + MnO ₂ (s) → 2H₂O(l) + MnCl₂(aq) + Cl₂(g)
= 146.0 g
According to above balanced chemical equation, 87g of MnO₂ reacts with 146 g of HCl
∴5.0 g of MnO₂ will react with
= \(\frac{146}{87} \times 5\)
= 8.39 g of HCI