RBSE Solutions for Class 5 Maths Chapter 14 परिमाप एवं क्षेत्रफल

Rajasthan Board RBSE Solutions for Class 5 Maths Chapter 14 परिमाप एवं क्षेत्रफल Textbook Exercise Questions and Answers.

RBSE Class 5 Maths Solutions Chapter 14 परिमाप एवं क्षेत्रफल

पातुगत प्रश्न:

पृष्ठ सं. 116:

प्रश्न 1. 
निर्मल की गणित की किताब में कुछ आकृतियों के परिमाप ज्ञात करने के सवाल हैं।

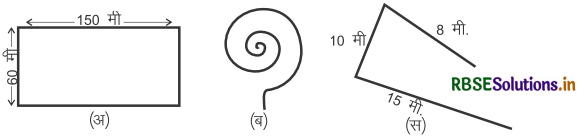
क्या आप इन तीनों आकृतियों का परिमाप ज्ञात कर सकते हो?
हल:
हम जानते हैं कि परिमाप केवल बंद आकृति का ही होता है। अतः यहाँ केवल आकृति (अ) का ही परिमाप ज्ञात किया जा सकता है। आकृति (ब) व (स) बन्द आकृतियाँ नहीं हैं। अतः इनका परिमाप ज्ञात नहीं किया जा सकता, ऐसी आकृतियों को खुली आकृतियाँ कहते हैं।

प्रश्न-नीचे कुछ आकृतियाँ दी गई हैं-

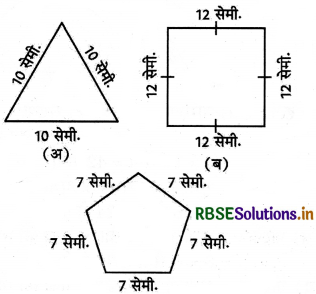
इन आकृतियों का परिमाप ज्ञात कीजिए।
हल-
(अ) हम जानते हैं कि नियमित आकृतियों का परिमाप = भुजाओं की संख्या - भुजा की माप
∴ परिमाप = 3 × 10 = 30 सेमी. 
(ब) परिमाप = 4 × 12 = 48 सेमी.
(स) परिमाप = 5 × 7 = 35 सेमी.

 

पृष्ठ सं. 117 (प्रयास कीजिए):

प्रश्न-सोचो क्या आयत नियमित आकृति है? अगर आपको आयत के परिमाप के लिए कोई नियम बनाना हो, तो आप क्या करेंगे?

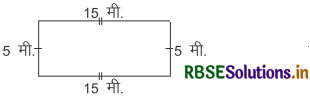
हल : 
दी गई आकृति एक आयत है, इसकी लम्बाई व चौड़ाई असमान (क्रमश: 15 व 5 मीटर) हैं, अतः यह नियमित आकृति नहीं है।
आयत के परिमाप के लिए नियम = लम्बाई + चौड़ाई + लम्बाई + चौड़ाई 
= 2 × लम्बाई + 2 × चौड़ाई
= 2(लम्बाई + चौड़ाई) 
अतः नियम यह हैआयत का परिमाप = 2(लम्बाई + चौड़ाई)
= 2 (15 + 5) = 2 (20) = 40 मीटर 

पृष्ठ सं. 119:

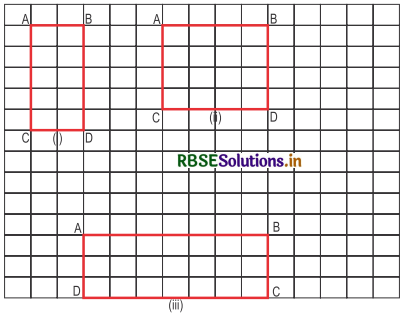
प्रश्न-नीचे दी गई ग्रिड पेपर पर आकृतियों (ii) व (iii) का क्षेत्रफल ज्ञात करो।

हल : 
प्रथम विधि-दो आकृतियों का क्षेत्रफल इस प्रकार है-सर्वप्रथम आकृतियों में खानों की संख्या गिनकर प्राप्त संख्या ही इनका क्षेत्रफल होता है-

(ii)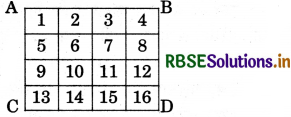

(iii)

अतः आकृति (ii) का क्षेत्रफल 16 वर्ग सेमी तथा 
आकृति (iii) का क्षेत्रफल 21 वर्ग सेमी है।

 

द्वितीय विधि:

आकृति (ii) एक वर्ग है जिसकी प्रत्येक भुजा = 4 सेमी. अतः वर्ग का क्षेत्रफल = भुजा × भुजा
4 × 4 = 16 वर्ग सेमी. 

आकृति (iii) एक आयत है जिसकी लम्बाई 7 सेमी. तथा चौड़ाई 3 सेमी. है। 
अतः आयतन का क्षेत्रफल = लम्बाई × चौड़ाई = 7 × 3 = 21 वर्ग सेमी.

पाठ्यपुस्तक के प्रश्न:

प्रश्नावली:

प्रश्न 1. 
नीचे दी गई आकृतियों का परिमाप ज्ञात कीजिए।

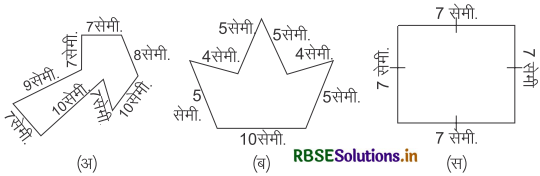
हल : 
(अ) परिमाप = भुजाओं का योग = 7 + 10 + 7 + 10 + 8 + 7 + 9 + 7 = 65 सेमी
(ब) परिमाप = भुजाओं का योग = 10 + 5 + 4 + 5 + 5 + 4 + 5 = 38 सेमी 
(स) परिमाप = भुजाओं का योग = 7 + 7 + 7 + 7 = 28 सेमी 

 

प्रश्न 2. 
निम्नलिखित माप की आयताकार आकृतियों का परिमाप ज्ञात कीजिए। 
(अ) लंबाई = 30 सेमी 
चौडाई = 48 सेमी

(ब) लंबाई = 20 सेमी 
चौड़ाई = 34 सेमी 

(स) लंबाई = 60 सेमी 
चौड़ाई = 20 सेमी 

(द) लंबाई = 30 सेमी
चौड़ाई = 12 सेमी
हल : 
(अ) परिमाप = 2(लम्बाई + चौड़ाई)
= 2(30 + 48) = 2(78) = 156 सेमी 

(ब) परिमाप = 2(लम्बाई + चौड़ाई)
= 2(20 + 34) = 2(54) = 108 सेमी 

(स) परिमाप = 2(लम्बाई + चौड़ाई)
= 2(60 + 20) = 2(80) = 160 सेमी 

(द) परिमाप = 2(लम्बाई + चौड़ाई)
= 2(30 + 12) = 2(42) = 84 सेमी 

 

प्रश्न 3. 
नियमित आकृतियों के परिमाप, सूत्र द्वारा ज्ञात कीजिए।

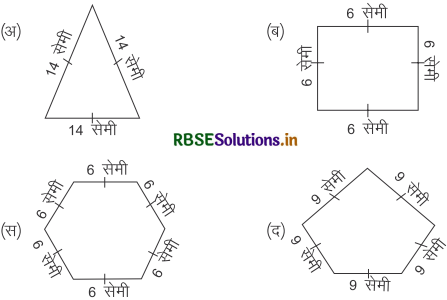
हल : 
(अ) परिमाप = भुजाओं की संख्या × भुजा की माप 
= 3 × 14 सेमी 
= 42 सेमी 

(ब) परिमाप = भुजाओं की संख्या × भुजा की माप
= 4 × 6 सेमी 
= 24 सेमी 

(स) परिमाप = भुजाओं की संख्या × भुजा की माप
= 6 × 6 सेमी 
= 36 सेमी 

(द) परिमाप = भुजाओं की संख्या × भुजा की माप
= 5 × 9 सेमी 
= 45 सेमी

 

प्रश्न 4. 
विजय ने एक आयत बनाया है। आप इसका परिमाप और क्षेत्रफल ज्ञात कीजिए। क्या आप इसकी लंबाई व चौड़ाई को इस प्रकार बढ़ा। सकते है कि इसका परिमाप व क्षेत्रफल समान हो जाये।
(लम्बाई व चौड़ाई दोनों को बढ़ाना जरुरी नहीं हैं)

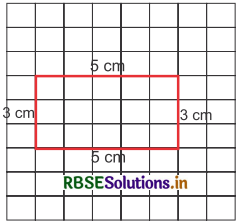
हल : 
आयत का परिमाप = भुजाओं का योग = 5 + 3 + 5 + 3 = 10 + 6 = 16 सेमी 
आयत का क्षेत्रफल = लम्बाई × चौड़ाई
= 5 × 3 = 15 वर्ग सेमी 
यदि आयत की लम्बाई 5 सेमी से 4 सेमी तथा चौड़ाई 3 सेमी से 4 सेमी कर दी जाए तो परिमाप = 4 × भुजा 
= 4 × 4 = 16 सेमी
क्षेत्रफल = (भुजा) × (भुजा)
= 4 × 4 = 16 वर्ग सेमी 
अतः परिमाप व क्षेत्रफल दोनों बराबर हो जायेंगे। 

 

प्रश्न 5. 
एक आयताकार मैदान की लंबाई 25 मीटर व चौड़ाई 30 मीटर है। इस मैदान का क्षेत्रफल ज्ञात कीजिए। 
हल : 
मैदान की लम्बाई = 25 मीटर
तथा चौड़ाई = 30 मीटर 
मैदान का क्षेत्रफल = लम्बाई × चौड़ाई
= 25 × 30 = 750 वर्ग मीटर 

प्रश्न 6. 
एक आयताकार टावेल की लंबाई 125 सेमी एवं चौड़ाई 60 सेमी है। इस टावेल का परिमाप कितना होगा? 
हल : 
टावेल की लम्बाई = 125 सेमी
तथा चौड़ाई = 60 सेमी 
∴ टावेल का परिमाप = 2(लम्बाई + चौड़ाई)
= 2 (125 + 60)
= 2 (185) = 370 सेमी. 

 

प्रश्न 7. 
एक वर्गाकार खेत के चारों ओर कटीले तारों का एक घेरा लगाने में 260 मीटर लम्बे कटीले तार की आवश्यकता हुई तो इस खेत की भुजा ज्ञात कीजिए। 
हल : 
तार की लम्बाई = खेत का परिमाप = 260 मीटर 
∴ खेत का परिमाप = 260 मीटर
⇒ 4 × भुजा = 260 मीटर
⇒ भुजा = = 65 मीटर 
अतः खेत की भुजा 65 मीटर की है। 

प्रश्न 8. 
एक कमरे के फर्श की लंबाई 8 मीटर तथा चौड़ाई 7 मीटर है। इस कमरे में ऐसी दरी बिछी है जो फर्श को पूरा-पूरा ढक लेती है। इस दरी का क्षेत्रफल ज्ञात कीजिए।
हल : 
फर्श की लम्बाई = 8 मीटर 
फर्श की चौड़ाई = 7 मीटर 
दरी का आवश्यक क्षेत्रफल = फर्श का क्षेत्रफल 
= लम्बाई × चौड़ाई = 8 × 7 = 56 वर्ग मीटर 
अतः दरी का क्षेत्रफल 56 वर्ग मीटर है। 

 

प्रश्न 9. 
एक वर्गाकार चौकी का परिमाप ज्ञात करो जिसकी भुजा 60 सेन्टीमीटर है। 
हल : 
चौकी की भुजा = 60 सेन्टीमीटर 
चौकी का परिमाप = 4 × भुजा
= 4 × 60 = 240 सेन्टीमीटर 
अत: चौकी का परिमाप 240 सेन्टीमीटर है।

प्रश्न 10. 
एक वर्गाकार खेत के दो चक्कर लगाने में देव को 40 मीटर चलना पड़ा। तो वर्गाकार खेत की भुजा ज्ञात कीजिए।
हल : 
दो चक्कर में चली दूरी = 40 मीटर 
1 चक्कर में चली दूरी = = 20 मीटर 
वर्गाकार खेत की चारों भुजाएँ समान होती हैं 
: 4 × भुजा = खेत का परिमाप 
⇒ 4 × भुजा = 20 मीटर 
⇒ भुजा = 7 मीटर = 5 मीटर 
अतः खेत की प्रत्येक भुजा 5 मीटर की है।

 

महत्वपूर्ण प्रश्न:

बहुविकल्पीय प्रश्न:

प्रश्न 1. 
एक आयताकार पार्क की लम्बाई L तथा चौड़ाई B हो, तो उसका क्षेत्रफल होगा-
(अ) 2 × (L + B) 
(ब) 2 × (L - B)
(स) 2 × (L ÷ B) 
(द) L × B
हल :
(द) L × B

प्रश्न 2. 
एक वर्गाकार खेत के चारों ओर एक चक्कर लगाने पर तय की गई दूरी होगी-
(अ) 4 × भुजा 
(ब) (भुजा)²
(स) भुजा ÷ 4 
(द) 4 भुजा²
हल :
(अ) 4 × भुजा 

प्रश्न 3. 
एक आयताकार चौक की लम्बाई 25 मीटर और चौड़ाई 15 मीटर है, तो उसका क्षेत्रफल होगा-
(अ) 80 वर्ग सेमी 
(ब) 375 वर्ग सेमी
(स) 40 वर्ग सेमी 
(द) 100 वर्ग सेमी 
हल :
(ब) 375 वर्ग सेमी

 

प्रश्न 4. 
एक वर्गाकार आकृति की एक भुजा 15 सेमी है, तो उसका क्षेत्रफल होगा-
(अ) 225 वर्ग सेमी 
(ब) 60 वर्ग सेमी
(स) 75 वर्ग सेमी 
(द) 100 वर्ग सेमी 
हल :
(अ) 225 वर्ग सेमी 

प्रश्न 5. 
एक आयताकार खेत की लम्बाई 10 मीटर तथा चौड़ाई 8 मीटर है। इसके चारों ओर तार की बाड़ लगानी है, तो तार की कुल लम्बाई होगी-
(अ) 80 मीटर 
(ब) 160 मीटर
(स) 36 मीटर 
(द) 18 मीटर
हल :
(स) 36 मीटर 

प्रश्न 6. 
एक त्रिभुज जिसकी भुजाएँ 10 सेमी, 8 सेमी और 5 सेमी हैं, तो त्रिभज का परिमाप होगा-
(अ) 40.5 सेमी 
(ब) 23 सेमी
(स) 22 सेमी. 
(द) 20 सेमी 
हल :
(ब) 23 सेमी

 

प्रश्न 7. 
वर्ग का परिमाप है
(अ) 4 × (एक भुजा की ल.)
(ब) 2 + (ल. × चौ.) 
(स) 2 × (ल. + चौ.) 
(द) चारों भुजाओं का गुणनफल
हल :
(अ) 4 × (एक भुजा की ल.)

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
क्षेत्रफल किसे कहते हैं ?
हल : 
कोई ज्यामितीय आकृति किसी समतल पर जितना क्षेत्र घेरती है, वह उसका क्षेत्रफल होता है।

प्रश्न 2. 
सम आकृतियाँ किसे कहते हैं ? 
हल : 
ऐसी बन्द आकृतियाँ जिसकी सभी भुजाएँ और कोण बराबर हों, बन्द सम आकृतियाँ कहलाती हैं।

प्रश्न 3.
परिमाप किसे कहते हैं ?
हल : 
एक बन्द आकृति के चारों ओर एक चक्कर लगाने में तय की गई दूरी, उस आकृति का परिमाप कहलाती है।

प्रश्न 4. 
एक सम पंचभुज का परिमाप ज्ञात कीजिए, जिसकी प्रत्येक भुजा की लम्बाई 3 सेमी
हल :
इस सम पंचभुज में 5 भुजाएँ हैं, जिसमें प्रत्येक भुजा की लम्बाई 3 सेमी है, सम पंचभुज का परिमाप = 5 × 3 सेमी = 15 सेमी.

 

लघूत्तरात्मक प्रश्न:

प्रश्न 1. 
दिए गए चित्र में त्रिभुज का क्षेत्रफल ज्ञात कीजिए।

हल : 
चित्र में त्रिभुज के अन्दर खानों को गिनकर इसका क्षेत्रफल ज्ञात करते हैं।
पूरे-पूरे खानों की संख्या = 27 
आधे या आधे से बड़े खानों की संख्या = 9
अतः त्रिभुज का क्षेत्रफल = 27 + 9 = 36 खाने या 36 वर्ग इकाई 

प्रश्न 2.
2 मी. 30 सेमी लम्बाई तथा 1 मी. 20 सेमी चौड़ाई वाले एक लोहे की छड़ का क्षेत्रफल वर्ग मीटर में ज्ञात कीजिए। 
हल : 
छड़ की लम्बाई = 2 मी. 30 सेमी = 2.30 मी.
छड़ की चौ. = 1 मी. 20 सेमी. = 1.20 मी. 
लोहे की छड़ का क्षेत्रफल = ल. × चौ.
= 2.30 × 1.20 
= 2.76 वर्ग मी.

 

प्रश्न 3. 
ग्राफ पेपर पर कोई एक वृत्त खींचिए। इस वृत्त में उपस्थित वर्गों की संख्या को गिनकर वृत्ताकार क्षेत्र का अनुमानित क्षेत्रफल ज्ञात कीजिए। 
हल : 
ग्राफ पेपर पर कोई एक वृत्त खींचा जिसका प्रत्येक वर्ग 1 सेमी × 1 सेमी माप का है।

पूर्ण वर्ग जो वृत्त में है = 1 
आधे से ज्यादा भरे वर्ग = 4 
आधे से कम भरे वर्ग = 4
पूरे वर्गों द्वारा घेरा गया क्षेत्रफल = (1× 1) वर्ग सेमी = 1 वर्ग सेमी 
आधे से ज्यादा भरे वर्गों द्वारा घेरा गया क्षेत्रफल = (4 × 1) वर्ग सेमी = 4 वर्ग सेमी 
आधे से कम भरे वर्गों द्वारा घेरा गया क्षेत्रफल = 4 × 0 वर्ग सेमी = 0 वर्ग सेमी 
∴ कुल क्षेत्रफल = 1 + 4 + 0 वर्ग सेमी = 5 वर्ग सेमी।

प्रश्न 4.
32 सेमी लम्बाई और 21 सेमी चौड़ाई वाले एक फोटो को लकड़ी की पट्टी से फ्रेम करना है। आवश्यक लकड़ी की पट्टी की लम्बाई ज्ञात कीजिए।
हल : 
फोटो का फ्रेम आयताकार होता है। 
∴ फ्रेम में आवश्यक लकड़ी का परिमाप = 2 × (ल. + चौ.) 
= 2 × (32 सेमी + 21 सेमी)
= 2 × (53 सेमी) = 106 सेमी 
अतः आवश्यक लकड़ी की पट्टी की लम्बाई = 106 सेमी 

 

प्रश्न 5. 
नीचे दी हुई आकृतियों का परिमाप ज्ञात कीजिए-

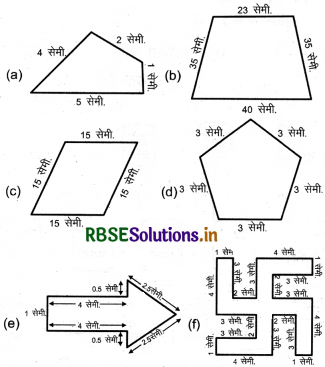
हल : 
(a) परिमाप = भुजाओं की लम्बाइयों का योग = 5 सेमी + 1 सेमी + 2 सेमी + 4 सेमी = 12 सेमी
(b) परिमाप = भुजाओं की लम्बाइयों का योग = 40 सेमी + 35 सेमी + 23 सेमी + 35 सेमी = 133 सेमी
(c) परिमाप = 4 × एक भुजा की लम्बाई
= 4 × 15 सेमी = 60 सेमी 
(d) परिमाप = 5 × एक भुजा की लम्बाई
= 5 × 3 सेमी = 15 सेमी 
(e) परिमाप = भुजाओं की लम्बाइयों का योग
= 4 सेमी + 0.5 सेमी + 2.5 सेमी + 2.5 सेमी + 0.5 सेमी + 4 सेमी + 1 सेमी = 15 सेमी. 
(f) परिमाप = भुजाओं की लम्बाई का योग
= 4 सेमी + 3 सेमी + 2 सेमी + 3 सेमी + 1 सेमी + 4 सेमी + 3 सेमी + 2 सेमी + 3 सेमी + 1 सेमी + 4 सेमी + 3 सेमी + 2 सेमी + 3 सेमी + 1 सेमी + 4 सेमी + 3 सेमी + 2 सेमी + 3 सेमी + 1 सेमी
= 52 सेमी 

 

प्रश्न 6. 
एक त्रिभुज का परिमाप ज्ञात कीजिए जिसकी भुजाएँ 10 सेमी, 14 सेमी तथा 15 सेमी हैं।
हल : 
त्रिभुज का परिमाप = भुजाओं की लम्बाइयों का योग 
= 10 सेमी + 14 सेमी + 15 सेमी = 39 सेमी 

प्रश्न 7. 
एक सम षट्भुज का परिमाप ज्ञात कीजिए, जिसकी प्रत्येक भुजा की माए 8 मोटर है। 
हल : 
एक सम षट्भुज में 6 समान भुजाएँ होती हैं। 
∴ इसका परिमाप = 6 × भुजा की लम्बाई
= 6 × (8 मीटर) = 48 मीटर 

प्रश्न 8. 
एक वर्ग की भुजा ज्ञात कीजिए, जिसका परिमाप 20 मीटर है।
हल : 
वर्ग का परिमाप = 20 मीटर 
∵ वर्ग में 4 समान भुजाएँ होती हैं।
∴ वर्ग की भुजा = परिमाप / 4 =  \(\frac{20}{4}\)
= 5 मीटर

 

प्रश्न 9. 
एक सम पंचभुज का परिमाप 100 सेमी है। प्रत्येक भुजा की लम्बाई ज्ञात कीजिए।
हल : 
सम पंचभुज का परिमाप = 100 सेमी
∵ सम पंचभुज में 5 समान भुजाएँ होती हैं।
∴ एक भुजा की लम्बाई = परिमाप / 5
= \(\frac{100}{5}\) = 20 सेमी