RBSE Solutions for Class 5 Maths Chapter 7 Equivalent Fractions

Rajasthan Board RBSE Solutions for Class 5 Maths Chapter 7 Equivalent Fractions Textbook Exercise Questions and Answers.

RBSE Class 5 Maths Solutions Chapter 7 Equivalent Fractions

Intext Questions:

Question 1.
Represent the equivalent fractions by filling colour in the following diagrams.

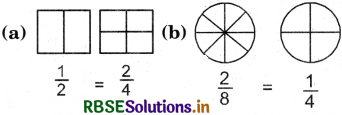
Solution:

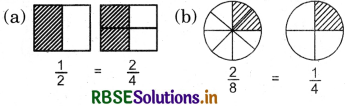
Question 2. 
Can we convert a fraction into equivalent fraction by multiplying numerator and denominator with the same number.
Solution: 
Yes we can. 
For example:

Question 3. 
Can we also convert a fraction into equivalent fraction by dividing numerator and denominator with the same number?
Solution: 
Yes, we can.
For example (a) \(\frac{6}{9}\), (b) \(\frac{2}{4}\)

(a) \(\frac{6}{9}=\frac{6 \div 3}{9 \div 3}=\frac{2}{3}\)

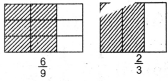
(b) \(\frac{2}{4}=\frac{2 \div 2}{4 \div 2}=\frac{1}{2}\)

Exercise:

Question 1. 
Convert the given fraction into equivalent fraction by multiplying numerator and denominator by 2.
Solution: 
(i) \(\frac{1}{2}\)
(ii) \(​​\frac{2}{3}\)
(iii) \(\frac{1}{5}\)
(iv) \(\frac{2}{5}\)
(v) \(\frac{2}{7}\)
Solution:
(i) \(\frac{1}{2}=\frac{1 \times 2}{2 \times 2}=\frac{2}{4}\)

(ii) \(\frac{2}{3}=\frac{2 \times 2}{3 \times 2}=\frac{4}{6}\)

(iii) \(\frac{1}{5}=\frac{1 \times 2}{5 \times 2}=\frac{2}{10}\)

(iv) \(\frac{2}{5}=\frac{2 \times 2}{2 \times 5}=\frac{4}{10}\)

(v) \(\frac{2}{7}=\frac{2 \times 2}{7 \times 2}=\frac{4}{14}\)

Question 2. 
Convert the given fraction into equivalent fraction by multiplying numerator and denominator by 3.
(i) \(\frac{1}{4}\)
(ii) \(\frac{3}{5}\)
(iii) \(\frac{2}{5}\)
(iv) \(\frac{2}{7}\)
(v) \(\frac{1}{6}\)
Solution:
(i) \(\frac{1}{4}=\frac{1 \times 3}{4 \times 3}=\frac{3}{12}\)

(ii) \(\frac{3}{5}=\frac{3 \times 3}{5 \times 3}=\frac{9}{15}\)

(iii) \(\frac{2}{5}=\frac{2 \times 3}{5 \times 3}=\frac{6}{15}\)

(iv) \(\frac{2}{7}=\frac{2 \times 3}{7 \times 3}=\frac{6}{21}\)

(v) \(\frac{1}{6}=\frac{1 \times 3}{6 \times 3}=\frac{3}{18}\)

Question 3. 
Convert the given fraction into equivalent fraction by multiplying numerator and denominator by 2, 3 and 4 respectively.
(i) \(\frac{1}{4}\)
(ii) \(\frac{2}{3}\)
(iii) \(\frac{2}{5}\)
(iv) \(\frac{3}{4}\)
Solution: 

Question 4. 
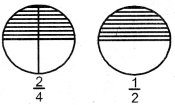
Represent the given equivalent fractions by filling colour in following diagrams.

(i)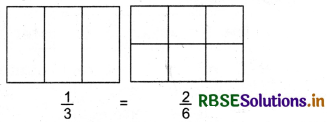

(ii)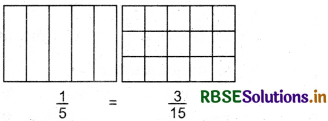

Solutions:

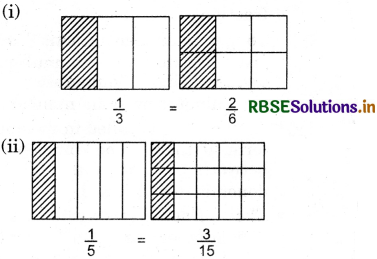
Question 5.
Fill in the blanks:

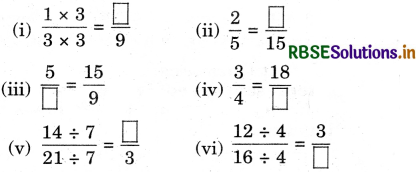
Solution:

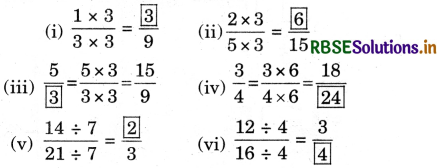
Question 6. 
Given some examples where we get after dividing equally and write down below.
\(\frac{1}{4}=\frac{2}{8}=\frac{3}{12}\) = .................
Solution:
\(\frac{1}{4}=\frac{2}{8}=\frac{3}{12}=\frac{4}{16}=\frac{5}{20}\) = \(\frac{6}{24}=\frac{7}{28}=\frac{8}{32}\)

Question 7.
Write four equivalent fractions of .
Solution:
\(\frac{1}{5}=\frac{1 \times 2}{5 \times 2}=\frac{1 \times 3}{5 \times 3}=\frac{1 \times 4}{5 \times 4}=\frac{1 \times 5}{5 \times 5}\)
⇒ \(\frac{1}{5}=\frac{2}{10}=\frac{3}{15}=\frac{4}{20}=\frac{5}{25}\)

Question 8.
Ranu bought 6 meter long ribbon from market, if she equally divides it among 4 friends, then what is the length of ribbon each friend will get?
Solution:
Each friend (out of 4) will get m. ribbon.
\(\frac{6}{4}=1+\frac{2}{4}\) i.e., 1\(\frac{1}{2}\)

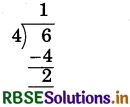
∴ Each will get 1 m ribbon.

Question 9.
Saraswati needs 1 meter of cloth to make a shirt. How much cloth she needs to make two such shirts?
Solution. 
Closth required for 1 shirt = 1\(\frac{1}{4}\) m
Cloth required for 2 shirts = (1\(\frac{1}{4}\) + 1\(\frac{1}{4}\))
= (1 + \(\frac{1}{4}\) + 1 + \(\frac{1}{4}\))
= (1 + 1 + \(\frac{1}{4}\) + \(\frac{1}{4}\))
= (2 + \(\frac{2}{4}\))
= (2 + \(\frac{1}{2}\))
= 2\(\frac{1}{2}\) m

Thus, 2\(\frac{1}{2}\) m cloth is required for 2 shirts.

Important Questions:

Multiple Choice Questions:

Question 1.    
If 20 litre milk is distributed in 5 houses, then numerator of simplest form of obtained fraction will be :
(a) 4    
(b) 5    
(c) 6    
(d) 7
Solution:
(a) 4

Question 2.    
Simplest form of \(\frac{35}{5}\) is :
(a) 4    
(b) 5    
(c) 6    
(d) 7
Solution:
(d) 7

Question 3.    
Solving 43 ÷ 3, remainder will be :
(a) 0    
(b) 1    
(c) 2    
(d) 3
Solution:
(b) 1

Question 4.    
2 litre kerosine is filled in one stove, then kerosine filled in 5 stoves will be :
(a) 8    
(b) 9    
(c) 10    
(d) 12
Solution:
(c) 10

Question 5.    
If 5 chapatis are distributed between 2 children, each will get:
(a) 2\(\frac{1}{2}\)
(b) 1\(\frac{1}{2}\)
(c) 2 
(d) 1
Solution:
(a) 2

Question 6.
\(\frac{2}{5}\) will be equivalent to:
(a) \(\frac{4}{10}\)
(b) \(\frac{6}{10}\)
(c) \(\frac{8}{10}\)
(d) \(\frac{10}{20}\)
Solution:
(a) \(\frac{4}{10}\)

Question 7.
\(\frac{3 \times 5}{5 \times 5}=\frac{\square}{25}\), empty box will have:
(a) 5
(b) 10
(c) 15
(d) 20
Solution:
(c) 15

Question 8.
Equivalent fraction of \(\frac{3}{4}\) is :
(a) 8/16    
(b) 12/16
(c) 8/12    
(d) None of these
Solution:
(b) 12/16

Short Answer Type Questions:

Question 1. 
Write three equivalent fraction of .
Solution: 
\(\frac{2}{3} \times \frac{2}{2}=\frac{4}{6}\)
\(\frac{2}{3} \times \frac{3}{3}=\frac{6}{9}\)
\(\frac{2}{3} \times \frac{4}{4}=\frac{8}{12}\)
Thus, three equivalent fractions of \(\frac{2}{3}\) are \(\frac{4}{6}\), \(\frac{6}{9}\) and \(\frac{8}{12}\).

Question 2. 
15 litre kerosine has to fill equally in 3 stoves. How much kerosine will be filled in each stove? 
Solution: 
∵ Total kerosine = 15 l and number of stoves to be filled with kerosine = 3 
Kerosine will be filled in each stove = (15 ÷ 3) = 5
Thus, each stove will be filled with 5 l kerosine.

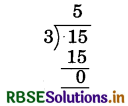
Question 3. 
10 litre milk is distributed among 20 children, then how much milk each child got?
Solution: 
∵ Total milk = 10 l
Number of children = 20 
Each child will get milk = (10 ÷ 20) = \(\frac{10}{20}=\frac{1}{2}\) l
Thus, each child got \(\frac{1}{2}\) l milk.
 
Question 4. 
If 20 chapati are distributed among 5 kids. Then how many chapati got by each one :
Solution: 
Total number of chapati = 20 
Total number of kids = 5 
⇒ Each kid get chapati = (20 ÷ 5) = \(\frac{20}{5}\) = 4 chapati

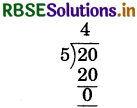
So, each kids got 4 chapati.

Question 5. 
A packet contains 5 candles then find how many prockets will be formed by 729 candles and how many candles will be left ?
Solution: 
∵ Total candles = 729
∴ packet contains 5 candles,number of packets = 729 ÷ 5

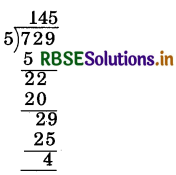
Number of packets So, 145 packets will be formed and 4 candles will be left.

Question 6. 
Sita bought 1\(\frac{1}{2}\) l milk. Her sister bought 2\(\frac{1}{2}\) l milk. How much milk will be collected in house. It rate of 1 l milk is ₹ 30, then how much money Sita and her sister spend separately?
Solution: 
∵ 1 l = 1000 ml
∴ \(\frac{1}{2}\) l = 500 ml
Sita bought milk = 1 \(\frac{1}{2}\) l {1l 500 ml)
Her sister bought milk = 2 \(\frac{1}{2}\)  (2l 500 ml)
Total milk bought milk = 1 l 500 ml + 2 l 500 l = l
Cost of 1l litre milk = ₹ 30
Cost of \(\frac{1}{2}\) l milk = \(\frac{30}{2}\) = ₹ 15
Sita has spent on 1\(\frac{1}{2}\) l milk (30 + 15)= ₹ 45
Her sister spent on 2\(\frac{1}{2}\)l milk = ₹ (30 + 30 + 15) = ₹ 75