RBSE Solutions for Class 5 Maths Chapter 4 वैदिक गणित

Rajasthan Board RBSE Solutions for Class 5 Maths Chapter 4 वैदिक गणित Textbook Exercise Questions and Answers.

RBSE Class 5 Maths Solutions Chapter 4 वैदिक गणित

प्रश्नावली 4.1:

घटाव कीजिए-(सूत्र का न्यूनेन् पूर्वेण तथा परम मित्र अंक की सहायता से घटाइए) 

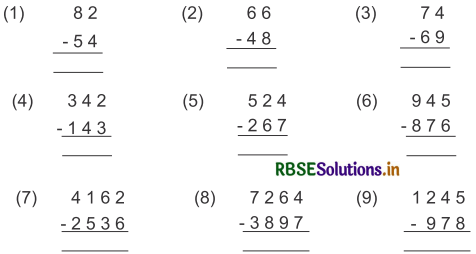
हल : 
(1)

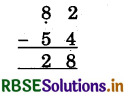
संकेत:
(i) 2 में से 4 नहीं घटाया जा सकता, अतः 4 के परम मित्र अंक 6 को अंक 2 में जोड़ा व योगफल = 8 नीचे लिखेंगे। 
(ii) 2 के पूर्वेण अंक 8 पर एक न्यून चिह्न लगाएगें।(8) 
(iii) 8 = 7 में से 5 घटाकर नीचे लिखेंगे। संख्या 28 प्राप्त होती है।

 

(2)

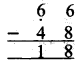
संकेत:
(i) 6 में से 8 नहीं घटाया जा सकता अतः 8 के परम मित्र 18. 2 को 6 में जोड़ा व योगफल 8 नीचे लिखेंगे। 
(ii) 6 के पूर्वेण अंक 6 पर एक न्यून चिह्न लगाएगें।(6) 
(iii) 6 = 5 में से 4.घटाकर नीचे लिखेंगे। संख्या 18 प्राप्त होती है।

(3)

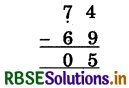
संकेत:
(i) 4 में से 9 नहीं घटाया जा सकता, अतः 9 के परम मित्र अंक 1 को अंक 4 में जोड़ा व योगफल =5 नीचे लिखेंगे।
(ii) 4 के पूर्वेण अंक 7 पर एक न्यून चिह्न लगाएगें। (7) 
(iii) 7 = 6 में से 6 घटाकर नीचे लिखेंगे। संख्या 5 प्राप्त होती है। 

(4)

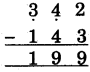
संकेत : 
(i) 2 में से 3 नहीं घटाया जा सकता, अतः 3 के परम मित्र अक 7 को अंक 2 में जोड़ा व योगफल = 9 नीचे लिखेगें। 
(ii) 2 के पूर्वेण अंक 4 पर एक न्यून चिह्न लगाएगें।
(iii) 4 = 3 में से 4 नहीं घटाया जा सकता अतः 4 के - परम मित्र अंक 6 को अंक 3 में जोड़ा व योगफल = 9 नीचे लिखेंगे। 
(iv) 4 के पूर्वेण अंक 3 पर एक न्यून चिह्न लगाएगें। 
(v) 3 = 2 में से 1 घटाया, 2 - 1 = 1 नीचे लिखेंगे। संख्या 199 प्राप्त होती है।

 

(5)

संकेत:
(i) 4 में से 7 नहीं घटाया जा सकता, अतः 7 के परम मित्र अंक 3 को अंक 4 में जोड़ा व योगफल = 7 नीचे लिखेगें। 
(ii) 4 के पूर्वेण अंक 2 पर एक न्यून चिह्न लगाएगें। (2) 
(iii) 2 = 1 में से 6 नहीं घटाया जा सकता अतः 6 के परम मित्र अंक 4 को अंक 1 में जोड़ा व योगफल = 5 नीचे लिखेगें। 
(iv) 2 के पूर्वेण अंक 5 पर एक न्यून चिह्न लगाएगें।
(v) 5 = 4 में से 2 घटाया, 4 - 2 = 2 नीचे लिखेंगे। संख्या 257 प्राप्त होती है।

(6)

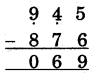
संकेत:
(i) 5 में से 6 नहीं घटाया जा सकता, अत: 6 के परम मित्र अंक 4 को अंक 5 में जोड़ा व योगफल = 9 नीचे लिखेगें। 
(ii) 5 के पूर्वेण अंक 4 पर एक न्यून चिह्न लगाएगें। (4)
(iii) 4 = 3 में से 7 नहीं घटाया जा सकता अतः 7 के परम मित्र अंक 3 को अंक 3 में जोड़ा व योगफल = 6 नीचे लिखेगें। 
(iv) 4 के पूर्वेण अंक 9 पर एक न्यून चिह्न लगाएगें।
(v) 9 = 8 में से 8 घटाया, 8-8 = 0 नीचे लिखेगें। संख्या 69 प्राप्त होती है।

 

(7)

संकेत:
(i) 2 में से 6 नहीं घटाया जा 4 1 6 2 सकता अतः 6 के परम मित्र 4 को 2 में जोड़ा व योगफल  6 नीचे लिखेगें एवं 2 के पूर्वेणं अंक 6 पर एक न्यून चिह्न लगाएगें। 
(ii) 6 = 5 में से 3 नहीं घटाया जा सकता है, अतः 6 - 3 = 2 नीचे लिखेंगे। 
(iii) अब 1 में से 5 नहीं घटाया जा सकता, अत: 5 के परम मित्र को 1 में जोड़ा एवं पूर्वेण अंक 4 पर न्यून लगाएंगे। (4) 
(iv) 4 - 3, अत: 3 - 2 = 1 लिखेगें। संख्या 1626 प्राप्त होती है।

(8)

संकेत:
(i) 4 में से 7 नहीं घटाया जा 72 6 4. सकता अतः 7 के परम मित्र - 3 8 9 7 3 को 4 में जोड़ा व योगफल  7 नीचे लिखेगें एवं 4 के पूर्वेण अंक 6 पर एक न्यून चिह्न लगाएगें। (6) 
(ii) 6 = 5 में से 9 नहीं घटाया जा सकता, अत: 9 के परम मित्र 1 को 5 में जोड़ा एवं 6 के पूर्वेण अंक 2 पर न्यून लगाएंगे। (2) 
(iii) 2 = 1 में से 8 नहीं घटाया जा सकता, अत:8 के परम मित्र 2 को 1 में जोड़ा एवं पूर्वेण अंक 7 पर न्यून लगाएंगे। (7)
(iv) 7 = 6, अत: 6 - 3 = 3 लिखेगें। संख्या 3367 प्राप्त होती है।

 

(9)

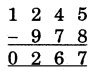
संकेत:
(i) 5 में से 8 नहीं घटाया जा सकता अतः 8 के परम मित्र को 5 में जोड़ा व योगफल  7 नीचे लिखेंगे एवं 5 के पूर्वेण अंक 4 पर एक न्यून चिह्न लगाएगें। (4) 
(ii) 4 = 3 में से 7 नहीं घटाया जा सकता, अत: 7 के परम मित्र 3 को 3 में जोड़ा एवं 4 के पूर्वेण अंक 2 पर न्यून लगाएंगे। (2) 
(iii) 2 = 1 में से 9 नहीं घटाया जा सकता, अत: 9 के परम मित्र 1 को 1 में जोड़ा एवं पूर्वेण अंक 1 पर न्यून लगाएंगे। (1) 
(iv) 1 = 0, अतः नीचे 0 लिखेगें। संख्या 267 प्राप्त होती है। 

 

प्रश्नावली 4.2:

घटाव कीजिए-(सूत्र-एकाधिकेन पूर्वेण + परम मित्र अंक)

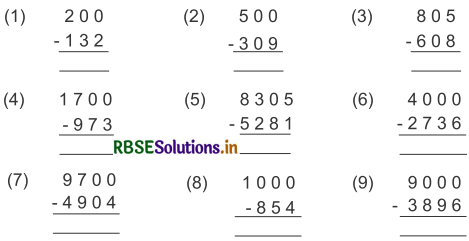
हल:
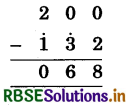
(1)

संकेत:
(i) 0 में से 2 नहीं घटाया जा सकता, अतः 2 के परम मित्र अक 8 को अंक 0 में जोडा व योगफल = 8 नीचे लिखेगें।
(ii) 2 के पूर्वेण अंक 3 पर एकाधिक चिह्न लगाएगें। (3) 
(iii) 0 में से 4 नहीं घटाया जा सकता अत: 4 के परम मित्र अंक 6 को अंक 0 में जोड़ा व योगफल = 6 नीचे लिखेगें।
(iv) 3 के पूर्वेण अंक 1 पर एकाधिक चिह्न लगाएगें। (1) 
(v) 2 में से 1 = 2 घटाया, 2 - 2 = 0 नीचे लिखेंगे। संख्या 68 प्राप्त होती है। 

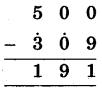
(2)

संकेत: 
(i) 0 में से 9 नहीं घटाया जा सकता, अतः 9 के परम मित्र अंक 1 को अंक 0 में जोड़ा व योगफल = 1 नीचे लिखेगें। 
(ii) 9 के पूर्वेण अंक 0 पर एकाधिक चिह्न लगाएगें। (0) 
(iii) 0 में से 0 = 1 नहीं घटाया जा सकता, अत: 1 के परम मित्र अंक 9 को अंक 0 में जोड़ा व योगफल = 9 नीचे लिखेगें। 
(iv) 0 के पूर्वेण अंक 3 पर एकाधिक चिह्न लगाएगें।
(v) 5 में से 3 = 4 घटाया, 5 - 4 = 1 नीचे लिखेगें। संख्या 191 प्राप्त होती है। 

 

(3)

संकेत:
(i) 5 में से 8 नहीं घटाया जा सकता, अतः 8 के परम मित्र अंक 2 को अंक 5 में जोड़ा व योगफल = 7 नीचे लिखेगें। 
(ii) 8 के पूर्वेण अंक 0 पर एकाधिक चिह्न लगाएगें। (0)
(iii) 0 में से =1 नहीं घटाया जा सकता, अतः 1 के परम मित्र अंक 9 को अंक 0 में जोड़ा व योगफल = 9 नीचे लिखेगें। 
(iv) 0 के पूर्वेण अंक 6 पर एकाधिक चिह्न लगाएगें। (6) 
(v) 8 में से 17 घटाया, 8-7 = 1 नीचे लिखेगें। संख्या 197 प्राप्त होती है। 

(4)

संकेत:
(i) 0 में से 3 नहीं घटाया जा सकता, अतः 3 के परम मित्र 7 को 0 में जोड़ा व योगफल 7 नीचे लिखेगें एवं 3 के पूर्वेण अंक 7 पर एकाधिक चिह्न लगाएगें। (i) 
(ii) 0 में से 18 नहीं घटाया जा सकता, अत: 8 के परम मित्र 2 को 0 में जोड़ा एवं 7 के पूर्वेण अंक पर एकाधिक लगाएंगे। (9) 
(iii) 7 में से 9 = 10 नहीं घटाया जा सकता, अत: 10 के परम मित्र 0 को 7 में जोड़ा एवं ; पूर्वेण अंक 0 पर एकाधिक लगाएंगे। (0) 
(iv) 1 में से 0 =1 घटाकर 0 पर एकाधिक लगाएंगे। (0).
(v) 1 में से 0 =1 घटाकर 0 नीचे लिखेंगे। संख्या 727 प्राप्त होती है। 

 

(5)

संकेत:
(i) 5 में से 1 घटाकर 4 नीचे लिखेंगे। 
(ii) 0 में से 8 नहीं घटाया जा सकता अत: 8 के परम मित्र 2 को 0 में जोड़ा व योगफल 2 नीचे लिखेगें एवं 8 के पूर्वेण अंक 2 पर एकाधिक चिह्न लगाएगें। (2) 
(iii) 3 में से 2 = 3 घटाकर 0 नीचे लिखेंगे। 
(iv) 8 में से 5 घटाकर 3 नीचे लिखेंगे। संख्या 3024 प्राप्त होती है।

(6)

संकेत:
(i) 0 में से 6 नहीं घटाया जा सकता, अतः 6 के परम मित्र 4 को 0 में जोड़ा व योगफल नीचे लिखेंगे एवं 6 के पूर्वेण अंक 3 पर एकाधिक चिह्न लगाएंगे। (3)
(ii) 0 में से 3 = 4 नहीं घटाया जा सकता, अत: 4 . के परम मित्र 6 को 0 में जोड़ा एवं 3 के पूर्वेण अंक पर एकाधिक लगाएंगे। (7) 
(iii) 0 में से 7 = 8 नहीं घटाया जा सकता, अतः 8 के परम मित्र 2 को 0 में जोड़ा एवं पूर्वेण अंक 2 पर एकाधिक लगाएंगे। (2) 
(iv) 4 में से 2 = 3 को घटाकर नीचे लिखते हैं। संख्या 1264 प्राप्त होती है।

 

(7)

संकेत:
(i) 0 में से 4 नहीं घटाया जा सकता अतः 4 के परम मित्र 6 को 0 में जोड़ा व योगफल न 6 नीचे लिखेंगे एव 4 के पूर्वण अंक 0 पर एकाधिक चिह्न लगाएंगे। (6) 
(ii) 0 में से 6 = 1 नहीं घटाया जा सकता, अत: 1 के परम मित्र 9 को 0 में जोड़ा एवं के पूर्वेण अंक पर एकाधिक लगाएंगे। (9) 
(iii) 7 में से 9 = 10 नहीं घटाया जा सकता, अतः 10 के परम मित्र 0 को 7 में जोड़ा एवं पूर्वेण अंक 4 पर एकाधिक लगाएंगे। (4) 
(iv) 9 में से 4 = 5 को घटाकर नीचे लिखते हैं। संख्या 4796 प्राप्त होती है। 

(8)

संकेत:
(i) 0 में से 4 नहीं घटाया जा सकता अतः 4 के परम मित्र के 4 6 को 0 में जोड़ा व योगफल 6 नीचे लिखेंगे एवं 4 के पूर्वेण 0 1 4 6 अंक 5 पर एकाधिक चिह्न लगाएगें।
(ii) 0 में से 5 = 6 नहीं घटाया जा सकता, अत: 6 के परम मित्र 4 को 0 में जोड़ा एवं 5 के पूर्वेण अंक पर एकाधिक लगाएंगे। (8) 
(iii) 0 में से हूं नहीं घटाया जा सकता, अतः 9 के परम मित्र 1 को 0 में जोड़ा एवं पूर्वेण अंक 0 पर एकाधिक लगाएंगे। (0) 
(iv) 1 में से 0 = 1 घटाकर 0 नीचे लिखेंगे। संख्या 146 प्राप्त होती है। 

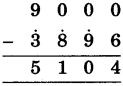
(9)

संकेत:
(i) 0 में से 6 नहीं घटाया जा सकता अतः 6 के परम मित्र 4 को 0 में जोड़ा व योगफल 4 नीचे लिखेंगे एवं6 के पूर्वेण 51 0 4 अंक 9 पर एकाधिक चिह्न लगाएंगे। (9) 
(ii) 0 में से 9 = 10 नहीं घटाया जा सकता, अतः 10 के परम मित्र 0 को 0 में जोड़ा एवं 9 के पूर्वेण अंक पर एकाधिक लगाएंगे। (8) 
(iii) 0 में से 8 = 9 नहीं घटाया जा सकता, अत: 9 के परम मित्र 1 को 0 में जोड़ा एवं पूर्वेण अंक 3 पर एकाधिक लगाएंगे। (3) 
(iv) 9 में से 3 = 4 घटाकर 5 नीचे लिखते हैं। संख्या 5104 प्राप्त होती है।

 

प्रश्नावली 4.3:

"10" के आधार पर विचलन लिखिए:

1. 14 का विचलन ............................. 
2. 11 का विचलन ............................. 
3. 8 का विचलन .............................
4. 9 का विचलन .............................
5. 13 का विचलन .............................
6. 19 का विचलन .............................
7. 7 का विचलन .............................
8. 6 का विचलन .............................
हल : 
1. 14 का विचलन = 14 - 10 = + 4
2. 11 का विचलन = 11 - 10 = + 1 
3. 8 का विचलन = 8 - 10 = - 2 
4. 9 का विचलन = 9 - 10 = - 1
5. 13 का विचलन = 13 - 10 = + 3
6. 19 का विचलन = 19 - 10 = + 9 . 
7. 7 का विचलन = 7 - 10 = - 3 
8. 6 का विचलन = 6 - 10 = - 4

 

प्रश्नावली 4.4:

प्रश्न-आधार 10 पर सूत्र निखिलम् द्वारा गुणा कीजिए। 
(1) 12 × 9
(2) 15 × 12 
(3) 13 × 17
(4) 8 × 9 
(5) 14 × 11 
(6) 9 × 16 
(7) 12 × 13
(8) 13 × 10 
हल : 
(1) 12 × 9

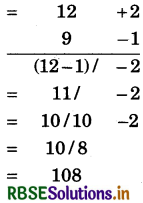
संकेत:
(i) निकटतम आधार = 10, अतः विचलन एवं -1 हैं।
(ii) विचलनों का गुणनफल = 2 × (- 1) = - 2 
(iii) बाएँ पक्ष में 12 - 1 = 11 या 9 + 2 = 11 लिखेंगे। 
(iv) दाईं ओर ऋणात्मक संख्या नहीं रखनी है, अतः धनात्मक के लिए बाईं ओर से 1 लेने पर बाईं ओर 1 × 10 = 10 लिखेंगे। 
(v) 11 - 1 = 10 बाईं ओर लिखेगें। अतः संख्या 108 प्राप्त हुई। 

(2) 15 × 12

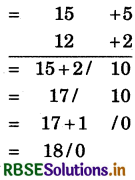
= 180

संकेत:
(i) निकटतम आधार = 10, अतः विचलन एवं + 2 हैं। 
(ii) विचलना का गुणनफल = 5 × 2 = 10
(iii) बाएँ पक्ष में 15 + 2 = 17 या 12 + 5 = 17 लिखेंगे। 
(iv) दाएँ पक्ष में दो अंक है अतः एक अंक बाईं ओर . स्थानांतरित करेंगे (क्योंकि आधार 10 में एक शून्य है, अतः एक अंक रहेगा।) 
(v) 17 + 1 = 18 लिखेंगे। अतः संख्या 180 प्राप्त।

 

(3) 13 × 17

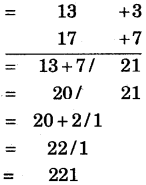
संकेत:
(i) निकटतम आधार = 10, अतः विचलन = + 3 एवं + 7 है।
(ii) विचलनों का गुणनफल = 3 × 7 = 21 
(iii) बाएँ पक्ष में 13 + 7 = 20 या 17 + 3 = 20 लिखेंगे। 
(iv) दाएँ पक्ष में दो अंक है अतः एक अंक बाईं ओर स्थानान्तरित करेंगे (क्योंकि आधार 10 में एक शून्य है अतः एक अंक रहेगा।) 
(v) 20 + 2 = 22 लिखेंगे। अतः संख्या 221 प्राप्त हुई। 

(4) 8 × 9

संकेत:
(i) निकटतम आधार =10, अतः विचलन = - 2 एवं - 1 हैं।
(ii) विचलनों का गुणनफल = (- 2) × (- 1) = 2 
(iii) बाएँ पक्ष में 9 - 2 = 7 या 8 - 1 = 7 लिखेंगे। अतः संख्या 72 प्राप्त हुई। 

 

(5) 14 × 11

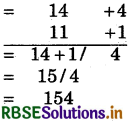
संकेत:
(i) निकटतम आधार = 10, अतः विचलन = + 4 और + 1 हैं।
(ii) विचलनों का गुणनफल = 4 × 1 = 4 
(iii) बाएँ पक्ष में लिखिए 14 + 1 = 5 या 11 + 4 = 15 लिखेंगे। अतः संख्या 154 प्राप्त हुई।

(6) 9 × 16

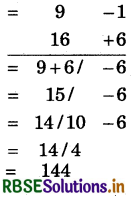
संकेत:
(i) निकटतम आधार = 10, अतः विचलन - 1 एवं + 6 हैं।
(ii) विचलनों का गुणनफल = (- 1) × 6 = - 6
(iii) बाएँ पक्ष में 9 + 6 = 15 या 16 - 1 = 15 लिखेंगे। 
(iv) दाईं ओर ऋणात्मक संख्या नहीं रखनी है अतः धनात्मक के लिए बाईं ओर से 1 लेने पर बाईं ओर 1 × 10 = -10 लिखेंगे। 
(v) 15 - 1 = 14 बाईं ओर लिखेंगे। अतः संख्या 144 प्राप्त हुई। 

 

(7) 12 × 13

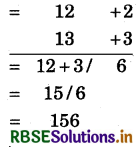
संकेत:
(i) निकटतम आधार = 10, अत: विचलन = + 2 और + 3 हैं।
(ii) विचलनों का गुणनफल = 2 × 3 = 6
(iii) बाएँ पक्ष में 2 + 3 = 15 या 13 + 2 = 15 लिखेंगे। अतः संख्या 156 प्राप्त हुई। 

(8) 13 × 10

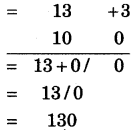
संकेत:
(i) निकटतम आधार = 10, अतः विचलन = + 3 और 0 हैं। 
(ii) विचलनों का गुणनफल = 3 × 0 = 0 
(iii) बाएँ पक्ष में 13 + 0 = 13 या 10 + 3 = 13 लिखेंगे। अतः संख्या 130 प्राप्त हुई।

 

महत्वपूर्ण प्रश्न:

बहुविकल्पीय प्रश्न:

प्रश्न 1. 
7564 - 3692 का मान है
(अ) 3872 
(ब) 4872 
(स) 3882 
(द) 3862 
हल : 
(अ) 3872 

प्रश्न 2. 
324 - 267 का मान है
(अ) 58 
(ब) 57 
(स) 56
(द) 55
हल : 
(ब) 57 

प्रश्न 3. 
2000 - 1854 का मान है| 
(अ) 246 
(ब) 244 
(स) 146 
(द) 145 
हल : 
(स) 146 

 

प्रश्न 4. 
7306 - 4291 का मान है
(अ) 3016 
(ब) 3017 
(स) 3014 
(द) 3015 
हल : 
(द) 3015 

प्रश्न 5. 
15 का 10 के आधार पर विचलन है
(अ) + 5 
(ब) - 5 
(स) 4 
(द) 6 
हल : 
(अ) + 5 

प्रश्न 6. 
4 का 10 के आधार पर विचलन है
(अ) - 4 
(ब) - 6
(स) + 6 
(द) + 4
हल : 
(ब) - 6

 

प्रश्न 7. 
15 × 13 का मान है
(अ) 185 
(ब) 175 
(स) 195 
(द) 205
हल : 
(स) 195

प्रश्न 8.
9 × 7 का मान है
(अ) 62 
(ब) 64 
(स) 73 
(द) 63. 
हल : 
(द) 63.

 

रिक्त स्थानों की पूर्ति कीजिए:

प्रश्न 1. 
किसी संख्या का चरम अंक उसका ................... का अंक होता है।
हल :
इकाई
 
प्रश्न 2. 
5 का एकाधिक ................... द्वारा व्यक्त किया जाता है।  
हल :
5

प्रश्न 3. 
8 का एक न्यून ................... होता है। 
हल :
3

प्रश्न 4. 
23 में अंक 3 का एकाधिक पूर्वेष ................... होता है। 
हल :
4

प्रश्न 5.
वैदिक गणित में गुणन संक्रिया की एक विधि ................... होती है। 
हल :
निखिलम् विधि।

 

अतिलघूत्तरीय/ लघूत्तरीय प्रश्न:

प्रश्न-1 व 2 को एक न्यूनेन पूर्वेण व परम मित्र अंक की सहायता से हल करो:

हल :
1.

संकेत:
(i) 4 से 5 नहीं घटाया जा सकता, अतः 5 के परम मित्र अंक 4 को अंक 4 में जोड़ा व योग फल = 9 नीचे लिखेंगे।
(ii) 4 के पूर्वेण अंक 6 पर एक न्यून चिह्न लगाएंगे। (6)
(iii) 6 = 5 में से 9 नहीं घटाया जा सकता अत:9 के परम मित्र अंक 1 को अंक 5 में जोड़ा व योगफल = 6 नीचे लिखेंगे। 
(iv) 6 के पूर्वेण अंक 8 पर एक न्यून चिह्न लगाएगे। (8) 
(v) 8 = 7, 7 में से 6 घटाया, 7 - 6 = 1 नीचे लिखेंगे। प्राप्त संख्या 169 है। 

2.

संकेत:
(i) 2 में से 5 नहीं घटाया जा सकता, अतः 5 के परम मित्र 5 को 2 में जोड़ा व योगफल  7 नीचे लिखेंगे एवं 2 के पूर्वेण अंक 3 पर एक न्यून चिह्न लगाएगें। (3) 
(ii) 3 = 2 में से 6 नहीं घटाया जा सकता, अतः 6 के परम मित्र 4 को 2 में जोड़ा एवं 3 के पूर्वेण अंक 4 पर न्यून लगाएंगे। (4) 
(iii) 4 = 3 में से 7 नहीं घटाया जा सकता, अतः 7 के परम मित्र 3 को 3 में जोड़ा एवं 4 के पूर्वेण अंक 9 पर न्यून लगाएंगे। (9) 
(iv) 9 = 8, अतः 8 - 8 = 0 लिखेंगे। प्राप्त संख्या 667 है।

 

प्रश्न 3. 
एकाधिकेन पूर्वेण तथा परम मित्र अंक की सहायता से हल कीजिए - 800 - 543
हल :

संकेत:
(i) 0 में से 3 नहीं घटाया जा सकता। अतः 3 के परम मित्र 7 को 0 में जोड़ा योगफल 7 नीचे लिखेगें नीचे की संख्या में 3 के पूर्वेण अंक 4 पर एकाधिक लगाएंगे। (4) 
(ii) 0 में से 4 = 5 नहीं घटाया जा सकता है, अतः 5 का परम मित्र 5 को अंक 0 में जोड़ा योगफल 5 नीचे लिखेगें।
(iii) 4 के पूर्वेण अंक 5 पर एकाधिक का चिह्न लगाएंगे। (5) 
(iv) 8 में से 5 = 6 घटाने पर, 8 - 6 = 2 लिखेगें। प्राप्त संख्या 257 है।

प्रश्न 4.
3 का विचलन 10 के आधार पर ज्ञात करो। 
हल : 
3 का 10 के आधार पर विचलन =3 - 10 = - 7 

प्रश्न 5. 
16 का विचलन 10 के आधार पर ज्ञात कीजिए।
हल : 
16 का 10 के आधार पर विचलन = 16 - 10 = + 6 

 

आधार 10 पर सूत्र निखिलम् द्वारा प्रश्न 6, 7. व 8 को हल कीजिए:

प्रश्न 6. 
12 × 16. 
हल : 

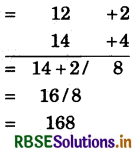
संकेत:
(i) निकटतम आधार = 10, अतः विचलन = + 2 और + 6 हैं।
(ii) विचलनों का गुणनफल = 2 × 4 = 8
(iii) बाएँ पक्ष में 12 + 4 = 16 या 14 + 2 = 16 लिखेगें। प्राप्त संख्या 168 है। 

प्रश्न 7.
8 × 12 

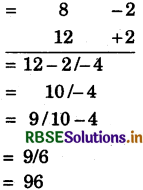
संकेत:
(i) निकटतम आधार = 10, अतः विचलन = - 2 एवं + 2 हैं।
(ii) विचलनों का गुणनफल (- 2) × (2) = - 4.
(iii) बाएँ पक्ष में 12 - 2 = 10 या 8 + 2 = 10 लिखेगें। 
(iv) दाईं ओर ऋणात्मक संख्या नहीं रखनी है अतः धनात्मक के लिए बाईं ओर से 1 लेने पर बाईं ओर 1 × 10 = 10 लिखेगें। 
(v) अतः 10 - 1 = 9 बाईं ओर लिखेगें प्राप्त संख्या 96 है।

 

प्रश्न 8. 
15 × 17 

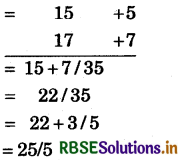
= 255

संकेत:
(i) निकटतम आधार = 10, अतः विचलन + 5 एवं + 7 हैं। 
(ii) विचलनों का गुणनफल = 5 × 7 = 35
(iii) बाएँ पक्ष में 15 + 7 = 22 या 17 + 5 = 22 लिखेंगे। 
(iv) दाएँ पक्ष में दो अंक है अतः एक अंक बाईं ओर स्थानांतरित करेंगे (क्योंकि आधार 10 में एक - शून्य है अतः एक अंक रहेगा।). 
(v) 22 + 3 = 25 लिखेगें।