RBSE Solutions for Class 5 Maths Chapter 4 Vedic Mathematics

Rajasthan Board RBSE Solutions for Class 5 Maths Chapter 4 Vedic Mathematics Textbook Exercise Questions and Answers.

RBSE Class 5 Maths Solutions Chapter 4 Vedic Mathematics

Exercise 4.1 

Subtract the following with the help of Ekanyunena Puryena and Param mitra (friendly number) Sutra:

Solution:    

(1)  

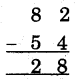
Hint:
(i) We cannot subtracted 4 from 2 so add param mitra number. 6 of 4, in 2 and write sum = 8 below the line.
(ii) Mark Ekanyunena mark at 8, purvena digit of 2 (8).
(iii) Subtract 5 from 8 = 7 and will write below the line, we get number 28.

(2)

Hint:
(i) 8 cannot subtracted from 6. So, add 2, param mitra of 8, in 6 and write sum 8 below the line.
(ii) Mark Ekanyunena mark at 6 purvena number, of 6 (6).
(iii) Subtract 4 from 6 = 5 and write bellow the line we get number 18.

(3)

Hint:
(i) 9 cannot subtracted from 4, so param mitra of 9 i.e., 1 is added to 4 and write sum = 5 below the line.
(ii) Mark Ekanyunena mark at 7 purvena digit of 4.
(iii) Subtract 6 from 7 = 6 and write below the line, we get number 5.

(4)

Hint: 
(i) 3 cannot subtracted from 2, so param mitra of 3 i.e., T is added to and write sum = 9 below the line.
(ii) Mark Ekanyunena mark at 4, purvena digit of 2 (4).
(iii) 4 cannot subtracted from 4 = 3, so param mitra digit of 4 i.e., 6 is added to 3 and write sum = 9 below the line.
(iv) Mark Ekanyunena mark at 3 purvena digit of 4.
(v) Subtract 1 from 3 = 2 write 2 - 1 = 1 below the line we, get number 199.

(5)

Hint:
(i) 7 cannot subtracted from 4 so param mitra of 7 i.e., 3 is added and write sum = 7 below the line.
(ii) Mark Ekanyunena sign at 2, purvena digit of 4(2).    .
(iii) 6 cannot subtracted from 2 = 1, so param mitra of 6 i.e., 4 is added to 1 and write s\im = 5 below the line.
(iv) Mark Ekanyunena sign at (5), purvena digit of 2 (5).
(v) Subtracts from 5 = 4, write 4 - 2 = 2 under the line, we get number 257.
 
(6)

Hint:
(i) 6 cannot subtracted from 5 so param mitra of 6 i.e., 4 is added to 5 and write sum = 9 below the line.
(ii) Mark purvena digit of 5 (4).
(iii) 7 cannot subtracted from from 4 = 3, so param mitra digit of 7 i.e., 3 is added to 3 and write sum = 6 under the line.
(iv) Mark Ekanyunena sign at 9, purvena digit of 4 (9).
(v) Subtract 8 from 9 = 8, write 8 - 8 = 0 under the line, we get number 69.

(7)

Hint:
(i) 6 cannot subtracted from 2. so param mitra of    6 i.e., 4 is added to 2 and write sum = 6 under the line and mark Ekanyunena sign at 6, purvena digit of 2.
(ii) 3 cannot subtracted from 6 = 5, so write 6-3 = 2 under the line.
(iii) Now, 5 cannot subtract from 1, so param mitra of 5 added to 1 and mark
Ekanyunena sign at purvena digit 4(4)
(iv) 4 - 3, so write 3 - 2 = 1, we get 1626. 

(8)

Hint:
7 cannot subtracted from 4, so param mitra of 7, i.e., 3 is added to 4 and write sum = 7 under the line and mark
Ekanyunena sign at 6, purvena digit of 4 (6).
(ii) 9 cannot subtracted from 6 = 5, so param mitra of 9 i.e., 1 is added to 5 and mark Ekanyunena sign at 2, purvena digit of 6 (2)
(iii) 8 cannot subtract from 2 = 1, so param mitra of 8 i.e., 2 is added ttf 1 and mark Ekunyunena sign at 7, purvena digit (7).
(iv) 7 = 6, so write 6 -3 = 3 we get number 3367.

(9)

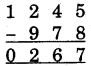
Hint:

(i) 8 cannot subtracted from 5, so param mitra of 8, 2 is added to 5 and write sum = 7 under the line and mark Ekanyunena sign at 4, purvena digit of 5 (4).
(ii) 7 cannot subtracted from 4 = 3, so param mitra of 7 i.e., 3 is added to 3 and mark Ekanyunena sign at 2, purvena digit of 2 (2).
(iii) 9 cannot subtracted from 2 = 1, so param mitra of 9 i.e., 1 is added to 1 and mark Ekanyunena sign at 1, purvena digit (1).
(iv) 1 = 0, so write 0 under the line, we get number 267.    

Exercise 4.2

Subtract the following with the help of Ekadhikena Purvena and Param mitra (best friend) Sutra:

(1)  

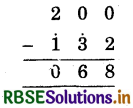
Hint:
(i) 2 cannot subtractrd from 0, so param mitra digit of 2, i.e., 8 is added to 0 and write sum = 8 under the line.
(ii) Mark Ekadhikena sign at 3, purvena digit of 2 (3).
(iii) 3 = 4 cannot subtracted from 0. Param mitra digit of 4 i.e., 6 is added to 0 and write sum = 6 under the line.
(iv) Mark Ekadhikena sign at 1, purvena digit of 3 (i).
(v) Subtract 1 = 2 from 2, write 2 - 2 = 0 under the line, we get number 68.

(2)

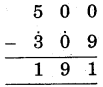
Hint:

(i) 9 cannot subtracted from 0, so param mitra digit of 9, i.e., 1 is added to 0 write sum = 1 under the line. 
(ii) Mark Ekadhikena sign at 0, purvena digit of 9(0).
(iii) 0 = 1 cannot subtract from 0 so param mitra digit of 1 i.e., 9 is added to 0 and write sum = 9 under the line.
(iv) Mark Ekadhikena sign at 3, purvena digit of 0.
(v) Subtract 3 = 4 from 5, write 5 - 4 = 1 under the line, we get number 191.

(3)

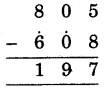
Hint:
(i) 8 cannot subtracted from 5, so param mitra digit of 8, i.e., 2 is added to 5 and write sum = 7 under the line.
(ii) Mark Ekadhikena sign at 0, purvena digit of 80).
(iii) Subtract 0 = 1 from 0, so pararn mitra digit of 1 i.e., 9 is added 0 and write sum = 9 under the line.
(iii) Mark Ekadhikena sign at 6, purvena digit of 0(6).
(iv) Subtract 6 = 7 from 8, write 8 - 7 = 1 under the line, we get number 197.

(4)

Hint:
(i) 3 cannot subtracted from 0, thus param mitra of 3 i.e 7 is added to 0 and write sum = 7 under the line
(ii) 7 = 8 cannot subtracted from 0, so param mitra of 8 i.e., 2 is added to 0 and mark Ekadhikena sign at purvena digit of 7 (9).
(iii) 9 = 10 cannot subtracted from 7, so param mitra of lo i.e., 0 is added to 7 and mark Ekadhikena sign at 0, purvena digit of 9(0).
(iv) Subtract 0 = 1 from 1 mark Ekadhikena sign (0).
(v) Subtract 0 = 1 from 1, write 0 under the line, we get number 727.

(5)

Hint:
(i) Subtract 1 from 5 write 4 under the line.
(ii) 8 cannot subtracted from 0, so param mitra of 8 i.e., 2 is added to 0 and write sum = 2 under the line and mark Ekadhikena sign at 2, purvena digit of 8 (2).
(iii) Subtract 2 = 3 from 3 write 0 under the line.
(iv) Subtract 5 from 8 write 3 under the line, we get number 3024.

(6)

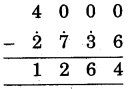
Hint:
(i) 6 cannot subtracted from 0, so param mitra of 6 i.e., 4 is added to 0 and write sum = 4 under the line and mark Ekadhikena sign at 3, purvena digit of 6(3).
(ii) 3 = 4 cannot subtracted from 0, so param mitra of 4 i.e., 6 is added to 0 and mark Ekadhikena sign at purvena digit of 3 (7).
(iii) 7 = 8 cannot subtracted from 0, so param mitra of 8 i.e., 2 is added to 0 and mark Ekadhikene sign at purvena digit 2(2).
(iv) Subtract 2 = 3 from 4 and write under the line we get number 1264.

(7)

Hint:
(i) 4 cannot subtracted from 0, so param mitra of 4 i.e, 6 is added to 0 and write sum 6 under the line and mark Ekadhikena sign at 0, purvena digit of 4 (6).
(ii) 6 = 1 cannot subtracted from 0, so param mitra of 1 i.e., 9 is added to 0 and mark Ekadhikena sign at purvena digit of 0 (9).
(iii) 9 = 10 cannot subtracted from 7, so param mitra of 10 i.e., 0 is added to 7 apd mark Ekadhikena sign at purvena digit 4(4).
(iv) Subtract 4 = 5 from 9 and write under the line we get number 4796.

(8)

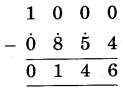
Hint:
(i) 4 cannot subtracted from 0, so param mitra of 4 i.e, 6 is added to 0 4 and Write sum = 6 under the line and mark Ekadhikena sign at 5, purvena digit of 4.
(ii) 5 = 6 cannot subtracted from 0, so param mitra of 6 i.e., 4 is added to 0 and mark Ekadhikena sign at purvena digit of 5(8).
(iii) 8 = 9 cannot subtracted from 0, so param mitra of 9 i.e., 1 is added to 0 and mark Ekadhikena sign at purvena digit 0(0).
(iv) Subtract 6 = 1 from 1 and write under the line, we get number 146.

(9)

Hint:
(i) 6 cannot subtracted fr0m 0, so param mitra of 6 i.e, 4 is added to 0 and write sum = 4 under the line and mark Ekadhikena sign at 9, purvena digit of 6 (9).
(ii) 9 = 10 cannot subtracted from 0, so param mitra of 10 i.e., 0 is added to 0 and mark Ekadhikena sign at purvena digit of 9 (8).
(iii) 8 = 9 cannot sutracted from 0, so param mitra of 9 i.e., 1 is added to 0 and mark Ekadhikena sign at purvena digit 3 (3).
(iv) Subtract 3 = 4 from 9 and write 5 under the line, we get number 5104.

Exercise 4.3
    
Question. 
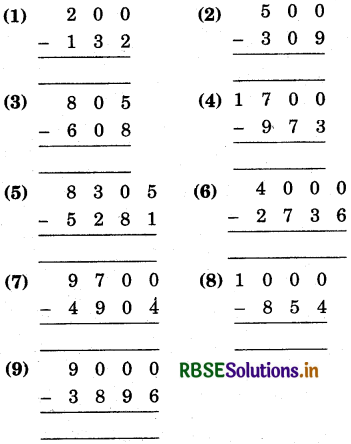
Write down the deviation of following on base 10.
1.    Deviation of 14 ........................    
2.    Deviation of 11 ........................                 
3.    Deviation of 8 ........................
4.    Deviation of 9 ........................
5.    Deviation of 13 ........................
6.    Deviation of 19 ........................
7.    Deviation of 7 ........................
8.    Deviation of 6 ........................
Solution: 
1. Deviation of 14 = 14 - 10 = + 4
2. Deviation of 11 = 11 - 10 = + 1
3. Deviation of 8 = 8 - 10 = - 2
4. Deviation of 9 = 9 - 10 = - 1
5. Deviation of 13 = 13 - 10 = + 3
6. Deviation of 19= 19 - 10 = + 9
7. Deviation of 7 = 7 - 10 = - 3
8. Deviation of 6 = 6 - 10 = - 4

Exercise 4.4

Question. 
Multiply by Nikilam Sutra at base 10.
(1) 12 × 9
(2) 15 × 12
(3) 13 × 17 
(4) 8 × 9
(5) 14 × 11 
(6) 9 × 16
(7) 12 × 13 
(8) 13 × 10
Solution: 
(1) 12 × 9

 
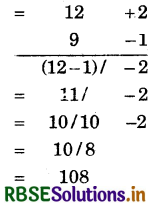
Hint:
(i) Closest base = 10, so deviation are + 2 and - 1.
(ii) Multiplication of deviations = 2 × (- 1) = - 2
(iii) In LH.S., write 12 - 1 = 11 or 9 + 2 = 11
(iv) Negative number cannot be put on R.H.S. So, borrow one carry from L.H.S. and make it + ve. Therefore, 10 × 1 = 10 on L.H.S.
(v) On left side, write 11 - 1 = 10, so we get number 108.

(2) 15 × 12

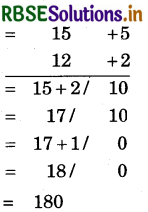
Hint:
(i) Closest base = 10, so deviations are + 5 and + 2.
(ii) Multiplication of deviations = 5 × 2 = 10
(iii) In L.H.S., write 15 + 2 = 17 or 12 + 5 = 17
(iv) On left side, there are 2 digits, so we have to shift one digit from right side (because base 10 has only one zero, therefore only one digit will remain on R.H.S.)
(v) On left side write 17 + 1 = 18, so we get number 180.

 

(3) 13 × 17

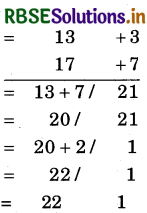
Hint:
(i) Closest base = 10, so deviations are + 3 and + 7.
(ii) Multiplication of deviations = 3 x 7 = 2i
(iii) In L.H.S., write 13 + 7 = 20 or 17 + 3 = 20
(iv) On left side, there are 2 digits, so we have to shift one digit from R.H.S. (because base 10 has only one zero, therefore only one digit will remain on R.H.S.)
(v) Write 20 + 2 = 22, so we get number 221.

(4) 8 × 9

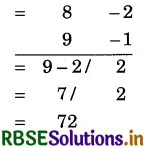
Hint:
(i) Closest base = 10, so deviations are - 2 and - 1.
(ii) Multiplication of . deviations = (- 2) × (- 1) = 2.
(iii) In L.H.S., write 9 - 2 = 7 or 8 - 1 = 7 Thus number obtained is 72.

(5) 14 × 11

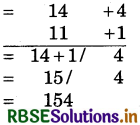
Hint:
(i) Closest base = 10, so deviations are + 4 and + 1.
(ii) Multiplication of deviations = 4 × 1 = 4
(iii)    In L.H.S., write 14 + 1 = 15 or 11 + 4 = 15, so we get number 154.

(6) 9 × 16

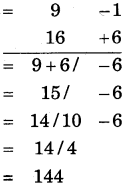
Hint:
(i) Closest base = 10, so deviations are - 1 and + 6.
(ii) Multiplication of deviations = (- 1) × 6 = - 6
(iii) In L.H.S., write 9 +6 = 15 or 16 - 1 = 15
(iv) Negative number cannot be put on R.H.S., so borrow one carry from L.H.S. and make it +ve. Therefore, write 1 × 10 = 10 in L.H.S.
(v) Write 15 - 1= 14 in L.H.S., so number obtained is 144.

(7) 12 × 13

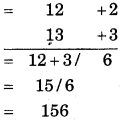
Hint:
(i) Closest base = 10, so deviations are + 2 and + 3.
(ii) Multiplication of deviations = 2 × 3 = 6 
(iii) In L.H.S. write 2 + 3 = 15 or 13 + 2 = 15, so we get number 156.

(8) 13 × 10

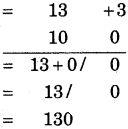
Hint
(i) Closest base = 10, so deviations are + 3 and 0.
(ii) Multiplication of deviations = 3 × 0 = 0
(iii) In L.H.S., write 13 + 0 = 13 or 10 + 3 = 13, so we get number 130.

 
Important Questions:

Multiple Choice Questions:

Question 1.    
The value of 7564 - 3642 is :
(a) 3922    
(b) 4872    
(c) 3882    
(d) 3862
Solution:
(a) 3922    

Question 2.    
The value of 324 - 267 is :
(a) 58    
(b) 57    
(c) 56    
(d) 55
Solution:
(b) 57    

Question 3.    
The value of 2000 - 1854 is :
(a) 246    
(b) 244    
(c) 146    
(d) 145
Solution:
(c) 146    

Question 4.    
The value of 7306 - 4291 is :
(a) 3016    
(b) 3017    
(c) 3014 
(d) 3015
Solution:
(d) 3015

Question 5.    
The deviation of 15 on base 10 is
(a) + 5    
(b) - 5    
(c) 4    
(d) 6
Solution:
(a) + 5    

Question 6.    
The deviation of 4 on base 10 is :
(a) - 4    
(b) - 6    
(c) + 6    
(d) + 4
Solution:
(b) - 6    

Question 7.    
The value of 15 x 13 is :
(a) 185    
(b) 175    
(c) 195    
(d) 205
Solution:
(c) 195

Question 8.    
The value of 9 × 7 is :
(a) 62    
(b) 64    
(c) 73    
(d) 63
Solution:
(d) 63

Fill in the blanks:

Question 1.    
The extreme digit of a number is its ................. digit.
Solution:
unit

Question 2.    
Ekadhik of 5 in shown by .................
Solution:
6

Question 3.    
Elenune of 8 in    .................
Solution:
7

Question 4.    
Ekadhik Poorvena of 3 in 23 is .................
Solution:
33

Question 5.        
................. is a method of multiplication operation in vedic mathematics.
Solution:
Nikhilam method.

Very Short / Short Answer Type Questions:

Question. 
Solve the following questions 1 and 2 with the help of Ekadhikena purvena and Param mitra digit.

(1)

Solution:
Hint
(i) 5 cannot subtracted from 4, so param mitra digit of 5 i.e., 5 is added to digit 4 and write sum = 9. 
(ii) Mark Ekanyunena digit of 4 (6). 
(iii) 9 cannot subtracted from 6 = 5, so param mitra digit of 9 i.e., 1 is added to 5 and write sum = 6 under the line.
(iv) Mark Ekanyunena sign at 8, purvena digit of 6.
(v) 8 = 7, subtract 6 from 7, 7 - 6 = 1. Write 1 under the line we get number 169.

2.    

Hint
(i) 5 cannot subtract from 2, so param mitra digit 0f 5 i.e 5 is 5 ie., added to 2 and write sum 7 under the line and markEkanyunena mark at 3 purvena digit of 3 (3)
(ii) 6 cannot subtracted from 3 = 2, so param mitra of 6 i.e., 4 is added to 2 and mark Ekanyunena sign at 4 purvena digit of 3 (4).
(iii) 7 cannot subtracted from 4 = 3, thus param mitra of 7 i.e., 3 is added to 3 and mark Ekanyunena sign 9, purvena digit of 4.
(iv) 9 = 8, so write 8 - 8 = 0. The number obtained is 667.

Question 3. 
With the help of Ekadhikena purvena and Param mitra digit, solve 800 - 543.
Solution:    

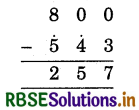
Hint:
(i) 3 cannot subtracted from 0, so param mitra digit of 3, i.e., 7 is added to zero write sum = 7 under the line. Mark Ekadhikena sign at 4, purvena digit of 3 (4)
(ii) 4 = 5 cannot subtracted from 0, so param mitra of 5 i.e., 5 is added to 0 and write sum 5 under the line.
(iii) Mark Ekadhik sign at 5, purvena digit of 4.
(iv)    Subtract 5 = 6 from 8, write 8 - 6 = 2. The number obtained is 257.

Question 4. 
Find deviation of 3 at the base 10. 
Solution: 
Deviation of 3 on the base 10 = 3 - 10 = - 7.

 
Question 5. 
Find deviation of 16 at the base 10. 
Solution: 
Deviation of 16 on the base 10 = 16 - 10 = + 6.

Solve Q. 6, 7 and 8 by Nikhilam Sutra at base 10.
Solution:

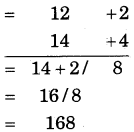
Hint:
(i) Closest base = 10, so deviations are + 2 and + 6.
(ii) Multiplication of deviations = 2 x 4 = 8
(iii) In L.H.S., write 12 + 4 = 16 or 14 + 2 = 16. The obtained number is 168.

 

Question 7.
8 × 12

Solution:

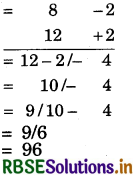
Hint:
(i)    Closest base = 10, so deviations are - 2 are + 2.
(ii)    Multiplication of deviations = (- 2) × (2) = - 4
(iii)    In L.H.S., write 12 - 2 = 10 or 8 + 2 = 10
(iv)    Negative number cannot be put on right side. So, borrow one carry from left side and make it positive. Therefore, write 1 × 10 = 10 on left side.
(v)    Write 10 - 1 = 9 on L.H.S. The number obtained is 96.

 

Question 8.
15 × 17

Solution:

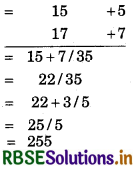
(i) Closest base = 10, so deviations are + 5 and + 7.
(ii) Multiplication of deviations = 5 × 7 = 35
(iii) In L.H.S.; write 15 + 7 = 22 or 17 + 5 = 22
(iv) There are two digits in the right side. So one digit will be transferred to the left side. (Because in base 10 one digit is zero so there will be one digit.
(v) We write 22 + 3 = 25.