RBSE Class 11 Economics Notes Chapter 6 Measures of Dispersion

These comprehensive RBSE Class 11 Economics Notes Chapter 6 Measures of Dispersion will give a brief overview of all the concepts.

RBSE Class 11 Economics Chapter 6 Notes Measures of Dispersion

Measures of Dispersion
Dispersion is the extent to which values in a distribution vary from the average of the distribution.

Measures of Dispersion

• Absolute measures - expressed in terms of original units of a data
• Relative measures - expressed in terms of percentage and ratios

Absolute measures of dispersion are range, quartile deviation, mean deviation and standard deviation.
Relative measures of dispersion are coefficient of range, coefficient of quartile deviation, coefficient of mean deviation and coefficient of variance.

Range and its Coefficient
Range is the difference between the highest (H) and lowest (L) value in a series. It can be calculated by using the formula:
Range = H - L
Higher value of range implies higher dispersion.
Range is unduly affected by extreme values.

Coefficient of range:
Coefficient of range is the ratio of the difference between the highest and lowest values to the sum of the lowest and highest values of the series.
Coefficient of Range = \(\frac{H-L}{H+L}\)

Quartile Deviation and its Coefficient
Inter-quartile range is the difference between the third (Q₃) and first (Q₁) quartile of a series, that is:
I Inter-quartile Range =  Q₃ - Q₁
It is based on the 50 per cent values in the distribution.

Half of the inter-quartile range is quartile deviation.
Quartile deviation can be calculated by using the formula:
Quartile Deviation = \(\frac{Q_3-Q_1}{2}\)

Coefficient of quartile deviation can be calculated as:
Coefficient of Quartile Deviation = \(\frac{Q_3-Q_1}{Q_3+Q_1}\)

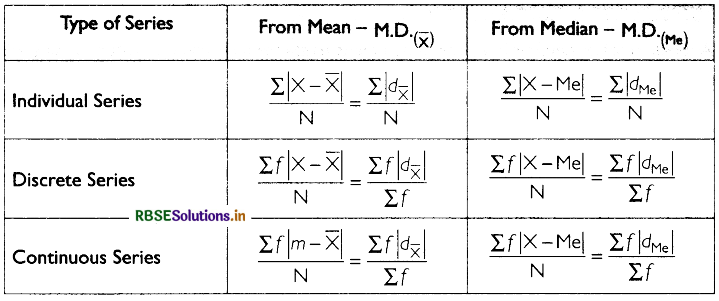
Mean Deviation and its Coefficient

• Mean deviation is the arithmetic average of the deviations of all the values taken from average value ; (mean or median) of the series.
• The algebraic signs (+ or -) of the deviations are ignored while calculating mean deviation.

Formulae for Calculating Mean Deviation

Standard Deviation and Coefficient of Variance
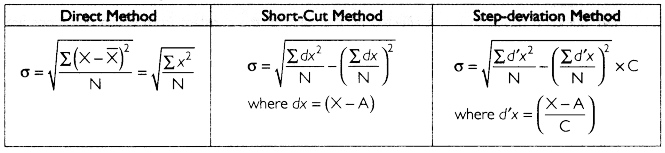
Standard deviation (σ) is the square root of the arithmetic mean of the squares of all deviations.
Formulae for Calculating Standard Deviation

Variance is the square of standard deviation: σ²

• Standard deviation is independent of origin, that is, it is not affected by the constant from which deviations are taken.
• Standard deviation is not independent of scale, that is, if the deviations are divided by a common factor, its value is used in the formula to obtain standard deviation.
• Coefficient of variation is the percentage variation in the mean. It can be calculated as:
  C.V. = \(\frac{\sigma}{\overline{\bar{x}}}\) × 100

Lorenz Curve

• Lorenz curve is the graphical representation of dispersion. It compares the variability of two or more distributions.
• Lorenz cunve indicates the degree of variability through the information expressed in a cumulative form.
• A 45° straight line in the Lorenz curve is the line of equal distribution.
• When there are two or more curves, the one which is the farthest from line of equal distribution has the highest dispersion.