RBSE Solutions for Class 11 Physics Chapter 9 ठोसों के यांत्रिक गुण

Rajasthan Board RBSE Solutions for Class 11 Physics Chapter 9 ठोसों के यांत्रिक गुण Textbook Exercise Questions and Answers.

RBSE Class 11 Physics Solutions Chapter 9 ठोसों के यांत्रिक गुण

RBSE Class 11 Physics ठोसों के यांत्रिक गुण Textbook Questions and Answers

प्रश्न 9. 1.
4. 7m लंबे व 3.0 x 10⁵ m² अनुप्रस्थ काट के स्टील के तार तथा 3.5mm लंबे व 4.0 x 10^-5 m² अनुप्रस्थ काट के ताँबे के तार पर दिये गये समान परिमाण के भारों को लटकाने पर उनकी लम्बाइयों में समान वृद्धि होती है। स्टील तथा ताँबे के यंग प्रत्यास्थता गुणांकों में क्या अनुपात है? 
उत्तर:
दिया गया है:
स्टील के तार के लिए
तार की लम्बाई L₁ = 4.7m
अनुप्रस्थ काट A₁ = 3.0 × 10 m² 
लम्बाई में समान वृद्धि l₁ = / (माना) है
तांबे के तार के लिए
तार की लम्बाई L₂ = 3.5m
अनुप्रस्थ काट A₂ = 4.0 × 10^-5 m²
लम्बाई में समान वृद्धि l² = / (माना)
दिया गया है:
F¹ = F² = F
माना कि स्टील व ताँबे के यंग गुणांक क्रमश Y₁ और Y₂ हैं

 

प्रश्न 9.2 
नीचे चित्र 9.11 में किसी दिये गये पदार्थ के लिये प्रतिबल - विकृति वक्र दर्शाया गया है। इस पदार्थ के लिये (a) यंग प्रत्यास्थता गुणांक (b) सन्निकट पराभव सामर्थ्य क्या है?

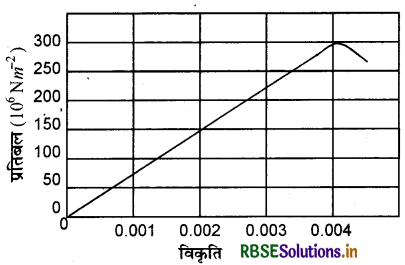
उत्तर:
प्रतिबल विकृति वक्र से स्पष्ट है कि 150 x 10⁶ N/m²
प्रतिबल के लिए 0.002 विकृति है।
(a) पदार्थ का यंग गुणांक (Y)

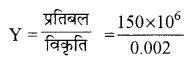
= 75 × 10⁹
= 7.5 × 10¹⁰ N/m² द्वारा दिया जाता है।

(b) पराभव शक्ति का अर्थ यह है कि अधिकतम वह प्रतिबल
जिसे वह सहन कर सके
आरेख से दत्त पदार्थ की पराभव सामर्थ्य लगभग
300 × 10⁶ N/m² = 3 x 10⁸ N/m² है।

प्रश्न 9.3.  
दो पदार्थों A और B के लिए प्रतिबल विकृति ग्राफ चित्र में दर्शाये गये हैं।

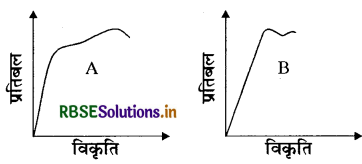
इन ग्राफों को एक ही पैमाना मानकर खींचा गया है। 
(a) दोनों पदार्थों में से यंग प्रत्यास्थता गुणांक किसका अधिक
(b) दोनों पदार्थों में कौन अधिक मजबूत है?
उत्तर:
(a) दोनों दत्त आरेखों की ढाल (slope ) से स्पष्ट है A के लिए प्रतिबल का मान B से अधिक है। इसलिए यंग गुणांक 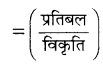का मान B की अपेक्षा A का अधिक है।
(b) किसी पदार्थ की सामर्थ्य उस प्रतिबल से निर्धारित की जाती है जो पदार्थ के विखण्डन बिन्दु के संगत उसको विखण्डित करे या उसमें विभंजन उत्पन्न करे। चूंकि B की अपेक्षा पदार्थ A की सामर्थ्य अधिक है क्योंकि B बिन्दु के संगत A बिना विखण्डित हुए अधिक भार वहन कर सकता है, B नहीं।

प्रश्न 9.4. 
निम्नलिखित दो कथनों को ध्यान से पढ़िये और कारण सहित बताइये कि वे सत्य हैं या असत्य
(a) इस्पात की अपेक्षा रबड़ का यंग गुणांक अधिक है। 
(b) किसी कुण्डली का तनन उसके अपरूपण गुणांक से निर्धारित होता है।
उत्तर:
(a) असत्य है। यह ऐसा इसलिए है कि यदि हम स्टील व रबर के समान लम्बाई व अनुप्रस्थ काट वाले तारों पर समान विरूपण बल लगाया जाये तो रबर की अपेक्षा स्टील में कम खिंचाव होता है। इसलिए Ys > Yr। दूसरे शब्दों में इसे इस प्रकार से कह सकते हैं। कि स्टील व रबर में समान विकृति उत्पन्न करने के लिए हमें स्टील पर अधिक प्रतिबल लगाना पड़ेगा।
(b) सत्य है। इसका कारण यह है कि न तो कुण्डलिनी कमानी की लम्बाई अर्थात् कमानी बनाने वाले तार की लम्बाई और न ही इसके आयतन में परिवर्तन होता है। चूंकि कुण्डली की आकृति में ही परिवर्तन होता है। अतः कुण्डली का तनन उसके अपरूपण गुणांक से निर्धारित होता है।

प्रश्न 9.5 
0.25 सेमी. व्यास के दो तार, जिनमें एक इस्पात का तथा दूसरा पीतल का है, चित्र के अनुसार भारित है। बिना भार लटकाये इस्पात तथा पीतल के तारों की लंबाइयाँ क्रमश: 1.5m तथा 1.0m हैं। यदि इस्पात तथा पीतल के यंग गुणांक क्रमशः 2.0 x 10¹¹ Pa तथा 0.91 x 10¹¹ Pa हों तो इस्पात तथा पीतल के तारों में विस्तार की गणना कीजिए।

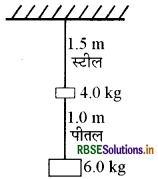
उत्तर:
स्टील तार के लिए
स्टील तार पर कुल बल का मान
F₁ = 4 + 6 = 10kg भार
F₁ = 10 × 9.8N
l₁ = 1.5m 
∆l₁ = ? 
2r₁ =0.25cm
\(r_1=\frac{0.25}{2}\)
= 0.125 × 10^-2 m
Y = 2.0 x 10¹¹ Pa
इस्पात तार के लिए
F₂ = 6.0kg भार = 6 × 9.8N
2r₂ = 0.25cm
∴ r₂ = 0.25/2 = 0.125cm
r₂ = 0.125 × 10^-2m
l₂ =1.0m.  ∆l₂ = ?
Y₂ = 0.91 × 10¹¹ Pa
हम जानते हैं

प्रश्न 9.6. 
ऐलुमिनियम के किसी घन के किनारे 10 सेमी. लंबे हैं। इसकी एक फलक किसी ऊर्ध्वाधर दीवार से कसकर जड़ी हुई है। इस घन के सम्मुख फलक से 100 किग्रा. का एक द्रव्यमान जोड़ दिया गया है। ऐलुमिनियम का अपरूपण गुणांक 25 GPa है। इस फलक का ऊर्ध्वाधर विस्थापन कितना होगा?
उत्तर:
दिया गया है:
यहाँ पर घन की भुजा
L = 10cm = 0.1m 
एक फलक का क्षेत्रफल
= L x L
= 0.1 × 0.1
= 0.01m²
∴ A = 0.01m²

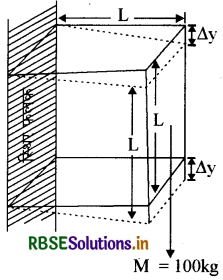
माना इस फलक का
ऊर्ध्वाधर विस्थापन ∆L है।
फलन 1 का संलग्न द्रव्यमान M = 100kg
M = 100kg
इस द्रव्यमान के कारण फलन 1 पर बल F का मान होगा
F = Mg = 100 × 9.8N
फलक पर अपरूपण प्रतिबल का मान = F/A
\(=\frac{100 \times 9.8}{0.01} \mathrm{~N} / \mathrm{m}^2\)
= 9.8 × 10⁴ N/m²
लेकिन दिया गया है ऐलुमिनियम का अपरूपण गुणांक
n = 25 G pa = 25 गीगा पास्कल
= 25 x 10⁹ पास्कल = 25 x 10⁹ N/m²

∴ फलक का ऊर्ध्वाधर विस्थापन ∆L = 4 x 10^-7m 

प्रश्न 9.7. 
मृदु इस्पात के चार समरूप खोखले बेलनाकार स्तम्भ 50,000 kg द्रव्यमान के किसी बड़े ढाँचे को आधार दिये हुए हैं। प्रत्येक स्तम्भ की भीतरी तथा बाहरी त्रिज्याएँ क्रमशः 30 तथा 60 cm हैं। भार वितरण को एकसमान मानते हुए प्रत्येक स्तम्भ की संपीडन विकृति की गणना कीजिए।
उत्तर:
दिया गया है:
प्रत्येक स्तम्भ पर संपीडन बल
\((F)=\frac{50000}{4} \mathrm{~kg}\)
\(\mathrm{F}=\frac{50000}{4} \times 9.8 \mathrm{~N}\)
एक स्तम्भ की आंतरिक त्रिज्या,
r₁ = 30cm = 0.3m
स्तम्भ की बाहरी त्रिज्या
r₂ = 60cm = 0.6m 
∴ प्रत्येक स्तम्भ की अनुप्रस्थ काट 
= A = (r₂² - r₁²) 
= π[(0.6)² - (0.3)²] 
= π[0.36 - 0.09]

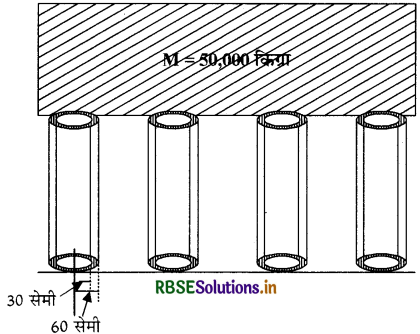
= 0.27πमीटर²
यंग का प्रत्यास्थता गुणांक, Y
= 2 × 10¹¹ Pa
प्रत्येक स्तम्भ की संपीडन विकृति = ?

∴ सभी स्तम्भों की संपीडन विकृति
= 0.722 × 10^-6 × 4
= 2.88 × 10^-6 (मात्रकहीन)

प्रश्न 9.8. 
ताँबे का एक टुकड़ा, जिसका अनुप्रस्थ परिच्छेद 15.2mm × 19.1 mm का है, 44,500 N बल के तनाव से खींचा जाता है, जिससे केवल प्रत्यास्थ विरूपण उत्पन्न हो। उत्पन्न विकृति की गणना कीजिए।
उत्तर:
दिया गया है:
Y = 1.1 × 10¹¹ N/m²
अनुप्रस्थ काट (A) = 15.2 × 10^-3 × 19.1 × 10^-3 m²
= 15.2 × 19.1 × 10^-6 m²
बल (F) = 44,500N
विकृति = ?
हम जानते हैं

= 0.00139 (मात्रकहीन) 

प्रश्न 9.9. 
1.5 cm का एक इस्पात का केबिल भार उठाने के लिए इस्तेमाल किया जाता है। यदि इस्पात के लिए अधिकतम अनुज्ञेय प्रतिबल 10 Nm² है तो उस अधिकतम भार की गणना कीजिए जिसे केबिल उठा सकता है।
उत्तर:
केबिल की त्रिज्या = 1.5cm = 1.5 × 10^-2 m
अधिकतम अनुज्ञेय प्रतिबल = 108 N/m²
= A = πr?
केबल का अनुप्रस्थ काट =
= π(1.5 × 10^-2)²
= π × 2.25 × 10^-4 m²
अधिकतम भार = अधिकतम बल = ?

अधिकतम बल = अधिकतम प्रतिबल x अनुप्रस्थ काट
= 108 x π x 2.25 × 10^-4
= 2.25 × 3.14 × 10⁴
= 7.065 × 10⁴N 

प्रश्न 9.10. 
15 kg द्रव्यमान की एक दृढ़ पट्टी को तीन तारों, जिनमें प्रत्येक की लंबाई 2m है, से सममित लटकाया गया है। सिरों के दोनों तार ताँबे के हैं तथा बीच वाला लोहे का है। तारों के व्यासों के अनुपात निकालिए, प्रत्येक पर तनाव उतना ही रहना चाहिए।
उत्तर:
माना ताँबे तथा लोहे के तारों का व्यास क्रमश: d₁ तथा d₂ है। तब उनके क्षेत्रफल

माना ताँबे तथा लोहे की यंग प्रत्यास्थता गुणांक क्रमश: Y1 तथा Y2
ताँबे के तार के लिये विकृति

d₁ : d₂ : : 131 : 1

प्रश्न 9.11. 
एक मीटर अतानित लंबाई के इस्पात के तार के एक सिरे से 14.5 kg का द्रव्यमान बाँध कर उसे एक ऊर्ध्वाधर वृत्त में घुमाया जाता है, वृत्त की तली पर उसका कोणीय वेग 2 rev/s है। तार के अनुप्रस्थ परिच्छेद का क्षेत्रफल 0.065 cm² है। तार में विस्तार की गणना कीजिए जब द्रव्यमान अपने पथ के निम्नतम बिंदु पर है।
उत्तर:
दिया गया है:
तार के 'एक सिरे पर लटका द्रव्यमान, m = 14.5 kg . 
लोहे के तार की लम्बाई l = Im. 
आवृत्ति n = 2 
चक्कर / सेकण्ड = 2 rps
∴ कोणीय आवृत्ति
ω = 2πv
= 2 x π x 2 
= 4π रेडियन
A = 0.065cm² = 0.065 × 10^-4m²
लोहे का यंग गुणांक Y = 2 x 10¹¹Pa 
F = m/ω²

= 17.61 x 10^-4 m
= 17.61 x 10^-2 cm
= 0.1761 cm = 0.180 cm

प्रश्न 9.12. 
नीचे दिये गये आँकड़ों से जल के आयतन प्रत्यास्थता गुणांक की गणना कीजिए; प्रारंभिक आयतन = 100.0 लीटर, दाब में वृद्धि = 100.0 atm (1 atm = 1.013 x 10⁵ Pa), अंतिम आयतन = 100.5 लीटर। नियत ताप पर जल तथा वायु के आयतन प्रत्यास्थता गुणांकों की तुलना कीजिए। सरल शब्दों में समझाइये कि यह अनुपात इतना अधिक क्यों है।
उत्तर:
दिया गया है:
आरंभिक आयतन v₁ = 100 
= 100 x 10^-3 m³
अंतिम आयतन v₂ = 100.5 
= 100.5 x 10^-3 m³
∴ आयतन में वृद्धि ∆V = v₂ - v₁
∆v = (100.5 - 100) x 10^-3 m³
= 0.5 x 10^-3 m³
∆p = 100 
= 100 x 1.013 x 10⁵ pa
(∵ 1 वायुमण्डल दाब = 1.013 x 10⁵ pa)
माना जल के आयतन प्रत्यास्थता गुणांक को यदि हम Kw से
प्रदर्शित करें तब सूत्र

यह सरल अनुपात का मान इतना अधिक इसलिए है चूंकि एक ही ताप पर वायु की विकृति पानी की विकृति की अपेक्षा बहुत अधिक होती है। अर्थात् द्रवों में गैसों की अपेक्षा अंतरा आण्विक दूरियाँ संगत दूरियों से कम होती हैं। अतः द्रवों में गैसों की अपेक्षा अंतरा - परमाण्विक बल बहुत अधिक होता है।

प्रश्न 9.13. 
जल का घनत्व उस गहराई पर जहाँ दाब 80.00 atm हो, कितना होगा? दिया गया है कि पृष्ठ पर जल का घनत्व 1.03 × 10³ kg m", जल का संपीड्यता- गुणांक 45.8 x 10^-11 Pa^-1
(1 Pa = 1 Nm^-2)
उत्तर:
दिया गया है:
दाब (P) = 80.0atm
= 80.0 × 1.013 × 10⁵ Pa
∵ latm = 1.013 × 10⁵ Pa
जल की संपीडता = 1/K
∴ 1/K = 45.8 × 10^-11 Pa^-1 (lPa = 1N/m²)
पृष्ठ पर जल का घनत्व p = 1.03 x 10³ kg/m
माना जल का घनत्व उस गहराई पर जहाँ दाब 80.00atm = p1
माना M द्रव्यमान का पृष्ठ तथा गहराई पर आयतन V एवं V1

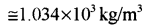
प्रश्न 9.14. 
काँच के स्लेब पर 10 atm का जलीय दाब लगाने पर उसके आयतन में भिन्नात्मक अन्तर की गणना कीजिये। 
उत्तर:
दिया गया है:
दाब P = 10atm 
= 10 x 1.013 x 10⁵Pa सारणी से काँच की पट्टी का आयतन गुणांक K = 37 x 10⁹
N/m² है। काँच की पट्टी के आयतन में आंशिक परिवर्तन = ∆V/V जो कि हमें ज्ञात करना है
हम जानते हैं:
आयतन गुणांक k = ∆p/∆V/V  सम्बन्ध का प्रयोग करने पर

प्रश्न 9.15. 
ताँबे के एक ठोस घन का एक किनारा 10 cm का है। इस पर 7.0 x 10 Pa का जलीय दाब लगाने पर इसके आयतन में संकुचन निकालिये।
उत्तर:
दिया गया है:
L = 10cm = 10 x 10^-2 m
K = ताँबे का आयतन गुणांक = 140 x 10⁹ Pa
( सारणी से ताँबे का आयतन गुणांक K = 140 x 10⁹ Pa है) 
P = 7 x 10⁶ Pa
∆V = ठोस ताँबे के घन में आयतन का संकुचन होना
V = L x L x L = L3 = (10 × 10^-2)³
= 1000 × 10^-6 = 10^-3 m³
= 0.001m³
सूत्र-

= - 0.05 × 10^-6 m³
= - 0.05 cm³
यहाँ पर ऋण आयतन में संकुचन दर्शाता है।

प्रश्न 9.16. 
एक लीटर जल पर दाब में कितना अन्तर किया जाये कि वह 0 10% से संपीडित हो जाये?
उत्तर:
दिया गया है:
V = 1 लीटर
∆V = - 0.10% यहाँ पर आयतन में कमी हो रही है।
∆V = -0.10/100 x 1 = -1/100 = 10^-3 लीटर
माना 1 लीटर पानी के संपीडन के लिये दाब में परिवर्तन 
पानी का आयतन गुणांक K = 2.2 x 10⁹ N/m²
सारणी से पानी का आयतन गुणांक K = 2.2 x 10⁹ N/m² है।
सूत्र \(\mathrm{K}=-\frac{\Delta \mathrm{P}}{\frac{\Delta \mathrm{V}}{\mathrm{V}}}\) का प्रयोग करने पर
\(\Delta \mathrm{P}=-\mathrm{K} \frac{\Delta \mathrm{V}}{\mathrm{V}}\)
मान रखने पर: 
\(=\frac{-2.2 \times 10^9 \times\left(\frac{-1}{1000}\right)}{1}\)
= 2.2 x 10⁶ N/m²

प्रश्न 9.17. 
हीरे के एकल क्रिस्टलों से बनी निहाइयों, जिनकी आकृति नीचे दिखाई गयी है, का उपयोग अति उच्च दाब के अन्तर्गत द्रव्यों के व्यवहार की जाँच के लिए किया जाता है। निहाई के संकीर्ण सिरों पर सपाट फलकों का व्यास 0.50mm है। यदि निहाई के चौड़े सिरों पर 50,000 N का बल लगा हो तो उसकी नोंक पर दाब ज्ञात कीजिए ।
उत्तर:
दिया गया है:
निहाई के चौड़े सिरों पर लगाया गया बल = संपीडन बल, F = 50,000 N
F = 5 × 10⁴ N
व्यास = 0.50mm
= 0.50 × 10^-3 m
= 50 × 10^-5 m
= 5 × 10^-4 m

∴ त्रिज्या r = 1/2 x व्यास हीरे के शंकु

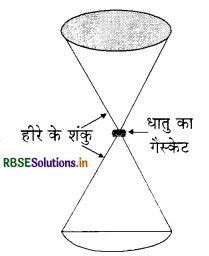
= 1/2 x 5 × 10^-4m
= 2.5 × 10^-4 m
क्षेत्रफल A = πr²

= 2.55 × 10¹¹ Pa
अतः निहाई के शिखर पर दाब P = 2.55 x 10¹¹ Pa 

प्रश्न 9.18. 
1.05 m लम्बाई तथा नगण्य द्रव्यमान की एक छड़ को बराबर लंबाई के दो तारों, एक इस्पात का (तार A ) तथा दूसरा ऐलुमिनियम का (तार B) द्वारा सिरों से लटका दिया गया है, जैसा कि चित्र में दिखाया गया है। A तथा B के तारों के अनुप्रस्थ परिच्छेद के क्षेत्रफल क्रमश: 1.0 mm और 2.0mm ² हैं। छड़ के किसी बिन्दु से एक द्रव्यमान m को लटका दिया जाए ताकि इस्पात तथा ऐलुमिनियम के तारों में (a) समान प्रतिबल तथा (b) समान विकृति उत्पन्न हो।

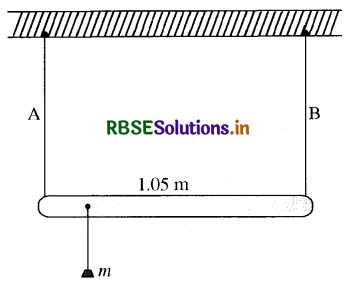
उत्तर:
स्टील के तार A के लिये
दिया गया है:
l1 = l
A1 = 1 mm²
Y1 = 2 × 10¹¹ N/m² (तालिका से लिया गया है)
ऐलुमिनियम के तार B के लिये
l2 = 1
A2 = 2 mm², 
Y2 = 7 x 10¹⁰ N/m²
(तालिका से लिया गया है)

(a) A और B पर प्रतिबल F1/A1 और F2/A2 क्रमश: हैं
प्रतिबल समान है

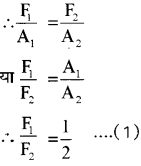
छड़ पर जिस बिन्दु पर द्रव्यमान लटका हुआ है उस बिन्दु के सापेक्ष बल आघूर्ण निकालने पर छड़ की कुल लम्बाई 1.05m 
द्रव्यमान तार A से (x) m की दूरी पर है और तार B से (1.05 - x ) m की दूरी पर होगा। आघूर्ण लेने पर
F1 x x = F2 × (1.05 - x )
या
\(\frac{\mathrm{F}_1}{\mathrm{~F}_2}=\frac{1.05-x}{x}\) ....(2)
समीकरण (1) से मान रखने पर
\(\frac{1}{2}=\frac{1.05-x}{x}\)
या 
x = 2.10 - 2x
या
x + 2x = 2.10
या 
3x = 2.10
या x = 2.10/3 = 0.70m
अतः तार A से 0.70m और तार B से 1.05 - 0.70 = 0.35 m की दूरियों पर प्रत्येक द्रव्यमान m को लटकाना चाहिये।

(b) माना कि तारों में तनाव F1 तथा F2 है।
∴ तार A के लिये विकृति = प्रतिबल/Y से प्राप्त करेंगे।
तार A के लिये विकृति = \(\frac{F_1 / A_1}{Y_1}=\frac{F_1}{A_1 Y_1}\)
और तार B के लिये विकृति = \(\frac{F_2 / A_2}{Y_2}=\frac{F_2}{A_2 Y_2}\)
चूँकि विकृतियाँ समान हैं।

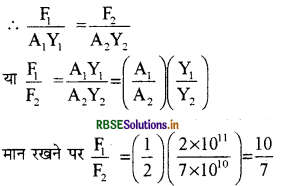
समीकरण ( 2 ) में मान रखने पर
\(\frac{10}{7}=\frac{1.05-x}{x}\)
या
10x = 7.35 - 7x
या
10x + 7x = 7.35
या
17x = 7.35
या
x = 7.35/17 = 0.43m
अर्थात् तार A के सिरे से 0.43m दूरी पर द्रव्यमान को लटकाना चाहिये।

प्रश्न 9.19. 
मृदु इस्पात के एक तार, जिसकी लंबाई 1.0m तथा अनुप्रस्थ परिच्छेद का क्षेत्रफल 0.50 x 10² cm है, को दो खम्बों के बीच क्षैतिज दिशा में प्रत्यास्थ सीमा के अन्दर ही तनित किया जाता है। तार के मध्य बिन्दु से 100g का एक द्रव्यमान लटका दिया जाता है। मध्य बिन्दु पर अवनमन की गणना कीजिए।

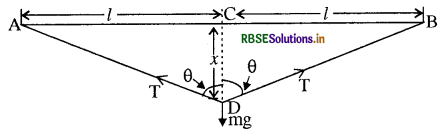
उत्तर:
मध्य बिन्दु पर बल लगने से मध्य बिन्दु माना x मीटर नीचे आ जाता है जैसा चित्र में दर्शाया गया है।
AC = AB = l = 1/2 = 0.5
m = 100 g = 0.100 g
AD = BD = (l² + x²)1/2
लम्बाई में वृद्धि ∆l = AD + DB - AB
= 2AD - AB 
∵ DB = AD

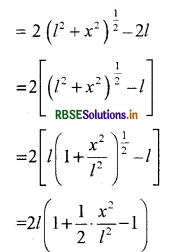
द्विपद प्रमेय का प्रयोग ∵ x<< l 
\(=2 l\left(\frac{1}{2} \cdot \frac{x^2}{l^2}\right)=\frac{x^2}{l}\)
यदि तार में तनाव T है तब
2T Cos θ = mg

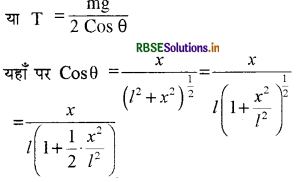
द्विपद प्रमेय का प्रयोग करने पर
यहाँ पर x<<l ∴ 1/2 x²/l²  का मान शून्य के बराबर होगा।

मान रखने पर:
\(=0.5\left(\frac{0.1 \times 10}{2 \times 10^{11} \times 0.5 \times 10^{-6}}\right)^{\frac{1}{3}}\)
= 1.074 x 10^-2 m
= 1.074 cm
अतः मध्य बिन्दु पर अवनमन का मान लगभग 1cm होगा। 

प्रश्न 9.20. 
धातु के दो पहियों के सिरों को चार रिवेट आपस में जोड़ दिया गया है। प्रत्येक रिवेट का व्यास 6mm है। या रिवेट पर अपरूपण प्रतिबल 6.9 x 107 Pa से अधिक नहीं बढ़ना हो तो रिवेट की हुई पट्टी द्वारा आरोपित तनाव का अधिकतम मान कितना होगा? मान लीजिए कि प्रत्येक रिवेट एक चौड़ाई भार वहन करता है।
उत्तर:
दिया गया है:
रिवेट का व्यास = 6mm = 6 x 10^-3m
त्रिज्या = \(\frac{6 \times 10^{-3}}{2}=3 \times 10^{-3} \mathrm{~m}\)
रिवेट पर अधिकतम अपरूपण प्रतिबल = 6.9 x 10⁷ pa
यदि कीलक द्वारा जड़ी पट्टी पर अधिकतम भार अर्थात् बल W_max हो तब 
W_max/4A = 6.9 x 10⁷ pa
∴ W_max = 4A x 6.9 x 10⁷ ................... (1)
A = πr² 
= 22/7 x (3 x 10^-3)²
= 22/7 x 9 x 10^-6 ............. (2)
समी. (2) का मान समी. (1) में रखने पर
∴ Wmax = 4 x 22/7 x 9 x 10^-6 x 6.9 x 10⁷
= 4 x 3.14 x 9 x 9.6 x 10
= 7.799 x 10³N
= 7.8 x 10³ N

प्रश्न 9.21. 
प्रशान्त महासागर में स्थित मैरिना नामक खाई एक स्थान पर पानी की सतह से 11 km. नीचे चली जाती है और उस खाई में नीचे तक 0.32 m' आयतन का इस्पात का एक गोला गिराया जाता है तो गोले के आयतन में परिवर्तन की गणना करें। खाई के तल पर जल का दाब 1.1 x 10⁸ Pa है और इस्पात का आयतन 160 GPa है |
उत्तर:
दिया गया है:
ऊँचाई (h) = 11km = 11 x 10³m
पानी का घनत्व p = 10³ kg/m³
g = 10m/s²
∴ 11 km पानी के स्तम्भ द्वारा खाई की पेंदी पर लगाया गया दाब
AP = hpg
= 11 x 10 x 10 x 10 Pa
= 1.1 × 10⁸ Pa
V = 0.32 m³
AV = ?
इस्पात का आयतन गुणांक = K = 160 G Pa
K = 160 × 10° N/m
K = [1.6 × 10] N/m²
हम जानते हैं-
\(\begin{aligned} \Delta \mathrm{V} & =\frac{\Delta \mathrm{PV}}{\mathrm{K}} \\ & =\frac{1.1 \times 10^8 \times 0.32}{1.6 \times 10^{11}} \end{aligned}\)
= 2.2 × 10^-4 m³