RBSE Class 11 Physics Important Questions Chapter 4 Motion in a Plane

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 4 Motion in a Plane Important Questions and Answers.

RBSE Class 11 Physics Chapter 4 Important Questions Motion in a Plane

Multiple Choice Questions

Motion In A Plane Extra Questions Question 1.
Which of the following quantities is a vector quantity:
(a) Velocity
(b) Speed
(c) Pressure
(d) None of these
Answer:
(a) Velocity

Motion In A Plane Class 11 Important Questions Question 2.
If the resultant of two forces F and F acting on a point is F, then the angle between them will be:
(a) 120°
(b) 90°
(c) 60°
(d) 0°
Answer:
(a) 120°

Motion In A Plane Class 11 Extra Questions Question 3.
Which of the following vector relations is wrong?
(a) \(\vec{A}+\vec{B}=\vec{B}+\vec{A}\)
(b) \(\vec{A}\) x \(\vec{B}\) = \(\vec{B}\) x \(\vec{A}\)
(c) \(\vec{A}\) + \(\vec{B}=\vec{A}+\vec{B}\)
(d) \(\vec{A}\) . \(\vec{B}\) = \(\vec{B}\) . \(\vec{A}\)
Answer:
(b) \(\vec{A}\) x \(\vec{B}\) = \(\vec{B}\) x \(\vec{A}\)

Class 11 Physics Chapter 4 Important Questions With Answers Question 4.
If \(\vec{P}\) x \(\vec{Q}\) = \(\vec{R}\) then magnitude of  \(\vec{P}\) . \(\vec{Q}\) will be:
(a) zero
(b) PR
(c) \(\frac{R}{P}\)
(d) \(\frac{P}{R}\)
Answer:
(a) zero

Motion In A Plane Important Questions Question 5.
Force acting on point \(\vec{r}\) = (3\(\hat{i}\) + 2\(\hat{j}\) + 3\(\hat{k}\)) is \(\vec{F}\) = (2\(\vec{i}\) - 3\(\vec{j}\) + 4\(\vec{k}\)) N, then moment of force about origin will be:
(a) -17\(\hat{i}\) + 6\(\hat{j}\) + 13\(\hat{k}\)
(b) 6\(\hat{i}\) - 6\(\hat{j}\) + 12\(\hat{k}\)
(c) 17\(\hat{i}\) - 6\(\hat{j}\) - 13\(\hat{k}\)
(d) -6\(\hat{i}\) + 6\(\hat{j}\) - 12\(\hat{k}\)
Answer:
(c) 17\(\hat{i}\) - 6\(\hat{j}\) - 13\(\hat{k}\)

Motion In A Plane Class 11 Important Questions And Answers Question 6.
A man moves 3 m towards east and then 4m towards north. The magnitude of its displacement is:
(a) 7 m
(b) 5 m
(c) \(\sqrt{5}\) m
(d) 1 m
Answer:
(b) 5 m

Motion In A Plane Class 11 Questions Question 7.
If \(\vec{P}\) + \(\vec{Q}\) = \(\vec{R}\) and R = \(\sqrt{|\vec{P}|^2+|\vec{R}|^2}\), then angle between \(\vec{P}\) and \(\vec{Q}\) will be:
(a) 60°
(b) 90°
(c) 120°
(d) 180°
Answer:
(b) 90°

Motion In A Plane Extra Questions Class 11 Question 8.
If \(\vec{A}\) = (5\(\hat{i}\) + 7\(\hat{j}\) - 3\(\hat{k}\)) and \(\vec{B}\) = -2\(\hat{j}\) + 2\(\hat{i}\) - C\(\hat{k}\) are perpendicular to each other, then value of C will be:
(a) 2
(b) 6
(c) -8
(d) -7
Answer:
(c) -8

Question 9.
Which of the following is a vector quantity?
(a) Acceleration
(b) Velocity
(c) Force
(d) All of these
Answer:
(d) All of these

Question 10.
A river is flowing from west to east with speed of 5 ms^-1. A man who can swim in still water with speed of 10 ms^-1, is at south bank of the river. He wants to cross the river in minimum time. He should swim in which direction?
(a) Towards north
(b) At 30° from north to east
(c) At 30° from north to west
(d) At 60° from north to east
Answer:
(a) Towards north

Question 11.
If θ be the angle between \(\vec{A}\) and \(\vec{B}\), then value of (\(\vec{B}\) x \(\vec{A}\)). \(\vec{A}\) will be:
(a) BA²sinθ
(b) BA² cosθ
(c) zero
(d) BA² sinθ cosθ
Answer:
(c) zero

Question 12.
The direction of a vector \(\vec{A}\) is vertically upward and that of \(\vec{B}\) is towards north. Dot product of vectors will be:
(a) towards west
(b) towards east
(c) zero
(d) vertically downwards
Answer:
(c) zero

Question 13.
If |\(\vec{A}\) x \(\vec{B}\)| = \(\vec{A}\) . \(\vec{B}\), then angle between \(\vec{A}\) and \(\vec{B}\) will be:
(a) 0
(b) π
(c) \(\frac{\pi}{4}\)
(d) \(\frac{\pi}{2}\)
Answer:
(c) \(\frac{\pi}{4}\)

Question 14.
A particle is moving X-Y plane and its co-ordinates at any point are (x,y,t) such that x = A sin ωt and y = A cos ωt, where ω is a constant quantity. The path of the particle will be:
(a) Linear
(b) Elliptical
(c) Circular
(d) Parabolic
Answer:
(c) Circular

Question 15.
Range of a bullet fired by gun with velocity a is R, then inclination of the barrel from horizontal will be:
(a) cos^-1(\(\frac{v_2}{Rg}\))
(b) cos^-1(\(\frac{Rg}{v_2}\))
(c) tan^-1(\(\frac{v_2}{Rg}\))
(d) \(\frac{1}{2}\)sin^-1(\(\frac{Rg}{v_2}\))
Answer:
(d) \(\frac{1}{2}\)sin^-1(\(\frac{Rg}{v_2}\))

Question 16.
The path of projectile is:
(a) Elliptical
(b) Linear
(c) Parabolic
(d) None of these
Answer:
(c) Parabolic

Question 17.
For same range at how many angle an a projectile be projected?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2

Question 18.
A particle moves on a circular path of radius r, on completing half circle, its displacement will be:
(a) 2r
(b) zero
(c) r
(d) r/2
Answer:
(a) 2r

Question 19.
A particle is moving on a circular path with constant speed, then acceleration of the particle will be:
(a) zero
(b) along tangent
(c) along radius
(d) along the circumference of the circle
Answer:
(c) along radius

Question 20.
A ball is projected at an angle θ with any velocity, the value of θ for maximum range will be:
(a) 0°
(b) 30°
(c) 60°
(d) 45°
Answer:
(d) 45°

Question 21.
A particle is moving on circular path with angular velocity \(\vec{\omega}\), linear velocity \(\vec{v}\), angular acceleration \(\vec{\alpha}\) and linear acceleration \(\vec{a}\), then which of the following options is not correct?
(a) \(\vec{\omega} \perp \vec{v}\)
(b) \(\vec{\omega} \perp \vec{\alpha}\)
(c) \(\vec{\omega} \perp \vec{a}\)
(d) \(\vec{\omega} \perp \vec{\alpha}\)
Answer:
(b) \(\vec{\omega} \perp \vec{\alpha}\)

Question 22.
In uniform circular motion:
(a) Velocity and acceleration both remain changing
(b) Velocity and acceleration both remain constant
(c) Velocity remains constant but acceleration changes
(d) Acceleration remains constant but velocity changes
Answer:
(a) Velocity and acceleration both remain changing

Question 23.
An object is moving with constant speed. Is acceleration possible in it?
(a) In linear motion
(b) In circular motion
(c) In parabolic motion
(d) Never
Answer:
(b) In circular motion

Question 24.
Initial velocity of a projectile is \(\vec{v}\) = (3\(\hat{i}\) + 4\(\hat{j}\)) ms^-1. At maximum height, its velocity will be:
(a) 3 ms^-1
(b) 4 ms^-1
(c) 5 ms^-1
(d) zero
Answer:
(a) 3 ms^-1

Question 25.
A particle is moving on a circular path of radius r with constant speed v and one cycle completes in time T. Acceleration of the particle is:
(a) \(\frac{2 \pi v}{T}\)
(b) \(\frac{2 \pi r}{T}\)
(c) \(\frac{2 \pi r_2}{T}\)
(d) \(\frac{2 \pi v_2}{T}\)
Answer:
(a) \(\frac{2 \pi v}{T}\)

Question 26.
If a_R and a_T are the radial and tangential accelerations, then the particle will do uniform circular motion if:
(a) a_R = 0 and a_T = 0
(b) a_R = 0 but a_T ≠ 0
(c) a_R ≠ 0 but a_T = 0
(d) a_R ≠ 0 and a_T ≠ 0
Answer:
(c) a_R ≠ 0 but a_T = 0

Question 27.
A man can throw a ball horizontal with maximum distance of 100 m. This player can through upto how much distance in vertical direction?
(a) 50 m
(b) 100 m
(c) 150 m
(d) 200 m
Answer:
(a) 50 m

Fill in the Blanks

Question 1.
A unit vector is a .............................. and ..............................
Answer:
unitless, dimensionless

Question 2.
When a vector \(\vec{A}\) is multipled by a scalar S, it becomes a vector .............................. whose unit is .............................. from the unit of vector \(\vec{A}\).
Answer:
S\(\vec{A}\)

Question 3.
The vector subtraction .............................. commutative law.
Answer:
does not follow

Question 4.
Those vectors which are having equal or unequal magnitudes and are acting along the parallel straight lines are called ..............................
Answer:
collinear vectors

Question 5.
The direction of centripetal acceleration is ..............................
Answer:
along the radius directed towards the centre of circular path

Question 6.
The angle of projection for a body to have same horizontal range and maximum height is ..............................
Answer:
tan^-1(u)

Question 7.
A jet of water issuing from a hole near the bottom of water tank is an ..............................
Answer:
example of projectile

Question 8.
A uniform circular motion is an example of .............................. motion.
Answer:
accelerated

Question 9.
When a projectile is projected with velocity v making an angle θ with the horizontal direction, the maximum horizontal range is ..............................
Answer:
\(\frac{v_2}{g}\)

Question 10.
The maximum height attained by a projectile is equal to .............................. of its maximum range.
Answer:
one fourth.

Very Short Answer Questions

Question 1.
Can any vector change with time?
Answer:
Yes.

Question 2.
Does the subtraction of vectors obey commutative law?
Answer:
No, because (\(\vec{A}\) - \(\vec{B}\)) ≠ (\(\vec{B}\) - \(\vec{A}\))

Question 3.
If unit vector in east direction is \(\hat{i}\), then if air is coming from east, then what will be unit vector of air?
Answer:
Unit vector with respect to an obsever standing at origin, the unit vector of air will be -\(\hat{i}\).

Question 4.
Can the scalar product of two vectors be negative?
Answer:
Yes, when the angle between them be between 90° to 270°.

Question 5.
Give any example of multiplication of a vector by scalar.
Answer:
Linear momentum \(\vec{p}\) = m \(\vec{m}\) and force \(\vec{F}\) = m \(\vec{a}\).

Question 6.
If a vector \(\vec{A}\) is multiplied by scalar m, then tell thte magntidue and direction of product.
Answer:
Resultant vector will be m \(\vec{A}\). Its magnitude will be mA and its direction will be same as that of \(\vec{A}\).

Question 7.
In which situation, the dot product of two non-zero vectors will be zero?
Answer:
When the angle between the vectors is 90° i.e. the vectors are at right angle to each other.

Question 8.
Froce \(\vec{F}\) displaces a stationary object by \(\vec{d}\). How will you show this process in vector symbols?
Answer:
Work done by the force,
W = \(\vec{F}\).\(\vec{d}\) = F.d. cosθ

Question 9.
What is the value of self product \(\vec{A}\).\(\vec{A}\)?
Answer:
\(\vec{A}\).\(\vec{A}\) = A A cos 0°= A²

Question 10.
Is subtraction process of vectors is associative?
Answer:
Yes, because (\(\vec{P}\) + \(\vec{Q}\)) - \(\vec{R}\) = \(\vec{P}\) + (\(\vec{Q}\) - \(\vec{R}\))

Question 11.
Can resultant of four non-coplanar vectors be zero?
Answer:
Yes.

Question 12.
If \(\vec{P}\).\(\vec{R}\) = \(\vec{Q}\), then will \(\vec{P}\) and \(\vec{Q}\) be always equal?
Answer:
\(\vec{P}\) and \(\vec{Q}\) will be equal only when each of both vectors make same angle with \(\vec{R}\).

Question 13.
What type of path of a projectile will appear when veiwed from another projectile?
Answer:
On viewing a projectile from other projectile, its path will appear to be linear.

Question 14.
Is the kinetic energy of projectile is zero at highest point of trajectory?
Answer:
No; because at highest point only vertical component of velocity is zero but horizon velocity remains unchanged. Therefore at highest point kinetic energy of projectile will be:
E_R = \(\frac{1}{2}\) m (u cosθ)²

Question 15.
An object is dropped freely from' the window of a train. Will the time of falling the object on ground remain same if:
(i) train is at rest.
(ii) train is moving with uniform velcoity v.
(iii) train is moving with uniform acceleration a.
Answer:
In each situation, the time of falling the object will be same.

Question 16.
A stone is dropped from the window of a moving train. What type of path will be seen by a person standing on the ground?
Answer:
Parabolic.

Question 17.
At which point, the speed of projectile will be minimum?
Answer:
At highest point.

Question 18.
What should be angle of projection for maximum horizontal range?
Answer:
45°.

Question 19.
An object is projected vertically upward and it returns on the same point of projection. Find the distance travelled and displacement.
Answer:
Displacement will be zero while distance travelled will be 2h, where h is maximum height.

Question 20.
A particle is moving in east direction. If force is applied on it in north direction, then will its path be one dimensional or two dimensional?
Answer:
Since initial velocity and acceleration both are in different directions, therefore its motion will be two dimensional.

Question 21.
At what angle of projection, maximum height and horizontal range both will be equal?
Answer:
θ = tan^-1 4 = 76°

Question 22.
An object is moving on current path with uniform speed. Give the nature of the acceleration.
Answer:
In this case the acceleration will be due to change in direction and it is in normal direction to velocity.

Question 23.
Angular velocity and angular acceleration, are both scalar or vector?
Answer:
Both are vector quantities.

Question 24.
An object is moving on circular path with uniform speed. What will be its tangential acceleration?
Answer:
Zero.

Question 25. 
What does remain constant among velocity, acceleration, force and kinetic energy for a particle moving with uniform speed on circular path?
Answer:
Only kinetic energy remains constant.

Question 26.
A particle is moving on circular path of radius R. What will be its distance and diplacemeht after completing half cycle?
Answer:
Displacement = 2R; distance = πR

Question 27.
When a projectile is projected at an angle, then which component of its velocity remains constant?
Answer:
Horizontal component of velocity remains constant.

Question 28.
Whether centripetal acceleration is uniform or variable?
Answer:
Variable.

Question 29.
Is circular motion possible without acceleration?
Answer:
No.

Question 30.
Is it possible that the speed of particle be constant but even then its motion be accelerated?
Answer:
Yes; in uniform circular motion, the speed remains constant but due to change in direction its velocity remains changing. Hence, centripetal acceleration is there in action.

Match the following:

Question (i)

Column-1	Column-2
(a) Range	(P) H = \(\frac{u^2 \sin ^2 \theta}{2 g}\)
(b) Maximum height	(Q) T = \(\frac{2 u \sin \theta}{g}\)
(c) Time of flight	(R) R = \(\frac{u^2 \sin 2 \theta}{g}\)

Answer:

Column-1	Column-2
(a) Range	(R) R = \(\frac{u^2 \sin 2 \theta}{g}\)
(b) Maximum height	(P) H = \(\frac{u^2 \sin ^2 \theta}{2 g}\)
(c) Time of flight	(Q) T = \(\frac{2 u \sin \theta}{g}\)

Question (ii)

Column-1	Column-2
(a) Angular velocity	(P) α = \(\frac{d \omega}{d t}\)
(b) Angular acceleration	(Q) a = \(\frac{v^2}{R}\)
(c) Centripetal acceleration	(R) ω = \(\frac{d \theta}{d t}\)

Answer:

Column-1	Column-2
(a) Angular velocity	(R) ω = \(\frac{d \theta}{d t}\)
(b) Angular acceleration	(P) α = \(\frac{d \omega}{d t}\)
(c) Centripetal acceleration	(Q) a = \(\frac{v^2}{R}\)

Short Answer Questions

Question 1.
When the resultant of two vectors equal in magnitudes will be:
(i) Zero
(ii) equal in magnitude of each vector?
Answer:
(i) When θ = 180°
(ii) When θ = 120°.

Question 2.
Can the resultant of two vectors equal in magnitude be zero?
Answer:
Magnitude of resultant of two vectors \(\vec{A}\) and \(\vec{B}\),

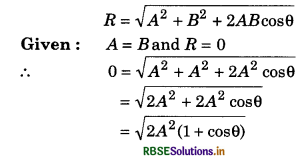
or 2A²(1 + cosθ) = 0
or 1 + cosθ = 0 [∵A ≠ 0]
or cosθ = -1
∴ θ = 180°

Question 3.
Is it correct to say zero vector as vector?
Answer:
Yes; because the sum and difference of two vectors is a vector quantity, therefore,
\(\vec{R}\) - \(\vec{R}\) = \(\overrightarrow{0}\) (zero vector)

Question 4.
Although force \(\vec{F}\) and displacement \(\vec{S}\) are vector quantities, even then work done W is a scalar quantity, why? If \(\vec{F}\) and \(\vec{S}\) both are non zero, even then W can be zero, when?
Answer:
Scalar product of force (\(\vec{F}\)) and displacement (\(\vec{S}\)) provides the work done (W); this is why W is a scalar quantity.
If angle between \(\vec{F}\) and \(\vec{S}\) is 90°, then
W = \(\vec{F}\).\(\vec{S}\) = F.S cos 90° = 0

Question 5.
Explain the law of parallelogram of vector addition with the help of diagram.
Answer:
Law of parallelogram of vector addition:
According to this law, “If two vectors can be represented in magnitude and direction both by two adjoining arms of a parallelogram, then resultant of these vectors will be represented in magnitude and direction both by that diagonal of the parallelogram which passes from the intersection point of the adjoining arms. See “Fig. 4.12”.
Thus the resultant of vectors \(\vec{P}\) and \(\vec{Q}\) will be

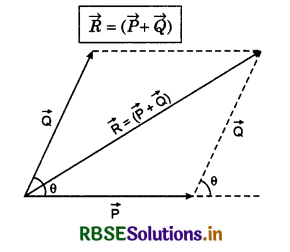
Question 6.
Give the differences between scalar product and vector product of two vectors with examples.
Answer:
There are two types of product of two vectors:
(i) Scalar product or dot product
(ii) Vector product or cross product.

(i) Scalar product or dot product: This product of two vectors is a scalar quantity, therefore it is called ‘scalar product’ and it is denoted by symbol
of dot (.) therefore it is called ‘Dot product’ also.
Scalar product of two vectors is given by,
\(\vec{A}\).\(\vec{B}\) = |\(\vec{A}\)| |\(\vec{B}\)| cosθ
or \(\vec{A}\).\(\vec{B}\) = AB cosθ
where |\(\vec{A}\)| = magnitude of \(\vec{A}\) = A
|\(\vec{B}\)| = magnitude of \(\vec{B}\) = B
and θ = angle between \(\vec{A}\) and \(\vec{B}\)
Examples:
1. Dot product of area vector \(\vec{A}\) and electric field vector \(\vec{E}\) provides electric flux ΦE

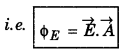
2. Dot product of magnetic field \(\vec{B}\) and area vector \(\vec{A}\) provides magnetic flux Φm. i.e.,

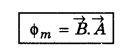
Vector product or cross-product: This product of two vectors is a vector quantity therefore it is called vector product and it is denoted by symbol of
cross (X), therefore it called cross-product also. Cross product of two vectors can be obtained by following relation:
\(\vec{A}\) x \(\vec{B}\) = |\(\vec{A}\)| |\(\vec{B}\)| sinθ \(\hat{n}\)
or \(\vec{A}\) x \(\vec{B}\) = AB sinθ\(\hat{n}\)
where, |\(\vec{A}\)| = magnitude of \(\vec{A}\)
|\(\vec{B}\)| = magnitude of \(\vec{B}\)
θ = angle between \(\vec{A}\) and \(\vec{B}\)

\(\hat{n}\) = unit vector at right angle to plane \(\vec{A}\) and \(\vec{B}\) and its direction is decided by right handed screw rule.
Rules for deciding the direction of \(\vec{A}\) x \(\vec{B}\)
These are following two rules to decide the direction of \(\vec{A}\) x \(\vec{B}\) i.e. the direction of \(\hat{n}\):
(i) Right hand screw rule
(ii) Right hand thumb rule
(i) Right hand screw rule: If we imagine to rotate a right handed screw along the direction at right angle to plane of \(\vec{A}\) and \(\vec{B}\) from \(\vec{A}\) to \(\vec{B}\), then the direction of motion of tip of the screw decides the direction of \(\hat{n}\) or \(\vec{A}\) x \(\vec{B}\) (fig. 4.42).

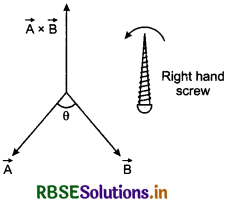
(ii) Right hand thumb rule: If we fold the fingers on right hand such that the direction of turn of fingers represents the direction of thumb will represent the direction of \(\vec{A}\) x \(\vec{B}\) (fig. 4.43).
Examples:
(i) Moment of force i.e. torque, \(\vec{\tau}=\vec{r} \times \vec{F}\)
(ii) Linear velocity, \(\vec{v}\) = \(\vec{\omega}\) x \(\vec{r}\)

Question 7.
Maximum height of a projectile is H and its time of flight is T, then prove that 8H = gT² and for height H, the projection velocity will be u = \(\frac{\sqrt{2 g H}}{\sin \theta}\).
Answer:

2gH = u² sin²θ
∴ u² = \(\frac{2 g H}{\sin ^2 \theta}\)

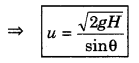
Question 8.
Prove that maximum range of a projectile is 4 times its maximum height.
Answer:
∵ R_max = \(\frac{u_2}{g}\)
It is obtained at θ = 45°, therefore at angle of projection

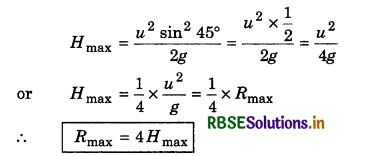
Question 9.
A projectile is projected with velocity u in θ direction. When it is at the highest point of its path, then:
(a) What are horizontal and vertical velocities in terms of u and θ?
(b) What will be its acceleration?
(c) What is relation between velocity and acceleration?
Answer:
(a) Horizontal velocity v_x = u cosθ
Vertical velocity v_y = 0 (zero)
(b) Acceleration = g
(c) Velcoity and acceleration will be perpendicular to each other i.e., \(\vec{a}\) ⊥ \(\vec{v}\)

Question 10.
Two objects of mass 10 kg and 5 kg are projected with horizontal velocity of 10 ms^-1 from height of 100 m. What will be ratio of times on reaching the ground?
Answer:
If time in falling the object is t, then from relation h = ut + \(\frac{1}{2}\)gt²
Here initial velocity in vertical direction is zero,
i.e., u = 0

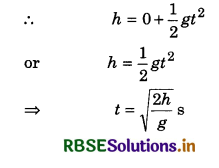
In this relation mass m is not involved, therefore both the objcet will reach the ground at same time.
∴ t₁ : t₂ = 1 : 1

Question 11.
Time of flight of a projectile is T and horizontal range is R. What will be angle of projection?
Answer:

Question 12.
What is the relation between velocity and acceleation at highest point of the trajectory?
Answer:
At highest point, the velocity is tangential to path i.e, in horizontal direction while acceleration (g) is vertically downward. Thus, both are perpendicular, i.e. \(\vec{\alpha}\) ⊥ \(\vec{v}\) at highest point.

Question 13.
Co-ordinates of a particle moving on circular path with constant angular velocity ω, at time 't' are x = A cosωt and y = A sin ωt. Find the radius of the circular path, velocity and acceleration of the particle.
Answer:
Given: x = Acos ωt ...................(1)
and    y = Asin ωt .................(2)
∴ X-component of velocity,
v_x = \(\frac{d x}{d t}=\frac{d}{d t}\)(A cos ωt) = -Aω sin ωt
or v_x = -Aω sin ωt .......................(3)
an Y-component of velocity,
v_y = \(\frac{d y}{d t}=\frac{d}{d t}\)(A sin ωt)
or v_y = Aω cos ωt ........................(4)
X-component of acceleration,
a_x = \(\frac{d v_x}{d t}=\frac{d}{d t}\)[-A sin ωt]
or a_x = -Aω² cos ωt ....................(5)
and Y-component a_y = \(\frac{d}{d t}\) v_y = \(\frac{d}{d t}\)[Aω cos ωt]
or a_y = -Aω² sin ωt .........................(6)
Now on adding squares of equation (1) and (2)
x² + y² = A² cos² ωt + A² sin² ωt
= A² (cos² ωt + sin² ωt)
or x² + y² = A² ...........................(7)
This equation (7) represents a circle whose centre is (0, 0) and its radius of A i.e.,
A = \(\sqrt{x^2+y^2}\)

Question 14.
If the speed of uniform circular motion is equal to velocity after falling freely the half of the radius of the circle, then prove that centripetal acceleration will be equal to acceleration of freely falling bodiy i.e., g.
Answer:
Centripetal acceleration
a_c = \(\frac{v_2}{r}\) ...........................(1)
∵ The velocity of freely falling body after falling from height h is

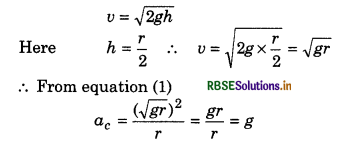
or a_c = g = Acceleration of freely falling body.

Question 15.
From the same height, one ball A is dropped freely and other ball B is projected horizontally at the same time. If air friction is negligible, then
(i) Which ball will strike the ground first?
(ii) Vertical velocity of which ball will be greater on reaching the ground?
(iii) Will both the ball fall on the same place?
(iv) On which factor will depend the range of B?
Answer:
(i) Both the ball will reach the ground at same time.
(ii) Vertical velocity of both balls will be same on reaching the ground.
(iii) No.
(iv) Range of B will depend on height h and horizontal velocity.

Question 16.
A particle on fourth part of a circular path. What will be ratio of distance and displacement?
Answer:
The particle moves from A to B.
∴ Distance S = \(\frac{1}{4}\) x 2πr = \(\frac{1}{2}\)πr

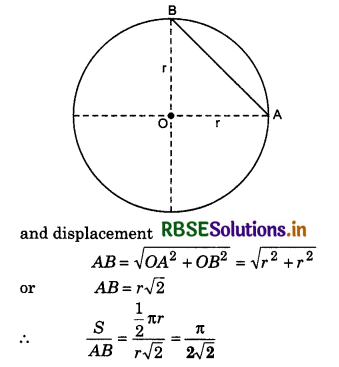
Question 17.
Earth completes one revolution around the Sun in time T with velocity v. Show that the acceleration directed from Earth to Sun will be \(\frac{2 \pi v}{T}\).
Answer:
∵ v = rω and centripetal acceleration

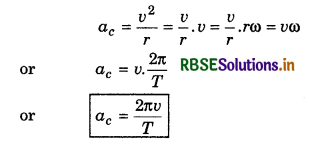
Question 18.
On doubling the speed of the particle in circular motion and radius of the path, what will be change in the centripetal acceleration of the particle?
Answer:
∵ a_c = \(\frac{v_2}{r}\)
On doubling v and r, a'_c = \(\frac{(2 v)^2}{2 r}=\frac{4 v^2}{2 r}=2 \cdot \frac{v^2}{r}\)
or a'_c = 2a_c
i.e., centripetal acceleration will also be doubled.

Question 19.
Many bullets are Bred with velocity v, in all directions. What will be the maximum area covered by the bullets?
Answer:
If r is the maximum range of each bullet, then effective covered area.
A = πr²
Now maximum range,

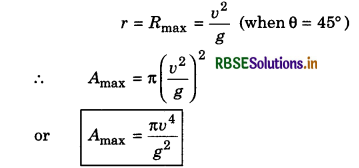
Question 20.
Range of a projectile projected at angle θ and (90° - θ) is same. If in both situations the time of flight is t₁ and t₂, then show that the range will directly proportional to product of t₁ and t₂.
Answer:

Question 21.
A particle is moving on arc of radius R. Its velocity is v = a\(\sqrt{s}\), where a is a constant.If α be the angle between net acceleration vector and velocity vector, then find the value of α in terms of R and s.
Answer:

∵ Tangential acceleration and velocity are in same direction, therefore if α be the angle between velocity and net acceleration, then
tanα = \(\frac{a_N}{a_T}=\frac{s a^2 / R}{a^2 / 2}=\frac{2 s}{R}\)

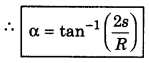
Question 22.
A bob is suspended from ceiling and it is vibrating. What will be path of the bob on cutting its cord in following conditions:
(i) When the bob is at its maximum displacement position and (ii) it is at its mean position?
Answer:
(i) At maximum displacement, the velocity of the bob will be zero, therefore it will fall freely. Therefore its path will be straight line, vertically downward.
(ii) A mean position, the velocity of the bob is maximum and in horizontal direction. Therefore, the path of the bob will be parabolic.

Question 23.
An object is moving along a circular path. Whether angular velocity or linear velocity of all particles of the object will be same?
Answer:
Angular velocity of all the particles will be same about axis of rotation but the distance of different, particles will be different from axis of rotation. Therefore, velocity of all particles will be different.

Question 24.
Answer with reason, whether following statements are true or false?
(i) In circular motion, the acceleration is always along the radius and towards the centre.
(ii) The velocity vector of a particle at any point is always along the direction of tangent at that point in circular motion.
(iii) The average of acceleration vector in uniform circular motion for one cycle is zero vector.
(iv) If a particle is moving on circular path with non-uniform speed,then radial component of its acceleration is \(\frac{v_2}{R}\).
Answer:
(i) False: it is true only for uniform circular motion.
(ii) True: because for uniform circular motion \(\vec{v}\).\(\vec{R}\) = 0: i.e, \(\vec{v}\) is always perpendicular to \(\vec{R}\).
(iii) True.
(iv) True.

Question 25.
A disc of radius r is rotating about its axis with angular velocity ω. What will be ratio of velocities on the disc situated at distance R/3 and R from the axis of rotation?
Answer:
∵ v = Rω
∴ v₁ = \(\frac{R}{3}\) ω and v₂ = Rω
∴ \(\frac{v_1}{v_2}=\frac{\frac{R \omega}{3}}{R \omega}=\frac{1}{3}\)
or v₁ : v₂ = 1 : 3

Question 26.
Why mud-guards are used on the wheels of vehicles?
Answer:
In circular motion, the velocity of particles is always in tangential direction. Therefore, mud particle when leave the wheels, they move in tangential direction. Hence, mud-guards are used on the wheels of vehicles.

Conceptual Questions

Question 1.
On multiplying a vector by scalar, does its nature change?
Answer:
On multiplying a vector by scalar, its nature can change or not also. For example: when a vector is multiplied by a pure digit (e.g., 1, 2, 3, ....), then the nature of vector does not change but on multiplying a vector by scalar physical quantity, the nature of the vector is changed. For example: when velocity vector is multiplied by mass then the product becomes linear momentum which is also a vector quantity but its nature is different from velocity.

Question 2.
Magnetic flux (scalar) attached with a plane placed in a magnetic Held at right angle to field lines is equal to product of intensity of magnetic field (vector) and area of the plane. Whether the area of the plane is a vector quantity or scalar quantity?
Answer:
Salar product of two vectors is a scalar quantity. Magnetic flux is obtained by
Φ = \(\vec{B}\).\(\vec{A}\)
Therefore area is a vector quantity.

Question 3.
Is the quantity having magnitude and direction both, certainly a vector quantity? Answer by giving example.
Answer:
NO, for example electric current has magnitudes and direction both but even then it is a scalar quantity because addition of two currents does not obey the law of vector addtion.

Question 4.
A person sitting in a bus moving with speed of 40 km.h^-1 from west to east, observes that the rain drops are falling vertically down-wards. At what angle will the rain drops be observed ,by a man standing on ground?
Answer:
Person is sitting in a bus which is going from west to east, he observes the rain fall vertically downwards.

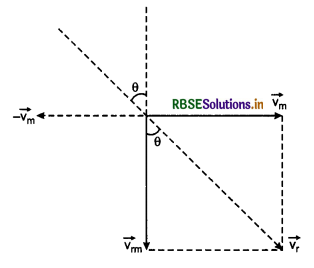
\(\vec{v_m}\) = velocity of the man
\(\vec{v_r}\) = velocity of rain fall
\(\overrightarrow{v_{r m}}\) = relative velocity of rain drops with respect of man.
For a man standing on the ground, the rain drops will appear to fall at an angle θ with vertical
tan θ = \(\frac{\left|\overrightarrow{v_m}\right|}{\left|\overrightarrow{v_{r m}}\right|}=\frac{v_m}{v_{r m}}\)
∴ θ = tan^-1(\(\frac{v_m}{v_rm}\))

Question 5.
Is there identity of position in gestalt except magnitude and direction of a vector? Can the physical effects of two vectors \(\vec{A}\) and \(\vec{B}\) be same, if there positions are different?
Answer:
Yes; for each vector, there is identity also in gestalt along with its direction and magnitude. Two vectors \(\vec{A}\) and \(\vec{B}\) of different positions, exhibit different effect.

Question 6.
Two persons pull a cord such that the cord remains stretched in horizontal position. On hanging a mass of 8.0 kg from the centre of the cord, it does not remain horizontal. Can the cord be made horizontal by applying the tension?
Answer:
Suppose the tension in cord is T and it makes an angle a with horizontal. Tension T is resolved in horizontal and vertical components. T cosα is horizontal component and T sinα is vertical component. Horizontal components T cosα balance each other while vertical components Tsinα add up and provide net vertical force 2T sinα which balances the weight W = 8kg-wt.

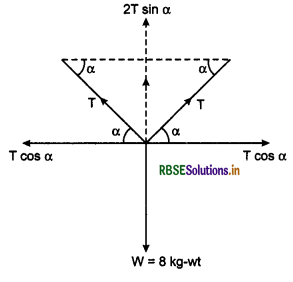
∴ 2T sinα = W
or T = \(\frac{W}{2 \sin \alpha}\)
For cord to be completely horizontal, α = 0°
∴ sin α = sin 0° = 0
Hence T = \(\frac{W}{0}\) = ∞ (infinite) which is not possible.
Therefore horizontal tension can not balance vertical weight.

Question 7.
We can express the events in order of time and it is a sense of time, in resolved form time is past, present and future. Can time be considered a vector?
Answer:
Time always goes from past to present and later on to future. Thus time can be given direction which is certain but not stable. Therefore time can not be considered as vector.

Question 8.
Is flying of a bird an example of vector addition?
Answer:
Yes; flying of a birds is an example of vector addition. Both wings of bird apply forces \(\vec{F_1}\) and \(\vec{F_2}\) on air in directions AO and BO respectively. As a result reactional forces R₁ and R₂ are applied by air on wings of the bird. Resultant of R₁ and R₂ is R (i.e., vector addition of \(\vec{R_1}\) and \(\vec{R_2}\), due to which bird moves ahead.

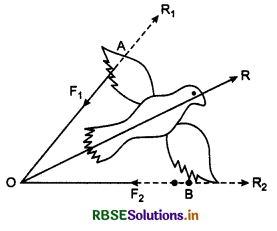
Question 9.
A man is moving with speed of 2 km h^-1 and he observes the rainfall vertically downwards. When he increases his velocity to 4 km h-1, the raindrops fall at an angle of 45°. Find the speed of rainfall and its direction also.
Answer:
Suppose velocity of man is \(\vec{v_1}\) and that of rain fall is \(\vec{v_2}\) which makes angle θ with vertical. Relative velocity of rain drops with respect to man,

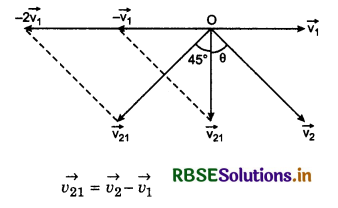
When the man increases his velocity to \(\overrightarrow{2 v_1}\) then relative velocity of rain drops with respect to man,
\(\overrightarrow{v_{21}}\) = \(\vec{v_2}\) - 2\(\vec{v_1}\)
From the figure,
sinθ = \(\frac{v_1}{v_2}\) and tan 45° = \(\frac{v_1}{v_21}\)

Question 10.
At what angle a player should through a javelin to achieve maximum range?
Answer:
∵ R = \(\frac{u^2 \sin 2 \theta}{2}\)
For R_max, sin 2θ = 1 or 2θ = 90° ⇒ θ = 45°
Therefore, javelin should be thrown at an angle of 45° for maximum range.

Question 11.
From the top of a tower on ball is projected horizontally and at the same time another ball is left freely.Answer:
(i) Will both the balls reach the ground at the same time?
(ii) Will the velocities of both the balls be equal at the ground?
Answer:
(i) Yes; because the vertical velocity of both the balls is zero.
(ii) No; their vertical velocities will be same at the time of striking the ground but horizontal velocities will be different. Horizontal velocity of the object projected horizontal will be same as initial velocity and that of second ball will be zero.

Question 12.
Speed of an object is constant, can the path of the object be of some other type besides linear and circular?
Answer:
All type of curved path are possible. If acceleration in motion is zero then the path will be linear. If magnitude of acceleration is constant but direction always changes such that it remains perpendicular to velocity, then object moves on circular path with constant speed. If the magnitude and direction of the acceleration changes such that it remain perpendicular to direction of motion, then object moves on curved path with constant speed.

Question 13.
A glass globule rolling with speed of u ms^-1 on a horizontal table of height h, falls down from the edge of the table. At how much distance from the base of the table, globule will reach the ground?
Answer:
It time taken by globule in falling is T, then
T = \(\sqrt{2h}{g}\) s
The globule will leave the table with horizontal velocity u which remains constant, therefore the horizontal distance covered by the globule.
d = u x T = u\(\sqrt{2h}{g}\) m

Question 14.
Prove that any projectile covers a same height in two different times and the sum of these two times is equal to time of flight.
Answer:
Suppose the times of covering the same height are t₁ and t₂ therefore

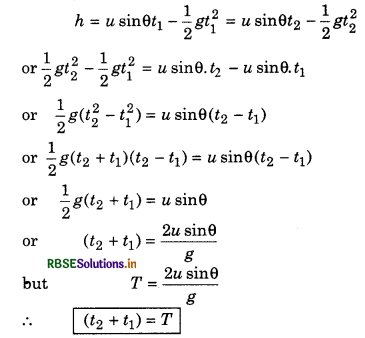
Question 15.
A gunner always keeps the barrel of the gun above the line of sight, why?
Answer:
A gunner keeps the barrel of gun above the line of sight because as the bullet leaves the barrel, it starts falling under gravity and its path becomes parabolic. Therefore, it is not done so, then the bullet will not hit the target.

Question 16. 
In long jump, is the importance of this factor that how height you take before jumping?
Answer:
Range R = \(\frac{u^2 \sin 2 \theta}{g}\)
For maximum range sin 2θ = 1 or 2θ = 90°
⇒ θ = 45°
For this angle of projection, maximum height
H = \(\frac{u^2 \sin ^2 45^{\circ}}{2 g}=\frac{u^2}{4 g}\) = constant
Thus to attain θ = 45°, H = \(\frac{u^2}{4 g}\) is necessary
This is why, in long jump, the player takes some height before jumping.

Question 17.
If horizontal range of a projectile be a and attained maximum height be b, then prove that the velocity of the projectile will be \(\left[2 g\left\{b+\frac{a^2}{16 b}\right\}\right]^{1 / 2}\).
Answer:
Maximum height
H = b = \(\frac{u^2 \sin ^2 \theta}{2 g}\)
⇒ sin2θ = \(\frac{2 g b}{u^2}\) ............................(1)

Question 18.
A ball is projected with same speed v from same point at different angles of projection. In both the situations range is same. If h₁ and h₂ be the maximum heights in these situations, then find the value of h₁ + h₂.
Answer:
For same range angle of projection will be θ and (90° - θ).

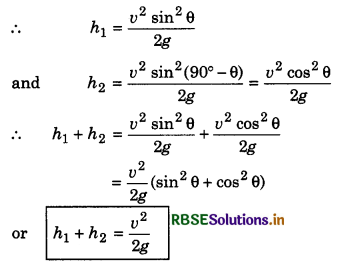
Question 19.
A man standing on the roof of a house of height h, throws a praticle downward and another particle is horizontal direction with same velocity u. What will be ratio of velocities of both particles an reaching the ground?
Answer:
Velocity of first particle
v₁² = u² + 2gh
∴ v₁ = \(\sqrt{u^2}+{2gh}\)
For second particle v_x = u and v²_y = 0 + 2gh

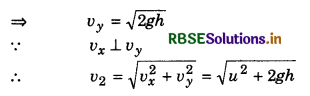
∴ v₁ : v₂ = 1 : 1 because v₁ = v₂

Question 20.
Prove that when the motion of one projectile is viewed from other projectiles then it seems to be linear.
Answer:
Suppose two projectiles are projected in X-Y plane with initial velocities u₁ and u₂ at projection angles θ₁ and θ₂. Also let us suppose that origin O i.e. the projection point. We consider two points A(x₁, y₁) and B(x₂, y₂) on the trajectories of both projectiles at same time t shown in fig.
Then x₁ = u₁ cosθ₁.t
and y₁ = u₁ sinθ₁.t - \(\frac{1}{2}\)gt²
and x₂ = u₂ cosθ₂.t
y₂ = u₂ sinθ₂t - \(\frac{1}{2}\)gt²
∴ x₂ - x₁ = (u₂ cosθ₂ - u₁ cosθ₁)t .............................(1)
and y₂ - y₁ = (u₂ sinθ₂ - u₁ sinθ₁)t .........................(2)
∴ From equations (1) and (2),
\(\frac{y_2-y_1}{x_2-x_1}=\frac{u_2 \sin \theta_2-u_1 \sin \theta_1}{u_2 \cos \theta_2-u_1 \cos \theta_1}\) = m (say) ...........................(3)
Suppose (x, y) are the co-ordinates with respect to second projectile, then

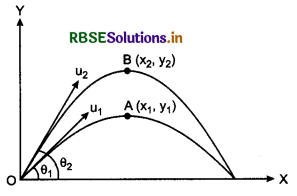
x₂ - x₁ = x and (y₂ - y₁) = y
∴ From equation (3)
\(\frac{y}{x}\) = m or y = mx
which is equation of straight line passing through origin.

Question 21.
A particle P is projected with velocity u₁ at an angle of 30° and another particle Q is projected vertically upward from the point below the highest point of P with velocity u₂. What will be necessary condition for colliding both particles?
Answer:
For collision of both particle at highest point A, time taken by both particles should be same (say t).
Time taken by P upto Q
t₁ = \(\frac{u_1 \sin 30^{\circ}}{g}\) ...........................(1)

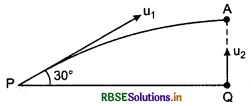
Time taken by Q upto A,
t₂ = \(\frac{u_2 \sin 90^{\circ}}{g}\) ..........................(2)
As is given in the question that;
t₁ = t₂
∴ \(\frac{u_1 \sin 30^{\circ}}{g} = \frac{u_2 \sin 90^{\circ}}{g}\)
or \(\frac{u_1}{2g}\) = \(\frac{u_2}{g}\)

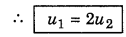
Question 22.
An object is slipping on a frictionless inclined plane while other object falls freely from the same point. Which object will strike the surface first?
Answer:
Acceleration of slipping object on inclined plane is g sinθ while that of freely falling object is g, where θ is angle of inclination of the plane.

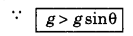
∴ Second object will reach the ground first.

Question 23.
A projectile of mass m is projected from the ground at an angle θ and its trajectory in vertical plane is given by relation y = ax - bx², where a and b are constants and x,y are the horizontal and vertical distances from the projection point. Find the maximum height attained by the projectile.
Answer:
On comparing y = ax - bx² with

∴ Maximum height attained by the projectlie,
h = \(\frac{a^2}{4b}\)

Question 24.
A particle of mass m is situated at point Pin a hemisphere of radius r. A horizontal acceleration a₀ is applied on the particle, if gravitational acceleration is considered negligible, then what will be the time taken by particle in touching the surface of hemisphere again?
Answer:
Suppose the particle touches the surface again at A,
Suppose PA = l
From ∆OPB,

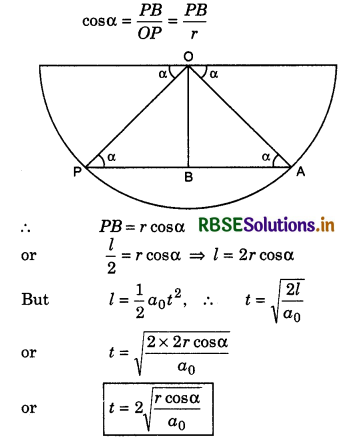
Question 25.
A ball of mass m moves on circular paths of radius r₁ and r₂ with speed v₁ and v₂ respectively. If r₁ < r₂ then establish the relation between v₁ and v₂ while centripetal acceleration in both situations is same.
Answer:
Centripetal acceleration, a_c = \(\frac{v_2}{r}\)
∵ a₁ = a₂ ∴ \(\frac{v_1^2}{r_1}\) = \(\frac{v_2^2}{r_2}\)
or \(\frac{v_1^2}{v_2^2}\) = \(\frac{r_1}{r_2}\) or \(\frac{v_1}{v_2}\) = \(\sqrt{r_1}{r_2}\) .........................(1)
∵ Given, r₁ < r₂
∴ Hence, v₁ < v₂

Question 26.
An object is projected such that its horizontal range and attained maximum height are same. At what angle with horizontal is it projected? (tan 76° = 4)
Answer:
Given, H = R
∴ \(\frac{u^2 \sin ^2 \theta}{2 g}=\frac{u^2 \sin 2 \theta}{g}\)
or \(\frac{\sin^2\theta}{2}\) = 2 sinθ.cosθ
or sinθ = 4 cosθ or tanθ = 4
But given, tan 76° = 4
∴ θ = 76°

Question 27.
Two cannon balls of mass 5 kg and 10 kg are projected by a cannon in same direction with same velocity. Which ball will reach the ground first? If the balls are projected with different velocities in same direction, then which ball reach the ground first?
Answer:
Time of flight,
T = \(\frac{2u\sin\theta}{g}\) ............................(1)
This formula does not contain mass m, therefore value of T does not depend on mass m. Hence both the balls will reach the ground at same time.
from equation (1), T ∝ u
∴ For greater value of u, value of T will also be more. Therefore the ball of lesser speed will reach first.

Question 28.
The equation of trajectory of a projectile is y = x -\(\frac{x^2}{80}\), where x and y area in 'm', what will be angle of velocity with horizontal after 4s. (g = 10 ms^-2)?
Answer:
On comparing the given equation y = x - \(\frac{x^2}{80}\) with standard equation of trajectory
y = x tanθ - \(\frac{g x^2}{2 u^2 \cos ^2 \theta}\)
we have, tanθ = 1 ⇒ θ = 45°

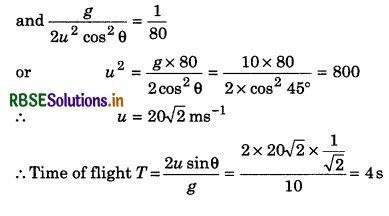
Therefore after 4 s, the projectile will strike the ground and at this time the angle of velocity with horizontal will be 45° downwards.

Question 29.
A particle, starting from origin moves in y-direction with constant acceleration a in X-Y plane. The equation of motion is y = ßx². Find its velocity in X-direction.
Answer:
Velocity in X-direction is constant.

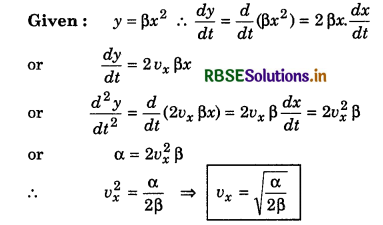
Question 30.
A particle is projected from height H with velocity v₀ at an angle θ (0 < θ < π/2). If v is velocity of a particle on reaching the ground and t is the time taken by particle in reaching upto ground then tell that what changes will appear in t and v with angle θ?
Answer:
From the diagram,

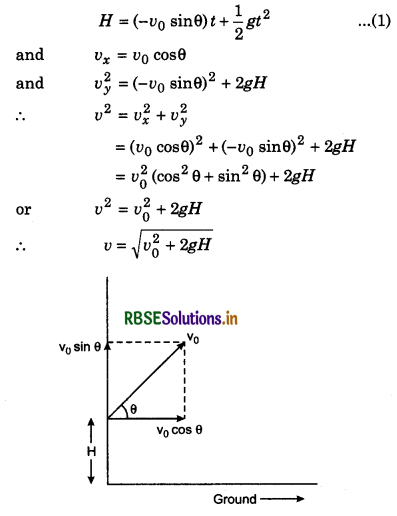
i.e., the speed does not depend upon the angle θ.
From equation (1).
\(\frac{1}{2}\)gt² = H + v₀t.sinθ
From this equation, it is clear that increasing the value of θ, time t will also increase.

Question 31.
Two objects are projected with velocity u at angles α and (90°- α) with horizontal. Find the ratio of their maximum heights and horizontal ranges.
Answer:
(i) Maximum height at angle of projection θ,

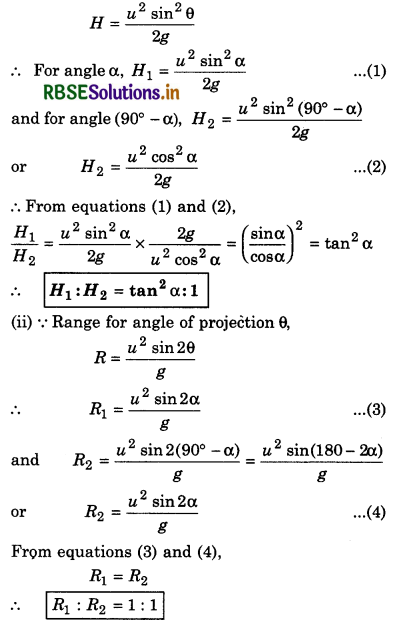
Question 32.
A projectile is projected with kinetic energy K. If it attains maximum range, then what will be its kinetic energy at maximum height?
Answer:
If the velocity of projection be v and mass of the projectile be m, then
K = \(\frac{1}{2}\)mv²
∵ The projectile attains maximum range, therefore angle of projection will be θ = 45°.
∴ At the time of projection,
v_x = v cos 45° = \(\frac{v}{\sqrt{2}}\) (horizontal velocity)
and v_y = v sin 45° = \(\frac{v}{\sqrt{2}}\) (vertical velocity)
∵ The horizontal velocity v_x remains unchanged and at heighest point, v_y becomes zero. Only v_x remains there.
∴ Kinetic energy at highest point,
K' = \(\frac{1}{2}\)mv_x² = \(\frac{1}{2}\)m(\(\frac{v}{\sqrt{2}}\))² = \(\frac{1}{2} \frac{mv^2}{2}\)
or K' = \(\frac{K}{2}\)

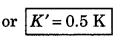
Long Answer Questions

Question 1.
What is law of parallelogram of vector addition? If \(\vec{P}\) and \(\vec{Q}\) are acting at a angle and their magnitudes are same, then prove that resultant R = 2P cos\(\frac{\alpha}{2}\)
Answer:
The multiplication of a vector by a real number either leaves the direction unchanged if the number is positive or reverses the direction. If the number is negative, while the magnitude of the vector is scaled by the magnitude of the number.

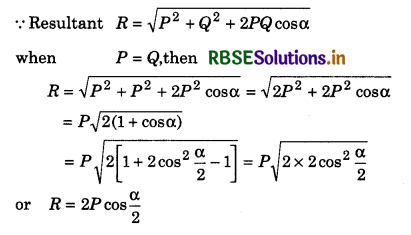
Question 2.
Give the triangle method for addition of two vectors. Prove that vector addition is commutative.
Answer:
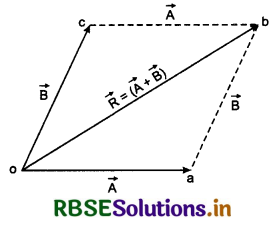
Law of triangle of vector addition:
Suppose there are two vectors \(\vec{A}\) and \(\vec{B}\) making an angle θ with each other (fig. 4.10). Addition method of these two vectors is given below.

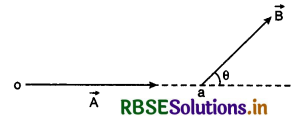
Method:
1. First of all we draw a base oa of length equal to magnitude of one vector along its direction.
2. Now we draw a line from final point of oa i.e., from a making an angle (180 - θ) with oa.
3. We cut an arc of length equal to magnitude of other vector. It represents vector \(\vec{B}\) with terminus as b.
4. Now initial point of \(\vec{A}\) and terminus of \(\vec{B}\) is joined which provides the resultant \(\vec{R}\) of \(\vec{A}\) and \(\vec{B}\). By measuring the length of \(\vec{R}\). We get the magnitude of resultant. This whole process is shown in fig. 4.11.

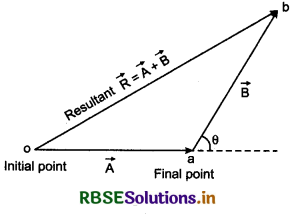
Addition of vector obeys commutative law:
if \(\vec{A}\) and \(\vec{B}\) are two vector quantities, then
\(\vec{A}\) + \(\vec{B}\) = \(\vec{B}\) + \(\vec{A}\).
Suppose oa = \(\vec{A}\) and ab = \(\vec{B}\), from law of triangle of vector addition for ∆oab
or \(\vec{ob}\) = \(\vec{oa}\) + \(\vec{ab}\)
or \(\vec{R} \) = \(\vec{A}\) + \(\vec{B}\) ........................(1)

On applying the same law of ∆acb
\(\vec{ob}\) = \(\vec{oc}\) + \(\vec{cb}\)
or \(\vec{R}\) = \(\vec{B}\) + \(\vec{A}\) ........................(2)
On comparing equations (1) and (2), we have

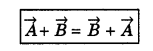
Question 3.
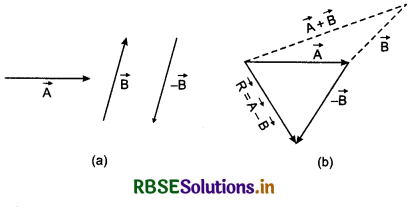
Prove that the magnitude of sum of two vector is maximum (A + B) and minimum (A - B) or (B - A).
Answer:
Addition of vector obeys commutative law:
if \(\vec{A}\) and \(\vec{B}\) are two vector quantities, then
\(\vec{A}\) + \(\vec{B}\) = \(\vec{B}\) + \(\vec{A}\).
Suppose oa = \(\vec{A}\) and ab = \(\vec{B}\), from law of triangle of vector addition for ∆oab
or \(\vec{ob}\) = \(\vec{oa}\) + \(\vec{ab}\)
or \(\vec{R}\) = \(\vec{A}\) + \(\vec{B}\) ........................(1)

On applying the same law of ∆acb
\(\vec{ob}\) = \(\vec{oc}\) + \(\vec{cb}\)
or \(\vec{R}\) = \(\vec{B}\) + \(\vec{A}\) ........................(2)
On comparing equations (1) and (2), we have

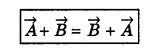
Vector addition obeys associative law:
(\(\vec{A}\) + \(\vec{B}\)) + \(\vec{C}\) = \(\vec{A}\) + (\(\vec{B}\) + \(\vec{C}\))
Suppose three vectors \(\vec{A}\), \(\vec{B}\) and \(\vec{C}\) are represented by \(\vec{oa}\), \(\vec{ab}\) and \(\vec{bc}\) respectively.

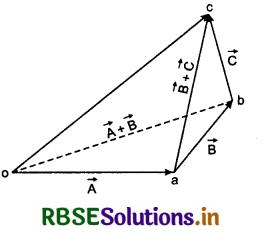
Applying law of triangle for vector addition in ∆oab
\(\vec{ob}\) = \(\vec{oa}\) + \(\vec{ab}\) = \(\vec{A}\) + \(\vec{B}\)
Similarly in ∆abc

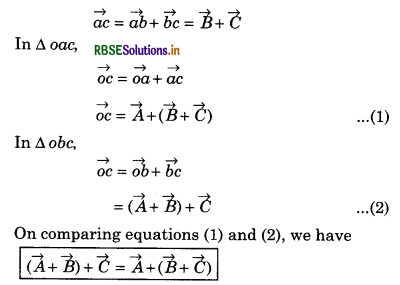
Subtraction of Vectors
Process of subtraction is also the process of addition. The vector to be subtracted is added with negative signs. i.e.
\(\vec{A}\) - \(\vec{B}\) = \(\vec{A}\) + (-\(\vec{B}\))
Suppose vectors \(\vec{A}\) and \(\vec{B}\) are as shown in following diagram [fig. 4.16 (a)], then subtract of \(\vec{B}\) from \(\vec{A}\) is expressed in the same diagram [fig. 4.16(b)].
In fig. (b), the difference in addition and subtraction is made clear.

If we have to subtract \(\vec{A}\) from \(\vec{B}\), then the process is shown in following diagram (fig. 4.17).

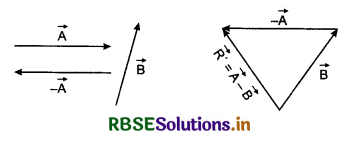
On comparing \(\vec{R}\) and \(\vec{R}^{\prime}\), we find that magnitude of both vectors is same but their directions are opposite i.e., \(\vec{R}\) = -\(\vec{R}^{\prime}\) or (\(\vec{A}\) - \(\vec{B}\)) = -(\(\vec{B}\) - \(\vec{A}\)).
Thus it is obvious that difference of two vectors is not commutative.
There is another method also for subtraction of vectors. In this method we draw both vectors from the same point. If \(\vec{B}\) is to be subtracted from \(\vec{A}\), then the head of \(\vec{B}\) is joined to head of \(\vec{A}\) (fig. 4.18. (b)). This vector \(\vec{R}\) = (\(\vec{B}\) - \(\vec{B}\)). On the other hand if \(\vec{A}\) is to be subtracted from \(\vec{B}\), then the head of \(\vec{A}\) is joined to \(\vec{B}\).
This provides \(\vec{R}^{\prime}\) = (\(\vec{B}\) - \(\vec{A}\)) [Fig. 4.18 (c)]

Question 4.
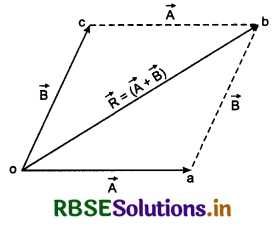
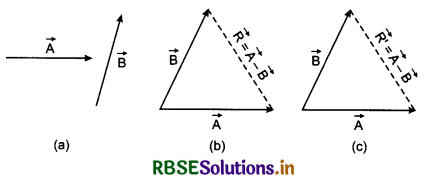
Explain polygon method for adding more than two vectors. Prove that the vector addtion obeys associative law.
Answer:
Polygon method of vector addition: This method of vector addition is pure graphical method and by this method two or more than two vectors can be added successfully. The process of addition is started by drawing any one vector in given direction and its length (magnitudes) according to appropriate scale chosen. From the head of this vector, second vector is drawn and from the head of second vector, third vector and so on. In the last the tail of first vector and head of last vector is joined which provides the resultant of all vectors. For example: following four vectors given, in fig. 4.13 (a) are to be added. In fig. 4.13 (b) the addition process is shown starting from \(\vec{A}\).

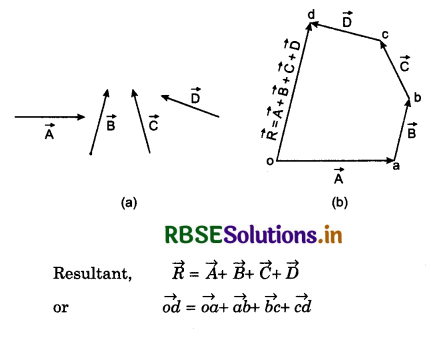
Vector addition obeys associative law:
(\(\vec{A}\) + \(\vec{B}\)) + \(\vec{C}\) = \(\vec{A}\) + (\(\vec{B}\) + \(\vec{C}\))
Suppose three vectors \(\vec{A}\), \(\vec{B}\) and \(\vec{C}\) are represented by \(\vec{oa}\), \(\vec{ab}\) and \(\vec{bc}\) respectively.

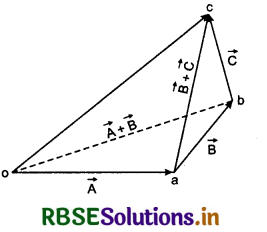
Applying law of triangle for vector addition in ∆oab
\(\vec{ob}\) = \(\vec{oa} + \vec{ab} = \vec{A} + \vec{B}\)
Similarly in ∆abc

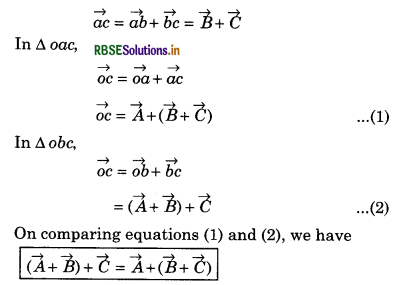
Question 5.
What do you understand by projectile? Prove that the path of projectile projected in horizonal direction from the top of a tower, is parabolic.
Answer:
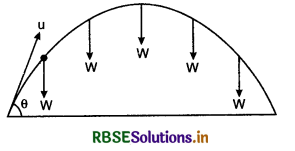
In accelerated motion in horizontal direction, the direction of acceleration is always in the direction of motion, therefore the magnitude of velocity (i.e., speed) remains changing with time while the direction remains unchanged. This type of motion is called ‘Linear motion’.

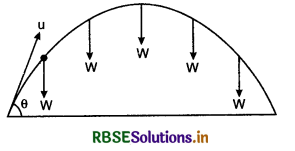
Now we study such motion in which the direction of acceleration remains in same direction but different with the direction of velocity. In this situation velocity of the particle remains changing with time. This motion is called “motion in a plane”. Simplest example of motion in plane is ‘projectile motion’. As shown in fig. 4.48 if an object is projected at an angle with horizontal in upward direction and air friction is neglected, then only one force (weight W of the object) acts on the object. Due to this force the path of the object becomes parabolic not straight. Thus, “the object which moves on parabolic path, is called projectile and its path of motion is called trajectory.” A packet left from an aeroplane, an object projected horizontally from a tower; an object projected at an angle upward from ground, the bullet fired by a gun etc. are the examples of projectile motion.
Therefore projectile motion can be resolved in two perpendicular linear motions.
(i) Horizontal motion and
(ii) Vertical motion
These two motions are totally independent on each other. Horizontal motion is accelerationless i.e, with uniform speed, but vertical motion is under gravitational acceleration, i.e, the object moves under gravitation acceleration acting always vertically downwards. As a result the velocity of a object decreases during upward motion, with the same rate it increases when moves vertically downward. Then the time taken by the object in reaching upto highest point is same as that from highest point to point of projection.

From above discussion, it is clear that projectile motion is such example in which the velocity of the object always keep on changing while its acceleration (g = 9.8ms^-2) remains constant.
Projection in Horizontal Direction from a Height
Suppose an object is projected in horizontal direction with initial velocity  from point O. In horizontal direction, its horizontal velocity will remain unchanged because air friction is considered negligible and no any other force is acting on object in horizontal direction. In the beginning vertical velocity at O is zero but as the object leaves the point O, its vertical velocity starts increasing with acceleration g. Therefore in this projection, after time t s, horizontal velocity = \(\vec{u}\) (which is initial velocity) ...................(i)
Vertical velocity \(\vec{v} = \vec{g}\)t (applying equation v = u + at) ................(ii)
∴ Resultant velocity \(\vec{v}\)R = \(\vec{u} + \vec{g}\)t .............................(1)
The direction of this resultant velocity can be obtained by drawing tangent on the trajectory at the point in reference as is shown at point A in fig. 4.49.

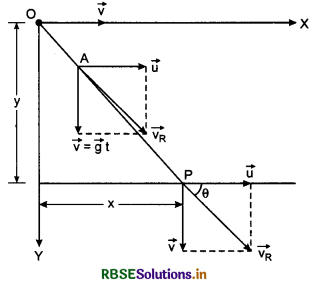
If the time taken by projectile in reaching point P, be T (which is called time of flight), then at point P,
Horizontal velocity of the projectile = \(\vec{u}\)
∴ Horizontal displacement, x = u T .......................(iii)
and vertical displacement y = \(\frac{1}{2}\)gT² .........................(iv)
(By formula h = ut + \(\frac{1}{2}\)gt² and u = 0)
∴ Resultant displacement
= \(\sqrt{x_2}+{y_2} = \sqrt{(u T)^2+\left(\frac{1}{2} g T^2\right)^2}\) .........................(2)
From equation (iii)
T = \(\frac{x}{u}\)
∴ From equation (iv),
y = \(\frac{1}{2}g\frac{x_2}{u_2} or \frac{2u_2}{g}\)y = x²
or x² = \(\frac{2u_2}{g}\)y .......................(3)

Question 6.
What is projectile? Find the expressions of the following:
(i) Maximum height
(ii) Time of flight 
(iii) Range of projectile projected at an angle θ with horizontal.
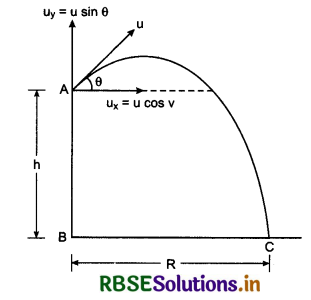
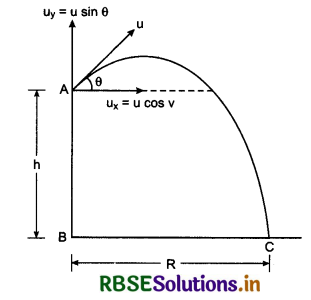
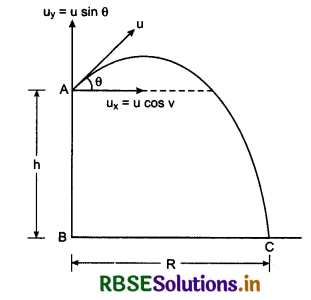
Answer:
If a projectile is projected upward from the tower of height h, making an angle θ with horizontal, then, horizontal component of initial velocity
u_x = u cosθ ............................(1)
and vertical component
u_y =  u sinθ ..........................(2)
On taking downward direction positive.
u_y = -u sinθ

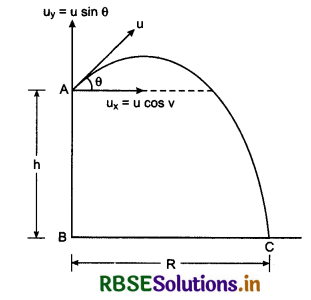
For time of flight: In vertical direction from A to B, from second equation of motion,

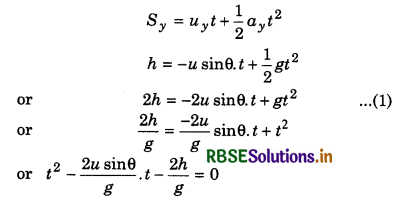
On comparing this quadratic equation with ax² + bx + c = 0, we have:
a = 1, b = \(-\frac{2 u \sin \theta}{g}\); c = \(\frac{-2 h}{g}\)
∴ t = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
On substituting the values in above relation, we can calculate the value of t.
For range: ∵ Range = horizontal velocity x time of flight

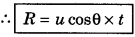
Question 7.
Projectile projected at angle θ, moves under gravity. Establish the equation of trajectory.
Answer:
If a projectile is projected upward from the tower of height h, making an angle θ with horizontal, then, horizontal component of initial velocity
u_x = u cosθ ............................(1)
and vertical component
u_y =  u sinθ ..........................(2)
On taking downward direction positive.
u_y = -u sinθ

For time of flight: In vertical direction from A to B, from second equation of motion,

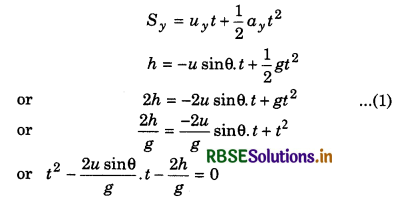
On comparing this quadratic equation with ax² + bx + c = 0, we have:
a = 1, b = \(-\frac{2 u \sin \theta}{g}\); c = \(\frac{-2 h}{g}\)
∴ t = _{\(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)}
On substituting the values in above relation, we can calculate the value of t.
For range: ∵ Range = horizontal velocity x time of flight

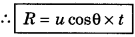
Question 8.
At what angle of projection, the maximum range (R_max) will be travelled by a projectile projected with initial velocity u and maximum height i.e., (H_max) will be obtained at what angle of projection? Also establish the relation between Rmax and Hmax.
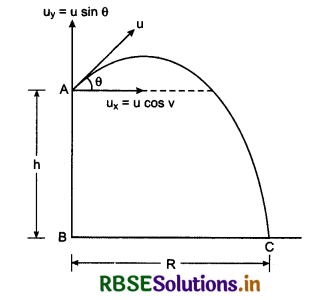
Answer:
If a projectile is projected upward from the tower of height h, making an angle θ with horizontal, then, horizontal component of initial velocity
u_x = u cosθ ............................(1)
and vertical component
u_y =  u sinθ ..........................(2)
On taking downward direction positive.
u_y = -u sinθ

For time of flight: In vertical direction from A to B, from second equation of motion,

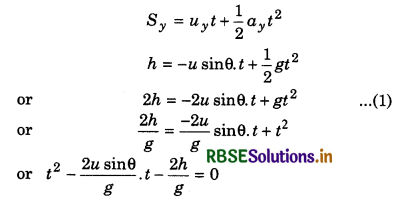
On comparing this quadratic equation with ax² + bx + c = 0, we have:
a = 1, b = \(-\frac{2 u \sin \theta}{g}\); c = \(\frac{-2 h}{g}\)
∴ t = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
On substituting the values in above relation, we can calculate the value of t.
For range: ∵ Range = horizontal velocity x time of flight

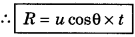
Question 9.
What is projectile? Prove that its range will be maximum for angle of projection θ = 45°.
Answer:
In accelerated motion in horizontal direction, the direction of acceleration is always in the direction of motion, therefore the magnitude of velocity (i.e., speed) remains changing with time while the direction remains unchanged. This type of motion is called ‘Linear motion’.

Now we study such motion in which the direction of acceleration remains in same direction but different with the direction of velocity. In this situation velocity of the particle remains changing with time. This motion is called “motion in a plane”. Simplest example of motion in plane is ‘projectile motion’. As shown in fig. 4.48 if an object is projected at an angle with horizontal in upward direction and air friction is neglected, then only one force (weight W of the object) acts on the object. Due to this force the path of the object becomes parabolic not straight. Thus, “the object which moves on parabolic path, is called projectile and its path of motion is called trajectory.” A packet left from an aeroplane, an object projected horizontally from a tower; an object projected at an angle upward from ground, the bullet fired by a gun etc. are the examples of projectile motion.
Therefore projectile motion can be resolved in two perpendicular linear motions.
(i) Horizontal motion and
(ii) Vertical motion
These two motions are totally independent on each other. Horizontal motion is accelerationless i.e, with uniform speed, but vertical motion is under gravitational acceleration, i.e, the object moves under gravitation acceleration acting always vertically downwards. As a result the velocity of a object decreases during upward motion, with the same rate it increases when moves vertically downward. Then the time taken by the object in reaching upto highest point is same as that from highest point to point of projection.
From above discussion, it is clear that projectile motion is such example in which the velocity of the object always keep on changing while its acceleration (g = 9.8ms^-2) remains constant.
Projection in Horizontal Direction from a Height
Suppose an object is projected in horizontal direction with initial velocity  from point O. In horizontal direction, its horizontal velocity will remain unchanged because air friction is considered negligible and no any other force is acting on object in horizontal direction. In the beginning vertical velocity at O is zero but as the object leaves the point O, its vertical velocity starts increasing with acceleration g. Therefore in this projection, after time t s, horizontal velocity = \(\vec{u}\) (which is initial velocity) ...................(i)
Vertical velocity \(\vec{v} = \vec{g}\)t (applying equation v = u + at) ................(ii)
∴ Resultant velocity \(\vec{v}\)R = \(\vec{u} + \vec{g}\)t .............................(1)
The direction of this resultant velocity can be obtained by drawing tangent on the trajectory at the point in reference as is shown at point A in fig. 4.49.

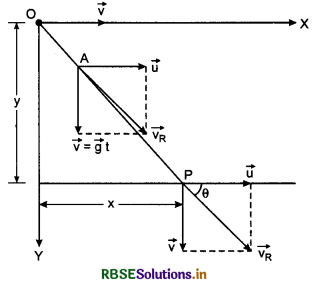
If the time taken by projectile in reaching point P, be T (which is called time of flight), then at point P,
Horizontal velocity of the projectile = \(\vec{u}\)
∴ Horizontal displacement, x = u T .......................(iii)
and vertical displacement y = \(\frac{1}{2}\)gT² .........................(iv)
(By formula h = ut + \(\frac{1}{2}\)gt² and u = 0)
∴ Resultant displacement
= \(\sqrt{x_2}+{y_2} = \sqrt{(u T)^2+\left(\frac{1}{2} g T^2\right)^2}\) .........................(2)
From equation (iii)
T = \(\frac{x}{u}\)
∴ From equation (iv),
y = \(\frac{1}{2}g\frac{x_2}{u_2}\) or \(\frac{2u_2}{g}\)y = x²
or x² = \(\frac{2u_2}{g}\)y .......................(3)

If a projectile is projected upward from the tower of height h, making an angle θ with horizontal, then, horizontal component of initial velocity
u_x = u cosθ ............................(1)
and vertical component
u_y =  u sinθ ..........................(2)
On taking downward direction positive.
u_y = -u sinθ

For time of flight: In vertical direction from A to B, from second equation of motion,

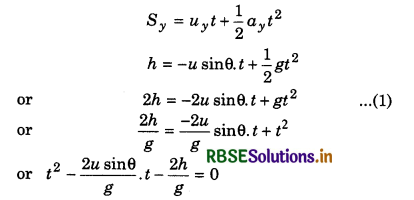
On comparing this quadratic equation with ax² + bx + c = 0, we have:
a = 1, b = \(-\frac{2 u \sin \theta}{g}\); c = \(\frac{-2 h}{g}\)
∴ t = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
On substituting the values in above relation, we can calculate the value of t.
For range: ∵ Range = horizontal velocity x time of flight

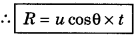
Question 10.
Find the resultant velocity of projectile at any point of trajectory when projected at an angle θ.
If a projectile is projected upward from the tower of height h, making an angle θ with horizontal, then, horizontal component of initial velocity
u_x = u cosθ ............................(1)
and vertical component
u_y =  u sinθ ..........................(2)
On taking downward direction positive.
u_y = -u sinθ

For time of flight: In vertical direction from A to B, from second equation of motion,

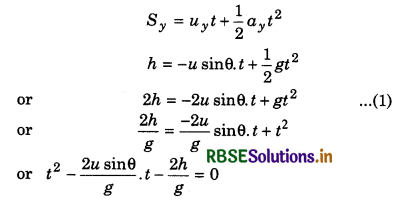
On comparing this quadratic equation with ax² + bx + c = 0, we have:
a = 1, b = \(-\frac{2 u \sin \theta}{g}\); c = \(\frac{-2 h}{g}\)
∴ t = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
On substituting the values in above relation, we can calculate the value of t.
For range: ∵ Range = horizontal velocity x time of flight

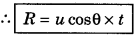
Question 11.
Prove that, at any time, change in momentum depends an angle of projection and projection velocity.
If a projectile is projected upward from the tower of height h, making an angle θ with horizontal, then, horizontal component of initial velocity
u_x = u cosθ ............................(1)
and vertical component
u_y =  u sinθ ..........................(2)
On taking downward direction positive.
u_y = -u sinθ

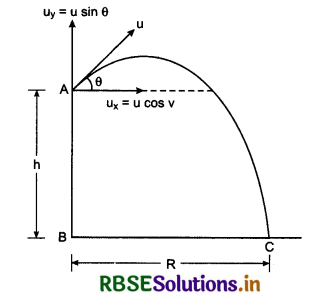
For time of flight: In vertical direction from A to B, from second equation of motion,

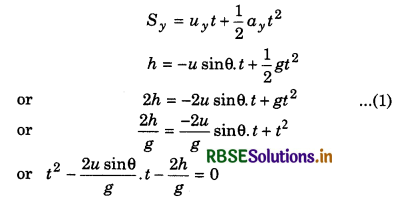
On comparing this quadratic equation with ax² + bx + c = 0, we have:
a = 1, b = \(-\frac{2 u \sin \theta}{g}\); c = \(\frac{-2 h}{g}\)
∴ t = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
On substituting the values in above relation, we can calculate the value of t.
For range: ∵ Range = horizontal velocity x time of flight

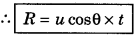
Question 12.
What do you understand by uniform circular motion? Define angular velocity of a particle and establish relation between linear velocity and angular velocity.
Answer:
When a particle moves on a circular path with uniform speed, then its motion is called uniform circular motion. In this motion, the magnitude of velocity of the particle remains constant (equal to speed of the particle) but the direction always remains changing. Therefore, for the motion of the particle under such acceleration the direction of particle remains changing always.

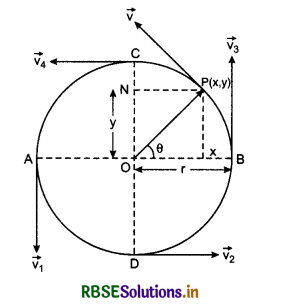
As is shown in fig. 4.60, a particle is moving with constant speed u on a circular path of radius r and centre O. At any time the position of the particle P can be expressed by angle θ which is made by radius vector (\(\vec{r}\)) with initial position OB. At any time the direction of the velocity is along the tangent on the circle and tangent is perpendicular to radius at that time. The magnitude of velocity remains constant. Therefore the magnitudes of the velocities shown at A, D, B and C,
\(|\vec{v_1}| = |\vec{v_2}| = |\vec{v_3}| = |\vec{v_4}|\) = v

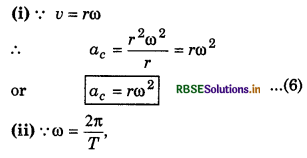
Angularvelocity (ω): "Rate of change of angular displacement with time is called angular velocity." It is denoted by ω and it is a vector quantity. Its unit is rad s^-1 and its direction is decided by right hand screw rule.
According to definition, "Angular velocity is angle by which radius vector rotates in 1 second."

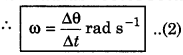
For very short time interval i.e., ∆t → 0

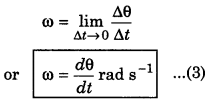
Since the angular displacement in one complete revolution is 2π and time taken is time period T, therefore

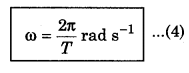
If the frequency of revolution be n, then
n = \(\frac{1}{T}\)
∴ ω = 2πn rad s^-1 ..........................(5)
If a particle is moving on circular path with uniform angular velocity, then angular displacement in time t will be θ = ωt.

Linear velocity: When a particle moves in straight line then its displacement remains changing with time. "Rate of change of displacement with time is called the velocity of the particle." It is denoted by v and it is a velocity quantity. Its unit is ms^-1. If the displacement of a particle in time interval ∆t is ∆s, then its average velocity,

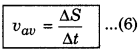
If ∆t → 0, then instantaneous velocity
v = \(\lim _{\Delta t \rightarrow 0} \frac{\Delta S}{\Delta t}\)

Question 13.
What do you understand by centripetal acceleration? Obtain the expressions for centripetal acceleration of a particle executing uniform circular motion.
Answer:
When a particle moves on a circular path with uniform speed, then its velocity remains changing at each point of the path due to changing the direction of velocity. In this situation an acceleration becomes active on the particle and the direction of this acceleration always remains towards the centre of the path. This acceleration is called centripetal acceleration or normal acceleration or radial acceleration.

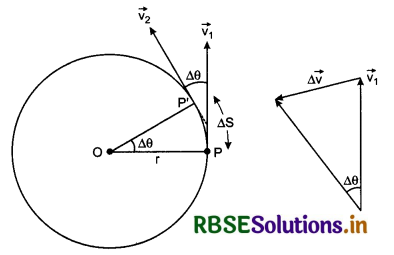
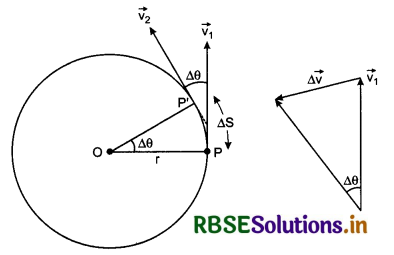
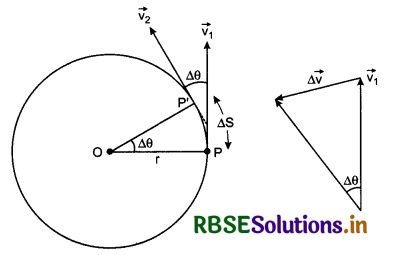
Suppose a particle is moving on circular path of radius r with uniform speed v. In time interval ∆t, it reaches from point P to P'. Velocity of the particle at these points is \(\vec{v_1}\) and \(\vec{v_2}\) and the distance along circular part i.e. arc is ∆S. Since the speed is constant;
∴ \(|\vec{v_1}| = |\vec{v_2}|\) = v (speed)
or v₁ = v₂ = v ..........................(1)
∵ Angle = \(\frac{\text { arc }}{\text { radius }}\)
∴ From fig.4.62, angle
∆θ = \(\frac{\Delta S}{r}\) ............................(2)
If we show vectors \(\vec{v_1}\) and \(\vec{v_2}\) on same vector diagram, then we get the diagram shown in fig. 4.63.
From this diagram,

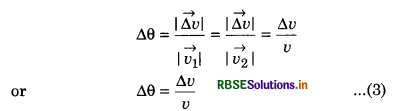
On comparing equation (2) and (3), we have
\(\frac{\Delta v}{v}=\frac{\Delta S}{r}\)

With the help of diagram 4.62, it can be proved \(\overrightarrow{\Delta v}\) will be towards the centre of the circular path. Therefore this acceleration is called 'Centripetal acceleration' and is denoted by a_c.

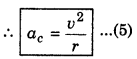
Since this acceleration, normal to velocity, therefore it is also called 'normal acceleration' and it is along radius of the path, hence it is called 'radial acceleration.'

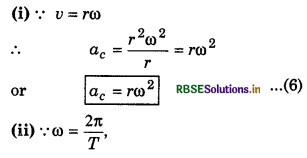
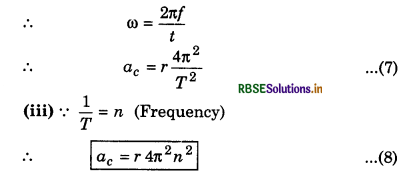
when the frequency is given in rotations

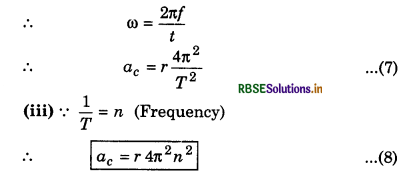
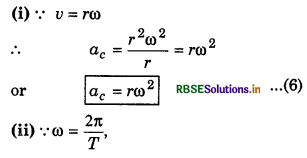
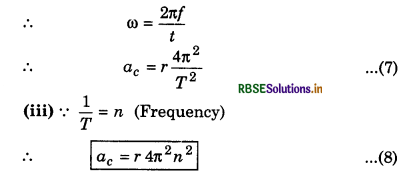
Since the magnitude of the particle velocity i.e., speed u is constant, therefore magnitude of a_c = \(\left(\frac{v^2}{r}\right)\) also remains constant but its direction remains changing due to changing the direction of particle velocity. However, its direction remains always perpendicular to velocity and towards centre of the path.

Question 14.
An object is moving on circular path of radius R with uniform speed. Its frequency is n. Prove that its centripetal acceleration will be a = 4π²n²R.
Answer:
When a particle moves on a circular path with uniform speed, then its velocity remains changing at each point of the path due to changing the direction of velocity. In this situation an acceleration becomes active on the particle and the direction of this acceleration always remains towards the centre of the path. This acceleration is called centripetal acceleration or normal acceleration or radial acceleration.

Suppose a particle is moving on circular path of radius r with uniform speed v. In time interval ∆t, it reaches from point P to P'. Velocity of the particle at these points is \(\vec{v_1}\) and \(\vec{v_2}\) and the distance along circular part i.e. arc is ∆S. Since the speed is constant;
∴ \(|\vec{v_1}| = |\vec{v_2}\)| = v (speed)
or v₁ = v₂ = v ..........................(1)
∵ Angle = \(\frac{\text { arc }}{\text { radius }}\)
∴ From fig.4.62, angle
∆θ = \(\frac{\Delta S}{r}\) ............................(2)
If we show vectors \(\vec{v_1}\) and \(\vec{v_2}\) on same vector diagram, then we get the diagram shown in fig. 4.63.
From this diagram,

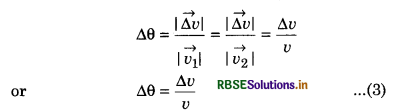
On comparing equation (2) and (3), we have
\(\frac{\Delta v}{v}=\frac{\Delta S}{r}\)

With the help of diagram 4.62, it can be proved \(\overrightarrow{\Delta v}\) will be towards the centre of the circular path. Therefore this acceleration is called 'Centripetal acceleration' and is denoted by a_c.

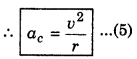
Since this acceleration, normal to velocity, therefore it is also called 'normal acceleration' and it is along radius of the path, hence it is called 'radial acceleration.'

when the frequency is given in rotations

Since the magnitude of the particle velocity i.e., speed u is constant, therefore magnitude of a_c = \(\left(\frac{v^2}{r}\right)\) also remains constant but its direction remains changing due to changing the direction of particle velocity. However, its direction remains always perpendicular to velocity and towards centre of the path.

Question 15.
Obtain the expression for centripetal acceleration. What will be resultant acceleration in non-uniform circular motion?
Answer:
When a particle moves on a circular path with uniform speed, then its velocity remains changing at each point of the path due to changing the direction of velocity. In this situation an acceleration becomes active on the particle and the direction of this acceleration always remains towards the centre of the path. This acceleration is called centripetal acceleration or normal acceleration or radial acceleration.

Suppose a particle is moving on circular path of radius r with uniform speed v. In time interval ∆t, it reaches from point P to P'. Velocity of the particle at these points is \(\vec{v_1}\) and \(\vec{v_2}\) and the distance along circular part i.e. arc is ∆S. Since the speed is constant;
∴ \(|\vec{v_1}| = |\vec{v_2}|\) = v (speed)
or v₁ = v₂ = v ..........................(1)
∵ Angle = \(\frac{\text { arc }}{\text { radius }}\)
∴ From fig.4.62, angle
∆θ = \(\frac{\Delta S}{r}\) ............................(2)
If we show vectors \(\vec{v_1}\) and \(\vec{v_2}\) on same vector diagram, then we get the diagram shown in fig. 4.63.
From this diagram,

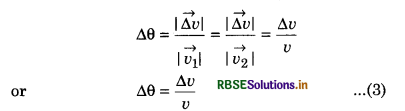
On comparing equation (2) and (3), we have
\(\frac{\Delta v}{v}=\frac{\Delta S}{r}\)

With the help of diagram 4.62, it can be proved \(\overrightarrow{\Delta v}\) will be towards the centre of the circular path. Therefore this acceleration is called 'Centripetal acceleration' and is denoted by a_c.

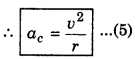
Since this acceleration, normal to velocity, therefore it is also called 'normal acceleration' and it is along radius of the path, hence it is called 'radial acceleration.'

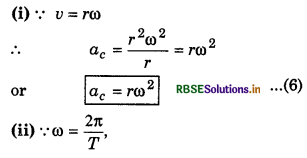
when the frequency is given in rotations

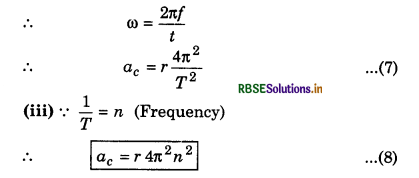
Since the magnitude of the particle velocity i.e., speed u is constant, therefore magnitude of a_c = \(\left(\frac{v^2}{r}\right)\) also remains constant but its direction remains changing due to changing the direction of particle velocity. However, its direction remains always perpendicular to velocity and towards centre of the path.

Question 16.
A particle of mass m is moving on circular path of radius r with uniform speed v. Find the value of centripetal acceleration and its direction, acting on the particle.
Answer:
When a particle moves on a circular path with uniform speed, then its velocity remains changing at each point of the path due to changing the direction of velocity. In this situation an acceleration becomes active on the particle and the direction of this acceleration always remains towards the centre of the path. This acceleration is called centripetal acceleration or normal acceleration or radial acceleration.

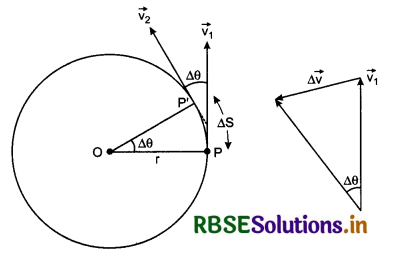
Suppose a particle is moving on circular path of radius r with uniform speed v. In time interval ∆t, it reaches from point P to P'. Velocity of the particle at these points is \(\vec{v_1}\) and \(\vec{v_2}\) and the distance along circular part i.e. arc is ∆S. Since the speed is constant;
∴ \(|\vec{v_1}| = |\vec{v_2}|\) = v (speed)
or v₁ = v₂ = v ..........................(1)
∵ Angle = \(\frac{\text { arc }}{\text { radius }}\)
∴ From fig.4.62, angle
∆θ = \(\frac{\Delta S}{r}\) ............................(2)
If we show vectors \(\vec{v_1}\) and \(\vec{v_2}\) on same vector diagram, then we get the diagram shown in fig. 4.63.
From this diagram,

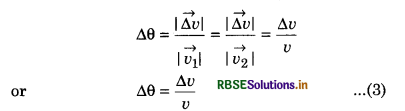
On comparing equation (2) and (3), we have
\(\frac{\Delta v}{v}=\frac{\Delta S}{r}\)

With the help of diagram 4.62, it can be proved \(\overrightarrow{\Delta v}\) will be towards the centre of the circular path. Therefore this acceleration is called 'Centripetal acceleration' and is denoted by a_c.

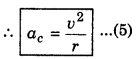
Since this acceleration, normal to velocity, therefore it is also called 'normal acceleration' and it is along radius of the path, hence it is called 'radial acceleration.'

when the frequency is given in rotations

Since the magnitude of the particle velocity i.e., speed u is constant, therefore magnitude of a_c = \(\left(\frac{v^2}{r}\right)\) also remains constant but its direction remains changing due to changing the direction of particle velocity. However, its direction remains always perpendicular to velocity and towards centre of the path.

Numerical Questions

Based on addition and subtraction of vectors

Question 1.
Two forces of 6N and 8N are acting at a point at right angle to each other. Determine their resultant by vector sketch.
Answer:
Given: F₁ = 6N, F₂ = 8N, θ = 90°
Scale 1 N = 1 cm
∴ F₁ = 6N = 6 cm
F₂ = 8N = 8 cm
Length of resultant force
\(\vec{F} = \vec{F_1} + \vec{F_2}\) = 10 cm
∴ F = 10N

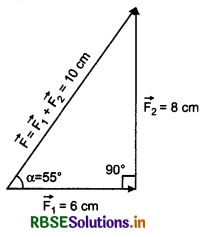
Direction of \(\vec{F}\) from \(\vec{F_1}\) = α = 53° (on measuring).

Question 2.
Two forces of 3N and 9N are acting at a point making an angle of 60° between them. Find their resultant by vector sketch.
Answer:
10.8 N, at an angle of 46° wiht 3N force

Question 3.
The magnitude of two forces acting on a body are F and F and that of their resultant is also F. Find the angle between them.
Answer:
Given: F₁ = F; F₂ = F; R = F; θ = ?
∵ R = \(\sqrt{F_1^2+F_2^2+2 F_1 F_2 \cos \theta}\)
or F = \(\sqrt{F^2+F^2+2 F^2 \cos \theta}\)
or F² = 2F² + 2F² cosθ
or 1 = 2 + 2 cosθ
or 2cosθ = 1 - 2 = -1
or cosθ = \(-\frac{1}{2}\)
∴ θ = cos^-1(-\(\frac{1}{2}\)) = 120°
or θ = 120°

Question 4.
Two forces of same magnitude of 3N are acting on an object at an angle of θ. The magnitude of resultant of these vectors is also 3N. Find the value of θ.
Answer:
θ = 120°

Based an resolution of vectors

Question 5.
A force of 50 N is acting on a body making an angle of 30° from east. Find the eastern and northern components of the force.
Answer:
Given: F = 50N
F_E = ?, F_N = ?

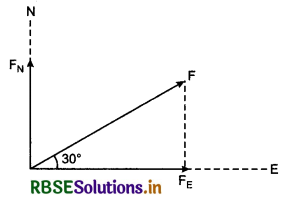
From the diagram,
Eastern component of force,
F_E = F cos 30° = 50 x \(\frac{\sqrt{3}}{2}\) = 25 x 1.732
or F_E = 43.3N
and F_M = F sin 30° = 50 x \(\frac{1}{2}\) = 25N

Question 6.
Vertical component of a force acting at 30° from horizontal; is 200 N. Find the value of applied force.
Answer:
Given: F_v = 200N
F = ?
From the figure

F_v = F sin 30° = F x \(\frac{1}{2}\)
or F = 2F_v = 2 x 200
or F = 400 N

Question 7.
Handle of roller is pulled by a force 50 N. If handle makes an angle of 30° with horizontal, then determine the vertical and horizontal components of the force.
Answer:
Given: F = 50N; θ = 30°
F_H = ?, Fv = ?
∵ F_H = F cosθ = F cos 30°
= 50 x \(\frac{\sqrt{3}}{2}\) = 43.3N

F_v = F sinθ = 50 x \(\frac{1}{2}\) = 25 N

Based on scalar product

Question 8.
If the magnitude of two vectors are 5 and 8 and their scalar product is 20\(\sqrt{2}\), then find the angle between the vectors.
Answer:
Given: A = 5; B = 8, \(\vec{A}.\vec{B}\) = 20\(\sqrt{2}\); θ = ?
∵ cosθ = \(\frac{\vec{A} \cdot \vec{B}}{A \cdot B}=\frac{20 \sqrt{2}}{5 \times 8}=\frac{1}{2} \times \sqrt{2}=\frac{1}{\sqrt{2}}\)
∴ θ = cos^-1(\(\frac{1}{\sqrt{2}}\) ) = 45°
or θ = 45°

Question 9.
If \(\vec{A} = 4\hat{i} + 3\hat{j}\) and \(\vec{B} = 5\hat{i} - 2\hat{j}\), then find the value of \(\vec{A}.\vec{B}\).
Answer:
Given: \(\vec{A} = 4\hat{i} + 3\hat{j}\), \(\vec{B} = 5\hat{i} - 2\hat{j}\)
\(\vec{A}.\vec{B}\) = ?
\(\vec{A}.\vec{B} = (4\hat{i} + 3\hat{j}).(5\hat{i} - 2\hat{j})\)
= \(20\hat{i}.\hat{i} - 8\hat{i}.\hat{j} + 15\hat{j}.\hat{i} - 6\hat{j}.\hat{j}\)
= 20 - 0 + 0 - 6
= 14

Question 10.
A force of 150 N is active on a body and the body gets displaced by 15 m making an angle of 60°. Calculate the work done by the force.
Answer:
Given: F = 150 N; θ = 60°; d = 15 m; W = ?
∵ W = \(\vec{F}.\vec{d}\) = F.d. cosθ
= 150 x 15 x cos 60°
= 150 x 15 x \(\frac{1}{2}\) = 75 x 15
= 1125 J

Question 11.
Magnitude of vector \(\vec{F}\) is 3.0 N and it makes an angle of 60° with displacement vector \(\vec{R}\) of magnitude 4.0 m. Obtain the value of scalar product \(\vec{F}.\vec{R}\).
Answer:
F = 3N; R = 4.0m; θ = 60°; \(\vec{F}.\vec{R}\) = ?
∴ \(\vec{F}.\vec{R}\) = F.R cosθ = 3 x 4 x cos 60°
= 3 x 4 x \(\frac{1}{2}\)
= 6J

Question 12.
A force of 10 N is acting on an object, then it gets displacement by 2m in the direction of the force. Calculate the work done.
Answer:
F = 10N; d = 2 m; θ = 0°; W = ?
W = \(\vec{F}.\vec{d}\) = F.d. cosθ
= 10 x 2 x cos 0°
= 20 x 1
= 20 J

Question 13.
If \(\vec{A} = \hat{i} - 10\hat{j}\) and \(\vec{B} = 3\hat{i} - 4\hat{j}\), then find \(\vec{A}.\vec{S}\).
Answer:
\(\vec{A} = \hat{i} - 10\hat{j}\); \(\vec{B} = 3\hat{i} - 4\hat{j}\); \(\vec{A}.\vec{B}\) = ?
\(\vec{A}.\vec{B} = (\hat{i} - 10\hat{j}).(3\hat{i} - 4\hat{j}) = 3\hat{i}.\hat{i} - 4\hat{i}.\hat{j} - 30\hat{j}.\hat{i} + 40\hat{j}.\hat{i} \)
= 3 - 0 - 0 + 40 = 43

Question 14.
If \(\vec{A} = 3\hat{i} - 6\hat{i} - 2\hat{k}\) and \(\vec{B} = \hat{i} + 2 \hat{j} - 3 \hat{k}\), then determine:
(i) magnitude of \(\vec{A}\), (ii) value of \(\vec{A}.\vec{B}\).
Answer:

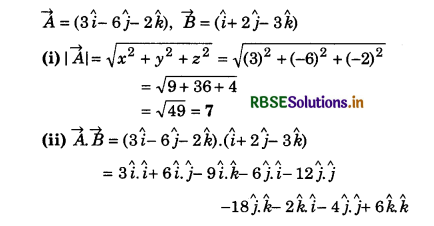
= 3 + 0 - 0 - 0 - 12 - 0 - 0 - 0 + 6
= -3

Question 15.
By applying a constant force \(\vec{F} = (5\hat{i} + 2\hat{j} + 3\hat{k})\)N on a body it is displaced by \(\vec{B} = (10\hat{i} + 12\hat{j} + 13\hat{k}) \)m. Calculate the work done on the body.
Answer:

Question 16.
Prove that vector \(\vec{A} = 2\hat{i} + 2\hat{j} - 2\hat{k}\) and vector \(\vec{B} = 7\hat{i} - 5\hat{j} + 2\hat{k}\) are perpendicular.
Answer:

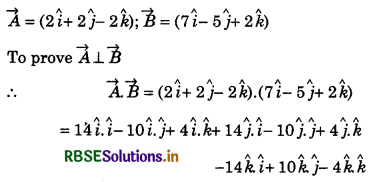
= 14 - 0 + 0 + 0 - 10 + 0 - 0 + 0 - 4
= 14 - 14
= 0
∴ θ = 90°
Hence \(\vec{A}\) ⊥ \(\vec{B}\).

Question 17.
For what value of p, \(\vec{A} = 5\hat{i} + 6\hat{j} + p\hat{k}\) and \(\vec{B} = 4\hat{i} - 5\hat{j} + 2\hat{k}\) will be at right angle to each other?
Answer:

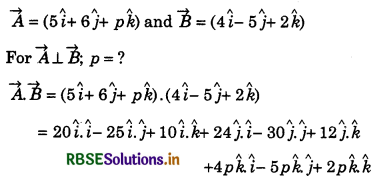
= 20 - 0 + 0 + 0 - 30 + 0 + 0 - 0 + 2p
= -10 + 2p
If \(\vec{A}\) ⊥ \(\vec{B}\)
then \(\vec{A}.\vec{B}\) = 0
∴ 2p - 10 = 0
or 2p = 10
∴ p = 5

Question 18.
(a) \(\vec{A} = 3\hat{i} + 4\hat{j}\) and \(\vec{B} = 12\hat{i} - 5\hat{j}\) where \(\hat{i}\) and \(\hat{j}\) are unit vectors along X and Y axes respectively. Find:
(i) magnitude of \(\vec{A}\) and (ii) value of \(\vec{A}.\vec{B}\).
(b) If \(\vec{A} = 2\hat{i} + 3\hat{j} - 5\hat{k}\), then find the magnitude of it.
Answer:
(a) \(\vec{A} = 3\hat{i} + 4\hat{j}\) and \(\vec{B} = 12\hat{i} - 5\hat{j}\)
(i) \(|\vec{A}| = \sqrt{(3)^2+(4)^2}=\sqrt{9+16}=\sqrt{25}\) = 5
∴ A = 5 unit
\(\vec{A}.\vec{B} = (3\hat{i} + 4\hat{j}).(12\hat{i} - 5\hat{j})\)
= \(36\hat{i}.\hat{i} - 15\hat{i}\hat{j} + 48\hat{j}.\hat{i} - 20\hat{j}.\hat{j}\)
= 36 - 0 + 0 - 20
(b) \(\vec{A} = 2\hat{i} + 3\hat{j} - 5\hat{k}\)
∴ \(|\vec{A}| = \sqrt{(2)^2+(3)^2+(-5)^2}=\sqrt{4+9+25}=\sqrt{38}\)
or A = \(\sqrt{38}\) unit

Question 19.
\(\vec{A} = 3\hat{i} + 4\hat{j}\) and \(\vec{B} = 2\hat{i} - 5\hat{j}\), where \(\hat{i}\) and \(\hat{j}\) are unit vectors along X and Y-axes respectively.
Determine the value of \(\vec{A}.\vec{B}\).
Answer:

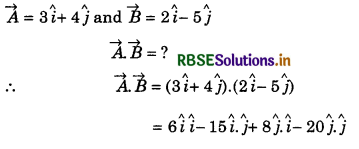
= 6 - 0 + 0 - 20
= -14

Question 20.
Determine the value of (\(2\hat{i} -\hat{j}\)). (\(4\hat{i} + 2\hat{j}\)).
Answer:
(\(2\hat{i} - \hat{j}\)).(\(4\hat{i} + 2\hat{j}\))
= (2)(4) + (-1)(2)
= 8 - 2 = 6

Question 21.
When a force of (\(5\hat{i} + 2\hat{j} + 3\hat{k}\)) is applied on an object, then it displaces by a displacement of (\(10\hat{i} + 12\hat{j} + 14\hat{k}\)) m. Calculate the work done by the force on the object.
Answer:

= 50 + 0 + 0 + 0 + 24 + 0 + 0 + 0 + 42
= 116 J

Question 22.
A force \(\vec{A} = (2\hat{i} + 3\hat{j} + 4\hat{k})\)N displaces a particle by \(\vec{d} = (5\hat{i} + 4\hat{j} + 3\hat{k})\) m. Calculate the work done.
Answer:

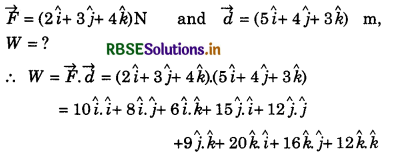
= 10 + 0 + 0 + 0 + 12 + 0 + 0 + 0 + 12
= 34 J

Question 23.
Find the condition under which (\(\vec{a}.\vec{b}\))² = a²b².
Answer:
(\(\vec{a}.\vec{b}\))² = a²b²
or (ab cosθ)² = a²b²
or a²b² cos²θ = a²b²
∴ cos²θ = \(\frac{a^2 b^2}{a^2 b^2}\) = 1
or cosθ = ±1
For cosθ = +1 ⇒ θ = 0°
For cosθ = -1 ⇒ θ = 180°
∴ For θ = 0° or 180°, the given relation will be true.

Question 24.
If vector \(\vec{A} = 3\hat{i} + x\hat{j} + 5\hat{k}\) and \(\vec{B} = 2\hat{i} + \hat{j} - 2\hat{k}\) are perpendicular to each other, then find the value of x.
Answer:

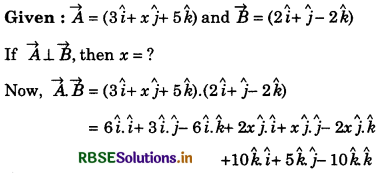
= 6 + 0 - 0 + 0 + x - 0 + 0 + 0 -10
= x - 4
∵ \(\vec{A} ⊥ \vec{B}\)
∴ \(\vec{A}.\vec{B}\) = 0
Therefore, x - 4 = 0 ⇒ x = 4

Question 25.
Three vectors \(\vec{A}\), \(\vec{B}\) and \(\vec{C}\) are such that \vec{A} = \vec{B} + \vec{C} and their magnitude are 5, 4 and 2 respectively. What will be angle between \vec{A} and \vec{C}?
Answer:

Question 26.
Determine the value of p for which \(\vec{A} = 2\hat{i} + 2\hat{j} + p\hat{k}\) and \(\vec{B} = 2\hat{i} - 3\hat{i} + \hat{k}\) will be perpendicular to each other.
Answer:

= 4 - 0 + 0 + 0 - 6 + 0 + 0 - 0 + p
= -2 + p
∵ \(\vec{A} ⊥ \vec{B} \)
∴ \(\vec{A}.\vec{B}\) = 0
Hence p = 2 = 0 ⇒ p = 2

Based on vector product

Question 27.
A force of \(\vec{F} = (2\hat{i} - 3\hat{j} + 4\hat{k})\) N is acting on a point. Its displacement vector about origin is \(\vec{S} = (3\hat{i} + 2\hat{j} + 3\hat{k})\) m. Calculate the torque of the force.
Answer:

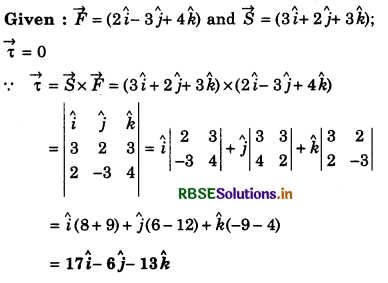
Question 28.
If \(\vec{A} = 3\hat{i} +2\hat{j} -\hat{k}\) and \(\vec{B} = 12\hat{i} + 5\hat{j} - 5\hat{k}\), then find the unit vector at right angle to plane of \(\vec{A}\) and \(\vec{B}\).
Answer:

Question 29.
If vector \(\vec{A} = 2\hat{i} + 2\hat{j} - 2\hat{k}\) and vector \(\vec{B} = 7\hat{i} - 5\hat{j} + 2\hat{k}\), then find the value of \(\vec{A}\) x \(\vec{B}\).
Answer:

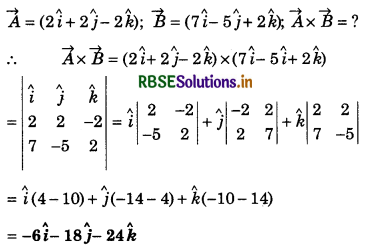
Based on scalar and vector product

Question 30.
If \(\vec{A} = 3\hat{i} + 2\hat{j} + \hat{k}\) and \(\vec{B} = -5\hat{i} - 5\hat{j} + 5\hat{k}\) then what will be the values of \(\vec{A}.\vec{B}\) and \(\vec{A}\) x \(\vec{B}\)?
Answer:

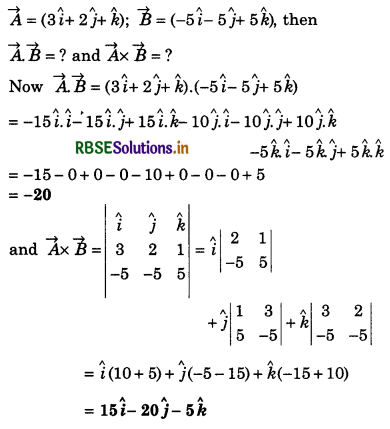
Question 31.
Prove that \(\vec{A} = 4\hat{i} -\hat{j} + 2\hat{k}\) and \(\vec{B} = \hat{i} + 2\hat{j} - \hat{k}\) are perpendicular to each other. Also find their vector product.
Answer:

= 4 + 0 - 0 - 0 - 2 + 0 + 0 + 0 - 2
= 4 - 4 = 0
∴ \(\vec{A}.\vec{B}\) = 0
or A.B. cosθ = 0
or cosθ = 0
∴ θ = 90°
∴ \(\vec{A} ⊥ \vec{B}\)
\(\vec{A} x \vec{B} = (4\hat{i} - \hat{j} + 2\hat{k}) x (\hat{i} + 2\hat{j} - \hat{k})\)

Based on river crossing

Question 32.
A boatman can move his boat with velocity of 10 kmh^-1 in still water. If the width of a river is 2 km and velocity of river flow is 5 kmh^-1, then tell that in which direction he should move his boat so that he may reach just opposite point of other river bank. Also find that how much time will he take to cross the river.
Answer:
Given: \(\vec{v_m}\) = 10 km.h^-1
\(\vec{v_r}\) = 5 km.h^-1
Starting from point A, to reach point B, the boatman should move his boat in opposite direction of river flow at an angle θ with AB.
From the figure,

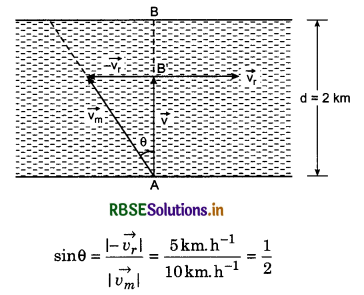
∴ θ = 30°
∴ Angle of boat motion with respect to river bank in anticlockwise direction = 90° + 30° = 120°
Resultant velocity, from the figure
|\(\vec{v}\)|² = |\(\vec{v_m}\)|₂² - |\(\vec{v_r}\)|²
or v² = (10)² - (5)² = 100 - 25 = 75
∴ v = \(\sqrt{75}\) km h^-1
∴ Time taken in crossing the river
t = \(\frac{d}{v}=\frac{2 \mathrm{~km}}{\sqrt{75} \mathrm{~km}^{-1}}=\frac{2}{\sqrt{75}} \mathrm{hr}\)
= \(\frac{2}{8.66}\) hr
= 0.2309 hr
= 0.2309 x 60 min
= 13.8568 min
= 13.86 min

Question 33.
A swimmer swims across the river which is flowing in east direction with velocity of 3 kmh^-1. If relative velocity of swimmer with respect to water is 4 kmh^-1 in north direction, then:
(a) What is relative velocity of swimmer with respect to river bank?
(b) If river be of 5 km width, then what will be time of crossing the river?
(c) On reaching the opposite bank, what will be distance of reaching point from starting point?
Answer:
As \(\vec{v_r}\) = 3 km^-1 in east; \(\vec{v_m}\) = 4 km h^-1 in north, d = 5 km.
(a) Velocity of swimmer wiht respect to river bank is \(\vec{v_m}\). From the figure:

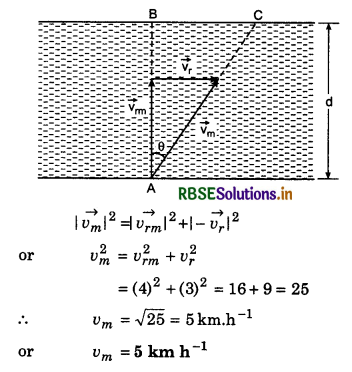
If \(\vec{v_m}\) makes an angle θ with \(\vec{v_rm}\), then
sinθ = \(\frac{\left|-\overrightarrow{v_r}\right|}{\left|\overrightarrow{v_m}\right|}=\frac{3 \mathrm{kmh}^{-1}}{5 \mathrm{kmh}^{-1}}=\frac{3}{5}\) = 0.6 or sinθ = 0.6
∴ θ = sin^-1(0.6) = 37°
(b) Time taken in crossing the river
t = \(\frac{d}{v_{r m}}=\frac{5 \mathrm{~km}}{4 \mathrm{~km} \cdot \mathrm{hr} r^{-1}}\) = 1.25 hr
(c) The distance which travelled along the bank of river
BC = vr x t
= 3 km.hr^-1 x 1.25 hr
= 3.75 km
= 3.75 x 1000 m
= 3750 m

Based on Umbrella Problem

Question 34.
A girl is running with speed of 3 km.h^-1 towards west. She observes that rain is falling vertically downward with speed of 4 km.h^-1. What will be the relative velocity of rain with respect to girl and in which direction should she handle the umbrella to make her safe from rain?
Answer:
\(\vec{v_g}\) = 3 km hr^-1 in west; \(\vec{v_rg}\) = 4 km h^-1 vertically downwards, \(\vec{v_r}\) = ?; θ = ?
Actual velocity of rain fall,
\(\vec{v_r} = \vec{v_rg} - \vec{v_g}\)

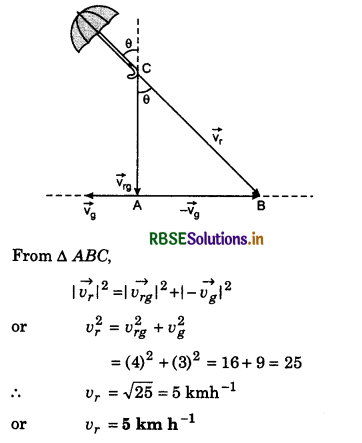
If the angle from vertical at which the girl should handle the umbrella for safety from rain, be θ then
tanθ = \(\frac{\left|-\overrightarrow{v_g}\right|}{\left|\overrightarrow{v_{r g}}\right|}=\frac{3}{4}\)
or θ = tan^-1(\(\frac{3}{4}\)) towards west
or θ = 37° towards west

Question 35.
Shivya is moving in east direction with the speed of 10 ms^-1. At the same time rain starts falling vertically downwards with velocity of 30 ms^-1. At what angle he should handle the umbrella for his safety from rain?
Answer:

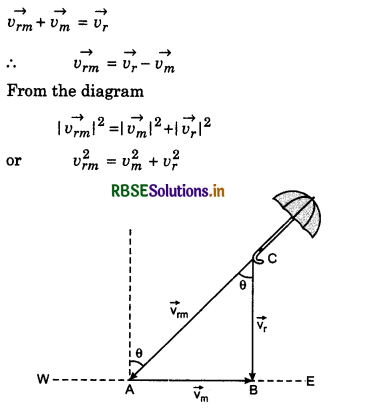
= (10)² + (30)²
= 100 + 900
= 1000
∴ v_rm = \(\sqrt{1000}\) = 10\(\sqrt{10} \)ms^-1
If the angle at which the umbrella is to be handled is θ from vertical, then
tanθ = \(\frac{\left|\overrightarrow{v_m}\right|}{\left|\overrightarrow{v_r}\right|}=\frac{10}{30}=\frac{1}{3}\)
∴ θ = tan^-1(\(\frac{1}{3}\))

Based on displacement velocity and acceleration of particle

Question 36.
The co-ordinates of a particle are x = (4t - 1)m and y = 8t² m. Calculate the following:
(i) Average velocity of the particle during time interval from t = 1 s to t = 2 s, and
(ii) Instantaneous velocity of particle at t = 2s.
Answer:
(i) Given: x = (4t - 1) and y = 8t²

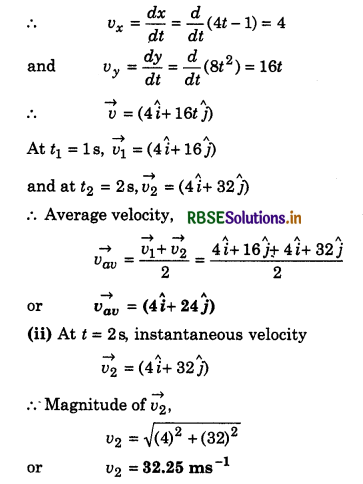
Question 37.
The position of a particle is given by \(\vec{r} = (3t\hat{i} + 4t3\hat{j} + 5\hat{k})\) m. Determine:
(i) Velocity and acceleration of the particle.
(ii) Magnitude of velocity and acceleration at t = 5 s.
Answer:
Given: \(\vec{r} = (3t\hat{i} + 4t3\hat{j} + 5\hat{k})\) m
(i) Velocity of the particle

Based on projectile projected in horizontal direction

Question 38.
A metallic bob Y suspended by a cord vibrates as shown in figure. When the bob is at a height of 10 m and moves with the velocity of 1 ms^-1 in horizontal direction, then the cord is broken. Find the horizotnal distance travelled by the bob.

Answer:
When the cord of sphere breaks, then sphere will behave as projectile porjected in horizontal direction with u = 1 ms^-1.
∴ The time taken by shpere to reach the ground,
t = \(\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 10}{10}}=\sqrt{2} \mathrm{~s}\)
∴ Range R = u x t = 1 x \(\sqrt{2}\) = 1.414 m

Question 39.
Three globules A, B and C are projected horizontally from the top of a tower with velocities 0.5 ms^-1, 1 ms^-1 and 2 ms^-1 respectively. Which globule will reach the ground first? Which globule will reach the ground at maximum distance From the base of the tower?
Answer:
v_A = 0.5 ms^-1; v_B = 1 ms^-1; v_C = 2 ms^-1
∵ Time of flight, T = \(\sqrt{2h}{g}\)
Mass m and horizontal velocity u is not involved in this formula. Therefore, time of flight does not depend upon m and u. Hence, all the three globules will reach the ground at same time.
∵ Horizontal range = horizontal velocity x time of flight
or R = u x T
For same T; R ∝ u
Therefore globule C will let the ground at maximum distance from base of the tower. 

Question 40.
A ball is projected from the top of a tower in horizontal direction with the speed of 40 ms^-1. Gravitation acceleration is 10 m/s².
(i) Determine the speed of the ball and the in direction of the ball with horizontal, after 4s from the time of projection.
(ii) If the ball reaches the ground in 4s, then calculate the height of the tower.
Answer:
(i) Given u = 40 ms^-1; g = 10 ms^-2. Suppose after 4s, the particle is at point P. There, v_x = u = 40 ms^-1, u_y = 0 ms^-1
and v_y = 0 + gt = 10 x 4 = 40 ms^-1
∴ v = \(\sqrt{v_x^2+v_y^2}=\sqrt{(40)^2+(40)^2}\)
= 40\(\sqrt{2} \)ms^-1

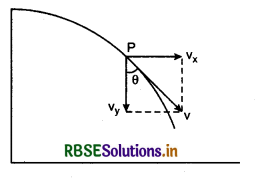
If \(\vec{v}\) makes an angle θ with vertical, then
sinθ = \(\frac{v_x}{v}=\frac{40}{40 \sqrt{2}}=\frac{1}{\sqrt{2}}\)
∴ θ = 45°
(ii) ∵ T = 4s
∴ Height of the tower by using relation
S = ut + ^{\(\frac{1}{2} \)}at²
h = 0 + \(\frac{1}{2}\)gT² = \(\frac{1}{2}\) x 10 x 4 x 4
or h = 80 m

Question 41.
An aeroplane is flying at the height of 1960 m with the velocity of 500/3 ms^-1 in horizontal direction. When the aeroplane is above a point A on the ground, a bomb is dropped from the plane, which strikes the ground at Q. What is the distance AQ?
Answer:
Given: h = 1960 m; u = \(\frac{500}{3}\) ms^-1

Based on the projection at an angle from the ground

Question 42.
A ball is thrown with the velocity of 30 ms^-1 making an angle of 60° with horizontal direction. Find:
(i) time of flight, (ii) maximum height, (iii) range, (iv) magnitude and direction of velocity when ball strikes the ground. (g = 10 ms^-2)
Answer:
u = 30 ms^-1; θ = 60°; g = 10 ms^-2

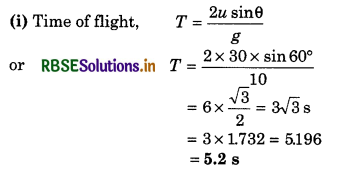
(ii) Maximum height,

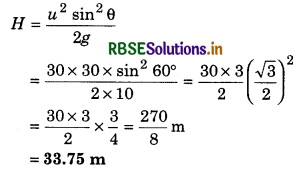
(iii) Range,
R = u cos 60° x T = 300 x\( \frac{1}{2}\) x 5.2
= 15 x 5.2
= 78.0 m
(iv) Velocity of the projectile on reaching the ground will be 30 ms^-1 at an angle of 60° downward with horizontal.

Question 43.
A stone is thrown from the bridge with velocity of 20 ms^-1 making an angle of 30° downwards with horizontal direction. If the stone strikes the water after 2.0 s then what is the height of the bridge from the level of water? (g = 9.8ms^-2)
Answer:
u = 20 ms^-1; θ = 30°; g = 9.8 ms^-2; T = 2s; h = ?

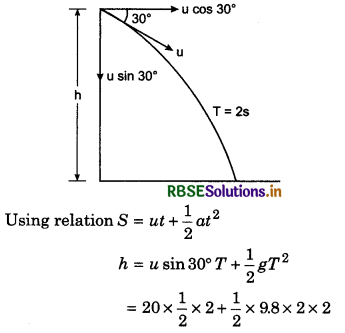
= 20 + 19.6
= 39.6 m

Question 44. 
A fighter plane is flying at the height of 2000 m with horizontal velocity of 540 km h^-1. before how much distance should it drop a bomb so that the bomb may hit the enemy camp? (g = 10ms^-1)
Answer:
h = 2000 m; u =\( 540\frac{\mathrm{km}}{\mathrm{hr}}\) = 540 x \(\frac{5}{18}\) = 150 ms^-1; g = 10 ms^-2; time of flight
T = \(\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 2000}{10}}=\sqrt{400}\)
or T = 20 s
∴ Range R = u x T = 150 x 20 m
= 3000 m
= 3 km

Question 45.
A projectile is projected with velocity of 20 ms^-1 at an angle of 60° with horizontal. A car is running on horizontal road with velocity of 5 ms^-1. At the time of projection, the car is 50 m ahead. Determine the time when the projectile will strike the back of car.
Answer:
v = 20 ms^-1, θ = 60°
Speed of car u = 5 ms^-1
Horizontal component of projectile velocity
v_x = v cos 60° = v x \(\frac{1}{2}\) = 20 x \(\frac{1}{2}\) = 10 ms^-1
∴ Relative velocity of projectile with respect to car
v_pc = v_p - v_c = 10 - 5 = 5 ms^-1
The distance of car, 50 m, will be covered with this velocity;
∴ 50 = v_pc x t = 5t
∴ t = \(\frac{50}{5}\) = 10s

Based on projection at an angle from some height

Question 46.
The top of a tower is 156 m high. From the top of the tower, a projectile is projected with velocity of 39 ms^-1 at an angle of 30° upwards with horizontal. Find the distance from the base of the tower where the projectile strikes the ground and the time taken by projectile in reaching the ground, (g = 9.8ms^-2)
Answer:
Given: u = 39 ms^-1; θ = 30°; h = 156 m; g = 9.8 ms^-2; T = ?; R = ?
v_y = u sin 30° = 39 x \(\frac{1}{2}\)
= 19.5 ms^-1
v_x = u cos 30° = 39 x \(\frac{\sqrt{3}}{2}\)
= 19.5 x 1.732
= 33.77 ms^-1

On applying relation S = ut + \(\frac{1}{2}\)at for vertical height h (height of the tower)
h = -uy(u)T + \(\frac{1}{2}\)gT², where T = time of flight
156 = -19.5T + \(\frac{1}{2}\) x 9.8 x T²
or 4.9T² - 19.5 T - 156 = 0
∴ T = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{19.5 \pm \sqrt{(19.5)^2+4 \times 4.9 \times 156}}{2 \times 4.9}\)
= 7.97s (Taking + sign)
∴ Range, R = v_x x T = 33.77 x 7.97 m
or R = 269.2 m

Question 47.
With what velocity should a ball be projected from tower of height 10 m at an angle of 30° with horizontal so that it may reach the ground at a distance of 17.3 m from the base of the tower. (g = 10 ms^-2)
Answer:
h = 10 m; v_x = u cos 30° = \(\frac{\sqrt{3}}{2}\).u
and v_y = u sin 30° = \(\frac{u}{2}\)
For vertical motion, h = -v_yT +\( \frac{1}{2}\)gT²

∴ 10 = -\(\frac{u}{2}\)T + \(\frac{1}{2}\) x 10 x T²
or 10T² - uT - 20 = 0 ....................(1)
∵ R = u cos 30° x T
17.3 = u x \(\frac{\sqrt{3}}{2}\) x T
or uT = \(\frac{2 \times 17.3}{\sqrt{3}}=\frac{2 \times 1.73 \times 10}{1.732}\) = 20
T = \(\frac{20}{u}\)
∴ From equation (1)

Question 48.
A stone is thrown with the velocity of 10 ms^-1 from the tower at an angle of 30° upwards with horizontal. It reaches the ground after 5 s. Calculate the height of the tower and range of the stone, (g = 10ms^-2).
Answer:
u = 10 ms^-1; θ = 30°; T = 5s; g = 10 ms^-2
∴ v_x = u cos 30° = 10 x \(\frac{\sqrt{3}}{2}\) = 5\(\sqrt{3}\) ms^-1
v_y = u sin 30° = 10 x \(\frac{1}{2}\) = 5 ms^-1

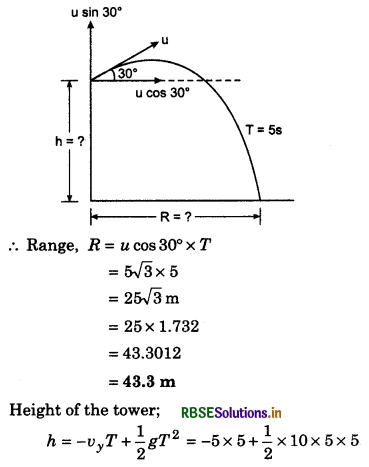
= -25 + 125
= 100 m

Question 49.
A ball is projected in horizontal direction with constant horizontal velocity of 15 ms^-1. Find the displacement of the ball after 4 s and draw its vector sketch. (g = 10 ms^-2)
Answer:
Let us consider, the projectile point as origin. Suppose after 4s the projectile is at P(x, y). Then
x = v_x x t = 15 x 4 = 60 m
and y = 0 + \(\frac{1}{2}\)gt² = \(\frac{1}{2}\) x 10 x 4 x 4
= 80 m

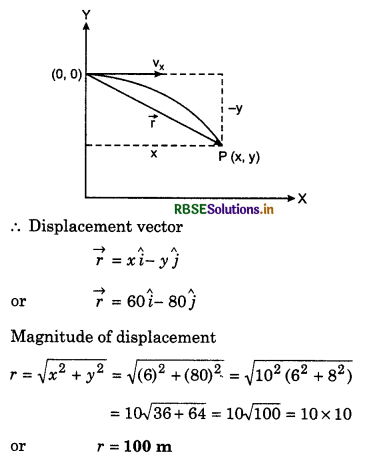
Based on circular motion

Question 50.
The lengths of needles of hour and minute of a clock are 4 cm and 6 cm respectively.
(i) Find the ratio of linear velocities of tips of the needles.
(ii) If the length of hour needle be 3 cm, then what will be the above ratio?
Answer:
(i) r₁ = 4 cm, T₁ = 12 hr
r₂ = 6 cm, T₂ = 1 hr
v₁ : v₂ = ?
∵ v = rω = r.\(\frac{2\pi}{T}\)
∴ \(\frac{v_1}{v_2}=\frac{r_1 \frac{2 \pi}{T_1}}{r_2 \frac{2 \pi}{T_2}}=\frac{r_1}{r_1} \times \frac{T_2}{T_1}=\frac{4 \mathrm{~cm}}{6 \mathrm{~cm}} \times \frac{1 \mathrm{hr}}{12 \mathrm{hr}}\)
= \(\frac{1}{18} \)∴ v₁ : v₂ = 1 : 18
(ii) If r₁ = 3 cm, then
\(\frac{v_1}{v_2}=\frac{r_1}{r_2} \times \frac{T_2}{T_1}=\frac{3 \mathrm{~cm}}{6 \mathrm{~cm}} \times \frac{1 \mathrm{hr}}{12 \mathrm{hr}}=\frac{1}{24}\)
∴ v₁ : v₂ = 1 : 24

Question 51.
A proton is moving on circular path of radius 0.1 m under centripetal acceleration of 2.5 x 10¹⁴ ms-2. Determine:
(i) angular velocity of proton, (ii) frequency, (iii) linear velocity of proton.
Answer:
r = 0.1 m; a_c = 2.5 x 10¹⁴ ms^-2
(i) ω = ?; (ii) n = ?; (iii) v = ?
(i) ∵ a_c = rω² ⇒ ω = \(\sqrt{\frac{a_c}{r}}=\sqrt{\frac{2.5 \times 10^{14}}{0.1}}\)
or ω = 5 x 10⁷ rads^-1
(ii) ∵ ω = 2πn ⇒ \(\frac{5 \times 10^7}{6.28}\)
= 7.96 x 10⁶ Hz
(iii) ∵ v = rω, ∴ v = 0.1 x 5 x 10⁷
or v = 5 x 10⁶ ms^-1

Question 52.
Length of second’s needle of a clock is 3.0 cm. Calculate the linear velocity and angular velocity of tip of the needle.
Answer:
r = 3.0 cm; T = 60s; ω = ?; v = ?
∴ ω = \(\frac{2 \pi}{T}=\frac{6.28}{60}\) = 0.105 rads^-1
and v = rω = 3 cm x 0.105 = 0.315 cms^-1

Based on centripetal acceleration and tangential acceleration

Question 53.
A particle is moving on circular path of radius 10 cm at the rate of 3 c.s^-1. Find the centripetal acceleration in terms of it.
Answer:
r = 10 cm; n = 3 cs^-1; a_c = ?
= 0.10 m
∵ ac = r.4π²n² = 0.1 x 4π² x 3 x 3
= 3.6π² ms^-2

Question 54.
With what horizontal velocity an object be projected so that it may move along equator parallel to earth surface? (radius of earth = 6.4 x 10⁶ m and g = 10ms^-2)
Answer:
v = ?; a_c = g = 10 ms^-2; Re = 6.4 x 10⁶ m
∵ a_c =\( \frac{v^2}{R_e}\) ⇒ v² = a_c.Re ⇒ v = \(\sqrt{a_c \cdot R_e}\)
v = \(\sqrt{10 \times 6.4 \times 10^6}\) = 8 x 10³ ms^-1
= 8 kms^-1

Question 55.
An artificial satellite is moving in circular orbit at height of 6.0 x 10⁵ m from earth’s surface and completes its on revolution in 93 minutes. Find the centripetal acceleration of the satellite. (Radius of earth = 6.4 x 10⁶ m)
Answer:
h = 6.0 x 10⁵ m = 0.6 x 10⁶ m; Re = 6.4 x 10⁶ m
r = Re + h = 6.4 x 10⁶ + 0.6 x 10⁶ = 7.0 x 10⁶ m
T = 93 min = 93 x 60s; a_c = ?
a_c = \(\frac{r .4 \pi^2}{T^2}=\frac{7.0 \times 10^6 \times 4 \times 9.86}{93 \times 60 \times 93 \times 60}\)
= 8.87 ms^-2

Question 56.
A motor car is moving on a circular path of radius 400 m with the velocity of 20 ms^-1. Its speed is increasing at the rate of 1.0 ms^-2. Find its acceleration.
Answer:
v = 20 ms^-1; r = 400m; a_T = 1.0 ms^-2; a = ?
a_c = \(\frac{v^2}{r}=\frac{20 \times 20}{400}\) = 1 ms^-2
∴ a = \(\sqrt{a_c^2+a_T^2}=\sqrt{(1)^2+(1)^2}=\sqrt{2}\) = 1.414 ms^-2

High Order Thinking Skills or HOTS

Question 1.
The position vector of a particle is given by \(\vec{r} = 3.0t.\hat{i} + 2.0t2.\hat{j} + 5.0\hat{k}\). where t is expressed in second Units of other multiples are such that unit of r may become in meter.
1. Find the velocityv(t) and acceleration \(\vec{a}\)(t) of the particle.
2. Magnitude and direction of v(t) at t = 1.0 s.
Solution:

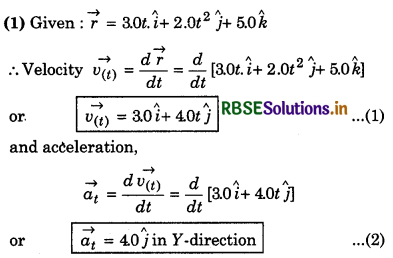
2. From equation (1) at t = 1 s
\(\overrightarrow{v_{(1)}}=3.0 \hat{i}+4.0 \hat{j}\)
∴ v(1) = \(\sqrt{v_x^2+v_y^2}=\sqrt{(3)^2+(4)^2}=\sqrt{9+16}=\sqrt{25}\)
or v(1) = 5 ms^-1
If angle between vt and v_x is θ, then
tanθ = \(\frac{v_y}{v_x}=\frac{4}{3}\)
∴ θ = tan^-1(\(\frac{4}{3}\)) = 53°

Question 2.
A particle moves in X-Y plane from point A(1, 2) to B(4, 3) in 5 second. Find the displacement of the particle in this period.
Solution:
Position vectors of point A and B are respectively


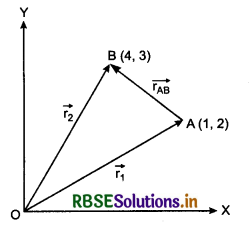
∴ Magnitude of displacement,
r_AB = \(\sqrt{x^2+y^2}=\sqrt{(3)^2+(1)^2}=\sqrt{9+1}=\sqrt{10}\)
or r_AB = \(\sqrt{10}\) = 3.162 unit

Question 3.
If there are two vectors \(\vec{A} = 2\hat{i} + \hat{j}\) and \(\vec{B} = 3\hat{i} + 4\hat{j}\), then find such vector which has magnitude equal to that \(\vec{B}\) and direction of \(\vec{A}\).
Solution:

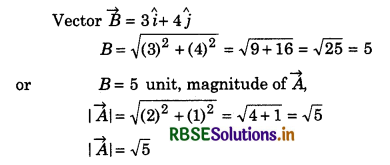
∴ Unit vector in direction of \(\vec{A}\),
\(\hat{A} = \frac{\vec{A}}{|\vec{A}|}=\frac{2 \hat{i}+\hat{j}}{\sqrt{5}}\)
Suppose the desired vector is \(\vec{C}\).

Question 4.
An object dropped freely from height H, strikes the inclined plane at height h from the ground. As a result its velocity becomes horizontal. From what value of \(\frac{h}{H}\), the object will take maximum time in reaching the ground?
Solution:
Suppose the object is dropped from point A and after falling (H - h) distance freeely, it strikes the inclined plane PQ at point B and attains horizontal velocity. Ultimately it reaches the ground at point C.

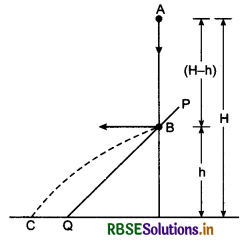
If the object takes time t₁ from A to B, then by relation S = ut + \(\frac{1}{2}\)t²

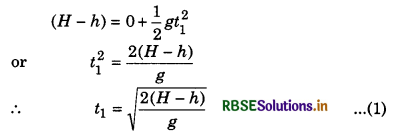
At point B, the vertical velocity of the object becomes zero. Therefore, if object takes time t₂ from B to C, then again from relation S = ut + \(\frac{1}{2}\)at²
h = 0 + \(\frac{1}{2}\)gt₂² ⇒ t₂ = \(\sqrt{2h}{g}\) ..........................(2)
∴ Total time taken from A to C,
t = t₁ + t₂
or t = \(\sqrt{\frac{2(H-h)}{g}}+\sqrt{\frac{2 h}{g}}\)
For maximum time,

Question 5.
Two particles P and Q of mass 20 g and 40 g respectively are projected simulaneously from point A and B with same velocity of 49 ms-1 making angles 45° and 135° with horizontal (figure). Distance between A and B is 245 m. Both the particles move in same plane. After collision particle P retraces its own path.

(i) Find the position of Q when it strikes the ground.
(ii) How much time is taken by Q in reaching the ground after collision?
Solution:
In horizontal direction,
Velocity of particle P = 49 cos 45° = \(\frac{49}{\sqrt{2}}\) ms^-1 and
Velocity of particle Q = 49 cos 135° = \(-\frac{49}{\sqrt{2}}\) ms^-1
Thus the speed of both particles in horizontal direction is equal and in opposite direction. Therefore both will collide above middle point of AB.
∴ Horizontal distance covered by both the particles = \(\frac{245}{2}\) m

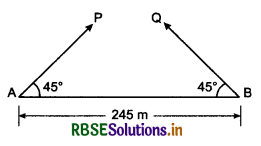
∵ Range R = \(\frac{u^2 \sin 2 \theta}{g}\)
= \(\frac{49 \times 49 \times \sin 90^{\circ}}{9.8}\)
= 245 m
Therefore, both particles will collide at highest point of their path where vertical velocity becomes zero.
∴ Before collision the velocity of P, v_P = \(\frac{49}{\sqrt{2}} \)ms^-1
and that of Q, v_Q = \(-\frac{49}{\sqrt{2}}\) ms^-1
After collision v'_P = \(-\frac{49}{\sqrt{2}}\) ms^-1
and v'_Q = ?
According to principle of conservation of momentum,
(20 x 10^-3) x \(\frac{49}{\sqrt{2}}\) + (40 x 10^-3) x (\(-\frac{49}{\sqrt{2}}\))
= (20 x 10^-3)(\(-\frac{49}{\sqrt{2}}\)) + (40 x 10^-3) x v'_Q
1 - 2 = -1 + 2 v'_Q
or 2 - 2 = 2 v'_Q
or v'_Q = 0
Therefore particle Q will fall freely after collision.
∵ Maximum height
H = \(\frac{u^2 \sin ^2 \theta}{2 g}=\frac{(49)^2 \times \frac{1}{2}}{2 \times 9.8}\) = 61.25 m
∴ Time taken by Q in falling upto ground
t = \(\sqrt{\frac{2 H}{g}}=\sqrt{\frac{2 \times 61.25}{9.8}}\)
or t = 3.53 s

Question 6.
Two cannons situated on a hill of height 10 m fire two balls one by one after some time interval with same speed of 5\(\sqrt{3}\) ms-1. One ball is projected in horizontal direction and other at angle of 600 upward with horizontal. Both balls collide in air at point A. Determine:
(i) Time interval between the projection of both balls.
(ii) Co-ordinates of point AP. Origin is taken on ground near the base of hill just bellow the mussel of connons and motion of ball in X-Y plane. (Given: g = 10 ms^-2).
Solution:
Suppose first ball is fired at an angle of 60° apwards with horizontal and after time t second ball is fired in horizontal direction. First ball reaches point P after time t₁ and second ball after time t₂. If horizontal distance of P from projection point A be x and vertical distance be y, then for first ball:
In horizontal direction x = 5\(\sqrt{3}\) cos 60° t₁
or x = \(\frac{5 \sqrt{3}}{2}\) t₁ ..........................(1)
and vertical direction,
y = (-5\(\sqrt{3}\) sin 60°)t₁ + \(\frac{1}{2}\)gt₁²
or y = -\(\frac{15}{2}\) t₁ + \(\frac{1}{2}\)gt₁² ........................(2)

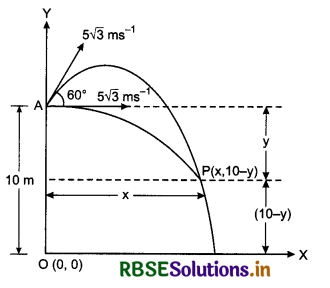
For second ball,
x = 5\(\sqrt{3}\)t₂ .......................(3)
and y = \(\frac{1}{2}\)gt₂² ..........................(4)
From equation (1) and (3),
\(\frac{5 \sqrt{3}}{2}\)t₁ = 5\(\sqrt{3}\) t₂
or t₁ = 2t₂ .....................(5)
From equations (2) and (4),
\(-\frac{15}{2} t_1+\frac{1}{2} g t_1^2=\frac{1}{2} g t_2^2\)
or \(-\frac{15}{2}\)t₁ + 5t₁² = 5t₂² ....................(1) (because g = 10 ms^-2)
From equation (5), t₂ = \(\frac{t_1}{2}\)
∴ From equation (6)
 \(-\frac{15}{2}\)t₁ + 5t₁² = 5\(\frac{t_1^2}{4}\)

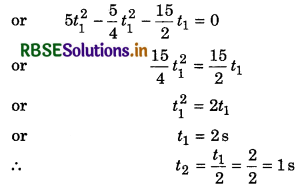
Hence the time interval between the projection of both balls,
∆t = t₁ - t₂ = 2 - 1 = 1 s or ∆t = 1 s
∴ From equation (1),
x = \(\frac{5 \sqrt{3}}{2} \times t_1=\frac{5 \sqrt{3}}{2} \times 2=5 \sqrt{3} \mathrm{~m}\) m
or x = 5\(\sqrt{3}\) m
From equation (4),
y = \(\frac{1}{2}\)gt₂² = \(\frac{1}{2}\) x 10 x (1)² = 5 m
∴ With respect to origin, x = 5\(\sqrt{3}\) m and y' = 10 - 5 = 5 m
Hence the co-ordinates of point P = (5\(\sqrt{3}\),5) m

Question 7.
In a sphere of radius R, a frictionless wire AB is fitted. A small globule slips on this wire. How much time will be taken by globule is slipping from A to B?
Solution:
If acceleration along AB be a then distance covered in this direction in time t, will be
r = \(\frac{1}{2}\)at²

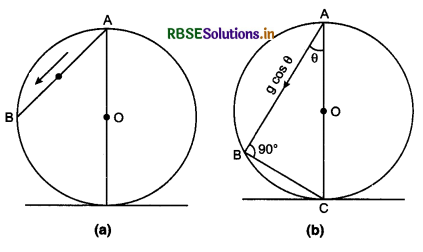
Component of gravitational acceleration g cosθ will be effective along AB
AB = \(\frac{1}{2}\)g cosθ x t²
But from the figure(b).

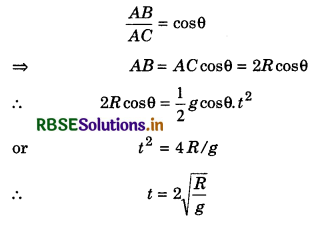
Question 8.
Kinetic energy of a particle in a circle of radius R is K which is given by K = as², where s = distance travelled by the particle. Find the acceleration acting on the particle.
Solution:
Given kinetic energy
K = as²
or \(\frac{1}{2}\) mv² = as² .........................(1)
On differentiating both sides with respect to t,

Therefore resultant acceleration

Questions for Competitive Examinations

Objective Type Questions

Question 1.
Rate of retardation of a body moving with speed of 6.25 ms^-1, is given by \(\frac{d v}{d t} = - 2.5\sqrt{v}\), where v is instantaneous speed. The time taken by the body in coming to rest is:
(a) 1s
(b) 2s
(c) 4s
(d) 8s
Answer:
Rate of retardation of the object:
\(\frac{d v}{d t}=-2.5 \sqrt{v} \text { or } \frac{d v}{\sqrt{v}}=-2.5 d t\)
On integrating both sides,

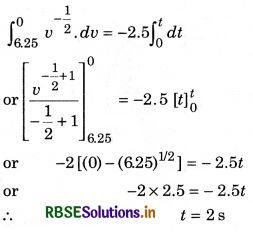
Hence, otpin (b) is correct.

Question 2.
A point P is moving on a circular path in anticlock wise direction as shown in adjoining diagram. The motion of P is such that it covers length s = t³ + 5, where s is in metres and t in seconds. Radius of the path is 20 m. When t = 2 s, then acceleration of P is approximately:

(a) 1.3 ms^-2
(b) 1.2 ms^-2
(c) 7.2 ms^-2
(d) 4 ms^-2
Answer:
Given: S = t³ + 5; r = 20 m
Linear velocity of the particle,
v = \(\frac{d s}{d t}=\frac{d}{d t}\)[t³ + 5] = 3t²
Velocity at t = 2s, v = 3(t)² = 3 x (2)²
= 3 x 4 = 12 ms^-1
Linear acceleration a = \(\frac{d v}{d t}=\frac{d}{d t}\)(3t²) = 6t
At t = 2s, a_T = 6 x 2 = 12 ms^-2
Radial acceleration
a_c = \(\frac{v^2}{r}=\frac{12 \times 12}{20}\) = 7.4 ms^-2
∴ Resultant acceleration
a = \(\sqrt{a_c^2+a_T^2}=\sqrt{(7.4)^2+(12)^2}\)
or a = 14 ms^-2
Hence, option (d) is correct.

Question 3.
In figure, two frictionless inclined planes, inclined at 30° and 60° with vertical, are shown. Two blocks A and B are placed on both planes. What is relative vertical acceleration of A with respect to B?

(a) 4.9 ms^-2 in horizontal direction
(b) 9.8 ms^-2 in vertical direction
(c) zero(0)
(d) 4.9 ms^-2 in vertical direction
Answer:
Vertical component of acceleartion of block A,
a_A = g sinθ.sinθ = g x sin 60°.sin 60° = g.\(\frac{3}{4}\)
Similarly, a_B = g sin30°.sin 30° = g x \(\frac{1}{4}\)
∴ Relative acceleration of object A with respect to B,
a_AB = a_A - a_B
= \(\frac{3}{4}\)g - \(\frac{1}{4}\)g
= \(\frac{2}{4}\)g = g/2 = \(\frac{9.8}{2}\) = 4.9 ms^-1
∴ Option (a) is correct.

Question 4.
For a particle moving on circular path of radius R with uniform speed. Acceleration \(\vec{a}\) for a particle (P)(R,θ) on the path is:

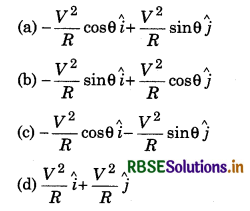
Answer:
For uniform circular motion.
\(\vec{a} = \frac{v^2}{R}\) (towards the centre of the circle)

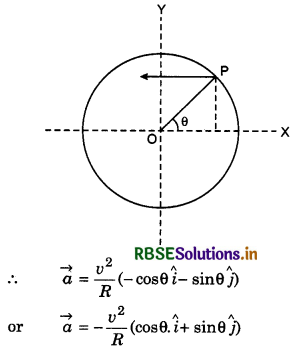
Thus, option (c) is correct.

Question 5.
A particle of mass m is projected with velocity v₀ in X-Y plane at an angle θ with X-axis as shown in figure. For time t < \(\frac{v_0 \sin \theta}{g}\), angular momentum of the particle is, where \(\hat{i}, \hat{j}\) and \(\hat{k}\) are unit vectors along X, Y and Z axes respectively:

(a) -mgv₀t² cosθ\(\hat{i}\)
(b) mgv₀t cosθ \(\hat{k}\)
(c) -\(\frac{1}{2}\) mgv₀t² cosθ \(\hat{k}\)
(d) \(\frac{1}{2}\) mgv₀²t² cosθ\(\hat{i}\)
Answer:
Angular momentum,
∵ \(\vec{L}\) = m(\(\vec{r}\) x \(\vec{v}\))
If (x, y, t) are the co-ordinates of point P, then
x = v₀.cosθ x t
and y = v₀ sinθ x t - \(\frac{1}{2}\)gt²

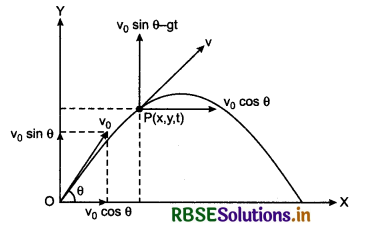
∴ Position vector of P,
\(\vec{r}\) = \(x\hat{i} + y\hat{j}\) = [v₀ cosθ.t\(\hat{i}\) + {v₀ sinθ x t - \(\frac{1}{2}\)gt²}\(\hat{j}\)]
AT point P,
v_x = v₀ cosθ
and v_y = v₀ sinθ - gt
∴ \(\vec{v}\) = v_x\(\hat{i} \)+ v_g \(\hat{j}\)
= v₀ cosθ.\(\hat{i}\) + (v₀ sinθ - gt)\(\hat{j}\)
Therefore angular momentum,

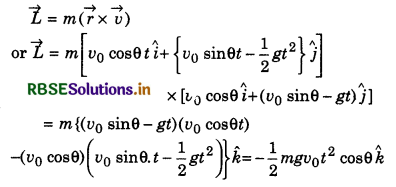
Therefore, option (c) is correct.

Question 6.
Imagine a rubber ball is falling freely from a height of 4.9 m on a horizontal elastic plate. Suppose that the time of collision is negligible and plate is perfectly elastic, the sketch of v-t and that of y-t (where v is velocity and y is displacement) will be:

Answer:
For ball, h = \(\frac{1}{2}\)gt²
For straight line v = -gt, after collision, v = gt because collision is perfectly elastic therefore the ball will go upto same height after each collision.

Hence, option (c) is correct.

Question 7.
Inital velocity of a particle is \((3\hat{i} + 4\hat{j})\) and acceleration is \((0.4\hat{i} + 0.3 \hat{j})\). Its speed after 10 s will be:
(a) 7\(\sqrt{2}\)
(b) 7 units
(c) 8.5 unit
(d) 10 unit
Answer:
∵ \(\vec{v} = \vec{u} + \vec{a}\)t
∴ \(\vec{v} = (3\hat{i} + 4\hat{j}) + (0.4\hat{i} + 0.3\hat{j})\) x 10
= \(3\hat{i} + 4\hat{j} + 4\hat{i} + 3\hat{j}\)
or \(\vec{v} = 7\hat{i} + 7\hat{j} \) ∴\(|\vec{v}| = \sqrt{7^2+7^2}=7 \sqrt{2}\)
Thus option (a) is correct.

Question 8.
Velocity of a particle is v = v₀ + gt + ft². If its position at t = 0 is x = 0, then its displacement in unit time i.e. t = 1 is:
(a) v₀ + 2g + 3f
(b) v₀ + \(\frac{g}{2} + \frac{f}{3}\)
(c) v₀ + g + f
(d) v₀ + \(\frac{g}{2}\) + f
Answer:
Given: v = v₀ + gt + ft²
or \(\frac{dx}{dt}\) = v₀ + gt + ft²
or dx = (v₀ + gt + ft²) dt
On integrating both sides,

Thus, alternative (b) is correct.

Question 9.
A particle is projected with kinetic energy K at an angle of projection 60°. At highest point the kinetic energy of the particle is:
(a) K
(b) Zero
(c) \(\frac{K}{4}\)
(d) \(\frac{K}{2}\)
Answer:
θ = 60°
K = \(\frac{1}{2}\) mu²
At highest point, v_x = v cos 60° = \(\frac{u}{2}\)
∴ Kinetic energy at highest point,
K' = \(\frac{1}{2}\) mv_x² = \(\frac{1}{2}m.\frac{u^2}{4}\) = \(\frac{1}{4}\) x \(\frac{1}{2}\) mv² = \(\frac{K}{4}\)
Thus, option (c) is correct.

Question 10.
A particle situated at x = 0, moves at t = 0 in positive X-direction with velocity u which changes according to relation u = \(\alpha \sqrt{x}\). Displacement of the particle changes with time in this way:
(a) t²
(b) t
(c) t^1/2
(d) t³
Answer:

Thus, x changes according to t². Hence option (a) is correct.

Question 11.
Calculate the angle of projection at which a projectile with velocity \(\sqrt{2gh}\) is projectile so that it just crosses a wall of height a.h situated at a distance of h from the point of projection:
(a) 15°
(b) 75°
(c) 60°
(d) 30°
Answer:
For vertical upward motion:
y = (u sinα) t - \(\frac{1}{2} \)gt²
∴ h = (u sinα)t - \(\frac{1}{2}\)gt²
or gt² - 2u sinα.t + 2h = 0 ...........................(1)
Solution of this quadratic equation.

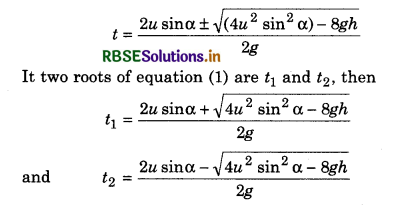
If the particle crosses the wall in time t₁ and t₂ then time of flight,

Thus, option (d) is correct.

Question 12.
Find the centripetal acceleration of a particle which takes 2 s in completing one revolution on a circular path of radius 100 m:
(a) 98.5 ms^-2
(b) 198.5 ms^-2
(c) 49.29 ms^-2
(d) 985.9 ms^-2
Answer:
Centripetal acceleration, a = rω² = 4π² n².r
∴ a_c = 4π²(\(\frac{1}{2}\))² x 10 = π² x 10
= 9.86 x 10 = 98.6 ms^-2
Thus, option (a) is correct.

Question 13.
A car is moving on a circular path of radius 500 m with speed of 30 ms^-1. If at any instant the speed of the car increases at the rate of 2 ms^-1, then find the resultant acceleration of the car:
(a) 4.7 ms^-2
(b) 3.8 ms^-2
(c) 3 ms^-2
(d) 2.7 ms^-2
Answer:
Centripetal acceleration,
a_c = \(\frac{v^2}{r}=\frac{(30)^2}{500}\) = 1.8 ms^-2
Tangential acceleration, a_T = 2 ms^-2
∴ Resultant acceleration
a = \(\sqrt{a_c^2+a_T^2}=\sqrt{(1.8)^2+(2)^2}\)
or a = 2.7 ms^-2
Thus, option (d) is correct.

Question 14.
A particle starts moving from rest. The graph plotted between its acceleration and time is shown in figure. Maximum speed of the particle will be:
(a) 110 ms^-1
(b) 55 ms^-1
(c) 550 ms^-1
(d) 660 ms^-1

Answer:
Area covered by acceleration-time graph and time axis provides change in velocity.
∴ v_max = \(\frac{1}{2}\) x (10) x 11 = 55 ms^-1
Hence, option (b) is correct.
Alternate method:

For maximum or minimum put \(\frac{dv}{dt}\) = 0
∴ t = 11 sec
At t = 11 sec,
\(\frac{d^2 v}{d t^2}=-\frac{10}{11}\) < 0
At t = 11 sec, v is maximum

Question 15.
A small block starts slipping on a smooth inclinded plane from rest. If the distance travelled in time interval from t = (n - 1) to t = n, be Sn, then the value \(\frac{S_n}{S_{n+1}}\) will be:
(a) \(\frac{(2 n-1)}{2 n} \)
(b) \(\frac{2 n+1}{2 n-1}\)
(c) \(\frac{2 n-1}{2 n+1}\)
(d) \(\frac{2 n}{2 n+1}\)
Answer:
Distance travelled in tth second
St = ut + \(\frac{1}{2} a (2t - 1)\)
or St = u + at - \(\frac{1}{2}\)a
It is given that u = 0
∴ St = at - \(\frac{1}{2}\)a
∴ \(\frac{S_n}{S_{n+1}}=\frac{a n-\frac{1}{2} a}{a(n+1)-\frac{1}{2} a}=\frac{2 n-1}{2 n+1}\)
Therefore, option (c) is correct.

Question 16.
A particle which can move only in Y-direction, a force \(\vec{F} = (-2\hat{i} + 15\hat{j} + 6\hat{k})\) N is applied on the particle. Due to this force if the particle gets displaced by 10 m in Y-direction then what will be work done?
(a) 20 J
(b) 150 J
(c) 160 J
(d) 190 J
Answer:
Froce \(\vec{F} = (-2\hat{i} + 15\hat{j} + 6\hat{k})\)N
Displacement on Y-axis, \(\vec{d} = 10\hat{j}\)
∴ W = \(\vec{F}.\vec{d} = (-2\hat{i} + 15\hat{j} + 6\hat{k}).(10\hat{j})\)
W = 150 J
∴ Option (b) is correct.

Question 17.
The pulleys and strings shown in figure are frictionless. What will be the value 0 for equilibrium of the system?

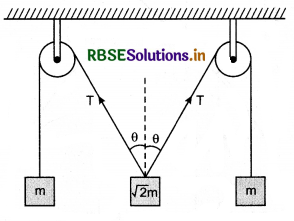
(a) 0°
(b) 30°
(c) 45°
(d) 60°
Answer:
In equilibrium,
2T cosθ = \(\sqrt{2}\) mg
∴ cosθ = \(\frac{\sqrt{2} m g}{2 T}=\frac{m g}{\sqrt{2} T}\)
∵ T = mg,
∴ cosθ = \(\frac{1}{\sqrt{2}}\) ⇒ θ = 45°
∴ Option (c) is correct.

Question 18.
What will be the value of α if vectors \(\vec{A} = (2\hat{i} + 3\hat{j} + 8\hat{k})\) and \(\vec{B} = -4\hat{i} - 4\hat{j} + α\hat{k}\) be perpendicular?
(a) -1
(b) \(\frac{1}{2}\)
(c) \(-\frac{1}{2}\)
(d) 1
Answer:
\(\vec{A} = 2\hat{i} + 3\hat{j} + 8\hat{k} and \vec{B} = -4\hat{i} - 4\hat{j} + α\hat{k}\)
∴ \(\vec{A}.\vec{B} = (2\hat{i} + 3\hat{j} + 8\hat{k}).(-4\hat{i} - 4\hat{j} + α\hat{k})\)
= -8 + 12 + 8α
= 4 + 8α
If \(\vec{A} ⊥ \vec{B}\), then \(\vec{A}.\vec{B}\) = 0
∴ 4 + 8α = 0 ⇒ α = -\(\frac{1}{2}\)
Thus, option (c) is correct.

Question 19.
If θ be the angle between \(\vec{A}\) and \(\vec{B}\), then the magnitude of (\(\vec{B}\) x \(\vec{A}\)).\(\vec{A}\) will be:
(a) BA² cosθ
(b) BA² sinθ
(c) BA² sinθ.cosθ
(d) Zero
Answer:
\(\vec{B}\) x \(\vec{A}\) = B.A. sinθ.\(\hat{i}\) = \(\vec{R}\)
The direction of \(\vec{R}\) will be at right angles to plane of \(\vec{A}\) and \(\vec{B}\).
i.e. \(\vec{R} ⊥ \vec{A}\)
Hence, (\(\vec{B}\) x \(\vec{A}\)).\(\vec{A}\) = \(\vec{R}.\vec{A}\) = R.A. cos 90° = 0 (zero)
Thus, alternative (d) is correct.

Question 20.
The motion of a particle along straight line is defined by x = 8 + 12t - t³, where x is in metres and t in seconds. Retardation of the particle when its velocity becomes zero, is:
(a) 24 ms^-2
(b) Zero
(c) 6 ms^-2
(d) 12 ms^-2
Answer:
x = 8 + 12t - t³
∴ Velocity v = \(\frac{d x}{d t}=\frac{d}{d t}\)(8 + 12t - t³)
or v = 12 - 3t²
If v = 0, then 12 - 3t² = 0 ⇒ t2 = 4 ⇒ t = 2s
Now acceleration
a = \(\frac{d v}{d t}=\frac{d}{d t}\)(12 - 3t²) = -6t
∴ For v = 0 i.e., at t = 2s
a = -6 x 2 = -12 ms^-2
∴ Retardation = 12 ms^-2
Hence, alternative (d) is correct.

Question 21.
A boy can throw a stone up to maximum height of 10 m. Upto which maximum distance in horizontal direction, can he throw the same stone?

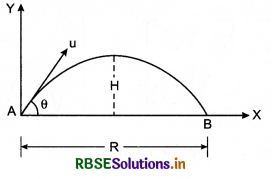
(a) 20\(\sqrt{2}\)
(b) 10 m
(c) 10\(\sqrt{2}\)
(d) 20 m
Answer:
For maximum height, if velocity is u, then
u = \(\sqrt{2 g h}=\sqrt{2 \times 10 \times 10}=10 \sqrt{2}\) ms^-1
For R_max, θ = 45°
∴ R_max = \(\frac{u^2 \sin 2 \theta}{g}=\frac{u^2 \sin 90^{\circ}}{g}=\frac{u^2}{g}\)
= \(\frac{(10 \sqrt{2})^2}{10}=\frac{10 \times 10 \times 2}{10}\) = 20 m
or R_max = 20 m
Thus, option (d) is correct.

Question 22.
The velocity of a projectile at point A is \((2\hat{i} + 3\hat{j})\) ms^-1, then its velocity at another point B will be:
(a) \((-2\hat{i} - 3\hat{j})\)
(b) \((2\hat{i} + 3\hat{j})\)
(c) \((2\hat{i} - 3\hat{j})\)
(d) \((3\hat{i} + 2\hat{j})\)
Answer:
Only vertical velocity of projectile changes.
∴ Velocity at B
v_B = \((2\hat{i} - 3\hat{j})\) ms^-1 because v_A = \((2\hat{i} + 3\hat{j})\) ms^-1
∴ Alternative (c) is correct.

Question 23.
Initial velocity of a projectile is \((\hat{i} + 2\hat{j})\) ms^-1, where \(\hat{i}\) and \(\hat{j}\) are unit vectors along horizontal and vertical directions respectively. If g = 10 ms then equation of its path is:
(a) y = x - 5x²
(b) y = 2x - 5x²
(c) 4y = 2x - 5x²
(d) 4y = 2x - 25x²
Answer:
Initial velcoity \(\vec{u} = (\hat{i} + 2\hat{j})\) ms-¹
∴ Magnitude of \(\vec{u}\)
u = \(\sqrt{(1)^2+(2)^2}=\sqrt{1+4}=\sqrt{5}\) ms^-1
From the equation of trajectory

∴ Option (b) is correct.