RBSE Solutions for Class 11 Physics Chapter 12 Thermodynamics

Rajasthan Board RBSE Solutions for Class 11 Physics Chapter 12 Thermodynamics Textbook Exercise Questions and Answers.

RBSE Class 11 Physics Solutions Chapter 12 Thermodynamics

RBSE Class 11 Physics Thermodynamics Textbook Questions and Answers

Question 12.1.
A geyser heats water flowing at the rate of 3.0 liters per minute from 27°C to 77°C. If the geyser operates on a gas burner, what is the rate of consumption of the fuel if its' heat of combustion is 4.0 x 104 J/g?
Solution:
The mass of water flowing per unit time = 3000 g per minute
= \(\frac{3000}{60}\) = 50 g/s
Heat required to heat this water from 27°C to 77°C
= 50 x 4.2 x 50 J/s
= 1.05 x 10⁴ J/s
Heat generated by combustion of 1 g of fuel = 4.0 x 10⁴ J
= \(\frac{1.05 \times 10^4}{4.0 \times 10^4}\) = 0.2625 g
or Fuel required to be burnt per minute
= 0.2625 x 60 = 15.75 ≅ 16 g

Question 12.2.
What amount of heat must be supplied to 2.0 x 10^-2 kg of nitrogen (at room temperature) to raise its temperature by 45°C at constant pressure? (Molecular mass of N₂ = 28; R = 8.3 J/mol¹/K¹)
Solution:
The mass of the gas
= 2.0 x 10^-2 kg = 20 g
∴ This mass of the gas is equivalent to \(\frac{20}{28}\) mole
= \(\frac{5}{7}\) mole
Now, the amount of heat required

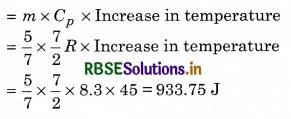
Question 12.3.
Explain why:
(a) Two bodies at different temperatures T₁ and T₂ if brought in thermal contact do not necessarily settle to the mean temperature \(\frac{T_1+T_2}{2}\).
(b) The coolant in a chemical or a nuclear plant (i.e., the liquid used to prevent the different parts of a plant from getting too hot) should have high specific heat.
(c) Air pressure in a car tyre increases during driving.
(d) The climate of a harbour town is more temperate than that of a town in a desert at the same latitude.
Solution:
(a) The two bodies in general do not have the equilibrium or the steady state temperature equal to \(\frac{T_1+T_2}{2}\) because they may have different masses and different specific heats.

(b) The coolant should have high specific heat so that it may take away larger quantity of heat with less increase in its temperature (without boiling).
The quantity of heat taken = Mass x Specific heat x Rise in temperature
or Q = ms ∆θ
Larger the value of s, larger will be the heat absorbed by the coolant for the same rise in its temperature.

(c) During driving, air inside the tube gets hot because of friction between the tyres and the road. Because the air inside the tube gets hot, its pressure increases (because volume of air is constant) in accordance with Charle’s law.

(d) The climate of a harbour town is more temperate because of the large amount of water vapour present in the air due to its proximity with sea.

Question 12.4.
A cylinder with a movable piston contains 3 moles of hydrogen at standard temperature and pressure. The walls of the cylinder are made of a heat insulator, and the piston is insulated by having a pile of sand on it. By what factor does the pressure of the gas increase if the gas is compressed to half its original volume?
Solution:
Since the process is adiabatic,
P₁V₁^γ = P₂V₂^γ
where \(\frac{V_1}{V_1}=\left(\frac{2}{1}\right)\)
γ = \(\frac{7}{5}\) for hydrogen
∴ Factor by which the pressure of the gas increases,
⇒ \(\frac{P_2}{P_1}=\left(\frac{V_1}{V_2}\right)^\gamma\) [From (1)]
⇒ \(\frac{P_2}{P_1}\) = (2)^7/5 = 2.64

Question 12.5.
In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B, an amount of work equal to 22.3 J is done on the system. If the gas is taken from state A to B via a proces in which the net heat absorbed by the system is 9.35 cal, how much is the net work done by the system in the latter case? (Take 1 cal = 4.19 J).
Solution:
Since the system is going from A and B and then back to A it is undergoing a cyclic change. Now, in cyclic change there is no change in internal energy (∆U = 0). From first law of thermodynamics
∆Q = ∆U + ∆W = ∆W    [∵ ∆U = 0]
The amount of heat absorbed by the system
= 9.35 cal - 22.3 J
= (9.35 x 4.19 - 22.3) J = 16.87 J
∴ The net work done by the system = 16.87 J

Question 12.6.
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
(a) What is the final pressure of the gas in A and B?
(b) What is the change in internal energy of the gas?
(c) What is the change in the temperature of the gas?
(d) Do the intermediate states of the system (before settling to the final equilibrium state) lie on its P-V-T surface?
Solution:
(a) The gas would rush from A to B. The change in pressure and volume will take place under adiabatic conditions. The final pressure in the two cylinders would be 0.5 atm.
(b) The change in internal energy of the gas will be zero.
(c) The change in temperature will be zero.
(d) Since the process is rapid, the intermediate states are non-equilibrium states and hence do not satisfy the gas equation. So, the intermediate states of the system do not lie on the P-V-T surface.

Question 12.7.
A steam engine delivers 5.4 x 10⁸ J of work per minute and services 3.6 x 10⁹ J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?
Solution:
Output i.e., useful work done per min. = 5.4 x 10⁸ J
Input i.e., heat absorbed per min. = 3.6 x 10⁹ J
Efficiency = \(\frac{\text { Output }}{\text { Input }}\)
= \(\frac{5.4 \times 10^8}{3.6 \times 10^9}\) = 0.15
= 0.15 x 100% = 15%
Heat energy wasted/minute = Heat absorbed/min - Useful work done/min
= 3.6 x 10⁹ - 5.4 x 10⁸ = 10⁹(3.6 - 0.54) = 3.06 x 10⁹ J

Question 12.8.
An electric heater supplies heat to a system at a rate of 100 W. If system performs work at a rate of 75 joules per second, at what rate is the internal energy increasing?
Solution:
Heat supplied per sec = \(\frac{\Delta Q}{\Delta t}\) = 100 watt

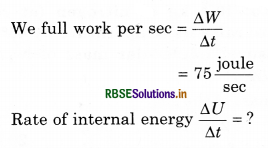
from Ist equation of thermodynamics ∆Q = ∆U + ∆W
The equation is divided by time interval

Question 12.9.
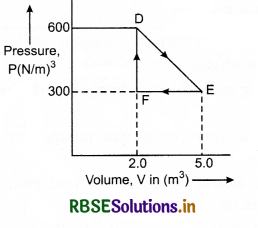
A thermodynamic system is taken from an original state to an intermediate state by the linear process shown in the figure. Its volume is then reduced to the original value from E to F by an isobaric process. Calculate the total work done by the gas from D to E to F. 

Solution:
As is clear from figure,
Change in pressure, dP = 600 - 300
= 300 N/m³
Change in volume = dV = (5 - 2) m³
= 3m³
Work by the gas from D to E to F
W = Area of ∆DEF
= \(\frac{1}{2}\) x DE x EF
= \(\frac{1}{2}\) x DP x dV = \(\frac{1}{2}\) x 300 x 3
= 450 Joule

Question 12.10.
A refrigerator is to maintain eatables kept inside at 10°C. If room temperature is 36°C, calculate the coefficient of performance.
Solution:
Here, T1 = 36° C = 36 + 273 = 309 K
T2 = 10°C = 10 + 273 = 283 K
ß = \(\frac{T_2}{T_1-T_2}=\frac{283}{309-283}\)
= \(\frac{283}{26}\) = 10.9