RBSE Solutions for Class 11 Physics Chapter 8 गुरुत्वाकर्षण

Rajasthan Board RBSE Solutions for Class 11 Physics Chapter 8 गुरुत्वाकर्षण Textbook Exercise Questions and Answers.

RBSE Class 11 Physics Solutions Chapter 8 गुरुत्वाकर्षण

RBSE Class 11 Physics गुरुत्वाकर्षण Textbook Questions and Answers

प्रश्न 8.1. 
निम्नलिखित के उत्तर दीजिए:
(a) आप किसी आवेश का वैद्युत बलों से परिरक्षण उस आवेश को किसी खोखले चालक के भीतर रखकर कर सकते हैं। क्या आप किसी पिण्ड का परिरक्षण, निकट में रखे पदार्थ के गुरुत्वीय प्रभाव से, उसे खोखले गोले में रखकर अथवा किसी अन्य साधनों द्वारा कर सकते हैं?
(b) पृथ्वी के परितः परिक्रमण करने वाले छोटे अन्तरिक्ष यान में बैठा कोई अन्तरिक्ष यात्री गुरुत्व बल का संसूचन नहीं कर सकता। यदि पृथ्वी के परितः परिक्रमण करने वाला अन्तरिक्ष स्टेशन आकार में बड़ा है, तब क्या वह गुरुत्व बल के संसूचन की आशा कर सकता है?
(c) यदि आप पृथ्वी पर सूर्य के कारण गुरुत्वीय बल की तुलना पृथ्वी पर चन्द्रमा के कारण गुरुत्व बल से करें, तो आप यह पाएंगे कि सूर्य का खिंचाव चन्द्रमा के खिंचाव की तुलना में अधिक है (इसकी जाँच आप स्वयं आगामी अभ्यासों में दिए गए आंकड़ों की सहायता से कर सकते हैं) तथापि चन्द्रमा के खिंचाव का ज्वारीय प्रभाव सूर्य के ज्वारीय प्रभाव से अधिक है। क्यों?
उत्तर:
(a) नहीं, वैद्युत बल मध्यवर्ती माध्यम की प्रकृति पर निर्भर है, जबकि गुरुत्व बल नहीं है, इसलिए गुरुत्वाकर्षण में इस प्रकार परिरक्षण का कार्य नहीं है, अर्थात् गुरुत्वीय कवच सम्भव नहीं है।
(b) हाँ, वह गुरुत्व बल का संसूचन तभी कर सकता है जब अन्तरिक्ष यान बहुत बड़ा हो, उस समय गुरुत्व का प्रभाव पर्याप्त होगा अतः अन्तरिक्ष यान को गुरुत्वीय क्षेत्र पर अन्तरिक्ष यान का प्रभाव मापने योग्य हो जायेगा।
(c) पृथ्वी चन्द्रमा के बीच की दूरी सूर्य और पृथ्वी की दूरी से बहुत कम है। ज्वार का प्रभाव दूरी के घन के व्युत्क्रमानुपाती होता है, अर्थात् यह वर्ग व्युत्क्रमानुपाती नियम जो कि गुरुत्वाकर्षण बल में लागू होता है, नहीं मानता, यही कारण है कि सूर्य की अपेक्षा चन्द्रमा का ज्वार पर प्रभाव अधिक होता है।

प्रश्न 8. 2. 
सही विकल्प का चयन कीजिए:
(a) बढ़ती तुंगता के साथ गुरुत्वीय त्वरण बढ़ता / घटता है। 
(b) बढ़ती गहराई के साथ (पृथ्वी को एक समान घनत्व को गोला मानकर) गुरुत्वीय त्वरण बढ़ता / घटता है।
(c) गुरुत्वीय त्वरण पृथ्वी के द्रव्यमान / पिण्ड के द्रव्यमान पर निर्भर नहीं करता।
(d) पृथ्वी के केन्द्र से r₂ तथा r₁ दूरियों के दो बिन्दुओं के बीच स्थितिज ऊर्जा अन्तर के लिए सूत्र GMm (1/r₂ - 1/r₁) सूत्र mg ( r₂ - r₁) से अधिक / कम यथार्थ है।
उत्तर:
(a) बढ़ती तुंगता के साथ गुरुत्वीय त्वरण कम होता है।
∵ h ऊँचाई पर गुरुत्वीय त्वरण
gh = g(1 - 2h/R)
अतः h बढ़ने पर gh का मान कम होता है।
(b) बढ़ती गहराई के साथ (पृथ्वी को एक समान घनत्व को गोला मानकर) गुरुत्वीय त्वरण घटता है।
∵ gd = (1 - d/R)
अतः d बढ़ने पर गुरुत्वीय त्वरण 8 का मान कम होता है।

(c) ∵ गुरुत्वीय त्वरण g = GM/R², जहाँ M = पृथ्वी का द्रव्यमान
∴ गुरुत्वीय त्वरण पिण्ड के द्रव्यमान (m) पर निर्भर नहीं करता है।

(d) पृथ्वी के केन्द्र से r₂ तथा r₁ दूरियों के दो बिन्दुओं के बीच स्थितिज ऊर्जा अन्तर के लिए सूत्र
-GMn(1/r₂ - 1/r₁) सूत्र mg (r₂ - r₁) से अधिक यथार्थ है।
∵ g का मान विभिन्न स्थितियों पर परिवर्तित होता रहता है।

प्रश्न 8.3. 
मान लीजिए एक ऐसा ग्रह है जो सूर्य के परितः पृथ्वी की तुलना में दो गुनी चाल से गति करता है, तब पृथ्वी की कक्षा की तुलना में इसका कक्षीय आमाप क्या है?
उत्तर:
जैसा कि हम जानते हैं-पृथ्वी सूर्य के चारों ओर एक चक्कर 1 वर्ष में लगा लेती है।
∴ TE = 1 वर्ष
जैसा कि दिया गया है:
Tp = 1/2 TE
rE = 1 AU, rp = ?
केपलर के तीसरे नियम से

प्रश्न 8.4. 
बृहस्पति के एक उपग्रह, आयो (lo) की कक्षीय अवधि 11.769 दिन तथा कक्षा की त्रिज्या 4.22 x 10⁸m है। यह दर्शाइए कि बृहस्पति का द्रव्यमान सूर्य के द्रव्यमान का लगभग 1/1000 गुना है। 
उत्तर:
माना बृहस्पति का द्रव्यमान M = ? 
सूर्य का द्रव्यमान M₂ = 2 x 10³⁰ kg 
बृहस्पति के उपग्रह I0 का परिभ्रमण काल
T = 1.769 × 24 x 3600 S
= 15.2841 × 10⁴s
बृहस्पति के परितः कक्षा की त्रिज्या
r = 4.22 x 10⁸m
G = 6.67 x 10^-11 Nm/kg²
सिद्ध करना है M₁ = 1/100M₂
GM/r³ = ω² का सम्बन्ध प्रयोग करने पर
\(\begin{aligned} \frac{\mathrm{GM}_1}{r^3} & =\left(\frac{2 \pi}{\mathrm{T}}\right)^2 \\ \mathbf{M}_1 & =\left(\frac{2 \pi}{\mathrm{T}}\right)^2 \times \frac{r^3}{\mathrm{G}} \end{aligned}\)
मान रखने पर

प्रश्न 8. 5. 
मान लीजिए कि हमारी आकाशगंगा में एक सौर द्रव्यमान के 2.5 x 10¹¹ तारे हैं। मंदाकिनीय केन्द्र से 50,000 ly दूरी पर स्थित कोई तारा अपनी एक परिक्रमा पूरी करने में कितना समय लेगा? आकाशगंगा का व्यास 10⁵ ly लीजिए।
उत्तर:
दिया गया है:
एक तारे की त्रिज्या (r) = आकाशगंगा के केन्द्र से तारे की दूरी 
= 50,000 प्रकाश वर्ष
= 50,000 × 9.46 x 10¹⁵ m 
= 4.73 × 10²⁰m
माना आकाशगंगा के तारों का द्रव्यमान
M = 2.5 x 10 x 2 x 10³⁰ kg
∵ एक सूर्य का द्रव्यमान = 2 x 10³⁰ kg
= 5 × 10⁴¹ kg
G = 6.67 x 10^-11 Nm²/kg²
T = एक चक्कर का परिभ्रमण काल = ? 
आकाशगंगा का व्यास = 10⁵ प्रकाश वर्ष
हम जानते हैं:

मान रखने पर

= 11.25 x 10¹⁵
= 1.26 x 10¹⁶ S
वर्ष में बदलने पर
\(=\frac{1.12 \times 10^{16}}{365 \times 24 \times 3600}\)
= 3.55 x 10⁸ m/s

प्रश्न 8.6. 
सही विकल्प का चयन कीजिए:
(a) यदि स्थितिज ऊर्जा का शून्य अनन्त पर है, तो कक्षा में परिक्रमा करते किसी उपग्रह की कुल ऊर्जा इसकी गतिज / स्थितिज ऊर्जा का ऋणात्मक है।
(b) कक्षा में परिक्रमा करने वाले किसी उपग्रह को पृथ्वी के गुरुत्वीय प्रभाव से बाहर निकालने के लिए आवश्यक ऊर्जा समान ऊंचाई (जितनी उपग्रह की है) के किसी स्थिर पिण्ड को पृथ्वी के प्रभाव से बाहर प्रक्षेपित करने के लिए आवश्यक ऊर्जा से अधिक / कम होती है। 
उत्तर:
(a) गतिज ऊर्जा (b) कम।

प्रश्न 8.7. 
क्या किसी पिण्ड की पृथ्वी से पलायन चाल (a) पिण्ड के द्रव्यमान, (b) प्रक्षेपण बिन्दु की अवस्थिति, (c) प्रक्षेपण की दिशा, (d) पिण्ड के प्रमोचन की अवस्थिति की ऊंचाई पर निर्भर करती है?
उत्तर:
(a) हम जानते हैं कि पलायन वेग \(v_{\mathrm{E}}=\sqrt{\frac{2 \mathrm{GM}_{\mathrm{E}}}{\mathrm{R}_{\mathrm{E}}}}\) होता है। जहाँ पर ME तथा RE पृथ्वी के द्रव्यमान तथा उसकी त्रिज्या हैं, स्पष्ट रूप से VE द्रव्यमान पर निर्भर नहीं है, अतः पलायन वेग भी द्रव्यमान पर निर्भर नहीं है।
(b) हाँ, चूँकि \(\mathrm{v}_{\mathrm{E}}=\sqrt{2 g \mathrm{R}_{\mathrm{E}}}\) होता है। यहाँ पर g का मान भिन्न-भिन्न ऊँचाइयों पर भिन्न-भिन्न होता है। यही कारण है कि VE भी ऊँचाई की स्थिति पर निर्भर है।
(c) नहीं, यह प्रक्षेप की दिशा पर निर्भर नहीं है। चूँकि VE प्रक्षेप की दिशा से स्वतंत्र है।
(d) हाँ, यह जहाँ से पिण्ड का प्रमोचन किया जाता है, जैसा कि (b) में बताया गया है। यह स्थिति की ऊँचाई पर निर्भर है।

प्रश्न 8.8. 
कोई धूमकेतु सूर्य की परिक्रमा अत्यधिक दीर्घवृत्तीय कक्षा में कर रहा है। क्या अपनी कक्षा में धूमकेतु की शुरू से अन्त तक (a) रैखिक चाल, (b) कोणीय चाल, (c) कोणीय संवेग, (d) गतिज ऊर्जा, (e) स्थितिज ऊर्जा, (f) कुल ऊर्जा नियत रहती है। सूर्य के अति निकट आने पर धूमकेतु के द्रव्यमान में हास को नगण्य मानिये।
उत्तर:
(a) संवेग संरक्षण के नियमानुसार जब धूमकेतु सूर्य के निकट होता है तो वह तीव्र गति से चलता है, लेकिन जब वह (ग्रह) दूर होता है तो धीरे चलता है। इसलिए हम कह सकते हैं कि रैखिक चाल स्थिर नहीं रहती है।
(b) धूमकेतु की कोणीय चाल भी थोड़ी-सी बदलती है।
(c) नियमानुसार धूमकेतु का कोणीय संवेग संरक्षित रहता है। 
(d) यहाँ पर रैखिक चाल समय-समय पर बदल रही है इसलिए इसकी गतिज ऊर्जा भी निरन्तर बदलती है।
(e) विभव ऊर्जा का मान सूर्य से पृथ्वी पर निर्भर करता है। यही कारण है कि दीर्घवृत्तीय कक्षा में स्थितिज ऊर्जा बदलती रहती है। जैसे- जैसे निरन्तर सूर्य और धूमकेतु की दूरी बदलती है।
(f) हम जानते हैं कि यांत्रिक ऊर्जा अर्थात् कुल ऊर्जा गतिज ऊर्जा तथा स्थितिज ऊर्जा के योग के बराबर होती है सदैव ऊर्जा संरक्षण के नियम के अनुसार स्थिर रहता है। कुल ऊर्जा नियत रहती है।

प्रश्न 8.9. 
निम्नलिखित में से कौनसे लक्षण अन्तरिक्ष में अन्तरिक्ष यात्री के लिए दुखःदायी हो सकते हैं:
(a) पैरों में सूजन, 
(b) चेहरे पर सूजन, 
(c) सिरदर्द, 
(d) दिविन्यास समस्या।
उत्तर:
अन्तरिक्ष यात्री, अन्तरिक्ष में (b) चेहरे पर सूजन, (c) सिरदर्द तथा (d) दिविन्यास समस्या से पीड़ित होगा।

प्रश्न 8.10. 
एक समान द्रव्यमान घनत्व की अर्धगोलीय खोलों द्वारा परिभाषित ढोल के पृष्ठ के केन्द्र पर गुरुत्वीय तीव्रता की दिशा [देखिए चित्र ] (i), (ii) b, (iii), (iv) 0 में किस तीर द्वारा दर्शायी जाएगी?

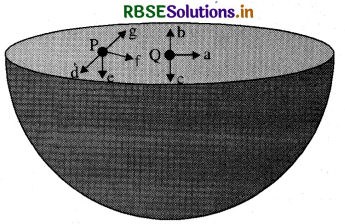
उत्तर:
हम जानते हैं- गुरुत्वीय विभव का मान खोखले गोले के अन्दर सभी बिन्दुओं पर स्थिर रहता है। इस कारण से गुरुत्वीय विभव प्रवणता का मान खोखले गोले के अन्दर शून्य होगा। इस कारण से गुरुत्वीय तीव्रता का मान गुरुत्वीय विभव प्रवणता के ऋणात्मक मान के बराबर होगा। इसलिए गुरुत्वीय तीव्रता का मान खोखले गोले के अन्दर सभी बिन्दुओं पर शून्य होगा।

उपर्युक्त बिन्दु यह दर्शाते हैं कि खोखले गोले के अन्दर किसी बिन्दु पर लगने वाले गुरुत्वाकर्षण बल आपस में सममित होते हैं। इसलिए यदि हम खोखले गोले के आधे हिस्से को हटा दें तो कण पर लगने वाला नेट गुरुत्वाकर्षण बल (केन्द्र पर) नीचे की ओर लगेगा जो कि गुरुत्वीय तीव्रता की दिशा में होगा। अतः सही उत्तर (iii) है।

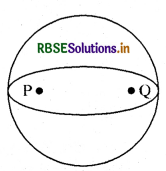
प्रश्न 8.11. 
उपर्युक्त समस्या में किसी यादृच्छिक बिन्दु P पर गुरुत्वीय तीव्रता किस तीर (i) d, (ii) e, (iii) f, (iv) g द्वारा व्यक्त की जाएगी?
उत्तर:
P तथा Q दोनों पर विभव नियत ( constant ) है तथा इसलिए तीव्रता = शून्य
अतः सही उत्तर (ii) है।

प्रश्न 8.12. 
पृथ्वी से किसी रॉकेट को सूर्य की ओर दागा गया है। पृथ्वी के केन्द्र से किस दूरी पर रॉकेट पर गुरुत्वाकर्षण बल शून्य है? सूर्य का द्रव्यमान = 2 x 10³⁰ kg, पृथ्वी का द्रव्यमान = 6 x10²⁴ kg अन्य ग्रहों आदि के प्रभावों की उपेक्षा कीजिए (कक्षीय त्रिज्या 1.5 x 10¹¹m)।
उत्तर:
माना कि पृथ्वी के केन्द्र से दूरी पर r

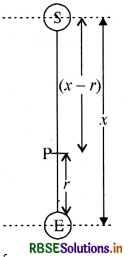
एक बिन्दु P है जिस बिन्दु पर पृथ्वी तथा सूर्य के गुरुत्वाकर्षण बल समान हैं। इस कारण से रॉकेट पर बल का मान शून्य होगा। सूर्य और पृथ्वी के बीच की दूरी माना x है।
सूर्य का द्रव्यमान Mg = 2 x 10³⁰ kg
पृथ्वी का द्रव्यमान ME = 6 x 10²⁴ kg सूर्य और पृथ्वी के बीच की
दूरी
x = 1.5 x 10¹¹m
माना रॉकेट का द्रव्यमान = m (माना )
बिन्दु P पर सूर्य और रॉकेट के बीच गुरुत्वाकर्षण बल = पृथ्वी तथा रॉकेट के बीच गुरुत्वाकर्षण बल



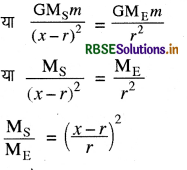
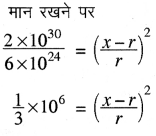
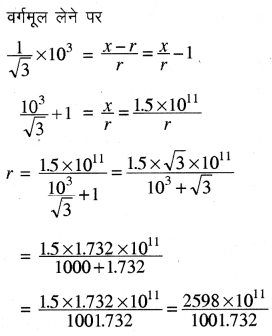
= 2.594 × 10⁸ m
= 2.6 × 10⁸ m
अतः पृथ्वी के केन्द्र से 2.6 x 10⁸m की दूरी पर गुरुत्वाकर्षण बल शून्य होगा। 

प्रश्न 8.13. 
आप सूर्य को कैसे तोलेंगे, अर्थात् उसके द्रव्यमान का आकलन कैसे करेंगे? सूर्य के परितः पृथ्वी की कक्षा की औसत त्रिज्या 1.5 x 10⁸ km है।
उत्तर:
दिया गया है:
पृथ्वी की कक्षा की त्रिज्या r = 1.5 x 10⁸ किमी. 
= 1.5 x 10 मी.
सूर्य के परितः पृथ्वी का चक्कर लगाने का समय
= 365 दिन
= 365 × 24 × 3600 s
अतः
G = 6.67 × 10^-11 Nm²/kg²
हम जानते हैं-
\(\frac{r}{\mathrm{~T}^2}=\frac{\mathrm{GM}_{\mathrm{S}}}{4 \pi^2 r^2}\)
यहाँ पर Ms = सूर्य का द्रव्यमान
\(M_S=\frac{4 \pi^2 r^3}{T^2 \mathrm{G}}\)
मान रखने पर

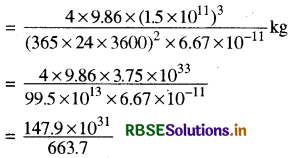
= 0.223 x 10³¹
= 2.23 × 10³⁰ kg
अर्थात् 2.0 x 10³⁰ kg 

प्रश्न 8.14. 
एक शनि-वर्ष एक पृथ्वी वर्ष का 29.5 गुना है। यदि पृथ्वी सूर्य से 1.5 x 10⁸ km दूरी पर है, तो शनि सूर्य से कितनी दूरी पर है?
उत्तर:
हम केप्लर के तीसरे नियम से जानते हैं कि ग्रह का सूर्य के परितः भ्रमणकाल का वर्ग α ( अर्धमुख्य अक्ष)
अर्थात्
T² α p³
यहाँ पर शनि के लिए rg और पृथ्वी के लिए PE और शनि के समय के लिए Ts और पृथ्वी के लिए TE लेंगे।
∴ शनि और पृथ्वी के लिए
और
Ts² α rs³
TE² α rE³ .............. (2)
समीकरण (1) में समीकरण (2) का भाग देने पर
\(\left(\frac{\mathrm{T}_{\mathrm{S}}}{\mathrm{T}_{\mathrm{E}}}\right)^2=\left(\frac{r_{\mathrm{S}}}{r_{\mathrm{E}}}\right)^3\)
दिया गया है:
Ts = 29.5 TE
या
T's/TE = 29.5
और
rE = पृथ्वी की सूर्य से दूरी = 1.5 x 10⁸ km
rs = शनि की सूर्य से दूरी = ?
\((29.5)^2=\left(\frac{r_{\mathrm{S}}}{1.5 \times 10^8}\right)^3=\frac{\left(r_{\mathrm{S}}\right)^3}{3.75 \times 10^{24}}\)
(rs)³ = (29.5) ² × 3.375 x 10²⁴
= 2937 × 10²⁴
rs = (2937 x (10²⁴)^1/3
rs = 14.3 x 10⁸ km
= 1.43 × 10° km 

प्रश्न 8.15. 
पृष्ठ पर किसी वस्तु का भार 63 N है। पृथ्वी की त्रिज्या की आधी ऊंचाई पर पृथ्वी के कारण इस वस्तु पर गुरुत्वीय बल कितना है?
उत्तर: 
दिया गया है:
पृथ्वी की सतह से ऊँचाई h = 1/2R
पृथ्वी की त्रिज्या = R
पृथ्वी के कारण इस वस्तु पर गुरुत्वीय बल = ?
W = mg = 63 N
हम जानते हैं:

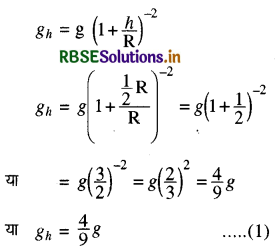
माना पिण्ड का द्रव्यमान = m
यदि Wतथा Wh पृथ्वी तल और पृथ्वी तल से ऊँचाई पर क्रमशः
भार है तब
W = mg = 63N
और
Wh = mgh = m x 4/9g ∵ gh = 4/9h
Wh = 4/9 mg
= 4/9 x 63 = 4 × 7 = 28N
∴ Wh = 28 N 

प्रश्न 8.16. 
यह मानते हुए कि पृथ्वी एक समान घनत्व का एक गोला है तथा इसके पृष्ठ पर किसी वस्तु का भार 250 N है, यह ज्ञात कीजिए कि पृथ्वी के केन्द्र की ओर आधी दूरी पर इस वस्तु का भार क्या होगा ?
उत्तर:
माना वस्तु का भार पृथ्वी के पृष्ठ पर W है और पृथ्वी से d
गहराई पर भार Wd है।
दिया गया है-
W = mg = 250 N ............. (1)
और
Wd = mgd ......... (2)
हम जानते हैं:
gd = g(1 - d/R) ................... (3)
दिया गया है:
d = 1⁄2R, R = पृथ्वी की त्रिज्या ................. (4)
मान रखने पर

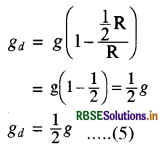
समीकरण (2) से मान रखने पर
\(\begin{aligned} \mathbf{W}_d & =m \times \frac{1}{2} g=\frac{1}{2} m g \\ & =\frac{1}{2} \mathbf{W}=\frac{1}{2} \times 250 \end{aligned}\)
Wd = 125 N
इस प्रकार पृथ्वी के केन्द्र की ओर आधी दूरी पर वस्तु का भार 125 N हो जाएगा।

प्रश्न 8.17. 
पृथ्वी के पृष्ठ से ऊर्ध्वाधरतः ऊपर की ओर कोई रॉकेट 5 kms¹ की चाल से दागा जाता है। पृथ्वी पर वापस लौटने से पूर्व यह रॉकेट पृथ्वी से कितनी दूरी तक जाएगा? पृथ्वी का द्रव्यमान = 6.0 x 10²⁴ kg; पृथ्वी की माध्य त्रिज्या = 6.4 x 10° m तथा G = 6.67 × 10^-11 Nm² kg²
उत्तर:
दिया गया है:
रॉकेट की आरम्भिक चाल = 5 km/s
= 5 x 10³ m/s
पृथ्वी का द्रव्यमान ME = 6.0 x 10²⁴ kg
RE = 6.4 x 10⁵ m
G = 6.67 × 10^-11 Nm/kg²
जब रॉकेट का वेग समाप्त हो जाता है तब यह पृथ्वी तल से ऊँचाई पर पहुँच जाता है। अर्थात् वेग शून्य हो जाता है। यदि 11 रॉकेट का द्रव्यमान है तब पृथ्वी तल पर इसकी कुल ऊर्जा
\(\mathrm{K} . \mathrm{E}+\mathrm{P} \cdot \mathrm{E}=\frac{1}{2} m \mathrm{v}^2-\frac{\mathrm{GM}_{\mathrm{E}} m}{\mathrm{R}_{\mathrm{E}}}\)............ (1)
जहाँ पर ME = पृथ्वी का द्रव्यमान RE = पृथ्वी की त्रिज्या G = सार्वत्रिक गुरुत्वाकर्षण स्थिरांक है।
उच्चतम बिन्दु पर KE = 0
और \(\mathrm{P} . \mathrm{E}=\frac{-\mathrm{GM}_{\mathrm{E}} m}{\mathrm{R}_{\mathrm{E}}+h}\) ...................... (2)
∴ h ऊँचाई पर रॉकेट की कुल ऊर्जा
= K.E+ P.E
= 0 + PE = PE = \(\frac{-\mathrm{GM}_{\mathrm{E}} m}{\mathrm{R}_{\mathrm{E}}+h}\)
\(=\frac{-\mathrm{GM}_{\mathrm{E}} m}{\mathrm{R}_{\mathrm{E}}+h}\) ............. (3)
ऊर्जा संरक्षण नियमानुसार समीकरण ( 1 ) तथा (3) से

v²(R_E + h) = 2g R_Eh
⇒ v²R_E + v²h = 2g R_Eh
⇒ v²R_E = 2g R_Eh - v²h
⇒ v²R_E = h [2gR_E - v²]
⇒ \(h=\frac{\mathrm{v}^2 \mathrm{R}_{\mathrm{E}}}{2 g \mathrm{R}_{\mathrm{E}}-\mathrm{v}^2}\) ............. (4)
मान रखने पर
\(\begin{aligned} h & =\frac{\left(5 \times 10^3\right)^2 \times 6.4 \times 10^6}{2 \times 9.8 \times 6.4 \times 10^6-\left(5 \times 10^3\right)^2} \\ & =\frac{25 \times 10^6 \times 6.4 \times 10^6}{125.44 \times 10^6-25 \times 10^6}=\frac{160 \times 10^6}{100.44} \end{aligned}\)
= 1.593 × 10 = 1.6 x 10 m
= 1600 km
∵ पृथ्वी के केन्द्र से दूरी
= RE + h
= 6.4 x 10⁶ + 1.6 x 10⁶
= 8.0 x 10⁶m 

प्रश्न 8.18. 
पृथ्वी के पृष्ठ पर किसी प्रक्षेप्य की पलायन चाल 11.2 kms^-1 है। किसी वस्तु को इस चाल की तीन गुनी चाल से प्रक्षेपित किया जाता है। पृथ्वी से अत्यधिक दूर जाने पर इस वस्तु की चाल क्या होगी ? सूर्य तथा अन्य ग्रहों की उपस्थिति की उपेक्षा कीजिए। 
उत्तर:
माना कि पृथ्वी की सतह पर प्रारम्भिक चाल v तथा पृथ्वी से
बहुत दूर प्रक्षेप्य की अन्तिम चाल v' है।
प्रक्षेप्य की प्रारम्भिक स्थितिज ऊर्जा (पृथ्वी तल पर)
= - GMm/R
तथा अन्तिम स्थितिज ऊर्जा (अनन्त पर) = 0 
इसलिए ऊर्जा संरक्षण के नियम से
प्रारम्भिक गतिज ऊर्जा + प्रारम्भिक स्थितिज ऊर्जा
= अन्तिम गतिज ऊर्जा + अन्तिम स्थितज ऊर्जा
mv
=> 1/2mv² - GMm/R = 1/2mv² + 0 .............. (1)
परन्तु वस्तु का पलायन वेग
\(\mathrm{v}_e=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}\)
∴ 1/2mv²e = GMm/R
∴ समीकरण (1) से
1/2mV² - 1/2mv²e = 1⁄2mv²
∴ प्रश्नानुसार
v = 3ve
∴ 1⁄2m(3ve)² - 1/2m² = 1⁄2mv²
=> 9ve² - ve² = v² 
ve = 8ve²
\(\mathrm{v}^{\prime}=\sqrt{8 \mathrm{v}_e}\)
v' = 2.83 × 11.2 Kms^-1
v' = 31.68 Kms^-1

प्रश्न 8.19. 
कोई उपग्रह पृथ्वी के पृष्ठ से 400km ऊंचाई पर पृथ्वी की परिक्रमा कर रहा है। इस उपग्रह को पृथ्वी के गुरुत्वीय प्रभाव से बाहर निकालने में कितनी ऊर्जा खर्च होगी? उपग्रह का द्रव्यमान = 200 kg; पृथ्वी का द्रव्यमान = 6.0 x 10²⁴ kg; पृथ्वी की त्रिज्या = 6.4 x 10^-11 m तथा G = 6.67 x 10^-11 N m² kg ²
उत्तर: 
उपग्रह को पृथ्वी के गुरुत्वीय प्रभाव से बाहर ले जाने में 
आवश्यक ऊर्जा = उपग्रह की बंधन ऊर्जा + 1/2 GMm/R + h
मान रखने पर

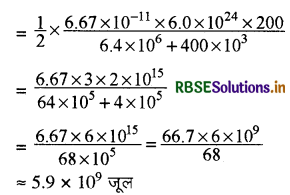
प्रश्न 8.20. 
दो तारे, जिनमें प्रत्येक का द्रव्यमान सूर्य के द्रव्यमान (2 x 10³⁰ kg) के बराबर है, एक-दूसरे की ओर सम्मुख टक्कर के लिए आ रहे हैं। जब वे 10 km दूरी पर हैं तब इनकी चाल उपेक्षणीय है। ये तारे किस चाल से टकराएंगे? प्रत्येक तारे की त्रिज्या 10⁴ km है। यह मानिए कि टकराने के पूर्व तक तारों में कोई विरूपण नहीं होता (G के ज्ञात मान का उपयोग कीजिए)।
उत्तर:
दिया गया है:
प्रत्येक तारे का द्रव्यमान, M = 2 × 10³⁰ kg
दो तारों के बीच की आरम्भिक दूरी
r = 109 km = 10² m
निकाय की आरम्भिक विभव ऊर्जा का मान
= -GM.M/r
तारों की कुल गतिज ऊर्जा = 1⁄2Mv² + 1/2Mv²
= Mv²
जहाँ पर तारों का वेग है, जिससे वे आपस में टकराते हैं। जब तारों में टक्कर होती है, तब उनके केन्द्रों के बीच की दूरी
r = 2R
∴ दो तारों की अन्तिम विभव ऊर्जा = -GM.M/2R
∴ ऊर्जा संरक्षण नियम से
imm
दिया गया है-
M = 2 × 10³⁰ kg
G = 6.67 x 10^-11 Nm² / kg² 
r = 10¹² m
R = 10⁷ m
मान रखने पर
\(\begin{aligned} & \mathrm{Mv}^2=-\frac{\mathrm{GMM}}{r}-\left(\frac{-\mathrm{GMM}}{2 \mathrm{R}}\right) \\ & \mathrm{Mv}^2=\frac{-\mathrm{GM} \cdot \mathrm{M}}{r}+\frac{\mathrm{GMM}}{2 \mathrm{R}} \end{aligned}\)
= - 2.668 x 10³⁸ +1.334 x 10⁴³
= 1.334 × 10⁴³

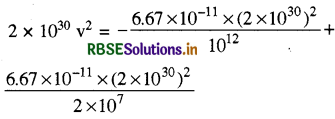
= 2.583 × 10⁵ m/s
v = 2.6 x 10⁵m/s 

प्रश्न 8.21. 
दो भारी गोले जिनमें प्रत्येक का द्रव्यमान 100 kg, त्रिज्या 0.10m है किसी क्षैतिज मेज पर एक-दूसरे से 1.0m दूरी पर स्थित हैं। दोनों गोलों के केन्द्रों को मिलाने वाली रेखा के मध्य बिन्दु पर गुरुत्वीय बल तथा विभव क्या है? संतुलन में होगा? यदि हां, तो यह क्या इस बिन्दु पर रखा कोई पिण्ड संतुलन स्थायी होगा अथवा अस्थायी? 
उत्तर:
माना कि A तथा B दो गोलों की विभिन्न स्थितियाँ हैं तथा AB का मध्यबिन्दु P है। A पर द्रव्यमान के कारण P पर गुरुत्वीय क्षेत्र

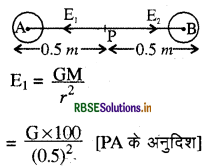
B पर द्रव्यमान के कारण P पर गुरुत्वीय क्षेत्र
\(\mathrm{L}_2=\frac{\mathrm{G} \times 100)}{(0.5)^2}\)
[PB के अनुदिश]
∵ E1 व E2 परिमाण में समान परन्तु विपरीत दिशा में होने से P पर परिणामी गुरुत्वीय क्षेत्र शून्य जिससे गुरुत्वीय बल शून्य होगा। 
∵ गुरुत्वीय विभव एक अदिश राशि है अतः P पर कुल गुरुत्वीय
विभव-
V = VA + VB

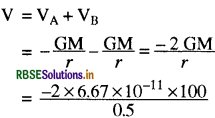
= - 2.668 × 10^-8 J/kg
= - 2.7 x 10⁸ J/kg
इस प्रकार पिण्ड संतुलन में होगा। परन्तु यह अस्थायी साम्यावस्था की स्थिति में होगा क्योंकि A तथा B स्थिति से थोड़ा सा भी विस्थापन संतुलन को अव्यवस्थित कर देगा जिसे पुनः स्थापित नहीं किया जा सकता है।

अभ्यास के अतिरिक्त प्रश्न:

प्रश्न 8.22. 
जैसा कि आपने इस अध्याय में सीखा है कि कोई तुल्यकाली उपग्रह पृथ्वी के पृष्ठ से लगभग 36,000 km ऊंचाई पर पृथ्वी की परिक्रमा करता है। इस उपग्रह के निर्धारित स्थल पर पृथ्वी के गुरुत्व बल के कारण विभव क्या है? (अनन्त पर स्थितिज ऊर्जा शून्य लीजिए।) पृथ्वी का द्रव्यमान = 6.0 x 10²⁴ kg पृथ्वी की त्रिज्या = 6400 km.
उत्तर:
पृथ्वी का द्रव्यमान M1 = 6.0 x 10²⁴ kg
पृथ्वी की त्रिज्या R1 = 6,400km
पृथ्वी के पृष्ठ से उपग्रह की ऊँचाई = 36,000km 
उपग्रह के स्थान पर पृथ्वी के गुरुत्वाकर्षण के कारण विभव

प्रश्न 8.23. 
सूर्य के द्रव्यमान से 2.5 गुने द्रव्यमान का कोई तारा 12 km आमाप से निपात होकर 1.2 परिक्रमण प्रति सेकण्ड से घूर्णन कर रहा है (इसी प्रकार के संहत तारे को न्यूट्रॉन तारा कहते हैं कुछ प्रेक्षित तारकीय पिण्ड, जिन्हें पल्सार कहते हैं, इसी श्रेणी में आते हैं)। इसके विषुवत् वृत्त पर रखा कोई पिण्ड, गुरुत्व बल के कारण, क्या इसके पृष्ठ से चिपका रहेगा? (सूर्य का द्रव्यमान = 2 x 10³⁰ kg)
उत्तर:
कोई पिण्ड तारे के पृष्ठ से गुरुत्वाकर्षण के कारण तभी चिपक सकता है यदि गुरुत्वाकर्षण के कारण गुरुत्वीय त्वरण का मान
अभिकेन्द्रीय त्वरण से सदैव अधिक होना चाहिए जिसमें पिण्ड घूर्णन कर रहा है। 
गुरुत्वाकर्षण के कारण गुरुत्वीय त्वरण
\(\begin{aligned} & g=\frac{\mathrm{GM}_{\mathrm{E}}}{\mathrm{R}_{\mathrm{E}}^2} \\ & g=\frac{6.67 \times 10^{-11} \times 2.5 \times 2 \times 10^{30}}{(12000)^2} \end{aligned}\)
g = 2.3 x 10¹² m/s²
अभिकेन्द्रीय त्वरण ac = rω² = r (2πn)²
= 12000 (2r x 1.2) ²
= 1.2 परिक्रमण प्रति सेकण्ड
= 68.15 × 10⁴ m/s
यहाँ पर g > rω², इसलिए पिण्ड तारे के पृष्ठ से चिपका रहता है।

प्रश्न 8.24. 
कोई अन्तरिक्ष यान मंगल पर ठहरा हुआ है। इस अन्तरिक्ष यान पर कितनी ऊर्जा खर्च की जाए कि इसे सौरमण्डल से बाहर धकेला जा सके। अन्तरिक्ष यान का द्रव्यमान का द्रव्यमान = 2 x 10³⁰ kg: मंगल का द्रव्यमान = 1000 kg; सूर्य 6.4 x 10²³ kg; मंगल की त्रिज्या = 3395 km; मंगल की कक्षा की त्रिज्या = 2.28 × 10⁸ km तथा G = 6.67 x 10^-11 Nm² kg²
उत्तर:
दिया गया है:
अंतरिक्ष यान का द्रव्यमान m = 1000 kg
सूर्य का द्रव्यमान M = 2 x 10³⁰ kg
मंगल का द्रव्यमान Ma = 6.4 x 10²³ kg 
मंगल की त्रिज्या Rm = 2.38 x 10⁸ km 
= 2.38 × 10¹¹ m
G = 6.67 × 10^-11 Nm²/kg²
सूर्य के परितः मंगल की त्रिज्या = 3395 km = 3395 x 10 m सूर्य के गुरुत्वाकर्षण बल के कारण अन्तरिक्ष यान की स्थितिज ऊर्जा
\(=\frac{-\mathrm{GM}_s m}{\mathrm{R}_m}\) ........ (1)
मंगल के गुरुत्वाकर्षण के कारण भी अन्तरिक्ष यान की विभव ऊर्जा
\(=\frac{-\mathrm{GM}_m m}{\mathrm{R}}\) .......... (2)
∴ जब अन्तरिक्ष यान मंगल के पृष्ठ पर स्थित है तो इसकी कुल
स्थितिज ऊर्जा
\(=\frac{-\mathrm{GM}_s m}{\mathrm{R}_m}-\frac{\mathrm{GM}_m m}{\mathrm{R}}\)
∴ अन्तरिक्ष यान की कुल ऊर्जा = KE + PE
= 0+ P.E = P.E
\(\begin{aligned} & =-\mathrm{G} m\left(\frac{\mathrm{M}_s}{\mathrm{R}_m}+\frac{\mathrm{M}_m}{\mathrm{R}}\right) \\ & =-\mathrm{G} m\left(\frac{\mathrm{M}_s}{\mathrm{R}_m}+\frac{\mathrm{M}_m}{\mathrm{R}}\right) \end{aligned}\)
∴ अन्तरिक्ष यान को सौरमण्डल से बाहर धकेलने के लिए ऊर्जा की
आवश्यकता पड़ेगी
\(\begin{aligned} & =-\left[-\mathrm{GM}\left(\frac{\mathbf{M}_s}{\mathbf{R}_m}+\frac{\mathbf{M}_m}{\mathbf{R}}\right)\right] \\ & =\mathrm{G} m\left[\frac{\mathbf{M}_s}{\mathrm{R}_m}+\frac{\mathbf{M}_m}{\mathbf{R}}\right] \end{aligned}\)
मान रखने पर

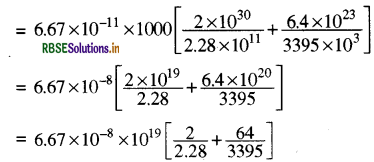
= 6.67 x 10 x [0.877 +0.0189]
= 6.67 × 10¹¹ x 0.9059
= 6 x 10¹¹ J 

प्रश्न 8. 25. 
किसी रॉकेट को मंगल के पृष्ठ से 2 kms^-1 की चाल से ऊर्ध्वाधर ऊपर दागा जाता है। यदि मंगल के वातावरणीय प्रतिरोध के कारण इसकी 20% आरंभिक ऊर्जा नष्ट हो जाती है, तो मंगल के पृष्ठ पर वापस लौटने से पूर्व यह रॉकेट मंगल से कितनी दूरी तक जाएगा? मंगल का द्रव्यमान = 6.4 x 10²³ kg; मंगल की त्रिज्या 3395 km तथा G = 6.67 x 10^-11 Nm² kg ² 
उत्तर:
माना रॉकेट का द्रव्यमान = m
मंगल ग्रह का द्रव्यमान = M
माना रॉकेट का आरम्भिक वेग = v है।
आरम्भिक गतिज ऊर्जा = 1⁄2mv²
आरम्भिक स्थितिज ऊर्जा = PE = \(\frac{-\mathrm{GMm}}{\mathrm{R}}\)
कुल आरम्भिक ऊर्जा का मान E = 1/2mv² - GMm/R
चूँकि 20% KE खो जाती है। केवल 80% ही ऊँचाई तक पहुँचने के लिए शेष रह जाती है अर्थात्
E का 80% = 80/10E = 4/5E
∴ \(\frac{4}{5}\left[\frac{1}{2} m \mathrm{v}^2-\frac{\mathrm{GM} m}{\mathrm{R}}\right]\)

h ऊँचाई पर रॉकेट की स्थितिज ऊर्जा
PE = - GMm/R + h
h ऊँचाई पर
K.E = 0
∴ ऊर्जा संरक्षण के नियम से-
कुल प्रारम्भिक ऊर्जा = कुल अन्तिम ऊर्जा प्रारम्भिक (KE + PE) = अन्तिम (KE + P.E)

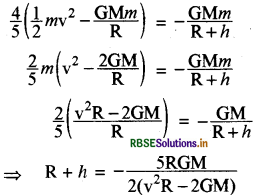
दिया है-
R = 3395 किमी.
= 3395 × 10³
G = 6.67 x 10^-11 न्यूटन x मी.² / किग्रा.² 
M = 6.4 x 10²³ किमी
v = 2 किमी / से. = 2000 मी./से.

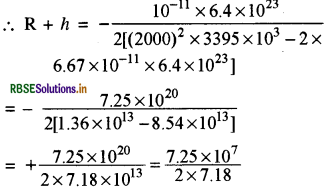
= 5.05 x 10⁶.
h = 5.05 x 10⁶ - R
5.05 x 10⁶ - 3395 × 10³
= 1655 x 10³ मी
= 1655 किमी.