RBSE Solutions for Class 11 Physics Chapter 7 कणों के निकाय तथा घूर्णी गति

Rajasthan Board RBSE Solutions for Class 11 Physics Chapter 7 कणों के निकाय तथा घूर्णी गति Textbook Exercise Questions and Answers.

RBSE Class 11 Physics Solutions Chapter 7 कणों के निकाय तथा घूर्णी गति

RBSE Class 11 Physics कणों के निकाय तथा घूर्णी गति Textbook Questions and Answers

प्रश्न 7.1. 
एकसमान द्रव्यमान घनत्व के निम्नलिखित पिण्डों में प्रत्येक के द्रव्यमान केंद्र की अवस्थिति लिखिए:
(a) गोला. 
(b) सिलिंडर,
(c) छल्ला तथा 
(d) घन। 
क्या किसी पिण्ड का द्रव्यमान केंद्र आवश्यक रूप से उस पिण्ड के भीतर स्थित होता है? 
उत्तर:
इन चारों स्थितियों में एकसमान द्रव्यमान घनत्व है इसलिए द्रव्यमान केन्द्र की स्थिति निम्न होगी:
(a) गोला के केन्द्र पर 
(b) बेलन के सममिति अक्ष के मध्य बिन्दु पर अर्थात् इसके ज्यामिति केन्द्र पर 
(c) छल्ले के केन्द्र पर 
(d) विकर्णों के कटान बिन्दु पर अर्थात् इसके ज्यामितीय केन्द्र पर नहीं, यह आवश्यक नहीं है कि किसी पिण्ड का द्रव्यमान केन्द्र पिण्ड के भीतर स्थित होना चाहिए। कुछ स्थितियों में जैसे छल्ला, खोखला बेलन, खोखला गोला तथा खोखले घन आदि पिण्डों में द्रव्यमान केन्द्र पिण्ड के बाहर हो सकता है। वृत्ताकार वलय स्थिति में द्रव्यमान केन्द्र वृत्ताकार वलय के केन्द्र पर स्थित होता है, जहाँ कोई भी द्रव्यमान नहीं होता है। 

 

प्रश्न 7.2. 
HCl अणु में दो परमाणुओं के नाभिकों के बीच पृथक्कन लगभग 1.27Å (1  = 10^-10 m ) है। इस अणु के द्रव्यमान केंद्र की लगभग अवस्थिति ज्ञात कीजिए। यह ज्ञात है कि क्लोरीन का परमाणु हाइड्रोजन के परमाणु की तुलना में 35.5 गुना भारी होता है तथा किसी परमाणु का समस्त द्रव्यमान उसके नाभिक पर केंद्रित होता है। 
उत्तर:
माना H परमाणु का द्रव्यमान (m₁) = m इकाई है। 
∴ Cl परमाणु का द्रव्यमान (m₂) = 35.5 m इकाई 
माना H परमाणु से द्रव्यमान केन्द्र (cm) x À  दूरी पर है। 

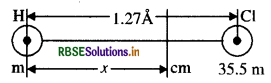
cm को उद्गम मानकर माना कि H तथा Cl परमाणुओं की स्थिति 
क्रमशः \(\overrightarrow{r_1}\) तथा \(\overrightarrow{r_2}\) अर्थात् cm की स्थिति सदिश शून्य है। 
अर्थात्  \(\overrightarrow{\mathrm{R}}_{c m}=0=\frac{m_1 \vec{r}_1+m_2 \vec{r}_2}{m_1+m_2}\)
या \(m_1 \vec{r}_1+m_2 \overrightarrow{r_2}=0\)
यहाँ r1 = -xi
और \(\overrightarrow{r_2}=(1.27-x) \hat{i}\)
समीकरण (1) से 
\(m(-x \hat{i})+35.5 \mathrm{~m}(1.27-x) \hat{i}=0\)
या mx = 35.5 m (1.27 - x) 
या x = 35.5 (1.27 - x) 
या x = 35.5 × 1.27 - 35.5 x 
या x + 35.5 x = 35.5 x 1.27 
या 36.5 x = 35.5 x 1.27 
या \(x=\frac{35.5 \times 1.27}{36.5}\)
x = 1.235Å = 1.24Å 
अतः द्रव्यमान केन्द्र H परमाणु से तथा H एवं Cl परमाणुओं को जोडने वाली रेखा पर स्थित होगा। 

प्रश्न 7.3. 
कोई बच्चा किसी चिकने क्षैतिज फर्श पर एकसमान चाल से गतिमान किसी लंबी ट्रॉली के एक सिरे पर बैठा है। यदि बच्चा खड़ा होकर ट्रॉली पर किसी भी प्रकार से दौड़ने लगता है, तब निकाय (ट्रॉली + बच्चा) के द्रव्यमान केंद्र की चाल क्या है? 
उत्तर:
(ट्रॉली + बच्चे ) के निकाय के द्रव्यमान केन्द्र की चाल अपरिवर्ती रहती हैं जो कि है। यदि बच्चा उठकर किसी भी प्रकार ट्रॉली पर दौड़ने लगता है। यह इसलिए है कि किसी भी निकाय की स्थिति उस पर लगे बाह्य बल के प्रयास से ही बदल सकती है और यहाँ पर कोई बाह्य बल कार्य नहीं करता। ट्रॉली पर दौड़ने में लगा बल निकाय के अन्दर से ही है। अर्थात् आन्तरिक बल है। 

प्रश्न 7.4. 
दर्शाइये कि \(\vec{a}\) एवं \(\vec{b}\) के बीच बने त्रिभुज का क्षेत्रफल \(\vec{a} \times \vec{b}\) है के परिमाण का आधा है। 
उत्तर:
माना \(\vec{a}, \overrightarrow{\mathrm{OP}}\) के द्वारा प्रदर्शित किया गया है और \(\vec{b}, \overrightarrow{\mathrm{OQ}}\) के द्वारा प्रदर्शित किया गया है। 
माना 
∠POQ = θ 
समान्तर चतुर्भुज OPRQ पूरा किया और विकर्ण PQ को मिलाया, लम्ब QN, OP पर खींचा गया है। 
त्रिभुज OQN में 
sin θ = \(\frac{\mathrm{QN}}{\mathrm{OQ}}=\frac{\mathrm{QN}}{b}\)
QN = b sin θ 
अब परिभाषा से 
| \(\vec{a} \times \vec{b}\) | = ab sin θ = (OP) (QN) 
\(=\frac{2(\mathrm{OP})(\mathrm{QN})}{2}\)
= 2 × ∆OPQ का क्षेत्रफल 
∴ ∆ OPQ का क्षेत्रफल = 1/2\(\vec{a} \times \vec{b}\) इति सिद्धम् 

प्रश्न 7.5. 
दर्शाइये कि a. (bx c) का परिमाण तीन सदिशों a, b एवं c से बने समान्तर षट्फलक के आयतन के बराबर है। 
उत्तर:
माना एक समान्तर षट्फलक तीन सदिशों \(\overrightarrow{\mathrm{OA}}=\vec{a}, \overrightarrow{\mathrm{OB}}=\vec{b}\) तथा \(\overrightarrow{\mathrm{OC}}=\vec{c}\) से बनता है। 

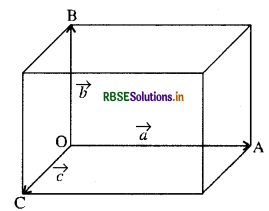
अब 
\(\begin{aligned} & \vec{b} \times \vec{c}=b c \sin 90^{\circ} \cdot \hat{n}=b c \hat{n} \\ & \vec{b} \times \vec{c}=b c \hat{n} \end{aligned}\)
जहाँ पर एक इकाई सदिश जो OA के अनुदिश है, और है तथा imm समतल के लम्बवत् है। 
अब 
\(\vec{a} \cdot(\vec{b} \times \vec{c})=\vec{a} \cdot b c \hat{n}\) = (a) (bc) cos 0° 
क्योंकि \(\vec{a}\) तथा bc n समान दिशा में हैं। 
= abc 
जो कि समान्तर षट्फलक के आयतन के परिमाण के बराबर है। इति सिद्धम् 

प्रश्न 7.6. 
एक कण, जिसके स्थिति सदिश के x, y, z अक्षों के अनुदिश अवयव क्रमश: x, y, z हैं, और रेखीय संवेग सदिश P के अवयव Px, P, P. हैं, के कोणीय संवेग 7 के अक्षों के अनुदिश अवयव ज्ञात कीजिए। दर्शाइये कि यदि कण केवल x-y तल में ही गतिमान हो तो कोणीय संवेग का केवल 7-अवयव ही होता है। 
उत्तर:
चित्र में OX, OY, OZ तीन लम्बवत् अक्ष हैं। माना कण P पर है जिसकी स्थिति सदिश \(\overrightarrow{\mathrm{OP}}=\vec{r}\) x - Y तल में है। 

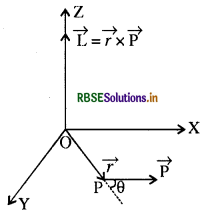
यहाँ कोण θ  स्थिति सदिश \(\vec{r}\) के बढ़े हुए का संवेग p के साथ कोण है। 
\(\vec{l}=\vec{r} \times \overrightarrow{\mathrm{P}}\) ............ (1)
यह एक सदिश राशि है, जिसकी दिशा का मान सदिशों की गुणा के दाहिने हाथ के नियम से दिया जाता है। 
यहाँ पर संवेग \(\overrightarrow{\mathrm{P}}\) XOY तल में स्थित है। अतः कोणीय संवेग \(\vec{l}\) अक्ष के अनुदिश कार्य करता है। 
\(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\)
तथा 
\(\mathrm{P}=\mathrm{P}_x \hat{i}+\mathrm{P}_y \hat{j}+\mathrm{P}_z \hat{k}\) .............. (2)
समीकरण ( 1 ) में मान रखने  पर 
\(\begin{aligned} \vec{l} & =(x \hat{i}+y \hat{j}+z \hat{k}) \times\left(\mathrm{P}_x \hat{i}+\mathrm{P}_y \hat{j}+\mathrm{P}_z \hat{k}\right) \\ & =\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ x & y & z \\ \mathrm{P}_x & \mathrm{P}_y & \mathrm{P}_z \end{array}\right| \end{aligned}\)
या 
\(l_x \hat{i}+l_y \hat{j}+l_z \hat{k}=\hat{i}\left(y P_z-z P_y\right)-\hat{j}\left(x \mathrm{P}_z-z \mathrm{P}_x\right)+\hat{k}\left(x \mathrm{P}_y-y \mathrm{P}_x\right)\)
दोनों तरफ तुलना करने पर 
lx = yP2 -  xPy 
ly = - (xPz - zPx) = zPx - xPz 
lz = xPy - yPx 
समीकरण (3) X, Y तथा Z अक्षों के अनुदिश \(\vec{l}\) के वांछित घटक दिया जाता है। 
यदि कण केवल X-Y तल में ही गतिमान हो तब Z = 0 तथा 
Pz = 0 
जिससे 
\(\vec{l}\)  = (xPy - yPx) 
∵ k, Z - अक्ष के अनुदिश एकांक सदिश होता है अतः कोणीय संवेग \(\vec{l}\) का केवल Z - अवयव ही अस्तित्व में होगा। 

प्रश्न 7.7. 
दो कण, जिनमें से प्रत्येक का द्रव्यमान mm एवं चाल v है, d दूरी पर, समान्तर रेखाओं के अनुदिश, विपरीत दिशाओं में चल रहे हैं। दर्शाइये कि इस द्विकण निकाय का सदिश कोणीय संवेग समान रहता है, चाहे हम जिस बिन्दु के परितः कोणीय संवेग लें। 
उत्तर:
इस द्विकण निकाय का कुल कोणीय संवेग 

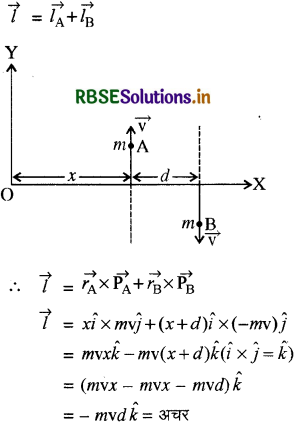
अतः\(\vec{l}\) का मान x पर निर्भर नहीं है अर्थात् यह उस बिन्दु की स्थिति पर निर्भर नहीं है जिसके परितः इसकी गणना की गई है। इस प्रकार इस द्विकण निकाय का कोणीय संवेग समान रहता है चाहे हम जिस बिन्दु के परितः कोणीय संवेग लें। 

प्रश्न 7.8. 
W भार की एक असमांग छड़ को, उपेक्षणीय भार वाली दो डोरियों से चित्र में दर्शाये अनुसार लटका कर विरामावस्था में रखा गया है। डोरियों द्वारा ऊर्ध्वाधर से बने कोण क्रमश: 36.9° एवं 53.1° हैं। छड़ 2m लम्बाई की है। छड़ के बाएँ सिरे से इसके गुरुत्व केन्द्र की दूरी d ज्ञात कीजिए। 

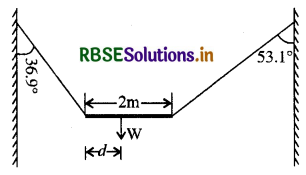
उत्तर:
चित्र से स्पष्ट है - θ1 = 36.9° और θ2 = 53.1° 

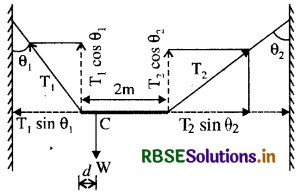
यदि T व T2 दो डोरियों के तनाव हों तब क्षैतिज दिशा में साम्यावस्था 
T1 sin θ 1 = T2 sin θ 2 
या 

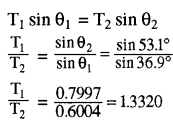
दिया गया है - छड़ के बायें सिरे से इसके गुरुत्व केन्द्र की दूरी d है।
बिन्दु C के सापेक्ष घूर्णन साम्यावस्था के लिए 
T₁ cos θ1 x d = T₂ cos θ2 (2 - d) 
चूँकि छड़ की लम्बाई = 2m है। 
T₁ cos 36.9° × d = T₂ cos 53.1° (2 – d) 
T₁ × 0.7997 x d = T₂ x 0.6004 (2 - d) 
या 
T₁/T₂ x 0.7997 x d = 0.6004 (2 - d) 
T₁/T₂ का मान रखने पर 
⇒ 1.3320 x 0.7997 x d = 0.6004 (2 - d) 
⇒ \(\frac{1.3320 \times 0.7997}{0.6004}=\frac{2-d}{d}\)
⇒ 1.7742 = 2/d - 1
⇒ 2.7742 = 2/d 
∴ \(d=\frac{2}{2.7742}=0.721 \mathrm{~m}\)
∴ d = 0.721 x 100 cm 
= 72.1 cm 

 
प्रश्न 7.9. 
एक कार का भार 1800 kg है। इसकी अगली और पिछली धुरियों के बीच की दूरी 1.8m है। इसका गुरुत्व केन्द्र, अगली धुरी से 1.05m पीछे है। समतल धरती द्वारा इसके प्रत्येक अगले और पिछले पहियों पर लगने वाले बल की गणना कीजिए। 
उत्तर:
दिया गया है:
कार का द्रव्यमान (m) = 1800 kg 
कार की अगली और पिछली धुरियों के बीच की दूरी = 1.8m कार का गुरुत्व केन्द्र, अगली धुरी से 1.05m की दूरी पर है। ekukfd R₁ तथा R₂ समतल भूमि द्वारा प्रत्येक पिछले पहिये (back wheel) तथा प्रत्येक अगले पहिये (front wheel) पर आरोपित प्रतिक्रिया 

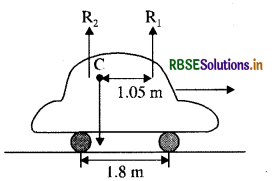
R₁ + R₂ = mg = 1800 x 9.8 
R₁ + R₂ = 1800 x 9.8 .....(1) 
घूर्णन साम्यावस्था C के लिए 
R₁ × 1.05 = R₂ (1.8 - 1.05 ) = R₂ x 0.75 
⇒ 1.05 R₁ = 0.75R₂ 

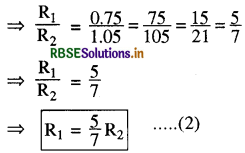
समीकरण (1) तथा (2) से R₁ तथा R₂ के मान निकालने पर R₁ का मान समीकरण (1) में रखने पर 
\(\frac{5}{7} R_2+R_2=1800 \times 9.8\)
= 150 × 9.8 × 7 
R₂ = 10290 N 
∴ R₁ = 5/7R₂ = 5/7 ×10290 = 7350 N 
⇒ R₁ = 7350 N 
प्रत्येक अगले पहिये पर बल 
R₂/2 = 10290/2
= 5145 N 

प्रश्न 7.10. 
(a) किसी गोले का, इसके किसी व्यास के परित जड़त्व आघूर्ण 2MR 2/5 है, जहाँ M गोले का द्रव्यमान एवं R इसक त्रिज्या है। गोले पर खींची गई स्पर्श रेखा के परितः इसका जड़त्व आघूप ज्ञात कीजिए। 
(b) M द्रव्यमान एवं R त्रिज्या वाली किसी डिस्क का इसके किसी व्यास के परितः जड़त्व आघूर्ण MR 2/4 है। डिस्क के लम्बवत इसकी कोर से गुजरने वाली अक्ष के परितः इस चकती का जड़त्व आघूर्ण ज्ञात कीजिए। 
उत्तर:
(a) माना R त्रिज्या तथा M द्रव्यमान के गोले के व्यास के परितः उसका जड़त्व आघूर्ण IAB है। 
∴ IAB = 2/5MR² ................. (1)
यहाँ पर गोला ठोस है। 

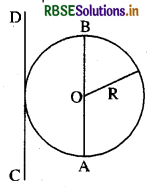
माना गोले के व्यास AB के समान्तर स्पर्शज्या CD है और दोनो समान्तर अक्षों के बीच की दूरी R है। यदि CD अक्ष के परितः इसका जड़त्व आघूर्ण ICD है तो समान्तर अक्ष प्रमेय से, 
IcD = IAB + MR² = 2/5MR² + MR² 
ICD = 7/5MR² 

(b) डिस्क का व्यास के परितः जड़त्व आघूर्ण = MR²/4 इसलिये चकती के केन्द्र से गुजरने वाली व तल के लम्बवत् अक्ष के सापेक्ष जड़त्व 
आघूर्ण 
Iz = Ix + ly 
लम्ब अक्ष प्रमेय से, 
∵ दोनों व्यास समान हैं। 
∴ Ix = ly 
Iz = Ix + Ix = 2Ix 
Iz = 2 × MR²/4 = MR²/2
∴ डिस्क के लम्बवत् कोर से गुजरने वाली अक्ष के परितः चकती का जड़त्व आघूर्ण (समान्तर अक्षों की प्रमेय से) 
Iz = Iz + MR² 
= 1⁄2 MR² + MR² 
Iz = 3/2 MR²

प्रश्न 7.11. 
समान द्रव्यमान और त्रिज्या के एक खोखले बेलन और एक ठोस गोले पर समान परिमाण के बल आघूर्ण लगाये गये हैं। बेलन अपनी सामान्य सममित अक्ष के परितः घूम सकता है और गोला अपने केन्द्र से गुजरने वाली किसी अक्ष के परितः एक दिये गये समय के बाद दोनों में कौन अधिक कोणीय चाल प्राप्त कर लेगा? 
उत्तर:
माना खोखले बेलन तथा ठोस गोले का द्रव्यमान एवं त्रिज्या क्रमश: M व R है। तब 
माना I₁ तथा I₂ खोखले बेलन का उसकी सममित अक्ष के परितः तथा ठोस गोले का इसके केन्द्र से जाने वाले अक्ष के परितः जड़त्व आघूर्ण है। 
तब 
I₁ = MR² ......... (1)
तथा 
I² = 2/5MR²  ................ (2)
समीकरण (1) में समीकरण (2) का भाग देने पर 
\(\frac{I_1}{I_2}=\frac{M^2}{\frac{2}{5} \mathrm{MR}^2}=\frac{5}{2}\)

I₁/I₂ = 5/2 ............ (3)
माना τ = बल आघूर्ण, जो उनमें से प्रत्येक पर लगाया जाता है, का परिमाण है। यदि बेलन व ठोस में उत्पन्न कोणीय त्वरण क्रमश: α1 तथा α2 है तब 
τ = I₁α1
और 
τ = I₂ α2
∴ I₁α1 = I₂α2
या 
\(\begin{aligned} \frac{\mathrm{I}_1}{\mathrm{I}_2}=\frac{\alpha_2}{\alpha_1} \\ \frac{5}{2}=\frac{\alpha_2}{\alpha_1} \end{aligned}\)
[समीकरण (3) से मान रखा गया है। 
α1 > α2
यदि t समय के पश्चात् बेलन की कोणीय चाल ω1 तथा ω2 है तब 
ω1 = ω0 + α1t .............. (4)
ω2 = ω0 + α2t ................. (5)
और 
जहाँ पर ω0 = आरम्भिक चाल है। 
α1 तथा α2 का मान रखने पर स्पष्ट है कि 
ω2 > ω1 
अतः दत्त समय के पश्चात् ठोस गोले की कोणीय चाल का मान बेलन की अपेक्षा अधिक होगा। 

प्रश्न 7.12.
20 kg द्रव्यमान का कोई ठोस सिलिंडर अपने अक्ष के परितः 100 rad s-1 की कोणीय चाल से घूर्णन कर रहा है। सिलिंडर की त्रिज्या 0.25m है। सिलिंडर के घूर्णन से संबद्ध गतिज ऊर्जा क्या है? सिलिंडर का अपने अक्ष के परितः कोणीय संवेग का परिमाण क्या है? 
उत्तर:
दिया गया है:
M = 20 kg 
R = 0.25 m 
ω = 100 Radian/s 
यदि बेलन का उसके अक्ष के परितः जड़त्व आघूर्ण I है तो 
I = 1/2 MR²
मान रखने पर 
I = 1/2 × 20 × (0.25)² 
= 1/2 ×20 × (1/4)² 
\(=\frac{1}{2} \times 20 \times\left(\frac{1}{4}\right)^2=\frac{20}{2 \times 16}\)
= 5/8kgm² 
∴ घूर्णन गतिज ऊर्जा (K.E) = 1/2Iω² 
मान रखने पर 
\(\begin{aligned} & =\frac{1}{2} \times \frac{5}{8} \times(100)^2 \\ & =\frac{5 \times 100 \times 100}{2 \times 8} \end{aligned}\)
= 5×25 × 25 
5 × 625 = 3125 J 
बेलन का अपने अक्ष के परितः कोणीय संवेग का परिमाण माना L 
कोणीय संवेग L = Iω 
= 5/8 x 100
= 62.5 kgm² s^-1 

प्रश्न 7.13. 
(a) कोई बच्चा किसी घूर्णिका ( घूर्णीमंच) पर अपनी दोनों भुजाओं को बाहर की ओर फैलाकर खड़ा है। घूर्णिका को 40 rev / min की कोणीय चाल से घूर्णन कराया जाता है। यदि बच्चा अपने हाथों को वापस सिकोड़ कर अपना जड़त्व आघूर्ण अपने आरंभिक जड़त्व आघूर्ण का 2/5 गुना कर लेता है, तो इस स्थिति में उसकी कोणीय चाल क्या होगी? यह मानिए कि घूर्णिका की घूर्णन गति घर्षणरहित है। 
(b) यह दर्शाइए कि बच्चे की घूर्णन की नयी गतिज ऊर्जा उसकी आरंभिक घूर्णन की गतिज ऊर्जा से अधिक है। आप गतिज ऊर्जा में हुई इस वृद्धि की व्याख्या किस प्रकार करेंगे? 
उत्तर:
(a) दिया गया है:
आरम्भिक कोणीय चाल, ω₁ = 40 rev/min 
ω₂ = ? 
अन्तिम जँड़त्व आघूर्ण, I₂ = 5 I₁, आरम्भिक जड़त्व आघूर्ण 
कोई भी बाह्य बल कार्य नहीं कर रहा 
∴ कोणीय संवेग L = स्थिरांक (constant ) 
∴ I₁
या ω₂ = I₁ω₁/I₂
मान रखने पर 
\(=\frac{\mathrm{I}_1 \times 40}{\frac{2}{5} \mathrm{I}_1}=\frac{40 \times 5}{2}\)
= 100 rev/min. 

(b) आरम्भिक घूर्णन K.E = E1 = 1/2I₁ω₁2 
अन्तिम घूर्णन K.E = E 2 = 1/2I₂ω₂² 
\(\frac{E_1}{E_2}=\frac{\frac{1}{2} I_1 \omega_1^2}{\frac{1}{2} I_2 \omega_2^2}\)

\(=\frac{I_1 \omega_1^2}{I_2 \omega_2^2}=\left(\frac{I_1}{I_2}\right)\left(\frac{\omega_1}{\omega_2}\right)^2\)
मान रखने पर 
\(\frac{E_1}{E_2}=\left(\frac{I_1}{\frac{2}{5} I_1}\right)\left(\frac{40}{100}\right)^2\)
\(=\frac{5}{2} \times\left(\frac{2}{5}\right)^2=\frac{5}{2} \times \frac{4}{25}=\frac{2}{5}\)
⇒ E₁/E₂ = 2/5
या E₂ = 2.5 E₁
अतः स्पष्ट है कि नई K. E जब बच्चा हाथ बाँध लेता है आरम्भिक घूर्णन K. E का 2.5 भाग है। 
हाथ बाँधने के पश्चात् बच्चे की घूर्णन गतिज ऊर्जा में वृद्धि उसकी अपनी आंतरिक ऊर्जा के उपयोग के कारण प्रतीत होती है। 

प्रश्न 7.14. 
3kg द्रव्यमान तथा 40 cm त्रिज्या के किसी खोखले सिलिंडर पर कोई नगण्य द्रव्यमान की रस्सी लपेटी गई है। यदि रस्सी को 30 N बल से खींचा जाए तो सिलिंडर का कोणीय त्वरण क्या होगा? रस्सी का रैखिक त्वरण क्या है? यह मानिए कि इस प्रकरण में कोई फिसलन नहीं है। 
उत्तर:
दिया गया है:

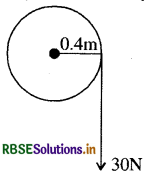
खोखले बेलन का द्रव्यमान M = 3 kg 
खोखले बेलन की त्रिज्या R = 40 cm 
= 4/100 = 0.4m 
स्पर्शीय बल F = 30 N 
बेलन का कोणीय त्वरण = α = ? 
माना रस्सी का रैखिक त्वरण = a = ? 
खोखले बेलन का जड़त्व आघूर्ण उसकी अक्ष के सापेक्ष 
I = MR² 
= 3 × (0.4)² = 3 x 0.16 
= 0.48 kgm² 
यदि τ = बेलन पर कार्यरत बल आघूर्ण है तब 
τ = F x R 
= 30 × 0.4 = 12 N^-m 
यदि α कोणीय त्वरण उत्पन्न होता है तब 
τ = I α से 
\(\alpha=\frac{\tau}{I}=\frac{12}{0.48}=\frac{1200}{48}\)
α = 25 radian/s² 
रैखिक त्वरण = Rα  
= 0.4 × 25 = 10 m/s² 

प्रश्न 7.15. 
किसी घूर्णक (रोटर) की 200 radst की एकसमान कोणीय चाल बनाए रखने के लिए एक इंजन द्वारा 180 Nm का बल आघूर्ण प्रेषित करना आवश्यक होता है। इंजन के लिए आवश्यक शक्ति ज्ञात कीजिए। (नोट- घर्षण की अनुपस्थिति में एकसमान कोणीय वेग होने में यह समाविष्ट है कि बल आघूर्ण शून्य है। व्यवहार में लगाए गए बल आघूर्ण की आवश्यकता घर्षणी बल आघूर्ण को निरस्त करने के लिए होती है ।) यह मानिए कि इंजन की दक्षता 100% है। 
उत्तर:
दिया गया है:
ω = 200 rad/s² 
t = 180 Nm. 
P ? 
P = TO सम्बन्ध का उपयोग करके हम 
= 180 × 200 = 36,000 W 
= 36 kW 

प्रश्न 7.16. 
R त्रिज्या वाली समांग डिस्क से R / 2 त्रिज्या का एक वृत्ताकार भाग काट कर निकाल दिया गया है। इस प्रकार बने वृत्ताकार सुराख का केन्द्र मूल डिस्क के केन्द्र से R/2 दूरी पर है। अवशिष्ट डिस्क के गुरुत्व केन्द्र की स्थिति ज्ञात कीजिए। 
उत्तर:
माना मूल डिस्क की त्रिज्या = R 
हटाये गये वृत्ताकार भाग की त्रिज्या = R/2
माना डिस्क का इकाई क्षेत्रफल का द्रव्यमान = m. 
∴ मूल डिस्क का द्रव्यमान = πR2 x m 
इसी तरह हटाये गये भाग का द्रव्यमान 

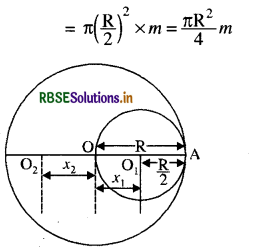
यदि मूल डिस्क तथा हटाये गये भागों के द्रव्यमान क्रमश: M तथा M1
और 
M = πR²m 
और 
M₁ = πR²/4m
यदि M₂ शेष भाग का द्रव्यमान है तब 
\(=\pi \mathrm{R}^2 m-\frac{\pi \mathrm{R}^2}{4} m=\frac{3}{4} \pi \mathrm{R}^2 m\)
तब 
माना O मूल बिन्दु है। 
यदि Rcm हटाये गये तथा शेष भाग का द्रव्यमान केन्द्र (c.m.) है 
तब 
\(\mathbf{R}_{\mathrm{cm}}=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\) सूत्र से 
यहाँ 
x1 = OO1 = OA - OA 
\(x_1=\mathrm{R}-\frac{\mathrm{R}}{2}=\frac{\mathrm{R}}{2}\)
M = 3/4πR²
लेकिन 
Rcm = 0 

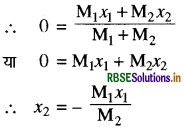
मान रखने पर
\(x_2=\frac{-\frac{\pi \mathrm{R}^2}{4} m}{\frac{3}{4} \pi \mathrm{R}^2 m} \times \frac{\mathrm{R}}{2}\)
यहाँ ऋण चिन्ह दर्शाता है कि शेष भाग का द्रव्यमान केन्द्र R/6 पर O के बायीं ओर है जो कि हटाये गये भाग की विपरीत दिशा में है।
 
प्रश्न 7.17. 
एक मीटर छड़ के केन्द्र के नीचे क्षुर-धार रखने पर वह इस पर संतुलित हो जाती है जब दो सिक्के, जिनमें प्रत्येक का द्रव्यमान 5g है, 12.0 cm के चिन्ह पर एक के ऊपर एक रखे जाते हैं तो छड़ 45.0 cm चिन्ह पर संतुलित हो जाती है। मीटर छड़ का द्रव्यमान क्या है? 
उत्तर:
माना छड़ का द्रव्यमान C पर m है। तब C पर बल लगेगा 
= mg 

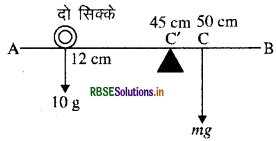
चूँकि छड़ साम्यावस्था में है अतः C' के परितः आघूर्ण समान है अर्थात् 
10 g (45 - 12 ) = mg (50 - 45)
⇒ 10 g x 33 = 5mg 
m = \(\frac{10 g \times 33}{5 g}\) = 66 g
अतः मीटर छड़ का द्रव्यमान = 66g 

प्रश्न 7.18. 
एक ठोस गोला, भिन्न नति के दो आनत तलों पर एक ही ऊँचाई से लुढ़कने दिया जाता है। (a) क्या वह दोनों बार समान चाल से तली में पहुँचेगा? (b) क्या उसको एक तल पर लुढ़कने में दूसरे से अधिक समय लगेगा? (c) यदि हाँ, तो किस पर और क्यों? 
उत्तर:
नत तल पर लुढ़कते गोले का त्वरण 
\(a=\frac{\mathrm{g} \sin \theta}{1+\frac{\mathrm{K}^2}{\mathrm{R}^2}}\)
जहाँ 
\(\frac{\mathrm{K}^2}{\mathrm{R}^2}=\frac{2}{5}\)
धरातल पर पहुँचने पर गोले का वेग 
\(v=\sqrt{\frac{2 g h}{1+\frac{\mathrm{K}^2}{\mathrm{R}^2}}}\)
(a) ∵ गोले का वेग नत तल की ऊँचाई पर निर्भर करता है। यहाँ पर दोनों नत तलों की ऊँचाई समान है। इस कारण से गोला दोनों नत तलों के आधार पर समान वेग से पहुँचेगा। 
(b) हाँ, गोले को एक तल पर लुढ़कने में दूसरे तल की तुलना में अधिक समय लगेगा। 
(c) त्वरण a α sin θ 
अतः जिस नत तल का आनत कोण 6 कम होगा, उस तल पर गोले का त्वरण a कम होगा तथा उस तल पर लुढ़कने में अधिक समय लगेगा। 

प्रश्न 7.19.
2m त्रिज्या के एक वलय (छल्ले) का भार 100 kg है। यह एक क्षैतिज फर्श पर इस प्रकार लोटनिक गति करता है कि इसके द्रव्यमान केन्द्र की चाल 20 cm/s हो। इसको रोकने के लिए कितना कार्य करना होगा ? 
उत्तर:
दिया गया है
त्रिज्या R = 2 m 
वलय का द्रव्यमान M = 100kg 
v = 20 cm/s = 0.2m/s 
छल्ले की कुल ऊर्जा = 1⁄2Mv² + 21002 
छल्ले का जड़त्व आघूर्ण I = MR ² 
∴ छल्ले की कुल ऊर्जा = 1⁄2Mv² + 2 MR²w² 
मान रखने पर 
लेकिन v = Rω
∴ v₂ = R₂ω² 
छल्ले की कुल ऊर्जा I = 1⁄2Mv² + 1/2Mv² 
= Mv² 
छल्ले को रोकने में किया गया कार्य = छल्ले की कुल ऊर्जा 
W = Mv² 
= 100 × (0.2)² 
= 100 × 0.04 
= 4J 

प्रश्न 7.20. 
ऑक्सीजन अणु का द्रव्यमान 5.30 x 10^-26 kg है तथा इसके केन्द्र से होकर गुजरने वाली और इसके दोनों परमाणुओं को मिलाने वाली रेखा के लम्बवत् अक्ष के परितः जड़त्व आघूर्ण 1.94 ×10^-46 kgm² है। मान लीजिए कि गैस के ऐसे अणु की औसत चाल 500 m/s है और इसके घूर्णन की गतिज ऊर्जा, स्थानान्तरण की गतिज ऊर्जा की दो-तिहाई है। अणु का औसत कोणीय वेग ज्ञात कीजिए। 
उत्तर:
दिया गया है:
ऑक्सीजन के अणु का द्रव्यमान m = 5.30 × 10^-20 kg
ऑक्सीजन अणु का जड़त्व आघूर्ण I = 1.94 x 10^-46 kg m² 
अणु की औसत चाल v = 500m/s 
अणु का औसत कोणीय वेग ω = ? 
घूर्णन की गतिज ऊर्जा KE = 2/3 × (स्थानान्तरण की गतिज ऊर्जा)  
या \(\frac{1}{2} \mathrm{I} \omega^2=\frac{2}{3} \times \frac{1}{2} m \mathrm{v}^2\)
या \(\frac{1}{2} \mathrm{I} \omega^2=\frac{1}{3} m \mathrm{v}^2\)
या \(\omega^2=\frac{\frac{2}{3} m \mathrm{v}^2}{\mathrm{I}}\)
∴ \(\omega=\sqrt{\frac{\frac{2}{3} m \mathrm{v}^2}{\mathrm{I}}}=\sqrt{\frac{2 m \mathrm{v}^2}{3 \mathrm{I}}}\)
मान रखने पर 

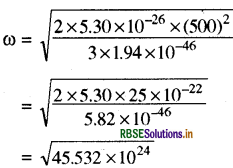
= 6.747 × 10² rad/s. 
= 6.75 x 10² rad/s. 

प्रश्न 7.21. 
एक बेलन 30° कोण बनाते आनत तल पर लुढ़कता हुआ ऊपर चढ़ता है। आनत तल की तली में बेलन के द्रव्यमान केन्द्र की चाल 5m/s है। 
(a) आनत तल पर बेलन कितना ऊपर जायेगा? 
(b) वापस तली तक लौट आने में इसे कितना समय लगेगा? 
उत्तर:
(a) दिया गया है:
θ = 30° 
v = 5m/s. 
माना बेलन समतल के ऊपर h ऊँचाई तक जाता है। 
ऊर्जा संरक्षण के नियम से 
1⁄2mv² + 1/2Iω² = mgh .....,..... (1) 
बेलन के लिए 
I = 1⁄2mR² 
समीकरण (1) में मान रखने पर 
1⁄2mv² + 1/2 (1⁄2mR²)ω² = mgh 
⇒ 1/2mv² + 1/4mv² = mgh
या 
3/4mv² = mgh
3/4 v² = gh
h = 3v²/4g
मान रखने पर 
\(h=\frac{3 \times(5)^2}{4 \times 9.8}\) = 1.91 m
यदि आनत तल पर बेलन s दूरी तय करता है तब हम जानते हैं
sin θ = h/s 
s = h/sinθ
S = 3.826 
s = 3.83m 

(b) माना T = बेलन द्वारा तलहटी पर वापस पहुँचने में लिया गया 
हम जानते हैं \(t=\sqrt{\frac{2 s\left(1+\frac{\mathrm{K}^2}{\mathrm{R}^2}\right)}{g \sin \theta}}\)
बेलन के लिए K²/R² का मान 1/2 होता है। 
∴  \(\begin{aligned} t & =\sqrt{\frac{2 \times 3.83\left(1+\frac{1}{2}\right)}{9.8 \sin 30^{\circ}}}=\sqrt{\frac{2 \times 3.83 \times 3}{2 \times 9.8 \times 0.5}} \\ t & =\sqrt{2.345}=1.53 \end{aligned}\)
T = 2 × t = 2 x 1.53 = 3.06 s 
T = 3s 

 
अभ्यास के 'अतिरिक्त प्रश्न:

प्रश्न 7.22. 
जैसा चित्र में दिखाया गया है, एक खड़ी होने वाली सीढ़ी के दो पक्षों BA और CA की लम्बाई 1.6m है और इनको A पर कब्जा लगा कर जोड़ा गया है। इन्हें ठीक बीच में, 0.5m लम्बी रस्सी DE द्वारा बाँधा गया है। सीढ़ी BA के अनुदिश B से 1.2m की दूरी पर स्थित बिन्दु F से 40 kg का एक भार लटकाया गया है। यह मानते हुए कि फर्श घर्षण रहित है और सीढ़ी का भार उपेक्षणीय है, रस्सी में तनाव और सीढ़ी पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए। (g = 9.8 m/s^-1 लीजिए) 
(संकेत-सीढ़ी के दोनों ओर के संतुलन पर अलग-अलग विचार कीजिए) 

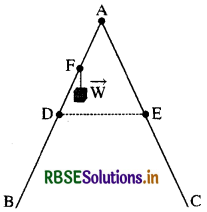
उत्तर:
दिया गया है:
AB = AC = 1.6m 
DE = 0.5m 
D तथा E मध्य बिन्दु हैं। 
∴ AD = DB = AE = EC 
= 1.6/2 = 0.8
BF = 1.2m 
AF = 0.4m 
T = रस्सी में तनाव = ? 

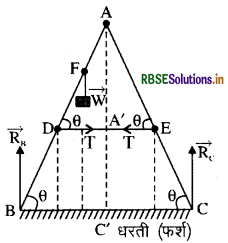
बिन्दु B तथा C पर फर्श द्वारा आयतित बल 
= RB, Rc = ? 
W = 40 kg भार 
= 40 × 9.8 N = 392 N 
माना 
∠ADE = ∠AED = 6 
= ∠ABC = ∠ACB 
यहाँ पर A, DE भुजा का मध्य बिन्दु है। 
∴ DA' = 0.5/2  = 25m 
DF' = 0.125 m 
चित्र से यह स्पष्ट है कि 
RB + Rc = W = 39.2 N ............. (1)
विभिन्न बलों के आघूर्ण A के परितः लेने पर 
RB = BC = W X DF + T × AA' 
(AB सीढ़ी के लिए) 
या 
RB X AB cosθ = T x 0.8 sinθ 
अब ∆DFF' में 
\(\cos \theta=\frac{\mathrm{DF}^{\prime}}{\mathrm{DF}}=\frac{0.125}{0.4}\)
0.3125 = cos 71.8° 
θ  = 71.8° 
sin 71.8° = 0.9500 
tan 71.8° = 3.0415 
समीकरण (2) व (4) से 
RB x 1.6 x 0.3125 = 392 x 0.125 + T x 0.8 x 0.9500
या  
0.5RB = 49 +0.76 T ......... (5)
या 
इसी प्रकार 
Rc × 1.6 x 0.3125 = T × 0.8 x 0.9500 
0.5 Rc = 0.76 T .................. (6)
समीकरण (5) तथा (6) से 
0.5 RB = 49 + 0.5 Rc 
या 
1⁄2 (RB - Rc ) = 49 
RB - Rc = 98 ................(7)
समीकरण (1) तथा (7) को जोड़ने पर 
2RB = 392 + 98 = 490 
RB = 420 = 245N उत्तर 
∴Rc = RB - 98 
Rc = 245 - 98 = 147 उत्तरं .......................... (8) 
समीकरण (6) तथा (8) से 
0.5 x 147 = 0.76 T 
या 
\(\mathrm{T}=\frac{0.5 \times 147}{0.76}\)
T = 96.7 N = 97 N 

प्रश्न 7.23. 
कोई व्यक्ति एक घूमते हुए प्लेटफॉर्म पर खड़ा है उसने अपनी दोनों बाँहें फैला रखी हैं और उनमें से प्रत्येक में 5 kg भा पकड़ रखा है। प्लेटफॉर्म की कोणीय चाल 30 rev/min है। फिर व व्यक्ति बाँहों को अपने शरीर के पास ले आता है जिससे घूर्णन अक्ष प्रत्येक भार की दूरी 90 cm से बदल कर 20 cm हो जाती है प्लेटफॉर्म सहित व्यक्ति के जड़त्व आघूर्ण का मान 7.6 kg ² ले सक हैं। 
(a) उसका नया कोणीय वेग क्या है? (घर्षण की उपेक्षा कीजिए (b) क्या इस प्रक्रिया में गतिज ऊर्जा संरक्षित होती है? यदि नही तो इसमें परिवर्तन का स्रोत क्या है? 
उत्तर:
(a) दिया गया है:
प्रत्येक हाथ का द्रव्यमान = 5 kg 
R₁ = 90 cm = 0.9m 
R₂ = 20 cm = 0.20m 
Io = व्यक्ति तथा प्लेटफॉर्म का जड़त्व आघूर्ण 
= 7.6 kgm² 
यदि R₁ तथा R₂ स्थितियों में जड़त्व आघूर्ण क्रमशः I₁ तथा I₂ है। 
तब सूत्र I = MR² सम्बन्ध का उपयोग करने पर 
I₁ = 2M × R₁2 
= 2 × 5 × (0.9)² = 8.1 kgm² 
I₂1 = 2 M × R₂² 
= 2 × 5 × (0.2) ² 
= 0.4 kg m² 
यदि निकाय के जड़त्व आघूर्ण अर्थात् 
(व्यक्ति + भार + प्लेटफॉर्म) के R₁ तथा R₂ दूरी क्रमशः I₁ तथा I₂ 
I₁ = I₁ + Io 
= 8.1 + 7.6 = 15.7 kg m² 
I₂ = I₂ + I₀ 
= 0.4 + 7.6 = 8.0kgm² 
प्लेटफॉर्म की कोणीय चाल = 30 rev / min 
= 30/60 rev/sec = 1/2 rev/sec
∴ आवृत्ति 
f = 1⁄2 rev/sec. 
∴ कोणीय चाल ω = 2πf 
= 2π x 1/2 =n radian/sec. 
माना R₂ स्थिति में नई कोणीय चाल ω² है। 
∴ संवेग संरक्षण के नियम के अनुसार 
Iω₁ = Iω₂
या 
15.7 × π = 8 × ω₂
या 
ω = 15.7π/8 
= 1.9625 n radian/sec. 
∴ कोणीय आवृत्ति f2 = imm
\(\begin{aligned} & =\frac{1.9625}{2} \mathrm{rev} / \mathrm{sec} \\ & =\frac{1.9625}{2} \times 60 \mathrm{rev} / \mathrm{min} . \end{aligned}\)
= 30 × 1.9625 = 58.88 rev/min. 
= 58.88 rpm 

(b) नहीं, इस प्रक्रिया में गतिज ऊर्जा संरक्षित नहीं रहती है। जैसे-जैसे जड़त्व आघूर्ण का मान कम होता है, तभी घूर्णन गतिज ऊर्जा का मान बढ़ता जाता है। यह परिवर्तन व्यक्ति के द्वारा अपनी बाँहों को अपने शरीर के पास लाने में किये गये कार्य के कारण होता है। 
जैसे नीचे स्पष्ट किया गया है:
I₁ω₁ = I₂ω₂
∴ I₁²ω₁² = I₂²ω₂²
या 
\(\frac{I_1}{I_2}=\frac{\frac{1}{2} I_2 \omega_2^2}{\frac{1}{2} I_1 \omega_1^2}\)
यहाँ पर 
I₁ > I₂ 
या I₁/I₂ > 1
अतः 
1/2I₂ω₂² > 1/2 I₁ω₁²
इति सिद्धम् 
इस प्रकार घूर्णन गतिज ऊर्जा, I के कम होने से बढ़ जाती है अर्थात् इस प्रक्रिया में गतिज ऊर्जा संरक्षित नहीं रहती है। गतिज ऊर्जा में यह परिवर्तन व्यक्ति द्वारा हाथों को समीप लाने में किये गये कार्य के कारण है। 

प्रश्न 7.24. 
10g द्रव्यमान और 500 m/s चाल वाली बन्दूक की गोली एक दरवाजे के ठीक केन्द्र में टकराकर उसमें अंतःस्थापित हो जाती है। दरवाजा 1.0m चौड़ा है और इसका द्रव्यमान 12 kg है। इसके एक सिरे पर कब्जे लगे हैं और यह इनसे गुजरती एक ऊर्ध्वाधर अक्ष के परितः लगभग बिना घर्षण के घूम सकता है। गोली के दरवाजे में अंतःस्थापन के ठीक बाद इसका कोणीय वेग ज्ञात कीजिए।
(संकेत- एक सिरे से गुजरती ऊर्ध्वाधर अक्ष के परितः दरवाजे का जड़त्व आघूर्ण ML 2/3 है)
उत्तर:
दिया गया है:
गोली का द्रव्यमान (m1) = 10g = 10 × 10³ kg 
गोली का वेग (v) = 500 m/s
दरवाजे की चौड़ाई (L) = 1.0m
दरवाजे का द्रव्यमान (M) = 12 kg 
कोणीय चाल ω = ?
गोली द्वारा दरवाजे को दिया गया कोणीय संवेग
= MV x (1/2)
∵ दरवाजे की चौड़ाई = 1m है।
और गोली उसके मध्य में लगी है।
= 10 × 10^-3 × 500 × 2
= 5 x 500 × 10³
= 2.5 kg m/sec.
जैसे कि दिया गया है-एक सिरे से गुजरती ऊर्ध्वाधर अक्ष के परितः
दरवाजे का जड़त्व आघूर्ण
\(I=\frac{\mathrm{MI}^2}{3}=\frac{12 \times(1)^2}{3}=4\)
1 = 4kgm²
कोणीय संवेग संरक्षण नियम से गोली का प्रारम्भिक कोणीय संवेग = दरवाजे का अन्तिम कोणीय संवेग
2.5 = Iω
2.5 = 4ω
ω = 2.5/4
= 0.625 rad/sec. 

प्रश्न 7.25. 
दो चक्रिकाएँ जिनके अपने-अपने अक्षों (चक्रिका के अभिलंबवत् तथा चक्रिका के केंद्र से गुजरने वाले) के परितः जड़त्व आघूर्ण I₁ तथा I₂ हैं ω₁ और जो  तथा ω₂ कोणीय चालों से घूर्णन कर रही हैं, को उनके घूर्णन अक्ष संपाती करके आमने-सामने लाया जाता है। (a) इस दो चक्रिका निकाय की कोणीय चाल क्या है? (b) यह दर्शाइए कि इस संयोजित निकाय की गतिज ऊर्जा दोनों चक्रिकाओं की आरंभिक गतिज ऊर्जाओं के योग से कम है। ऊर्जा में हुई इस हानि की आप कैसे व्याख्या करेंगे? लीजिए।
उत्तर:
दो चक्रिकाओं का जड़त्व आघूर्ण क्रमशः I₁ तथा I₂ है और उनकी कोणीय चाल क्रमशः ω₁ तथा ω₂ है। जब इन्हें सम्पर्क में लाया जाता है तो चक्रिकाओं के निकाय का जड़त्व आघूर्ण I₁ + I₂ होगा। माना संयुक्त निकाय की कोणीय चाल = 0 है।
(a) ∴ दोनों चक्रिकाओं का कुल आरम्भिक कोणीय संवेग 
I₁ = I₁ + I₂
संयुक्त निकाय का कुल अन्तिम कोणीय संवेग
I₂ = (I₁ + I₂) ω
कोणीय संवेग संरक्षण के नियमानुसार
L₂ = L₁
या
(I₁ + I₂)_ω = I₁ω₁ + I₂ω₂
या
\(\omega=\frac{I_1 \omega_1+I_2 \omega_2}{I_1+I_2}\)  ................. (1)

(b) दोनों चक्रिकाओं की आरम्भिक गतिज ऊर्जा
\(\mathrm{L}_1=\frac{1}{2} \mathrm{I}_1 \omega_1^2+\frac{1}{2} \mathrm{I}_2 \omega_2^2\)
संयुक्त निकाय की अन्तिम गतिज ऊर्जा
\(\mathrm{E}_2=\frac{1}{2}\left(\mathrm{I}_1+\mathrm{I}_2\right) \omega^2\)
समीकरण (1) से ω का मान रखने पर

जो कि एक धनात्मक संख्या है। इसलिए > 0 होगा।
या
E₁ - E₂ > 0
E₁ > E₂
या E₂ < E₁
अर्थात् संयुक्त निकाय की कुल ऊर्जा दोनों वस्तुओं की आरम्भिक ऊर्जा के योग से कम है। अतः दोनों चक्रिकाओं को मिलाने से गतिज ऊर्जा की हानि होती है क्योंकि दोनों चक्रिकाओं की सतहों के बीच में घर्षण बल होता है। दोनों चक्रिकाओं को शामिल करने पर ये बल. एक साझी कोणीय चाल उत्पन्न करते हैं। यह किसी प्रकार आंतरिक हास है जिसके कारण कोणीय संवेग परिवर्तित नहीं होता है।

प्रश्न 7.26. 
(a) लम्बवत् अक्षों के प्रमेय की उपपत्ति करें। (संकेत- (x,y ) तल के लम्बवत् मूल बिन्दु से गुजरती अक्ष से किसी बिन्दु x-y की दूरी का वर्ग (x² + y² ) है।
(b) समांतर अक्षों के प्रमेय की उपपत्ति करें। (संकेत-यदि द्रव्यमान केन्द्र को मूल बिन्दु ले लिया जाये तो ∑miri = 0) 
उत्तर:

 दिया गया है:
AB = AC = 1.6m 
DE = 0.5m 
D तथा E मध्य बिन्दु हैं। 
∴ AD = DB = AE = EC 
= 1.6/2 = 0.8
BF = 1.2m 
AF = 0.4m 
T = रस्सी में तनाव = ? 

बिन्दु B तथा C पर फर्श द्वारा आयतित बल 
= RB, Rc = ? 
W = 40 kg भार 
= 40 × 9.8 N = 392 N 
माना 
∠ADE = ∠AED = 6 
= ∠ABC = ∠ACB 
यहाँ पर A, DE भुजा का मध्य बिन्दु है। 
∴ DA' = 0.5/2  = 25m 
DF' = 0.125 m 
चित्र से यह स्पष्ट है कि 
RB + Rc = W = 39.2 N ............. (1)
विभिन्न बलों के आघूर्ण A के परितः लेने पर 
RB = BC = W X DF + T × AA' 
(AB सीढ़ी के लिए) 
या 
RB X AB cosθ = T x 0.8 sinθ 
अब ∆DFF' में 
\(\cos \theta=\frac{\mathrm{DF}^{\prime}}{\mathrm{DF}}=\frac{0.125}{0.4}\)
0.3125 = cos 71.8° 
θ  = 71.8° 
sin 71.8° = 0.9500 
tan 71.8° = 3.0415 
समीकरण (2) व (4) से 
RB x 1.6 x 0.3125 = 392 x 0.125 + T x 0.8 x 0.9500
या  
0.5RB = 49 +0.76 T ......... (5)
या 
इसी प्रकार 
Rc × 1.6 x 0.3125 = T × 0.8 x 0.9500 
0.5 Rc = 0.76 T .................. (6)
समीकरण (5) तथा (6) से 
0.5 RB = 49 + 0.5 Rc 
या 
1⁄2 (RB - Rc ) = 49 
RB - Rc = 98 ................(7)
समीकरण (1) तथा (7) को जोड़ने पर 
2RB = 392 + 98 = 490 
RB = 420 = 245N उत्तर 
∴Rc = RB - 98 
Rc = 245 - 98 = 147 उत्तरं .......................... (8) 
समीकरण (6) तथा (8) से 
0.5 x 147 = 0.76 T 
या 
\(\mathrm{T}=\frac{0.5 \times 147}{0.76}\)
T = 96.7 N = 97 N 

प्रश्न 7.27. 
सूत्र \(\mathrm{v}^2=\frac{2 g h}{\left(1+k^2 / \mathrm{R}^2\right)}\) को गतिकीय दृष्टि (अर्थात् बलों तथा बल आघूणों के विचार) से व्युत्पन्न कीजिए। जहाँ लोटनिक गति करते पिंड (वलय, डिस्क, बेलन या गोला) का आनत तल की तली में वेग है। आनत तल पर / वह ऊँचाई है जहाँ से पिंड गति प्रारंभ करता है। सममित अक्ष के परितः पिंड की घूर्णन त्रिज्या है और R पिंड की त्रिज्या है।
उत्तर:
डिस्क को लुढ़काने के लिए एक बल आघूर्ण की आवश्यकता होती है, जो हमें केवल स्पर्शीय बल के द्वारा ही प्राप्त किया जा सकता है। इस समस्या में केवल घर्षण बल ही स्पर्शीय बल दे सकता है। इसके लिए आवश्यक है:
(a) B बिन्दु पर घर्षण बल वेग के विरुद्ध है इसलिए संपर्क बिन्दु पर घर्षण बल उसी दिशा में है जिसमें तीर दिखाया गया है। घर्षण बल आघूर्ण की दिशा इस प्रकार है कि यह कोणीय गति का विरोध करता है। क्योंकि CO अन्दर की ओर कागज के तल अविलम्ब है, घर्षण बल आघूर्ण की दिशा कागज के अविलम्ब उसमें से बाहर की ओर होगी।
(b) घर्षण बल संपर्क बिन्दु B के वेग को घटा देता है। जब यह वेग शून्य होता है तो डिस्क की लोटनी गति आदर्श सुनिश्चित हो जाती है। एक बार ऐसा हो जाने पर घर्षण बल शून्य हो जाता है।

प्रश्न 7.28. 
अपने अक्ष पर (D) कोणीय चाल से घूर्णन करने वाली किसी चक्रिका को धीरे से (स्थानान्तरीय धक्का दिए बिना) किसी पूर्णतः घर्षणरहित मेज पर रखा जाता है। चक्रिका की त्रिज्या R है। चित्र में दर्शाई चक्रिका के बिंदुओं A, B तथा C पर रैखिक वेग क्या है ? क्या यह चक्रिका चित्र में दर्शाई दिशा में लोटनिक गति करेगी?

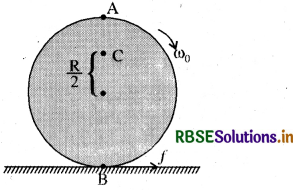
उत्तर:
हमें ज्ञात है:
v = Rω
∴ बिन्दु A का रैखिक वेग VA = Rω₀ तीर की दिशा में
B बिन्दु के लिए VB = Rω₀ (तीर की विपरीत दिशा में)
यदि चक्रिका का केन्द्र निदेश तंत्र के केन्द्र पर है तो B का प्रासंगिक निर्देश - R है।
बिन्दु C के लिए Vc = ( R/22 )ω₀ तीर की दिशा में
अतः चक्रिका निर्दिष्ट दिशा में चक्रण नहीं करेगी। इसका मुख्य कारण यह है कि चक्रिका को घर्षण रहित मेज के ऊपर रख दिया जाये तो घर्षण की अनुपस्थिति में कोई पिण्ड लोटनिक गति नहीं कर सकता है। 

प्रश्न 7.29. 
स्पष्ट कीजिए कि पिछले प्रश्न में दिए चित्र में अंकित दिशा में चक्रिका की लोटनिक गति के लिए घर्षण होना आवश्यक क्यों है?
(a) B पर घर्षण बल की दिशा तथा परिशुद्ध लुढ़कन आरंभ होने से पूर्व घर्षणी बल आघूर्ण की दिशा क्या है ?
(b) परिशुद्ध लोटनिक गति आरंभ होने के पश्चात् घर्षण बल क्या है?
उत्तर:
डिस्क को लुढ़काने के लिए एक बल आघूर्ण की आवश्यकता होती है, जो हमें केवल स्पर्शीय बल के द्वारा ही प्राप्त किया जा सकता है। इस समस्या में केवल घर्षण बल ही स्पर्शीय बल दे सकता है। इसके लिए आवश्यक है:
(a) B बिन्दु पर घर्षण बल वेग के विरुद्ध है इसलिए संपर्क बिन्दु पर घर्षण बल उसी दिशा में है जिसमें तीर दिखाया गया है। घर्षण बल आघूर्ण की दिशा इस प्रकार है कि यह कोणीय गति का विरोध करता है। क्योंकि CO अन्दर की ओर कागज के तल अविलम्ब है, घर्षण बल आघूर्ण की दिशा कागज के अविलम्ब उसमें से बाहर की ओर होगी।
(b) घर्षण बल संपर्क बिन्दु B के वेग को घटा देता है। जब यह वेग शून्य होता है तो डिस्क की लोटनी गति आदर्श सुनिश्चित हो जाती है। एक बार ऐसा हो जाने पर घर्षण बल शून्य हो जाता है।

प्रश्न 7.30.
10 cm त्रिज्या की कोई ठोस चक्रिका तथा इतनी ही त्रिज्या का कोई छल्ला किसी क्षैतिज मेज पर एक ही क्षण 10 x rad st की कोणीय चाल से रखे जाते हैं। इनमें से कौन पहले लोटनिक गति आरंभ कर देगा। गतिज घर्षण गुणांक μk = 0.21
उत्तर:
दिया गया है:
द्रव्यमान केन्द्र का आरम्भिक वेग शून्य है।
∴ u = 0
घर्षण बल के कारण द्रव्यमान केन्द्र त्वरित होता है।
uk x mg = ma 
V = u + at
∴ a = μkg....... (1)
∴ v = 0 + Hagt
v = μkgt ...... (2)
 माना घर्षण बल आघूर्ण आरम्भिक कोणीय वेग ch में मंदन उत्पन्न करता है।
μkmg x R = - Iα
\(\alpha=-\frac{\mu_k m g \mathrm{R}}{I}\) .......(3)
ω = ω0 + αt 
∴ \(\omega=\omega_0-\frac{\mu_{\mathrm{k}} \mathrm{mgRt}}{I}\) ................ (4)
जब लुढ़कना प्रारम्भ करता है तब v = Ro
समीकरण (2) तथा (4) से
\(\mu_k \mathrm{gt}=\mathrm{R} \omega_0-\frac{\mu_{\mathrm{k}} \mathrm{mgR}^2 \mathrm{t}}{\mathrm{I}}\) ................ (5)
छल्ले के लिए
I= mR²
\(\omega_0=\frac{\mu_k g t+\mu_k g t}{R}=\frac{2 \mu_k g t}{R}\)
या
\(t=\frac{\omega_0 R}{2 \mu_k g}\) ................(6)
ठोस चक्रिका के लिए
I = 1⁄2 mR²
समीकरण (5) से
μkgt = Rω0 - 2μkgt
3μkgt = Rω0

∴ \(t=\frac{\omega_0 R}{3 \mu_k g}\) ..................(7)
समीकरण (6) तथा (7) में मान रखकर समय ज्ञात करने पर
दिया गया है:
R = 0.1m
ω0 = 10 n radian/sec.
μk = 0.2
8 = 9.8m/s²
छल्ले का समय
\(\begin{aligned} t & =\frac{\omega_0 \mathrm{R}}{2 \mu_k g} \\ & =\frac{10 \pi \times 0.1}{2 \times 0.2 \times 9.8}=\frac{10 \times 3.14 \times 0.1}{2 \times 0.2 \times 9.8} \end{aligned}\)
t = 0.8 se ..............(8)
ठोस चक्रिका का समय
\(\begin{aligned} t & =\frac{\omega_0 \mathrm{R}}{3 \mu_k g} \\ & =\frac{10 \pi \times 0.1}{3 \times 0.2 \times 9.8}=\frac{10 \times 3.14 \times 0.1}{3 \times 0.2 \times 9.8} \end{aligned}\)
t = 0.53 sec.
समीकरण (8) तथा (9) से स्पष्ट है कि ठोस चक्रिका पहले लुढ़कना शुरू कर देगी।

प्रश्न 7.31. 
10 kg द्रव्यमान तथा 15 cm त्रिज्या का कोई सिलिंडर किसी 30° झुकाव के समतल पर परिशुद्धतः लोटनिक गति कर रहा है। स्थैतिक घर्षण गुणांक A = 0.25 है।
(a) सिलिंडर पर कितना घर्षण बल कार्यरत है?
(b) लोटन की अवधि में घर्षण के विरुद्ध कितना कार्य किया जाता
(c) यदि समतल के झुकाव 6 में वृद्धि कर दी जाए तो 6 के किस
मान पर सिलिंडर परिशुद्धतः लोटनिक गति करने की बजाय फिसलना आरंभ कर देगा? 
उत्तर:
दिया गया है:
द्रव्यमान (m) = 10 kg
त्रिज्या R = 15 cm = 15/100m = 0.15m
θ = 30°,  μs = 0.25
हम जानते हैं नत तल पर लोटनी गति करती हुई वस्तु का त्वरण निम्न सूत्र से ज्ञात करते हैं-
\(a=\frac{g \sin \theta}{\left(1+\frac{\mathrm{K}^2}{\mathrm{R}^2}\right)}\)
यहाँ पर वस्तु बेलन है इसलिए K²/R² का मान 1/2 होता है।
\(a=\frac{g \sin \theta}{\left(1+\frac{1}{2}\right)}=\frac{2}{3} g \sin \theta\) ................... (1)
a = 2/3 × 9.8 × sin30° = 98/3m/s?
(a) बेलन पर कार्यरत घर्षण बल
F = mg sinθ - ma 
F = m (gsinθ - a )
\(\begin{aligned} & =10\left(9.8 \sin 30^{\circ}-\frac{9.8}{3}\right) \\ & =10\left(9.8 \times \frac{1}{2}-\frac{9.8}{3}\right)=\frac{1}{6} \times 10 \times 9.8 \end{aligned}\)
= 16.333N 

(b) क्योंकि घर्षण बल बेलन के विस्थापन के लम्बवत् कार्य करता है अतः लुढ़कने में घर्षण के विरुद्ध किया गया कार्य शून्य है।

(c) बेलन पर कार्यरत घर्षण बल
F = mg sinθ - ma
= m (g sinθ - a)
समी (1) से
a = 2/3sinθ
F = m(gsinθ - 2/3gsinθ)
= 1/3mgsinθ
फिसलने के लिये प्रतिबन्ध
\(\begin{aligned} \frac{\mathrm{F}}{\mathrm{R}} & \leq \mu_{\mathrm{s}} \\ \frac{\frac{1}{3} m g \sin \theta}{m g \cos \theta} & \leq \mu_{\mathrm{s}} \\ \frac{1}{3} \tan \theta & \leq \mu_{\mathrm{s}} \end{aligned}\)
नत तल का वह कोण जिस पर सिलिंडर बिना लुढ़के फिसलता है, वह कोण 6 है। तब
tanθ = 3μs
=> tan θ = 3 x 0.25 = 0.75
θ = tan^-1 (0.75)

प्रश्न 7.32. 
नीचे दिए गए प्रत्येक प्रकथन को ध्यानपूर्वक पढ़िए तथा कारण सहित उत्तर दीजिए कि इनमें से कौन-सा सत्य है और कौन-सा असत्य है।
(a) लोटनिक गति करते समय घर्षण बल उसी दिशा में कार्यरत होता है जिस दिशा में पिण्ड का द्रव्यमान केंद्र गति करता है। 
(b) लोटनिक गति करते समय संपर्क बिंदु की तात्क्षणिक चाल शून्य होती है।
(c) लोटनिक गति करते समय संपर्क बिंदु का तात्क्षणिक त्वरण शून्य होता है।
(d) परिशुद्ध लोटनिक गति के लिए घर्षण के विरुद्ध किया गया म कार्यशून्य होता है।
(e) किसी पूर्णत: घर्षणरहित आनत समतल पर नीचे की ओर गति करते पहिए की गति फिसलन गति (लोटनिक गति नहीं होगी ।
उत्तर:
(a ) 'सत्य, जब पिण्ड लोटनिक गति करता है तब घर्षण बल द्रव्यमान केन्द्र की गति की दिशा में होता है क्योंकि धरातल के साथ संपर्क बिन्दु की गति द्रव्यमान केन्द्र की गति के विपरीत दिशा में होती है।
(b) यह सत्य है एक लोटनिक पिण्ड को पृथ्वी से उसके संपर्क बिन्दु में से गुजरने वाले अक्ष के परितः घूमता हुआ मान सकते हैं और परिणामस्वरूप तात्क्षणिक चाल शून्य है।
(c) यह असत्य है। चूँकि घूर्णन करती हुई वस्तु का तात्क्षणिक त्वरण शून्य नहीं होता है।
(d) यह सत्य है। चूँकि जैसे ही पिण्ड पूर्णरूप से लुढ़कना शुरू करता है, तब उसका घर्षण बल शून्य हो जाता है। अतः घर्षण बल के विरुद्ध किया गया कार्य शून्य होगा।
(e) यह सत्य है। पिण्ड एवं उस पर लगने वाले घर्षण बल के कारण लोटनिक गति करता है। यदि चक्र एक पूर्णतः घर्षण रहित आनत तल पर नीचे की ओर चल रहा है तो यह केवल अपने भार के प्रभाव में है। चूँकि भार इसके द्रव्यमान केन्द्र से ऊर्ध्वाधर में कार्य करता है। चक्र चक्रण नहीं करेगा। यह फिसलता रहेगा अर्थात् घर्षण की अनुपस्थिति में यह लोटनिक गति नहीं कर सकता और पिण्ड केवल स्थानान्तरीय बल के कारण फिसल सकता है।

प्रश्न 7.33. 
कणों के किसी निकाय की गति को इसके द्रव्यमान केन्द्र की गति और द्रव्यमान केन्द्र के परितः गति में अलग-अलग करके विचार करना। दर्शाइये कि:
(a) p = \(\overrightarrow{p_i^{\prime}}+m_i \vec{v}\), जहाँ pi (m: द्रव्यमान वाले) i-वें कण का संवेग है, और \(\overrightarrow{p_i^{\prime}}=m_i \overrightarrow{v_i^{\prime}}\)। ध्यान दें कि द्रव्यमान केन्द्र के सापेक्ष - वें कण का वेग है। द्रव्यमान केन्द्र की परिभाषा का उपयोग करके यह भी सिद्ध कीजिए कि \(\Sigma \overrightarrow{p_i^{\prime}}=0\)

(b) K = K + 1/2MV²
K कणों के निकाय की कुल गतिज ऊर्जा, K' = निकाय की कुल गतिज ऊर्जा जबकि कणों की गतिज ऊर्जा द्रव्यमान केन्द्र के सापेक्ष ली MV²/2 संपूर्ण निकाय के (अर्थात् निकाय के द्रव्यमान केन्द्र के) स्थानान्तरण की गतिज ऊर्जा है। इस परिणाम का उपयोग पाठ्यपुस्तक के अनुच्छेद 7.14 में किया गया है।

(c) \(\overrightarrow{\mathbf{L}}=\overrightarrow{\mathbf{L}}^{\prime}=\mathbf{R} \times \mathbf{M} \overrightarrow{\mathbf{V}}\)
जहाँ \(\overrightarrow{\mathbf{L}}^{\prime}=\mathbf{\Sigma} \overrightarrow{r_i^{\prime}} \times \overrightarrow{p_i^{\prime}}\), द्रव्यमान के परितः निकाय का कोण संवेग है जिसकी गणना में वेग द्रव्यमान केन्द्र के सापेक्ष मापे गये हैं। याद कीजिए \(\overrightarrow{r_i^{\prime}}=\overrightarrow{r_i}-\overrightarrow{\mathbf{R}}\) शेष सभी चिह्न अध्याय में प्रयुक्त विभिन्न राशियों के मानक चिन्ह हैं। ध्यान दें कि ' द्रव्यमान केन्द्र के परितः निकाय का कोणीय संवेग एवं \(M \vec{R} \times \overrightarrow{\mathbf{V}}\)  इसके द्रव्यमान केन्द्र का कोणीय संवेग है।

(d) \(\frac{d \overrightarrow{\mathrm{L}^{\prime}}}{d t}=\sum \overrightarrow{r_i^{\prime}} \times \frac{\overrightarrow{d p^{\prime}}}{d t}\)
यह भी दर्शाइये कि \(\frac{d \overrightarrow{\mathrm{L}^{\prime}}}{d t}=\overrightarrow{\tau_{e x t}}\)
(जहाँ \(\overrightarrow{\tau_{e x t}^{\prime}}\) द्रव्यमान केन्द्र के परितः निकाय पर लगने वाले सभी बाह्य बल आघूर्ण हैं।)
[संकेत- द्रव्यमान केन्द्र की परिभाषा एवं न्यूटन के गति के तृतीय नियम का उपयोग कीजिए। यह मान लीजिए कि किन्हीं दो कणों के बीच के आन्तरिक बल उनको मिलाने वाली रेखा के अनुदिश कार्य करते हैं।]
उत्तर:
(a) i गतिशील कणों का निकाय लेने पर
ith कण का द्रव्यमान = mi
∴ ith 'कण का वेग = \(\overrightarrow{\mathrm{v}}_i\)
द्रव्यमान केन्द्र का वेग = V
ith कण का वेग द्रव्यमान केन्द्र के निकाय के सापेक्ष
\(\overrightarrow{\mathrm{V}}_i^{\prime}=\overrightarrow{\mathrm{V}}_i-\overrightarrow{\mathrm{V}}\) ............. (1)
दोनों तरफ m का गुणा समीकरण (1) में करने पर
\(\begin{aligned} m_i \overrightarrow{\mathrm{V}}_i^{\prime} & =m_i \overrightarrow{\mathrm{V}}_i-m_i \overrightarrow{\mathrm{V}} \\ \overrightarrow{\mathrm{P}_i^{\prime}} & =\overrightarrow{\mathrm{P}}_i-m_i \overrightarrow{\mathrm{V}} \end{aligned}\)
जहाँ पर \(\overrightarrow{\mathrm{P}_i^{\prime}}=m_i \overrightarrow{\mathrm{V}_i^{\prime}}\)
= ith कण का संवेग द्रव्यमान केन्द्र के निकाय के सापेक्ष
हम जानते हैं-
\(\overrightarrow{\mathrm{P}_i^{\prime}}=m_i \overrightarrow{\mathrm{V}}_i^{\prime}\)
सभी कणों का संवेगों का योग द्रव्यमान केन्द्र के निकाय के सापेक्ष करने पर

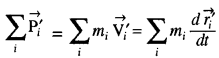
\(\frac{\overrightarrow{r_i^{\prime}}}{\overrightarrow{\mathrm{V}_i^{\prime}}}=i\) कणों का स्थिति सदिश द्रव्यमान केन्द्र के सापेक्ष
\(\overrightarrow{\mathrm{V}}_i^{\prime}=\frac{d \vec{r}_i^{\prime}}{d t}\)
द्रव्यमान केन्द्र की परिभाषा के अनुसार

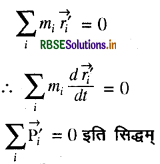
(b) किसी भी निकाय की गतिज ऊर्जा के दो अंग होते हैं। स्थानान्तरीय गतिज ऊर्जा (K) तथा घूर्णीय गतिज ऊर्जा (K1 ) अर्थात् द्रव्यमान केन्द्र की गति की गतिज ऊर्जा (1/2 mV²) और कणों के निकाय
के द्रव्यमान केन्द्र के परितः घूर्णीय गतिज ऊर्जा K' होती है। इस प्रकार निकाय की कुल गतिज ऊर्जा
K = 1⁄2mV² + 1/2Iw²
K = 1/2mV² + K1

(c) ith कणों का स्थिति सदिश मूल बिन्दु के सापेक्ष = \(\vec{r}_i\)
ith कणों का स्थिति सदिश द्रव्यमान केन्द्र के सापेक्ष = \(\vec{r}_i\)
द्रव्यमान केन्द्र का स्थिति सदिश मूल बिन्दु के सापेक्ष = \(\overrightarrow{\mathrm{R}}\)
दिया गया है
\(\begin{aligned} & \overrightarrow{r_i^{\prime}}=\overrightarrow{r_i}-\vec{R} \\ & \vec{r}_i=\overrightarrow{r_i^{\prime}}+\mathrm{R} \end{aligned}\)
प्रथम खण्ड (a) से हम जानते हैं-
\(\overrightarrow{\mathrm{P}}_i=\overrightarrow{\mathrm{P}}_i^{\prime}+m_i \overrightarrow{\mathrm{V}}\)
दोनों तरफ का सदिश गुणनफल करने पर 

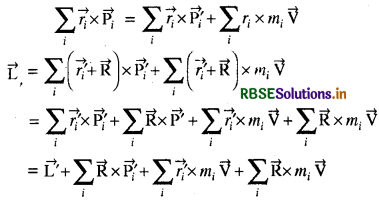
जहाँ पर \(\overrightarrow{\mathrm{R}} \times \sum_i \overrightarrow{\mathrm{P}}_i^{\prime}=0\) और
\(\sum_i \overrightarrow{r_i^{\prime}} \times \mathrm{M} \overrightarrow{\mathrm{V}}=0\)
∴ \(\overrightarrow{\mathrm{L}}=\overrightarrow{\mathrm{L}^{\prime}}+\mathrm{R} \times \mathrm{M} \overrightarrow{\mathrm{V}}\)

(d) कणों के एक निकाय को आकाश में लीजिए। उन कणों पर एक बल आघूर्ण लग रहा है। माना किसी कण के लिए x y व z अक्ष की अनुदिश सदिश के घटक क्रमशः L_x, L_y, L_z रैखिक संवेग के घटक P_x, P_y, तथा P_z हैं।
∴ L_x = YP_z - ZP_y
L_y = ZP_x - XP_z
L_z = X P_y - Y Px
∴ \(\begin{aligned} \overrightarrow{\mathrm{L}}_i & =\mathrm{L}_x \hat{i}+\mathrm{L}_y \hat{j}+\mathrm{L}_z \hat{k} \\ & =\left(\mathrm{Y} \mathrm{P}_z-\mathrm{Z} \mathrm{P}_y\right) \hat{\mathrm{i}}+\left(\mathrm{ZP}_x-\mathrm{XP} \mathrm{P}_z\right) \hat{\mathrm{j}}+ \\ & \quad\left(\mathrm{XP}_y-\mathrm{Y} \mathrm{P}_x\right) \hat{\mathrm{j}} \end{aligned}\)

∴ किसी कण के संवेग परिवर्तन की दर को

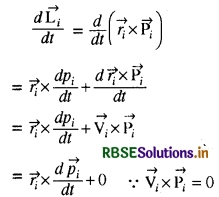
यदि निकाय का कुल कोणीय संवेग \(\overrightarrow{\mathrm{L}^{\prime}}\) है, तब

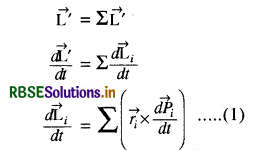
इति सिद्धम्
हम यह जानते हैं कि निकाय पर कार्यरत कुल बाह्य बल

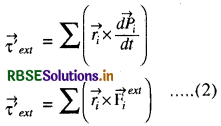
∵ बाह्य बल सदैव युग्म में होते हैं तथा एक-दूसरे को निरस्त कर देते हैं। 
समीकरण (1) तथा (2) से
\(\frac{\overrightarrow{\mathrm{L}}_i}{d t}={\overrightarrow{\tau^{\prime}}}_{\text {ext }}\)
इति सिद्धम्