RBSE Solutions for Class 11 Physics Chapter 6 कार्य, ऊर्जा और शक्ति

Rajasthan Board RBSE Solutions for Class 11 Physics Chapter 6 कार्य, ऊर्जा और शक्ति Textbook Exercise Questions and Answers.

RBSE Class 11 Physics Solutions Chapter 6 कार्य, ऊर्जा और शक्ति

RBSE Class 11 Physics कार्य, ऊर्जा और शक्ति Textbook Questions and Answers

प्रश्न 6.1. 
किसी वस्तु पर किसी बल द्वारा किए गए कार्य का चिन्ह समझना महत्त्वपूर्ण है। सावधानीपूर्वक बताइए कि निम्नलिखित 
राशियाँ धनात्मक हैं या ऋणात्मक:
(a) किसी व्यक्ति द्वारा किसी कुएँ में से रस्सी से बँधी बाल्टी को रस्सी द्वारा बाहर निकालने में किया गया कार्य। 
(b) उपर्युक्त स्थिति में गुरुत्वीय बल द्वारा किया गया कार्य। 
(c) किसी आनत तल पर फिसलती हुई किसी वस्तु पर घर्षण द्वारा किया गया कार्य। 
(d) किसी खुरदरे क्षैतिज तल पर एकसमान वेग से गतिमान किसी वस्तु पर लगाए गए बल द्वारा किया गया कार्य। 
(e) किसी दोलायमान लोलक को विरामावस्था में लाने के लिए वायु के प्रतिरोधी बल द्वारा किया गया कार्य। 
उत्तर:
हम जानते हैं कि किया गया कार्य 
W = \(\overrightarrow{\mathrm{F}} \cdot \vec{S}\) = FScosθ 
जहाँ θ, F (बल) तथा विस्थापन ड में छोटा कोण है। 
(a) किसी व्यक्ति द्वारा किसी कुएँ में से रस्सी से बँधी बाल्टी को रस्सी द्वारा बाहर निकालने पर किया गया कार्य धनात्मक होगा। चूँकि बाल्टी को ऊर्ध्वाधर ऊपर की ओर उठाने के लिए उसके भार के बराबर बल की आवश्यकता है तथा बाल्टी भी बल की दिशा के अनुदिश चलती है। 
इस प्रकार 
θ = 0° 
∴ W = FS cos () = FS ' x 1 
W = FS जो कि धनात्मक है। 

(b) उपर्युक्त स्थिति में गुरुत्वीय बल द्वारा किया गया कार्य ऋणात्मक होगा। चूँकि बाल्टी ऊर्ध्वाधर अधोमुखी कार्य करने वाले गुरुत्वाकर्षण बल के विपरीत चलती है। 
अतः 
∴ θ = 180° 
∴ cos 180° = - 1 
W = FS × (- 1) = - FS 
अतः यहाँ पर W ऋणात्मक है। 

(c) एक आनत तल पर नीचे की ओर फिसलने वाले पिण्ड पर घर्षण बल द्वारा किया गया कार्य ऋणात्मक है। चूँकि घर्षण बल, गति का विरोध 
करता है, अतः 
∴ θ = 180° 
∴ W = FS cos 180
= FS (-1)
W = - FS

(d) किसी 'खुरदरे क्षैतिज तल पर एकसमान वेग से गतिमान किसी वस्तु पर लगाये गये बल द्वारा किया गया कार्य धनात्मक होगा। चूँकि θ = शून्य है। 
∴ W = FS cos θ° = FS x 1
W = FS

(e) यह कार्य ऋणात्मक है। चूँकि वायु का प्रतिरोध बल लोलक के दोलन की दिशा के विपरीत कार्य करता है जो कि विस्थापन के विपरीत है। अर्थात् θ = 180° 

प्रश्न 6.2.
2 kg द्रव्यमान की कोई वस्तु जो आरंभ में विरामावस्था में है, 7N के किसी क्षैतिज बल के प्रभाव से एक मेज पर गति करती है। मेज का गतिज घर्षण गुणांक 0.1 है। निम्नलिखित का परिकलन कीजिए और अपने परिणामों की व्याख्या कीजिए:
(a) लगाए गए बल द्वारा 10s में किया गया कार्य।
(b ) घर्षण द्वारा 10s में किया गया कार्य। 
(c) वस्तु पर कुल बल द्वारा 10s में किया गया कार्य। 
(d) वस्तु की गतिज ऊर्जा में 10s में परिवर्तन। 
उत्तर:
दिया गया है:
वस्तु का द्रव्यमान (m) = 2 kg 
वस्तु विरामावस्था में है। 
∴ प्रारम्भिक वेग u = 0 
गतिज घर्षण गुणांक μK = 0.1 
समय (t) = 10 s 
F = 7N 
घर्षण बल f = μKR 
लेकिन R = mg
घर्षण बल f
घर्षण बल 
∴ नेट बल F = F - f
= 7 - 1.96
= 5.04 N
∴ नेट त्वरण जिससे पिण्ड चल रहा है:

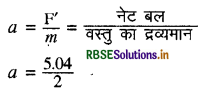
10 सेकण्ड में तय की गई दूरी अर्थात् विस्थापन का मान ज्ञात
s = ut + 1/2 at²
= 0 x 10 + 1/2 x 2.52 x (10)²
= 0 + 1/2 x 2.52 x 100
= 1.26 x100
= 126.00 m
अतः S = 126 m 
∴ विस्थापन (d) = 126m 

(a) आरोपित बल द्वारा किया गया है। 
W1 = FS = 7 x 126 = 882 J 

(b) घर्षण बल द्वारा 10 सेकण्ड में किया गया कार्य
W2 = -f x s 
1.96 × 126 
= - 246.96 J 
= - 247 J 

(c) वस्तु पर कुल बल द्वारा 10 सेकण्ड में किया गया कार्य 
W3 = F× S 
= 5.04 x 126 

(d) कार्य - ऊर्जा प्रमेय से 
गतिज ऊर्जा में परिवर्तन = किया गया कार्य 
= 635.04 J 

 

प्रश्न 6.3. 
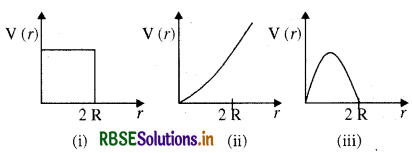
चित्र में कुछ एकविमीय स्थितिज ऊर्जा फलनों के उदाहरण दिए गए हैं। कण की कुल ऊर्जा कोटि-अक्ष पर क्रॉस द्वारा निर्देशित की गई है। प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइए, यदि कोई हैं तो, जिनमें दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता। इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए। कुछ ऐसे भौतिक संदर्भों के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हों। 


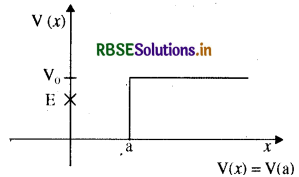
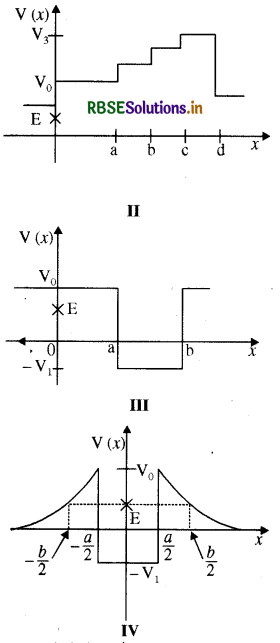
उत्तर:
हम जानते हैं कि पिण्ड की कुल ऊर्जा E = K.E. + PE. 
या 
K.E. = E - P.E = 1⁄2mv² 
 ∵ K. E. कभी भी ऋणात्मक नहीं हो सकती, अतः P.E. का मान सदैव E से कम ही होगा। 
(i) x = a और x = 0 के बीच क्षेत्र में P.E. शून्य है अतः गतिज ऊर्जा (K.E.) धनात्मक है। 
x > a क्षेत्र में P.E. (Vo) का मान E से अधिक है। 
अतः इस क्षेत्र में K. E. ऋणात्मक होगी। इस प्रकार x > a क्षेत्र में कण उपस्थित नहीं हो सकता। 

इस स्थिति में कण में न्यूनतम कुल ऊर्जा शून्य है। 
(ii) x < a और x > b के लिए, P.E. (Vo) > E 
∴ KE. का मान ऋणात्मक होगा। इस कारण से वस्तु x < a और x > b के क्षेत्र में उपस्थित नहीं रह सकती है। क्षेत्र x > a तथाx < b में PE ऋणात्मक है। इसका अर्थ है कि गतिज ऊर्जा का मान धनात्मक है इसीलिए क्षेत्र x > a और x < b में कण पाया जा सकता है। इस स्थिति में जो कुल ऊर्जा कण में हो सकती है, वह V1 है। 

(iii) कण किसी भी क्षेत्र में दिखाई नहीं देगा चूँकि प्रत्येक क्षेत्र में PE. (Vo) > E है।

अतः क्षेत्र - ∞ < x < ∞ में कण उपस्थित नहीं हो सकता है। 
इस स्थिति में कण की न्यूनतम ऊर्जा - V1 हो सकती है 

(iv) इस स्थिति में कण की कुल ऊर्जा PE. उसकी कुल ऊर्जा से अधिक है। 
इसी आधार से क्षेत्र -b/2 < x < -a/2, a/2 < x < b/2 नहीं हो सकता है। 
इस प्रकार तीनों क्षेत्रों में गतिज ऊर्जा ऋणात्मक होगी इस प्रकार कण इन क्षेत्रों में उपस्थित नहीं होगा। 
-b/2 , x < - a/2 तथा a/2 < x < b/2 
इस स्थिति में कण की न्यूनतम कुल ऊर्जा - V1 हो सकती है। 

प्रश्न 6.4. 
रेखीय सरल आवर्त गति कर रहे किसी कण का स्थितिज ऊर्जा फलन V(x) = kx²/2 है, जहाँ k दोलक का बल नियतांक है। k = 0.5 Nm^-1 के लिए V(x) व x के मध्य ग्राफ चित्र में दिखाया गया है। यह दिखाइए कि इस विभव के अंतर्गत गतिमान कुल 1J ऊर्जा वाले कण को अवश्य ही 'वापिस आना' चाहिए जब यह x = + 2m पर पहुँचता है। 

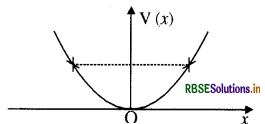
उत्तर:
किसी भी क्षण किसी दोलक की कुल ऊर्जा E का मान उसकी आरम्भिक स्थितिज ऊर्जा (P.E.) तथा उसकी आंशिक गतिज ऊर्जा (K.E.) के योग के बराबर होती है। अतः इसको इस प्रकार से लिखा जा सकता है:
E = KE + PE. 
E = 1⁄2mv² + 21⁄2kx² .....(1) 
समीकरण (1) में m = कण का द्रव्यमान 
V = कण का वेग 
तथा K बल स्थिरांक है, जिसका मान 
k = 0.5 N/m और विस्थापन x है। 
E = 1 जूल ( दिया गया है) 
किसी क्षण कण वापस आता है, तब उसका v = 0 समीकरण (1) में सभी मान रखने पर 
1 जूल  = 1/2 x m x 0 + 1/2 x 0.5 x x²
1 = 0 + 5/20 x²
1 = 1/u x²
x² = 4
अथवा 
\(x=\pm \sqrt{4}=\pm 2 m\)
अतः x = + 2m प्राप्त करते हैं। 

प्रश्न 6.5. 
निम्नलिखित का उत्तर दीजिए:
(a) किसी रॉकेट का बाह्य आवरण उड़ान के दौरान घर्षण के कारण जल जाता है। जलने के लिए आवश्यक ऊष्मीय ऊर्जा किसके व्यय पर प्राप्त की गई - राकेट या वातावरण? 
(b) धूमकेतु सूर्य के चारों ओर बहुत ही दीर्घवृत्तीय कक्षाओं में घूमते हैं। साधारणतया धूमकेतु पर सूर्य का गुरुत्वीय बल धूमकेतु के लंबवत् नहीं होता है। फिर भी धूमकेतु की संपूर्ण कक्षा में गुरुत्वीय बल द्वारा किया गया कार्य शून्य होता है। क्यों? 
(c) पृथ्वी के चारों ओर बहुत ही क्षीण वायुमण्डल में घूमते हुए किसी कृत्रिम उपग्रह की ऊर्जा धीरे-धीरे वायुमण्डलीय प्रतिरोध (चाहे यह कितना ही कम क्यों न हो) के विरुद्ध क्षय के कारण कम होती जाती है फिर भी जैसे-जैसे कृत्रिम उपग्रह पृथ्वी के समीप आता है तो उसकी चाल में लगातार वृद्धि क्यों होती है? 
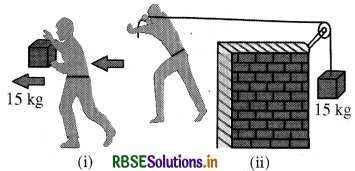
(d) चित्र (i) में एक व्यक्ति अपने हाथों में 15kg का कोई द्रव्यमान लेकर 2m चलता है। चित्र (ii) में वह उतनी ही दूरी अपने पीछे रस्सी को खींचते हुए चलता है। रस्सी घिरनी पर चढ़ी हुई है और उसके दूसरे सिरे पर 15 kg का द्रव्यमान लटका हुआ है। परिकलन कीजिए कि किस स्थिति में किया गया कार्य अधिक है? 

उत्तर:
(a) रॉकेट 
उड़ान में रॉकेट की कुल ऊर्जा उसके द्रव्यमान पर निर्भर करती है। 
∴P.E. + K.E. = mgh + 1/2 mv² 
जब रॉकेट का बाह्य आवरण घर्षण के कारण जल जाता है, तो उसका द्रव्यमान कम हो जाता है। रॉकेट की कुल ऊर्जा घटती है, जो रॉकेट की ऊर्जा घटती है वही ऊर्जा रॉकेट के आवरण को जलाती है। 
(b) ∵ गुरुत्वीय बल संरक्षी बल (Conservating force) होता है जिसके अन्तर्गत बन्द पथ में किया गया कुल कार्य शून्य होता है अतः धूमकेतु की सम्पूर्ण कक्षा में गुरुत्वीय बल द्वारा किया गया कार्य शून्य होता है। 
(c) जैसे-जैसे उपग्रह पृथ्वी के निकट आता जाएगा, उसकी स्थितिज ऊर्जा कम होती जाएगी। ऊर्जा संरक्षण के नियम के अनुसार, स्थितिज तथा गतिज ऊर्जा का योग स्थिर रहना चाहिए इसलिए उपग्रह की गतिज ऊर्जा और उसका वेग बढ़ जाते हैं, लेकिन उपग्रह की कुल ऊर्जा कम होती जाती है । कुछ घर्षण के कारण ऊर्जा में क्षय होने से अर्थात् वायु प्रतिरोध के कारण क्षय होने से। 
(d) चित्र (i) की स्थिति में व्यक्ति 15 kg द्रव्यमान पर ऊर्ध्वाधर ऊपरमुखी बल लगाता है लेकिन वह 2m क्षैतिज दिशा में चलता है। यहाँ पर बल और विस्थापन डे के बीच कोण 90° है। 
अतः किया गया कार्य W = FS cos 90° = 0 
अतः किया गया कार्य W = शून्य है। चित्र (ii) में 15 kg द्रव्यमान पर ऊर्ध्वाधर ऊपरमुखी बल लगाया जाता है। पिण्ड का भार तथा द्रव्यमान भी ऊपर की ओर उठाया जाता है। अतः θ = 0 
∵ W = mgs 
= 0 
= 15 × 9.8 x 2 = 294 जूल 
इस प्रकार से द्वितीय स्थिति में किया गया कार्य अधिक है। 

प्रश्न 6.6. 
सही विकल्प को रेखांकित कीजिए:
(a) जब कोई संरक्षी बल किसी वस्तु पर धनात्मक कार्य करता है तो वस्तु की स्थितिज ऊर्जा बढ़ती है / घटती है / अपरिवर्ती रहती है। 
(b) किसी वस्तु द्वारा घर्षण के विरुद्ध किए गए कार्य का परिणाम हमेशा इसकी गतिज / स्थितिज ऊर्जा में क्षय होता है । 
(c) किसी बहुकण निकाय के कुल संवेग परिवर्तन की दर निकाय के बाह्य बल / आंतरिक बलों के जोड़ के अनुक्रमानुपाती होती है। 
(d) किन्हीं दो पिंडों के अप्रत्यास्थ संघट्ट में वे राशियाँ, जो संघट्ट के बाद नहीं बदलती हैं; निकाय की कुल गतिज ऊर्जा / कुल रेखीय संवेग / कुल ऊर्जा हैं। 
उत्तर:
(a) जब कोई संरक्षी बल किसी वस्तु पर धनात्मक कार्य करता है, तो वस्तु की स्थितिज ऊर्जा कम हो जाती है। चूँकि संरक्षित बल पिण्ड पर धनात्मक कार्य करता है, जब यह बल की दिशा में पिण्ड को विस्थापित करता है। इस कारण से पिण्ड बल के केन्द्र की ओर अग्रसर होता है और इस प्रकार से x का मान कम कर देता हैं। यही कारण है कि उसकी स्थितिज ऊर्जा कम हो जाती है। 
(b) किसी वस्तु द्वारा घर्षण के विरुद्ध किए गए कार्य का परिणाम हमेशा इसकी गतिज ऊर्जा में क्षय होता है। इसका मुख्य कारण यह है कि घर्षण के विरुद्ध किया गया कार्य पिण्ड की गतिज ऊर्जा को कम कर देता है। 
(c) किसी निकाय के कुल संवेग को आंतरिक बल में नहीं बदल सकते अतः अनेक कणों वाले निकाय में कुल संवेग की परिवर्तन दर निकाय पर लगे बाह्य बल के अनुपाती है। 
(d) किन्हीं दो पिण्डों के अप्रत्यास्थ संघट्ट में वे राशियाँ, जो संघट्ट के बाद नहीं बदलती हैं, वे हैं निकाय का कुल रैखिक संवेग तथा उसकी कुल ऊर्जा (यदि निकाय वियुक्त है)। निकाय की कुल गतिज ऊर्जा (KE.) संरक्षित नहीं रहती क्योंकि यह ऊर्जा के किसी और रूप में बराबर मात्रा में बदल सकती है। 

प्रश्न 6.7. 
बतलाइए कि निम्नलिखित कथन सत्य हैं या असत्य अपने उत्तर के लिए कारण भी दीजिए:
(a) किन्हीं दो पिंडों के प्रत्यास्थ संघट्ट में, प्रत्येक पिंड का संवेग व ऊर्जा संरक्षित रहती है। 
(b) किसी पिंड पर चाहे कोई भी आंतरिक व बाह्य बल क्यों न लग रहा हो, निकाय की कुल ऊर्जा सर्वदा संरक्षित रहती है। 
(c) प्रकृति में प्रत्येक बल के लिए किसी बंद लूप में, किसी पिंड की गति में किया गया कार्य शून्य होता है। 
(d) किसी अप्रत्यास्थ संघट्ट में, किसी निकाय की अंतिम गतिज ऊर्जा, आरंभिक गतिज ऊर्जा से हमेशा कम होती है। 
उत्तर:
(a) कथन असत्य है। चूँकि निकाय का कुल संवेग तथा कुल ऊर्जा बजाय किसी पिण्ड के संरक्षित है। 
(b) कथन असत्य है। चूँकि किसी निकाय पर बाह्य बल उसकी कुल ऊर्जा को कम या अधिक कर सकता है। 
(c) कथन असत्य है। किसी बंद लूप में किसी पिण्ड की गति में किया गया कार्य शून्य होता है, जब बल संरक्षी हो (जैसे गुरुत्वीय तथा स्थिर वैद्युतीय बल)। यह उस समय शून्य नहीं होता है जब बल असंरक्षित है, जैसे घर्षण बल आदि। 
(d) कथन सत्य है व आमतौर पर हमेशा नहीं क्योंकि अप्रत्यास्थ संघट्ट में कुछ गतिज ऊर्जा, ऊर्जा के अन्य रूप में रूपान्तरित हो जाती है। 

प्रश्न 6.8. 
निम्नलिखित का उत्तर ध्यानपूर्वक, कारण सहित दीजिए:
(a) किन्हीं दो बिलियर्ड गेंदों के प्रत्यास्थ संघट्ट में, क्या गेंदों के संघट्ट की अल्पावधि में (जब वे संपर्क में होती हैं) कुल गतिज ऊर्जा संरक्षित रहती है? 
(b) दो गेंदों के किसी प्रत्यास्थ संघट्ट की लघु अवधि में क्या कुल रेखीय संवेग संरक्षित रहता है? 
(c) किसी अप्रत्यास्थ संघट्ट के लिए प्रश्न (a) व (b) के लिए आपके उत्तर क्या हैं? 
(d) यदि दो बिलियर्ड - गेंदों की स्थितिज ऊर्जा केवल उनके केंद्रों के मध्य, पृथक्करण दूरी पर निर्भर करती है तो संघट्ट प्रत्यास्थ होगा या अप्रत्यास्थ? ( ध्यान दीजिए कि यहाँ हम संघट्ट के दौरान बल के संगत स्थितिज ऊर्जा 
की बात कर रहे हैं, न कि गुरुत्वीय स्थितिज ऊर्जा की) 
उत्तर:
(a) नहीं दत्त प्रत्यास्थ संघट्ट में गतिज ऊर्जा संरक्षित नहीं रहती है क्योंकि छोटे से समय अन्तराल में जब गेंदें संघट्ट की स्थिति में होती हैं, तो गतिज ऊर्जा का कुछ भाग उनमें विकृति उत्पन्न करने में काम आ जाता है तथा यह स्थितिज ऊर्जा में परिवर्तित हो जाती है। एक प्रत्यास्थ संघट्ट में, संघट्ट से पहले और बाद में गतिज ऊर्जा संरक्षित रहती है। 
(b) हाँ, दो गेंदों के किसी प्रत्यास्थ संघट्ट की लघु अवधि में कुल रेखीय संवेग संरक्षित रहता है। 
(c) किसी अप्रत्यास्थ संघट्ट में संघट्ट के दौरान या उसके बाद भी गतिज ऊर्जा संरक्षित नहीं रहती है। कुल रैखिक संवेग फिर भी संघट्ट के समय और उसके पश्चात् भी संरक्षित रहता है। 
(d) संघट्ट प्रत्यास्थ है। 

प्रश्न 6.9. 
कोई पिंड जो विरामावस्था में है, अचर त्वरण से एकंविमीय गति करता है। इसको किसी समय पर दी गई शक्ति अनुक्रमानुपाती है:
(i) t^-1/2 
(ii) t
(iii) t^3/2 
(iv) t² 
उत्तर:
पिण्ड में अचर त्वरण = m
प्रारम्भिक वेग u = 0 
और t समय पर वेग = v है 
∴ गति के प्रथम समी. से 
V = u + at 
V = 0 + at = at
बल F = ma (अचर) 
शक्ति P = E. v. 
= ma . at = ma²t 
P α t 

प्रश्न 6.10. 
एक पिंड अचर शक्ति के स्रोत के प्रभाव में एक ही दिशा में गतिमान है। इसका समय में विस्थापन, अनुक्रमानुपाती है:
(i) t^1/2 
(ii) t
(iii) t^3/2  
(iv) t² 
उत्तर:
∵ शक्ति P = E.v. 
लेकिन F = ma और v = at 
∵ v = u + at ⇒ v = 0 + at 
v = at 
मान रखने पर 
P = ma x at = ma²t 

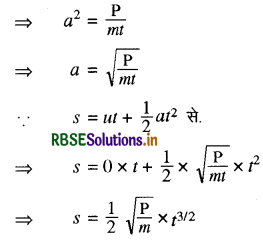
∵ प्रश्नानुसार P = अचर 
∴ s α t^3/2
अतः सही उत्तर (iii) 

प्रश्न 6.11. 
किसी पिंड पर नियत बल लगाकर उसे किसी निर्देशांक प्रणाली के अनुसार 7-अक्ष के अनुदिश गति करने के लिए बाध्य किया गया है जो इस प्रकार है:
\(\mathrm{F}=(-\hat{i}+2 \hat{j}+3 \hat{k}) \mathbf{N}\)
जहाँ \(\hat{i}, \hat{j}, \hat{k}\) क्रमशः x, y- एवं z - अक्ष के अनुदिश एकांक सदिश हैं। इस वस्तु को 7-अक्ष के अनुदिश 4m की दूरी तक गति कराने के लिए आरोपित बल द्वारा किया गया कार्य कितना होगा? 
उत्तर:
दिया गया है:
\(\overrightarrow{\mathrm{F}}=(-\hat{i}+2 \hat{j}+3 \hat{k}) \mathrm{N}\)
\(\overrightarrow{\mathrm{s}}\) = 4 k
∵ दूरी 2-अक्ष के अनुदिश 4 m 
W = ? 
हम जानते हैं: W = \(\overrightarrow{\mathrm{F}} . \overrightarrow{\mathrm{S}}\)
W = \((-\hat{i}+2 \hat{j}+3 \hat{k}) \cdot 4 \hat{k}\)
= \(-4(\hat{i} \cdot \hat{k})+8(\hat{j} \cdot \hat{k})+12(\hat{k} \cdot \hat{k})\)
हम जानते हैं- 
\(\begin{aligned} & \hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=0 \\ & \hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1 \end{aligned}\)
और 
W = - 4 × 0 + 8 × 0 + 12 x 1 
= 0 + 0 + 12 = 12 J 

प्रश्न 6.12. 
किसी अंतरिक्ष किरण प्रयोग में एक इलेक्ट्रॉन और एक प्रोटॉन का संसूचन होता है जिसमें पहले कण की गतिज ऊर्जा 10 keV है और दूसरे कण की गतिज ऊर्जा 100 keV है। इनमें कौन-सा तीव्रगामी है, इलेक्ट्रॉन या प्रोटॉन ? इनकी चालों का अनुपात ज्ञात कीजिए। (इलेक्ट्रॉन का द्रव्यमान = 9.11 x 10^-31 kg, प्रोटॉन का द्रव्यमान = 1.67 × 10^-27 kg, I ev = 1.60 x 10^-19J) 
उत्तर:
दिया गया है:
E1 = 10 kev 
= 10 × 10³ ev 
= 10 × 10³ x 1.6 × 10^-19 J 
= 16 × 10^-16 J
लेकिन E1 = 1/2 me ve²
∴ 1/2me ve² = 16 x 10^-16 J ............. (1)
इसी प्रकार से 
E2 = 100 kev 
= 100 × 10³ ev 
= 100 × 10³ x 1.6 × 10^-19 J 
= 160 × 10^-16 J
लेकिन E2 = 1/2 mp vp²
∴1/2 mp vp² = 160 x 10^-16 J ................. (2)
समीकरण (1) में समीकरण (2) का भाग देने पर

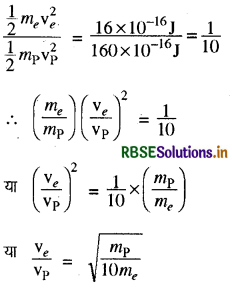
मान रखने पर 
= \(\sqrt{\frac{1.67 \times 10^{-27}}{10 \times 9.11 \times 10^{-31}}}=13.53\)
\(\frac{v_e}{v_{\mathrm{p}}}=13.53\)

प्रश्न 6.13.
2 mm त्रिज्या की वर्षा की कोई बूँद 500m की ऊँचाई से पृथ्वी पर गिरती है। यह अपनी आरंभिक ऊँचाई के आधे हिस्से तक (वायु के श्यान प्रतिरोध के कारण ) घटते त्वरण के साथ गिरती है और अपनी अधिकतम (सीमान्त ) चाल प्राप्त कर लेती है, और उसके बाद एकसमान चाल से गति करती है। वर्षा की बूँद पर उसकी यात्रा के पहले व दूसरे अर्ध भागों में गुरुत्वीय बल द्वारा किया गया कार्य कितना होगा? यदि बूँद की चाल पृथ्वी तक पहुँचने पर 10ms¹ हो तो संपूर्ण यात्रा में प्रतिरोधी बल द्वारा किया गया कार्य कितना होगा? 
उत्तर:
दिया गया है:
वर्षा की बूँद की त्रिज्या r = 2 mm = 2 x 10 m 
पानी की बूँद का घनत्व p = 10³ kg/m³ 
पृथ्वी से ऊँचाई जहाँ से बूँद गिरना प्रारम्भ करती है 
H = 500m 
आधी यात्रा में तय की गई दूरी 
= 1/2 H
= 1/2 x 500 = 250m
गोलाकार बूँद का आयतन 
= 4/3 πr³
या \(V=\frac{4}{3} \times \frac{22}{7} \times\left(2 \times 10^{-3}\right)^3 \mathrm{~m}^3\)
यदि वर्षा की बूँद का द्रव्यमान m हो तो द्रव्यमान 
m = आयतन x घनत्व 
m = V x p 
मान रखने पर 

≈ 33.52 x 10^-6
≈ 3.35  x  10^-5 kg 
बूँद पर गुरुत्वीय बल
F = mg
F = 3.35 X 10^-5 X 9.8N
गुरुत्वीय बल द्वारा बूँद पर किया गया कार्य 
W = F x d 
= 3.35 × 105 x 9.8 x 250 
W = 0.082 J 
माना कि वर्षा की बूँद आरम्भ में विराम अवस्था में है अर्थात् U = () 
पृथ्वी से टकराने पर अन्तिम वेग v = 10m/s 
वर्षा की बूँद की गतिज ऊर्जा में परिवर्तन 
∆Ek = 1/2mv² - 1/2mu² 
= 1⁄2mv² -1⁄2m x 0 = 1⁄2mv² - 0 
= 1/2mv² 
= 1/2 × 3.35 × 10^-5 × (10)² 
= 1.675 × 10^-5 x 10² 
= 1.675 × 10³ J 
= 0.00167 J 
गुरुत्वीय बल द्वारा किया गया कार्य = mgh 
= 3.35 × 10^-5 x 9.8 x 500 
= 0.16415 J 
प्रतिरोधी बल द्वारा कुल यात्रा में किया गया कार्य 
= गतिज ऊर्जा में परिवर्तन - गुरुत्वीय बल द्वारा किया गया कार्य 
= 0.001675 - 0.16415 
अर्थात् प्रतिरोधी बल द्वारा किया गया कार्य ऋणात्मक है 
= 0.163 J

प्रश्न 6.14. 
किसी गैस पात्र में कोई अणु 200ms^-1 की चाल से अभिलंब के साथ 30° का कोण बनाता हुआ क्षैतिज दीवार से टकराकर पुन: उसी चाल से वापस लौट जाता है। क्या इस संघट्ट में संवेग संरक्षित है? यह संघट्ट प्रत्यास्थ है या अप्रत्यास्थ? 
उत्तर:
हाँ, चाहे संघट्ट प्रत्यास्थ हो या अप्रत्यास्थ, संघट्ट में रैखिक संवेग सदैव संरक्षित रहता है। अतः दत्त स्थिति में संवेग संरक्षित है। चूँकि अणु की चाल संघट्ट के पहले व बाद में समान रहती है। अतः अणु की गतिज ऊर्जा भी संरक्षित है। इसलिए संघट्ट प्रत्यास्थ है। इसको इस प्रकार से भी समझ सकते हैं:
यदि गैस के अणु का द्रव्यमान m हो और दीवार का द्रव्यमान M हो तब प्रत्यास्थ के बाद कुल गतिज ऊर्जा 
E2 = 1/2m(200)² + 1/2M× (0)² 
E2 = 2 × 104 m J 

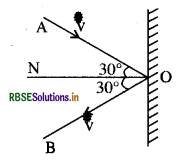
संघट्ट से पहले अणु की गतिज ऊर्जा
E₁ = 1/2m(200)² = 2 x 10⁴ mj
E₁ = E₂
अतः संघट्ट प्रत्यास्थ है।

प्रश्न 6.15. 
किसी भवन के भूतल पर लगा कोई पंप 30m³ आयतन की पानी की टंकी को 15 मिनट में भर देता है। यदि टंकी पृथ्वी तल से 40m ऊपर हो और पंप की दक्षता 30% हो तो पंप द्वारा कितनी विद्युत शक्ति का उपयोग किया गया? 
उत्तर:
दिया गया है:
पानी का आयतन = 30m³ 
समय 1 = 15 मिनट = 15 x 60 सेकण्ड 
ऊँचाई = 900 s 
h = 40m 
पम्प की दक्षता n = 30% 
पानी का घनत्व p = 103 kg/m³ 
ऊपर खींचे जाने वाले पानी का द्रव्यमान (m) 
= आयतन x पानी का घनत्व 
m = 30 × 10³ = 3 × 104 kg 
∴ टंकी को भरने के लिए पम्प द्वारा किया गया कार्य 
W = mgh 
या 
W = 3 × 10⁴ × 9.8 × 40 
= 1.176 × 107 J 
वांछित शक्ति (P) = \(\frac{\mathrm{W}}{t}=\frac{1.176 \times 10^7}{900}\)
= 13070 V
\(=\frac{13070}{100} k \mathrm{~W}\)

= 13.07 Kw
हम जानते हैं:

प्रश्न 6.16. 
दो समरूपी बॉल-बियरिंग एक-दूसरे के संपर्क में हैं और किसी घर्षणरहित मेज पर विरामावस्था में हैं। इनके साथ समान द्रव्यमान का कोई दूसरा बॉल-बियरिंग, जो आरंभ में v चाल से गतिमान है, सम्मुख संघट्ट करता है। यदि संघट्ट प्रत्यास्थ है तो संघट्ट के पश्चात् सामने (चित्र) में से कौन-सा परिणाम संभव है? 

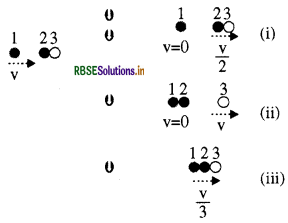
उत्तर:
माना कि प्रत्येक बॉल - बियरिंग का द्रव्यमान m है। टक्कर से पूर्व निकाय की कुल गतिज ऊर्जा 
= 1/2 mv² 
टक्कर के पश्चात् निकाय की कुल गतिज ऊर्जा 
स्थिति(i) =  \(=0+\frac{1}{2}(2 m)\left(\frac{v}{2}\right)^2=\frac{1}{4} m v^2\)
स्थिति(ii) =  \(0+\frac{1}{2} m \mathrm{v}^2=\frac{1}{2} m \mathrm{v}^2\)
स्थिति (iii) = \(\frac{1}{2}(3 m)\left(\frac{\mathrm{v}}{3}\right)^2=\frac{1}{6} m \mathrm{v}^2\)
इस प्रकार स्थिति (ii) में ही गतिज ऊर्जा संरक्षित है। अतः टक्कर के पश्चात् केवल स्थिति (ii) ही सम्भव है। 

प्रश्न 6.17. 
किसी लोलक के गोलक A को, जो ऊर्ध्वाधर से 30° का कोण बनाता है, छोड़े जाने पर मेज पर, विरामावस्था में रखे दूसरे गोलक B से टकराता है जैसा कि चित्र में प्रदर्शित है। ज्ञात कीजिए कि संघट्ट के पश्चात् गोलक A कितना ऊँचा उठता है? गोलकों के आकारों की उपेक्षा कीजिए और मान लीजिए कि संघट्ट प्रत्यास्थ है। 

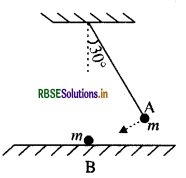
उत्तर:
हम जानते हैं कि जब दो समान द्रव्यमान वाले पिण्ड सीधा संघट्ट करते हैं तो संघट्ट के बाद उनके वेग आपस में बदल जाते हैं। यह प्रक्रिया पूर्णतः प्रत्यास्थ टक्कर में ही होती है। वर्तमान स्थिति में गोलक A किसी चाल से चल रहा है तथा गोलक B विराम की स्थिति में है । अतः संघट्ट के बाद गोलक A विराम की स्थिति में आ जाता है तथा गोलक B उसी चाल से चलता है जिसमें गोलक A संघट्ट से पहले चल रहा था । गोलक A संघट्ट में गोलक B को अपना सम्पूर्ण संवेग हस्तांतरित कर देता है और संघट्ट के पश्चात् गोलक A बिल्कुल ऊपर नहीं उठता। 

प्रश्न 6.18. 
किसी लोलक के गोलक को क्षैतिज अवस्था से छोड़ा गया है। यदि लोलक की लंबाई 1.5m है तो निम्नतम बिंदु पर आने पर गोलक की चाल क्या होगी ? यह दिया गया है कि इसकी आरंभिक ऊर्जा का 5% अंश वायु प्रतिरोध के विरुद्ध क्षय हो जाता है। 
उत्तर:
बिन्दु A पर लोलक की ऊर्जा पूर्णतः स्थितिज ऊर्जा है। बिन्दु B पर लोलक की ऊर्जा सम्पूर्ण रूप से गतिज ऊर्जा है। इसका अर्थ यह हुआ कि जब लोलक का गोलक A से B की ओर आता है तो स्थितिज ऊर्जा कम हो जाती है और गतिज ऊर्जा के मान में 

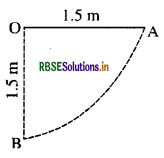
वृद्धि होती जाती है। इस प्रकार B पर गतिज ऊर्जा = स्थितिज ऊर्जा, लेकिन स्थितिज ऊर्जा का 5% भाग प्रतिरोध के विरुद्ध क्षय हो जाता 
है। 
यदि B पर वेग का मान v हो तब
K.E. = 1/2 mv² = 95% P.E., A ................. (1)
दिया गया है: m = गोलक का द्रव्यमान
बिन्दु B पर चाल = v
h = B की अपेक्षा A बिन्दु की ऊँचाई = 1.5~m
समीकरण (i) में मान रखने पर:

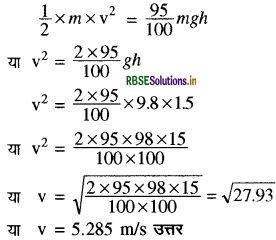
प्रश्न 6.19. 
300 kg द्रव्यमान की कोई ट्रॉली, 25 kg रेत का बोरा लिए हुए किसी घर्षणरहित पथ पर 27 kmh^-1 की एकसमान चाल से गतिमान है। कुछ समय पश्चात् बोरे में किसी छिद्र से रेत 0.05 kgs^-1 की दर से निकलकर ट्राली के फर्श पर रिसने लगती है। रेत का बोरा खाली होने के पश्चात् ट्रॉली की चाल क्या होगी? 
उत्तर:
यहाँ पर ट्रॉली एकसमान चाल से गतिमान है। इसका अर्थ यह है कि ट्रॉली तथा रेत के बोरे के निकाय पर कोई भी बाह्य बल कार्य नहीं कर रहा है। यदि एक छेद में से रेत ट्रॉली पर गिरता है तो यह ट्रॉली पर किसी बाह्य बल को उत्पन्न नहीं करता है। इसलिए बोरे के रिसने से ट्रॉली की चाल पर कोई अन्तर नहीं आयेगा, चाहे सारा रेत का बोरा खाली क्यों न हो जाए। यह इसलिए होता है कि रेत के भार को फर्श की प्रतिक्रिया संतुलित कर लेती है। दोनों गति की दिशा के लम्बात्मक है इसलिए रेत के रिसने पर न तो ट्रॉली के ऊपर न ही ट्रॉली द्वारा बल से कोई कार्य किया जाता है। इसलिए चाल वहीं रहती है। 
चाल = 27 km/h 

प्रश्न 6.20.
0.5 kg द्रव्यमान का एक कण v = a x 3/2 वेग से सरल रेखीय गति करता है जहाँ a = 5m^-1/2s ^-1 है x = 0 से x = 2m तक इसके विस्थापन में कुल बल द्वारा किया गया कार्य कितना होगा? 
उत्तर:
दिया गया है:
द्रव्यमान (m) = 0.5 kg 
वेग (v) = ax 
a = 5 m^-1/2s^-1 
यदि x = 0 से 2m तक इसके विस्थापन में किया गया कार्य W हो तो हमें कार्य W का मान ज्ञात करना है 
x = 0 पर कण का प्रारम्भिक वेग V1 = a x 0 
V1 = 0 
x = 2 पर कण का अन्तिम वेग V2 = a (2)^3/2 
= 5 × (2)^3/2 
किया गया कार्य W = गतिज ऊर्जा में वृद्धि 
= 1/2 m(v₂² - v₁²)
मान रखने पर:
\(\begin{aligned} & =\frac{1}{2} \times 0.5 \times\left(\left(5 \times 2^{3 / 2}\right)^2-0\right) \\ & =\frac{5}{20} \times(25 \times 8-0)=\frac{5 \times 200}{20} \end{aligned}\)
= 50 J 

प्रश्न 6.21. 
किसी पवनचक्की के ब्लेड, क्षेत्रफल A के वृत्त जितना क्षेत्रफल प्रसर्प करते हैं। (a) यदि हवा v वेग से वृत्त के लंबवत् दिशा में बहती है तो । समय में इससे गुजरने वाली वायु का द्रव्यमान क्या होगा? (b) वायु की गतिज ऊर्जा क्या होगी ? (c) मान लीजिए कि पवनचक्की हवा की 25% ऊर्जा को विद्युत ऊर्जा में रूपान्तरित कर देती है। यदि A = 30m 2, और v = 36 km h ^-1 और वायु का घनत्व 1.2 kgm है तो उत्पन्न विद्युत शक्ति का परिकलन कीजिए। 
उत्तर:
दिया गया है- 
(a) पवनचक्की के पंखों द्वारा प्रसर्पित वृत्तीय क्षेत्रफल = A 
हवा का वेग = V 
माना वायु का घनत्व = p 
अतः t समय में वायु द्वारा तय की गई दूरी = vt 
इसलिए वृत्तीय क्षेत्रफल A से जाने वाली वायु का आयतन 
= क्षेत्रफल x लम्बाई 
= A x vt = Avt 
∴ t समय में हवा का द्रव्यमान = आयतन x घनत्व 
= Avt × p 
= Av pt 

(b) हवा की K. E. = 1⁄2mv² 
= 1/2 x (Avpt) x v²
= 1/2 Av³pt

(c) उत्पन्न वैद्युत ऊर्जा = 25/100 x हवा की K. E.
= 25/100 x 1/2Av³pt = 1/8 Av³pt

लेकिऩ दिया गया है:
A = 30 m²
v = 36 Km/h
= 36 x 5/18 = 10 m/s
 p = 1.2 kg/m³
 
समी. (1) में मान रखने पर:

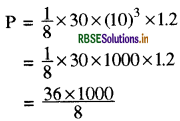
= 36 x 125 = 4500
w = 4.5 KW

प्रश्न 6.22. 
कोई व्यक्ति वजन कम करने के लिए 10 kg द्रव्यमान को 0.5m की ऊँचाई तक 1000 बार उठाता है। मान लीजिए कि प्रत्येक बार द्रव्यमान को नीचे लाने में खोई हुई ऊर्जा क्षयित हो जाती है। (a) वह गुरुत्वाकर्षण बल के विरुद्ध कितना कार्य करता है ? (b) यदि वसा 3.8 x 107 J ऊर्जा प्रति किलोग्राम आपूर्ति करता हो जो कि 20% दक्षता की दर से यांत्रिक ऊर्जा में परिवर्तित हो जाती है तो वह कितनी वसा खर्च कर डालेगा? 
उत्तर:
दिया गया है:
m = 10 kg 
h = 0.5m 
n = 1000 
∴ कुल ऊँचाई H = 0.5 × 1000 = 500m 
(a) गुरुत्वाकर्षण बल के विपरीत किया गया कार्य 
= mgH 
= 10 × 9.8 × 500 
= 49,000 J 
(b) प्रति किलोग्राम चर्बी द्वारा दी गई ऊर्जा 
= 3.8 × 10⁷ x 20/100
= 0.76 × 10⁷ J kg 
∴ वह वसा खर्च कर डालेगा = \(\frac{1 \mathrm{~kg}}{0.76 \times 10^7} \times 49,000\)
= 6.45 x 10^-3 kg

प्रश्न 6.23. 
कोई परिवार 8 kW विद्युत-शक्ति का उपभोग करता है। (a) किसी क्षैतिज सतह पर सीधे आपतित होने वाली सौर ऊर्जा की औसत दर 200 Wm^-2 है। यदि इस ऊर्जा का 20% भाग लाभदायक विद्युत ऊर्जा में रूपान्तरित किया जा सकता है तो 8 kW की विद्युत आपूर्ति के लिए कितने क्षेत्रफल की आवश्यकता होगी ? (b) इस क्षेत्रफल की तुलना किसी विशिष्ट भवन की छत के क्षेत्रफल से कीजिए। 
उत्तर:
परिवार द्वारा विद्युत शक्ति का उपभोग = 8 kW 
= 8 × 1000 = 8000 W 
(a) क्षैतिज सतह पर सीधे आपतित होने वाली सौर ऊर्जा की औसत दर 
= 200 W/m² 
लाभकारी वैद्युत ऊर्जा में परिवर्तित ऊर्जा 
= 200 W/m² की 20% 
= 20/100 × 200 = 40 W/m² 
परिवार द्वारा वांछित कुल शक्ति = 8000 W 
अतः उतनी वैद्युत ऊर्जा उत्पन्न करने के लिए वांछित क्षेत्रफल 
= 8000/40 = 200 m²

(b) माना छत का एक किनारा x है 
अतः छत का क्षेत्रफल = x x x = x2 
इस प्रकार से 
x2 = 200 m² 
\(x=\sqrt{200}=10 \sqrt{2}\)
= 10 × 1.414 = 14.14 
अतः छत का क्षेत्रफल लगभग 14m x 14m का होना चाहिए।
 
अभ्यास के अतिरिक्त प्रश्न:

प्रश्न 6.24 
0.012 kg द्रव्यमान की कोई गोली 70ms^-1 की क्षैतिज चाल से चलते हुए 0.4 kg द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरंत ही विरामावस्था में आ जाती है। गुटके को छत से पतली तारों द्वारा लटकाया गया है। परिकलन कीजिए कि गुटका किस ऊँचाई तक ऊपर उठता है? गुटके में पैदा हुई ऊष्मा की मात्रा का भी अनुमान लगाइए। 
उत्तर:
दिया गया है:
m1 = 0.012 Kg
u1 = 70 m/s
m2 = 0.4 kg
u2 = 0
गोली लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरन्त ही विरामावस्था में आ जाती है।
माना संघट्ट के पश्चात् संयुक्त रूप से चलती गोली व गुटके की चाल = vm/s
संवेग संरक्षण के नियमानुसार
(गोली + गुटके) का संघट्ट से पहले संवेग = संघट्ट के पश्चात्
गोली तथा गुटके का अन्तिम संवेग
m₁u₁ + m₂u₂ = (m₁ + m₂)v
मान रखने पर:
⇒ 0.012 x 70 + 0.4 x 0 = (0.012 + 0.4)v
⇒ 0.840 + 0 = 0.412 v
⇒ v = \(=\frac{0.840}{0.412}=\frac{840}{412}\)
⇒ v = 2.04 m/s
माना संघट्ट के बाद गुटका h ऊँचाई तक उठता है।
∴ संघट्ट के पश्चात् गुटके तथा गोली की K.E. में हानि = संघट्ट के पश्चात् (गुटके + गोली) की गतिज ऊर्जा में वृद्धि
1/2(m₁ + m₂)v² = (m₁ + m₂)gh
था
1/2v² = gh
\(h=\frac{\mathrm{v}^2}{2 g}=\frac{2.04 \times 2.04}{2 \times 9.8}\)
h = 0.212 m = 21.2 cm
अब गुटके में उत्पन्न ऊष्मा की गणना करने के लिए हम ऊर्जा की कमी को ज्ञात करेंगे।
∴ W = गोली की प्रारम्भिक गतिज ऊर्जा - गुटके तथा गोली की KE. 
= 1/2 m₁u₁² - 1/2(m₁ + m₂)v²
= 1⁄2 × 0.012 × (70)² - 1⁄2 (0.012 + 0.4) × (2.04)² 
= 29.4 - 0.86 = 28.54 J 

प्रश्न 6.25. 
दो घर्षणरहित आनत पथ, जिनमें से एक की ढाल अधिक है और दूसरे की ढाल कम है, बिंदु A पर मिलते हैं। बिंदु A से प्रत्येक पथ पर एक-एक पत्थर को विरामावस्था से नीचे सरकाया जाता है (चित्र)। क्या ये पत्थर एक ही समय पर नीचे पहुँचेंगे? क्या वे वहाँ एक ही चाल से पहुँचेंगे? व्याख्या कीजिए। यदि 01 = 30°, 2 = 60° और h = 10m दिया है तो दोनों पत्थरों की चाल एवं उनके द्वारा नीचे पहुँचने में लिए गए समय क्या हैं? 

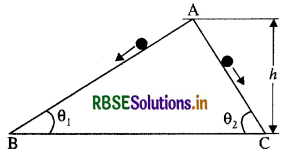
उत्तर:
चित्र में OA तथा OB दो चिकने आनत तल हैं जो क्षैतिज से θ1 तथा θ2 कोण बनाते हैं। दोनों समतलों की ऊँचाई समान है। इस कारण से दोनों पत्थर नीचे समान चाल से पहुँचेंगे। 

∴ 
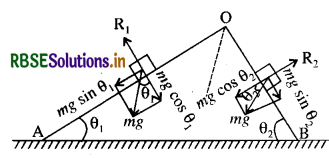
P.E. = K.E. 
= mgh = 1/2mv₁² = 1/2 mv₂². 
1⁄2mv₁² = 1⁄2 mv₂² 
V₁ = V₂ 
यदि पत्थर (1) व (2) में उत्पन्न त्वरण क्रमशः a 1 तथा a2 है तब 
a1 = g sinθ1 
a2 = g sinθ2
θ2 > θ1
a2 > a1
गति के प्रथम समीकरण से
v = u + at = 0 + at 
t = v/a
t α 1/a और a2 > a1
∴  t₂ < t₁
अर्थात् पहले पत्थर की अपेक्षा दूसरा पत्थर कम समय लेगा और तलहटी पर पहले पहुँचेगा अर्थात् अधिक झुकाव वाले तल पर पत्थर पहले तलहटी पर पहुँचेगा। 
h = 10 m
वेग \(\mathrm{v}=\sqrt{2 g h}=\sqrt{2 \times 9.8 \times 10}\)

= 14 m/s
θ1 = 30
v = u + at
v = g sinθ1

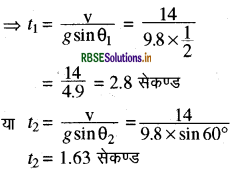
प्रश्न 6.26. 
किसी रूक्ष आनत तल पर रखा हुआ 100 Nm^-1 स्प्रिंग नियतांक वाले 1 kg द्रव्यमान का गुटका किसी स्प्रिंग से दिए गए चित्र के अनुसार जुड़ा है। गुटके को स्प्रिंग की बिना खिंची स्थिति में, विरामावस्था से छोड़ा जाता है। गुटका विरामावस्था में आने से पहले आनत तल पर 10 cm नीचे खिसक जाता है। गुटके और आनत तल के मध्य घर्षण गुणांक ज्ञात कीजिए। मान लीजिए कि स्प्रिंग का द्रव्यमान उपेक्षणीय है और घिरनी घर्षणरहित है। 

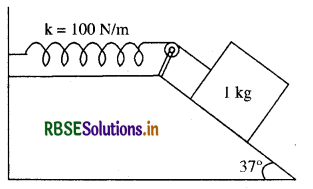
उत्तर:
दिया गया है:
गुटके का द्रव्यमान m = 1 kg 
g = 10m/s² 
स्प्रिंग नियतांक k = 100 N/m² 
sin 37° = 0.6018 
cos 37° = 0.7996 
और x = 10 cm = 0.1m 
यदि गुटके को xm दूरी से नीचे की ओर चलने में किया गया कार्य W है, तब 
W = (mg sin 0 - μ mg cos 0) × x ....(1) 
∴ कार्य (W) = बल (F) x विस्थापन (x) साम्यावस्था की स्थिति में कार्य = स्प्रिंग की स्थितिज ऊर्जा 
अब स्प्रिंग की स्थितिज ऊर्जा = 1/2 kx² ................. (2)
समीकरण (1) तथा (2) से 
1/2kx² = mg (sinθ - μ cos θ)x
kx = 2 mg (sinθ - μ cos θ)
⇒ kx = 2 mg sin θ - 2 μ mg cosθ
⇒  2 μ mg cosθ = 2 mg sinθ - kx

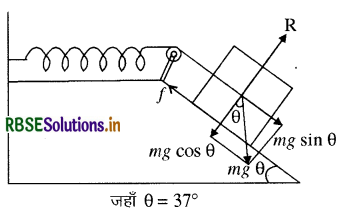
मान रखने पर 
\(\begin{aligned} & \mu=\frac{2 \times 1 \times 10 \times 0.6018-100 \times 0.1}{2 \times 1 \times 10 \times 0.7996} \\ & \mu=\frac{12.0360-10}{15.9920}=0.127 \end{aligned}\)
∴ μ = 0.217

प्रश्न 6.27 
0.3 kg द्रव्यमान का कोई बोल्ट 7 ms^-1 की एकसमान चाल से नीचे आ रही किसी लिफ्ट की छत से गिरता है। यह लिफ्ट के फर्श से टकराता है (लिफ्ट की लंबाई = 3m) और वापस नहीं लौटता है। टक्कर द्वारा कितनी ऊष्मा उत्पन्न हुई ? यदि लिफ्ट स्थिर होती तो क्या आपका उत्तर इससे भिन्न होता? 
उत्तर:
दिया गया है:
वोल्ट का द्रव्यमान m = 0.3 kg 
लिफ्ट की ऊँचाई h = 3m 
छत पर वोल्ट की स्थितिज ऊर्जा = mgh 
= 0.3 × 9.8 × 3 
= 8.82 J 
चूँकि वोल्ट प्रक्षिप्त नहीं होता अतः सम्पूर्ण स्थितिज ऊर्जा ऊष्मा में परिवर्तित हो जाती है जो ऊर्जा संरक्षण के नियमानुसार होती है। चूँकि सभी जड़त्वीय निर्देश तंत्रों में गुरुत्व जनित त्वरण का मान समान होता है, अतः चाहे उत्थापक गतिमान हो या स्थिर उत्तर वही रहेगा। 

प्रश्न 6.28.
200 kg द्रव्यमान की कोई ट्रॉली किसी घर्षणरहित पथ पर 36 km h^-1 की एकसमान चाल से गतिमान है। 20 kg द्रव्यमान का कोई बच्चा ट्रॉली के एक सिरे से दूसरे सिरे तक (10m दूर) ट्रॉली के सापेक्ष 4 ms^-1 की चाल से ट्रॉली की गति की विपरीत दिशा में दौड़ता है और ट्रॉली से बाहर कूद जाता है। ट्रॉली की अंतिम चाल क्या है? बच्चे के दौड़ना आरंभ करने के समय से ट्रॉली ने कितनी दूरी तय की? 
उत्तर:
दिया गया है: 
ट्रॉली का द्रव्यमान m₁ = 200kg 
बच्चे का द्रव्यमान m₂ = 20 kg 
ट्रॉली की चाल, u₁ = 36km/h 
= 36× 5/18/s = 10m/s 
बच्चे के दौड़ने से पहले मात्र निकाय का आरम्भिक संवेग 
Pi = (m₁ + m₂) u₁ 
Pi = (200 + 20) × 10 
अब ट्रॉली का नया वेग 
= 220 × 10 = 2200kg m/s 
= V2 
जब बच्चा 4 m/s के वेग से ट्रॉली के चलने की विपरीत दिशा में 
दौड़ता है तब पृथ्वी की अपेक्षा बच्चे की चाल = V₂ - 4 
∴ जब बच्चा दौड़ रहा है तो निकाय का अन्तिम संवेग 
Pf = m₁V₁ + m₂V₂ 
= 200 (v₂) + 200 ( V₂ - 4) 
चूँकि निकाय पर कोई बाह्य बल नहीं लगाया गया है 
अतः pi = pf
या 2200 = 200 v₂ + 20 ( V₂ - 4) 
या 2200 = 200 v₂ + 20 v₂ - 80 
या 2200 + 80 = 220 v₂ 
या 2280 = 220 V₂ 
या v₂ = \(\frac{2280}{220}=10.36 \mathrm{~m} / \mathrm{s}\)

प्रश्न 6.29. 
नीचे दिए गए चित्र में दिए गए स्थितिज ऊर्जा वक्रों में से कौन-सा वक्र संभवतः दो बिलियर्ड गेंदों के प्रत्यास्थ संघट्ट का वर्णन नहीं करेगा? यहाँ गेंदों के केंद्रों के मध्य की दूरी है और प्रत्येक गेंद का अर्धव्यास R है। 


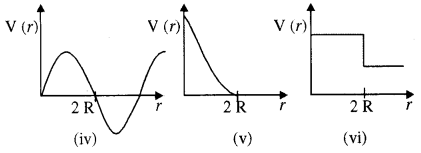
उत्तर:
दो द्रव्यमानों के निकाय के बीच स्थितिज ऊर्जा उनके बीच दूरी के व्युत्क्रमानुपाती होती है अर्थात् V(r) α 1/r जब दो बिलियर्ड गेंदें आपस में एक-दूसरे को स्पर्श करती हैं तब PE का मान शून्य होता है। 
∵ r = R + R = 2 R 
V (r) = 0 दिये गये स्थितिज ऊर्जा वक्रों में से वक्र (v) दो शर्तों को सन्तुष्ट करता है इसलिए चित्र (v) को छोड़कर सभी स्थितिज ऊर्जा वक्र दो बिलियर्ड गेंदों के बीच प्रत्यास्थ संघट्ट को प्रदर्शित नहीं कर सकते। 

प्रश्न 6.30. 
विरामावस्था में किसी मुक्त न्यूट्रॉन के क्षय पर विचार कीजिए n → p + e- 
प्रदर्शित कीजिए कि इस प्रकार के द्विपिंड क्षय से नियत ऊर्जा का कोई इलेक्ट्रॉन अवश्य उत्सर्जित होना चाहिए, और इसलिए यह किसी न्यूट्रॉन या किसी नाभिक के B-क्षय में प्रेक्षित सतत ऊर्जा वितरण का स्पष्टीकरण नहीं दे सकता ( चित्र 

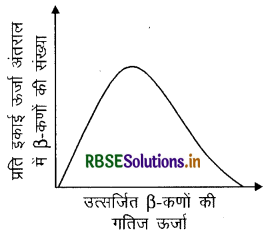
उत्तर:
इस अभिक्रिया में वैज्ञानिक पॉली ने सुझाव दिया कि इसमें एक अन्य कण जिसे न्यूट्रिनो (v) कहा जाता है, उत्सर्जित होता है। यह उदासीन व द्रव्यमान रहित कण है जिसका चक्रण 1/2 है। अतः सही अभिक्रिया निम्न है:
n → p + e + v