RBSE Solutions for Class 11 Physics Chapter 4 समतल में गति

Rajasthan Board RBSE Solutions for Class 11 Physics Chapter 4 समतल में गति Textbook Exercise Questions and Answers.

RBSE Class 11 Physics Solutions Chapter 4 समतल में गति

RBSE Class 11 Physics समतल में गति Textbook Questions and Answers

प्रश्न 4. 1. 
निम्नलिखित भौतिक राशियों में से बतलाइए कि कौन-सी सदिश हैं और कौन-सी अदिश
आयतन, द्रव्यमान, चाल, त्वरण, घनत्व, मोल संख्या, वेग, कोणीय आवृत्ति, विस्थापन, कोणीय वेग। 
उत्तर:
अदिश राशियाँ: आयतन द्रव्यमान, चाल, घनत्व, मोल संख्या, कोणीय आवृत्ति। 
सदिश राशियाँ: त्वरण, वेग, विस्थापन, कोणीय वेग। 

 

प्रश्न 4.2. 
निम्नांकित सूची में से दो अदिश राशियों को छाँटिए:
बल, कोणीय संवेग, कार्य, धारा, रैखिक संवेग, विद्युत क्षेत्र, औसत वेग, चुंबकीय आघूर्ण, आपेक्षिक वेग। 
उत्तर:
कार्य, धारा। 

प्रश्न 4.3. 
निम्नलिखित सूची में से एकमात्र सदिश राशि को छाँटिए: 
ताप, दाब, आवेग, समय, शक्ति, पूरी पथ-लंबाई, ऊर्जा, गुरुत्वीय विभव, घर्षण गुणांक, आवेश।  
उत्तर:
आवेग = संवेग में परिवर्तन = बल x समय 
यहाँ पर संवेग और बल दोनों ही सदिश राशियाँ हैं। इसलिए आवेश सदिश राशि होगी। 

प्रश्न 4. 4. 
कारण सहित बताइए कि अदिश तथा सदिश राशियों के साथ क्या अग्रलिखित बीजगणितीय संक्रियाएँ अर्थपूर्ण हैं? 
(a) दो अदिशों को जोड़ना, 
(b) एक ही विमाओं के एक सदिश व एक अदिश को जोड़ना, 
(c) एक सदिश को एक अदिश से गुणा करना, 
(d) दो अदिशों का गुणन, 
(e) दो सदिशों को जोड़ना, 
(f) एक सदिश के घटक को उसी सदिश से जोडना। 
उत्तर:
(a) नहीं, क्योंकि दो अदिशों में एक ही प्रकृति का योग किया जा सकता है। 
(b) नहीं, किसी अदिश राशि में उसी विमा के सदिश का संकलन अर्थपूर्ण नहीं है क्योंकि एक ही विमा के अदिशों का संकलन किया जा सकता है। एक अदिश तथा एक सदिश के साथ संकलित नहीं किया जा सकता है। 
(c) किसी सदिश का अदिश से गुणा सम्भव है। बीजगणित प्रक्रिया 
है, क्योंकि जब किसी सदिश को अदिश के साथ गुणा करते हैं तो हमें अदिश बार सदिश प्राप्त होता है, जो कि सदिश का परिमाण देता है। अर्थात् त्वरण \((\vec{a})\) को द्रव्यमान (m) से गुणा करते हैं तो हमें बल \(\vec{F}=m \vec{a}\) प्राप्त होता है, जो कि एक सार्थक प्रक्रिया है। 
(d) हाँ, दो अदिशों की गुणा एक सार्थक परिणाम देती है। चूँकि जब हम शक्ति P को समय (t) से गुणा करते हैं तो हमें कार्य W P x t = Pt प्राप्त होता है, जो कि एक उपयोगी बीजगणितीय प्रक्रिया हैं। 
(e) नहीं, चूँकि एक ही दिशा के दो सदिशों को जोड़ा जा सकता है अतः यह महत्त्वपूर्ण बीजगणितीय प्रक्रिया नहीं है। 
(f) हाँ, एक सदिश में उसी के घटक को जोड़ा जा सकता है क्योंकि वे दोनों सदिश एक ही प्रवृत्ति के होते हैं अर्थात् समान विमा के। उदाहरणार्थ, किसी वेग का घटक उसमें जोड़ा जा सकता है।
 
प्रश्न 4.5. 
निम्नलिखित में से प्रत्येक कथन को ध्यानपूर्वक पढ़िए और कारण सहित बताइए कि यह सत्य है या असत्य:
(a) किसी सदिश का परिमाण सदैव एक अदिश होता है, 
(b) किसी सदिश का प्रत्येक घटक सदैव अदिश होता है, 
(c) किसी कण द्वारा चली गई पथ की कुल लंबाई सदैव विस्थापन सदिश के परिमाण के बराबर होती है, 
(d) किसी कण की औसत चाल (पथ तय करने में लगे समय द्वारा विभाजित कुल पथ - लंबाई ) समय के समान अंतराल में कण के औसत वेग के परिमाण से अधिक या उसके बराबर होती है। 
(e) उन तीन सदिशों का योग जो एक समतल में नहीं हैं, कभी भी शून्य सदिश नहीं होता। 
उत्तर:
(a) सत्य है, चूँकि किसी सदिश का परिमाण सदैव एक संख्या होती है। 
(b) गलत है, चूँकि प्रत्येक सदिश का घटक भी एक सदिश होता है। 
(c) असत्य, यह तभी सत्य होता है जब कण उसी दिशा में एक सरल रेखा के अनुदिश गतिशील होता है। 
(d) सत्य, क्योंकि कुल पथ की लम्बाई विस्थापन सदिश के बराबर अथवा बड़ी होती है। अतः औसत चाल औसत वेग के परिमाण से बड़ी या बराबर होती है। 
(e) सत्य, शून्य सदिश प्राप्त करने के लिये तीसरे सदिश का परिमाण समान परन्तु दिशा विपरीत होनी चाहिये। 

प्रश्न 4.6. 
निम्नलिखित असमिकाओं की ज्यामिति या किसी अन्य विधि द्वारा स्थापना कीजिए- 

इनमें समिका (समता) का चिह कब लागू होता है? 
उत्तर:
दो सदिश \(\vec{a}\) और \(\vec{b}\) है पर विचार करते हैं जो कि समान्तर चतुर्भुज OPSQ की भुजा \(\overrightarrow{\mathrm{OP}}\) और \(\overrightarrow{\mathrm{OQ}}\) द्वारा निरूपित होते हैं। समान्तर चतुर्भुज के योग सदिश नियम से \((\vec{a}+\vec{b})\) को \(\overrightarrow{\mathrm{OS}}\) सदिश द्वारा निरूपित किया गया है। 

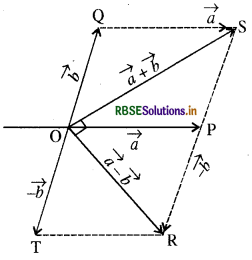
चित्र से OP = \(|\vec{a}|\) = OQ = PS = \(|\vec{b}|\) 
और OS = \(|\vec{a}+\vec{b}|\)

(a) सिद्ध करना है: \(|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|\)
प्रमाण - हम जानते हैं कि किसी त्रिभुज में एक भुजा की लम्बाई सदैव शेष रही दो भुजाओं की लम्बाई के योग से कम होती है। 
इसलिए ∆OPS में 
या 
OS < OP + PS 
या 
OS < OP + OQ 
\(|\vec{a}+\vec{b}|<|\vec{a}|+|\vec{b}|\) ............. (1)
यदि दोनों सदिश एक ही सरल रेखा के अनुदिश एक ही दिशा समरैखिक हैं, तब में कार्य कर रहे हैं। अर्थात् 
\(|\vec{a}+\vec{b}|=|\vec{a}|+|\vec{b}|\) .............. (2)
समीकरण (1) तथा (2) की शर्त को शामिल करते 
\(|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|\)
बराबर का चिन्ह तभी लागू होता है जब सदिश समरेखीय तथा एक ही दिशा में कार्यरत हो। इति सिद्धम् 

(b) सिद्ध करना है: \(|\vec{a}+\vec{b}| \geq|\vec{a}|-|\vec{b}| \mid\)
प्रमाण: किसी त्रिभुज में एक भुजा अन्य दो भुजाओं के अन्तर से 
अधिक होती है। 
∆OPS में 
OS + PS > OP 
या 
OS > | OP - PS | 
या 
OS > |OP - OQ| .....(3) 
∵ PS = OQ 
(OP - OQ) का मापांक लिया जा चुका है इसलिए LHS सदैव धनात्मक होगा। लेकिन RHS का मान ऋणात्मक भी हो सकता है यदि OP < PS | इस प्रकार समीकरण (3) से 
\(|\vec{a}+\vec{b}|>|\vec{a}|-|\vec{b}|\) .............. (4)
यदि दो सदिश तथा है एक ही सरल रेखा के अनुदिश विपरीत दिशा में कार्य कर रहे हैं, तब 
\(|\vec{a}+\vec{b}|=|| \vec{a}|-| \vec{b} \mid\) .............. (5)
समीकरण (4) तथा (5) को शामिल करने पर 
\(|\vec{a}+\vec{b}| \geq|| \vec{a}|-| \vec{b}||\) इति सिद्धम् 

(c) सिद्ध करना है: \(|\vec{a}-\vec{b}| \leq|\vec{a}|+|\vec{b}|\)
प्रमाण - फिर ∆OPR में 
\(\mathrm{OP}=|\vec{a}|, \mathrm{PR}=|-\vec{b}|=\vec{b}, \mathrm{OR}=|\vec{a}-\vec{b}|\)
अब त्रिभुज से 
OR < OP + PR 
या 
\(|\vec{a}-\vec{b}|<|\vec{a}|+|\vec{b}|\) ................... (6)
अब यदि सदिश \(\vec{a}\) व \(\vec{b}\) एक ही रेखा के अनुदिश विपरीत  दिशाओं में कार्यरत हैं तो 
\(|\vec{a}-\vec{b}|=|\vec{a}|+|\vec{b}|\) ................ (7)
समीकरण (6) तथा (7) को शामिल करने पर 
\(|\vec{a}-\vec{b}| \leq|\vec{a}|+|\vec{b}|\)

(d) सिद्ध करना है: \(|\vec{a}-\vec{b}| \geq|\vec{a}|-|\vec{b}| \mid\)
चूँकि किसी भी त्रिभुज में एक भुजा दोनों भुजाओं के अन्तर से अधिक होती है, अतः 
∆OPR से 
या
OR + PR > OP 
या 
 OR > | OP - PR | 
OR > | OP - Or | ........ (8)
∵ OT = PR 
यहाँ पर (OP - OT) का मापांक सदैव धनात्मक ही प्राप्त होगा । इसका अर्थ यह है कि LHS का मान सदैव धनात्मक ही होगा, लेकिन RHS का मान ऋणात्मक भी हो सकता है यदि 
OP < OT 
तब समीकरण (8) से \(|\vec{a}-\vec{b}|>|| \vec{a}|-| \vec{b} \mid\) ......(9) 
यदि दोनों सदिश व एक सरल रेखा के अनुदिश एक ही दिशा में कार्य करते हैं, तब 
\(|\vec{a}-\vec{b}|=|\vec{a}|-|\vec{b}|\) ................ (10)

समीकरण (9) तथा (10) को शामिल करने पर 
\(|\vec{a}-\vec{b}| \geq|| \vec{a}|-| \vec{b} \mid\)
 

प्रश्न 4.7. 
दिया है \(\vec{a}+\vec{b}+\vec{c}+\vec{d}=0\) नीचे दिए गए कथनों में से कौन-सा सही है- है। 
(a) \(\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}\) तथा \(\overrightarrow{\mathbf{d}}\) में से प्रत्येक शून्य सदिश है, 
(b) \((\vec{a}+\vec{c})\) का परिमाण \((\vec{b}+\vec{d})\) के परिमाण के बराबर है, 
(c) \(\overrightarrow{\mathbf{a}}\) का परिमाण \(\overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}\) है, तथा \(\overrightarrow{\mathrm{d}}\) के परिमाणों के योग से कभी भी अधिक नहीं हो सकता, 
(d) यदि \(\overrightarrow{\mathbf{a}}\) तथा व \(\overrightarrow{\mathbf{d}}\) संरेखीय नहीं हैं तो \(\vec{b}+\vec{c}\) अवश्य ही \(\overrightarrow{\mathbf{a}}\) तथा \(\overrightarrow{\mathbf{d}}\) के समतल में होगा, और यह है तथा के अनुदिश होगा यदि वे संरेखीय हैं। 
उत्तर:
(a) गलत, क्योंकि \(\vec{a}+\vec{b}+\vec{c}+\vec{d}\) का मान के \(\vec{a}, \vec{b}, \vec{c}\) तथा \(\vec{d}\)  शून्य सदिश होने के अतिरिक्त भी अनेक प्रकार से शून्य हो सकता 
(b) सही, क्योंकि \(\vec{a}+\vec{b}+\vec{c}+\vec{d}=0\)
या 
\(\vec{a}+\vec{c}=-(\vec{b}+\vec{d})\)
या \(|\vec{a}+\vec{c}|=|\vec{b}+\vec{d}|\)
अतः \((\vec{a}+\vec{c})\) का परिमाण \((\vec{b}+\vec{d})\) के परिमाण के बराबर है। 

(c) सही, क्योंकि \(\vec{a}+\vec{b}+\vec{c}+\vec{d}=0\)
\(\vec{a}=-(\vec{b}+\vec{c}+\vec{d})\)
या 
\(|\vec{a}|=|\vec{b}+\vec{c}+\vec{d}|\) .....(1) 
समीकरण (1) से स्पष्ट है कि \(\vec{a}\) का परिमाण सदिश \(\vec{b}+\vec{c}+\vec{d}\) के परिमाण के तुल्य है। चूँकि \(\vec{b}+\vec{c}+\vec{d}\) का परिमाण के परिमाण से अधिक या बराबर हो सकता है अतः \(\vec{a}\) का परिमाण है, \(\vec{b}, \vec{c}\) व \(\vec{d}\) के संकलन के परिमाण से कभी भी अधिक नहीं हो सकता। 
(d) सही, \(\vec{a}+\vec{b}+\vec{c}+\vec{d}=0\)
या 
\(\vec{a}+(\vec{b}+\vec{c})+\vec{d}=0\)
तीन सदिशों \(\vec{a},(\vec{b}+\vec{c})\) तथा \(\vec{d}\) का परिणामी योगफल तभी शून्य हो सकता है जबकि \(\vec{a}\) व \(\vec{d}\) संरेखीय हों तब \((\vec{b}+\vec{c})\) को \(\vec{a}\) व \(\vec{d}\)की रेखा में होना चाहिए। 

प्रश्न 4.8. 
तीन लड़कियाँ 200 m त्रिज्या वाली वृत्तीय बर्फीली सतह पर स्केटिंग कर रही हैं। वे सतह के किनारे के बिंदु P से स्केटिंग शुरू करती हैं तथा P के व्यासीय विपरीत बिंदु Q पर विभिन्न पथों से होकर पहुँचती हैं जैसा कि चित्र में दिखाया गया है। प्रत्येक लड़की के विस्थापन सदिश का परिमाण कितना है? किस लड़की के लिए यह वास्तव में स्केट किए गए पथ की लंबाई के बराबर है? 

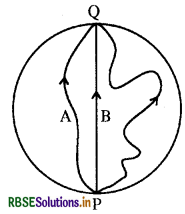
उत्तर:
प्रत्येक लड़की का विस्थापन 

∴  विस्थापन का परिमाण प्रत्येक लड़की के लिए होगा 
= PQ की लम्बाई 
= वृत्तीय बर्फीली सतह का व्यास 
= 2 × 200 = 400m 
प्रत्येक लड़की के लिए विस्थापन सदिश का परिमाण 
= | PQ | = 400m 
चित्र से स्पष्ट है कि B लड़की के विस्थापन का परिमाण स्केच द्वारा तय कुल वास्तविक दूरी के बराबर है। 

प्रश्न 4.9. 
कोई साइकिल सवार किसी वृत्तीय पार्क के केंद्र 0 से चलना शुरू करता है तथा पार्क के किनारे P पर पहुँचता है। पुनः वह पार्क की परिधि के अनुदिश साइकिल चलाता हुआ Q0 के रास्ते (जैसा चित्र में दिखाया गया है) केंद्र पर वापस आ जाता है। पार्क की त्रिज्या 1 km है। यदि पूरे चक्कर में 10 मिनट लगते हों तो साइकिल सवार का (a) कुल विस्थापन, (b) औसत वेग, तथा (c) औसत चाल क्या होगी? 

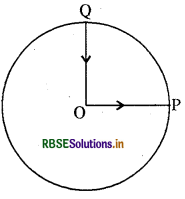
उत्तर:
(a) यहाँ पर दिया गया है:
वृत्तीय पथ की त्रिज्या = 1 km. 
साइकिल का विस्थापन = शून्य होगा 
चूँकि आरम्भिक बिन्दु की स्थिति और अन्तिम बिन्दु की स्थिति एक है।

(b) साइकिल सवार का माध्य वेग =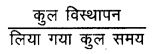
साइकिल सवार का औसत =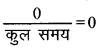

= 3.57 × 6 = 21.42 km/h 

प्रश्न 4.10. 
किसी खुले मैदान में कोई मोटर चालक एक ऐसा रास्ता अपनाता है जो प्रत्येक 500m के बाद उसके बाईं ओर 60° के कोण पर मुड़ जाता है। किसी दिए मोड़ से शुरू होकर मोटर चालक का तीसरे, छठे व आठवें मोड़ पर विस्थापन बताइए। प्रत्येक स्थिति में मोटर चालक द्वारा इन मोड़ों पर तय की गई कुल पथ-लंबाई के साथ विस्थापन के परिमाण की तुलना कीजिए। 
उत्तर: 
यहाँ पर मोटर चालक द्वारा चला हुआ पथ बंद षट्कोण ABCDEF है जिसकी एक भुजा का मान 500 मीटर है। 

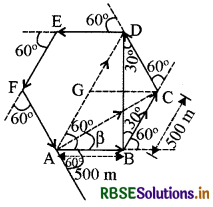
मोटर चालक अपनी यात्रा बिन्दु A से आरम्भ करता है। तीसरे मोड़ के अन्त में वह D पर पहुँचता है तथा 6वें मोड़ के अन्त में A पर पहुँचता है तथा बिन्दु C पर 8वें मोड़ के अन्त में पहुँचता है। 
(i) तीसरा मोड़ - तीसरा मोड़ D पर है। 
D पर विस्थापन सदिश = Ab = 2 × AG 
2 × 500 = 1000 m = 1 km 
कुल पथ की लम्बाई A से D तक 
= AB + BC + CD 
= 500 +500 + 500 
= 1500 m 
\(=\frac{1500}{1000} \mathrm{~km}\) = 1.5 Km
अब 

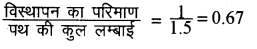
(ii) छठा मोड़-छठे मोड़ के अन्त में चालक आरम्भिक बिन्दु A पर है। अतः इसका विस्थापन सदिश शून्य होगा। 
जबकि पंथ की कुल लम्बाई = AB + BC + CD + DE + EF + FA 
= 500 +500 +500 +500 + 500 + 500 
= 6 × 500 = 3000m 
\(=\frac{3000}{1000} \mathrm{~km}\)
अब =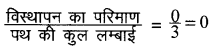

(iii) आठवाँ मोड़ - मोटर चालक इस मोड़ पर बिन्दु C पर होता है। 
∴ मोटर चालक का विस्थापन 
\(\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}\)
∴ AC का परिमाण 

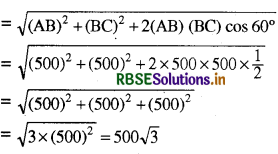
= 500 × 1,732 
= 866 m 

दिशा निर्धारण 
माना आठवें मोड़ की दिशा β कोण पर है। 

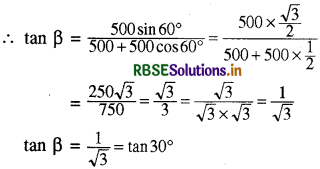
β = 30° 
अतः आठवें मोड़ पर चालक का विस्थापन 500 √3 मी. दिशा AB की प्रारम्भिक दिशा से 30° पर। 
पथ की कुल लम्बाई = 8 × 500 
= 4000 मी. 
= 4 किमी. 

\(=\frac{\sqrt{3}}{8}=0.22\)

प्रश्न 4.11. 
कोई यात्री किसी नए शहर में आया है और वह स्टेशन से किसी सीधी सड़क पर स्थित किसी होटल तक, जो 10 km दूर है, जाना चाहता है। कोई बेईमान टैक्सी चालक 23 km के चक्करदार रास्ते से उसे ले जाता है और 28 मिनट में होटल में पहुँचता है। 
(a) टैक्सी की औसत चाल, और 
(b) औसत वेग का परिमाण क्या होगा? क्या वे बराबर हैं? 
उत्तर: 
दिया गया है:
वास्तविक तय की गई कुल दूरी = 23 km 
विस्थापन का परिमाण = 10 km 
कुल समय = 28 मिनट = \(\frac{28}{60}\)घण्टा

(a) टैक्सी की माध्य चाल ( औसत चाल) 

(b) औसत वेग का परिमाण 

यहाँ पर औसत चाल का मान औसत वेग के परिमाण के बराबर नहीं है। 

प्रश्न 4.12. 
वर्षा का पानी 30m s^-1 की चाल से ऊर्ध्वाधर नीचे गिर रहा है। कोई महिला उत्तर से दक्षिण की ओर 10ms^-1 की चाल से साइकिल चला रही है। उसे अपना छाता किस दिशा में रखना चाहिए? 
उत्तर:  
OA के अनुदिश वर्षा ऊर्ध्वाधर नीचे की ओर 30km/h से हो रही है। स्त्री OS के अनुदिश 10km/h की चाल से जा रही है। वर्षा से अपने आपको बचाने के लिए स्त्री को अपनी छतरी उसकी अपेक्षा पड़ रही वर्षा की आपेक्षिक गति की दिशा में रखनी चाहिए।

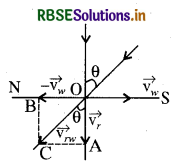
इस प्रकार से वर्षा की दो चाल होंगी:
(i) इसका अपना वेंग OA के अनुदिश 30 m/s तथा 
(ii) वेग OS के अनुदिश = 10 m/s 
वर्षा का आपेक्षिक वेग \(\overrightarrow{v_{n w}}=\vec{v}_r+\left(\overrightarrow{-v_w}\right)\) दोनों वेगों का परिमाण 

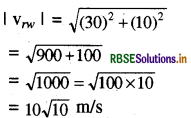
माना कि आपेक्षिक वेग ऊर्ध्वाधर से 8 कोण बनाता है। तब ∆OCA में चित्र से 
\(\tan \theta=\frac{\mathrm{AC}}{\mathrm{OA}}=\frac{\mathrm{OB}}{\mathrm{OA}}=\frac{10}{30}=\frac{1}{3}\)
tan Ꮎ = 0.3333 
Ꮎ = 18°26' 
अतः स्त्री को ऊर्ध्वाधर से 18°26' के कोण पर छतरी को रखना चाहिए जिससे वह वर्षा में भीगने से बच जाये।  

प्रश्न 4.13. 
कोई व्यक्ति स्थिर पानी में 4.0km/h की चाल से तैर सकता है। उसे 1.0 km चौड़ी नदी को पार करने में कितना समय लगेगा यदि नदी 300km/h की स्थिर चाल से बह रही हो और वह नदी के बहाव के लंब तैर रहा हो? जब वह नदी के दूसरे किनारे पहुँचता है तो वह नदी के बहाव की ओर कितनी दूर पहुँचेगा? 
उत्तर: 

व्यक्ति की चाल = 4 km/h 
तय की गई दूरी = 1 km 
नदी की चाल = 3 km/h 
माना समय नदी को पार करने में लिया जाता है। 

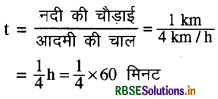
= 15 मिनट 

व्यक्ति द्वारा तय की गई दूरी (15 मिनट में ) = 3 km/h x 1 /4h 
\(\begin{aligned} & =\frac{3}{4} \mathrm{~km} \\ & =\frac{3}{4} \times 1000 \mathrm{~m} \end{aligned}\)
3 × 250 = 750m 

प्रश्न 4.14. 
किसी बंदरगाह में 72 km/h की चाल से हवा चल रही है और बंदरगाह में खड़ी किसी नौका के ऊपर लगा झंडा N-E दिशा में लहरा रहा है। यदि वह नौका उत्तर की ओर 51 km/ h चाल से गति करना प्रारंभ कर दे तो नौका पर लगा झंडा किस दिशा में लहराएगा? 
उत्तर:

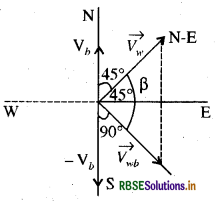
माना Vw = N-E दिशा में वायु का वेग है। 

Vb = N दिशा में नाव का वेग है। 
जब नाव बंदरगाह में खड़ी है तो झंडा N-E दिशा में लहराता है। अतः वायु का वेग N-E दिशा में है। जब नाव N दिशा में चलना शुरू करती है तो नाव की अपेक्षा वायु में आपेक्षिक वेग की दिशा में झंडा लहराने लगेगा 
V = 30km/h N-E दिशा में 
Vb = 51 km/h N दिशा में 
\(\vec{V}_{w b}=\vec{V}_w+\left(-\vec{V}_b\right)\)
यहाँ पर 
\(\begin{aligned} \left|\vec{V}_w\right| & =72 \mathrm{~km} / \mathrm{h} \\ \left|-\vec{V}_b\right| & =51 \mathrm{~km} / \mathrm{h} \end{aligned}\)
चित्र से स्पष्ट है कि Vw तथा -Vb के बीच कोण 90° + 45° = 135° है। 
यदि Vwb तथा Vw के बीच β कोण है तो समान्तर चतुर्भुज के नियमानुसार झंडे के फहराने की दिशा 

tan β = tan 45.1° 
∴ β = 45.1° 45° 
अर्थात् imm की दिशा लगभग पूर्व की ओर होगी अतः झण्डा पूर्व की ओर लहरायेगा। 

प्रश्न 4.15. 
किसी लंबे हॉल की छत 25m ऊँची है। वह अधिकतम क्षैतिज दूरी कितनी होगी जिसमें 40ms^-1 की चाल से फेंकी गई कोई गेंद छत से टकराए बिना गुजर जाए? 
उत्तर:
दिया गया है:
अधिकतम ऊँचाई H = 25m 
गेंद का प्रारम्भिक वेग u = 40m/s 
g = 9.8 m/s² 
माना गेंद को θ कोण से फेंका जाता है, जिसमें वह अधिकतम क्षैतिज दूरी प्राप्त करता है। 
अधिकतम ऊँचाई H = \(\frac{u^2 \sin ^2 \theta}{2 g}\)
मान रखने पर 
\(\begin{aligned} & 25=\frac{(40)^2 \sin ^2 \theta}{2 \times 9.8} \\ & 25=\frac{1600 \times \sin ^2 \theta}{19.6} \end{aligned}\)
⇒ 25 × 19.6 = 1600 sin2 θ 
⇒ sin² θ = \(\frac{25 \times 19.6}{1600}=\frac{19.6}{64}\) = 0.30625
sin² θ = 0.30625 
∴  \(\sin \theta=\sqrt{0.30625}\)
sin θ = 0.5534 
∴ θ = sin-t(0.5534) = 33.6° 
∴ अधिकतम परास 

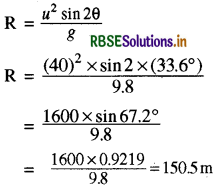
अधिकतम क्षैतिज दूरी होगी = 150.5m 

प्रश्न 4.16. 
क्रिकेट का कोई खिलाड़ी किसी गेंद को 100m की अधिकतम क्षैतिज दूरी तक फेंक सकता है। वह खिलाड़ी उसी गेंद को जमीन से ऊपर कितनी ऊँचाई तक फेंक सकता है? 
उत्तर:
दिया गया है: 
Rmax = 100 m 
H = ? 
हम जानते हैं कि क्षैतिज परास R = \(\frac{u^2 \sin 2 \theta}{g}\)
R = Rmax के लिए 0 = 45° होना चाहिए। 

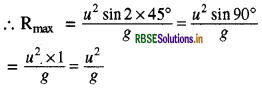
लेकिन 
Rmax = 100 .....(1) 
∴ 100 = u²/g
माना गेंद H ऊँचाई तक जा सकती है, जब क्रिकेट खिलाड़ी इसे u वेग से फेंकता है। चूँकि गेंद का अन्तिम वेग V = 0 
v² - u² = 2 (-g) H 
∴ यहाँ पर v = 0, a = - g, s = H 
या 
u² = 2gH 
\(\mathrm{H}=\frac{u^2}{2 g}=\frac{1}{2}\left(\frac{u^2}{g}\right)\)
समीकरण (1) से मान रखने पर 
H = 1⁄2 × 100 = 50m 
अतः वह खिलाड़ी उसी गेंद को जमीन से 50m ऊँचाई तक फेंक सकता है। 

प्रश्न 4.17. 
80 cm लंबे धागे के एक सिरे पर एक पत्थर बाँधा गया है और इसे किसी एकसमान चाल के साथ किसी क्षैतिज वृत्त में घुमाया जाता है। यदि पत्थर 25s में 14 चक्कर लगाता है तो पत्थर के त्वरण का परिमाण और उसकी दिशा क्या होगी? 
उत्तर:
दिया गया है:
r = 80cm. = 0.8 m 
आवृत्ति n = 14/25 प्रति सेकण्ड 
∴ कोणीय वेग ω = 2πn = 2 x 22/7 x 14/5 
ω = 88/25 रेडियन/सेकण्ड 
∴ अभिकेन्द्रीय त्वरण का मान 
ac = rω² 
ac = 0.8 x \(\left(\frac{88}{25}\right)^2\)
\(=\frac{0.8 \times 88 \times 88}{25 \times 25}\)
= 9.91 m/s² 
प्रत्येक बिन्दु पर त्वरण की दिशा त्रिज्या के अनुदिश तथा केन्द्र की ओर होगी। 

प्रश्न 4.18. 
कोई वायुयान 900kmh^-1 की एकसमान चाल से उड़ रहा है और 1.00 km त्रिज्या का कोई क्षैतिज लूप बनाता है। इसके अभिकेंद्र त्वरण की गुरुत्वीय त्वरण के साथ तुलना कीजिए। 
उत्तर:
दिया गया है: 
V = 900 km/h 
= 900 × 5/18 m/s 
= 50 × 5 = 250m/s 
r = 1.00 km = 1000
अभिकेन्द्रीय त्वरण ac = rω² = r x (v/r)²
\(=\frac{\mathrm{v}^2}{r}=\frac{(250)^2}{1000}=\frac{250 \times 250}{1000}\)
ac = 62.5 m/s² 

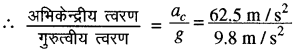
= 6.38 

प्रश्न 4.19. 
नीचे दिए गए कथनों को ध्यानपूर्वक पढ़िए और कारण देकर बताइए कि वे सत्य हैं या असत्य
(a) वृत्तीय गति में किसी कण का नेट त्वरण हमेशा वृत्त की त्रिज्या के अनुदिश केन्द्र की ओर होता है। 
(b) किस बिंदु पर किसी कण का वेग सदिश सदैव उस बिंदु पर कण के पथ की स्पर्श रेखा के अनुदिश होता है। 
(c) क्रिसी कण का एकसमान वृत्तीय गति में एक चक्र में लिया गया औसत त्वरण सदिश एक शून्य सदिश होता है। 
उत्तर:
(a) असत्य, क्योंकि एकसमान वृत्तीय गति (नियत चाल) में ही त्वरण त्रिज्या के अनुदिश तथा केन्द्र की ओर (अभिकेन्द्रीय त्वरण) होता है। 
(b) सत्य, वेग सदिश सदैव गति के पथ के स्पर्शी होता है। 
(c) सत्य, क्योंकि इस दशा में विस्थापन शून्य होता है। 

प्रश्न 4.20. 
किसी कण की स्थिति सदिश निम्नलिखित है:
\(\vec{r}=\left(3.0 \mathrm{t} \hat{i}-2.0 \mathrm{t}^2 \hat{j}+4.0 \hat{k}\right) \mathrm{m}\)
समय t सेकंड में है तथा सभी गुणकों के मात्रक इस प्रकार से हैं कि r में मीटर में व्यक्त हो जाएँ। 
(a) कण का \(\overrightarrow{\mathbf{v}}\) तथा \(\overrightarrow{\mathbf{a}}\) निकालिए, 
(b) t = 2.0s पर कण के वेग का परिमाण तथा दिशा कितनी होगी? 
उत्तर:
(a) वेग \(\overrightarrow{\mathrm{v}}=\frac{d \vec{r}}{d t}\)
लेकिन दिया गया है:

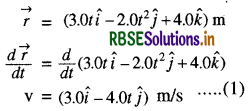
कण का त्वरण 

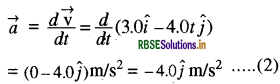
(b) t = 2s, पर 

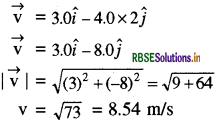
यदि θ कोण वेग v के साथ x -अक्ष से बनाता है। 
तब 
tan θ = \(\frac{v_y}{v_x}=-\frac{8}{3}=-2.667\)
tan θ = - tan 69.5° 
∴ θ = 69.5° x - अक्ष से नीचे की ओर 

प्रश्न 4.21. 
कोई कण t = 0 क्षण पर मूल बिंदु से 10\(\hat{j}\) ms^-1 के वेग से चलना प्रारम्भ करता है तथा x y समतल में एकसमान त्वरण \((8.0 \hat{i}+2.0 \hat{j}) m^{-2}\)से गति करता है। 
(a) किंस क्षण कण का x - निर्देशांक 16m होगा? इसी समय इसका y- निर्देशांक कितना होगा? 
(b) इस क्षण कण की चाल कितनी होगी? 
उत्तर:
दिया गया है:
\(\vec{u}=10.0 \hat{j} \mathrm{~m} / \mathrm{s}\)
समय t = 0 पर 
\(\vec{a}=(8.0 \hat{i}+2.0 \hat{j}) \mathrm{m} / \mathrm{s}^2\)

(a) हमें ज्ञात है, स्थिति 

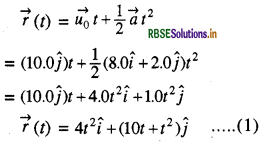
समीकरण (1) में कण के x तथा y के निर्देशांक हैं 
x (t) = 4.0 t² ................ (2)
y (t) = 10.0 t + 1.0t² .............. (3)
परन्तु 
x (t) = 16 m 
समीकरण (2) तथा (4) से 
4t² = 16 
\(t^2=\frac{16 m}{4}=4\)
∵ t = 2s
t का मान समीकरण (3) में रखने पर निर्देशांक 
y (t) = 10.0 t + 1.0 t² 
= 10.0 × 2 + 1.0 x (2)² 
= 20 + 4 = 24
∴ y (t) = 24 m .............. (5)

(b) कण की चाल
हम जानते हैं कण का वेग 
\(\vec{v}=\frac{d}{d t}(\vec{r})\)
मान रखने पर 

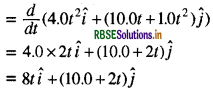
t = 2s पर 
\(v(t)=8 \times 2 \hat{i}+(10.0+2 \times 2) \hat{j}\)
था
\(v(t)=16 \hat{i}+14 \hat{j}\)
t = 2s पर कण की चाल 
\(\begin{aligned} |\vec{v}| & =\sqrt{v_x^2+v_y^2}=\sqrt{(16)^2+(14)^2} \\ & =\sqrt{256+196}=\sqrt{452} \end{aligned}\)
= 21.26m/s

प्रश्न 4.22. 
\(\hat{i}\) व \(\hat{j}\) क्रमश: x- व y-अक्षों के अनुदिश एकां सदिश हैं। सदिशों \(\hat{i}+\hat{j}\) तथा \(\hat{i}-\hat{j}\) का परिमाण तथा दिशा क होगा? सदिश A = \(2 \hat{i}+3 \hat{j}\) के \(\hat{i}+\hat{j}\) के दिशाओं के अनुदि घटक निकालिए। [आप ग्राफी विधि का उपयोग कर सकते हैं ]
उत्तर:
\(|\hat{i}+\hat{j}|=\sqrt{(1)^2+(1)^2}=\sqrt{2}\) इकाई 
tan θ = 1/1
1 = tan 45° 
 अतः \((\hat{i}+\hat{j})\) x-अक्ष से 45° कोण बनाता है। 
 
(ii) 
\(|\hat{i}-\hat{j}|=\sqrt{(1)^2+(-1)^2}=\sqrt{2}=1.414\) इकाई 
tan θ = -1/1 = 1 
θ = 45° 
अतः \((\hat{i}-\hat{j})\) x-अक्ष से - 45° कोण बनाता है। 

(iii) सदिश \(\overrightarrow{\mathrm{A}}=(2 \hat{i}+3 \hat{j})\) के घटक \((\hat{i}+\hat{j})\) की दिशा ज्ञात करने के लिए माना कि 
\(\overrightarrow{\mathrm{B}}=(\hat{i}+\hat{j})\)
तब 
\(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}\) = AB cos θ 
(A cos θ) B 

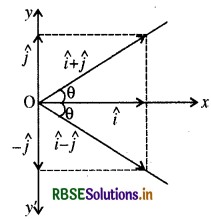
अतः B की दिशा में A का घटक ( A cos θ) = \(\frac{\vec{A} \cdot \vec{B}}{B}\)
\(=\frac{(2 \hat{i}+3 \hat{j}) \cdot(\hat{i}+j)}{\sqrt{(1)^2+(1)^2}}=\frac{2+3}{\sqrt{2}}\)
\(=\frac{5}{\sqrt{2}}\) इकाई 
यदि \(\overrightarrow{\mathbf{B}}=(\hat{i}-\hat{j})\) हो तब im की दिशा में im का घटक 
\(\cos \theta)=\frac{\vec{A} \cdot \vec{B}}{B}\)
\(\begin{aligned} & =\frac{(2 \hat{i}+3 \hat{j}) \cdot(\hat{i}-\hat{j})}{\sqrt{(1)^2+(-1)^2}} \\ & =\frac{2-3}{\sqrt{2}}=-\frac{1}{\sqrt{2}} \end{aligned}\)
इकाई 

प्रश्न 4.23. 
किसी दिक्स्थान पर एक स्वेच्छ गति के लिए निम्नलिखित संबंधों में से कौन-सा सत्य है? 

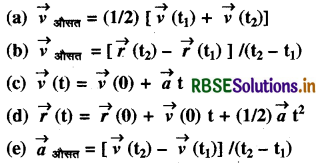
यहाँ 'औसत' का आशय समय अंतराल t₂ व t₁ से संबंधित भौतिक राशि के औसत मान से है। 
उत्तर:
सम्बन्ध (b) व (e) आकाश में किसी भी यादृच्छिक गति के लिए सही हैं। 
सम्बन्ध (a), (c) तथा (d) गलत हैं क्योंकि वे एकसमान त्वरित गति के लिए हैं। 

प्रश्न 4.24. 
निम्नलिखित में से प्रत्येक कथन को ध्यानपूर्वक पढ़िए तथा कारण एवं उदाहरण सहित बताइए कि क्या यह सत्य है। 
या असत्य:
अदिश यह राशि है जो 
(a) किसी प्रक्रिया में संरक्षित रहती है, 
(b) कभी ऋणात्मक नहीं होती, 
(c) विमाहीन होती है, 
(d) किसी स्थान पर एक बिंदु से दूसरे बिंदु के बीच नहीं बदलती, 
(e) उन सभी दर्शकों के लिए एक ही मान रखती है चाहे अक्षों से उनके अभिविन्यास भिन्न-भिन्न क्यों न हों। 
उत्तर:
(a) कथन असत्य है, क्योंकि प्रक्रम में कई अदिश राशियाँ संरक्षित नहीं हैं; जैसे कि ऊर्जा एक अदिश राशि है जो कि अप्रत्यास्थ संघट्ट में संरक्षित नहीं होती है। 
(b) कथन असत्य है, क्योंकि कुछ अदिश राशियाँ प्रक्रम में ऋणात्मक हैं। जैसे ताप अदिश राशि होते हुए भी ऋणात्मक हो सकती है, इसी प्रकार से आवेश भी अदिश राशि है और यह भी ऋणात्मक हो सकती है। 
(c) कथन असत्य है, क्योंकि अनेक अदिश राशियाँ विमाहीन नहीं होतीं। उदाहरणस्वरूप, द्रव्यमान, घनत्व, आवेश आदि अदिश राशि की परन्तु इनकी विमा होती है। 
(d) यह कथन असत्य है, क्योंकि कई अदिश राशियाँ आकाश में एक बिन्दु से दूसरे बिन्दु तक बदल जाती हैं। जैसे द्रव का घनत्व, ताप, गुरुत्वीय विभव, आवेश घनत्व एक बिन्दु से दूसरे पर बदलता है। 
(e) यह कथन सत्य है। निर्देशांक अक्षों के घुमाव से अदिश राशि का मान नहीं बदलता। जैसे- द्रव्यमान निर्देशांकों के अक्षों से स्वतन्त्र है। 

प्रश्न 4.25. 
कोई वायुयान पृथ्वी से 3400m की ऊँचाई पर उड़ रहा है। यदि पृथ्वी पर किसी अवलोकन बिंदु पर वायुयान की 10.0s की दूरी की स्थितियाँ 30° का कोण बनाती हैं तो वायुयान की चाल क्या होगी? 
उत्तर:
चित्र के अनुसार O प्रेक्षण बिन्दु है। A और B वायुयान की दो स्थितियाँ हैं जिसके लिए ∠AOB = 30° बिन्दु O से AB पर लम्ब डाला गया है। यहाँ पर OC = 3400m और ∠AOC = ∠COB 15° है। वायुयान का समय बिन्दु A से बिन्दु B तक 10 सेकण्ड लगते हैं। 

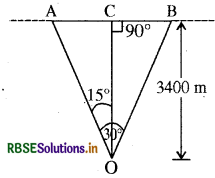
∆AOC में, 
AC = OC tan 15° 
= 3400 x 0.2679 
= 910.86 m 
AB = AC + CB = AC + AC = 2AC 
= 2 x 910.86 m 
वायुयान की चाल v =
\(=\frac{2 \times 910.86}{10}=\frac{910.86}{5}\)
= 182.2 m/s 

अभ्यास के अतिरिक्त प्रश्न:

प्रश्न 4.26.
किसी सदिश में परिमाण व दिशा दोनों होते हैं। क्या दिकस्थान में इसकी कोई स्थिति होती है? क्या यह समय के साथ परिवर्तित हो सकता है? क्या दिक्स्थान में भिन्न स्थानों पर दो बराबर सदिशों a व b का समान भौतिक प्रभाव अवश्य पड़ेगा? अपने उत्तर के समर्थन में उदाहरण दीजिए। 
उत्तर:
हाँ, परिमाण तथा दिशा के साथ प्रत्येक सदिश की एक स्थिति भी होती है। यह समय के साथ बदल सकती है। दो सदिश व समान होते हुए भी रिक्त स्थान में उनकी स्थितियाँ भिन्न होने से उनके भौतिक प्रभाव एक जैसे नहीं होते हैं । जैसे 3 kg वाले पिण्ड पर आपतित एक 15 N के बल का पृथ्वी पर तथा वैसे ही पिण्ड पर चन्द्रमा- पर भिन्न प्रभाव होता है। 

प्रश्न 4.27. 
किसी सदिश में परिमाण व दिशा दोनों होते हैं। क्या इसका यह अर्थ है कि कोई राशि जिसका परिमाण व दिशा हो, वह अवश्य ही सदिश होगी? किसी वस्तु के घूर्णन की व्याख्या घूर्णन - अक्ष की दिशा और अक्ष के परितः घूर्णन कोण द्वारा की जा सकती है। क्या इसका यह अर्थ है कि कोई भी घूर्णन एक सदिश है? 
उत्तर:
कोई भौतिक राशि जिसका परिमाण एवं दिशा दोनों हों, आवश्यक नहीं कि वह सदिश राशि हो। बहुत-सी भौतिक राशियाँ हैं जो दिशा और परिमाण रखती हैं लेकिन वे सदिश राशि नहीं हैं, वे सदिश संयोजन के नियमों का पालन नहीं करती हैं, जो कि आवश्यक है। उनको सदिश संयोजन का पालन करना चाहिए। आमतौर पर एक अक्ष के परितः किसी पिण्ड का घूर्णन एक सदिश नहीं होता। यद्यपि उसका परिमाण एवं दिशा दोनों होते हैं। क्योंकि निश्चित घूर्णन सदिश संकलन के प्रमुख नियम, सदिश विनिमय के नियम का पालन नहीं करता है, जो कि सदिश संकलन का एक प्रमुख नियम है। लेकिन अतिसूक्ष्म घूर्णन सदिश संकलन के विनिमय नियम का पालन करता है। अति सूक्ष्म घूर्णन को सदिश कह सकते हैं। 

प्रश्न 4.28. 
क्या आप निम्नलिखित के साथ कोई सदिश संबद्ध कर सकते हैं:
(a) किसी लूप में मोड़ी गई तार की लंबाई, 
(b) किसी समतल क्षेत्र, 
(c) किसी गोले के साथ? व्याख्या कीजिए। 
उत्तर:
(a) एक तार को छल्ले के रूप में मोड़े होने के कारण इसे सदिश नहीं कर सकते हैं क्योंकि इसकी कोई समान दिशा नहीं है। 
(b) हम समतल क्षेत्रफल A के साथ सदिश लगा सकते हैं क्योंकि 
क्षेत्रफल A = लम्बाई (1) x चौड़ाई (b) 
यहाँ पर लम्बाई 1 व चौड़ाई b दोनों ही सदिश हैं। 
(c) एक गोले का क्षेत्रफल एक शून्य सदिश लिया जा सकता है। यद्यपि गोले का आयतन किसी विशेष दिशा की ओर इंगित नहीं होता है। 

प्रश्न 4.29. 
कोई गोली क्षैतिज से 30° के कोण पर दागी गई है और वह धरातल पर 300km दूर गिरती है। इसके प्रक्षेप्य के कोण का समायोजन करके क्या 5.0 km दूर स्थित किसी लक्ष्य का भेद किया जा सकता है? गोली की नालमुख चाल को नियत तथा वायु के प्रतिरोध को नगण्य मानिए। 
उत्तर: 
स्थिति I दिया गया है: 
प्रक्षेप्य कोण 6 = 30° 
क्षैतिज परास R = 3 km 3 × 1000 = 3000m 

माना u प्रक्षेप्य वेग है, तब 
क्षैतिज परास \(\mathbf{R}=\frac{u^2 \sin 2 \theta}{g}\)
⇒ Rg = u² sin 2θ 
⇒ \(u^2=\frac{\mathrm{Rg}}{\sin 2 \theta}\)
मान रखने पर 

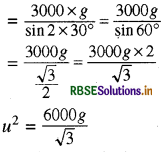
स्थिति II - माना 6' = नया प्रक्षेप्य कोण है और नया क्षैतिज परार R' है। R' = 5 km 
R' = 5000m, पुनः ॥ उतना ही है, जितना पहले था। 
क्षैतिज परास \(\mathrm{R}^{\prime}=\frac{u^2 \sin 2 \theta^{\prime}}{g}\)
मान रखने पर 

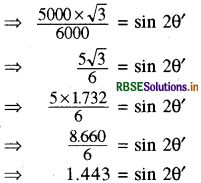
स्पष्ट रूप से sin 2θ > 1, जो कि सम्भव नहीं है। अतः हम इस निष्कर्ष पर पहुँचते हैं कि केवल प्रक्षेप्य कोण का समायोजन करने से ह 5 किमी. क्षैतिज परास प्राप्त करना कठिन होगा, जबकि नलिका चाल क नहीं बदला जाये। 

प्रश्न 4.30. 
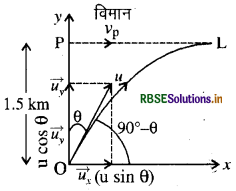
कोई लड़ाकू जहाज 1.5 km की ऊँचाई पर 72 km/h की चाल से क्षैतिज दिशा में उड़ रहा है और किसी वायुयान भेर्द तोप के ठीक ऊपर से गुजरता है। ऊर्ध्वाधर से तोप की नाल का क्य कोण हो जिससे 600ms^-1 की चाल से दागा गया गोला वायुयान प वार कर सके। वायुयान के चालक को किस न्यूनतम ऊँचाई पर जहा को उड़ाना चाहिए जिससे गोला लगने से बच सके। (g = 10ms^-2) 

उत्तर: 
दिया गया है:
g = 10m/s²
लड़ाकू विमान का वेग 
vp = 720 km/h 
= 720 x 5/18 m/s 
= 200 m/s 
u = गोले के नाल की चाल 
= 600 m/s 

(a) माना तोप ऊर्ध्वाधर (1) अक्ष से ) 9 कोण बनाता है। 
u का क्षैतिज घटक = u cos (90 - θ) 
= usinθ 
तथा ॥ का ऊर्ध्वाधर घटक = u sin (90 - θ) 
= u cos θ 
गोला दागने के बाद माना वह t समय बाद वायु के पंख पर लगता है। 
t समय वायुयान द्वारा तय की गई दूरी 
Xp = Vp x t 
= 200 × t 
Xp = 200t .............. (1)
t समय में गोले द्वारा तय की गई क्षैतिज दूरी 
वायुयान पर गोला लगेगा यदि 
Xs = 200 t = (600 sin 0) t .....(2) 
Xp = Xs 
200t = (600 sin 8) t 
\(\sin \theta=\frac{200}{600}=\frac{1}{3}=0.3333\)
∴ θ = 19.5° ऊर्ध्वाधर से 

(b) वायुयान गगनभेदी तोप से बच सकता है यदि इसकी ऊँचाई गोले की अधिकतम ऊँचाई के बराबर या अधिक हो। 
\(\mathrm{H}=\frac{u_y^2}{2 g}=\frac{(u \cos \theta)^2}{2 g}=\frac{u^2 \cos ^2 \theta}{2 g}\)
मान रखने पर 
\(\mathrm{H}=\frac{(600)^2 \cos ^2 19.5}{2 \times 10}=\frac{3,60,000}{2 \times 10} \times \frac{8}{9}\)
या 
H = 16 km 
\(\cos ^2 \theta=1-\sin ^2 \theta=1-\left(\frac{1}{3}\right)^2=\frac{8}{9}\)
वायुयान को कम से कम उड़ना पड़ेगा = 16 km 

प्रश्न 4.31 
एक साइकिल सवार 27 km/h की चाल से साइकिल चला रहा है। जैसे ही सड़क पर वह 80m त्रिज्या के वृत्तीय मोड़ पर पहुँचता है, वह ब्रेक लगाता है और अपनी चाल को 0.5m/ s की एकसमान दर से कम कर लेता है। वृत्तीय मोड़ पर साइकिल सवार के नेट त्वरण का परिमाण और उसकी दिशा निकालिए। 
उत्तर: 
दिया गया है:
v = 27 km/h 
\(\begin{aligned} & =\frac{27 \times 5}{18} \mathrm{~m} / \mathrm{s} \\ & =\frac{3 \times 5}{2}=7.5 \mathrm{~m} / \mathrm{s} \end{aligned}\)
= 7.5 m/s 
r = 80m 

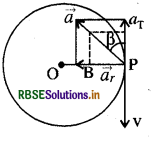
हम जानते हैं:
\(a_c=\frac{v^2}{r}\)
मान रखने पर 
\(a_{c^{\prime}}=\frac{(7.5)^2}{80}=\frac{7.5 \times 7.5}{80}\)
ac = 0.7m/s² 
माना कि साइकिल वाला बिन्दु P पर ब्रेक लगाता है तब स्पर्शी त्वरण ar (जो कि ऋणात्मक होगा) वेग के विपरीत दिशा में होगा (जैसा कि चित्र में दिखाया गया है) 
दिया गया है- 
\(a_{\mathrm{T}}=-\frac{0.5}{1.0}-\) 0.5 मी./से. ² 
ат और ac के बीच का कोण 90° है। 
सूत्र 
\(\begin{aligned} a & =\sqrt{a_c^2+a_T^2} \\ & =\sqrt{(0.7)^2+(0.5)^2}=\sqrt{0.49+0.25} \end{aligned}\)
= 0.86 m/s² 
माना परिणामी त्वरण स्पर्शी त्वरण से B कोण बनाती है। 
तब tan B = \(\frac{a_c}{a_T}=\frac{0.7}{0.5}\)
\(=\frac{7}{5}=1.4\)
β = 54°28′ 

प्रश्न 4.32. 
(a) सिद्ध कीजिए कि किसी प्रक्षेप्य के x-अक्ष तथा उसके वेग के बीच के कोण को समय के फलन के रूप में निम्न प्रकार से व्यक्त कर सकते हैं: 
\(\theta(t)=\tan ^{-1}\left(\frac{\mathbf{v}_{o y}-g t}{v_{o x}}\right)\)
(b) सिद्ध कीजिए कि मूल बिंदु से फेंके गए प्रक्षेप्य कोण का मान \(\theta_0=\tan ^{-1}\left(\frac{4 h_m}{R}\right)\) होगा। यहाँ प्रयुक्त प्रतीकों के अर्थ सामान्य 
उत्तर: 
(a) माना समय 1 पर प्रक्षेप्य बिन्दु P पर है। माना समय पर प्रक्षेप्य का वेग v है जो P पर वक्र की स्पर्शज्या की ओर कार्य करता है। माना 1 समय पर वेग v के क्षैतिज तथा ऊर्ध्वाधर घटक क्रमश: Vy हैं। अब oy के अनुदिश 0 से P तक प्रक्षेप्य की ऊर्ध्वाधर गति को लेते हैं। 

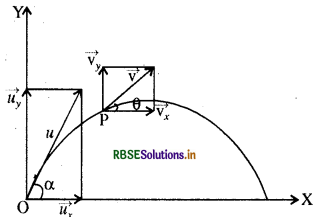
Vy = Uy + ay t का उपयोग करने पर 
Vy = Uy - gt  .................. (1) 
यहाँ पर ay = -g है 
OX के अनुदिश 
Vx = ux + 0 = ux ............... (2)
माना बिन्दु P पर परिणामी वेग क्षैतिज से 0 कोण बनाता है। 
\(\tan \theta=\frac{v_y}{v_x}\) .................. (3)
समीकरण (1), (2) तथा (3) से 
या 

इति सिद्धम् 

(b) α = समय 1 = 0 पर मूल () से प्रक्षेप्य कोण 
hm = प्रक्षेप्य द्वारा प्राप्त अधिकतम ऊँचाई 
R = प्रक्षेप्य का क्षैतिज परास 
u = समय t = 0 पर प्रक्षेप वेग 
यदि t = 0 पर u के घटक क्षैतिज uy तथा ऊर्ध्वाधर हैं तो 
ux = u cos α 
तथा 
uy = u sin α 
हम जानते हैं:
\(\mathrm{R}=\frac{u^2 \sin 2 \alpha}{g}\) ............. (4)
तथा 
\(h_m=\frac{u^2 \sin ^2 \alpha}{2 g}\) .............. (5)
समीकरण (5) में (4) का भाग देने पर