RBSE Solutions for Class 11 Physics Chapter 3 सरल रेखा में गति

Rajasthan Board RBSE Solutions for Class 11 Physics Chapter 3 सरल रेखा में गति Textbook Exercise Questions and Answers.

RBSE Class 11 Physics Solutions Chapter 3 सरल रेखा में गति

RBSE Class 11 Physics सरल रेखा में गति Textbook Questions and Answers

प्रश्न 3.1.
नीचे दिए गए गति के कौनसे उदाहरणों में वस्तु को लगभग बिंदु वस्तु माना जा सकता है।
(a) दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी।
(b) किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बंदर।
(c) जमीन से टकरा कर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद।
(d) किसी मेज के किनारे से फिसल कर गिरा कोई बीकर। 
उत्तर:
(a) चूंकि दो स्टेशनों के बीच की दूरी बहुत अधिक है तुलनात्मक वस्तु से अतः रेलगाड़ी को बिन्दु वस्तु माना जा सकता है।
(b) बन्दर द्वारा तय की गई दूरी अधिक है। अतः बन्दर को वस्तु बिन्दु माना जा सकता है। 
(c) जमीन से टकराकर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद की गति बाधा रहित नहीं है, जिससे गेंद उपयुक्त समय में अधिक दूरी तय नहीं करेगी और गेंद को बिन्दु वस्तु नहीं माना जा सकता है। 
(d) किसी मेज के किनारे से फिसल कर गिरा कोई बीकर बिन्दु वस्तु नहीं माना जा सकता है क्योंकि इस स्थिति में उपयुक्त समय में बीकर अधिक दूरी तय नहीं करता है। 

 

प्रश्न 3.2. 
दो बच्चे A व B अपने विद्यालय 0 से लौट कर अपने-अपने घर क्रमश: P तथा Q को जा रहे हैं। उनके स्थिति-समय 1) ग्राफ चित्र में दिखाए गए हैं। नीचे लिखे कोष्ठकों में सही प्रविष्टियों को चुनिए:

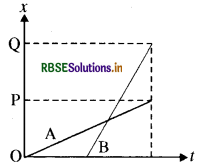
(a) B / A की तुलना में A/B विद्यालय से निकट रहता है।
(b) B / A की तुलना में A/B विद्यालय से पहले चलता है।
(c) B / A की तुलना में A/B तेज चलता है।
(d) A और B घर (एक ही / भिन्न) समय पर पहुंचते हैं। 
(e) A/B सड़क पर B/A से (एक बार / दो बार ) आगे हो जाते हैं। 
उत्तर:
(a) OP < OQ, A स्कूल के निकट रहता है B की अपेक्षा। 
(b) A के लिये x = 0 पर 1 = 0 होता है। लेकिन B के लिये x = 0 पर t का कुछ सीमित (finite ) मान प्राप्त होता है। 
अतः A स्कूल से 
B की अपेक्षा पहले चलता है। 
(c) समान गति में वेग (x - 1 ) ग्राम में ढाल के बराबर होता है। यहां पर B का ढाल, A के ढाल से ज्यादा है अतः A की अपेक्षा B तेज चलेगा 
(d) ग्राफ से स्पष्ट है कि A और B घर पर एक ही समय में पहुंचते हैं। क्योंकि P व Q से ग्राफ पर खींचे गये लम्ब 1 समय पर मिलते हैं। 
(e) इस (x - 1 ) ग्राफ में A और B एक ही बार प्रतिच्छेद कर रहे हैं और B स्कूल के लिये बाद में चलना प्रारम्भ करता है अतः यही कारण है कि B, A से आगे रहेगा। 

प्रश्न 3.3. 
एक महिला अपने घर से प्रातः 9.00 बजे 2.5 km दूर अपने कार्यालय के लिये सीधी सड़क पर 5 km h -1 चाल से चलती है। वहां वह सायं 5.00 बजे तक रहती है और 25km h ^-1 की चाल से चल रही किसी ऑटो रिक्शा द्वारा अपने घर लौट आती है। उपयुक्त पैमाना चुनिए तथा उसकी गति का x - t ग्राफ खींचिए। 
उत्तर:
दिया गया है 
x = 2.5 km 
माना सीधी सड़क पर चाल v1 = 5 km/h 
और अपने कार्यालय तक पहुंचने का लगा समय = t1 
\(t_1=\frac{x}{v_1}=\frac{2.5 \mathrm{~km}}{5 \mathrm{~km} / \mathrm{h}}\)
यदि दोनों अक्षों के लिये शून्य को उद्गम माना जाये तब t = 9.00 am, x = 0 तथा t = 9.30am पर x = 2.5 km और महिला चलकर अपने ऑफिस पहुँच जाती है, जहाँ पर वह सायं 5.00 बजे तक रहती है, जो कि सरल रेखा AB द्वारा दिखाया गया है। अतः लौटने में 
लगा समय 

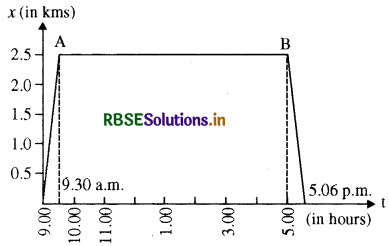
t₂ = 10 h = 6 मिनट 
अतः वह 5.06 pm पर घर लौट आती है । ग्राफ में पैमाना लेने 
x अक्ष पर 1 भाग = 1 घण्टा 
y अक्ष पर 1 भाग = 0.5 km. 

प्रश्न 3.4. 
कोई शराबी किसी तंग गली में 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, उसके बाद फिर 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, और इसी तरह वह चलता रहता है। उसका हर कदम 1m लंबा है और 1s समय लगता है। उसकी गति का x - t ग्राफ खींचिए । ग्राफ से तथा किसी अन्य विधि से यह ज्ञात कीजिए कि वह जहां से चलना प्रारंभ करता है वहाँ से 13m दूर किसी गड्ढे में कितने समय पश्चात् गिरता है। 
उत्तर:
शराबी का (x - 1 ) ग्राफ निम्न प्रकार का होगा:

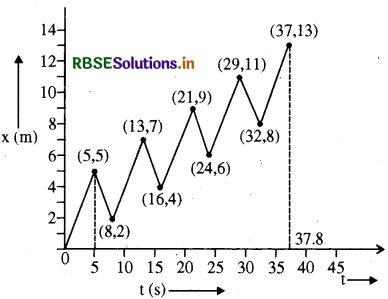
दिया गया है
1 मीटर चलने में लगा समय 1 सेकण्ड है। 
अतः पहले 5 मीटर चलने में लगा समय = 5 सेकण्ड 5 कदम आगे चलकर वह 3 कदम पीछे चलता है । अतः चली गई कुल दूरी = 53 = 2 मीटर 
इस दूरी को तय करने में लगा समय = 5 + 3 = 8 सेकण्ड अतः 32 सेकण्ड में तय की गई दूरी = 8 मीटर 
गड्ढे तक शेष दूरी 
= 13 - 8 = 5 मीटर 
अर्थात् शराबी अगले 5 कदमों में गड्ढे में गिर जायेगा जिसमें उसे 5 सेकण्ड का समय और लगेगा। 
अतः शराबी को गड्ढे में गिरने में लगा कुल समय t = 32 + 5 = 37 सेकंण्ड 

प्रश्न 3.5. 
कोई जेट वायुयान 500kmh^-1 की चाल से चल रहा है और यह जेट यान के सापेक्ष 1500kmh की चाल से अपने दहन उत्पादों को बाहर निकालता है। जमीन पर खड़े किसी प्रेक्षक के सापेक्ष इन दहन उत्पादों की चाल क्या होगी? 
उत्तर:
माना जेट वायुयान निष्कासित गैस व जमीन पर प्रेक्षक के वेग क्रमश: V1, V2 तथा V3 हैं। 
माना जेट वायुयान R. H.S. की तरफ (+ दिशा) में चल रहा है। निष्कासित गैस L. H.S. की तरफ चलेगी ( - दिशा में ) 
∴ प्रश्नानुसार 
V1 = 500 km/h 
 ∵ प्रेक्षक जमीन पर है ∴ विराम अवस्था में है। 
V3 = 0 
अब जहाज का आपेक्षिक वेग प्रेक्षक के सापेक्ष 
= V1 - V3 =
= 500 - 0  = 500 km/h 
= 500 km/h  ...(1) 
V2 - V1 = - 1500km/h  ...(2) 
जेट जहाज के सापेक्ष दहन उत्पादों की आपेक्षिक गति 
( - ) ॠण चिन्ह दर्शाता है कि जेट की दिशा के विपरीत दहन उत्पाद चलते हैं। 
समीकरण ( 1 ) तथा (2) का योग करने पर 
V1 - V3 + V2 - V1 = 500 + (- 1500) 
V2- V3 = 1000 km/h 
( - ) ऋण चिन्ह यह बताता है कि प्रेक्षक के सापेक्ष निष्कासित गैसों की दिशा ऋणात्मक या बाईं ओर है अर्थात् जेट जहाज की गति की विपरीत दिशा में। 

प्रश्न 3.6. 
सीधे राजमार्ग पर कोई कार 126 kmh^-1 की चाल से चल रही है। इसे 200m की दूरी पर रोक दिया जाता है। कार के मंदन को एकसमान मानिए और इसका मान निकालिए। कार को रुकने में कितना समय लगा? 
उत्तर:
हल दिया गया है u = 126 km/h 
\(=\frac{126 \times 1000}{60 \times 60} \mathrm{~m} / \mathrm{s}\)
m/s = 35m/s 
v = 0 
s = 200 m 
a = ? और t = ? 
हम जानते हैं गति के तीसरे समीकरण से 
u² = u² + 2as
0 = (35)² + 2 × a × 200 
या 
\(a=\frac{-(35)^2}{2 \times 200}=\frac{-35 \times 35}{400}\)
\(a=\frac{-49}{16}\)
a = = - 3.06 m/s² 
अतः कार समान रूप से a = 3.06m/s² से मंदित होती है। 
\(\mathrm{t}=\frac{v-u}{a}=\frac{0-35 \mathrm{~m} / \mathrm{s}}{-3.06 \mathrm{~m} / \mathrm{s}^2}\)
= 11.44 सेकण्ड 

प्रश्न 3. 7. 
दो रेलगाड़ियाँ A व B दो समांतर पटरियों पर 72 kmh^-1 की एकसमान चाल से एक ही दिशा में चल रही हैं। प्रत्येक गाड़ी 400m लंबी है और गाड़ी A गाड़ी B से आगे है । B का चालक A से आगे निकलना चाहता है तथा 1ms^-2 से इसे त्वरित करता है। यदि 50s के बाद B का गार्ड A के चालक से आगे हो जाता है तो दोनों के बीच आरंभिक दूरी कितनी थी? 
उत्तर: 
हल - गाड़ी A के लिये u = 72 km/h 
\(=\frac{72 \times 1000}{60 \times 60}\)
= 20m/s 
t = 50, a = 0, S = SA 
गति के दूसरे समीकरण से 
s = ut + 1/2 at²
∴ SA = 20 x 50 + 1/2 x 0 x (50)²
= 1000 + 0 = 1000 m
गाड़ी B के लिये 
s = 72 km/s = 20 m/s 
a = 1m/s², t = 50 s 
S = SB 
S = ut + 1/2 at² 
∴ SB  = 20 × 50 + × 1 × (50)² 
= 1000 + 1/2  × 2500 
1000 + 1250 = 2250 m 
∴ रेलगाड़ी के बीच आरम्भिक दूरी = 2250 - 1000 
= 1250m 

प्रश्न 3.8. 
दो लेन वाली किसी सड़क पर कार A 36kmh^-1 की चाल से चल रही है। एक-दूसरे की विपरीत दिशाओं में चलती दो कारें B व C जिनमें से प्रत्येक की चाल 54 km h^-1 है, कार A तक पहुँचना चाहती हैं। किसी क्षण जब दूरी AB दूरी AC के बराबर है तथा दोनों 1 km है, कार B का चालक यह निर्णय करता है कि कार C के कार A तक पहुँचने के पहले ही वह कार A से आगे निकल जाए। किसी दुर्घटना से बचने के लिए कार B का कितना न्यूनतम त्वरण जरूरी है? 
उत्तर: 
कार A की चाल = 36 km/h. 
\(=\frac{36 \times 1000}{60 \times 60} \mathrm{~m} / \mathrm{s}\)
= 10m/s. 

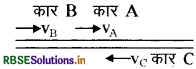
कार B व कार C की चाल = 54 km/h 
\(=\frac{54 \times 1000}{60 \times 60}=15 \mathrm{~m} / \mathrm{s}\)
कार B की चाल कार A के सापेक्ष VBA 
तो 
VBA = VB - VA = 15 - 10 = 5m/s. 
कार C की कार A के सापेक्ष आपेक्षिक चाल VCA = VC - VA 
VCA = VC - VA 
VC बायीं ओर गतिशील है अतः 
VCA = - [15 + 10] 
VCA = - 25 m/s 
∴ VAC = - VCA = + 25 m/s 
दूरी तय करने में लिया समय = t 
∴ AB = AC = 1 km = 1000 m. 
माना कार C द्वारा AC 
समय t = \(\frac{\mathrm{S}}{\mathrm{V}}=\frac{\mathrm{AC}}{\mathrm{v}_{\mathrm{CA}}}=\frac{1000}{25}\) = 40s. 
यदि कार B, a त्वरण उत्पन्न करती है, जब वह कार C के कार A तक पहुँचने के पहले ही कार A से आगे निकल जाये। 
s = ut + 1⁄2 at² का उपयोग करने पर 
AB =  VBA. t + 1/2 at²
at 2 
या 
1000 = 5 x 40 + 1/2 x a a (40)²
या 
1000 - 200 = 800 a 
या 
1000 = 200 + 800 a 
800a = 800 
a = 1 m/s² 

प्रश्न 3.9. 
दो नगर A व B नियमित बस सेवा द्वारा एक-दूसरे से जुड़े हैं और प्रत्येक T मिनट के बाद दोनों तरफ बसें चलती हैं। कोई व्यक्ति साइकिल से 20km h^-1 की चाल से A से B की तरफ जा रहा है और यह नोट करता है कि प्रत्येक 18 मिनट के बाद एक बस उसकी गति की दिशा में तथा प्रत्येक 6 मिनट बाद उसके विपरीत दिशा में गुजरती है। बस सेवाकाल T कितना है और बसें सड़क पर किस चाल (स्थिर मानिए) से चलती हैं? 
उत्तर: 
हल माना प्रत्येक बस की चाल = V1 km/h 
तथा साइकिल सवार की चाल = V2 km/h (A) साइकिल सवार की दिशा में बसों की आपेक्षिक चाल अर्थात् 
चाल A से B की ओर 
= V1 - V2 = (V1 - 20 ) km/h 
∴ V2 = 20 km/h 
चूँकि बस साइकिल सवार व्यक्ति की प्रत्येक 18 मिनट अर्थात् (18/60) घण्टा में पार करती है। 
अतः साइकिल सवार के 
= (V1 - 20) × 18/60 ...(1) 
बस द्वारा T मिनट में दूरी 
= v1 x T/60 ........ (2)
समीकरण (1) तथा (2) को बराबर करने पर 
(V1 - 20) x 18/60 = v1 x T/60
या 18 (v1 -  20)  = v1 × T 
\(\mathrm{v}_1-20=\frac{\mathrm{v}_1 \times \mathrm{T}}{18}\) ... (3) 

(B) साइकिल सवार के सापेक्ष शहर B से A की ओर आने वाली बस की आपेक्षिक चाल अर्थात् उस बस की आपेक्षिक चाल जो साइकिल सवार के विपरीत दिशा में गतिशील है। 
= (v1 + 20 ) km/h 
 ∵ विपरीत दिशा 
6 मिनट में बस द्वारा तय दूरी 
= (V1 + 20) x 6/60 km  ...(4) 
बस द्वारा T समय में तय दूरी 
= v1 x T/60 km ........... (5)
समीकरण (4) व (5) को बराबर रखने पर 
(v1 + 20)x 6/60 = v1 x T/60
(V1 + 20) = \(\frac{v_1 \times T}{6}\)
समीकरण (6) में समीकरण (3) से भाग देने पर 
\(\frac{v_1+20}{v_1-20}=\frac{18}{6}=3\)
या 
V1 + 20 = 3(V1 - 20) 
V1 + 20 = 3v1 - 60 
या 
20 + 60 = 3v1 - V1 = 2V1 
या 
V1 = 80/2 = 40 km/h 
समीकरण ( 3 ) में v का मान रखने पर 
40 - 20 = 40 x T /18 
या 
\(20=\frac{40 \mathrm{~T}}{18}\)
या 
\(\frac{20 \times 18}{40}=\mathrm{T}\)
या 
T = 9 मिनट 
v1 = 40 km/h, T = 9 मिनट 

प्रश्न 3.10. कोई खिलाड़ी एक गेंद को ऊपर की ओर आरंभिक चाल 29ms^-1 से फेंकता है, 
(i) गेंद की ऊपर की ओर गति के दौरान त्वरण की दिशा क्या होगी?
(ii) इसकी गति के उच्चतम बिन्दु पर गेंद के वेग व त्वरण क्या होंगे?
(iii) गेंद के उच्चतम बिन्दु पर स्थान व समय को x = 0 व t = 0 चुनिए, ऊर्ध्वाधर नीचे की ओर की दिशा को x-अक्ष की धनात्मक दिशा मानिए। गेंद की ऊपर की व नीचे की ओर गति के दौरान स्थिति, वेग व त्वरण के चिन्ह बताइए  
(iv) किस ऊँचाई तक गेंद ऊपर जाती है और कितनी देर के बाद गेंद खिलाड़ी के हाथों में आ जाती है?
[g = 9.8 m s± तथा वायु का प्रतिरोध नगण्य है।] 
उत्तर: 
(i) गुरुत्वीय त्वरण की दिशा ऊर्ध्वाधर नीचे की तरफ होगी चूँकि गेंद गुरुत्वीय प्रभाव में ऊपर की ओर घूम रही है। 
(ii) उच्चतम बिन्दु पर गेंद का अन्तिम वेग शून्य हो जायेगा । परन्तु 9.8 m/s² त्वरण ऊर्ध्वाधर अधोमुखी कार्य करता रहता है। 
(iii) जब x = 0 तथा t = 0 उच्चतम बिन्दु पर लिये जाते हैं तथा ऊर्ध्वाधर अधोमुखी दिशा को धनात्मक माना जाता है तब 
ऊपरमुखी गति के लिये स्थिति का चिन्ह ऋणात्मक, वेग का चिन्ह ऋणात्मक तथा त्वरण का चिन्ह धनात्मक होगा। v < 0, a > 0 
अधोमुखी गति में (नीचे की तरफ गति) - स्थिति का चिन्ह धनात्मक, वेग का चिन्ह धनात्मक तथा त्वरण का चिन्ह भी धनात्मक है अर्थात् v > (0, a > 0 
(iv) माना उच्चतम बिन्दु पर गेंद जाती है और समय 1 सेकण्ड लगता है, H = पृथ्वी से उच्चतम बिन्दु की ऊँचाई 
 ∵ आरम्भिक वेग u = - 29m/s 
a = g = 9.8 m/s² 
अन्तिम वेग v = 0, s = H = ?, t = ? 
v² - u² = 2as के सम्बन्ध को प्रयोग 
करने पर 
(0)² - (-29)² = 2 × 9.8 × H 
0 - 29 × 29 = 2 × 9.8 × H 
\(\mathrm{H}=\frac{-29 \times 29}{2 \times 9.8}\)
H = - 42.91m 
ऋण चिन्ह दर्शाता है कि तय की गयी दूरी ऊर्ध्वाधर ऊपर मुखी 
समीकरण 
या 
v = u + at 
0 = - 29 + 9.8 t 
या 
t = 29/9.8 = 2.96 सेकण्ड 
यहाँ पर पिण्ड केवल गुरुत्व के प्रभाव में गतिशील होता है । इसलिये गेंद का वापस आने का समय भी 2.96 सेकण्ड ही होगा। 
 ∵ कुल समय जिसमें गेंद खिलाड़ी के हाथ में वापस आ जाती है = 2 x 2.96 = 5.92 सेकण्ड 

 
प्रश्न 3.11. 
नीचे दिए गए कथनों को ध्यान से पढ़िए और कारण बताते हुए व उदाहरण देते हुए बताइए कि वे सत्य हैं या असत्य, एकविमीय गति में किसी कण की 
(a) किसी क्षण चाल शून्य होने पर भी उसका त्वरण अशून्य हो सकता है। 
(b) चाल शून्य होने पर भी उसका वेग अशून्य हो सकता है। 
(c) चाल स्थिर हो तो त्वरण अवश्य ही शून्य होना चाहिए। 
(d) चाल अवश्य ही बढ़ती रहेगी, यदि उसका त्वरण धनात्मक 
उत्तर:
(a) कथन सत्य है, चूँकि यदि गेंद की गति ऊपर मुखी है तो उच्चतम बिन्दु पर इसकी चाल शून्य होगी लेकिन अधोमुखी दिशा में त्वरण का मान 9.8m/s² जो गुरुत्वीय त्वरण के बराबर है, जो नीचे की ओर कार्य करता रहेगा। 
(b) कथन असत्य है। 
क्योंकि चाल, वेग का परिमाण होता है। चाल शून्य होने पर वेग का परिमाण शून्य होगा, इसलिये वेग का मान शून्य होगा। 
(c) सत्य, जब कोई एक कण समान चाल से एक सरल रेखा में गति कर रहा हो तब उसका वेग समय के साथ स्थिर रहता है। इसलिये 

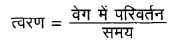
उदाहरण: किसी प्रत्यास्थ वस्तु का प्रत्यास्थ तल से संघट्ट। 
(d) असत्य, क्योंकि यदि हम गुरुत्वीय त्वरण की ऊर्ध्वाधर अधोमुखी दिशा को धनात्मक मान लें तो ऊपर की ओर ऊर्ध्वाधर दिशा में फेंकी गई गेंद की चाल धीमी होती जायेगी, परन्तु कथन सत्य भी हो सकता है यदि गति की दिशा ही त्वरण धनात्मक दिशा मान ली जाये। 

प्रश्न 3.12. 
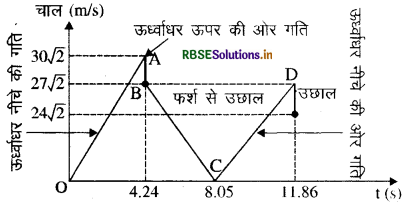
किसी गेंद को 90m की ऊँचाई से फर्श पर गिराया जाता है। फर्श के साथ प्रत्येक टक्कर में गेंद की चाल 1/10 कम हो जाती है। इसकी गति का t = 0 से 12s के बीच चाल - समय ग्राफ खींचिए। 
उत्तर:
दिया गया है- गेंद का प्रारम्भिक वेग u = 0, g = 10m / s², h = 90m, t = ?, v = ? 
गति के दूसरे समीकरण से 
h = ut + 1/2gt²
h = 0 x t + 1/2gt² 
h = 1/2 gt² 
2h = gt² 
\(\begin{aligned} \mathrm{t} & =\sqrt{\frac{2 h}{g}} \\ \mathrm{t} & =\sqrt{\frac{2 \times 90}{10}} \end{aligned}\)
\(\sqrt{18}=\sqrt{9 \times 2}=3 \sqrt{2}\)
t = 3√2 = 3 × 1.414 = 4.242 t = 4.2 सेकण्ड 
गति के तीसरे समीकरण से 
v² = u² + 2gh 
v² = 0 + 2gh = 2gh 
\(\mathrm{v}=\sqrt{2 g h}=\sqrt{2 \times 10 \times 90}\)
\(=\sqrt{900 \times 2}=30 \sqrt{2}\)

\(=30 \sqrt{2} \mathrm{~m} / \mathrm{s}\)
टक्कर के बाद गेंद का वेग 
u' = v - 1/10 v
\(\begin{aligned} & u^{\prime}=\frac{9}{10} v \\ & u^{\prime}=\frac{9}{10} \times 30 \sqrt{2} \end{aligned}\)
u' = 27√2 m/s. 
= 27 × 1.414 = 38.18 m/s. 
उच्चतम बिन्दु तक पहुँचने का समय 
\(\mathbf{t}^{\prime}=\frac{\mathrm{u}^{\prime}}{g}=\frac{27 \sqrt{2}}{10}\)
t' = 2.7 √2 = 3.81 सेकण्ड 
कुल समय = t + t' 
= 4.24 + 3.81 = 8.05 सेकण्ड गेंद फर्श पर पुन: 3.81 सेकण्ड बाद टकरायेगी जहाँ पर टकराने से पहले उसका वेग imm होगा। 
गेंद का टकराने के बाद पुनः वेग 
तब इसका समय होगा 
\(\begin{aligned} & =\frac{9}{10} \times 27 \sqrt{2} \\ & =24.3 \sqrt{2} \mathrm{~m} / \mathrm{s} . \end{aligned}\)
= 24.3 √2 m/s. 
= 8.05 + 3.81 = 11.86 सेकण्ड 

प्रश्न 3.13. 
उदाहरण सहित निम्नलिखित के बीच के अन्तर को स्पष्ट कीजिए:
(a) किसी समय अंतराल में विस्थापन के परिमाण (जिसे कभी-कभी दूरी भी कहा जाता है) और किसी कण द्वारा उसी अंतराल के दौरान तय किए गए पथ की कुल लंबाई। 
(b) किसी समय अंतराल में औसत वेग के परिमाण और उसी अंतराल में औसत चाल (किसी समय अंतराल में किसी कण की औसत चाल को समय अंतराल द्वारा विभाजित की गई कुल पथ-लंबाई के रूप में परिभाषित किया जाता है)। प्रदर्शित कीजिए कि (a) व (b) दोनों में ही दूसरी राशि पहली से अधिक या उसके बराबर है। समता का चिन्ह कब सत्य होता है ? ( सरलता के लिए केवल एकविमीय गति पर विचार कीजिए।) 
उत्तर:
(a) विस्थापन का परिमाण या पिण्ड द्वारा दत्त समय में तय दूरी वस्तु की अंतिम एवं प्रारम्भिक स्थितियों मैं अन्तर के बराबर है। इसे हम F - | से प्रदर्शित कर सकते हैं। पिण्ड द्वारा तय की गयी पथ की लम्बाई 

इसके द्वारा तय वास्तविक दूरी के बराबर है। पथ की कुल लम्बाई या तो अधिक या फिर विस्थापन के परिमाण के बराबर होती है। 

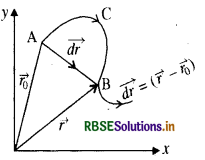
(b) माना समय 1 तथा 12 पर कण की स्थिति A व B पर है। 
∴ t1 व 12 के बीच माध्य वेग = \(\frac{A B}{t_2-t_1}\)
माध्य वेग 
\(\mathrm{v}_a=\lim _{\Delta t \rightarrow 0} \frac{\Delta r}{\Delta t}=\frac{d r}{d t}\)
जहाँ पर 
∆t = t₂ - t₁
माध्य वेग से यह स्पष्ट नहीं होता है कि कण की गति पथ AB या ACB के अनुदिश थी तथा समय 1 तथा 12 के बीच गति स्थायी थी या नहीं। माध्य वेग ज्ञात करने के लिये तय की गयी कुल दूरी में कुल समय का भाग देकर ज्ञात करते हैं। माना कि एक व्यक्ति 2 km दूर स्थित स्कूल में जाकर 2 घंटे में वापस आ जाता है (दोनों ओर की यात्रा ) 
∴ व्यक्ति की माध्य चाल = imm
= 2 km/h 
परन्तु माध्य वेग शून्य है क्योंकि 2 घण्टे के समय में उसका विस्थापन शून्य है। इस प्रकार (a) या (b) में द्वितीय राशि प्रथम राशि की अपेक्षा या तो अधिक है या उसके तुल्य । बराबर का चिन्ह उस समय सत्य है जब विस्थापन दूरी के बराबर हो। 

प्रश्न 3.14. 
कोई व्यक्ति अपने घर से सीधी सड़क पर 5km h^-1 की चाल से 2.5 km दूर बाजार तक पैदल चलता है। परन्तु बाजार बंद देखकर वह उसी क्षण वापस मुड़ जाता है तथा 7.5 km h^-1 की चाल से घर लौट आता है। 
समय अन्तराल (i) 0-30 मिनट, (ii) 0-50 मिनट, (iii) 0 - 40 मिनट की अवधि में उस व्यक्ति (a) के माध्य वेग का परिमाण तथा (b) का माध्य चाल क्या है? (नोट: आप इस उदाहरण से समझ सकेंगे कि औसत चाल को औसत वेग के परिमाण के रूप में परिभाषित करने की अपेक्षा समय द्वारा विभाजित कुल पथ-लंबाई के रूप में परिभाषित करना अधिक अच्छा क्यों है। आप थक कर घर लौटे उस व्यक्ति को यह बताना नहीं चाहेंगे कि उसकी औसत चाल शून्य थी ।) 
उत्तर:
माना व्यक्ति घर से बाजार जाने में 11 समय लेता है। 

और t₂ समय बाजार से घर जाने में लेता है। 
∴
∴ कुल समय लिया गया = t₁ + t₂ 
\(=\frac{1}{2} h+\frac{1}{3} h=\frac{5}{6} h\)
\(=\frac{5}{6} \times 60=50\) मिनट 

(i) समय अन्तराल 0 से 30 मिनट 
x 60 = 50 मिनट 
(a)

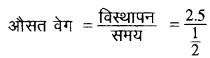
= 5 km/h 
(b)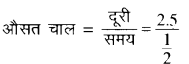 
(ii) समय अन्तराल 0 से 50 मिनट 
तय की गयी कुल दूरी = 2.5 + 2.5 
= 5 km. 

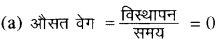
∵ यात्रा में लिया गया कुल समय = 20 + 300 = 50 मिनट है 
अतः व्यक्ति घर पर वापस आ जाता है जिससे कुल विस्थापन शून्य होगा। 

 
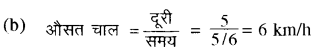
(iii) समय अन्तराल 0 से 40 मिनट 
30 मिनट में तय की गयी दूरी (घर से बाजार तक) 
= 2.5 km 
10 मिनट में तय की गयी दूरी (बाजार से घर तक) 
= 7.5 km/h 
\(=7.5 \times \frac{10}{60}\)
= 1.25 km 
∴ विस्थापन = 2.50 - 1.25 = 1.25 km. 
तय की गयी दूरी = 2.5 + 1.25 = 3.75 km. 

= 5.625 km/h. 
उपर्युक्त स्थितियों से यह स्पष्ट है कि माध्य वेग शून्य है परन्तु माध्य चाल शून्य नहीं है अतः माध्य चाल को कुल दूरी तथा कुल समय के अनुपात के रूप में व्यक्त करना माध्य वेग के परिमाण के रूप में परिभाषित करने से अच्छा है।

 
प्रश्न 3.15. 
हमने अभ्यास 3.13 तथा 3.14 में औसत चाल व औसत वेग के परिमाण के बीच के अन्तर को स्पष्ट किया है। यदि हम तात्क्षणिक चाल व वेग के परिमाण पर विचार करते हैं तो इस तरह का अंतर करना आवश्यक नहीं होता। तात्क्षणिक चाल हमेशा तात्क्षणिक वेग के बराबर होती है। क्यों? 
उत्तर:
किसी वस्तु का तात्क्षणिक वेग उस क्षण वस्तु के वेग के बराबर होता है। माध्य वेग का सीमान्तक तात्क्षणिक चाल कहलाता है। इस प्रकार जब समय अन्तराल सूक्ष्म हो तो विस्थापन का परिमाण ही प्रभावी रूप से वस्तु द्वारा उसी सूक्ष्म समय अन्तराल में तय दूरी के बराबर होता है। अतः इस मामले में क्षणिक वेग तथा क्षणिक चाल बराबर है। इसको निम्न द्वारा समझ सकते हैं:

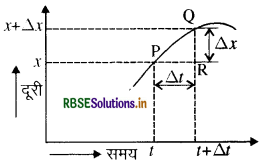
गतिमान वस्तु का तात्क्षणिक वेग उसके औसत वेग के बराबर होगा यदि उसके दो समयों (t तथा t + At ) के बीच का अन्तराल At 
अनन्तः सूक्ष्म हो। 
समय अन्तराल Δt में माध्य वेग 
\(=\frac{\Delta x}{\Delta t}\)
क्षण t पर क्षणिक वेग  \(=\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=\frac{d x}{d t}\) ....... (1)

यहाँ पर PQ = PQ रेखा की लम्बाई है। 
ΔPQR से (PQ ) 2 = (PR ) 2 + (QR) 2 
जैसे Δt → 0, PQ → QR या PQ → Δx 
समीकरण (2) से क्षणिक चाल = \(\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=\frac{d x}{d t}\)
जो कि क्षणिक वेग का परिमाण है। 

प्रश्न 3.16. 
चित्र में (a) से (d) तक के ग्राफों को ध्यान से देखिए और देखकर बताइए कि इनमें से कौन-सा ग्राफ एकविमीय गति को संभवतः नहीं दर्शा सकता। 

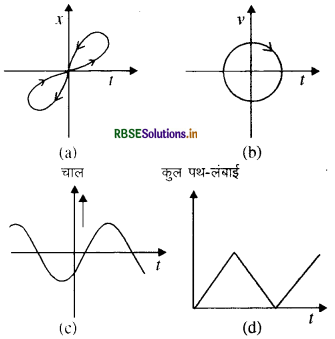
उत्तर:
(a) यह ग्राफ एकविमीय गति को संभवतः नहीं दर्शा सकता है। चूँकि इसमें किसी समय कण की दो स्थितियाँ हैं, जो कि एकविमीय गति को नहीं बताती हैं। 
(b) यह ग्राफ एकविमीय गति को संभवतः नहीं दर्शा सकता है। चूँकि किसी समय कण की दो स्थितियाँ या दो चाल / गति दर्शाई गयी हैं, जो कि एकविमीय गति में संभव नहीं हैं। 
(c) यह ग्राफ एकविमीय गति को नहीं दर्शाता है। चूँकि यह ग्राफ बतलाता है कि कण ऋणात्मक चाल रखता है, किन्तु कण की चाल कभी भी ऋणात्मक नहीं हो सकती है चाल सदैव धनात्मक होती है। 
(d) यह ग्राफ भी एकविमीय गति प्रदर्शित नहीं करता, चूँकि यह प्रदर्शित कर रहा है कि कुल पथ की लम्बाई एक निश्चित समय के `पश्चात् घट रही है, परन्तु गतिमान कण की कुल पथ - लम्बाई कभी भी समय के साथ नहीं घटती ग्राफ d से भी स्पष्ट है कि किसी समय में कुल पथ दूरी कम हो जाती है जो कि एकविमीय गति में संभव नहीं है। अतः हम कह सकते हैं कि (a) से (d) तक के बीच कोई आरेख 
एकविमीय गति नहीं दर्शाता है। 

प्रश्न 3.17. 
चित्र में किसी कण की एकविमीय गति का x - t ग्राफ दिखाया गया है। ग्राफ से कण t < 0 के लिए किसी सरल परवलीय पथ में गति करता है। उचित भौतिक संदर्भ का सुझाव दीजिए। 
क्या यह कहना ठीक होगा कि यह रेखा में और t > 0 के लिए किसी यदि नहीं, तो ग्राफ के संगत किसी 

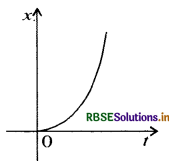
उत्तर: 
यह असत्य है कि < 0 पर कण सरल रेखा में तथा t > 0 पर वह परवलीय मार्ग पर चलता है, क्योंकि चित्र में x - 1 में आरेख कण की गति का पथ नहीं दर्शाता । ग्राफ से पता चलता है 1 = 0 पर x = 0 है। 
संदर्भ - समुच्चित संदर्भ एक पिण्ड का स्वतंत्र पतन है । जैसे - किसी वस्तु का किसी मीनार से स्वतंत्र पतन अर्थात् t = 0 पर x = 0 है।
ग्राफ द्वारा t = 0 पर x = 0 प्रदर्शित है, अतः ग्राफ गुरुत्व के अन्तर्गत ऊँचाई से गिरती हुई किसी वस्तु की गति प्रदर्शित कर सकता 
 
प्रश्न 3.18. 
किसी राजमार्ग पर पुलिस की कोई गाड़ी 30 km/h की चाल से चल रही है और उसी दिशा में 192 km/h की चाल से जा रही किसी चोर की कार पर गोली चलाती है। यदि गोली की नालमुखी चाल 150 m/s है तो चोर की कार को गोली किस चाल के साथ आघात करेगी? 
(नोट- उस चाल को ज्ञात कीजिये जो चोर की कार को हानि पहुँचाने में प्रासंगिक हो।) 
उत्तर:
दिया गया है: 
पुलिस की गाड़ी की चाल v 
\(=\frac{30 \times 5}{18}=\frac{25}{3} \mathrm{~m} / \mathrm{s}\)
चोर की कार की चाल = 192 km/h 
\(\mathrm{v}_1=\frac{192 \times 5}{18}=\frac{160}{3} \mathrm{~m} / \mathrm{s}\)
गोली की नालमुखी चाल = 150m/s. 
गोली की कुल चाल = गोली की नालमुखी चाल + पुलिस की गाड़ी की चाल 
\(\left(v_2^{\prime}\right)=150+\frac{25}{3}=\frac{475}{3} \mathrm{~m} / \mathrm{s}\)
∴ चोर की गाड़ी के सापेक्ष गोली का आपेक्षिक वेग = V2 - V 
( चूँकि दिशा एक ही है) 
\(\frac{475}{3}-\frac{160}{3}=\frac{315}{3}\)
= 105 m/s 

प्रश्न 3.19. 
चित्र में दिखाए गए प्रत्येक ग्राफ के लिए किसी उचित भौतिक स्थिति का सुझाव दीजिए:

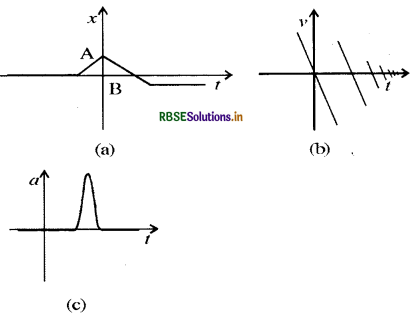
उत्तरं:
(a) जब किसी चिकने फर्श पर रखी गेंद को ठोकर मारी जाती है तो उसका x - t वक्र नीचे दिये हुए वक्र की तरह प्राप्त होता है। जब वह दीवार से टकराकर मंदित होती है तो रेखा B से उसकी गति दिखायी जा सकती है । बाद में वह किसी और दीवार से विश्राम में लायी जाती है जो x - 1 आरेख पर 1 के समान्तर रेखा से दिखायी गयी है । 

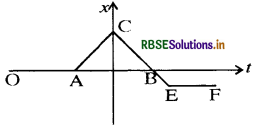
(b) आरेख (b) में किसी गेंद को किसी प्रारम्भिक वेग से ऊपर की ओर फेंका गया है जो बार - बार नीचे की ओर फर्श पर गिरकर उससे टकराकर कम गति से ऊपर उठती है। प्रत्येक टक्कर के बाद उसकी चाल ऊपर की ओर कम होती जाती है। 

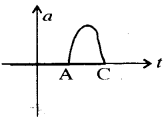
(c) यह ग्राफ त्वरण व समय में है। यह समान चाल से चलती क्रिकेट की गेंद बैट से टकराकर वापस आने का आरेख है। ग्राफ में यह छोटे से समय अन्तराल के लिये दिखाया गया है। 

प्रश्न 3. 20. 
चित्र में किसी कण की एकविमीय सरल आवर्ती गति के लिए x - t ग्राफ दिखाया गया है। ( इस गति के बारे में आप अध्याय 14 में पढ़ेंगे) समय t = 0.3s, 12 s, - 1.2 s पर कण के स्थिति, वेग व त्वरण के चिन्ह क्या होंगे? 

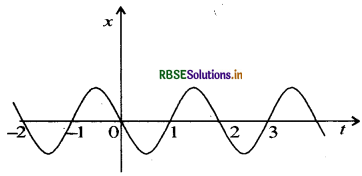
उत्तरं:
सरलं आवर्त गति में, 
त्वरण a = - ω²x  ......... (1)
तथा वेग 
v = dx/dt ........ (2) 
(जहाँ पर ω स्थिरांक है) 
(i) जब t = 0.1 सेकण्ड तथा x ऋणात्मक है। 
x - t ग्राफ का ढाल ऋणात्मक है जिससे v भी ऋणात्मक है। समीकरण (1) से त्वरण a धनात्मक है। 
(ii) जब t = 1.2 सेकण्ड तब x धनात्मक है। 
x - t ग्राफ का ढाल धनात्मक है जिससे v धनात्मक है। 
समीकरण ( 1 ) से त्वरण a ऋणात्मक है। 
(iii) जब t = - 1.2 सेकण्ड तब x ऋणात्मक है।  
x - t ग्राफ का ढाल धनात्मक है जिससे v समीकरण (1) से त्वरण a धनात्मक है। 

प्रश्न 3. 21. 
चित्र किसी कण की एकविमीय गति का ग्राफ दर्शाता है। इसमें तीन समान अंतराल दिखाए गए हैं। किस अंतराल में औसत चाल अधिकतम है और किसमें न्यूनतम है? प्रत्येक अंतराल के लिए औसत वेग का चिन्ह बताइए

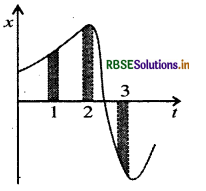
उत्तरं:
हम जानते हैं कि छोटे से समय अन्तराल में औसत वेग का मान, (x - t) आरेख की उस समय अन्तराल की प्रवणता के बराबर होता है अतः अन्तराल 3 में औसत चाल अधिकतम है, क्योंकि इसमें आरेख की प्रवणता (ढाल) अधिकतम है तथा (x - t) आरेख की प्रवणता 2 में न्यूनतम है । अतः औसत वेग भी 2 में न्यूनतम होगा। अन्तराल 1 व 2 में माध्य वेग धनात्मक परन्तु 3 में ऋणात्मक है। क्योंकि अन्तराल 1, 2 में x₂ - X₁ धनात्मक है तथा अन्तराल 3 में यह ऋणात्मक है। 

प्रश्न 3.22. 
चित्र में किसी नियत (स्थिर) दिशा के अनुदिश चल रहे कण का चाल-समय ग्राफ दिखाया गया है। इसमें तीन समान समय अंतराल दिखाए गए हैं। किस अंतराल में औसत त्वरण का परिमाण अधिकतम होगा? किस अंतराल में औसत चाल अधिकतम होगी? धनात्मक दिशा को गति की स्थिर दिशा चुनते हुए तीनों अंतरालों में तथा a के चिन्ह बताइए A, B, C व D बिंदुओं पर त्वरण क्या होंगे? 

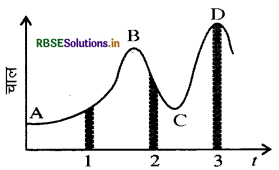
उत्तरं:
(i) हम जानते हैं कि औसत त्वरण छोटे समय अन्तराल में वह (v - t) आरेख का उस समय अन्तराल में प्रवणता के बराबर होता है। 
अर्थात् औसत त्वरण का परिमाण =
अन्तराल 1 व 3 की अपेक्षा अन्तराल 2 में (v - t) आरेख की प्रवणता अधिकतम है। अतः माध्य त्वरण का परिमाण अन्तराल 2 में अधिकतम है। 
(ii) औसत वेग अन्तराल 3 में अधिकतम है तथा (1) में न्यूनतम है क्योंकि चाल अक्ष पर D का उठाव उच्चतम पर है। 
(iii) तीनों अन्तराल में धनात्मक है अर्थात् v > 0 है। (1) में त्वरण धनात्मक, (2) में त्वरण ऋणात्मक तथा (3) में त्वरण शून्य है। 
(iv) समय अन्तराल 1 व 3 में प्रवणता धनात्मक होने के कारण त्वरण (a) का मान धनात्मक होगा, लेकिन अन्तराल 2 में प्रवणता ऋणात्मक होने के कारण त्वरण a का मान भी ऋणात्मक है अर्थात् a > 0 समय अन्तराल 1 और 3 में a < 0 अन्तराल 2 में  
(v) बिन्दुओं A, B, C तथा D पर वेग समय आरेख x अक्ष के समान्तर है। इस कारण से इन सभी बिन्दुओं पर त्वरण a का मान शून्य होगा। (इन चारों बिन्दुओं पर चाल समान है।) 

अभ्यास के अतिरिक्त प्रश्न:

प्रश्न 3. 23. 
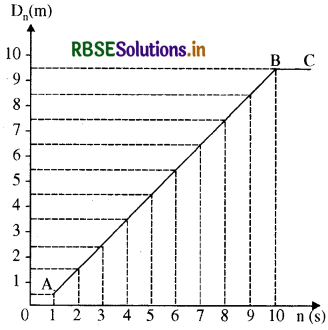
कोई तीन पहिये वाला स्कूटर अपनी विरामावस्था से गति प्रारंभ करता है। फिर 10s तक किसी सीधी सड़क पर 1ms^-2 के एकसमान त्वरण से चलता है। इसके बाद वह एकसमान वेग से चलता है। स्कूटर द्वारा nवें. सेकंड (n = 1, 2, 3.......) में तय की गई दूरी को n के सापेक्ष आलेखित कीजिए। आप क्या आशा करते हैं कि त्वरित गति के दौरान यह ग्राफ कोई सरल रेखा या कोई परवलय होगा? 
उत्तरं:
हल दिया गया है u = 0, त्वरण (a) = 1 m/s² 
t = 10 सेकण्ड 
यदि nth सेकण्ड में तय की गयी दूरी Sn हो तो समान त्वरण तथा प्रारंभिक वेग u होने पर 
sn = u+ 1⁄2 a (2n - 1) 
मान रखने पर 
sn = 0 + 1/2 × 1× (2 n -1) = 1⁄2 (2n -1 = 1/2 (2n-1)
n = 1, 2, 3, 4, 5, .................. रखने पर 
s1 = 1/2(2 × 1 -1) = 0.5m 
S2 = 1/2 (2 × 2 -1) = 1.5m 
S3 = 1⁄2 (2 × 3 - 1) = 2.5m 
S4 = 1/2 (2 × 4 - 1) = 3.5m. 
...................................
...................................
...................................
S10  = 1/2(2 × 10 - 1) = 19/2 
= 9.5m. 
nth सेकण्ड में तय दूरी Sn निम्न तालिका में दी गयी है:

n	1	2	3	4	5	6	7	8	9	10
Sn	0.5	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5

इन बिन्दुओं को ग्राफ पेपर पर आलेख करने पर हमको AB एक सरल रेखा प्राप्त होती है। चूँकि यहाँ पर Sn है, 10 सेकण्ड बा ग्राफ पर एक सरल रेखा BC है जो x - अक्ष के समान्तर है। 

प्रश्न 3.24. 
किसी स्थिर लिफ्ट में (जो ऊपर से खुली है) कोई बालक खड़ी है। वह अपने पूरे जोर से एक गेंद ऊपर की ओर फेंकत है जिसकी प्रारंभिक चाल 49ms है। उसके हाथों में गेंद के वापस आने में कितना समय लगेगा? यदि लिफ्ट ऊपर की ओर 5ms की एकसमान चाल से गति करना प्रारंभ कर दे और वह बालक फिर गेंद को अपने पूरे जोर से फेंकता तो कितनी देर में गेंद उसके हाथ में लौट आएगी? 
उत्तरं:
Case I - जब लिफ्ट स्थिर है। 
u = 49 मी./से. v = 0 मी./से. 
v = u - gt 
∴ 0 = 49 - 9.8 x t 

⇒ t = 49/9.8 = 5 सेकण्ड 
∴ कुल समय = 5 + 5 = 10 सेकण्ड 
∵ गेंद को ऊपर जाने में लगा समय = नीचे आने में लगा समय 
Case II - जब लिफ्ट समान वेग से गतिमान हो जाती है। 
जब लिफ्ट 5m/s की चाल से ऊपर की ओर अग्रसर होती है तो गेंद की आपेक्षिक गति वस्तु के सापेक्ष में कोई परिवर्तन नहीं होता, क्योंकि लिफ्ट में त्वरण के अभाव में चालक की गति 49 m/s ही रहती है। 
अतः प्राकृतिक रूप से गेंद बालक के हाथ में 10 सेकण्ड के बाद वापस आ जायेगी। 

प्रश्न 3.25. 
क्षैतिज में गतिमान कोई लंबा पट्टा (चित्र) 4 km/ h की चाल से चल रहा है। एक बालक इस पर (पट्टे के सापेक्ष) 9 km/h की चाल से कभी आगे कभी पीछे अपने माता-पिता के बीच दौड़ रहा है। माता व पिता के बीच 50m की दूरी है। बाहर किसी स्थिर प्लेटफार्म पर खड़े एक प्रेक्षक के लिए, निम्नलिखित का मान प्राप्त करिए:
चाल, 
(a) पट्टे की गति की दिशा में दौड़ रहे बालक की चाल, (b) पट्टे की गति की दिशा के विपरीत दौड़ रहे बालक की 
(c) बच्चे द्वारा (a) व (b) में लिया गया समय यदि बालक की गति का प्रेक्षण उसके माता या पिता करें तो कौन-सा उत्तर बदल जाएगा? 

उत्तरं: 
माना बायीं ओर से दायीं ओर की दिशा धनात्मक है। बालक की चाल पट्टे के सापेक्ष 
V 1 = 9 km/h. 
लम्बे पट्टे की चाल v2 = 4 km/h 
(a) जब बालक पट्टे की गति की विपरीत दिशा में दौड़ता है तो स्थिर प्रेक्षक की अपेक्षा बालक की चाल 
V = V1 + V2 
= 9 +4 = 13 km/h. (बायें से दायें) 
(b) जब बालक पट्टे की गति की विपरीत दिशा में दौड़ता है, 
v' = 4 - 9 = −5 km/h (दायें से बायें) ऋण चिन्ह यह बताता है कि बालक पट्टे की गति की विपरीत दिशा में दौड़ता हुआ प्रतीत होता है 
(c) माता-पिता के बीच की दूरी = s = 50 m. 
= 0.050 km. 
चूँकि बालक और माता-पिता एक ही पट्टे पर स्थित हैं अतः किसी भी स्थिर प्रेक्षक के लिये बालक की चाल पिता से माता की ओर सरल रेखा में गति 
या माता से पिता की ओर 9 km/h होगी अर्थात् बालक की चाल किसी भी माता या पिता की अपेक्षा 9 km/h ही होगी। 
∴ Case (a) व (b) में बालक द्वारा लिया गया समय 
\(\mathrm{t}=\frac{0.05 \mathrm{~km}}{9 \mathrm{~km} / \mathrm{h}}=\frac{.05}{9}\)
t = 0.5/9 x 60 x 60 = 20 सेकण्ड 
समय 20 सेकण्ड रह जायेगा यदि माता या पिता बालक की गति का प्रेक्षण करते हैं। 
यदि कोई एक माता या पिता गति को देखता है तो भी (a) व (b) के लिये उत्तर अपरिवर्तनीय होगा। यह इसलिये है कि किसी एक माता या पिता की अपेक्षा बालक की चाल 9 km/h है।
 
प्रश्न 3.26. 
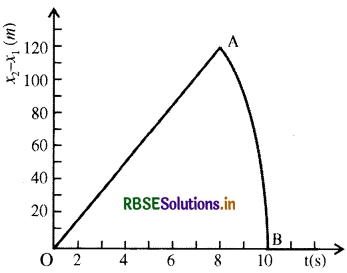
किसी 200 m ऊँची खड़ी चट्टान के किनारे से दो पत्थरों को एक साथ ऊपर की ओर 15ms^-1 तथा 30ms^-1 की प्रारंभिक चाल से फेंका जाता है। इसका सत्यापन कीजिए कि सामने दिखाया गया ग्राफ (चित्र) पहले पत्थर के सापेक्ष दूसरे पत्थर की आपेक्षिक स्थिति का समय के साथ परिवर्तन को प्रदर्शित करता है। वायु के प्रतिरोध को नगण्य मानिए और यह मानिए कि जमीन से टकराने के बाद पत्थर ऊपर की ओर उछलते नहीं। मान लीजिए g = 10 ms^-21 ग्राफ के रेखीय व वक्रीय भागों के लिए समीकरण लिखिए। 

उत्तरं: 
पहले पत्थर के t समय के लिए ऊर्ध्वाधर गति लेते हुए 
xo = 200m. 
u = 15m/s. 
a = - 10 m/s², t = t, x = x1 
X = Xo + ut + 1/2 at² 
∴ x1 = 200 + 15t + 1/2 (-10)ť² 
x1 = 200+ 15t - 5t² ........... (1)
जब पहला पत्थर जमीन पर टकराता है। 
x1 = 0
∴ समीकरण (1) से 
0 = 200 + 15t - 5t² 
5t² - 15t - 200 = 0 
या 
t² - 3t - 40 = 0 
या (t - 8) (t + 5) = 0 
∴ t = 8 सेकण्ड या t = -5 सेकण्ड 
∵ t = -5 सेकण्ड (अर्थहीन है) 
∴ t = 8 सेकण्ड 

दूसरे पत्थर के लिये जब दूसरा पत्थर जमीन से टकराता है 
x² = 0
इसलिये समीकरण (2) से 
0 = 200 + 30t - 5t² 
या 5t² - 30t - 200 = 0 
या  t - 6t - 40 = 0 
(t - 10) (t + 4 ) = 0 
∴ t = 10 सेकण्ड या t = 4 सेकण्ड 
∵ t = 4 सेकण्ड (अर्थहीन है) 
∴ t = 10 सेकण्ड 
समीकरण ( 2 ) व समीकरण ( 1 ) 
x₂ - x₁ = 15t ....(3) 
यहाँ पर (x₂ - x₁) और t दोनों ही एकघातीय सम्बन्ध से जुड़े हैं। इसलिये आरेख एक सरल रेखा होगी। 
∴ वक्र का भाग OA एक सरल रेखा t = 8 सेकण्ड पर दोनों पत्थरों के बीच दूरी अधिकतम होगी, क्योंकि पत्थर (1) पृथ्वी पर आ जाता है जबकि दूसरा पत्थर गति में रहता है। 
x₂ - x = 15 x 8 = 120m 
8 सेकण्ड बाद केवल दूसरा पत्थर 2 सेकण्ड के लिए गति में होगा | ग्राफ 8 सेकण्ड से 10 सेकण्ड के बीच द्विघात समीकरण x₂ = 200 + 301 - 5t² के अनुसार होगा अर्थात् यह परवलीय है। 

प्रश्न 3.27. 
किसी निश्चित दिशा के अनुदिश चल रहे किसी कण का चाल- समय ग्राफ चित्र में दिखाया गया है। कण द्वारा (a) t = 0 s से t= 10s, (b) t = 2s से 6s के बीच तय की गई दूरी ज्ञात कीजिए। 

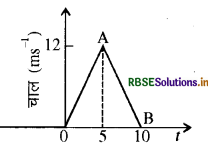
(a) तथा (b) में दिए गए अंतरालों की अवधि में कण की औसत चाल क्या है? 
उत्तरं: 
(a) (i) हम जानते हैं कि किसी समय में किसी वस्तु द्वारा तय की गयी दूरी उसके चाल- समय आरेख के क्षेत्रफल के बराबर होती है। 
t = (0) से t = 10 सेकण्ड समय में कण द्वारा तय दूरी 
= ∆OAB का क्षेत्रफल 
= 1/2आधार x ऊँचाई 
= 1⁄2 × 10 × 12 = 60m 
दिये गये समय अन्तराल में कण की माध्य चाल 

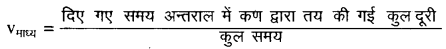
() सेकण्ड से 10 सेकण्ड में माध्य चाल, 
v_{माध्य}  = \(\frac{60}{10}=6 \mathrm{~m} / \mathrm{s}\)

(b) (i) 2 सेकण्ड से 6 सेकण्ड में तय दूरी ज्ञात करने के लिये 
t = 0 पर u = 0 तथा 
\(a=\frac{\mathrm{v}-\mathrm{u}}{\mathrm{t}}\) ..... (1)
t = 5 सेकण्ड पर v = 12 m/s 
\(a=\frac{12-0}{5}=\frac{12}{5}\)
= 2.4 m/s² 

समीकरण (1) का उपयोग करते हुये 2 सेकण्ड बाद V1 चाल 
V1 = 0 + 2.4 x 2 = 4.8 m/s 
∵ u = 0, a = 2.4, t = 2 सेकण्ड 
माना x1 = 2 सेकण्ड से 5 सेकण्ड में तय दूरी निम्न करते हैं:
x = ut + 1/2at² .......... (2)
x1 = 4.8 × 3 + 1/2 × 2.4 × (3)² 
x = 14.4 + 1.2 × 9 = 14.4 + 10.8 
= 25.2 मीटर प्राप्त करते हैं। 
x² = 5 से 6 सेकण्ड में तय दूरी 
a² = 5 से 10 सेकण्ड तक त्वरण 
V² = 5 सेकण्ड के पश्चात् चाल = 12m/s. 
v = 10 सेकण्ड पश्चात् अन्तिम वेग = () 
t = 10 - 5 = 5 सेकण्ड 
त्वरण (मंदन) = \(a_2=\frac{v-v_2}{t}=\frac{0-12}{5}\)
= - 2.4 m/s² 
समीकरण (2) का उपयोग करने पर 
x² = 12 × 1 + 1/2 × (-2.4) × (1)2 
= 12 - 1.2 = 10.8 m प्राप्त करते हैं । 
∵ यहाँ पर 
V = V2 = 12m/s 
a = - 2.4 m/s2, t = 1 सेकण्ड 
यदि x = 2 सेकण्ड से 6 सेकण्ड में कुल तय दूरी 
तब x = x1 + x2 
= 36 m 

(ii) समयान्तराल में माध्य चाल 

= 9 m/s. 

प्रश्न 3.28. 
एकविमीय गति में किसी कण का वेग-समय ग्राफ चित्र में दिखाया गया है:

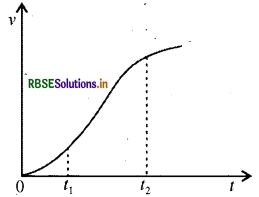
नीचे दिये सूत्रों में t₁ से t₂ तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही हैं:
(i) x(t₂) = x (t₁) + v (t₁) (t₂ - t₁) + (1/2)a (t ₂ - t₁)² 
(ii) V(t₂) = V(t₁) + a (t₂ - t₁) 
(iii) Vaverage= [x(t₂) - x (t₁)]/ (t₂ - t₁) 
(iv) aaverage = [ V(t₂ ) - v (t₁)] / (t₂ - t₁) 
(v) x(t₂) = x(t₁) + Vaverage (t₂ - t₁) + (1/2) aaverage (t₂ - t₁)² 
(vi) x(t₂ ) - x (t₁) = t - अक्ष तथा दिखाई गई बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल। 
उत्तरं: 
ग्राफ से स्पष्ट है कि वक्र का ढलान ( slope ) स्थिर तथा एकसमान नहीं है। अतः सम्बन्ध (i), (ii) तथा (v) सही नहीं हैं, लेकिन सम्बन्ध (iii), (iv) तथा (vi) सही हैं।