RBSE Solutions for Class 11 Physics Chapter 15 तरंगें

 Rajasthan Board RBSE Solutions for Class 11 Physics Chapter 15 तरंगें Textbook Exercise Questions and Answers.

RBSE Class 11 Physics Solutions Chapter 15 तरंगें

RBSE Class 11 Physics तरंगें Textbook Questions and Answers

प्रश्न 1.
2.50 kg द्रव्यमान की 20m लम्बी तानित डोरी पर 200 N बल का तनाव है। यदि इस डोरी के एक सिरे को अनुप्रस्थ झटका दिया जाए तो उत्पन्न विक्षोभ कितने समय में दूसरे सिरे तक पहुँचेगा?
उत्तर:
दिया गया है:
तानित डोरी का द्रव्यमान M = 2.50 kg
डोरी की लम्बाई l = 20.0m 
डोरी में तनाव T = 200 N
∴ इकाई लम्बाई की डोरी का द्रव्यमान
\(m=\frac{\mathbf{M}}{l}=\frac{2.50}{20.0}\)
m = 0.125kg/m
अनुप्रस्थ तरंगों का वेग \(\mathrm{v}=\sqrt{\frac{\mathrm{T}}{m}}\)
मान रखने पर
\(\begin{aligned} v & =\sqrt{\frac{200}{0.125}}=\sqrt{\frac{200 \times 1000}{125}} \\ & =\sqrt{200 \times 8}=\sqrt{1600} \end{aligned}\)
= 40m/s
उत्पन्न विक्षोभ को दूसरे सिरों तक पहुँचने का समय माना है
अतः समय

= l/v = 20/40 = 0.5s

प्रश्न 2.
300m मीनार के शीर्ष से गिराया गया पत्थर मीनार के आधार पर बने तालाब के पानी से टकराता है। यदि वायु में ध्वनि की चाल 340ms^-1 है तो पत्थर के टकराने की ध्वनि मीनार के शीर्ष पर पत्थर गिराने के कितनी देर बाद सुनाई देगी? (g = 9.8ms^-2 )
उत्तर:
दिया गया है:
मीनार की ऊंचाई h = 300m
g = 9.8m/s^-2
ध्वनि की चाल v = 340m/s.
माना पत्थर पानी से t1 समय के बाद टकराता है। तब गति के 
दूसरे समीकरण से:
s = ut + 1/2at²
मान रखने पर
300 = 0 × t₁ + 1/2 × 9.8 × t₁²
चूँकि पत्थर का प्रारम्भिक वेग u = Om/s
300 = 4.9t₁²
\(\begin{aligned} t_1^2 & =\frac{300}{4.9}=\frac{3000}{49} \\ t_1 & =\sqrt{\frac{3000}{49}}=7.82 \mathrm{~s} \end{aligned}\)
पत्थर टकराने के बाद ध्वनि का शीर्ष तक पहुँचने का समय माना t₂ है
\(t_2=\frac{h}{v}=\frac{300}{340}\)
शीर्ष पर टकराने की ध्वनि सुनने में लिया गया समय
t = t1 + l2 = 7.82 + 0.88 = 8.7s

प्रश्न 3.
12.0m लम्बे स्टील के तार का द्रव्यमान 2.10 kg है। तार में तनाव कितना होना चाहिये ताकि उस तार पर किसी अनुप्रस्थ तरंग की चाल 20° C पर शुष्क वायु में ध्वनि की चाल (343m 51 ) के बराबर हो।
उत्तर:
स्टील के तार की लम्बाई = 12.0m
द्रव्यमान M= 2.10 kg
तान में तनाव T = ?
इकाई लम्बाई के तार का द्रव्यमान
\(m=\frac{\mathrm{M}}{l}=\frac{2.10}{12.0}\)
= 0.175 kg/m
शुष्क वायु में ध्वनि की चाल = 343m/s
हम जानते हैं imm
या v₂ = T/m
या T = v₂m
मान रखने पर
= (343)² × 0.175
= 343 × 343 × 0.175
= 2.06 × 10⁴N

प्रश्न 4. 
सूत्र \(\mathbf{v}=\sqrt{\frac{\gamma \mathrm{P}}{\rho}}\) कि का उपयोग करके स्पष्ट कीजिये वायु में ध्वनि की चाल क्यों
(a) दाब पर निर्भर नहीं करती? 
(b) ताप के साथ बढ़ जाती है? तथा 
(c) आर्द्रता के साथ बढ़ जाती है? 
उत्तर:
(a) ध्वनि में वायु का वेग सूत्र
\(\mathbf{v}=\sqrt{\frac{\gamma \mathrm{P}}{\rho}}\) ................ (1)
यहाँ पर y = दी गयी गैस के लिये नियतांक है।
p =  गैस का घनत्व है।
गैस समीकरण से
PV = RT ∴ P = RT/v
समीकरण (1) में P का मान रखने पर
\(\mathrm{v}=\sqrt{\frac{\gamma \mathrm{RT}}{\mathrm{V} \rho}}\)
लेकिन द्रव्यमान M आयतन (V) घनत्व p
∴ \(\mathrm{v}=\sqrt{\frac{\gamma \mathrm{RT}}{\mathrm{M}}}\) .................. (2)
दी गयी गैस के लिये M स्थिर है और R भी स्थिर है। यदि T स्थिर हो तब समीकरण (2) से हम निष्कर्ष निकालते हैं कि ताप स्थिर रहने पर वायु (गैस) के दाब से v स्वतंत्र है।

(b) ताप का प्रभाव:
गैस समीकरण से
PV = RT
या
P = RT/V
\(\begin{aligned} \mathrm{v} & =\sqrt{\frac{\gamma \mathrm{P}}{\rho}} \\ & =\sqrt{\frac{\gamma \mathrm{RT}}{\rho \mathrm{V}}}=\sqrt{\frac{\gamma \mathrm{RT}}{\mathrm{M}}} \end{aligned}\)
यहाँ पर M = p, V = गैस का अणुभार
इस प्रकार यदि Y, R तथा M नियत या स्थिर है
इसलिये
\(V \propto \sqrt{T}\)
अर्थात् वायु या गैस में ध्वनि का वेग उसके ताप के वर्गमूल के समानुपाती होता है। इस प्रकार से कहा जा सकता है कि वायु में ध्वनि का वेग ताप बढ़ने के साथ बढ़ेगा।
(c) आर्द्रता का प्रभाव- वायु में पानी की वाष्प की उपस्थिति, वायु का घनत्व परिवर्तित कर देती है। इस प्रकार से आर्द्रता के साथ वायु में ध्वनि का वेग भी परिवर्तित हो जाता है।
माना
शुष्क वायु का वेग = Vd 
आर्द्रवायु में ध्वनि का वेग = Vm
शुष्क वायु का घनत्व = Pd
आर्द्र वायु का घनत्व = Pm

हम यह जानते हैं कि पानी की वाष्प का घनत्व शुष्क वायु के
घनत्व से कम होता है।
Pm < Pd
या
\(\frac{\rho_d}{\rho_m}>1\) .............. (4)
समीकरण (3) तथा (4) से हमें vm/vd > 1  प्राप्त होता है।
या
vm > vd
अर्थात् आर्द्रता के साथ ध्वनि का वायु में वेग बढ़ जाता है। यानी ध्वनि का वेग शुष्क वायु की अपेक्षा आर्द्र वायु में अधिक होता है। इसलिये ध्वनि शुष्क दिन की अपेक्षा बरसाती दिन में अधिक तेज चलती है।

प्रश्न 5. 
आपने यह सीखा कि एक विमा में कोई प्रगामी तरंग फलन y = f (x,t) द्वारा निरूपित की जाती है जिसमें x तथा को x - vt अथवा x + vt अर्थात् y = f (x +- ut) संयोजन में प्रकट होना चाहिये। क्या इसका प्रतिलोम भी सत्य है ? नीचे दिये गये के प्रत्येक फलन का परीक्षण करके यह बताइये कि वह किसी प्रगामी तरंग को निरूपित कर सकता है:
(a) (x - ut)²
(b) log [(x + ut)/x]
(c) l/(x + vt)
उत्तर:
नहीं, इसका प्रतिलोम सत्य नहीं है। प्रगामी तरंग निरूपित करने के लिये इसका मूल प्रतिबंध यह है किx और के सभी मानों के लिये तरंग फलन का मान सीमित होना चाहिये । y के दिये गये फलनों में से कोई भी इस प्रतिबन्ध को संतुष्ट नहीं करता है। इस कारण से यह फलन प्रगामी तरंगें प्रदर्शित नहीं करते हैं।

प्रश्न 6. 
कोई चमगादड़ वायु में 100 kHz आवृत्ति की पराश्रव्य ध्वनि उत्सर्जित करता है। यदि यह ध्वनि जल के पृष्ठ से टकराती है, तो (a) परावर्तित ध्वनि तथा (b) पारगमित ध्वनि की तरंगदैर्घ्य ज्ञात कीजिए। वायु तथा जल में ध्वनि की चाल क्रमशः 340ms^-1 तथा 1486ms^-1 है।
उत्तर:
दिया गया है
आवृत्ति n = 1000K Hz = 106 Hz. 
वायु में ध्वनि की चाल va = 340m/s 
जल में ध्वनि की चाल vw = 1486m/s 
(a) परावर्तित ध्वनि की तरंगदैर्ध्य
\(\begin{aligned} & \lambda_a=\frac{v_a}{n} \\ & \lambda_a=\frac{340}{10^6} \end{aligned}\)
= 3.4 x 10^-4 m
(b) पारगमित ध्वनि की तरंगदैर्ध्य
\(\begin{aligned} & \lambda_w=\frac{v_w}{n} \\ & \lambda_w=\frac{1486}{10^6} \end{aligned}\)
= 1.49 × 10^-3 m

प्रश्न 7. 
किसी अस्पताल में ऊतकों में ट्यूमरों का पता लगाने के लिये पराश्रव्य स्कैनर का प्रयोग किया जाता है। इस ऊतक में ध्वनि में तरंगदैर्ध्य कितनी है जिसमें ध्वनि की चाल 1.7 kms है ? स्कैनर की प्रचालन आवृत्ति 4.2 MHz है।
र दिया गया है।
उत्तर:
ध्वनि की चाल v = 1.7 km/s
v = 1.7 x 10³ m/s
आवृत्ति n = 4.2 MHz = 4.2 × 10⁶Hz
तरंगदैर्ध्य  λ = ?
हम जानते हैंतरंगदैर्घ्य \(\lambda=\frac{\mathrm{v}}{n}=\frac{1.7 \times 10^3}{4.2 \times 10^6}\)
= 0.405 × 10^-3 m = 0.405m.m.
अर्थात् तरंगदैर्ध्य
λ = 0.41m.m.

प्रश्न 8. 
किसी डोरी पर कोई अनुप्रस्थ गुणावृत्ति तरंग का वर्णन y(x,t) = 3.0sin (36t + 0.018x + π/4) द्वारा किया जाता है। जहाँ x तथा धनात्मक दिशा बाएँ से दाएँ है।
(a) क्या यह प्रगामी तरंग है अथवा अप्रगामी? यदि यह प्रगामी तरंग है तो इसकी चाल तथा संचरण की दिशा क्या है? 
(b) इसका आयाम तथा आवृत्ति क्या है?
(c) उद्गम के समय इसकी आरंभिक कला क्या है? 
(d) इस तरंग में दो क्रमागत शिखरों के बीच की न्यूनतम दूरी क्या है?
उत्तर:
अनुप्रस्थ गुणावृत्ति तरंग का दिया गया समीकरण
y(x,t) = 3.0sin(36t + 0.018x + π/4) है..... (1)
प्रगामी तरंग का मानक समीकरण
y(x,t) = a sin(2π/ λ(vt - x) + Φ)
= a sin(2π/Tt - 2π/λx + Φ)
[∵ 1/T = v/λ] ................... (2)
(a) समीकरण (1) तथा (2) की तुलना करने पर
2π/T  = 36
तथा
- 2π/ λ = 0.018
या
λ = -2π/0.018 ............ (3)
2πn = 36 .................. (4)
समीकरण (3) और (4) को गुणा करने पर
\(2 \pi n \lambda=\frac{-2 \pi \times 36}{0.018}\)
या \(n \lambda=\frac{-36 \times 1000}{18}\)
वेग (v) = 2000 cm/s = -20m/s
यहाँ पर ऋण चिन्ह यह दर्शाता है कि तरंग दाहिने से बाँये की ओर गतिमान है।

(b) दिया गया है चाल = 20 m/s
a = 3.0 cm = 3.0 × 10-2 m
2π/T = 36
1/T = 36/2π = 18/π 
आवृत्ति
n = 18/3.14
= 5.73Hz.

(c) कला कोण Φ = π/4 रेडियन

(d) दो क्रमागत शिखरों के बीच न्यूनतम दूरी = तरंगदैर्घ्य = λ
\(\begin{aligned} & =\frac{2 \pi}{0.018} \\ & =\frac{2 \times 3.14}{0.018}=348.9 \mathrm{~cm} \\ & \simeq 349 \mathrm{~cm} \\ & \simeq \frac{349}{100} \mathrm{~m}=3.49 \mathrm{~m} \end{aligned}\)

प्रश्न 9. 
प्रश्न 8 में वर्णित तरंग के लिये x = 0cm, 2cm तथा 4 cm के लिये विस्थापन (1) और समय (1) के बीच ग्राफ आलेखित कीजिये। इन ग्राफों की आकृति क्या है? आयाम, आवृत्ति अथवा कला में से किन पहलुओं में प्रगामी तरंग से दोलनी गति एक बिंदु से दूसरे बिंदु पर भिन्न है?
उत्तर:
दिया गया तरंग समीकरण
y(x,t) = 3.0sin(36t + 0.018x + π/4) 
विस्थापन का मान x = 0, 2 तथा 4 cm
y, (0,t) = 3.0sin (36t + π/4) ............(2)
y, ( 2, t) = 3.0sin (36t + 0.036 + π/4) ............. (3)
और y3 (4, t) = 3.0sin (36t + 0.072 + π/4) .............. (4)
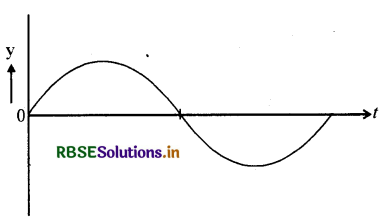
समीकरण (2), (3) तथा (4) से स्पष्ट है कि ग्राफ आगे दिखाये अनुसार ज्या वक्रीय होते हैं - प्रगामी तरंगों में दोलनी गतियां एक बिन्दु से दूसरे बिन्दु पर के कला में ही अलग होती हैं जो नीचे दी गयी हैं।
समीकरण (2), (3) और (4) के लिये यह क्रमशः π/4 , π/4 + 0.036 और π/4 + 0.072 है।

प्रश्न 10. 
प्रगामी गुणावृत्ति तरंग
y(x,t) = 2.0cos 2x (10-0.0080.x + 0.35)
जिसमें x तथा y को cm में तथा कोs में लिया गया है, के लिए उन दो दोलन बिंदुओं के बीच कलांतर कितना है जिनके बीच की दूरी है
(a) 4m
(b) 0.5m
(c) 12/2
(d) 31./4
उत्तर:
प्रगामी गुणावृत्ति तरंग का समीकरण
y (x, 1) = 2.0cos2π (10t0.0080x + 0.35) है। 
y (x, t) = 2.0 cos (2 x 10t - 2π  x 0.0080x + 2π x 0.35) ............ (1)
प्रगामी गुणावृत्ति तरंग का मानक समीकरण
y(x,t) = a cos(2π/λ(vt - x) + Φ) होता है। ....(2)
समीकरण (1) और (2) में x के गुणकों की तुलना करने पर
2π/λ = 2π x 0.0080
हम जानते हैं कलान्तर = 2π/ λ  x पथान्तर
(a) जब पथान्तर = 4m = 400cm है।
कलान्तर = 2π/ λ  x 400
समीकरण (3) से मान रखने पर
= 2π × 0.0080 × 400
= 6.4π rad

(b) जब पथान्तर = 0.5m = 50 cm है।
तब कलान्तर = 2π x 0.0080 × 50
= 0.8π rad

(c) जब पथान्तर = λ/2 है। 
कलान्तर = 2π/λ x λ/2 = πrad

(d) जब पथान्तर = 3λ/4 है।
तब कलान्तर = 2π/λ x 3λ/4 = 6π/4
= 3/2πrad

प्रश्न 11. 
दोनों सिरों पर परिबद्ध किसी तानित डोरी पर अनुप्रस्थ विस्थापन को इस प्रकार व्यक्त किया गया है:
y(x,t) = 0.06sin(2π/3x)cos(120π t)
जिसमें x तथा को तथा को में लिया गया है। इसमें डोरी की लम्बाई 1.5 m है जिसकी संहति 3.0 x 10^-2 kg है। निम्नलिखित का उत्तर दीजिये
(a) यह फलन प्रगामी तरंग अथवा अप्रगामी तरंग में से किसे निरूपित करता है?
(b) इसकी व्याख्या विपरीत दिशाओं में गमन करती दो तरंगों के अध्यारोपण के रूप में करते हुए प्रत्येक तरंग की तरंगदैर्घ्य, आवृत्ति तथा चाल ज्ञात कीजिये।
(c) डोरी में तनाव ज्ञात कीजिये।
उत्तर:
दिया गया फलन
y (x, t) = 0.06sin(2πx/3) cos (120π t) है। ........................ (1)
प्रगामी तरंग का समीकरण निरूपित करते हैं:
y(x,t) = asin 2π/λ(vt - x)
और अप्रगामी तरंग के समीकरण को निरूपित करते हैं:
y(x,t) = -2asin(2π/λ) cos(2πvt/λ)
(a) चूँकि दिया गया फलन अप्रगामी तरंग को निरूपित करने वाले फलन के समान है। इसलिये दिया गया फलन अप्रगामी तरंग निरूप्रित करता है।
जब एक तरंग x अक्ष के अनुदिश धनात्मक दिशा में गमन करती
(b) y1 = asin2π /λ(vt - x)
\(\begin{aligned} & =a\left[2 \cos \frac{\frac{2 \pi}{\lambda}(v t-x+\mathrm{v} t+x)}{2}\right] \sin \left(\frac{\frac{2 \pi}{\lambda}(v t-x-\mathrm{v} t-x)}{2}\right) \\ & =a\left[2 \cos \left(\frac{2 \pi}{\lambda} \mathrm{v} t\right) \sin \left(\frac{-2 \pi}{\lambda} x\right)\right] \\ & =-2 a \sin \left(\frac{2 \pi}{\lambda} x\right) \cos \left(\frac{2 \pi}{\lambda} \mathrm{v} t\right) \end{aligned}\)
और परावर्तित तरंग
\(\begin{aligned} \frac{2 \pi}{\lambda} & =\frac{2 \pi}{3} \text { या } \lambda=3 \mathrm{~m} . \\ \frac{2 \pi}{\lambda} \mathrm{v} & =120 \pi \end{aligned}\)
समीकरण (1) तथा (2) की तुलना करने पर
या 
आवृत्ति n = v/ λ = 180/3 =60HZ
अनुप्रस्थ तरंग का वेग
\(\mathrm{v}=\sqrt{\frac{\mathrm{T}}{m}} \text { } \mathrm{v}^2=\frac{\mathrm{T}}{m}\)
T = v² x m
m = इकाई लम्बाई का द्रव्यमान = M/l
\(=\frac{3 \times 10^{-2} \mathrm{~kg}}{1.5 \mathrm{~m}}\)
m = 2 x 10^-2 kg/m
तरंग की चाल v = 180m/s
(c) T = डोरी में तनाव = ?
समीकरण ( 3 ) में मान रखने पर
T = (180)² × (2 × 10²)
= 32400 × 2 × 10²
= 648N

प्रश्न 12. 
(i) प्रश्न 11 में वर्णित डोरी पर तरंग के लिये बताइये कि क्या डोरी के सभी बिंदु समान (a) आवृत्ति, (b) कला, (c) आयाम से कंपन करते हैं? अपने उत्तरों को स्पष्ट कीजिये।
(ii) एक सिरे से 0.375mm दूर के बिंदु का आयाम कितना है? 
उत्तर:
(i) डोरी के सभी बिन्दु केवल निस्पंदों को छोड़कर, आवृत्ति और कला समान हैं, लेकिन आयाम समान नहीं है। इसका कारण है कि समीकरण y(x,t) = 0.06sin(2π /3 x) cos(120πt)
तरंग निरूपित करता है। जिसके अलग-अलग बिन्दुओं पर अलग-अलग आयाम होते हैं। निस्पंद पर शून्य और प्रस्पंद पर कुछ अधिकतम आयाम सहित लेकिन कण की आवृत्ति और दोलनकाल समान रहता है।

(ii) दिया गया समीकरण
y (x, t ) = 0.06sin(2π/3x)cos(120πt)
इस तरंग का आयाम
a = 0.06sin(2π/3x)
x = 0.375m पर
a = 0.06sin(2π/3 x 0.375)
= 0.06sin(π/4) = 0.06 x \(\frac{1}{\sqrt{2}}\)
\(=\frac{0.06}{1.414}\) = 0.042m

प्रश्न 13. 
नीचे किसी प्रत्यास्थ तरंग (अनुप्रस्थ अथवा अनुदैर्घ्य) के विस्थापन को निरूपित करने वाले x तथा के फलन दिए गए हैं। यह बताइए कि इनमें से कौन (i) प्रगामी तरंग को, (ii) अप्रगामी तरंग को, (iii) इनमें से किसी भी तरंग को नहीं निरूपित करता है:
(a) y = 2 cos (3x) sin 10t
(b) y = \(2 \sqrt{x-v t}\)
(c) y = 3sin(5x - 0.5t) + 4cos (5x - 0.5t)
(d) y = cosxsint + cos 2.xsin 2t
उत्तर:
(a) दिया गया समीकरण दो गुणावृत्ति फलन x और में है। इसलिये यह एक अप्रगामी तरंग निरूपित करती है।
(b) दिया गया समीकरण कोई भी आवृत्ति फलन नहीं है। इसलिये यह कोई तरंग निरूपित नहीं करता है।
(c) दिये गये फलन में ज्या और कोज्या फलन के कोणांक समान हैं। इस कारण से यह फलन एक प्रगामी / गमनशील आवर्ती तरंग के समीकरण को निरूपित करता है।
(d) दिया गया समीकरण दो फलनों cosx.sint और cos 2x.sin 21 का योग है। जिसमें से प्रत्येक अप्रगामी तरंग निरूपित करती है। अतः दिया गया समीकरण दो अप्रगामी तरंगों का अध्यारोपण निरूपित करती है।

प्रश्न 14. 
दो दृढ़ टैंकों के बीच तानित तार अपनी मूल विधा में 45 Hz आवृत्ति से कंपन करता है। इस तार का द्रव्यमान 3.5 x 10^-2 kg तथा रैखिक द्रव्यमान घनत्व 4.0 x 10^-2 kgm^-1 है। (a) तार पर अनुप्रस्थ तरंग की चाल क्या है तथा (b) तार में तनाव कितना है?
उत्तर:
दिया गया है:
आवृत्ति n = 45Hz
तार का द्रव्यमान M = 3.5 x 10² kg
m = इकाई लम्बाई का द्रव्यमान रैखिक द्रव्यमान घनत्व
= 4.0 x 10² kg/m 
यदि माना तार की लम्बाई / है
\(l=\frac{\mathrm{M}}{m}=\frac{3.5 \times 10^{-2}}{4 \times 10^{-2}}\)
= 0.875m
(a) तार पर अनुप्रस्थ तरंग की चाल = ? 
(b) तार में तनाव T = ?
(a) दोलन की मूल विधा की आवृत्ति
\(n=\frac{\mathrm{v}}{\lambda}=\frac{\mathrm{v}}{2 l}\)
∵ मूल विधा दोलन में
L =  λ/2
या
 λ = 2l
चाल v = n x 2l
मान रखने पर
v = 45 x 2 x 0.875
= 78.75m/s
= 79m/s

(b) तार में तनाव निम्न सूत्र से ज्ञात कर सकते हैं-
\(\mathrm{v}=\sqrt{\frac{\mathrm{T}}{m}}\)
या
T =  v² x m
मान रखने पर
T = ( 78.75 )² × 4 × 10²
= 248.06N

प्रश्न 15. 
एक सिरे पर खुली तथा दूसरे सिरे पर चलायमान पिस्टन लगी 1 mm लंबी नलिका, किसी नियत आवृत्ति के स्रोत (340 Hz आवृत्ति का स्वरित्र त्रिभुज) के साथ, जब नलिका में वायु कॉलम 25.5 cm अथवा 79.3 cm होता है तब अनुनाद दर्शाती है। प्रयोगशाला के ताप पर वायु में ध्वनि की चाल का आकलन कीजिये। कोर प्रभाव को नगण्य मान सकते हैं।
उत्तर:
नलिका पिस्टन सहित बंद आर्गन नली बनाती है। माना l₁ तथा l₂ और (r+1) वे अनुनादों की क्रमशः लम्बाइयाँ हैं जो कि बन्द नली के क्रमश: दोलन हैं।
दिया गया है-
l₁ = 25.5cm
l₂ = 79.3cm
ध्वनि का तरंग वेग v है और आवृत्तियाँ क्रमश: n₁ और n₂ हैं। इन विधाओं के लिये आवृत्तियों के मान
n₁ = (2r -1) v/4l₁ ............. (1)
और
n₂ = (2r + l) - 1)v/4l₂
n₂ = (2r + 1)v/4l₂ .............. (2)
दिया गया है- दोनों विधाओं को 340 Hz की आवृत्ति के साथ
अनुनादित करते हैं।
\(\begin{aligned} (2 r-1) \frac{\mathrm{v}}{4 l_1} & =(2 r+1) \frac{\mathrm{v}}{4 l_2}=340 \\ \frac{(2 r-1)}{4 l_1} & =\frac{(2 r+1)}{4 l_2} \\ \frac{(2 r-1)}{2 r+1} & =\frac{l_1}{l_2}=\frac{25.5}{79.3}=\frac{1}{3} \end{aligned}\)
या
3 (2r - 1 ) = 2r + 1
⇒ 6r - 3 = 2r + 1
⇒ 4r = 4
r = 1
\(\frac{(2 r-1) \mathrm{v}}{4 l_1}\) = 340 में = 1 रखने पर
या \(\frac{(2 \times 1-1) \mathrm{v}}{4 l_1}=340\)
या 
v = 4 x 340 × l₁
मान रखने पर
v = 4 x 340 x 25.5
= 34680cm/s
= 346.80 m/s
v = 347m/s

प्रश्न 16. 
100 cm लंबी स्टील- छड़ अपने मध्य बिंदु पर परिबद्ध है। इसके अनुदैर्घ्य कंपनों की मूल आवृत्ति 2.53 kHz है। स्टील में ध्वनि की चाल क्या है?
उत्तर:
प्रश्नानुसार छड़ के कम्पनों को इस तरह से व्यक्त कर सकते हैं:

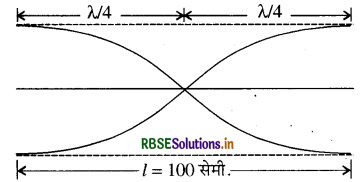
दिया है
n = 2.53 kHz = 2.53 × 10³ Hz
तथा
λ/4 + λ/4 = l
=> λ/2 = 1 मी. λ =  2 मी.
अतः चाल
v = nλ = 2.53 × 10³ × 2 
= 5.06 × 10³ मी./से. = 5.06 किमी./से. 

प्रश्न 17. 
20 cm लंबाई के पाइप का एक सिरा बंद है। 430 Hz आवृत्ति के स्रोत द्वारा इस पाइप की कौन-सी गुणावृत्ति विधा अनुनाद द्वारा उत्तेजित की जाती है? यदि इस पाइप के दोनों सिरे खुले हों तो भी क्या यह स्रोत इस पाइप के सभी अनुनाद करेगा? वायु में ध्वनि की चाल 340ms है।
उत्तर:
दिया गया है:
v = 340m/s
उत्प्रेरक स्रोत की आवृत्ति = 430 Hz.
हम जानते हैं कि बंद नली की वीं विधा की दोलन आवृत्ति
\(n=(2 r-1) \frac{\mathrm{v}}{4 l}\)
मान रखने पर
\(430=\frac{(2 r-1) \times 340}{4 \times 0.2}\)
था
\(\frac{430 \times 4 \times 0.2}{340}=2 r-1\)
1.012 = 2 - 1
2.012 = 2r
∴ R = 2.012/2 = 1.006 = 1.01
अर्थात् ऑर्गन नली पहली गुणावृत्ति या दोलन की मूल विधायें
खुली नलिका की स्थिति में वीं विधा की दोलन आवृत्ति
nR = r.v/2l होती है।
जहाँ मूल विधा में लम्बाई λ = 2l
मान रखने पर

r का माम पूर्णांक होना चाहिये अर्थात् वही स्रोत खुली ऑर्गन नलिका से अनुनाद में नहीं हो सकती है।

प्रश्न 18. 
सितार की दो डोरियाँ A तथा B एक साथ 'गा' स्वर बजा रही हैं तथा थोड़ी-सी बेसुरी होने के कारण 6 Hz आवृत्ति के विस्पंद उत्पन्न कर रही हैं। डोरी A का तनाव कुछ घटाने पर विस्पंद की आवृत्ति घटकर 3 Hz रह जाती है। यदि A की मूल आवृत्ति 324 Hz है तो B की आवृत्ति क्या है?
उत्तर:
हम जानते हैं कि आवृत्ति \(n \propto \sqrt{\mathrm{T}}\)
यहाँ पर T तनाव है। किसी डोरी के तनाव में कमी उसकी आवृत्ति को कम कर देती है। इसलिये कहा जाता है कि A की आवृत्ति B की आवृत्ति से अधिक है।
∴ nA - nB = 6Hz दिया गया है
तथा
nA = 324 Hz
324 - nB = 6 
324 - 6 = nB
या
nB = 318 Hz
A का तनाव कम करने पर
∆n = 3Hz
∴ A की आवृत्ति 324 - 3 = 321 हो जाती है।
nB = 318 Hz

प्रश्न 19.
स्पष्ट कीजिये क्यों (अथवा कैसे) 
(a) किसी ध्वनि तरंग में विस्थापन निस्पंद दाब प्रस्पंद होता है और विस्थापन प्रस्पंद दाब निस्पंद होता है।
(b) आँख न होने पर भी चमगादड़ अवरोधकों की दूरी, दिशा, प्रकृति तथा आकार सुनिश्चित कर लेते हैं।
(c) वायलिन तथा सितार के स्वरों की आवृत्तियाँ समान होने पर भी हम दोनों से उत्पन्न स्वरों में भेद कर लेते हैं।
(d) ठोस अनुदैर्घ्य तथा अनुप्रस्थ दोनों प्रकार की तरंगों का पोषण कर सकते हैं जबकि गैसों में केवल अनुदैर्घ्य तरंगें ही संचरित हो सकती हैं, तथा
(e) परिक्षेपी माध्यम में संचरण के समय स्पंद की आकृति विकृत हो जाती है।
उत्तर:
(a) ध्वनि तरंग में निस्पंद वह बिन्दु है, जहाँ पर दोलन का आयाम अर्थात् विस्थापन शून्य होता है। चूँकि यहाँ पर एक संपीड़न और एक विरलन मिलते हैं। जिस कारण से दाब का मान अधिकतम होता है। इसे हम दाब प्रस्पंद भी कहते हैं। जबकि प्रस्पंद वह बिन्दु है, जहाँ दोलन आयाम अधिकतम होता है, अर्थात् विस्थापन अधिकतम है। परन्तु दाब न्यूनतम अतः यह बिन्दु दाब निस्पंद कहलाता है। इसलिये विस्थापन निस्पंद दाब प्रस्पंद से और विस्थापन प्रस्पंद दाब निस्पंद के सम्पाती होते हैं।
(b) जब चमगादड़ उड़ते हैं तो वह बहुत अधिक आवृत्ति (अर्थात् कम तरंगदैर्घ्य) की पराश्रव्य ध्वनि उत्पन्न करते हैं। यह पराश्रव्य ध्वनियाँ अवरोध से टकराकर परावर्तित होने पर उनके द्वारा प्राप्त की जाती हैं। उनके कान इतने संवेदनशील और प्रशिक्षित होते हैं कि वह केवल अवरोध की दूरी के विषय में सूचना प्राप्त करते हैं और वह परावर्तक पृष्ठ की प्रकृति के विषय में भी जान लेते हैं।
(c) वायलिन तथा सितार के स्वरों की आवृत्तियाँ समान होने पर भी इन दोनों से उत्पन्न स्वरों में भेद कर लेते हैं। चूँकि भिन्न स्थितियों में वायलिन या सितार द्वारा उत्पन्न ध्वनियों में अधिस्वरों की संख्या अलग-
अलग होती है इसलिये उनके द्वारा उत्पन्न स्वरों में हम विभेद कर सकते हैं।
(d) ऐसा इसलिये है कि ठोसों में दोनों आयतन प्रत्यास्थता और आकार प्रत्यास्थता होती है। इसलिये दोनों अनुप्रस्थ और अनुदैर्घ्य तरंगें उनमें से गुजर सकती हैं। जबकि दूसरी ओर गैसों में केवल आयतन प्रत्यास्थता ही होती है और अपरूपण प्रत्यास्थता नहीं, इसलिये गैसों में केवल अनुदैर्ध्य तरंगें ही प्रचारित हो सकती हैं।
(c) एक परिक्षेपी माध्यम में, विभिन्न तरंगदैयों की तरंगें अलग- अलग दिशाओं में अलग-अलग चालों से गमन करती हैं। अतः स्पंद का आकार विकृत हो जाता है, अर्थात् अपरिक्षेपी माध्यम में समतल तरंगाग्र, परिक्षेपी माध्यम में समतल तरंगाग्र नहीं रहता है।

प्रश्न 20. 
रेलवे स्टेशन के बाह्य सिग्नल पर खड़ी कोई रेलगाड़ी शांत वायु में 400 Hz आवृत्ति की सीटी बजाती है। (i) प्लेटफॉर्म पर खड़े प्रेक्षक के लिये सीटी की आवृत्ति क्या होगी जबकि रेलगाड़ी (a) 10ms चाल से प्लेटफॉर्म की ओर गतिशील है, तथा (b) 10ms चाल से प्लेटफॉर्म से दूर जा रही है ? (ii) दोनों ही प्रकरणों में ध्वनि की चाल क्या है? शांत वायु में ध्वनि की चाल 340ms लीजिए।
उत्तर:
दिया गया है
आवृत्ति = 400Hz
शान्त वायु में ध्वनि की चाल = 340m/s
स्रोत की चाल v. = 10m/s
(i) (a) जब रेलगाड़ी 'S' प्लेटफार्म की ओर गतिशील है, तब प्लेटफार्म पर प्रेक्षक 'O' द्वारा सुनी जाने वाली आवृत्ति

(b) जब रेलगाड़ी प्लेटफार्म से दूर जा रही है। अर्थात् प्रेक्षक द्वारा सुनी जाने वाली आभासी आवृत्ति

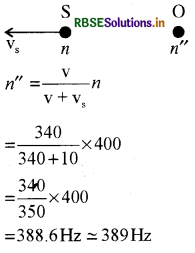
(ii) चूँकि दोनों स्थितियों में केवल स्रोत गतिशील है, माध्यक नहीं अतः ध्वनि की चाल दोनों स्थितियों में 340 मी./से. होगी।

प्रश्न 21. 
स्टेशन यार्ड में खड़ी कोई रेलगाड़ी शांत वायु में 400 Hz आवृत्ति की सीटी बजा रही है। (a) तभी 10m st चाल से बार्ड से स्टेशन की ओर वायु बहने लगती है। स्टेशन के प्लेटफॉर्म पर खड़े किसी प्रेक्षक के लिये ध्वनि की आवृत्ति, तरंगदैर्घ्य तथा चाल क्या हैं ? (b) क्या यह स्थिति तथ्यतः उस स्थिति के समरूप है जिसमें वायु शांत हो तथा प्रेक्षक 10ms चाल से यार्ड की ओर दौड़ रहा हो ? शांत वायु में ध्वनि की चाल 340ms ले सकते हैं।
उत्तर:
दिया गया है
(a) आवृत्ति = 400Hz
Vm = 10m/s
v = 340m/s
चूँकि ध्वनि उसी दिशा में है जिसमें वायु बहती है। 
अतः ध्वनि का आभासी वेग = 340 + 10 = 350m/s
∴ विश्राम में प्रेक्षक के लिये ध्वनि की तरंगदैर्ध्य
\(\lambda=\frac{\mathrm{v}+\mathrm{v}_m}{n}=\frac{350}{400}\) = 0.875m

(b) जब वायु शांत है vm = 0
प्रेक्षक की चाल
VL = 10m/s
Vs = 0
इसलिये आभासी आवृत्ति
\(\begin{aligned} n^{\prime} & =\left(\frac{\mathrm{v}+\mathrm{v}_{\mathrm{L}}}{\mathrm{v}}\right) \times n \\ & =\frac{340+10}{340} \times 400 \\ & =\frac{350}{340} \times 400 \end{aligned}\)
n = 411.8Hz.

स्त्रोत शान्त है इसलिये तरंगदैर्घ्य का मान नहीं बदलेगा।
अर्थात्
λ = λ = 0.875m
ध्वनि की चाल
= v + vm = 340 + 0
= 340m/s
इस प्रकार हम यह निष्कर्ष निकालते हैं कि स्थिति a तथा b पूर्ण रूप से समान नहीं हैं।

अतिरिक्त अभ्यास:

प्रश्न 22. 
किसी डोरी पर कोई प्रगामी गुणावृत्ति तरंग इस प्रकार व्यक्त की गई है:
y (x, t) = 7.5sin (0.0050x + 12t + π/4)
(a) x = 1 cm तथा t = 1s पर किसी बिंदु का विस्थापन तथा दोलन की चाल ज्ञात कीजिये। क्या यह चाल तरंग संचरण की चाल के बराबर है?
(b) डोरी के उन बिंदुओं की अवस्थिति ज्ञात कीजिये जिनका अनुप्रस्थ विस्थापन तथा चाल उतनी ही है जितनी x = 1 cm पर स्थित बिंदु की समय =2s, 5 s तथा 11 s पर है।
उत्तर:
(a) y(x, t) = 7.5sin(0.0050x + 12t + π/4)
उपरोक्त समीकरण को निम्न सामान्य प्रगामी तरंग के समीकरण से तुलना करने पर
y = asin [kx + ωt + Q]
अतः k = 0.0050 एवं ω = 12
तरंग वेग = v = nλ = (2πn) x λ/2π = ω/k
तरंग वेग (v) = 12/0.0050 = 12000/5 = 2400cm/s
v = 2400/100m/s = 24m/s
दिये गये समीकरण में x = 1 cm, t = 1 सेकण्ड पर विस्थापन
y (11) = 7.5sin(0.005 + 12 + π/4)
( दिये गये समी. में मान रखा गया है।)
= 7.5 sin (12,005 + π/4)
= 7.5sin (12.005 + 3.14/4)
= 7.5 sin (12.005 + 0.785)
= 7.5sin (12.79)
= 7.5sin (12.79 x 180/π)
[ π रेडियन = 180° ]
= 7.5sin (732.83°)
= 7.5sin (720° + 12.83°)
= 7.5sin12.83°
y (1, 1) = 7.5 x 0.2215
बिन्दु के दोलन की चाल
v = dy/dt
v = 7.5 x 12cos (0.0050x + 12t + π/4)
= 90.0cos (0.0050x + 12t + π/4)
x = 1 cm, r = 1 सेकण्ड पर
v = 90cos (0.005 x 1 + 12 × 1 + 0.785)
= 90cos(12.79)
= 90 cos (732.83° = 90 cos 12.83°)
= 90 × 0.9751 = 87.76cm/s
अतः बिन्दु की दोलन चाल = 88cm/s
लेकिन तरंग की चाल = 24m / s है।
अतः स्पष्ट है कि बिन्दु के दोलन की चाल तरंग गति की चाल से अलग है। अतः तुल्य नहीं है।

(b) दिया गया समीकरण
y = 7.5sin(0.0050x + 12t + 2 + π/2)
प्रगामी तरंग समीकरण
y = asin (ωt + kx + Φ) से तुलना करने पर k = 0.005 रेडियन / सेमी.
\(\lambda=\frac{2 \pi}{\mathrm{k}}=\frac{2 \times 3.142}{0.005}\)
=12.57m
अनुप्रस्थ तरंग में सभी बिन्दुओं का विस्थापन समान होता है। जो 3λ, 2λ, 3λ .... आदि की दूरियों पर होते हैं। इसलिये 12.57m 25.14m, 37.71m आदि के सभी बिन्दुओं का विस्थापन समान होगा। जैसा कि x= 1 सेमी. दूरी पर है।
इस प्रकार सभी बिन्दु जो π. जहाँ पर x = 1, 2, ±3, ±4, ....x = 1 cm से 12.57m 25.14 m......... आदि दूरियों पर है, पर विस्थापन समान होगा।

प्रश्न 23. 
ध्वनि का कोई सीमित स्पंद (उदाहरणार्थ सीटी का 'पिप' ) माध्यम में भेजा जाता है। (a) क्या इस स्पंद की कोई निश्चित (i) आवृत्ति, (ii) तरंगदैर्घ्य, (iii) संचरण की चाल है? (b) यदि स्पंद दर 1 स्पंद प्रति 20 सेकंड है अर्थात् सीटी प्रत्येक 20s के पश्चात् सेकंड के कुछ अंश के लिए बजती है, तो सीटी द्वारा उत्पन्न स्वर की आवृत्ति (1/20) Hz अथवा 0.05 Hz है?
उत्तर:
(a) सीटी का सीमित स्पंद अर्थात् स्पंद की न तो निश्चित तरंगदैर्ध्य और न ही निश्चित आवृत्ति है लेकिन एक अविवर्तन माध्यम में संचरण की चाल होती है। जो ध्वनि का वायु में वेग के तुल्य है।
(b) नहीं, सीटी द्वारा उत्पन्न स्वर की आवृत्ति न तो 1/20 ही 0.05 Hz है, अपितु यह 0.05 Hz सीटी की छोटी पिप आवृत्ति है अर्थात् स्पंद।

प्रश्न 24.
8.0 × 10^-3 kg m रैखिक द्रव्यमान घनत्व की किसी लंबी डोरी का एक सिरा 256 Hz आवृत्ति के विद्युत चालित स्वरित्र द्विभुज से जुड़ा है। डोरी का दूसरा सिरा किसी स्थिर घिरनी के ऊपर गुजरता हुआ किसी तुला के पलड़े से बँधा है। जिस पर 90 kg के बाट लटके हैं। घिरनी वाला सिरा सारी आवक ऊर्जा को अवशोषित कर लेता है जिसके कारण इस सिरे से परावर्तित तरंगों का आयाम नगण्य होता है। t = 0 पर डोरी के बाएँ सिरे (द्विभुज वाले सिरे ) x = 0 पर अनुप्रस्थ विस्थापन शून्य है ( = 0) तथा वह की धनात्मक दिशा के अनुदिश गतिशील है। तरंग का आयाम 5.0 cm है। डोरी पर इस तरंग का वर्णन करने वाले अनुप्रस्थ विस्थापन को x तथा के फलन के रूप में लिखिये |
उत्तर:
दिया गया है:
तुला का द्रव्यमान
M = 90kg
T = Mg
= 90 × 9.8 = 882.0N
रैखिक द्रव्यमान घनत्व m = 8 x 10^-3 kg/m 
डोरियों में अनुप्रस्थ तरंग का वेग
\(\mathrm{v}=\sqrt{\frac{\mathrm{T}}{m}}\)
मान रखने पर
\(\mathrm{v}=\sqrt{\frac{882}{8 \times 10^{-3}}}\)
= 3.32 × 10²
= 332m/s
x की धन दिशा में प्रगामी तरंग का समीकरण
y = asin (ωt - kx) ....(1)
जहाँ पर
ω = 2πn और
n = 256Hz
a = 5.0cm a = 0.05m
0 = 2π x 256 = 2 × 3.14 × 256 = 1607.68 रेडियन प्रति सेकण्ड
= 1.61 × 10³ रेडियन प्रति सेकण्ड
संचरण नियतांक
\(\mathrm{k}=\frac{\omega}{\mathrm{v}}=\frac{2 \pi \times 256}{3.32 \times 10^2}\)
\(=\frac{1607.68}{3.32 \times 10^2}\)
= 4.84 प्रति मीटर
चूँकि तरंग धनात्मक x दिशा के अनुदिश संचारित हो रही है तो तरंग का समीकरण होगा
या
y = a sin (wt - kx)
y = 0.05sin (1.6 x 10³t - 4.84x )
यहाँ पर x तथा मीटर में हैं और समय सेकण्ड में है।

प्रश्न 25. 
किसी पनडुब्बी से आबद्ध कोई 'सोनार' निकाय 40.0 kHz आवृत्ति पर प्रचलन करता है। कोई शत्रु - पनडुब्बी 360 kmht चाल से इस सोनार की ओर गति करती है। पनडुब्बी से परावर्तित ध्वनि की आवृत्ति क्या है? जल में ध्वनि की चाल 1450mst है। 
उत्तर:
'सोनार निकाय की आवृत्ति
n = 40 kHz
= 40 x 10³ Hz
पहले एक प्रेक्षक कार्य करते पनडुब्बी की ओर सोनार निकाय
v = 360km/h
= 360 x 5/18 m/s = 100m/s
ध्वनि की पानी में चाल
v = 1450m/s
∴ ध्वनि तरंगों की आभासी आवृत्ति जो शत्रु पनडुब्बी द्वारा
सुनी जायेगी

= 4.28 × 10⁴ Hz = 42.8kHz ............. (1)
यह आवृत्ति शत्रु पनडुब्बी द्वारा सुनी ध्वनि की आवृत्ति है। अब शत्रु- पनडुब्बी ' आवृत्ति की तरंग परावर्तित करेगी और इस प्रकार यह एक स्रोत का कार्य करेगी जो कि सोनार की ओर v, चाल से गति करती है vg = 100m/s. v = 0


प्रश्न 26. 
भूकंप पृथ्वी के भीतर तरंगें उत्पन्न करते हैं। गैसों के विपरीत, पृथ्वी अनुप्रस्थ (S) तथा अनुदैर्घ्य (P) दोनों प्रकार की तरंगों की अनुभूति कर सकती है। S तरंगों की प्रतिरूपी चाल लगभग 4.0kms^-1, तथा P तरंगों की प्रतिरूपी चाल लगभग 8.0km s^-1 है। कोई भूकंप-लेखी किसी भूकंप की P तथा S तरंगों को रिकॉर्ड करता है। पहली P तरंग पहली S तरंग की तुलना में 4 मिनट पहले पहुँचती है । यह मानते हुये कि तरंगें सरल रेखा में गमन करती हैं यह ज्ञात कीजिये कि भूकंप घटित होने वाले स्थान की दूरी क्या है?
उत्तर:
दिया है:
अनुप्रस्थ (S) तरंगों की चाल v₁ = 4 किमी./से.
भूकम्पमापी तक पहुँचने का समय = t₁
अनुदैर्घ्य तरंगों (P) की चाल v₂ = 8 किमी./से.
भूकम्पमापी तक पहुँचने का समय = t₂
चूँकि दोनों तरंगें एक ही स्थल पर उत्पन्न होंकर भूकम्पमापी तक
पहुँचती हैं अतः दोनों समान दूरी l तय करेंगी अतः
l = v₁ t₁ = v₂t₂
⇒ 4t₁ = 8t₂ ⇒ t₁ = 2t₂ ............ (1)
तथा दिया है t₁ = t₂ + (4 x 60) .............. (2)   
समीकरण (1) में मान रखने पर
t₂ = 240
t₁ = 2t₂ = 480
भूकम्प घटित होने वाले स्थान की दूरी
t = vt₁ t₁ = 4 x 480 = 1920 

प्रश्न 27. 
कोई चमगादड़ किसी गुफा में फड़फड़ाते हुए पराश्रव्य ध्वनि उत्पन्न करते हुए उड़ रहा है। मान लीजिए चमगादड़ द्वारा उत्सर्जित पराश्रव्य ध्वनि की आवृत्ति 40k Hz है। किसी दीवार की ओर सीधा तीव्र झपट्टा मारते समय चमगादड़ की चाल ध्वनि की चाल की 0.03 गुनी है। चमगादड़ द्वारा सुनी गई दीवार से परावर्तित ध्वनि की आवृत्ति क्या है?
उत्तर:
चमगादड़ द्वारा उत्सर्जित पराश्रव्य ध्वनि की आवृत्ति = 40kHz
ध्वनि का वायु में वेग v = 340 m/s
माना चमगादड़ की चाल vs = 0.03v
vs = 0.03 x 340
= 10.20m/s
चमगादड़ दीवार की ओर गमन कर रहा है। यह एक स्रोत का कार्य करता है तथा दीवार से परावर्तित ध्वनि तरंगों के लिये भी यह एक. गतिमान प्रेक्षक का कार्य करता है। अतः स्रोत तथा प्रेक्षक एक-दूसरे की ओर समान चाल से आगे बढ़ते हैं।
vs = vo = 10.2m/s
चमगादड़ द्वारा सुनी परावर्तित ध्वनि तरंगों की आवृत्ति
\(\begin{aligned} n^{\prime} & =\frac{340+10.2}{340-10.2} \times 40 k \mathrm{~Hz} \\ & =\frac{350.2}{329.8} \times 40 \mathrm{kHz} \end{aligned}\)
= 42.47kHz