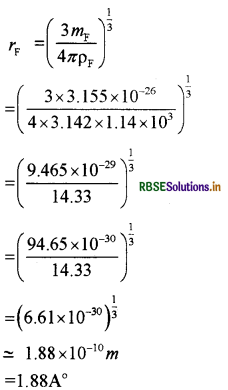RBSE Solutions for Class 11 Physics Chapter 13 अणुगति सिद्धांत

Rajasthan Board RBSE Solutions for Class 11 Physics Chapter 13 अणुगति सिद्धांत Textbook Exercise Questions and Answers.

RBSE Class 11 Physics Solutions Chapter 13 अणुगति सिद्धांत

RBSE Class 11 Physics अणुगति सिद्धांत Textbook Questions and Answers

प्रश्न 1. 
ऑक्सीजन के अणुओं के आयतन और STP पर इनके द्वारा घेरे गये कुल आयतन का अनुपात ज्ञात कीजिये। ऑक्सीजन के एक अणु का व्यास 3A लीजिये।
उत्तर:
STP पर ऑक्सीजन (O₂) का एक ग्राम मोल
= 22400 × 10^-6m³ आयतन घेरता है।
दिया गया है
ऑक्सीजन का एक अणु का व्यास = 3A = 3 x 10^-10 m
\(r=\frac{3}{2} \times 10^{-10} \mathrm{~m}\)
ऑक्सीजन के एक मोल में अणुओं का आयतन = ऑक्सीजन के एक अणु का आयतन x  आवोगाद्रो संख्या (N)
∴ = 4/3πr³ x NA
= 4/3π x (3/2 x 10^-10)³ x 6.023 x 10²³
= 4/3π x 27/8 x 10^-30 x 6.023 x 10²³
= 9π/2 x 6.023 x 10^-7
∴ ऑक्सीजन द्वारा घेरे वास्तविक अणु आयतन का अंश = दोनों आयतनों का अनुपात
\(\begin{aligned} & =\frac{\frac{9 \pi}{2} \times 6.023 \times 10^{-7}}{22400 \times 10^{-6}}=\frac{9 \pi \times 6.023 \times 10^{-7}}{2 \times 22400 \times 10^{-6}} \\ & =\frac{9 \times 3.14 \times 6.023 \times 10^{-3}}{2 \times 224} \end{aligned}\)
= 0.38 × 10^-3
= 3.8 × 10^-4
= 4 x 10^-4

प्रश्न 2. 
मोलर आयतन, STP पर किसी गैस (आदर्श) के 1 मोल द्वारा घेरा गया आयतन है। ( STP : 1 atm दाब, 0°C ) दर्शाइये कि यह 22.4 लीटर है। लीटर है।
उत्तर:
दिया गया है:
P = 1 atm = पारे के 0.76m
= hpg
= 0.76 × 13.6 × 10³ × 9.8
= 1.013 × 10⁵ N/m²
T = 0°C = 273K
R = 8.31 joule gm mol^-1 K^-1
हमें सिद्ध करना है कि 1 मोल द्वारा घेरा गया आयतन V = 22.4
∴ गैस समीकरण PV = nRT का उपयोग करके हम
\(\begin{aligned} V & =\frac{\mathrm{nRT}}{\mathrm{P}} \\ & =\frac{1 \times 8.31 \times 273}{1.013 \times 10^5} \end{aligned}\)
= 22.4 x 10^-3 m^-3
V = 22.4 लीटर

प्रश्न 3. 
चित्र में ऑक्सीजन के 1.00 x 10^-3 kg द्रव्यमान के लिये PVT एवं P में दो अलग-अलग तापों पर ग्राफ दर्शाये गये हैं।

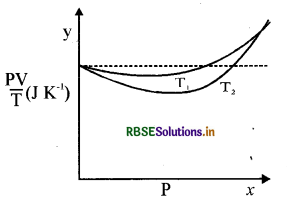
(a) बिंदुकित रेखा क्या दर्शाती है?
(b) क्या सत्य है T1 > T2 अथवा T1 < T 2?
(c) y अक्ष पर जहाँ वक्र मिलते हैं वहाँ PVT का मान क्या है?
(d) यदि हम ऐसे ही ग्राफ 1.00 x 10^-3 kg हाइड्रोजन के लिए बनाएँ तो भी क्या उस बिंदु पर जहाँ वक्र y अक्ष से मिलते हैं PVT का मान यही होगा? यदि नहीं तो हाइड्रोजन के कितने द्रव्यमान के लिए PV/T का मान ( कम दाब और उच्च ताप के क्षेत्र के लिए वही होगा ? H का अणु द्रव्यमान = 2.02u, O₂ का द्रव्यमान = 32.0u, R = 8.31Jmol^-1 K^-1)
उत्तर:
(a) बिन्दुकित रेखा आदर्श गैस का व्यवहार दर्शाती है, चूंकि यहाँ पर यह P-अक्ष के समानान्तर है और यह बताती है कि P के बदलने के बाद भी pv/T का मान वही रहता है।

(b) PV/T की उच्च स्थिति दर्शाती है कि T के लिये इसका मान कम है। इस प्रकार T1 > T2 यह इस कारण से है कि T1 का वक्र बिन्दुकित रेखा के समीप है T2 के वक्र की अपेक्षा क्योंकि वास्तविक गैस का आचरण आदर्श गैस के आचरण को छूता है जैसे-जैसे ताप बढ़ता है।

(c) जहाँ पर दो वक्र मिलते हैं, PV/T   का मान Y अक्ष पर nR के 
n को ज्ञात करना:  हमें ज्ञात है कि O के 32 x 10^-23 kg = 1 मोल
∴ O2 के 1.00 x 10^-3 kg = 1/32
R = 8.31JK^-1 mol^-1
\(\frac{\mathrm{PV}}{\mathrm{T}}=\frac{1}{32} \times 8.31\)
= 0.26JK^-1

(d) नहीं, हाइड्रोजन के लिये PV/T का वही मान प्राप्त नहीं होगा क्योंकि यह मान द्रव्यमान पर निर्भर है तथा हाइड्रोजन का द्रव्यमान, ऑक्सीजन के द्रव्यमान से कम है।
माना PV/T के समान मान के लिये H₂ के mkg वांछित हैं।
\(\mathrm{n}=\frac{m}{2.02 \times 10^{-3}}\) ............ (1)
PV/T = nR = 0.26JK^-1 [समीकरण (1) से]
अतः
n = 0.26/R
\(=\frac{0.26 \mathrm{JK}^{-1}}{8.31 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}}\)
n = 0.0313 mol ................. (2)
समीकरण (1) से
n = 0.0313mol
m = 2.02 × 10^-3n
अब n का मान समीकरण (2) से रखने पर
= 2.02 × 10^-3 × 0.0313
= 0.0632 × 10^-3kg
= 6.32 × 10^-5 kg

प्रश्न 4. 
एक ऑक्सीजन सिलिंडर जिसका आयतन 30 लीटर है, में ऑक्सीजन का आरंभिक दाब 15 atm एवं ताप 27°C है। इसमें से कुछ गैस निकाल लेने के बाद प्रमापी (गेज ) दाब गिर कर 11 atm एवं ताप गिर कर 17°C हो जाता है। ज्ञात कीजिए कि सिलिंडर से ऑक्सीजन की कितनी मात्रा निकाली गई है। (R = 8.31Jmol^-1K^-1, ऑक्सीजन का अणु द्रव्यमान 0 = 32u )। 
उत्तर:
दिया गया है-
V = 30 लीटर = 30 x 10^-3 मी.³ 
P₁ = 15 वायुमण्डलीय दाब तथा
T₁ = 27°C  T₁ = 27 + 273 = 300 K 
V₂ = 30 लीटर = 30 x 10^-3 मी. ³
P₂ = 11 वायुमण्डलीय दाब
T₂ = 17°C = 17 + 273 = 290K 
R = 8. 31 जूल / मोल / केल्विन
O₂ का अणुभार Mo₂ = 32 इकाई एवं 1 वायुमण्डलीय दाब = 1.013 x 10⁵ न्यूटन/मी^{. 2}
अतः प्रारम्भ में O₂ के मोलों की संख्या
\(\begin{aligned} \mathrm{n}_1 & =\frac{\mathrm{P}_1 \mathrm{~V}_1}{\mathrm{RT}_1} \\ & =\frac{15 \times 1.013 \times 10^5 \times 30 \times 10^{-3}}{8.31 \times 300} \end{aligned}\)
= 18.285 मोल
अतः प्रारम्भ में O₂ की मात्रा 
M₁ = n₁ × Mo₂
= 18.285 × 32 
= 585.12 ग्राम
अन्तिम अवस्था में O₂ मोलों की संख्या
\(\begin{aligned} \mathrm{n}_2 & =\frac{\mathrm{P}_2 \mathrm{~V}_2}{\mathrm{kT}_2} \\ & =\frac{11 \times 1.013 \times 10^5 \times 30 \times 10^{-3}}{8.31 \times 290} \end{aligned}\)
= 13.871 मोल
O₂ की मात्रा M₂ = n₂ x Mo₂
= 13.871 × 32 = 443.87 ग्राम
अत: O₂ की निकाली गयी मात्रा 
∆M = M₁ - M₂ 
= 585.12 - 443.87
= 141.25 ग्राम
= 0.14 किलो ग्राम

प्रश्न 5. 
वायु का एक बुलबुला, जिसका आयतन 1.0cm है, 40m गहरी झील की तली से जहाँ ताप 12°C है, उठकर ऊपर पृष्ठ पर आता है जहाँ ताप 35°C है। अब इसका आयतन क्या होगा? 
उत्तर:
दिया गया है-
V₁ = 1.0 cm³ = 1.0 × 10^-6 m³
T₁ = 12°C = 12 + 273 = 285K
P₁ = 1 atm + h1pg
= 1.01 × 10⁵ + 40 × 10³ × 9.8
= 101 × 10³ + 392 × 10³
= (101 + 392) × 10³
= 493 × 10³ = 493000 Pa
जब वायु का बुलबुला झील के पृष्ठ पर पहुँचता है तब
V₂ = ?,T = 35°C = 35 + 273 = 308K
P₂ = 1 atm = 1.01 × 10⁵ Pa
अब
\(\frac{P_1 V_1}{T_1}=\frac{P_2 V_2}{T_2}\)
या
मान रखने पर

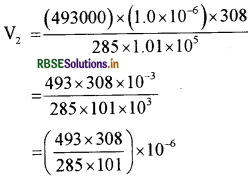
= 5.275 × 10^-6 m³
= 5.3 x 10^-6 m³

प्रश्न 6. 
एक कमरे में जिसका आयतन 25.0m है, 27°C ताप और 1atm दाब पर, वायु के कुल अणुओं (जिनमें नाइट्रोजन, ऑक्सीजन, जलवाष्प और अन्य सभी अवयवों के कण सम्मिलित हैं) की संख्या ज्ञात कीजिए।
उत्तर:
दिया गया है:
V = 25.0m³
अब
T = 27°C = 27 + 273 = 300K 
k = 1.38 × 10^-23 JK^-1
PV = nRT
= n(NAk)T 
= (nNA)kT = N1kT
जहाँ nN = N₁ = (हवा के अणु गैस में)
\(\mathrm{N}^1=\frac{\mathrm{PV}}{\mathrm{K}_{\mathrm{B}} \mathrm{T}}\)
मान रखने पर
\(=\frac{\left(1.01 \times 10^5\right)(25)}{\left(1.38 \times 10^{-23}\right) \times 300}\)
= 6.10 × 10²⁶ अणु 

प्रश्न 7. 
हीलियम परमाणु की औसत तापीय ऊर्जा का आकलन कीजिये (i) कमरे के ताप (27°C) पर। (ii) सूर्य के पृष्ठीय ताप (6000 K) पर। (iii) 100 लाख केल्विन ताप ( तारे के क्रोड का प्रारूपिक ताप ) पर।
उत्तर: 
दिया गया है
(i) T = 27°C = 27 + 273 = 300K
औसत ऊष्मीय ऊर्जा = 3/2KBT
मान रखने पर
= 3/2 × 1.38 × 10^-23 x 300
∵ kb = 1.38 × 10^-2" होता है
= 6.2 × 10^-21J
(ii) T = 6000K पर औसत ऊष्मीय ऊर्जा
= 3/2kBT
= 3/2 × 1.38 × 10^-23 × 6000
= 1.24 × 10^-19J
T = 100 लाख केल्विन पर
T = 10 million K = 10 7K

औसत ऊष्मीय ऊर्जा = 3/2kBT
= 3/2 × 1.38 × 10² × 10⁷
= 2.1 × 10^-16J

प्रश्न 8. 
समान धारिता के तीन बर्तनों में एक ही ताप और दाब पर गैसें भरी हैं। पहले बर्तन में नियॉन (एकपरमाणुक) गैस है, दूसरे में क्लोरीन (द्विपरमाणुक) गैस है और तीसरे में यूरेनियम हेक्साफ्लोराइड (बहुपरमाणुक) गैस है। क्या तीनों बर्तनों में गैसों के संगत अणुओं की संख्या समान है? क्या तीनों प्रकरणों में अणुओं की Vrms (वर्ग माध्य मूल चाल) समान है।
उत्तर:
समान दाब व ताप पर तीनों बर्तनों में समान आयतन होगा इसलिये आवोगाद्रो की परिकल्पना के अनुसार ताप और दाब की समान दशा रहने पर सभी गैसों के समान आयतनों में अणुओं की संख्या समान होती है। इसलिये विभिन्न गैसों से भरे तीनों पात्रों में अणुओं की संख्या समान होनी चाहिये अर्थात् तीनों पात्रों में क्रमश: अणुओं की संख्या समान है।
आवोगाद्रो संख्या NA = 6.023 x 10 ²³ अणु/ ग्राम मोल हम यह भी जानते हैं कि गैस का r.m.s. वेग
\(C_{\mathrm{rms}}=\sqrt{\frac{3 R T}{M}} \text { } C_{\mathrm{rms}} \alpha \frac{1}{\sqrt{\mathrm{M}}}\)
द्वारा दिया जाता है जहाँ M अणु द्रव्यमान है जो अलग- इसलिये तीनों गैसों में C_rms अलग गैसों के लिये अलग-अलग है, भिन्न-भिन्न होगा, नियॉन का द्रव्यमान सबसे कम है। इस कारण से नियॉन की स्थिति में r.m.s. वेग का मान अधिकतम होगा।

प्रश्न 9. 
किस ताप पर आर्गन गैस सिलिंडर में अणुओं की C_rms - 20°C पर हीलियम गैस परमाणुओं की C_rms के बराबर होगी ? (Ar का परमाणु द्रव्यमान = 39.9u एवं हीलियम का परमाणु द्रव्यमान = 4.0u)
उत्तर:
दिया गया है
M = 39.9, M1 = 4.0
T = ?
T = 20 + 273 = 253K
अब \(\mathrm{C}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}}=\sqrt{\frac{3 \mathrm{RT}}{39.9}}\) ........... (1)
इसी तरह से
\(\begin{aligned} & C^l=\sqrt{\frac{3 R T^1}{M^1}} \\ & C^l=\sqrt{\frac{3 R \times 253}{4}} \end{aligned}\) ................(2)
∵ T₁ = 253
लेकिन
C = C₁
\(\sqrt{\frac{3 \mathrm{RT}}{39.9}}=\sqrt{\frac{3 \mathrm{R} \times 253}{4}}\)
वर्ग करने पर
\(\frac{3 \mathrm{RT}}{39.9}=\frac{3 \mathrm{R} \times 253}{4}\)
या
\(\mathrm{T}=\frac{253 \times 39.9}{4}\)
T = 2.524 × 10³K

प्रश्न 10. 
नाइट्रोजन गैस के एक सिलिंडर में 2.0 atm दाब एवं 17°C ताप पर नाइट्रोजन अणुओं के माध्य मुक्त पथ एवं संघट्ट आवृत्ति का आकलन कीजिए। नाइट्रोजन अणु की त्रिज्या लगभग 1.0 A लीजिए। संघट्ट- काल की तुलना अणुओं द्वारा दो संघट्टों के बीच स्वतंत्रतापूर्वक चलने में लगे समय से कीजिए। (नाइट्रोजन का आण्विक द्रव्यमान = 28.0u)
उत्तर:
मैक्सवेल की त्रुटि सुधार के अनुसार, एक गैस अणु का
औसत मुक्त पथ
\(\lambda=\frac{1}{\sqrt{2} \pi n_0 d^2}\)
जहाँ पर d = एक अणु का व्यास
दिया गया है:
NA = 6.023 x 10²³ अणु / ग्राम मोल
P = 2atm = 2 × 1.013 × 10² N/m² 
R = 8.3JK^-1 mol^-1
\(n_0=\frac{6.023 \times 10^{23} \times 2 \times 1.013 \times 10^5}{8.3 \times 290}\)
= 5.07 × 1025 = 5.10 x 1025m^-3
r = 1A° = 1 × 10^-10m
∴ 2r = 2 x 10^-10 m
d = 2r = 2 x 10^-10 m

मान रखने पर

= 1.11 × 10^-7m 1.0 x 10^-7m 
r.m.s. वेग C = imm द्वारा दिया जाता है।
यहाँ पर दिया हुआ है कि M = 28 x 10^-3 kg और T = 17 + 273 = 290K
मान रखने पर
\(C=\sqrt{\frac{3 \times 8.31 \times 290}{28 \times 10^{-3}}}\)
C = 5.08 x 10²m/s = 5.1 x 10²m/s
∴ संघट्ट आवृत्ति v = C/λ
\(=\frac{5.1 \times 10^2}{1.0 \times 10^{-7}}\)
= 5.1 x 10⁹ प्रति सेकण्ड 
माना दो क्रमिक संघट्टों के बीच का समय अन्तराल T1 है।
\(\mathrm{T}^1=\frac{\lambda}{\mathrm{C}}=\frac{1.0 \times 10^{-7}}{5.1 \times 10^2}\)
T1 = 2.0 × 10^-10S ....(1)
माना संघट्ट का समय है
\(t=\frac{d}{\mathrm{C}}=\frac{2 \times 10^{-10}}{5.10 \times 10^2}\)
t = 4 x 10^-13S ........ (2)
समीकरण (1) में समीकरण (2) का भाग देने पर
\(\frac{\mathrm{T}^{\mathrm{i}}}{\mathrm{t}}=\frac{2.0 \times 10^{-10}}{4 \times 10^{-13}}\)
T = 500t
अर्थात् क्रमागत संघट्टों के मध्य लगा समय एक संघट्ट के लिये गये समय से 500 गुना है। इससे यह सिद्ध होता है कि गैस में अणु अधिकांश समय तक स्वतंत्र रूप से चलता है।

अतिरिक्त अभ्यास:

प्रश्न 11. 
एक मीटर लंबी सँकरी ( और एक सिरे पर बंद ) नली क्षैतिज रखी गई है। इसमें 76 cm लंबाई भरा पारद सूत्र, वायु के 15 cm स्तंभ को नली में रोककर रखता है। क्या होगा यदि खुला सिरा नीचे की ओर रखते हुए नली को ऊर्ध्वाधर कर दिया जाए?
उत्तर:
जब नली को क्षैतिज अवस्था में रखा जाता है तो पारे का 76 cm सूत्र 15 cm लम्बाई की वायु को फँसा लेता है। खुले सिरे पर नली की 9 cm लम्बाई छोड़ दी जायेगी। नली में बंद वायु का दाब वायुमण्डलीय दाब होगा।
माना नली की अनुप्रस्थ काट 1 सेमी है।
P₁ = 76cm, V₁ = 15 cm
जब नली को ऊर्ध्वाधर रखा जाता है तो वायु को 15 cm के अतिरिक्त दूसरे 9cm वायु के ( क्षैतिज स्थिति से दाहिने हाथ की ओर भरी) मिल जाते हैं।

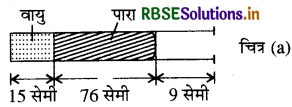
माना कि पारे के h cm वायुमण्डलीय दाब को संतुलित रखने के लिये बाहर प्रवाहित हो जाती हैं।

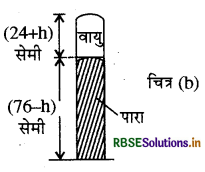
उस स्थिति में वायु स्तम्भ और पारे के स्तम्भ की ऊँचाइयाँ क्रमश: ( 24 + h) सेमी. और (76 - h) सेमी. हैं। तब वायु का
दाब = 76 - (76 - h) = पारे के सेमी.
V2 = (24 + h) cm³, P₂ = hcm
माना कि ताप स्थिर रहता है।\
P₁V₁ = P₂V₂,
या 76 x 15 = h x (24 + h)
या 76 × 15 = 24h + h₂
या h₂ + 24h - 76 x 15 = 0

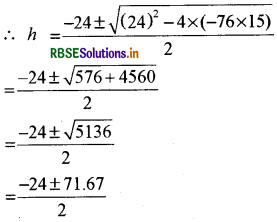
h = 23.8cm या - 47.8cm
= 24 cm या - 48cm
चूंकि h ऋणात्मक नहीं हो सकता इसलिए अधिक पारा नली के अन्दर नहीं प्रवाहित हो सकता।
∴ h = 24 cm
इस प्रकार नली की ऊर्ध्वाधर स्थिति में पारे का 24 सेमी. बाहर प्रवाहित हो जाता है, अर्थात् पारे का सूत्र लम्बाई में 24 सेमी. कम हो जायेगा ।
वायु स्तम्भ की लम्बाई = 24 + h = 48 सेमी.
तथा पारा स्तम्भ की लम्बाई = 76h = 52 सेमी. होगी।

प्रश्न 12. 
किसी उपकरण से हाइड्रोजन गैस 28.7 cm³s^-1 की दर से विसरित हो रही है। उन्हीं स्थितियों में कोई दूसरी गैस 7.2cm³s^-1 की दर से विसरित होती है। इस दूसरी गैस को पहचानिए।
[संकेत: ग्राहम के विसरण नियम R₁/ R₂ = (M₂ /M₁)^1/2 का उपयोग कीजिए, यहाँ R, R, क्रमशः गैसों की विसरण दर तथा M₁ एवं M₂ उनके आण्विक द्रव्यमान हैं। यह नियम अणुगति सिद्धांत का एक सरल परिणाम है।]
उत्तर:
ग्राहम के विसरण नियम के अनुसार
\(\frac{r_1}{r_2}=\sqrt{\frac{\mathrm{M}_2}{\mathrm{M}_1}}\)
जहाँ पर r₁ = गैस 1 के लिये विसरण दर = 28.7cm/s
r₂ गैस 2 के लिये विसरण दर = 7.2cm/s M₁ तथा M₂ क्रमश: उनके अणु द्रव्यमान हैं
\(\begin{aligned} \frac{28.7}{7.2} & =\sqrt{\frac{\mathrm{M}_2}{2}} \\ \mathrm{M}_2 & =\left(\frac{28.7}{7.2}\right)^2 \times 2 \end{aligned}\)
था = (3.99)2 x 2
था = (15.9) x 2 = 31.8
था M₂ = 32
हमें ज्ञात है कि ऑक्सीजन का अणुभार 32 है। अतः अज्ञात गैस O₂ है।

प्रश्न 13. 
साम्यावस्था में किसी गैस का घनत्व और दाब अपने सम्पूर्ण आयतन में एकसमान है। यह पूर्णतया सत्य केवल तभी है जब कोई भी बाह्य प्रभाव न हो। उदाहरण के लिए, गुरुत्व से प्रभावित किसी गैस स्तंभ का घनत्व (और दाब) एकसमान नहीं होता है। जैसा कि आप आशा करेंगे इसका घनत्व ऊँचाई के साथ घटता है। परिशुद्ध
निर्भरता 'वातावरण के नियम n₂ = n₁ exp\(\left[-\frac{m g}{k_B T}\left(h_2-h_1\right)\right]\) से दी जाती है, यहाँ n₂,n₁ क्रमशः h₂ व h₁ ऊँचाइयों पर संख्यात्मक घनत्व को प्रदर्शित करते हैं। इस संबंध का उपयोग द्रव स्तंभ में निलंबित किसी कण के अवसादन साम्य के लिए समीकरण  n₂ = n₁ exp\(\left[-\frac{m g}{k_B T}\left(h_2-h_1\right)\right]\) को व्युत्पन्न करने के लिए कीजिए, यहाँ निलंबित कण का घनत्व तथा p' चारों तरफ के माध्यम का घनत्व है। N आवोगाद्रो संख्या तथा R सार्वत्रिक गैस नियतांक है। [संकेत : निलंबित कण के आभासी भार को जानने के लिए आर्किमिडीज के सिद्धांत का उपयोग कीजिए।]
उत्तर:
कण का भार W = mg = 4/3πr³ pg
चूँकि द्रव्यमान = आयतन घनत्व
m = 4/3πr³ x p
यहाँ पर कण और अणु को गोलीय माना है जहाँ पर r कण की त्रिज्या है और p कण का घनत्व है।
∴ W = 4/3πr³Pg ................... (1)
गुरुत्व में इसकी चाल इस पर ऊपर की ओर उत्प्लावन बल उत्पन्न करती है जो कि
उत्प्लावन बल (B) = 4/3πr³p₁g .............. (2)
यहाँ पर p1 घेरने वाले माध्यम का घनत्व है। यदि कण पर नीचे की ओर कार्यरत बल F है।
तब
F = W - B
F = 4/3πr³pg - 4/3πr³p₁g
= 4/3πr³(p₁ -p)g  ....(3)
वायुमण्डलीय दाब के नियमानुसार
\(n_2=n_1 \exp \left(\frac{-m g}{\mathrm{k}_{\mathrm{B}} \mathrm{T}}\left(h_2-h_1\right)\right)\) .............(4)
जहाँ पर KB = वोल्ट्जमान स्थिरांक है।
h₁ तथा h₂ ऊँचाई पर क्रमश: n₁ व n₂ संख्या घनत्व है। समीकरण (3) में कार्यरत बल F = mg से विस्थापित करने पर

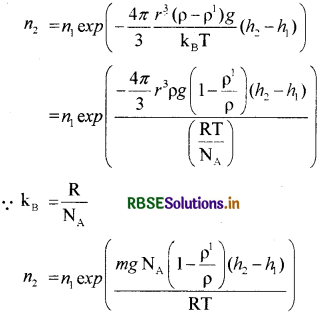
जो कि वांछित सम्बन्ध है। जहाँ पर 4/3πr³pg = कण का द्रव्यमान g = mg

प्रश्न 14. 
नीचे कुछ ठोसों व द्रवों के घनत्व दिए गए हैं। उनके परमाणुओं की आमापों का आकलन (लगभग ) कीजिए।

[ संकेत मान लीजिए कि परमाणु ठोस अथवा द्रव प्रावस्था में 'दृढ़ता से बँधे हैं तथा आवोगाद्रो संख्या के ज्ञात मान का उपयोग कीजिए। फिर भी आपको विभिन्न परमाण्वीय आकारों के लिए अपने द्वारा प्राप्त वास्तविक संख्याओं का बिल्कुल अक्षरशः प्रयोग नहीं करना चाहिए; क्योंकि दृढ़ संवेष्टन सन्निकटन की रुक्षता के परमाणवीय आकार कुछ A के परास में हैं।]
उत्तर:
यदि अणु की त्रिज्या r है तब प्रत्येक अणु का आयतन
= 4/3πr³
पदार्थ के 1 मोल में सभी अणुओं का आयतन

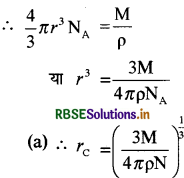
यहाँ पर rc → कार्बन के अणु की त्रिज्या है।
कार्बन के लिये M = 12.01 x 10^-3 kg
Pc = 2.22 x 10³ kg/m³

= 1.29 × 10^-10
= 1.29À
(b) स्वर्ण परमाणु का द्रव्यमान
M = 1.97 × 10^-3 kg
∴ प्रत्येक स्वर्ण परमाणु का द्रव्यमान
M = 1.97 × 10^-3 kg
∴ प्रत्येक स्वर्ण परमाणु का द्रव्यमान
\(=\frac{\mathrm{M}}{\mathrm{N}_{\mathrm{A}}}=\frac{1.97 \times 10^{-3}}{6.023 \times 10^{23}}\)
= 3.271 × 10^-25 kg
Pg = 19.32 × 10³ kg/m³
rs = प्रत्येक स्वर्ण परमाणु की त्रिज्या
∴ आयतन = 4/3πr³g = m/pg
या
\(r_g=\left(\frac{3 m}{4 \pi \rho_{\mathrm{g}}}\right)^{\frac{1}{3}}\)
\(=\left(\frac{3 \times 3.271 \times 10^{-25}}{4 \times 3.142 \times 19.32 \times 10^3}\right)^{\frac{1}{3}}\)
= 0.159 × 10^-9 m
= 1.59 × 10^-10m = 1.59 A°
(c) यहाँ नाइट्रोजन परमाणु का द्रव्यमान
M = 14.01 × 10^-3 kg
∴ प्रत्येक परमाणु का द्रव्यमान
\(m=\frac{\mathrm{M}}{\mathrm{N}_{\mathrm{A}}}=\frac{14.01 \times 10^{-3} \mathrm{~kg}}{6.023 \times 10^{23}}\)
= 2.3261 × 10^-25 kg
माना, rn = प्रत्येक परमाणु की त्रिज्या
pr = 1 x 10³  kg/m³

\(\begin{aligned} r_n & =\left(\frac{3 m}{4 \pi \rho_n}\right)^{\frac{1}{3}} \\ & =\left(\frac{3 \times 2.3261}{4 \times 3.142 \times 1 \times 10^3}\right)^{\frac{1}{3}} \end{aligned}\)

= 1.77 × 10¹⁰ m = 1.77 A

(d) यहाँ MLi = 6.94 x 10^-3 kg
PLi = 0.53 x 10³ kg/m³
MLi = प्रत्येक लीथियम परमाणु का द्रव्यमान
\(\begin{aligned} m_{\mathrm{F}} & =\frac{\mathbf{M}_{\mathrm{F}}}{\mathrm{N}_{\mathrm{A}}} \\ & =\frac{19 \times 10^{-3}}{6.023 \times 10^{23}} \end{aligned}\)
= 1.152 × 10^-26 kg
rLi = प्रत्येक लीथियम परमाणु की त्रिज्या है।

= 1.73 × 1010m = 1.73Å

(e)
MF = 19 × 10^-3kg 
Pg = 1.14 × 10³ kg/m³
प्रत्येक फ्लोरीन परमाणु का द्रव्यमान
\(\begin{aligned} r_n & =\left(\frac{3 m}{4 \pi \rho_n}\right)^{\frac{1}{3}} \\ & =\left(\frac{3 \times 2.3261}{4 \times 3.142 \times 1 \times 10^3}\right)^{\frac{1}{3}} \end{aligned}\)
= 3.155 × 10^-26kg
यदि rF , प्रत्येक क्लोरीन परमाणु की त्रिज्या है, तब