RBSE Solutions for Class 11 Physics Chapter 12 ऊष्मागतिकी

Rajasthan Board RBSE Solutions for Class 11 Physics Chapter 12 ऊष्मागतिकी Textbook Exercise Questions and Answers.

RBSE Class 11 Physics Solutions Chapter 12 ऊष्मागतिकी

RBSE Class 11 Physics ऊष्मागतिकी Textbook Questions and Answers

प्रश्न 1. 
कोई गीजर 3.0 लीटर प्रति मिनट की दर से बहते हुए जल को 27°C से 77°C तक गर्म करता है। यदि गीजर का परिचालन गैस बर्नर द्वारा किया जाए तो ईंधन के व्यय की क्या दर होगी? बर्नर के ईंधन की दहन - ऊष्मा 4.0 × 10⁴ Jg^-1 है।
उत्तर:
दिया गया है:
गर्म किये गये पानी के आयतन प्रवाह की दर (V) = 3.0 litre / min.
पानी की विशिष्ट ऊष्मा (s)  = 4.2 × 10³ Jkg^-1 C^-1 
पानी का घनत्व
= 3 x 10³ × 10^-6m³/min.
= 3 × 10^-3m³/min.
P = 10 kg/m
∴ गर्म किये गये पानी के प्रवाह की दर किग्रा / मिनट में
m = pV
= 10³ × 3 × 10^-3 kg/min.
= 3kg/min.
पानी के ताप में वृद्धि ∆T = T₂ - T₁
= 77 - 27 = 50°C
पानी की विशिष्ट ऊष्मा
s = 4.2Jkg^-1 C^-1
प्रयोग की गयी ऊष्मा ∆Q = ms∆T
= 3 x 4.2 × 10³ × 50J / min.
= 63 × 10⁴ J/min. .............. (1)
दिया गया है- बर्नर के ईंधन की दहन ऊष्मा,
= 40 × 10⁴Jg^-1
= 4.0 × 10⁴ × 10³Jkg^-1
= 4.0 × 10⁷Jkg^-1
माना ईंधन की mkg/min की दहन दर है
= m × 4 × 10⁷ J/min. ....(2)
समीकरण (1) तथा (2) को बराबर करने पर
m × 4 × 10⁷ = 63 x 10⁴
\(m=\frac{63 \times 10^4}{4 \times 10^7}=15.75 \times 10^{-3}\)
या
m = 15.75 × 10^-3 kg/min.
m = 15.75 × 10^-3 × 10 g/min. 
m = 15.75 g/min.
अर्थात् ईंधन की दहन दर 16g/min 

प्रश्न 2. 
स्थिर दाब पर 2.0 x 10 kg नाइट्रोजन ( कमरे ताप में 45°C वृद्धि करने के लिए कितनी ऊष्मा के ताप पर) के की आपूर्ति की जानी चाहिए? ( N₂ का अणुभार R = 8.3 Jmol ^-1 K^-1)
उत्तर:
दिया गया है:
गैस का द्रव्यमान m = 2 × 10^-2kg
= 2 × 10^-2  x 10³g = 20 g 
ताप में वृद्धि ∆T = 45°C
N₂ का अणुभार = 28g
m ग्राम गैस में " मोल हो तो n = \(\frac{m}{M}=\frac{20}{28}=\frac{5}{7}\)
R = 8.3Jmol^-1 K^-1
चूँकि नाइट्रोजन द्विपरमाणुक गैस है, अतः स्थिर दाब पर गैस की विशिष्ट ऊष्मा का मान
\(\mathrm{C}_{\mathrm{P}}=\frac{7}{2} \mathrm{R}=\frac{7}{2} \times 8.3 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}\)
माना ऊष्मा की आवश्यकता
∆Q = ?
∴ ∆Q = nCp∆T
\(=\frac{5}{7} \times \frac{7}{2} \times 8.3 \times 45 \mathrm{~J}\)
= 933.75J
= 934J

प्रश्न 3. 
व्याख्या कीजिए कि ऐसा क्यों होता है-
(a) भिन्न-भिन्न तापों I व I के दो पिण्डों को यदि ऊष्मीय सम्पर्क में लाया जाए तो यह आवश्यक नहीं कि उनका अंतिम ताप (T, + T ) / 2 ही हो।
(b) रासायनिक या नाभिकीय संयंत्रों में शीतलक ( अर्थात् द्रव जो संयंत्र के भिन्न-भिन्न भागों को अधिक गर्म होने से रोकता है) की विशिष्ट ऊष्मा अधिक होनी चाहिए।
(c) कार को चलाते चलाते उसके टायरों में वायुदाब बढ़ जाता है।
(d) किसी बंदरगाह के समीप के शहर की जलवायु समान अक्षांश के किसी रेगिस्तानी शहर की जलवायु से अधिक शीतोष्ण होती है।
उत्तर:
(a) इसका कारण यह है कि दोनों पिण्डों के द्रव्यमान भिन्न हो सकते हैं और उनकी विशिष्ट ऊष्मा भी भिन्न हो सकती है। जब दोनों पिण्ड सम्पर्क में आते हैं तब उच्च ताप वाले पिण्ड से भिन्न ताप वाले पिण्ड की ओर ऊष्मा का प्रवाह होता है। जब तक कि दोनों पिण्डों के ताप समान नहीं हो जाते हैं। अन्तिम ताप दोनों तापों का अन्तर हो सकता है अर्थात् T₁ + T₂/2 केवल तभी जबकि दोनों पिण्डों की ऊष्मा - धारितायें समान हों।
(b) यह इसलिये है कि पदार्थ द्वारा अवशोषित ऊष्मा पदार्थ की विशिष्ट ऊष्मा के अनुपाती है। जितनी अधिक विशिष्ट ऊष्मा होगी उतनी ही अधिक ऊष्मा उसी ताप वृद्धि के लिये शीतलक अवशोषित करेगा। 
(c) सड़क और टायर के बीच घर्षण के कारण वाहन चालन में टायर और उनके बीच वायु का ताप बढ़ जाता है और टायर का आयतन अपरिवर्तित रहता है। चार्ल्स के नियम से P α T ताप बढ़ने के कारण टायर के अन्दर वायुदाब बढ़ जाता है।
(d) यह इसलिये है चूँकि किसी बंदरगाह के समीप के शहर को आर्द्रता का मान किसी रेगिस्तानी शहर की तुलना में अधिक होता है।

प्रश्न 4. 
गतिशील पिस्टन लगे किसी सिलिंडर में मानक ताप द पर 3 मोल हाइड्रोजन भरी है। सिलिंडर की दीवारें ऊष्मारोधी पदार्थ की बनी हैं तथा पिस्टन को उस पर बालू की परत लगाकर ऊष्मारोधी बनाया गया है। यदि गैस को उसके आरंभिक आयतन के आधे आयतन तक संपीडित किया जाए तो गैस का दाब कितना बढ़ेगा?
उत्तर:
किसी भी ऊष्मा का आदान-प्रदान अनुमत नहीं है। अतः प्रक्रम रुद्धोष्म है। अब रुद्धोष्म परिवर्तन के लिये दिया गया है।
माना

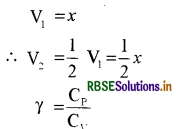
द्विपरमाणुक गैस या हाइड्रोजन के लिये

अतः दाब को प्रारम्भिक दाब का 2.64 गुना अधिक करना होगा। 

प्रश्न 5. 
रुद्धोष्म विधि द्वारा किसी गैस की अवस्था परिवर्तन करते समय उसकी एक साम्यावस्था A से दूसरी साम्यावस्था B तक ले जाने में निकाय पर 22.3J कार्य किया जाता है। यदि गैस की दूसरी प्रक्रिया द्वारा अवस्था A से अवस्था B में लाने से निकाय द्वारा अवशोषित नेट ऊष्मा 9.35 cal है तो बाद के प्रकरण में निकाय द्वारा किया गया नेट कार्य कितना है? (1 cal = 4.19 J)
उत्तर:
यहाँ पर रुद्धोष्म प्रक्रम है ∆Q = 0
∆W = - 23.3 J
ऊष्मागतिकी के प्रथम नियम से
∆Q = dU + ∆W
मान रखने पर
0 = dU - 22.3
या
∆U = 22.3 J
दूसरी प्रक्रिया में ∆Q= 9.35 कैलोरी
= 9.35 × 4.2 J = 39.3 जूल
∆W= ?
∆Q = dU + ∆W
 ∆W = ∆Q - ∆U
= 39.3 - 22.3 J
= 17.0 J

प्रश्न 6. 
समान धारिता वाले दो सिलिंडर A तथा B एक- दूसरे से स्टॉपकॉक के द्वारा जुड़े हैं। A में मानक ताप व दाब पर गैस भरी है जबकि B पूर्णतः निर्वातित है। स्टॉपकॉक यकायक खोल दी जाती है। निम्नलिखित का उत्तर दीजिए-
(a) सिलिंडर A तथा B में अंतिम दाब क्या होगा?
(b) गैस की आंतरिक ऊर्जा में कितना परिवर्तन होगा? 
(c) गैस के ताप में क्या परिवर्तन होगा?
(d) क्या निकाय की माध्यमिक अवस्थाएँ (अंतिम साम्यावस्था प्राप्त करने के पूर्व) इसके P-V-T पृष्ठ पर होंगी?
उत्तर:
(a) जब स्टॉपकॉक यकायक खोल दी जाती है, तब एक वायुदाब पर उपलब्ध गैस का आयतन दुगुना हो जाता है और दाब घटकर आधा हो जायेगा अर्थात् 0.5 वायुदाब।
(b) गैस की आंतरिक ऊर्जा में कोई भी परिवर्तन नहीं होगा, क्योंकि गैस पर या उसके द्वारा कोई भी कार्य नहीं किया जाता है।
(c) यदि गैस को आदर्श माना जाये तो उसके ताप में कोई परिवर्तन नहीं होगा क्योंकि प्रसार में यह कोई कार्य नहीं करती है। अर्थात् ∆T = 0
(d) नहीं, क्योंकि गैस का मुक्त प्रसार हो रहा है, अतः प्रक्रिया को नियंत्रित नहीं किया जा सकता (तीव्र प्रक्रम) अतः मध्यवर्ती अवस्थाओं में गैस साम्यावस्था प्राप्त नहीं करेगी। हाँ, कुछ समय पश्चात् अवश्य गैस साम्यावस्था प्राप्त कर लेगी तथा गैस की अवस्था P. V. T पृष्ठ पर स्थित होगी।

प्रश्न 7. 
एक वाष्प इंजन अपने बॉयलर से प्रति मिनट 3.6 × 10J ऊर्जा प्राप्त करता है जो प्रति मिनट 5.4 x 10 J कार्य देता है। इंजन की दक्षता कितनी है? प्रति मिनट कितनी ऊष्मा अपशिष्ट होगी?
उत्तर:
Q₁ = प्रति मिनट अवशोषित ऊर्जा
= 3.6 × 10⁴ J/minute
W =  वाष्प इंजन के द्वारा किया गया कार्य प्रति मिनट
= 5.4 × 10⁸ J/minute
Q₂ = अपव्यय (अस्वीकृत) ऊर्जा का मान प्रति मिनट n % = इंजन की दक्षता प्रतिशत में

∴ n = 0.15 x 100 = 15%
सम्बन्ध Q₁ = W + Q₂
Q₂ = Q₁ - W
= 3.6 x 10⁹ - 5.4 x 10⁸
= 36 x 10⁸ - 5.4 x 10⁸
= 30.6 x 10⁸ = 3.06 x 10⁹J

प्रश्न 8. 
एक हीटर किसी निकाय को 100 W की दर से ऊष्मा प्रदान करता है। यदि निकाय 75Js की दर से कार्य करता है, तो आंतरिक ऊर्जा की वृद्धि किस दर से होगी?
उत्तर:
दिया गया है-
ऊष्मा प्रदान की गयी,
∆Q = 100 W
∆Q = 100 J/s
तो किया गया कार्य
∆W = 75 J/s
आन्तरिक ऊर्जा में वृद्धि दर प्रति सेकण्ड dU = ?
ऊष्मागतिकी के प्रथम नियम से
या
∆Q= dU + ∆W
∴ dU = ∆Q - ∆W
= 100 - 75 = 25 J/s
dU = 25 W

प्रश्न 9. 
किसी ऊष्मागतिकीय निकाय को मूल अवस्था से मध्यवर्ती अवस्था तक चित्र में दर्शाये अनुसार एक रेखीय प्रक्रम द्वारा ले जाया गया है।

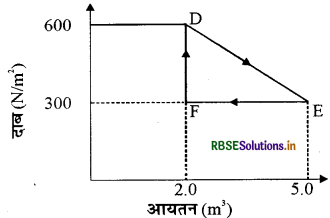
एक समदाबी प्रक्रम द्वारा इसके आयतन को E से F तक ले जाकर मूल मान तक कम कर देते हैं। गैस द्वारा D से E तथा E से F तक कुल किए गए कार्य का आकलन कीजिए।
उत्तर:
दिये गये चित्र से प्रक्रम DE में
आयतन में वृद्धि dv = 5.0 - 20 = 3m³
दाब में वृद्धि dp = 600 - 300 = 300N/m²
गैस के द्वारा किया गया कार्य (D से E से F तक )
= ∆DEF का क्षेत्रफल
W = 1/2 x DF × EF
= 1/2(600 - 300) (5 - 2)
= 1/2300 N/m² x 3m³
= 450 N-m.
= 450J

प्रश्न 10. 
खाद्य पदार्थ को एक प्रशीतक के अंदर रखने पर वह उसे 9°C पर बनाए रखता है। यदि कमरे का ताप 36 °C है तो प्रशीतंक के निष्पादन गुणांक का आकलन कीजिए।
उत्तर:
दिया गया है-
T1 = 273 + 36 = 309K
T2 = 9°C = 273 + 9282K
α =?
सम्बन्ध \(\alpha=\frac{T_2}{T_1-T_2}\) का उपयोग करके
\(\begin{aligned} & \alpha=\frac{282}{309-282} \\ & =\frac{282}{27}=10.44 \\ & \alpha=10.44 \\ & \end{aligned}\)