RBSE Solutions for Class 11 Physics Chapter 11 द्रव्य के तापीय गुण

Rajasthan Board RBSE Solutions for Class 11 Physics Chapter 11 द्रव्य के तापीय गुण Textbook Exercise Questions and Answers.

RBSE Class 11 Physics Solutions Chapter 11 द्रव्य के तापीय गुण

RBSE Class 11 Physics द्रव्य के तापीय गुण Textbook Questions and Answers

प्रश्न 1. 
निऑन तथा CO₂ के त्रिक बिन्दु क्रमशः 24.57K तथा 216.55K हैं। इन तापों को सेल्सियस तथा फारेनहाइट मापक्रमों व्यक्त कीजिए।
उत्तर:
सेल्सियस और केल्विन पैमाने में सम्बन्ध:
t = 1 - 273.15
जहां tc, tk = सेल्सियस और केल्विन पैमाने का तापमान है।
निऑन के लिए:
tc = 24.57 - 273.15 = 248.58°C
CO₂ के लिए:
t = 216.55 - 273.15 = -56.60°C
केल्विन और फारेनहाइट पैमाने में सम्बन्ध
\(\frac{t_{\mathrm{F}}-32}{180}=\frac{t_{\mathrm{k}}-273.15}{100}\)
मान रखने पर
\(t_F-32=\frac{180}{100}\left(t_k-273.15\right)\)
∴ \(t_{\mathrm{F}}=\frac{180}{100}\left(\mathrm{t}_{\mathrm{k}}-273.15\right)+32\)
निऑन के लिये
tF = 180/100 (24.57 - 273.15) + 32
= 1.80 (-248.58) + 32
= - 447.444 + 32 = - 415.444°F 
CO₂ के लिये
TF = 180/100(216.55 - 273.15) + 32
= 1.80(-56.6) + 32
= -101.88 + 32 = -69,88°F

प्रश्न 2. 
दो परम ताप मापक्रमों A तथा B पर जल के त्रिक बिन्दु को 200 A तथा 350 B द्वारा परिभाषित किया गया है। T तथा T में क्या संबंध है?
उत्तर:
दिया गया है:
जल का त्रिक बिन्दु पैमाने A पर 200A 
जल का त्रिक बिन्दु पैमाने B पर 350B 
प्रश्नानुसार 200A = 350B = 273.16K
या \(1 A=\frac{273.16}{200} K\)
और \(1 B=\frac{273.16}{350} K\)
यदि TA और TB जल के त्रिक बिन्दु पैमाने A और B पर हों त

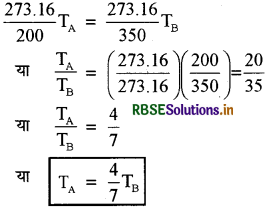
प्रश्न 3. 
किसी तापमापी का ओम में विद्युत प्रतिरोध ताप के साथ निम्नलिखित सन्निकट नियम के अनुसार परिवर्तित होता है R = Ro [1 + α (T - To)] यदि तापमापी का जल के त्रिक बिन्दु 273.16K पर प्रतिरोध 101.62Ω तथा लैंड के सामान्य संगलन बिन्दु (600.5K ) पर प्रतिरोध 165.552Ω है तो वह ताप ज्ञात कीजिए जिस पर तापमापी का प्रतिरोध 123.452Ω है।
उत्तर:
दिया गया है:
यहाँ पर R = 101.652. 
T_o = 273. 16K 
स्थिति (i) R₁ = 165.502, T₂ = 600.5K 
स्थिति (ii) R₂ = 123.452, T₂ = ? 
सम्बन्ध का प्रयोग करने में
R = R0 [1 +  α (T - T0)]
स्थिति (i) के लिए मान रखने पर
165.5 = 101.6[1 + α (600.5 - 273.16)]

स्थिति (ii) में
123.4 = 101.6[1 + α (T₂ - 273.16)]
123.4/101.6 = [1 + α(T₂ - 273.16)]
\(\frac{(123.4-101.6)}{101.6}\) = α(T₂ - 273.16)
a का मान रखने पर
\(\begin{aligned} & \Rightarrow \quad \frac{21.8}{101.6}=\frac{63.9}{327.34 \times 101.6}\left(\mathrm{~T}_2-273.16\right) \\ & \Rightarrow \quad \frac{21.8 \times 327.34}{63.9}=\mathrm{T}_2-273.16 \\ & \end{aligned}\)
⇒ 111.67 + 273.16 = T₂
⇒ 384.83 = T₂
या
⇒ T₂ = 384.83
⇒ T₂ = 385K.

प्रश्न 4. 
निम्नलिखित के उत्तर दीजिए:
(a) आधुनिक तापमिति में जल का त्रिक बिन्दु एक मानक नियत बिन्दु है, क्यों? हिम के गलनांक तथा जल के क्वथनांक को मानक नियत बिंदु मानने में (जैसा कि मूल सेल्सियस मापक्रम में किया गया था) क्या दोष है?
(b) जैसा कि ऊपर वर्णन किया जा चुका है कि मूल सेल्सियस मापक्रम में दो नियत बिंदु थे जिनको क्रमशः 0°C तथा 100°C संख्याएं निर्धारित की गईं थीं। परम ताप मापक्रम पर दो में से एक नियत बिंदु जल का त्रिक बिंदु लिया गया है जिसे केल्विन परम ताप मापक्रम पर संख्या 273.16 K निर्धारित की गई है। इस मापक्रम (केल्विन परम ताप ) पर अन्य नियत बिंदु क्या है?
(c) परम ताप (केल्विन मापक्रम ) T तथा सेल्सियस मापक्रम पर ताप tc में संबंध इस प्रकार है लिखा?
tc = T - 273.15
इस संबंध में हमने 273.15 लिखा है 273.16 क्यों नहीं
(d) उस परम ताप मापक्रम पर, जिसके एकांक अंतराल का आमाप फोरनहाइट के एकांक अंतराल की आमाप के बराबर है, जल के त्रिक बिन्दु का ताप क्या होगा?
उत्तर:
(a) क्योंकि जल का त्रिक बिन्दु (273.16K) एक निश्चित बिन्दु है तथा इसके संगत दाब व आयतन के मान भी निश्चित ही होते हैं। जबकि हिम के गलनांक तथा जल के क्वथनांक के मान दाब व आयतन के साथ परिवर्तनीय होते हैं।
(b) दूसरी ओर OK परम ताप पैमाने पर निश्चित ताप है। यह उस ताप के संगत है जिस पर गैस का ताप व दाब शून्य हो जाता है।
(c) त्रिक बिन्दु 0°C की अपेक्षा 0.01°C है। इस प्रकार से सेल्सियस डिग्री को केल्विन डिग्री के बराबर करने के लिए हिम बिन्दु 273.16 की अपेक्षा 27315K का केल्विन पैमाने पर उपयोग में लाते हैं और 273.15K के संगत सेल्सियस पैमाने पर 0°C है जो कि सम्बन्ध t = T - 273.15 से स्पष्ट है। यदि हम उपर्युक्त सम्बन्ध में 273.15 के स्थान पर 273.16 का प्रयोग करते हैं तो सेल्सियस पैमाने पर हिम बिन्दु 0 - 0.01°C होगा जो स्थिति नहीं है।
(d) हम जानते हैं

यदि t¹_K - t_K = 1k
तब t¹_F - t_F = 9/5
त्रिक बिन्दु तापक्रम के लिये
t = 273.16
नये पैमाने पर तापक्रम होगा = 273. 16 x 9/5 = 491.69

प्रश्न 5. 
दो आदर्श गैस तापमापियों A तथा B में क्रमशः ऑक्सीजन तथा हाइड्रोजन प्रयोग की गई हैं। इनके प्रेक्षण निम्नलिखित हैं;

(a) तापमापियों A तथा B के द्वारा लिए गए पाठ्यांकों के अनुसार सल्फर के सामान्य गलनांक का परमताप क्या है?
(b) आपके विचार से तापमापियों A तथा B के उत्तरों में थोड़ा अंतर होने का क्या कारण है? (दोनों तापमापियों में कोई दोष नहीं है)। दो पाठ्यांकों के बीच की विसंगति को कम करने के लिए इस प्रयोग में और क्या प्रावधान आवश्यक हैं?
उत्तर:
(a) माना गंधक का गलनांक T है। हमें यह भी ज्ञात है
कि पानी का त्रिक बिन्दु T = 273.16K
थर्मामीटर A के लिए
p_tr = 1.250 × 10⁵ P_a
P = 1.797 × 10⁵ P_aT = ?
हम जानते हैं

= 392.69K
B तापमापी के लिये
P_tr = 0.200 x 10⁵ P_a
P = 0.287 × 10⁵Pa
\(=273.16 \times \frac{0.287 \times 10^5}{0.200 \times 10^5}\)
= 391.98K

(b) तापमापियों A तथा B के उत्तरों में थोड़ा अन्तर होने का मुख्य कारण यह है कि ऑक्सीजन तथा हाइड्रोजन पूर्ण रूप से आदर्श गैस नहीं हैं। दो पाठ्यांकों के बीच की विसंगति को कम करने के लिए माप कम से कम दाब पर और त्रिक बिन्दु पर परम दाब और ताप के बीच में आरेख खींचकर बहिर्वेशन द्वारा ताप को प्राप्त किया जाता है। यदि PO प्रतिबन्ध में जब गैस आदर्श गैस की भांति व्यवहार करने की ओर अग्रसर होती है तब दाब शून्य की ओर बढ़ता है, यही प्रतिबंध है।

प्रश्न 6. 
किसी 1m लंबे स्टील के फीते का यथार्थ अंशांकन 27.0°C पर किया गया है। किसी तप्त दिन जब ताप 45°C था तब इस फीते से किसी स्टील की छड़ की लम्बाई 63.0cm मापी गई। उस दिन स्टील की छड़ की वास्तविक लंबाई क्या थी? जिस दिन ताप 27.0°C होगा उस दिन इसी छड़ की लम्बाई क्या होगी ? स्टील का रेखीय प्रसार गुणांक 1.20 × 10^-5K।
उत्तर:
स्टील के फीते का यथार्थ अंशांकन 27.0°C किया गया है। इसका अर्थ है कि फीता 27°C पर सही माप देगा अर्थात् स्टील फीते पर 1 सेमी. का परिमाण सही है।
∴ 27°C पर स्टील छड़ की लम्बाई l = 63cm.
और α = 1.2 × 10^-5 K^-1 जब ताप 27°C से 45°C तक अर्थात् 18°C बढ़ता है तब ∆l स्टील की छड़ की लम्बाई में वृद्धि हो तब
∆l = αl∆T
मान रखने पर
= 1.2 × 10^-5 × 63 × 18
[ ∆T = 45 - 27 = 18°C ]
= 1.2 × 63 × 18 × 10^-5 = 1360.8 × 10^-5 cm.
= 0.0136cm.
∴ स्टील की छड़ की लम्बाई (45°C पर)
= l + ∆l
= 63 + 0.0136
= 63.0136cm.
समान स्टील छड़ की लम्बाई 27°C तापक्रम वाले दिन होगी
= 63 x 1 = 63cm.

प्रश्न 7. 
किसी बड़े स्टील के पहिए को उसी पदार्थ की किसी धुरी पर ठीक बैठाना है। 27°C पर धुरी का बाहरी व्यास 8.70 cm तथा पहिए के केन्द्रीय छिद्र का व्यास 8.69 cm है। सूखी बर्फ द्वारा धुरी को ठंडा किया गया है। धुरी के किस ताप पर पहिया धुरी पर चढ़ेगा? यह मानिए कि आवश्यक ताप परिसर में स्टील का रैखिक प्रसार गुणांक नियत रहता है 
उत्तर:
दिया गया है T = 27°C  = 300K
T₁ K ताप पर लम्बाई l₁ = 8.70cm. 
T₂ K ताप पर लम्बाई /l₂ = 8.69cm.
लम्बाई में वृद्धि = l₂ - l₁ = -8.69 - 8.70
हम जानते हैं ∆l = -0.01cm. ∆l = l₁α (T₁ - T₂)
मान रखने पर
-0.01 = 8.70 × 1.20 × 10^-5 (T₂ - 300)
[ ∵ α = 1.20 × 10^-5 K^-1]

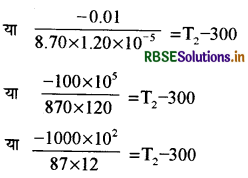
-0.958 × 10² =T₂ - 300
-95.8 + 300 = T₂
T₂ = 204.2K
T₂ = 204.2 - 273
= -68.8°C

प्रश्न 8. 
तांबे की चादर में एक छिद्र किया गया है। 27.0° C पर छिद्र का व्यास 4.24 cm है। इस धातु की चादर को -227° C तक तप्त करने पर छिद के व्यास में क्या परिवर्तन होगा? ताँबे का रेखीय प्रसार गुणांक 1.70 × 10^-5 K^-1 
उत्तर:
दिया गया है:
ताप T₁ = 27°C = 27 + 273 = 300K 
T₂ = 227°C = 227 + 273 = 500K
छिद्र का व्यास D₁ = 4.24 सेमी
α = 1.70 x 10^-5 प्रति केल्विन
प्रसार के पश्चात् माना छिद्र का व्यास D₂ हो जाता है।
अतः
L₂ = L₁ (1 + α∆T)
2πr² = 2πr (1 + α∆T)
D₂ = D₁ [1 + α∆T]
अतः व्यास में परिवर्तन
D₂ = D₁ + D₁ α∆T
∆D = D₁ α∆T = D₁ α(T₂ - T₁)
मान रखने पर
∆D = 4.24 × 1.70 x 10 [500 - 300] 
∆D = 4.24 × 1.70 x 10 x 200
= 0.0144 cm
= 1.44 x 10² cm. = 0144cm.
अर्थात् छिद्र के व्यास में 0.0144 सेमी. की बढ़ोतरी हो जायेगी। 

प्रश्न 9. 
27° C पर 1.8 cm लंबे किसी पीतल के तार को दृढ़ टेकों के बीच अल्प तनाव रखकर थोड़ा कसा गया है। यदि तर को -39° C ताप तक शीतित करें तो तार में कितना तनाव त्पन्न हो जाएगा? तार का व्यास 2.0 mm है। पीतल का रेखीय सार गुणांक = 2.0 x 10^-5 K^-1, पीतल का यंग प्रत्यास्थता गुणांक = 0.91 × 10¹¹ Pal
उत्तर:
दिया गया है:
l₁ = 1.8m.
t₁ = 27°C, t₂ = -39°C 
∴ ∆t = t₂ - t₁ = -39°C  - 27°C
= -66°C
माना t₂ °C पर लम्बाई = l₂ है।
पीतल के लिये α = 2 × 10^-5 C^-1
Y = 0.91 × 10¹¹ Pa
तार का व्यास D = 2.0mm = 2 × 10^-3m.

\(\mathrm{A}=\pi\left(\frac{\mathrm{D}}{2}\right)^2=\frac{1}{4} \pi \mathrm{D}^2\)
= 3.14 × (2 × 10^-3)²
= 3.14 × 10^-6 m^-2
यदि इस दौरान तार में उत्पन्न तनाव F हो तब

लेकिन
∆l = l₁α ∆t
अतः मान रखने पर
F = YA _o ∆t
F = 0.91 × 10¹¹ x 3.14 x 10^-6 x 2 x 10^-5 x 66
= 377.17 N
अतः तार में 377 N का तनाव उत्पन्न हो जाएगा।

प्रश्न 10. 
50 cm लंबी तथा 3.0 mm व्यास की किसी तांबे की छड़ को उसी लंबाई तथा व्यास की किसी स्टील की छड़ से जोड़ा गया है। यदि ये मूल लंबाइयां 40°C पर हैं, तो 250°C पर संयुक्त छड़ की लम्बाई में क्या परिवर्तन होगा? क्या संधि पर कोई तापीय प्रतिबल उत्पन्न होगा? छड़ के सिरों को प्रसार के लिए मुक्त रखा गया है। (ताँबे तथा स्टील के रेखीय प्रसार गुणांक क्रमशः = 2.0 × 10⁵ K^-1, स्टील = 1.2 x 10⁵ K हैं।) 
उत्तर: 
दिया गया है:
तांबे की छड़ का (α) = 2.0 x 10^-5 K^-1 
l₁ = 50cm, t₁ = 40°C t₂ = 250°C
∴ ∆t = 2 - 1 = 250 - 40 = 210°C
यदि l₂°C पर माना लम्बाई = l₂, तब
l₂ = l₁ (1 + α∆t )
∴ तांबे के लिए
∆l = l₂ - l₁
= αl₁ ∆t
= 2 × 10⁵ x 50 x 210
= 0.21 cm.
स्टील की छड़ के लिए
t₁ =40°C, t₂ = 250°C
∆t = t₂ - t₁ = 250°C - 40°C = 210°C 
a = 1.2 × 10^-5K^-1
l₁ = 50.0cm ∆t  = l¹₂ - l₁¹
l¹2 = l11(1 + α∆t)
स्टील के लिए ∆l1 = l21 - l11
∆l1 = αl11 ∆t1
मान रखने पर ∆l1 = 1.2 x 10^-5 x 50 x 210 = 0.126 cm.
∴ 250°C पर संयुक्त छड़ की लम्बाई
= 50.21 + 50.126
= 100.336cm.
और 40°C पर संयुक्त छड़ की लम्बाई
= 4 + 4 = 50 + 50
= 100cm.
∴ संयुक्त छड़ की लम्बाई में वृद्धि
= 100.336 - 100
= 0.336cm.
= 0.34cm.
छड़ें स्वतंत्र रूप से प्रसारित होती हैं, अतः जोड़ों पर कोई ऊष्मीय प्रतिबल उत्पन्न नहीं होता है।

प्रश्न 11. 
ग्लिसरीन का आयतन प्रसार गुणांक 49 × 10^-5 K है। ताप में 30°C की वृद्धि होने पर इसके घनत्व में क्या आंशिक परिवर्तन होगा?
उत्तर: 
दिया गया है: γ = 49 × 10^-5 °C
ताप में वृद्धि ∆T = 30°C
माना ग्लिसरीन का इसका आयतन V0 है तब आरम्भिक आयतन Vt है और 30°C पर
Vt = Vo (1 + γ∆T )
= V(1 + 49 × 10^-5 × 30)
= V(1 + 1470 × 10^-5)
= Vo (1 + 0.01470)
= 1.01470 Vo
\(\frac{\mathrm{V}_{\mathrm{t}}}{\mathrm{V}_{\mathrm{O}}}=1.01470\) ............ (1)
माना Po और P1 ग्लिसरीन के आरम्भिक तथा अन्तिम घनत्व हैं।
तब Po = m/v0 और P1 = m/v1
∴ घनत्व में भिन्नीय परिवर्तन = \(\frac{\rho_1-\rho_0}{\rho_o}\)
\(\begin{aligned} & =\frac{\frac{\mathrm{m}}{\mathrm{V}_{\mathrm{t}}}-\frac{\mathrm{m}}{\mathrm{V}_{\mathrm{O}}}}{\frac{\mathrm{m}}{\mathrm{V}_{\mathrm{O}}}}=\frac{\mathrm{V}_{\mathrm{O}}-\mathrm{V}_{\mathrm{t}}}{\mathrm{V}_{\mathrm{t}}} \\ & =\frac{\mathrm{V}_{\mathrm{O}}}{\mathrm{V}_{\mathrm{t}}}-1=\frac{1}{1.01470}-1 \end{aligned}\)
= 0.986 - 1 = -0.014
यहां पर ऋण चिह्न यह दर्शाता है कि ताप बढ़ने के साथ घनत्व कम हो जाता है।
Δρ/Po = 0.014 = 14 × 10^-3 = 1.4 × 10^-2

प्रश्न 12. 
8.0 kg द्रव्यमान के किसी ऐलुमिनियम के छोटे ब्लॉक में छिद्र करने के लिए किसी 10kw की बरमी का उपयोग किया गया है। 2.5 मिनट में ब्लॉक के ताप में कितनी वृद्धि हो जाएगी? यह मानिए कि 50% शक्ति तो स्वयं बरमी को गर्म करने में खर्च हो जाती है अथवा परिवेश में लुप्त हो जाती है। ऐलुमिनियम की विशिष्ट ऊष्माधारिता = 0.91 JgTK+ है।
उत्तर:
दिया गया है
ब्लॉक का द्रव्यमान m = 8 किग्रा.
ऐलुमिनियम की विशिष्ट ऊष्मा
S = 0.91 जूल / ग्राम - केल्विन
S = 0.91 × 10^-3 जूल / किग्रा. केल्विन
बरमी की शक्ति = P10 किलोवाट
= 10 x 10³ वाट = 10⁴ जूल / से.
अतः बरमी द्वारा 2.5 मिनट में उत्पन्न ऊष्मा
या
H = P x t = 10⁴ x 2.5 x 60 
H = 1.5 x 10⁶ जूल
ऐलुमिनियम ब्लॉक को प्राप्त ऊष्मा = 1/2H = mSΔT
ताप वृद्धि imm
= 103.02°C
= 103°C

प्रश्न 13. 
2.5 kg द्रव्यमान के ताँबे के गुटके को किसी भट्टी में 500°C तक तप्त करने के पश्चात् किसी बड़े हिम-ब्लॉक पर रख दिया जाता है। गलित हो सकने वाली हिम की अधिकतम मात्रा क्या है? ताँबे की विशिष्ट ऊष्माधारिता = 0.39Jg K^-1; बर्फ की संगलन ऊष्मा = 335 Jg^-1 है।
उत्तर:
दिया गया है:
धातु के गुटके का द्रव्यमान m = 2.5kg
m = 2500g
भट्टी का ताप T = 500°C
ताँबे की विशिष्ट ऊष्मा S = 0.39Jg^-1 °C^-1
हिमांकन की गुप्त ऊष्मा L = 335Jg^-1
माना बर्फ पिघलने की मात्रा का द्रव्यमान = m, है।
अतः बर्फ द्वारा प्राप्त की गई ऊष्मा = ताँबे द्वारा खोई गई ऊष्मा
m1L = mS∆T
m1 = mS∆T/L
मान रखने पर
\(=\frac{2500 \times 0.39 \times 500}{335}\)
= 1500g = 1.5kg 

प्रश्न 14. 
किसी धातु की विशिष्ट ऊष्माधारिता के प्रयोग में 0.20kg के धातु के गुटके को 150°C पर तप्त करके किसी ताँबे के ऊष्मामापी (जल तुल्यांक = 0.025 kg.), जिसमें 27°C का 150 cm जल भरा है, में गिराया जाता है। अंतिम ताप 40°C है। धातु की विशिष्ट ऊष्माधारिता परिकलित कीजिए। यदि परिवेश में क्षय ऊष्मा उपेक्षणीय न मानकर परिकलन किया जाता है, तब क्या आपका उत्तर धातु की विशिष्ट ऊष्माधारिता के वास्तविक मान से अधिक मान दर्शाएगा अथवा कम?
उत्तर:
दिया गया है:
धातु का द्रव्यमान m = 0.20 kg = 200g
धातु के तापक्रम में गिरावट ∆ T = 150 - 40 = 110°
यदि धातु की विशिष्ट ऊष्मा S हो तब धातु की ऊष्मा में कमी
∆Q = mS∆ T
∆ Q = 200 × S × 110
पानी का आयतन = 150c.c. = 150cm'
∴ पानी का द्रव्यमान m' = 150g
ऊष्मामापी का जल तुल्यांक w = 0.025kg
= 25 g
ऊष्मामापी और पानी के ताप में वृद्धि ∆T 1 = 40 - 27
इसके अतिरिक्त माना पानी की विशिष्ट ऊष्मा = 4.2 जूल ग्राम^-1 C^-1
पानी और ऊष्मामापी की ऊष्मा में वृद्धि = 4
∆Q1 = (m1 + W ) S1∆T
(150 + 25) × 4.2 × 13 ....(2)
समीकरण (1) तथा (2)
200 x S × 110 = 175 × 13 × 4.2
से
∴ ∆Q = ∆Q
\(S=\frac{175 \times 13 \times 4.2}{200 \times 110}\)
S = 0.434JKgK^-1 
यदि वातावरण में क्षय ऊष्मा उपेक्षणीय न हो तो गुटके द्वारा प्रदान सम्पूर्ण ऊष्मा, जल एवं ऊष्मामापी को प्राप्त नहीं होगी तथा इस स्थिति में गुटके की परिकलित विशिष्ट ऊष्मा, वास्तविक मान से कम होगी।

प्रश्न 15. 
कुछ सामान्य गैसों के कक्ष ताप पर मोलर विशिष्ट ऊष्माधारिताओं के प्रेक्षण नीचे दिए गए हैं:

इन गैसों की मापी गई मोलर विशिष्ट ऊष्माधारिताएं एकपरमाणुक गैसों की मोलर विशिष्ट ऊष्माधारिताओं से सुस्पष्ट रूप से भिन्न हैं। प्रतीकात्मक रूप में, किसी एकपरमाणुक गैस की मोलर विशिष्ट ऊष्माधारिता 2.92cal/mol K होती है। इस अंतर का स्पष्टीकरण कीजिए। क्लोरीन के लिए कुछ अधिक मान (शेष की अपेक्षा) होने से आप क्या निष्कर्ष निकालते हैं?
उत्तर:
चूंकि दत्त गैसें द्विपरमाणुक और अधिक स्वतंत्र कोटि की हैं अर्थात् दूसरी गति की विधायें हैं अर्थात् स्थानांतरित स्वतंत्र कोटि के अतिरिक्त घूर्णन और कम्पन ताप की कुछ मात्रा में बढ़ाने के लिए ऊष्मा ऊर्जा का सभी विधाओं में बढ़ाना आवश्यक है।
परिणामस्वरूप द्विपरमाणुक गैसों की गोलीय विशिष्ट ऊष्मा एकपरमाणुक गैसों से अधिक होती है। यह दर्शाया जा सकता है कि यदि केवल गति की घूर्णन विधि को ही लिया जाये,
द्विपरमाणुक गैसों की मोलर विशिष्ट ऊष्मा लगभग 5/2 R = 2.5 x  1.985
= 4.962cal mol'K है जो कि उपर्युक्त दत्त तालिका में क्लोरीन के अतिरिक्त सभी गैसों के लिये प्रेक्षण से मिलती है। क्लोरीन की विशिष्ट ऊष्मा का अधिक मान दर्शाता है कि स्थानांतरीय चाल के अतिरिक्त कमरे के ताप पर क्लोरीन में कम्पन विधा भी उपस्थित होती है।

प्रश्न 16. 
CO₂ के PT प्रावस्था आरेख पर आधारित निम्नलिखित प्रश्नों के उत्तर दीजिए:

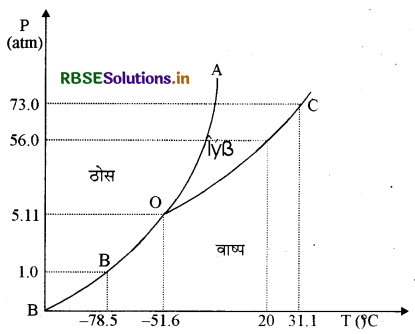
(a) किस ताप व दाब पर CO₂ की ठोस, द्रव तथा वा प्रावस्थाएं साम्य में सहवर्ती हो सकती हैं?
(b) CO₂ के गलनांक तथा क्वथनांक पर दाब में कमी क क्या प्रभाव पड़ता है?
(c) CO₂ के लिए क्रांतिक ताप तथा दाब क्या हैं? इनक क्या महत्व है?
(d) (i) - 70°C ताप व 1 atm दाब (ii) -60°C ताप 10 atm दाब, (iii)- 15°C ताप व 56 atm दाब पर CO₂ ठोस द्रव अथवा गैस में से किस अवस्था में होती है?
उत्तर:
(a) CO₂ ठोस, द्रव तथा वाष्प प्रावस्थाओं में त्रि बिन्दु पर संतुलन अवस्था में हो सकती है।
जिसके संगत P = 5.11atm तथा
T = 56.6°C द्वारा दिया जाता है।
(b) वक्र I तथा II से स्पष्ट है कि दोनों CO के क्वथनांक एवं हिमांक तापक्रम दाब में कमी करने पर कम हो जाते हैं।
(c) CO₂ के लिए क्रान्तिक दाब Pc = 73.0atm तथा T = 37. 1°C है। इस ताप के ऊपर बहुत अधिक दाब पर संपीडित करने पर भी CO₂ द्रवित नहीं होगी।
(d) 1 atm व 70°C
(i) ताप पर CO₂ वाष्प है चूंकि यह बिन्दु वाष्प क्षेत्र में स्थित
(ii) 10atm दाब और 60°C ताप पर CO₂ ठोस अवस्था में है क्योंकि यह बिन्दु ठोस क्षेत्र में है।
(iii) 15°C और 56atm दाब के अन्तर्गत CO₂ द्रव अवस्था में है। चूंकि यह बिन्दु द्रव क्षेत्र में है।

प्रश्न 17. 
CO2 के PT प्रावस्था आरेख पर आधारित निम्नलिखित प्रश्नों के उत्तर दीजिए-
(a) 1 atm दाब तथा - 60°C ताप पर CO2 का समतापी संपीडन किया जाता है? क्या यह द्रव प्रावस्था में जाएगी?
(b) क्या होता है जब 4 atm दाब पर CO₂ का दाब नियत रखकर कक्ष ताप पर शीतन किया जाता है?
(c) 10 atm दाब तथा 65°C ताप पर किसी दिए गए द्रव्यमान की ठोस CO₂ को दाब नियत रखकर कक्ष ताप तक तप्त करते समय होने वाले गुणात्मक परिवर्तनों का वर्णन कीजिए।
(d) CO₂ को 70°C तक तप्त तथा समतापी संपीडित किया जाता है। आप प्रेक्षण के लिए इसके किन गुणों में अंतर की अपेक्षा करते हैं?
उत्तर:
(a) Iatm दाब तथा 60°C ताप पर CO₂ का समतापी संपीडन करने पर यह सीधी ठोस अवस्था में सीधे बिना द्रव अवस्था में गये हुए बदल जाती है।
(b) 4atm दाब और कमरे के ताप (माना 25°C) पर CO₂ वाष्प है। यदि इसे स्थिर दाब पर ठंडा किया जाये तो यह बिना द्रव में बदले ठोस अवस्था को प्राप्त कर लेती है। यह आरम्भिक बिन्दु से केवल क्षैतिज रेखा ऊर्ध्वपातन वक्र (III) को काटती है।
(c) 10 atm और 65°C पर CO₂ ठोस है। समान स्थिर दाब पर CO₂ को गर्म किया जाता है तो यह द्रव अवस्था में होकर फिर वाष्प अवस्था में जाती है। यह ऐसा इसलिए है कि मूल बिन्दु से होकर जाने वाली रेखा हिमांकन और वक्रों को काटती है। हिमांकन और क्वथन बिन्दु इन बिन्दुओं से ज्ञात किये जा सकते हैं। जहाँ पर 10 atm पर क्षैतिज रेखा PT वक्र पर क्रमशः वक्रों को काटती है।
(d) यह द्रव अवस्था की स्पष्ट अवस्था परिवर्तन प्रदर्शित नहीं करता है। फिर भी CO₂ गैस आदर्श गैस आचरण से दाब बढ़ने के साथ अधिक से अधिक दूर हो जाएगी।

प्रश्न 18. 
101°F ताप ज्वर से पीड़ित किसी बच्चे को एन्टीपायरिन (ज्वर कम करने की दवा) दी गई जिसके कारण उसके शरीर से पसीने के वाष्पन की दर में वृद्धि हो गईं। यदि 20 मिनट में ज्वर 98°F तक गिर जाता है तो दवा द्वारा होने वाले अतिरिक्त वाष्पन की औसत दर क्या है? यह मानिए कि ऊष्मा ह्रास का एकमात्र उपाय वाष्पन ही है। बच्चे का द्रव्यमान 30 kg है। मानव शरीर की विशिष्ट ऊष्माधारिता जल की विशिष्ट ऊष्माधारिता के लगभग बराबर है तथा उस ताप पर जल के 580cal g^-1 है।
उत्तर:
दिया गया है:
ताप में गिरावट = ∆T = 101 - 98 = 3°F
\(\begin{aligned} & =3 \times \frac{5}{9}{ }^{\circ} \mathrm{C} \\ & =\frac{5}{3}{ }^{\circ} \mathrm{C} \end{aligned}\)
बच्चे का द्रव्यमान m = 30kg
मानव शरीर की विशिष्ट ऊष्मा = पानी की विशिष्ट ऊष्मा
S = 1000cal/kg x °C
∴ बच्चे द्वारा खोयी गई ऊष्मा ∆Q = mS∆T
= 30 × 1000 x 5/3 = 50000 कैलोरी
यदि m ग्राम पानी 20 मिनट में वाष्पन होता हो तब
mL = ∆Q
या
\(m=\frac{\Delta \mathrm{Q}}{\mathrm{L}}=\frac{50000}{580}\)
∴ अतिरिक्त वाष्पन की औसत दर = 86.2/20
= 4.31 ग्राम / मिनट

प्रश्न 19.
थर्मोकोल का बना 'हिम बॉक्स' विशेषकर र्मियों में कम मात्रा के पके भोजन के भंडारण का सस्ता तथा दक्ष धन है। 30 cm भुजा के किसी हिम बॉक्स की मोटाई 5.0 cm है। दे इस बॉक्स में 4.0 kg हिम रखा है तो 6h के पश्चात् बचे हिम मात्रा का आकलन कीजिए। बाहरी ताप 45°C है तथा थर्मोकोल की ऊष्मा चालकता 0.01 Js^-1 m^-1K^-1 है (हिम की मंगलन ऊष्मा = 335 x 10³ Jkg^-1) करती है।
उत्तर:
दिया गया है:
प्रत्येक भुजा की लम्बाई l = 30cm = 0.3m
प्रत्येक भुजा की मोटाई ∆r = 5cm = 0.05m
कुल पृष्ठीय क्षेत्रफल जिसमें से बॉक्स के अन्दर ऊष्मा प्रवेश
(A) = 6 × (भुजा)²
(A) = 6 × (03)²
(A) = 6 × 0.09 = 0.54m²
तापान्तर ∆T = 45 - 0 = 45°C
ऊष्मा चालकता K = 0.01J^-1s^-1m^-1C^-1
समय ∆t = 6hrs. = 6 × 60 x 60S
बॉक्स में रखा हुआ हिम M = 4.0kg
हिमांकन की ऊष्मा, L = 335 × 10³ J/kg
माना m द्रव्यमान की बर्फ इस समय में पिघलती है इसलिए m मात्रा की हिम पिघलाने में खर्च ऊष्मा
∴ ∆Q = mL = KA\(\left(\frac{\Delta \mathrm{T}}{\Delta x}\right) \Delta \mathrm{t}\)
या
m = KA\(\frac{\Delta \mathrm{T}}{\Delta x} \cdot \frac{\Delta \mathrm{t}}{\mathrm{L}}\)
मान रखने पर m = 0.01 × 0.54 x \(\frac{45}{0.05} \times \frac{6 \times 60 \times 60}{335 \times 10^3}\)
= 313.36 × 10^-3 kg.
= 0.313kg.
शेष रही हिम की मात्रा = M - m
= 4 - 0.313
= 3.687
= 3.7kg.

प्रश्न 20. 
किसी पीतल के बॉयलर की पेंदी का क्षेत्रफल 0.15m तथा मोटाई 1.0 cm है। किसी गैस स्टोव पर रखने पर इसमें 6.0 kg/min की दर से जल उबलता है। बॉयलर के सम्पर्क की ज्वाला के भाग का ताप आकलित कीजिए। पीतल की ऊष्मा चालकता = 109Js^-1 m K^-1; जल की वाष्पन ऊष्मा = 2256 x 10³ Jkg^-1 है।
उत्तर: 
बॉयलर की पेंदी का क्षेत्रफल A = 0.15m²
मोटाई Δx = 1.0cm = 10²m
K = 109J^-1s^-1 m^-1K^-1
T₂ = 100°C
माना स्टोव के सम्पर्क में बॉयलर के भाग का ताप = T₁ 
यदि बॉयलर के आधार से प्रति सेकण्ड प्रवाहित ऊष्मा Q है
\(\begin{aligned} \mathrm{Q} & =\mathrm{KA} \times \frac{\Delta \mathrm{T}}{\Delta x} \\ \mathrm{Q} & =\frac{109 \times 0.15 \times\left(\mathrm{T}_1-100\right)}{10^{-2}} \end{aligned}\)
Q = 1635 (T1 - 100 ) J/s. ....(1)
पानी की वाष्पन की ऊष्मा
L = 2256 x 10³ J/kg
बॉयलर में पानी के क्वथन की दर
M = 6.0kg/min = 6.0/60
= 0.1kg/s
∴ पानी द्वारा प्रति सेकण्ड प्राप्त ऊष्मा, Q = ML
Q = 0.1 x 2256 × 10³ J/s.
= 2256 × 10₂ J/s.
समीकरण (1) तथा (2) से
1635 (T₁ - 100) = 2256 × 10²
या
T₁ - 100 = \(\frac{2256 \times 10^2}{1635}=\frac{225600}{1635}\)
या
T₁ - 100 = 138
T₁ = 138 + 100
= 238°C
अतः स्टोव के सम्पर्क में बॉयलर के भाग का ताप 238°C 

प्रश्न 21. 
स्पष्ट कीजिए कि क्यों:
(a) अधिक परावर्तकता वाले पिण्ड अल्प उत्सर्जक होते हैं। 
(b) कंपकंपी वाले दिन लकड़ी की ट्रे की अपेक्षा पीतल का ग्लास कहीं अधिक शीतल प्रतीत होता है।
(c) कोई प्रकाशिक उत्तापमापी (उच्च तापों को मापने की युक्ति) जिसका अंशांकन किसी आदर्श कृष्णिका के विकिरणों के लिए किया गया है, खुले में रखे किसी लाल तप्त लोहे के टुकड़े का ताप काफी कम मापता है, परन्तु जब उसी लोहे के टुकड़े को भट्टी में रखते हैं, तो वह ताप का सही मान मापता है।
(d) बिना वातावरण के पृथ्वी अशरणीय शीतल हो जाएगी।
(e) भाप के परिचालन पर आधारित तापन निकाय तप्त जल के परिचालन पर आधारित निकायों की अपेक्षा भवनों को उष्ण बनाने में अधिक दक्ष होते हैं।
उत्तर:
(a) कृष्णिका वस्तुओं के लिये परिभाषित किरकौफ के नियम से अच्छे उत्सर्जक अच्छे अवशोषक होते हैं तथा इसका विलोम भी सत्य है। यदि किसी वस्तु की परावर्तन क्षमता अधिक है तो उसकी
अवशोषण क्षमता कम होगी। इसलिये ऐसी वस्तुएँ अच्छी उत्सर्जक नहीं होंगी। 
(b) पीतल की ऊष्मा चालकता का मान उच्च होता है अर्थात् पीतल ऊष्मा का सुचालक है इसलिये जब पीतल के गिलास को छुआ जाता है तो ऊष्मा शीघ्रता से मानव शरीर से पीतल के गिलास में चली जाती है। इस कारण से गिलास ठण्डा प्रतीत होता है। जबकि लकड़ी ऊष्मा की कुचालक है। इस कारण से ऊष्मा मानव शरीर से लकड़ी की ट्रे में नहीं प्रवाहित होती और वह अपेक्षाकृत गर्म प्रतीत होती है।
(c) माना भट्टी का ताप T हो तब स्टेफैन के नियम के अनुसार प्रति सेकण्ड प्रति इकाई क्षेत्रफल द्वारा उत्सर्जित ऊष्मा की मात्रा E = σ T' से ज्ञात करते हैं। जब पिण्ड को खुले ताप T पर रखा जाता है तब प्रति सेकण्ड प्रति इकाई क्षेत्रफल द्वारा उत्सर्जित ऊर्जा E = σ ( T4 - T 4) द्वारा दिया जाता है।
दोनों समीकरणों से स्पष्ट है कि E < E इसलिए प्रकाशिक उत्तापमापी अवरक्त उष्ण खुले में लोहे के टुकड़े का ताप का मान बहुत कम देगा।
(d) पृथ्वी के चारों ओर जो वायुमण्डल है वह अवरोधी आवरण का कार्य करता है और वह ऊष्मा के पलायन को रोकता है बल्कि इसे वापस पृथ्वी पर परावर्तित कर देता है। यदि यह वायुमण्डल अनुपस्थित होता तो यह पृथ्वी प्राकृतिक रूप से ठण्डी होती क्योंकि इससे सारी ऊष्मा पलायन कर चुकी होती।
(e) 100°C पर जल वाष्प में 100°C पर उबलने वाले जल की अपेक्षा अधिक ऊष्मा होती है क्योंकि जल वाष्प की गुप्त ऊष्मा 540 कैलोरी / ग्राम है। इस प्रकार स्पष्ट रूप से पानी की अपेक्षा वाष्प भवन को अच्छी प्रकार गर्म करेगी।

प्रश्न 22. 
किसी पिण्ड का ताप 5 मिनट में 80°C से 50°C हो जाता है। यदि परिवेश का ताप 20°C है, तो उस समय का परिकलन कीजिए जिसमें उसका ताप 60°C से 30°C हो जाएगा।
उत्तर:
न्यूटन के शीतलन नियम से शीतलन की दर x तापान्तर
पहली स्थिति दिया गया है T₁ = 80°C. T₂ = 50°C
ताप में परिवर्तन = T₁ - T₂ = 80°C - 50°C = 30°C
औसत ताप = \(\frac{\mathrm{T}_1+\mathrm{T}_2}{2}=\frac{80^{\circ}+50^{\circ}}{2}\)
= 65°C है।
वातावरण का ताप = 20°C
∴ ताप आधिक्य ∆T = 65 - 20 = 45°C
पिण्ड पाँच मिनट में 30°C ठण्डा हो जाता है।

या
30° = K × 45
6° = K × 45 ....(1)
दूसरी स्थिति में आसत ताप
\(\frac{60^{\prime \prime} \mathrm{C}+30^{\circ} \mathrm{C}}{2}\) = 45°C
जो कमरे के ताप से 25°C अधिक है। माना वह समय t है।
जिसमें पिण्ड का ताप 60°C से 30°C तक हो जायेगा।
\(\frac{30}{t}=K \times 25\) ............ (2)
जहाँ K समान परिस्थिति में पूर्व स्थिति के समान है। समीकरण (1) में समीकरण (2) का भाग देने पर
\(\begin{aligned} \frac{6}{30 / \mathrm{t}} & =\frac{\mathrm{K} \times 45}{\mathrm{~K} \times 25}=\frac{9}{5} \\ \frac{6 \mathrm{t}}{30} & =\frac{9}{5} \end{aligned}\)
t = 9 min.
अर्थात् वह समय 9 min होगा जिसमें पिण्ड का ताप 60°C से 30°C हो जायेगा।