RBSE Solutions for Class 11 Physics Chapter 10 तरलों के यांत्रिकी गुण

Rajasthan Board RBSE Solutions for Class 11 Physics Chapter 10 तरलों के यांत्रिकी गुण Textbook Exercise Questions and Answers.

RBSE Class 11 Physics Solutions Chapter 10 तरलों के यांत्रिकी गुण

RBSE Class 11 Physics तरलों के यांत्रिकी गुण Textbook Questions and Answers

प्रश्न 10.1. 
स्पष्ट कीजिए क्यों
(a) मस्तिष्क की अपेक्षा मानव का पैरों पर रक्तचाप अधिक
(b) 6 km ऊँचाई पर वायुमण्डलीय दाब समुद्रतल पर वायुमण्डलीय दाब का लगभग आधा हो जाता है, यद्यपि वायुमण्डल का विस्तार 100 km से भी अधिक ऊँई तक है।
(c) यद्यपि दाब, प्रति एकांक क्षेत्रफल पर लगने वाला बल होता है तथापि द्रवस्थैतिक दाब एक अदिश राशि है।
उत्तर:
(a) मस्तिष्क की अपेक्षा मानव का पैरों पर रक्तचाप अधिक होता है क्योंकि पैरों पर रक्त स्तम्भ की ऊँचाई अधिक है। परिणामस्वरूप मानव के पैरों पर मस्तिष्क की अपेक्षा रक्तचाप अधिक होता है।
(b) हम जानते हैं कि वायुमण्डल दाब पृथ्वी के पृष्ठ के निकट अधिकतम होता है, जो ऊँचाई के साथ-साथ तीव्रता से कम हो जाता है और 6 km ऊँचाई पर इसका मान समुद्रतल के मान से आधा हो जाता है। वायु का घनत्व 6 km ऊँचाई के बाद बहुत धीरे-धीरे कम होता है। इस कारण से 6 km ऊँचाई पर वायुमण्डलीय दाब इसके समुद्रतल पर मान का आधा हो जाता है।
(c) द्रव पर बल लगने के कारण पास्कल के नियम से दाब सभी दिशाओं में समान रूप से संचारित होता है। इस प्रकार से द्रव में दाब के लिए कोई निश्चित दिशा नहीं है। अतः द्रव स्थैतिक दाब एक अदिश राशि है।

 

प्रश्न 10.2. 
स्पष्ट कीजिए क्यों
(a) पारे का काँच के साथ स्पर्श कोण अधिक कोण होता है जबकि जल का काँच के साथ स्पर्श कोण न्यून कोण होता है।
(b) काँच के स्वच्छ समतल पृष्ठ पर जल फैलने का प्रयास करता है जबकि पारा उसी पृष्ठ पर बूँदें बनाने का प्रयास करता है। (दूसरे शब्दों में जल काँच को गीला कर देता है जबकि पारा ऐसा नहीं करता है।)
(c) किसी द्रव का पृष्ठ तनाव पृष्ठ के क्षेत्रफल पर निर्भर नहीं करता है।
(d) जल में घुले अपमार्जकों के स्पर्श कोणों का मान कम होना चाहिए।
(e) यदि किसी बाह्य बल का प्रभाव न हो, तो द्रव बूँद की आकृति सदैव गोलाकार होती है।
उत्तर:
(a) जब काँच पर थोड़ा-सा द्रव डाला जाता है तब द्रव- वायु, ठोस वायु और ठोस द्रव में अन्तरापृष्ठ बन जाता है।
इन तीनों अन्तरापृष्ठों के संगत पृष्ठ तनाव अर्थात् T_la T_sa और T_sl 
क्रमशः द्रव का ठोस के साथ सम्पर्क कोण से सम्बन्ध
\(\cos \theta=\frac{T_{\mathrm{sa}}-T_{s l}}{T_{h a}}\)
कोण होगा।

पारे और काँच की स्थिति में T_sa < T_sl
∴ cosθ का मान ऋणात्मक मिलेगा अर्थात् θ > 90° अर्थात् अधिक
द्रव तथा काँच की स्थिति में T_sa > T_sl
∴ cosθ  का मान धनात्मक मिलता है।
या θ < 90° अर्थात् यहाँ पर न्यूनकोण होगा।

(b) पारे और काँच के लिए सम्पर्क कोण अधिक कोण है। सम्पर्क कोण का मान अधिक कोण हो इसके लिए पारा बूँद का रूप धारण करने का
प्रयत्न करता है परन्तु पानी-काँच के संदर्भ में सम्पर्क
इस कारण से संतुलन के लिए समीकरण imm संतुष्ट नहीं होगा।
सम्पर्क कोण का मान न्यून कोण रखने के लिये पानी फैलने का प्रयत्न करता है।
कोण न्यून कोण है,

(c) पृष्ठ तनाव की परिभाषा द्रव पृष्ठ पर खींची एक काल्पनिक रेखा की इकाई लम्बाई पर, जो द्रव पृष्ठ के स्पर्शीय खींची गई है, अभिलम्ब बल के रूप में दी जाती है। चूंकि बल द्रव पृष्ठ के क्षेत्रफल से स्वतंत्र है, अतः पृष्ठ तनाव भी द्रव पृष्ठ के क्षेत्रफल से स्वतंत्र है।

(d) हम जानते हैं कि कपड़ों में महीन कोशिकाओं के रूप में छोटा-छोटा स्थान होता है। केशिका में द्रव की ऊँचाई का बढ़ना cos) के समानुपाती होता है। (यदि ) का मान बहुत अल्प होगा तो cost का मान बड़ा होगा और अपमार्जक कपड़े में छोटे-छोटे स्थानों से अधिक ऊपर उठेगा। चूंकि अपमार्जक का सम्पर्क कोण छोटा होता है, इसलिए वह अधिक प्रवेश उसके गर्द को कपड़े से निकाल देगा।

(e) बाह्य बलों की अनुपस्थिति में द्रव पर केवल पृष्ठ तनाव के कारण ही बल कार्य करेगा पृष्ठ तनाव के गुण के कारण एक द्रव की बूँद न्यूनतम पृष्ठ क्षेत्रफल रखना चाहती है। चूंकि द्रव के दिये आयतन के लिए किसी गोलीय द्रव बूंद का पृष्ठ क्षेत्रफल न्यूनतम होता है, अतः यह सदैव गोलीय आकृति ही ग्रहण करेंगी।

प्रश्न 10.3. 
प्रत्येक प्रकथन के साथ संलग्न सूची में से उपयुक्त शब्द छाँटकर उस प्रकथन के रिक्त स्थान की पूर्ति कीजिए: 
(a) व्यापक रूप से द्रवों का पृष्ठ तनाव ताप बढ़ने पर ......................... है। (घटता / बढ़ता )
(b) गैसों की श्यानता ताप बढ़ने पर ............................... "है, जबकि द्रवों की श्यानता ताप बढ़ने पर प्रतिबल ......................  है। (घटती / बढ़ती )
(c) दृढ़ता प्रत्यास्थता गुणांक वाले ठोसों के लिए अपरूपण -के अनुक्रमानुपाती होता है, जबकि दवों के लिए -के अनुक्रमानुपाती होता है। (अपरूपण विकृति / अपरूपण विकृति की दर )
(d) किसी तरल के अपरिवर्ती प्रवाह में आए किसी संकीर्णन पर प्रवाह की चाल में वृद्धि में -का अनुसरण होता है। ( संहति का संरक्षण / बरनूली सिद्धांत )
(e) किसी वायु सुरंग में किसी वायुयान के मॉडल में प्रक्षोभ की चाल वास्तविक वायुयान के प्रक्षोभ के लिए क्रांतिक चाल की -होती है। (अधिक / कम )
उत्तर:
(a) घटता
(b) बढ़ती घटती
(c) अपरूपण विकृति, अपरूपण विकृति की दर 
(d) संहति का संरक्षण सिद्धान्त
(e) अधिक

प्रश्न 10.4. 
निम्नलिखित के कारण स्पष्ट कीजिए: 
(a) किसी कागज की पट्टी को क्षैतिज रखने के लिए आपको उस कागज पर ऊपर की ओर हवा फूँकनी चाहिए, नीचे की ओर नहीं ।
(b) जब हम किसी जल टोंटी को अपनी उँगलियों द्वारा बंद करने का प्रयास करते हैं, तो उँगलियों के बीच की खाली जगह से तीव्र जलधाराएँ फूट निकलती हैं।
(c) इंजेक्शन लगाते समय डॉक्टर के अंगूठे द्वारा आरोपित दाब की अपेक्षा सुई का आकार दवाई की बहिः प्रवाही धारा को अधिक अच्छा नियंत्रित करता है।
(d) किसी पात्र के बारीक छिद्र से निकलने वाला तरल उस पर पीछे की ओर प्रणोद आरोपित करता है।
(e) कोई प्रचक्रमान क्रिकेट की गेंद वायु में परवलीय प्रपथ का अनुसरण नहीं करती।
उत्तर:
(a) यदि हम कागज के ऊपर की ओर फूँक मारें तो कागज के नीचे की अपेक्षा ऊपर वेग का मान अधिक होगा। कागज के ऊपर की गतिज ऊर्जा अधिक हो जायेगी। इसलिए कागज के टुकड़े के नीचे दाब अधिक हो जायेगा। वायुमण्डलीय दाब के कारण यह नीचे न गिर कर क्षैतिज रहेगा।
दूसरी ओर यदि कागज के नीचे से फूँक मारी जाये तो वहाँ पर वायुदाब कम हो जायेगा, कागज के ऊपर वायुदाब इसे नीचे की ओर झुका देगा। इसलिये कागज क्षैतिज नहीं रहेगा।
(b) जब हम किसी जल टोंटी को अपनी उँगलियों द्वारा बंद करने का प्रयास करते हैं, तो उँगलियों के बीच की खाली जगह से तीव्र जलधारायें फूट निकलती हैं। इसका कारण सांतत्य समीकरण AV, AN, से मिलता है। उँगलियों से पानी के जेट की निर्गत अनुप्रस्थ काट काफी कम हो जाती है, क्योंकि हमारी उँगलियों के बीच स्थान कम क्षेत्रफल का हो जाता है। क्षेत्रफल कम होने से पानी का वेग काफी बढ़ जाता है और हमारी उँगलियों के बीच के स्थान से पानी का तीव्र जेट निकलता है।
(c) हम जानते हैं P + 1/2pv² + pgh = स्थिरांक
इसलिए सूई का आकार प्रवाह वेग और अंगूठे का दाब, दाब को नियंत्रित करते हैं।
उपर्युक्त समीकरण में दाब (P) एक घातीय है जबकि वेग दो घात के रूप में विद्यमान है। इस कारण से वेग का प्रभाव अधिक होगा। इसलिए पिचकारी की सुई का वेग प्रवाह पर अच्छा प्रभाव होगा।
(d) किसी पात्र के बारीक छिद्र में से तरल बाहर निकलता है तो अधिक वेग प्राप्त कर लेता है और इसलिए अधिक संवेग होता है। चूंकि निकाय पर कोई बाह्य बल कार्य नहीं करता, इसलिए पात्र द्वारा पीछे की ओर संवेग संरक्षण के नियम से वेग प्राप्त करना चाहिये। इसके परिणामस्वरूप पात्र द्वारा एक आवेग (पीछे की ओर प्रणोद) का अनुभव होगा। 
(e) ऐसा मेगनस प्रभाव के कारण होता है। माना R.H.S. की ओर चलती एक गेंद को इसके शीर्ष पर फिरकाते हैं। गेंद के नीचे की अपेक्षा शीर्ष पर वायु का वेग अधिक है। इसलिए बरनूली सिद्धान्त से गेंद के शीर्ष पर दाब तल की तुलना में कम होता है, अतः फिरकी गेंद पर अपरमुखी नेटबल कार्य करेगा, इसलिए गेंद एक वक्र पथ का अनुसरण करेगी। इस प्रभाव को मेगनस प्रभाव कहते हैं।

प्रश्न 10.5. 
ऊँची एड़ी के जूते 50 kg संहति की कोई बालिका अपने शरीर को 1.0 cm व्यास की एक ही वृत्ताकार एड़ी पर संतुलित किए हुए है। क्षैतिज फर्श पर एड़ी द्वारा आरोपित दाब ज्ञात कीजिए। 
उत्तर:
दिया गया है:
द्रव्यमान (m) = 50kg
त्रिज्या r = 1/2 D = 1/2 x 1  = 0.5 cm
r = 0.5 × 10^-2 m

= 62.36 × 10⁵  = 6.24 x 10⁶ N/m²
= 6.24 × 10⁶Pa

प्रश्न 10.6. 
टॉरिसिली के वायुदाब मापी में पारे का उपयोग किया गया था। पास्कल ने ऐसा ही वायुदाबमापी 984 kg m घनत्व की फ्रेंच शराब का उपयोग करके बनाया। सामान्य वायुमंडलीय दाब के लिए शराब - स्तंभ की ऊँचाई ज्ञात कीजिए।
उत्तर:
दिया गया है:
सामान्य वायुदाब 
माना शराब स्तंभ की ऊँचाई = h
∴ शराब के स्तंभ की ऊँचाई h  के तुल्य यदि दाब P1 है तब-
p1 = hprg
यहाँ पर शराब का घनत्व = 984kg/m³
∴ p1 = h x 984 x 9.8
प्रश्नानुसार p1 = P
P1 = 1.013 x 10 N/m
∴ = h × 984 × 9.8 = 1.013 × 10⁵
\(h=\frac{1.013 \times 10^5}{984 \times 9.8}\)
अतः सामान्य वायुमण्डलीय दाब के लिए शराब स्तम्भ की ऊँचाई 10.5m होगी।

प्रश्न 10.7. 
समुद्र तट से कोई ऊर्ध्वाधर संरचना 10' Pa के अधिकतम प्रतिबल को सहन करने के लिए बनाई गई है। क्या यह संरचना किसी महासागर के भीतर किसी तेल कूप के शिखर पर रखे जाने के लिए उपयुक्त है ? महासागर की गहराई लगभग 3km है। समुद्री धाराओं की उपेक्षा कीजिए।
उत्तर:
दिया गया है:
पानी के स्तम्भ की ऊँचाई
h = 3km
= 3 × 1000m
= 3 × 10³m
पानी का घनत्व
p = 10³ kg/m³
यदि इस गहराई पर दाब P हो तब
P = hpg
P = 3 × 10³ × 10³ × 9.8
= 3 × 9.8 × 10⁶ 
Pa = 29.4 × 10⁶Pa
समुद्र तट से दूर कोई ऊर्ध्वाधर संरचना 10⁹ Pa को अधिकतम प्रतिबल को सहन करने के लिये बनायी गयी है और समुद्री पानी द्वारा अपरमुखी लगाया प्रणोद 29.4 x 10⁶ Pa है।
तब
29.4 x 10⁶ Pa < 10⁹ Pa
यहाँ पर संरचना द्वारा वहन अधिकतम प्रतिबल से यह प्रतिबल काफी कम है। अतः हम निष्कर्ष निकालते हैं कि संरचना इस प्रतिबल के लिए हमें उपयुक्त है।

प्रश्न 10.8. 
किसी द्रवचालित ऑटोमोबाइल लिफ्ट की संरचना अधिकतम 3000 kg संहति की कारों को उठाने के लिए की गई है। बोझ को उठाने वाले पिस्टन की अनुप्रस्थ काट का क्षेत्रफल 425 cm है। छोटे पिस्टन को कितना अधिकतम दाब सहन करना होगा?
उत्तर:
दिया गया है:
बोझ को उठाने वाले पिस्टन द्वारा वहन किये जाने वाला बल
F = 3000 kg भार
= 3000 × 9,8N
पिस्टन का क्षेत्रफल
A = 425cm² = 425 x 10^-4 m²
बड़े वाले पिस्टन पर अधिकतम दाब
\(\begin{aligned} P & =\frac{F}{A} \\ & =\frac{3000 \times 9.8}{425 \times 10^{-4}} \end{aligned}\)
= 6.92 × 10⁵Pa
चूंकि द्रव्य सभी दिशाओं में दाब को समान रूप से संचारित करता है, अतः छोटे पिस्टन द्वारा वहन अधिकतम बल = 6.92 x 10⁵ Pa होगा। 

प्रश्न 10.9. 
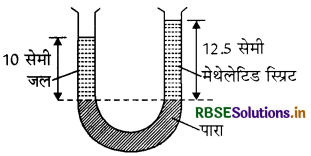
किसी नली की दोनों भुजाओं में भरे जल तथा मेथेलेटिड स्पिरिट को पारा एक-दूसरे से पृथक् करता है। जब जल तथा पारे के स्तम्भ क्रमश: 10cm तथा 12.5cm ऊँचे हैं, तो दोनों भुजाओं में पारे का स्तर समान है। स्पिरिट का आपेक्षिक घनत्व ज्ञात कीजिए। 
उत्तर:
U-नली की एक भुजा में पानी के स्तम्भ के लिये
h1 = 10.0cm
घनत्व
P1 = 1 g / cm³
U-नली की दूसरी भुजा में पारे के स्तम्भ के लिये hg = 12.5cm 
घनत्व P2 = ?
चूंकि UU-नली की दोनों भुजाओं में पारे के स्तम्भ समान हैं, इसलिए दाब दोनों के समान होंगे।

P₁ = P₂ 
h₁p₁g = h₂P₂g 
था h₁P₁ = h₂P₂
\(\rho_2=\frac{h_1 \rho_1}{h}\)
मान रखने पर
\(=\frac{10.0 \times 1}{12.5}=\frac{4}{5}\)
P₂ = 0.8 g/cm³
इसलिए स्पिरिट का विशिष्ट घनत्व = 
\(=\frac{0.8}{1}=0.8\)

प्रश्न 10.10
यदि प्रश्न 10.9 की समस्या U-नली की दोनों की समस्या -नली की दोनों भुजाओं में इन्हीं दोनों द्रवों को और उड़ेलकर दोनों दवों के स्तंभों की ऊँचाई 15 cm और बढ़ा दी जाये, तो दोनों भुजाओं में पारे के स्तरों में क्या अंतर होगा ? ( पारे का आपेक्षिक घनत्व = 13.6 ) 
उत्तर:
U-नली की दोनों भुजाओं में क्रमश: 15 cm पानी और स्पिरिट डालने पर स्पिरिट वाली भुजा में पारा ऊपर चढ़ जाएगा। माना दोनों भुजाओं में पारे के स्तरों का अंतर है और पारे का घनत्व है।
मरकरी स्तम्भ में h ऊँचाई द्वारा लगाया गया दाब = स्पिरिट के द्वारा लगाये गये दाब के अंतर के बराबर होगा।
hpg = h₁p₁g - h₂p₂g
hp = h₁p₁ - h₂P₂ ........... (1)
दिया गया है:
P = 13.6 g / cm³
P₁ =1 g/cm³
P₂ = 0.8 g / cm³
h₁ = 15 + 10 = 25cm
h₂ = 15 + 12.5 = 27.5cm
समीकरण (1) में मान रखने पर
h × 13.6 = 25 x 1 - 27.5 × 0.8 
13.6h = 25 - 22.00 = 3
\(h=\frac{3}{13.6}\)
अतः दोनों भुजाओं में पारे के स्तरों का अंतर = 0.22 cm 

प्रश्न 10.11. 
क्या बरनूली समीकरण का उपयोग किसी नदी की किसी क्षिप्रिका के जल प्रवाह का विवरण देने के लिए किया जा सकता है? स्पष्ट कीजिए।
उत्तर:
नहीं, चूंकि बरनूली समीकरण का उपयोग केवल धारारेखीय प्रवाह के लिए किया जाता है और एक क्षिप्रिका में जल प्रवाह धारा प्रवाह नहीं होता है।

प्रश्न 10.12. 
बरनूली समीकरण के अनुप्रयोग में यदि निरपेक्ष दाब के स्थान पर प्रमापी दाब ( गेज दाब) का प्रयोग करें तो क्या इससे कोई अंतर पड़ेगा? स्पष्ट कीजिए।
उत्तर:
नहीं, इसमें कोई अंतर नहीं पड़ता क्योंकि निरपेक्ष दाब को गैज से बरनूली समीकरण लगाने के लिए मापा जाये क्योंकि जिन दो बिन्दुओं पर बरनूली समीकरण का प्रयोग करते हैं उन पर जब तक वायुमण्डल दाब सार्थक रूप से भिन्न न हो उस स्थिति में निरपेक्ष दाब के स्थान पर प्रमापी दाब लिया जा सकता है।

प्रश्न 10.13. 
किसी 1.5 m लम्बी 1.0cm त्रिज्या की क्षैतिज नली से ग्लिसरीन का अपरिवर्ती प्रवाह हो रहा है। यदि नली के एक सिरे पर प्रति सेकंड एकत्र होने वाली ग्लिसरीन का परिमाण 4.0 x 10^-3 kgs^-1 है, तो नली के दोनों सिरों के बीच दाबांतर ज्ञात कीजिए। (ग्लिसरीन का घनत्व = 1.3 x 10³ kgm^-3 तथा ग्लिसरीन की श्यानता = 0.83 Pas ) आप यह भी जाँच करना चाहेंगे कि क्या इस नली में स्तरीय प्रवाह की परिकल्पना सही है?
उत्तर:
दिया गया है:
नली की लम्बाई l = 1.5m
त्रिज्या (r) = 1.0cm = 10^-2 m
प्रति सेकण्ड एकत्र होने वाली ग्लिसरीन का द्रव्यमान = 4.0 × 10^-3 kg/sec.
ग्लिसरीन का घनत्वp = 1.3 x 10³ kg/m³
ग्लिसरीन की श्यानता = 0.83Pas = 0.83N/m² x sec. 
माना नली के दोनों सिरों पर दाबान्तर P = ?
ग्लिसरीन का प्रति सेकण्ड प्रवाहित आयतन = V

नली में प्रवाह की जाँच करने के लिए हम रेनों संख्या का मान निकालते हैं।
\(\operatorname{Re}=\frac{\rho v_t \mathrm{D}}{\eta}\)  ................ (1)
यहाँ पर v1 = क्रांतिक वेग

स्तरीय प्रवाह में R का मान 0 से 2000 के बीच में होता है।
समीकरण (1) तथा (2) से
\(\mathrm{R}_{\mathrm{e}}=\frac{\rho D}{\eta} \times\left(\frac{\mathrm{M}}{\rho}\right) \times \frac{1}{\pi r^2}\)
यहाँ पर D = 2r है।
\(\begin{aligned} & =\frac{2 r \mathrm{M}}{\pi r^2 \eta} \\ & =\frac{2 \mathrm{M}}{\pi \mathrm{r} \eta}=\frac{2 \times 4 \times 10^{-3}}{3.14 \times 10^{-2} \times 0.83} \end{aligned}\)
= 3.07 × 10¹ =  0.307 = 0.31
इसलिए बहाव स्तरीय है।

प्रश्न 10.14. 
किसी आदर्श वायुयान के परीक्षण प्रयोग में वायु- सुरंग के भीतर पंखों के ऊपर और नीचे के पृष्ठों पर वायु-प्रवाह की गतियाँ क्रमश: 70ms तथा 63ms हैं। यदि पंख का क्षेत्रफल 2.5m ² है, तो उस पर आरोपित उत्थापक बल परिकलित कीजिए। वायु का घनत्व 1.3 kg m लीजिए।
उत्तर:
माना पंख के ऊपर तथा नीचे के पृष्ठों पर वायु की चाल क्रमश: V₁ व V₂ है और ऊपरी तथा निचले पृष्ठों पर वायुदाब P₁ और P₂ हैं
तब
v = 70m/s v₂ = 63m/s
और
p = 1.3kg/m³
बली प्रमेय से

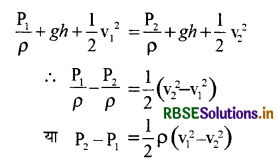
या
P₂ - P₁ = 1/2P(v₁² - v₂²)
मान रखने पर
= 1/2 x 1.3 × [(70)² - (63)²]
= 1/2 × 1.3 × (4900 - 3969)
= 1/2 × 1.36 × 931 = 1210.3/2
= 605.15 Pa
वायुयान पर भार = दाबान्तर x पंखे का क्षेत्रफल
= 605.15 × (2.5 ) = 1.51 x 10³N 

प्रश्न 10.15. 
चित्र (a) तथा (b) किसी द्रव (श्यानताहीन ) का अपरिवर्ती प्रवाह दर्शाते हैं। इन दोनों चित्रों में से कौन सही है? कारण स्पष्ट कीजिए।

उत्तर:
चित्र (a) सही नहीं है।
सांतत्य समीकरण के अनुसार Av = स्थिरांक
यदि छोटा क्षेत्रफल है तो द्रव का प्रवाह वेग अधिक होता है। अतएव बरनूली सिद्धान्त के अनुसार सँकरे भाग में दाब कम होना चाहिए। लेकिन चित्र में सँकरे भाग को बड़ा दिखाया गया है और इसका दाब भी अधिक दिखाया गया है।

प्रश्न 10.16. 
किसी स्प्रे पंप की बेलनाकार नली की अनुप्रस्थ काट का क्षेत्रफल 8.0cm है। इस नली के एक सिरे पर 1.0 mm व्यास के 40 सूक्ष्म छिद्र हैं। यदि इस नली के भीतर द्रव के प्रवाहित होने की दर 1.5mmin^-1 है, तो छिद्रों से होकर जाने वाले द्रव की निष्कासन- चाल ज्ञात कीजिए।
उत्तर:
दिया गया है:
अनुप्रस्थ काट का क्षेत्रफल A1 = 8.0cm
∴ A1 = 8 × 10⁴m²
सूक्ष्म छिद्रों की संख्या = 40
प्रत्येक छिद्र का व्यास d = 1.0mm
∴ प्रत्येक छिद्र की त्रिज्या (r) = 1/2d
= 1/2 x 1 = 0.5mm
∴ r = 0.5 × 10^-2 m
r = 5 × 10^-4 m
∴ प्रत्येक छिद्र की अनुप्रस्थ काट = πr²
= π x (5 × 10^-4)²
= 25π × 10^-8m²
∴ 40 छिद्रों का क्षेत्रफल = 40 x 25π x 10^-8
A₂ = π × 10^-5m²
नली में से द्रव का प्रवाह

V₁ = 1.5m/min = 1.5/60m/sec
= 1/40m/s.

माना द्रव निष्कासन का वेग V₂ = ?
∴ सांतत्य समीकरण से
A₁V₁ = A₂V₂
∴ v₂ = A₁V₁/A₂
मान रखने पर
\(\begin{aligned} & =\frac{8 \times 10^{-4} \times \frac{1}{40}}{\pi \times 10^{-5}}=\frac{1 \times 10}{5 \pi} \\ & =\frac{2}{\pi}=\frac{2 \times 7}{22} \end{aligned}\)
= 7/11 = 0.64 m/s

प्रश्न 10.17. 
U-आकार के किसी तार को साबुन के विलयन में डुबोकर बाहर निकाला गया जिससे उस पर एक पतली साबुन की फिल्म बन गई। इस तार के दूसरे सिरे पर फिल्म के सम्पर्क में एक फिसलने वाला हल्का तार लगा है जो 1.5 x 10^-2N भार ( जिसमें इसका अपना भार भी सम्मिलित है) को सँभालता है। फिसलने वाले तार की लंबाई 30 cm है। साबुन की फिल्म का पृष्ठ तनाव कितना है? 
उत्तर:
हम जानते हैं कि साबुन की झिल्ली में दो स्वतंत्र पृष्ठ होते हैं। झिल्ली को सहारा देने वाली लम्बाई
l = 2 x 30cm = 60cm
= 60 × 10^-2m = 6 × 10m.
W = 1.5 × 10^-2N
F = T × 2l =T × 6 × 10^-1 N
संतुलन स्थिति में पृष्ठ तनाव के कारण सरकन पर बल F सरकन द्वारा अवलम्बित भार W के बराबर होना चाहिए।
F = W = mg
T × 0.6 = 1.5 × 10^-2
\(\mathrm{T}=\frac{1.5 \times 10^{-2}}{0.6}\)
= 2.5 × 10^-2N/m. = 0.6

प्रश्न 10.18. 
निम्नांकित चित्र (a) में किसी पतली द्रव फिल्म को 4.5 x 10^-2 N का छोटा भार सँभाले दर्शाया गया है। चित्र (b) तथा (c) में बनी इस द्रव की फिल्में इसी ताप पर कितना भार सँभाल सकती हैं? अपने उत्तर को प्राकृतिक नियमों के अनुसार स्पष्ट कीजिए।

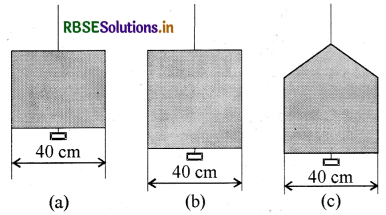
उत्तर:
भार को अवलम्ब प्रदान करने वाली झिल्ली की लम्बाई
= 40cm = 40 × 10²m
= 4 × 10m = 0.4m
कुल अवलम्बित भार= 4.5 × 10² N
पृष्ठ तनाव T = ?
झिल्ली की कुल लम्बाई = 2l = 2 x 0.4
= 0.8 ( ∵ इसके दो पृष्ठ होते हैं।)

= 5.625 × 10² N/m
स्थिति b तथा c में भी पृष्ठ तनाव समान होगा चूंकि द्रव और ताप समान हैं।
अतः पृष्ठ तनाव का मान 5.625 x 10^-2 N/m ही होगा। चित्र (b) और (c) में भार को अवलम्बन प्रदान करने वाली 

झिल्ली की लम्बाई का मान भी उतना ही होगा जितना कि (a) में है। अतः कहा जा सकता है कि प्रत्येक स्थिति में अवलम्बित कुल भार 4.5 x 10^-2N ही होगा। 

प्रश्न 10.19.
3.00mm त्रिज्या की किसी पारे की बूंद के भीतर कमरे के ताप पर दाब क्या होगा ? 20°C ताप पर पारे का पृष्ठ तनाव 4.65 x 10 Nm है। यदि वायुमंडलीय दाब 1.01 x 10⁵ Pa है, तो पारे की बूँद के भीतर दाब - आधिक्य भी ज्ञात कीजिए। 
उत्तर:
दिया गया है:
पारे की बूँद की त्रिज्या = 2.00mm
= 2 × 10^-3m
पारे का पृष्ठ तनाव
T = 4.65 × 10^-1 N/m 
P = 1.01 x 10⁵ Pa
पारे की बूँद के भीतर दाब-आधिक्य P = 2T/r
\(P=\frac{2 \times 4.65 \times 10^{-1}}{3 \times 10^{-3}}\)
= 310 Pa
बूँद के भीतर कुल दाब का मान होगा
= P + Po
= 310 + 1.01 × 10⁵Pa
= 1.0131 × 10⁵ Pa 

प्रश्न 10.20.
5.00mm त्रिज्या के किसी साबुन के विलयन के बुलबुले के भीतर दाब - आधिक्य क्या होगा? 20°C ताप पर साबुन के विलयन का पृष्ठ तनाव 2.50 x 10^-2 Nm है। यदि इसी विमा का कोई वायु का बुलबुला 1.20 आपेक्षिक घनत्व के साबुन के विलयन से भरे किसी पात्र में 40.0 cm गहराई पर बनता है, तो इस बुलबुले के भीतर क्या दाब होता, ज्ञात कीजिए। (1 वायुमंडलीय दाब = 1.01 × 10⁵Pa)।
उत्तर:
दिया गया है:
तनाव (T) = 2.5 × 10 ² N/m
त्रिज्या (r) = 5.00mm= 5 x 10^-3 m
साबुन के विलयन का घनत्व p = 1.2 x 10³ kg/m² 
साबुन के बुलबुले के भीतर दाब आधिक्य का मान
\(\begin{aligned} P & =\frac{4 \mathrm{~T}}{\mathrm{r}} \\ & =\frac{4 \times 2.5 \times 10^{-2}}{5 \times 10^{-3}}=20 \mathrm{~Pa} \end{aligned}\)
हवा के बुलबुले के भीतर दाब आधिक्य का मान
\(\begin{aligned} P_1 & =\frac{2 \mathrm{~T}}{\mathrm{r}} \\ & =\frac{2 \times 2.5 \times 10^{-2}}{5 \times 10^{-3}}=10 \mathrm{~Pa} \end{aligned}\)
साबुन के विलयन में h गहराई पर वायु के बुलबुले के अंदर दाब,
= P₁ + वायुमण्डलीय दाब + hpg
= 10 + 1.01 × 10 + 0.4 × 1.2 × 10³ × 9.8 
= 10 + 1.01 × 10⁵ + 4 × 12 × 98 
= 4714 + 1.01 × 10⁵
= 4714 + 101000
= 105714 = 1.06 × 10⁵Pa 

अतिरिक्त अभ्यास:

प्रश्न 10.21.
1.0m² क्षेत्रफल के वर्गाकार आधार वाले किसी टैंक को बीच में ऊर्ध्वाधर विभाजक दीवार द्वारा दो भागों में बाँटा गया है। विभाजक दीवार में नीचे 20 cm क्षेत्रफल का कब्जेदार दरवाजा है। टैंक का एक भाग जल से भरा है तथा दूसरा भाग 1.7 आपेक्षिक घनत्व के अम्ल से भरा है। दोनों भाग 4.0m ऊँचाई तक भरे गए हैं। दरवाजे को बंद रखने के आवश्यक बल परिकलित कीजिए। 
उत्तर:
पानी वाले उपखण्ड कक्ष के लिए:
h = 4m
P₁ = 10³ kg/m³

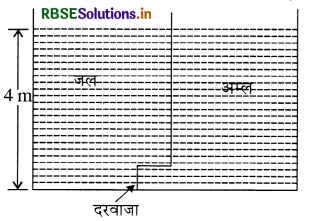
यदि पेंदी पर स्थित दरवाजे पर पानी द्वारा लगाने वाला दाब P, हो
P₁ = h₁p₁g
= 4 × 10³ × 9.8 = 3.92 × 10⁴Pa
अम्ल वाले उपखण्ड कक्ष के लिए:
h = 4.0mp₂ = 1.7 x 10³ kg/m³
 ∵ तेजाब का आपेक्षिक घनत्व = 1.7 x 10³ kg/m³ 
यदि पेंदी पर लगे दरवाजे पर अम्ल का दाब P₂ हो तब
P₂ = h₂P₂g
= 4.0 × 1.7 × 10³ × 9.8
= 6.664 × 10⁴Pa
दोनों दाबों का अन्तर = P₂ - P₁
∆P = 6.664 × 10⁴ - 3.92 × 10⁴
∆P = (6.664 - 3.92) × 10⁴
∆P = 2.774 × 10⁴ Pa
दरवाजे का क्षेत्रफल A = 20cm²
A = 20 × 10^-4m²
∴ दरवाजे पर बल = दाबांतर क्षेत्रफल
= ∆P × A
= (2.774 × 10⁴) × (20 × 10⁴)
= 54.88 N  = 55N
पानी वाले उपखण्ड से तेजाब वाले उपखण्ड की ओर 55 N क्षैतिज बल लगाकर दरवाजे को बंद किया जा सकता है।

प्रश्न 10.22. 
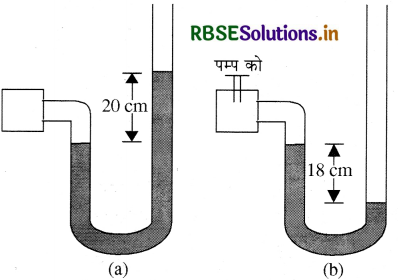
चित्र (a) में दर्शाए अनुसार कोई मैनोमीटर किसी बर्तन में भरी गैस के दाब का पाठ्यांक लेता है। पंप द्वारा कुछ गैस बाहर निकालने के पश्चात् मैनोमीटर चित्र (b) में दर्शाए अनुसार पाठ्यांक लेता है। मैनोमीटर में पारा भरा है तथा वायुमंडलीय दाब का मान 76 cm (Hg) है।
(i) प्रकरणों (a) तथा (b) में बर्तन में भरी गैस के निरपेक्ष दाब तथा प्रमापी दाब cm (Hg) के मात्रक में लिखिए।
(ii) यदि मैनोमीटर की दाहिनी भुजा में 13.6 cm ऊँचाई तक जल (पारे के साथ अमिश्रणीय) उड़ेल दिया जाए तो प्रकरण (b) में स्तर में क्या परिवर्तन होगा? (गैस के आयतन में हुए थोड़े परिवर्तन की उपेक्षा कीजिए।)

उत्तर:
दिया गया है:
(i) वायुमण्डलीय दाब Pa = 76 सेमी पारे के स्तम्भ के समान है बर्तन में भरी गैस का दाब = p
चित्र (a) में मैनोमीटर के अनुसार दाबांतर = 20 सेमी पारे के स्तम्भ के समान
अतः बर्तन में गैस का कुल दाब = P = 76 + 20 = 96 सेमी पारे के स्तम्भ के समान
चित्र (b) में मैनोमीटर के अनुसार दाबांतर = -18 सेमी पारे के स्तम्भ के समान
(क्योंकि बर्तन में से कुछ गैस बाहर निकाल ली गई है अतः दाब कम हो गया है।)
चित्र (b) में बर्तन में गैस का दाब = 76 + (-18) = 58 सेमी पारे के स्तम्भ के समान
(ii) यहाँ दाहिनी भुजा में पानी के 13.6 cm का अर्थ 13.6/13.6 = पारे के स्तम्भ का 1 cm
अर्थात् h1 = पारे का 1 cm [ यह चित्र में प्रदर्शित नहीं किया गया है।]
इसका मान निम्न प्रकार से किया जा सकता है
साम्यावस्था के लिए h.pmg = hwpwg
या
\(\begin{gathered} h_m=\frac{h_w \rho_w}{\rho_m}=\frac{h_w}{\rho_m / \rho_w} \\ h_m=\frac{13.6}{13.6}=1 \mathrm{~cm} \end{gathered}\)
= पारे के स्तम्भ के समान 1 cm
पारा बायीं भुजा में इस प्रकार उठेगा कि दोनों भुजाओं में पारे की स्तम्भ की ऊँचाइयों में
= 20cm - 1cm
= पारे के 19 cm स्तम्भ के समान 

प्रश्न 10.23. 
दो पात्रों के आधारों के क्षेत्रफल समान हैं परन्तु आकृतियाँ भिन्न-भिन्न हैं। पहले पात्र में दूसरे पात्र की अपेक्षा किसी ऊँचाई तक भरने पर दो गुना जल आता है। क्या दोनों प्रकरणों में पात्रों के आधारों पर आरोपित बल समान हैं? यदि ऐसा है तो भार मापने की मशीन पर रखे एक ही ऊँचाई तक जल से भरे दोनों पात्रों के पाठ्यांक भिन्न-भिन्न क्यों होते हैं?
उत्तर:
चूंकि दाब पानी के स्तम्भ की ऊँचाई पर निर्भर करता है। और भिन्न आकार वाले दो पात्रों में पानी के स्तम्भ की ऊँचाई एक समान है। इस कारण से प्रत्येक पात्र की पेंदी पर दाब समान होगा। चूंकि दोनों पात्रों के आधार का क्षेत्रफल समान है, इसलिए पानी के कारण दोनों पात्रों के आधार क्षेत्रफल पर समान बल कार्य करेगा। पानी पात्रों की दीवारों पर भी बल लगता है। यदि पात्र की दीवारें आधार के लम्बवत् नहीं हैं तो दीवार पर लगने वाले बल का ऊर्ध्वाधर घटक अशून्य होगा। चूंकि पानी की मात्रा दूसरे पात्र की अपेक्षा पहले में अधिक है। यही कारण है कि दोनों पात्रों में यद्यपि पानी समान ऊँचाई तक भरा गया है, फिर भी भारोत्तोलक यंत्र पर यह भिन्न माप देंगे।

प्रश्न 10.24 
रुधिर आधान के समय किसी शिरा में, जहाँ दाब 2000 Pa है, एक सुई धँसाई जाती है। रुधिर के पात्र को किस ऊँचाई पर रखा जाना चाहिए ताकि शिरा में रक्त ठीक-ठीक प्रवेश कर सके। (सम्पूर्ण रुधिर का घनत्व सारणी 10.1 में दिया गया है।)

तरल	P(kg/m3)
पानी	1.00 x 103
समुद्री पानी	1.03 x 103
पारा	13.6 x 103
इथाइल ऐल्कोहॉल	0.806 x 103
पूर्ण रक	1.06 x 103
वायु	1.29
ऑक्सीजन	1.43
हाइड्रोजन	9.0 x 10-2
अन्तर तारकीय स्थान	10-22

उत्तर:
दिया गया है:
गेज दाब, P = 2000 Pa
शिरा में रक्त ठीक-ठीक प्रवेश कर सके 
उसका घनत्व = 1.06 × 10³ kg/m³
g = 9.8m/s²
माना रुधिर के पात्र को ऊँचाई पर रखा जाना चाहिए
P = hpg
h = P/pg
मान रखने पर
\(\begin{aligned} & =\frac{2000}{1.06 \times 10^3 \times 9.8} \mathrm{~m} \\ & =\frac{2000}{106 \times 98}=\frac{2000}{10,388} \end{aligned}\)
h = 0.1925 0.2m
इस ऊँचाई पर पात्र रखने पर सूई पर रुधिर दाब एवं सिरा में रुधिर दाब समान, रक्त के शिरा में ठीक-ठीक प्रवेश के लिए सूई पर रुधिर दाब कुछ अधिक होना चाहिये। अतः पात्र को कुछ अधिक ऊँचाई लगभग 20 सेमी. ऊँचाई पर रखना चाहिए।

प्रश्न 10.25. 
बरनूली समीकरण व्युत्पन्न करने में हमने नली में भरे तरल पर किए गए कार्य को तरल की गतिज तथा स्थितिज ऊर्जाओं में परिवर्तन के बराबर माना था। (a) यदि क्षयकारी बल उपस्थित है, तब नली के अनुदिश तरल में गति करने पर दाब में परिवर्तन किस प्रकार होता है? (b) क्या तरल का वेग बढ़ने पर क्षयकारी बल अधिक महत्वपूर्ण हो जाते हैं? गुणात्मक रूप से चर्चा कीजिए।
उत्तर:
(a) बरनूली प्रमेय से हम जानते हैं-
दाब ऊर्जा में प्रति सेकण्ड कमी = वृद्धि + प्रति सेकण्ड स्थितिज ऊर्जा में वृद्धि + प्रति सेकण्ड गतिज ऊर्जा में
यदि हम श्यान बलों को नगण्य मानते हैं तब हम देखते हैं कि जब तरल निचले किनारे से ऊपरी किनारे की ओर प्रवाहित होता है, दाब कम होने के कारण दाब ऊर्जा कम हो जाती है। यदि क्षैयिक बल उपस्थित हो, तब दाब ऊर्जा का एक भाग द्रव प्रवाह के समय इनको पराभूत करने के काम आ जाता है, इसलिए दाब में जब द्रव नली के अनुदिश बहता है, कमी अधिक होगी।

(b) हाँ, जब तरल वेग बढ़ता है तो क्षैयिक बल अधिक प्रमुख हो जाते हैं। न्यूटन के नियम से हम जानते हैं कि श्यान बल
\(\mathrm{F}=-\eta \mathrm{A} \frac{d v}{d x}\)
यहाँ पर जैसे-जैसे V का मान बढ़ता है वैसे ही विभव प्रवणता का मान बढ़ता है। इस कारण से श्यान बल का मान भी बढ़ जाता है।

प्रश्न 10.26. 
(a) यदि किसी धमनी में रुधिर का प्रवाह पटलीय प्रवाह ही बनाए रखना है तो 2 x 10³m त्रिज्या की किसी धमनी में रुधिर - प्रवाह की अधिकतम चाल क्या होनी चाहिए? (b) तदनुरूपी प्रवाह - दर क्या है ? ( रुधिर की श्यानता 2.084 x 10^-3 Pas लीजिए) 
उत्तर:
पूर्ण रक्त का घनत्व p = 1.06 × 10³kg/m³ 
रक्तवाहिनी का व्यास D = 2 x त्रिज्या = 2 x 2 x 10m = 4 x 10^-3 m
रुधिर की श्यानता = 2.084 × 10^-3 Pas
रुधिर के स्तरीय प्रवाह के लिए Re = 2000
(a) माना रुधिर वाहिनी में रुधिर प्रवाह का औसत वेग = v = ?
हम जानते हैं:
\(\begin{aligned} \operatorname{Re} & =\frac{\rho \mathrm{v} d}{\eta} \\ \mathrm{v} & =\frac{\operatorname{Re} \eta}{\rho d} \end{aligned}\)
मान रखने पर
\(=\frac{2000 \times 2.084 \times 10^{-3}}{1.06 \times 10^3 \times 2 \times 10^{-3}}\)
= 0.983m / s = 0.98m/s

(b) प्रति सेकण्ड प्रवाहित रुधिर का आयतन V1 = ?
= रुधिर वाहिनी की अनुप्रस्थ काट x रुधिर प्रवाह का वेग
= πr²v
लेकिन त्रिज्या
\(\begin{aligned} r & =\frac{1}{2} \mathrm{D} \\ & =\pi\left(\frac{1}{2} \mathrm{D}\right)^2 \times \mathrm{v}=\frac{\pi \mathrm{D}^2 \mathrm{v}}{4} \end{aligned}\)
मान रखने पर
= π/4 × (4 × 10^-3)² × 0.98 = 5 × 16 × 10^-6 x 0.98
= π x 4 × 10^-6 × 0.98
= 3.14 × 4 × 10^-6 x 0.98
= 12.3088 x 10⁶ m³s
= 1.23 x 10^-5 m³s^-1

प्रश्न 10.27. 
कोई वायुयान किसी निश्चित ऊँचाई पर किसी नियत चाल से आकाश में उड़ रहा है तथा इसके दोनों पंखों में प्रत्येक का क्षेत्रफल 25 m' है। यदि वायु की चाल पंख के निचले पृष्ठ पर 180 kmht तथा ऊपरी पृष्ठ पर 234 km
है, तो वायुयान की संहति ज्ञात कीजिए। (वायु का घनत्व 1 kg m लीजिए।) 
उत्तर:
दिया गया है:
V = 180km/h
= 180 x 5/18m/s = 50m/s
V2 = 234 x 5/18 = 65 m/s
प्रत्येक पंखे का क्षेत्रफल = 25m²
∴ इसके कुल पंखे का क्षेत्रफल = 2 x 25 = 50m
p = वायु का घनत्व = 1 kg/m³
∴ ∆P पंखों के पृष्ठों के बीच दाबान्तर है, 
तब बरनूली सिद्धान्त से
∆P = 1/2p(v₂² - v₁²)
= 1/2 × 1 × [(65)² -  (50)²]
= (65 + 50) (65 - 50)
= 1/2 x 115 × 15
∴ उत्थापक बल = ∆P x A
= 1/2 × 115 × 15 x 50 
= 115 × 15 × 25 = 43125 N
वायुयान का भार दाबान्तर के कारण उत्पन्न अपरमुखी प्रणोद द्वारा
संतुलित है। अर्थात् mg = ∆PA
या
\(\mathrm{m}=\frac{\Delta \mathrm{P} \times \mathrm{A}}{g}\)
मान रखने पर
\(\mathrm{m}=\frac{43125}{9.8}\)
m = 4400.5 kg

प्रश्न 10.28. 
मिलिकन तेल बूँद प्रयोग में 2.0 × 10^-5 m त्रिज्या तथा 1.2 x 10³ kg m घनत्व की किसी बूँद की सीमांत चाल क्या है ? प्रयोग के ताप पर वायु की श्यानता 1.8 × 10^-5 pa इस चाल पर बूँद पर श्यान बल कितना है? (वायु के उत्प्लावन बल की उपेक्षा कीजिए)
उत्तर:
दिया गया है:
त्रिज्या 
r = 2.0 x 10 m
P = 1.2 x 10³ kg/m³
[n] = 1.8 × 10^-5 Pas
V1 = ?
F = ?
यहाँ पर वायु के कारण बूँद पर उत्प्लावन बल की उपेक्षा की गयी है।
∴ σ = 0 वायु के लिए

= 58.07 + 10^-3
= 5.8 × 10m/s = 5.8 cm/s
स्टोक के नियम के अनुसार बूँद पर श्यान बल
F = 6πnrv₁

मान रखने पर
= 6 × 22/7 × (1.8 × 10^-5) × (2 × 10^-5) × (5.8 × 10²)
= 6 × 3.14 × 1.8 × 2 × 5.8 × 10^-12
= 393.38 x 10^-12
= 3.934 × 10^-10 N

प्रश्न 10.29. 
सोडा काँच के साथ पारे का स्पर्श कोण 140° है। यदि पारे से भरी द्रोणिका में 1.00 mm त्रिज्या की काँच की किसी ली का एक सिरा डुबोया जाता है, तो पारे के बाहरी पृष्ठ के स्तर की तुलना में नली के भीतर पारे का स्तर कितना नीचे चला जाता है? (पारे का घनत्व = 13.6 x 10 kgm )
उत्तर:
दिया गया है
सम्पर्क कोण θ = 140°
त्रिज्या r = 1mm = 10^-3 m. 
पृष्ठ तनाव T = 0.465N/m.
पारे का घनत्व p = 13.6 x 10 kg/m³
ऊँचाई h = ?
cosθ = cos140° = - cos 40°
= -0.7660
\(h=\frac{2 \mathrm{TC} \cos \theta}{r \rho g}\)
मान रखने पर
\(\begin{aligned} h & =\frac{2 \times 0.465 \times \cos 140^{\circ}}{10^{-3} \times 13.6 \times 10^3 \times 9.8} \\ & =\frac{2 \times 0.465 \times(-0.7660)}{10^{-3} \times 13.6 \times 10^3 \times 9.8} \end{aligned}\)
= -5.34 × 10^-3 m
= -5.34mm
अतः पारे के बाहरी पृष्ठ के स्तर की तुलना में नली के भीतर का स्तर 5.34mm नीचे चला जाएगा।
अतः अवनति = 5.34mm

प्रश्न 10.30.
3.0mm तथा 6.0mm व्यास की दो संकीर्ण नलियों को एक साथ जोड़कर दोनों सिरों से खुली एक U-आकार की नली बनाई जाती है। यदि इस नली में जल भरा है, तो इस नली की दोनों भुजाओं में भरे जल के स्तरों में क्या अंतर होगा? प्रयोग के ताप पर जल का पृष्ठ तनाव 7.3 x 10^-2Nm है। स्पर्श कोण शून्य लीजिए तथा जल का घनत्व 1.0 × 10³ kg m लीजिए। (g = 9.8ms^-2)
उत्तर:
दिया गया है:
पानी का पृष्ठ तनाव (T) = 7.3 x 10^-2N/m
पानी का घनत्व (p) = 1 × 10³ kg/m³
सम्पर्क कोण θ = 0°
g = 9.8m/s²
व्यास d1 = 3.0mm
r1 = 1.5mm
r1 = 1.5 × 10^-3m
इसी प्रकार से d2 = 6.0mm
∴ r2 = 1/2d² = 1/2 x 6.0mm
∴ r2 = 3.00mm = 3 x 10^-3 m
माना U-नली की दो भुजाओं में अर्थात् नलिका एक व नलिका दो में पानी के स्तर की ऊँचाइयाँ क्रमश: h₁ व h₂ हैं।
∴ \(h_1=\frac{2 \mathrm{~T} \cos \theta}{\mathrm{r}_1 \rho g}\)
और 
∴ \(h_2=\frac{2 \mathrm{~T} \cos \theta}{\mathrm{r}_2 \rho g}\)

∴ U-नली की दोनों भुजाओं में पानी के स्तर में अन्तर

= 0.497 × 10²m = 0.497cm
= 4.97mm = 5.00mm

परिकलित्र / कम्प्यूटर आधारित प्रश्न:

प्रश्न 10.31. 
(a) हम जानते हैं कि वायु के घनत्व p ऊँचाई y (मीटरों में) के साथ इस संबंध के अनुसार घटता है:
P = p₀e^-y/y0
यहाँ समुद्र तल पर वायु का घनत्व po = 1.25 kg m^-3 तथा y0 एक नियतांक है। घनत्व में इस परिवर्तन को वायुमंडल का नियम कहते हैं। यह संकल्पना करते हुए कि वायुमंडल का ताप नियत रहता है । (समतापी अवस्था ) इस नियम को प्राप्त कीजिए। यह भी मानिए किg का मान नियत रहता है।
(b) 1425m³ आयतन का हीलियम से भरा कोई बड़ा गुब्बारा 400 kg के किसी पेलोड को उठाने के काम में लाया जाता है। यह मानते हुए कि ऊपर उठते समय गुब्बारे की त्रिज्या नियत रहती है, गुब्बारा कितनी अधिकतम ऊँचाई तक ऊपर उठेगा?
[yo = 8000m तथा P. = 0.18kgm लीजिए।
उत्तर:
(a) हम जानते हैं कि हवा के घनत्व में कमी की दर ऊँचाई (y) के समानुपाती होती है।
या
\(\frac{-\mathrm{d} \rho}{\mathrm{dy}} \propto \rho\)
\(\frac{d \rho}{d y}=-K \rho\)
यहाँ पर K समानुपाती स्थिरांक है। ऋणात्मक चिन्ह यह दर्शाता है कि जब हवा के घनत्व में कमी होती है तो ऊँचाई (y) का मान बढ़ता है।
\(\frac{d \rho}{\rho}=-\mathrm{K} d y\)
सीमा के अन्तर्गत समाकलन करने पर y का मान o से y तक बदलता है और हवा का घनत्व P0 से p तक बदलता है।
\(\int_\rho^\rho \frac{d \rho}{\rho}=-\mathrm{K} \int_0^y \mathrm{~K} d y\)
(log_ep)^p_p0 = -Ky
या
log_ep - log_ep₀ = -Ky
या log_e p/p₀ = - Ky
या p/p₀ = e^-ky या p = p₀e^-ky

यहाँ पर K एक स्थिरांक है। कल्पना कीजिए कि y0 एक स्थिरांक है। इस तरह से
K = 1/yo तब 
P = P₀e^-y/y0 ....(1)
(b) माना गुब्बारा y ऊँचाई तक ऊपर उठेगा, जहाँ पर उसका घनत्व हवा के घनत्व के बराबर होगा।

समीकरण (1) में मान रखने पर-


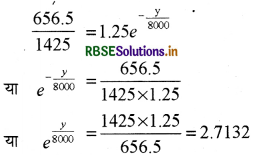
y = 8000m = 8km
या
यदि ऊँचाई के साथ 1 के मान में परिवर्तन को लिया जाये तो ऊँचाई लगभग 8.2 km आयेगी।