RBSE Solutions for Class 11 Economics Chapter 7 सहसंबंध

Rajasthan Board RBSE Solutions for Class 11 Economics Chapter 7 सहसंबंध Textbook Exercise Questions and Answers.

RBSE Solutions for Class 11 Economics Chapter 7 सहसंबंध

RBSE Class 11 Economics सहसंबंध InText Questions and Answers

पृष्ठ : 100

प्रश्न 1.
निम्नलिखित सारणी को देखें। वर्तमान कीमत पर राष्ट्रीय आय में वार्षिक वृद्धि तथा (सकल घरेलू उत्पाद के प्रतिशत के रूप में) सकल घरेलू बचत के बीच r का परिकलन कीजिए।
सारणी

वर्ष	राष्ट्रीय आय की वार्षिक वृद्धि	सकल घरेलू ब (GDP के प्रति के रूप में )
1992 - 93	14	23
1993 - 94	17	26
1994 - 95	18	27
1995 -96	17	25
1996 – 97	16	23
1997 – 98	12	25
1998 – 99	16	24
1999 – 2000	11	25
2000 – 01	8	24
2001 – 2002	10	23

उत्तर:

राष्ट्रीय आय में वार्षिक वृद्धि तथा सकल घरेलू बचत के बीच सहसम्बन्ध

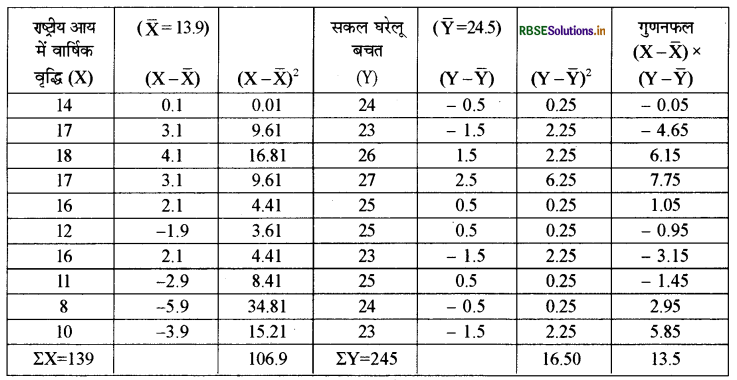
समान्तर माध्य = \(\overline{\mathbf{X}}=\frac{\Sigma \mathbf{X}}{\mathrm{N}}\)
\(=\frac{139}{10}=13.9\)

\(\begin{aligned} \overline{\mathrm{Y}} &=\frac{\Sigma \mathrm{Y}}{\mathrm{N}} \\ &=\frac{245}{10}=24.5 \end{aligned}\)

सहसम्बन्ध की गणना:

\(\mathrm{r}=\frac{\Sigma(\mathrm{X}-\overline{\mathrm{X}})(\mathrm{Y}-\overline{\mathrm{Y}})}{\sqrt{\Sigma(\mathrm{X}-\overline{\mathrm{X}})^{2}} \sqrt{\Sigma(\mathrm{Y}-\overline{\mathrm{Y}})^{2}}}\)

\(\begin{aligned} &=\frac{13.5}{\sqrt{106.9} \sqrt{16.50}} \\ &=\frac{13.5}{10.34 \times 4.06} \\ &=\frac{13.5}{41.98} \end{aligned}\)

= 0.32

RBSE Class 11 Economics सहसंबंध Textbook Questions and Answers

प्रश्न 1. 
कद (फुटों में) तथा वजन (किलोग्राम में) के बीच सहसम्बन्ध गुणांक की इकाई है।
(क) कि.ग्रा./फुट 
(ख) प्रतिशत 
(ग) अविद्यमान
उत्तर:
(ग) अविद्यमान

 

प्रश्न 2. 
सरल सहसम्बन्ध गुणांक का परास निम्नलिखित होगा।
(क) 0 से अनन्त तक 
(ख) 1 से + 1 तक
(ग) ऋणात्मक अनन्त से धनात्मक अनन्त तक
उत्तर:
(ख) 1 से + 1 तक

प्रश्न 3. 
यदि । धनात्मक है तो x और y के बीच का सम्बन्ध इस प्रकार का होता है।
(क) जब y बढ़ता है तो x बढ़ता है। 
(ख) जब y घटता है तो x बढ़ता है। 
(ग) जब । बढ़ता है तो x नहीं बढ़ता है।
उत्तर:
(क) जब y बढ़ता है तो x बढ़ता है। 

प्रश्न 4. 
यदि = 0 तब चर x और y के बीच
(क) रेखीय सम्बन्ध होगा 
(ख) रेखीय सम्बन्ध नहीं होगा
(ग) स्वतन्त्र होगा
उत्तर:
(ग) स्वतन्त्र होगा

प्रश्न  5. 
निम्नलिखित तीनों मापों में, कौनसा माप किसी भी प्रकार के सम्बन्ध की माप कर सकता है
(क) कार्ल पियरसन सहसम्बन्ध गुणांक 
(ख) स्पीयरमैन का कोटि सहसम्बन्ध 
(ग) प्रकीर्ण आरेख
उत्तर:
(क) कार्ल पियरसन सहसम्बन्ध गुणांक 

प्रश्न  6. 
यदि परिशुद्ध रूप से मापित आँकड़े उपलब्ध हों, तो सरल सहसम्बन्ध गुणांक।
(क) कोटि सहसम्बन्ध गुणांक से अधिक सही होता है। 
(ख) कोटि सहसम्बन्ध गुणांक से कम सही होता
(ग) कोटि सहसम्बन्ध की ही भाँति सही होता
उत्तर:
(ग) कोटि सहसम्बन्ध की ही भाँति सही होता

प्रश्न 7. 
साहचर्य के माप के लिए को सहप्रसरण से अधिक प्राथमिकता क्यों दी जाती है?
उत्तर:
साहचर्य के माप के लिए " को सहप्रसरण से अधिक प्राथमिकता दी जाती है। इसका कारण है कि सहसम्बन्ध (1) सह-प्रसरण का मापन करता है न कि कार्य-कारण सम्बन्ध का। दो चरों x तथा y के बीच सहसम्बन्ध की उपस्थिति का अर्थ है कि जब एक चर का मान किसी दिशा में बदलता है, तो दूसरा चर भी किसी निश्चित दिशा में बदलेगा। अतः सह-प्रसरण की माप के कारण ही सहसम्बन्ध को अधिक प्राथमिकता दी जाती है। 

प्रश्न 8. 
क्या आंकड़ों के प्रकार के आधार पर r,-1 तथा +1 के बाहर स्थित हो सकता है?
उत्तर:
ऑकड़ों के प्रकार के आधार पर 1,-1 तथा +1 के बाहर स्थित नहीं हो सकता है, क्योंकि सहसम्बन्ध का न्यूनतम मान -1 तथा अधिकतम मान +1 होता है।

प्रश्न 9. 
क्या सहसम्बन्ध के द्वारा कार्य-कारण सम्बन्ध की जानकारी मिलती है?
उत्तर:
सहसम्बन्ध से कार्य-कारण की जानकारी नहीं मिलती है, बल्कि सहसम्बन्ध सह - प्रसरण का मापन करता है। दो चरों x और y के बीच सहसम्बन्ध की उपस्थिति का अर्थ है कि जब एक चर का मान किसी दिशा में बदलता है तो दूसरे चर का मान या तो उसी दिशा में बदलेगा या फिर विपरीत दिशा में बदलेगा।

प्रश्न 10. 
सरल सहसम्बन्ध गुणांक की तुलना में कोटि सहसम्बन्ध गुणांक कब अधिक परिशुद्ध होता है?
उत्तर:
सरल सहसम्बन्ध गुणांक की तुलना में कोटि सहसम्बन्ध गुणांक उन परिस्थितियों में अधिक परिशुद्ध होता है, जबकि तथ्यों को प्रत्यक्ष रूप से संख्या में मापना सम्भव न हो; परन्तु उन्हें एक निश्चित क्रम में रखा जा सकता है, जैसे-कुशलता, सुन्दरता, बुद्धिमता, योग्यता, स्वास्थ्य इत्यादि । इसके अतिरिक्त, कभी-कभी चरम मानों वाले दो चरों के बीच सहसम्बन्ध गुणांक, चरम मान से रहित गुणांक से अत्यन्त भिन्न हो सकता है। इन परिस्थितियों में कोटि सहसम्बन्ध साधारण सहसम्बन्ध की तुलना में बेहतर विकल्प प्रदान करता है।

प्रश्न 11. 
क्या शून्य सहसम्बन्ध का अर्थ स्वतन्त्रता है?
उत्तर:
जब सहसम्बन्ध शून्य होता है तो दो चर आपस में सह-सम्बन्धित नहीं होते हैं। ऐसी स्थिति में सहसम्बन्ध का अभाव पाया जाता है तथापि इन चरों के बीच किसी दूसरे प्रकार का सहसम्बन्ध पाया जा सकता है। सामान्यतः शून्य सहसम्बन्ध का अर्थ स्वतन्त्रता ही है; क्योंकि इसमें सहसम्बन्ध की अनुपस्थिति पाई जाती है।

प्रश्न 12. 
क्या सरल सहसम्बन्ध गुणांक किसी भी प्रकार के सम्बन्ध को माप सकता है?
उत्तर:
सरल सहसम्बन्ध गुणांक केवल दो चरों के बीच पाए जाने वाले सहसम्बन्ध को माप सकता है। जब दो चरों से अधिक चरों के मध्य सम्बन्ध पाया जाए जैसेगेहूँ की पैदावार पर वर्षा एवं तापमान के प्रभाव का अध्ययन करना, तो ऐसी स्थिति में सरल सहसम्बन्ध गुणांक सहसम्बन्ध को नहीं माप सकता है। अतः सरल सहसम्बन्ध गुणांक से सभी प्रकार के सम्बन्धों को नहीं मापा जा सकता है। यह दो चरों के मध्य पाए जाने वाले किसी भी प्रकार के सम्बन्ध को माप सकता है।

प्रश्न 13. 
एक सप्ताह तक अपने स्थानीय बाजार में 5 प्रकार की सब्जियों की कीमतें प्रतिदिन एकत्र करें। उनका सहसम्बन्ध गुणांक परिकलित कीजिए। इसके परिणाम की व्याख्या कीजिए।
उत्तर:
उपर्युक्त स्थिति में सहसम्बन्ध गुणांक के परिकलन को अग्र उदाहरण द्वारा स्पष्ट कर सकते हैं।

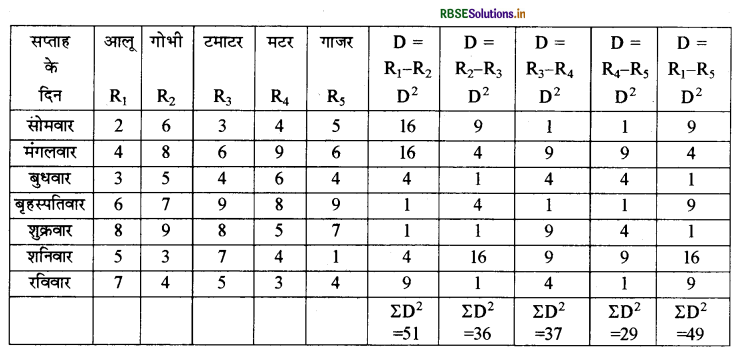
आलू तथा गोभी के मध्य सहसम्बन्ध
\(\begin{aligned} \mathrm{r}_{\mathrm{S}} &=1-\frac{6 \Sigma \mathrm{D}^{2}}{\mathrm{~N}^{3}-\mathrm{N}} \\ &=1-\frac{6 \times 51}{(343-7)}=1-\frac{306}{336} \end{aligned}\)

= 1 - 0.911
= 0.089

गोभी और टमाटर के मध्य सहसम्बन्ध
\(\begin{aligned} \mathrm{r}_{\mathrm{S}} &=1-\frac{6 \Sigma \mathrm{D}^{2}}{\mathrm{~N}^{3}-\mathrm{N}} \\ &=1-\frac{6 \times 36}{(343-7)}=1-\frac{216}{336} \end{aligned}\)

= 1- 66.4 = 0.36

टमाटर और मटर के मध्य सहसम्बन्ध
\(\begin{aligned} r_{S} &=1-\frac{6 \Sigma D^{2}}{N^{3}-N} \\ &=1-\frac{6 \times 37}{343-7} \\ &=1-\frac{222}{336} \end{aligned}\)

= 1 - 0.66 = 0.34

मटर और गाजर के मध्य सहसम्बन्ध
\(\begin{aligned} r_{S} &=1-\frac{6 \Sigma D^{2}}{N^{3}-N} \\ &=1-\frac{6 \times 29}{343-7} \end{aligned}\)

\(=1-\frac{174}{336}\)
= 1 - 0.52 = 0.48

गाजर और आलू के मध्य सहसम्बन्ध
\(\begin{aligned} \mathrm{r}_{\mathrm{S}} &=1-\frac{6 \Sigma \mathrm{D}^{2}}{\mathrm{~N}^{3}-\mathrm{N}} \\ &=1-\frac{6 \times 49}{343-7} \\ &=1-\frac{294}{336} \end{aligned}\)

= 1 - 0.875 = 0.125

परिणामों की व्याख्या: यहाँ सप्ताह भर की पाँच सब्जियों की कीमतें एकत्र कर उनके मध्य सहसम्बन्ध की गणना की गई। आलू तथा गोभी के मध्य सहसम्बन्ध की गणना करने पर सहसम्बन्ध गुणांक 0.089 आया। गोभी एवं टमाटर के मध्य सहसम्बन्ध गुणांक 036 निकला। टमाटर तथा मटर के मध्य सहसम्बन्ध गुणांक 0.34 निकला तथा मटर एवं गाजर के बीच सहसम्बन्ध गुणांक 048 निकला। इसी प्रकार गाजर और आलू के बीच सहसम्बन्ध गुणांक 0.125 निकला। इन पाँच सब्जियों में से मटर तथा गाजर के बीच सहसम्बन्ध गुणांक सबसे अधिक अर्थात् 0.48 पाया गया अतः इसमें उच्च कीमतें पाई गई।

प्रश्न 14. 
अपनी कक्षा के सहपाठियों के कद मापिए। उनसे उनके बेंच पर बैठे सहपाठी का कद पूछिए। इन दो चरों का सहसम्बन्ध गुणांक परिकलित कीजिए और परिणाम का निर्वचन कीजिए।
उत्तर:
उपर्युक्त स्थिति में सहसम्बन्ध गुणांक के परिकलन को अग्र उदाहरण द्वारा स्पष्ट कर सकते हैं।

सहपाठियों की संख्या	1	2	3	4	5	6	7	8	9	10
सहपाठियों द्वारा बताया गया कद (U)	60	58	62	56	59	63	65	66	68	60
वास्तविक कद (V)	62	64	53	60	72	56	68	60	69	65

सहसम्बन्ध की गणना

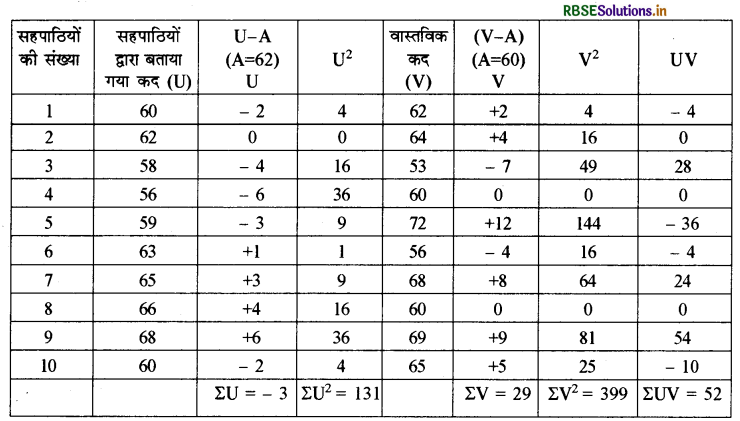
\(\begin{aligned} r &=\frac{\Sigma U V-\frac{(\Sigma U)(\Sigma V)}{N}}{\sqrt{\Sigma U^{2}-\frac{(\Sigma U)^{2}}{N}} \sqrt{\Sigma V^{2}-\frac{(\Sigma V)^{2}}{N}}} \\ r &=\frac{52-\frac{(-3)(29)}{10}}{\sqrt{131-\frac{(-3)^{2}}{10}} \sqrt{399-\frac{(29)^{2}}{10}}} \\ r &=\frac{52-\frac{(-87)}{10}}{\sqrt{131-.9} \sqrt{399-84.1}} \\ r &=\frac{52-(-8.7)}{\sqrt{130.1} \sqrt{314.9}} \end{aligned}\)

\(\begin{aligned} &r=\frac{52+8.7}{11.4 \times 17.7} \\ &r=\frac{60.7}{201.78} \end{aligned}\)
r = 0.301
अतः विद्यार्थियों द्वारा बताए गए कद तथा वास्तविक माप द्वारा निकाले गए कद में मध्यम स्तर का धनात्मक सहसम्बन्ध पाया गया।

प्रश्न 15. 
कुछ ऐसे चरों की सूची बनाएँ, जिनका परिशुद्ध मापन कठिन हो।
उत्तर:
कुछ ऐसे सम्बन्ध होते हैं, जो मात्र संयोग होते हैं, ऐसे चरों का परिशुद्ध मापन कठिन होता है। इनका उदाहरण निम्न प्रकार है

1. किसी पक्षी विहार में प्रवासी पक्षियों के आने के साथ उस क्षेत्र में जन्म दरों के सहसम्बन्ध का मापन।
2. आपकी जूते की माप तथा जेब में पैसों के बीच सहसम्बन्ध का मापन।
3. चीन का मौसम तथा भारत में चाय की मांग के बीच सहसम्बन्ध का मापन।
4. चीन में वर्षा की मात्रा तथा भारत में कपड़े की मांग के बीच सहसम्बन्ध का मापन आदि।

प्रश्न 16.
1 के विभिन्न मानों +1,-1 तथा 0 की व्याख्या करें।
उत्तर:
जब का मान +1 होता है तो दो चरों के बीच पाए जाने वाला रेखीय सम्बन्ध पूर्णतया धनात्मक होता है। यदि का मान -1 होता है तो दो चरों के बीच पाया जाने वाला सहसम्बन्ध पूर्णतया ऋणात्मक होता है। यदि का मान शून्य (0) होता है तो दो चरों के बीच सहसम्बन्ध का अभाव पाया जाता है, किन्तु ऐसी स्थिति में चरों के बीच रेखीय सम्बन्ध के अलावा किसी दूसरी प्रकार का सम्बन्ध पाया जा सकता है।

प्रश्न 17.
पियरसन सहसम्बन्ध गुणांक से कोटि सहसम्बन्ध गुणांक क्यों भिन्न होता है?
उत्तर:
कोटि सहसम्बन्ध गुणांक, पियरसन सहसम्बन्ध गुणांक से भिन्न होता है। कोटि सहसम्बन्ध गुणांक का प्रयोग तब किया जाता है जब चरों को सार्थक रूप से नहीं मापा जा सकता है; जैसे-कुशलता, सुन्दरता, बुद्धिमानी इत्यादि। जब गुणवत्ताओं पर आधारित चरों का सहसम्बन्ध ज्ञात किया जाता है तब उन्हें परिमाणीकरण करने के बजाय उनकी कोटि निर्धारित करना अधिक अच्छा विकल्प है, अत: कोटि सहसम्बन्ध गुणांक का उपयोग किया जाता है। जब कभी चरम मानों वाले दो चरों के बीच सहसम्बन्ध गुणांक, चर मान से रहित गुणांक से अत्यन्त भिन्न होता है तब कोटि सहसम्बन्ध गुणांक, पियरसन गुणांक की तुलना में बेहतर विकल्प प्रदान करता है।

प्रश्न 18. 
पिताओं (X) और उनके पुत्रों (Y) के कदों का माप नीचे इंचों में दिया गया है, इन दोनों के बीच सहसम्बन्ध गुणांक को परिकलित कीजिए।

X	65	66	57	67	68	69	70	72
Y	67	56	65	68	72	72	69	71

उत्तर:
सम्बन्ध गुणांक
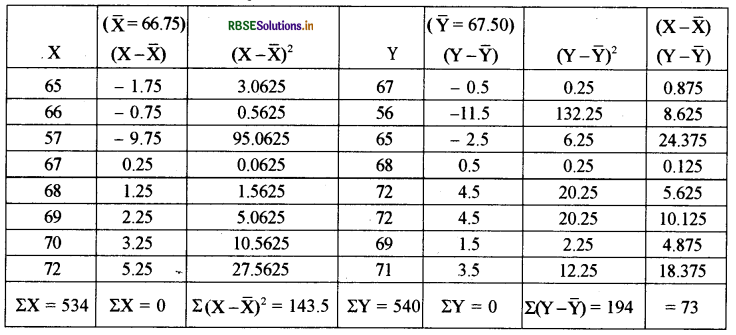सहसम्बन्ध गुणांक 
\(\begin{aligned} \overline{\mathbf{X}} &=\frac{\Sigma \mathbf{X}}{\mathrm{N}} \\ &=\frac{534}{8}=66.75 \end{aligned}\)

\(\begin{aligned} \bar{Y} &=\frac{\Sigma Y}{N} \\ &=\frac{540}{8}=67.50 \end{aligned}\)

सहसम्बन्ध गुणांक की गणना:
\(\begin{aligned} r &=\frac{\Sigma(X-\bar{X})(Y-\bar{Y})}{\sqrt{\Sigma(X-\bar{X})^{2}} \sqrt{\Sigma(Y-\bar{Y})^{2}}} \\ &=\frac{73}{\sqrt{143.5} \sqrt{194}} \\ &=\frac{73}{11.98 \times 13.93} \\ &=\frac{73}{166.88} \end{aligned}\)
r = 0.43
अतः पिता तथा पुत्रों के कदों की नाप में मध्यम स्तर का धनात्मक सहसम्बन्ध है।

प्रश्न 19.
X और Y के बीच सहसम्बन्ध गुणांक को परिकलित कीजिए और उनके सम्बन्ध पर टिप्पणी कीजिए।

X	-3	-2	-1	1	2	3
Y	9	4	1	1	4	9

उत्तर:
हसम्बन्ध गुणांक की गणना

X	X2	Y	Y2	XY
-3	9	9	81	-27
-2	4	4	16	-8
-1	1	1	1	-1
1	1	1	1	1
2	4	4	16	8
3	9	9	81	27
∑X	∑X2 = 28	∑Y =28	∑Y2 = 196	∑XY = 0

\(\begin{aligned} r &=\frac{\Sigma x y-\frac{(\Sigma X)(\Sigma Y)}{N}}{\sqrt{\Sigma X^{2}-\frac{(\Sigma X)^{2}}{N} \sqrt{\Sigma Y^{2}-\frac{(\Sigma Y)^{2}}{N}}}} \\ &=\frac{0-\frac{(0)(28)}{6}}{\sqrt{28-\frac{(0)^{2}}{6}} \sqrt{196-\frac{(28)^{2}}{6}}} \\ &=\frac{0}{\sqrt{28} \sqrt{196-130.67}} \\ &=\frac{0}{5.3 \times 8.08}=\frac{0}{42.824}=0 \end{aligned}\)