RBSE Solutions for Class 11 Economics Chapter 6 परिक्षेपण के माप

Rajasthan Board RBSE Solutions for Class 11 Economics Chapter 6 परिक्षेपण के माप Textbook Exercise Questions and Answers.

RBSE Class 11 Economics Solutions Chapter 6 परिक्षेपण के माप

RBSE Class 11 Economics परिक्षेपण के माप InText Questions and Answers

पृष्ठ: 76 

प्रश्न 1. 
निम्नलिखित मानों को देखें।
20, 30, 40, 50, 200 
(i) परास का परिकलन कीजिए।
(ii) यदि आँकड़ा समुच्चय में मान 200 नहीं हो तो परास क्या होगा?
(iii) यदि 50 के स्थान पर 150 हो तो परास क्या होगा? 
उत्तर:
(i) परास = L - S
यहाँ L = अधिकतम मान
S -  न्यूनतम मान परास = 200 - 20
= 180 

(ii) यदि आँकड़ा समुच्चय में 200 न हो तो आंकड़ा समुच्चय निम्न होगा
20, 30, 40, 50 अत: परास = L - S
= 50 - 20 = 30 

(iii) यदि आँकड़ा समुच्चय में 50 के स्थान पर 150 हो तो परास पर कोई प्रभाव नहीं पड़ेगा। 50 के स्थान पर 150 होने पर आंकड़ा समुच्चय निम्न प्रकार होगा
20, 30, 40, 150, 200 '
परास = L - S
= 200 - 20 = 180 

RBSE Class 11 Economics परिक्षेपण के माप Textbook Questions and Answers

प्रश्न 1. 
"किसी बारम्बारता वितरण के समझने के परिक्षेपण का माप केन्द्रीय मान का एक अच्छा सम्पूरक है।" टिप्पणी करें।
उत्तर:
यह कथन सत्य है कि किसी बारम्बारता वितरण को समझने में परिक्षेपण का माप केन्द्रीय मान का एक अच्छा सम्पूरक है। केन्द्रीय मान औसत वितरण के केवल एक पहलू को ही बताता है अर्थात् वह मानों के प्रतिनिधि आकार को बताता है। उदाहरण के लिए दो परिवारों का औसत आय एकसमान हो किन्तु हो सकता है कि उन परिवारों की व्यक्तिगत आय में असमानता है, केन्द्रीय माप इस असमानता को नहीं दर्शाता। अतः वितरण को बेहतर ढंग से जानने के लिए हमें परिक्षेपण के मानों की आवश्यकता पड़ती है। परिक्षेपण यह दर्शाता है कि वितरण का मान उसके औसत मान से कितना भिन्न है अर्थात परिक्षेपण का माप आंकड़ों के बिखराव को दर्शाता है, किसी श्रृंखला के वितरण के बारे में परिक्षेपण का माप आंकड़ों की बेहतर जानकारी देता है।

 

प्रश्न 2. 
परिक्षेपण का कौनसा माप सर्वोत्तम है और कैसे?
उत्तर:
परिक्षेपण के निम्न चार प्रमुख माप हैं
(1) परास (2) चतुर्थक विचलन (3) माध्य विचलन (4) मानक विचलन। यद्यपि परिक्षेपण के उपर्युक्त चारों मापों की अपनी-अपनी विशेषताएँ एवं सीमाएँ हैं। परिक्षेपण के इन मापों में मानक विचलन को सर्वोत्तम माना जाता है क्योंकि यह सभी मानों पर आधारित होता है। किसी भी मान में परिवर्तन, मानक विचलन के मान को प्रभावित करता है। इसकी गणना में बीजगणितीय चिह्नों को ध्यान में रखा जाता है। बीजगणितीय गुणों के कारण यह अन्य प्रमापों से उत्तम है। यह उद्गम से स्वतन्त्र है किन्तु स्केल से नहीं है। इसके साथ - साथ यह कुछ उच्च सांख्यिकीय विधियों में भी प्रयुक्त होता है।

प्रश्न 3.
"परिक्षेपण के कुछ माप मानों के प्रसरण पर निर्भर करते हैं, लेकिन कुछ केन्द्रीय मान से मानों के विचरण को परिकलित करते हैं।" क्या आप सहमत हैं?
उत्तर:
हम इस कथन से सहमत हैं कि परिक्षेपण के कुछ माप मानों के प्रसरण पर निर्भर करते हैं लेकिन कुछ केन्द्रीय मान के मानों के विचरण को परिकलित करते हैं। परिक्षेपण के कुछ माप जैसे परास तथा चतुर्थक विचलन मानों के प्रसरण पर निर्भर करते हैं लेकिन कुछ माप जैसे माध्य विचलन तथा मानक विचलन औसत से मानों के विचलनों पर आधारित होते हैं।

प्रश्न 4. 
एक कस्बे में 25% लोग रु.45,000 से अधिक आय अर्जित करते हैं, जबकि 75% लोग रु. 18,000 से अधिक अर्जित करते हैं। परिक्षेपण के निरपेक्ष एवं सापेक्ष मानों का परिकलन कीजिए।
उत्तर:
परिक्षेपण की निरपेक्ष माप. परास = L - S
345,000 - 18,000
= 27.000 

 परिक्षेपण की सापेक्ष माप
 परास गुणांक = \(\frac{L-S}{L+S}\)
\(=\frac{45000-18000}{45000+18000}\)
\(=\frac{27000}{63000}\)
= 0.428 
= 0.43

प्रश्न 5. 
एक राज्य में 10 जिलों की प्रति एकड़ गेहूँ व चावल फसल की उपज अग्रवत् है।

प्रत्येक फसल के लिए परिकलन करें
(क) परास 
(ख) चतुर्थक विचलन 
(ग) माध्य से माध्य विचलन 
(घ) मध्यिका से माध्य विचलन 
(ङ) मानक विचलन 
(च) किस फसल में अधिक विचरण है?
(छ) प्रत्येक फसल के लिए विभिन्न मापकों के मानों की तुलना कीजिए।
उत्तर:
(क) परासपरास की गणना निम्न सूत्र द्वारा की जाएगी
परास = L - S 
यहाँ L= वितरण में अधिकतम मान
s= वितरण में न्यूनतम मान गेहूँ का परास = L - S
25 - 9 = 16 
चावल का परास = L - S
= 34 - 12 = 22 

(ख) चतुर्थक विचलनचतुर्थक विचलन ज्ञात करने का सूत्र निम्न प्रकार

\(\text { Q.D. }=\frac{Q_{3}-Q_{1}}{2}\)
(i) गेहूँ का चतुर्थक विचलन-सर्वप्रथम श्रेणी को आरोही क्रम में व्यवस्थित करेंगे
 9, 10, 10, 12, 15, 16, 18, 19,21,25
N = 10 
प्रथम चतुर्थक (Q₁) का मान
= Size of \(\left(\frac{N+1}{4}\right)^{t h}\) item
= Size of \(\left(\frac{10+1}{4}\right)^{\text {th }}\) item
= Size of 2.75th item 
= Size of 2nd item + \(\frac{3}{4}\) (Size of 3rd item - Size of 2nd item) 
= 10+ \(\frac{3}{4}\) (10-10) 
Q₁ = 10
तृतीय चतुर्थक (Q₃) का मान
 = Size of 3 x \(\left(\frac{N+1}{4}\right)^{t h}\) item 
 Q₃ =  Size of 3 x \(\left(\frac{10+1}{4}\right)^{\text {th }}\) item 
 = Size of \(\frac{33}{4}^{\text {th }}\) item 
 = Size of 8.25th item
= Size of 8th item + \(\frac{1}{4}\) (Size of 9th item - Size of 8th item) 
= 19 + \(\frac{1}{4}\) (21 - 19)
= 19 + \(\frac{1}{4}\) x 2
= 19 + 0.5 = 19.5 

अतः चतुर्थक विचलन (Q.D.)
\(\begin{aligned} &=\frac{Q_{3}-Q_{1}}{2} \\ &=\frac{19.5-10}{2}=\frac{9.5}{2} \end{aligned}\) 
= 4.75 
अतः गेहूँ का चतुर्थक विचलन = 4.75

(ii) चावल का चतुर्थक विचलन: चावल का चतुर्थक विचलन निकालने हेतु सर्वप्रथम श्रेणी को आरोही क्रम में लिखना होगा
12, 12, 12, 15, 18, 18, 22, 23, 29, 34 
N = 10
प्रथम चतुर्थक (Q₁) का आकार
= Size of \(\left(\frac{N+1}{4}\right)^{t h}\) item 
= Size of \(\left(\frac{10+1}{4}\right)^{\text {th }}\) item
= Size of 2.75th item 
= Size of 2nd item + (Size of 3rd item - Size of 2nd item) 
= 12+ \(\frac{3}{4}\) (12 - 12)
Q₁ = 12 

तृतीय चतुर्थक (Q₃) का मान
Q₃ = Size of 3 x \(\left(\frac{N+1}{4}\right)^{t h}\) item
Size of 3 x \(\left(\frac{10+1}{4}\right)^{\text {th }}\) item 
= Size of 8.25th item
= Size of 8th item + 1 (Size of 8th item - Size of 9th item) 
= 23 + 4 (29 - 23) 
= 23 + 16
= 23 + 1.5 
Q₃ = 24.5 
चावल का चतुर्थक विचलन (Q.D.)
\(=\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
\(=\frac{24.5-12}{2}=\frac{12.5}{2}=6.25\)

गेहूँ का समान्तर माध्य
माध्य से माध्य विचलन (M.D) निकालते समय के सभी मानों को धनात्मक माना जाता है।
\(=\frac{\Sigma(\mathrm{d})}{\mathrm{N}}\)
\(\Sigma|\mathrm{d}|=\Sigma(\mathrm{X}-\overline{\mathrm{X}})\) 
N = पदों की संख्या

गेहूँ तथा चावल का माध्य से माध्य विचलन निकालने हेतु निम्न सारणी बनाई जाएगी:

जिला	गेहूँ x	विचलन \((X-\bar{X})=|d|\)	चावल  Y	विचलन \((\mathbf{Y}-\overline{\mathbf{Y}}=|\mathrm{d}|)\)
1	12	3.5	22	2.5
2	10	5.5	29	9.5
3	15	0.5	12	7.5
4	19	3.5	23	3.5
5	21	5.5	18	1.5
6	16	0.5	15	4.5
7	18	2.5	12	7.5
8	9	6.5	34	14.5
9	25	9.5	18	7.5
10	\(\Sigma \mathbf{X}=155\)	\(\Sigma|\mathrm{d}|=43\)	\(\Sigma \mathbf{X}=195\)	\(\Sigma|\mathrm{d}|=60\)

चावल का समान्तर माध्य:
\(\begin{aligned} &=\frac{\Sigma Y}{N} \\ &=\frac{195}{10} \\ &=19.5 \end{aligned}\)

(माध्य से माध्य विचलन निकालते समय Y - 1 के सभी मानों को धनात्मक मान लिया जाता है।)

गेहूँ का माध्य विचलन

\(\text { M.D. } \overline{\mathrm{x}}=\frac{\Sigma|\mathrm{d}|}{\mathrm{N}}\)

\(\begin{aligned} &=\frac{43}{10} \\ &=4.3 \end{aligned}\)

चावल का माध्य विचल
\(\text { M.D. } \overline{\mathrm{x}}=\frac{\Sigma|\mathrm{d}|}{\mathrm{N}}\)
\(=\frac{60}{10}\)

= 6
(घ ) मध्यिका से माध्य विचलन-मध्यिका से माध्य विचलन निकालने का सूत्र निम्न प्रकार है
\(\text { M. D. }=\frac{\Sigma|\mathrm{d}|}{\mathrm{N}} \text { } \Sigma|\mathrm{d}|\) = X - Medain

मध्यिका का माध्य विचलन (आरोही क्रम के अनुसार)

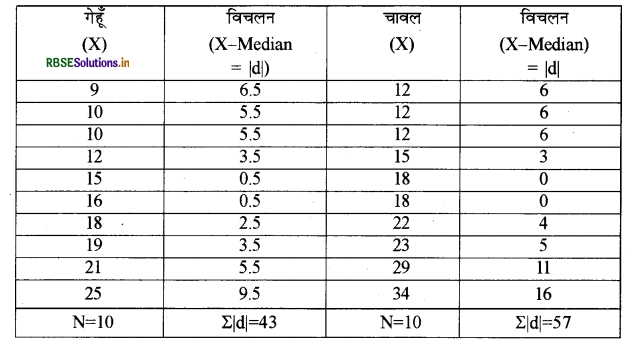
गेहूँ का मध्यिका मूल्य 
मध्यिका = Size of \(\left(\frac{\mathrm{N}+1}{2}\right)^{\mathrm{th}}\) item
= Size of \(\left(\frac{10+1}{2}\right)^{\text {th }}\) item = Size of 5.5th item 
\(\begin{aligned} &=\frac{\text { Size of } 5^{\text {th }} \text { item }+\text { Size of } 6^{\text {th }} \text { item }}{2} \\ &=\frac{15+16}{2}=15.5 \end{aligned}\)

गेहूँ का माध्य विचलन 
\(\text { M.D. }=\frac{\Sigma|d|}{N}\)

चावल का मध्यिका मूल्य

मध्यिका = Size of \(\left(\frac{\mathrm{N}+1}{2}\right)^{\mathrm{th}}\) item
= Size of \(\left(\frac{10+1}{2}\right)^{\text {th }}\) item = Size of 5.5th item
\(=\frac{\text { Size of } 5^{\text {th }} \text { item }+\text { Size of } 6^{\text {th }} \text { item }}{2}\)

\(=\frac{18+18}{2}=18\)
चावल का माध्य विचलन
\(\text { M.D. }=\frac{\Sigma|d|}{N}\)

(ङ) मानक विचलन-किसी श्रेणी का मानक विचलन निकालने हेतु कई सूत्र हैं किन्तु वास्तविक माध्य विधि का निम्न सूत्र है जिसकी सहायता से मानक विचलन निकाला जा सकता है
यहाँ \(\sigma=\sqrt{\frac{\Sigma \mathrm{d}^{2}}{\mathrm{~N}}}\)
\(\Sigma \mathrm{d}^{2}=(\mathbf{X}-\overline{\mathbf{X}})^{2}\)
गेहूँ तथा चावल के मानक विचलन की गणना

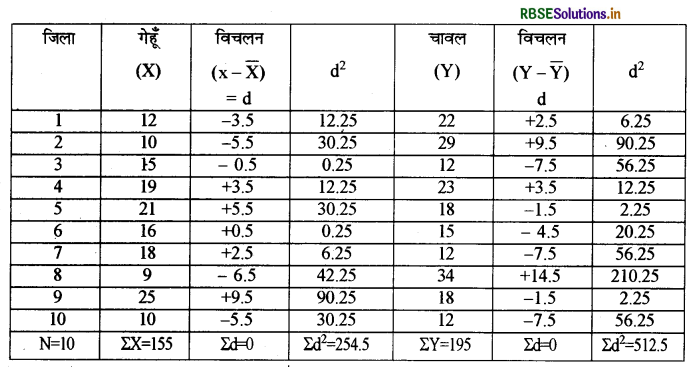
गेहूँ का समान्तर माध्य 
\(=\frac{\Sigma X}{N}=\frac{155}{10}=15.5\)
गेहूँ का मानक विचलन
\(\begin{aligned} \sigma &=\sqrt{\frac{\Sigma \mathrm{d}^{2}}{\mathrm{~N}}} \\ &=\sqrt{\frac{2545}{10}} \\ &=\sqrt{25.45} \\ &=5.04 \end{aligned}\)

चावल का समान्तर माध्य
\(\frac{\Sigma Y}{N}=\frac{195}{10}=19.5\)
चावल का मानक विचलन
\(\begin{aligned} \sigma &=\sqrt{\frac{\Sigma \mathrm{d}^{2}}{\mathrm{~N}}} \\ &=\sqrt{\frac{512.5}{10}} \\ &=\sqrt{51.25} \\ &=7.16 \end{aligned}\)

(च) किस फसल में अधिक विचरण है? 

\(\begin{aligned} &=\frac{5.04}{15.5} \times 100 \\ &=\frac{504}{15.5}=32.52 \end{aligned}\)
चावल का विचरण गुणांक 
\(\begin{aligned} &=\frac{\sigma}{\bar{X}} \times 100 \\ &=\frac{7.16}{19.5} \times 100 \\ &=\frac{716}{19.5}=36.72 \end{aligned}\)

अत: चावल का विचरण गुणांक अधिक है।
(छ) प्रत्येक फसल के लिए विभिन्न मापकों के मानों की तुलना

1. परास - गेहूँ की फसल का परास 16 है तथा चावल की फसल का परास 22 है। अतः चावल की फसल का परास अधिक है।
2. चतुर्थक विचलन - गेहूँ की फसल का चतुर्थक विचलन 4.75 है जबकि चावल की फसल का चतुर्थक विचलन 6.25 है। अतः चावल की फसल का चतुर्थक विचलन अधिक है।
3. माध्य से माध्य विचलन - गेहूँ की फसल का माध्य से माध्य विचलन 43 है जबकि चावल की फसल का माध्य से माध्य विचलन 6 है अतः चावल की फसल का माध्य से माध्य विचलन अधिक है।
4. मध्यिका से माध्य विचलन - गेहूँ की फसल का मध्यिका से माध्य विचलन 43 है जबकि चावल की फसल का मध्यिका से माध्य विचलन 5.7 है। अत: चावल की फसल का मध्यिका से माध्य विचलन अधिक है।
5.  मानक विचलन - गेहूं की फसल का मानक विचलन 5.04 है जबकि चावल की फसल का मानक विचलन 7.16 है। अतः चावल की फसल का मानक विचलन अधिक है।
6. विचरण गुणांक - गेहूँ की फसल का विचरण गुणांक 3252 है जबकि चावल की फसल का विचरण गुणांक 36.72 है। अतः चावल की फसल का विचरण गुणांक अधिक है।

प्रश्न 6. 
पूर्ववर्ती प्रश्न में विचरण के सापेक्ष मापों को परिकलित कीजिए और वह मान बताइए जो आपके विचार में सर्वाधिक विश्वसनीय हो।
उत्तर:
(क) विस्तार अथवा परास गुणांक
विस्तार अथवा परास गुणांक = \(\frac{L-S}{L+S}\)
(i) गेहूँ का परास गुणांक
L = 25, S = 9
परास गुणांक = \(\frac{25-9}{25+9}=\frac{16}{34}=0.47\)

(ii) चावल का परास गुणांक
L = 34, S = 12
परास गुणांक = \(\frac{34-12}{34+12}=\frac{22}{46}=0.48\)

(ख) चतुर्थक विचलन गुणांक
चतुर्थक विचलन गुणांक का सूत्र = \(\frac{Q_{3}-Q_{1}}{Q_{3}+Q_{1}}\)
(i) गेहूं की फसल का चतुर्थक विचलन गुणांक
\(=\frac{19.5-10}{19.5+10}=\frac{9.5}{29.5}\) = 0.34

(ii) चावल की फसल का चतुर्थक विचलन गुणांक
\(=\frac{24.5-12}{24.5+12}=\frac{12.5}{36.5}=0.34\)

(ग) माध्य से माध्य विचलन गुणांक
\(\frac{\text { M.D. }(\overline{\mathrm{X}})}{\overline{\mathrm{X}}}\)

(i) गेहूँ की फसल का माध्य से माध्य विचलन गुणांक
\(=\frac{\text { M. } D_{\cdot(\bar{X})}}{\bar{X}}=\frac{4.3}{15.5}=0.28\)

(ii) चावल की फसल का माध्य से माध्य विचलन
\(=\frac{\text { M. } D_{\cdot}(\bar{X})}{\bar{X}}=\frac{6}{19.5}=0.31\)

 (घ) मध्यिका से माध्य विचलन गुणांक
\(\frac{\text { M.D. }(\overline{\mathrm{X}})}{\overline{\mathrm{X}}}\)

(i) गेहूं की फसल के लिए माध्य विचलन गुणांक
\(=\frac{4.3}{15.5}=0.28\)

(ii) चावल की फसल के लिए माध्य विचलन

\(=\frac{5.7}{18}=0.32\)

(ङ) मानक विचलन से विचरण गुणांक
\(=\frac{\sigma}{\overline{\mathrm{X}}} \times 100\)
(i) गेहूँ की फसल के लिए विचरण गुणांक
\(=\frac{5.04}{15.5} \times 100=32.52\)

(ii) चावल की फसल के लिए विचरण गुणांक

\(=\frac{7.16}{19.5} \times 100=36.72\)
उपर्युक्त सभी मानकों में मानक विचलन से विचरण

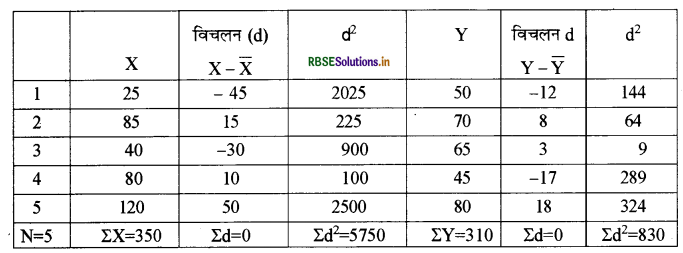
 श्रेणी का समान्तर माध्य
\(\begin{aligned} \bar{X} &=\frac{\Sigma \mathbf{X}}{\mathrm{N}} \\ &=\frac{350}{5}=70 \end{aligned}\)
मानक विचलन \(\sqrt{\frac{\Sigma \mathrm{d}^{2}}{\mathrm{n}}}\)
\(\sigma_{\mathrm{X}}=\sqrt{\frac{5750}{5}}=33.91\)
 विचरण गुणांक = \(\frac{\sigma}{\bar{X}} \times 100\)
\(\begin{aligned} &=\frac{33.91}{70} \times 100 \\ &=48.44 \% \end{aligned}\)

प्रश्न 7. 
किसी क्रिकेट टीम के लिए एक बल्लेबाज का चयन करना है। यह चयन x और के बीच पाँच पूर्ववर्ती टेस्टों के स्कोर के आधार पर करना है, जो निम्नवत् है

किस बल्लेबाज को टीम में चुना जाना चाहिए? 
(क) अधिक रन स्कोर करने वाले को या 
(ख) अधिक भरोसेमंद बल्लेबाज को।
उत्तर:
इस प्रश्न के उत्तर हेतु हमें समान्तर माध्य तथा मानक विचलन से विचरण गुणांक की गणना करनी होगी जो निम्न प्रकार है
Y श्रेणी का समान्तर माध्य
\(\overline{\mathbf{Y}}=\frac{\Sigma \mathbf{Y}}{\mathbf{N}}\)
\(=\frac{310}{5}=62\)
मानक विचलन = \(\sqrt{\frac{\Sigma \mathrm{d}^{2}}{n}}\)
\(\sigma_{Y}=\sqrt{\frac{830}{5}}=12.88\)
विचरण गुणांक \(=\frac{\sigma}{\bar{Y}} \times 100\)
\(\begin{aligned} &=\frac{12.88}{62} \times 100 \\ &=20.77 \% \end{aligned}\)

(क) यदि अधिक रन बनाने वाले बल्लेबाज का चुनाव करना हो तो हमें X का चुनाव करना होगा क्योंकि इसका समान्तर माध्य Y से अधिक है।

(ख) यदि हमें अधिक भरोसेमंद बल्लेबाज का चुनाव करना हो तो बल्लेबाज Y का चुनाव करना होगा क्योंकि बल्लेबाज Y का विचरण गुणांक कम है जो अधिक संगतता को दर्शाता है।

प्रश्न 8. 
दो ब्रांडों के बल्बों की गुणवत्ता जांचने के लिए, ज्वलन अवधि घंटों में उनके जीवनकाल को, प्रत्येक ब्रांड के 100 बल्बों के आधार पर निम्नानुसार अनुमानित किया गया है।

जीवन काल (घण्टों में)	बल्बों की संख्या
	ब्रांड क	ब्रांड ख
0 – 50 50 -100 100 – 150 150 -200 200 – 250	15 20 18 25 22	2 8 60 25 2
	100	100

उत्तर:

इस प्रश्न को हल करने हेतु समान्तर माध्य, मानक विचलन तथा विचरण गुणांक निकालना होगा।

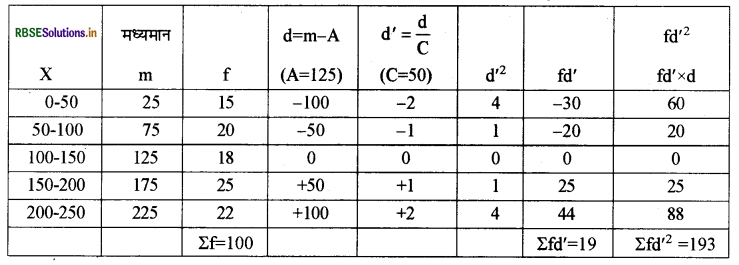समान्तर माध्य
\(\begin{aligned} &=\mathrm{A}+\frac{\Sigma \mathrm{fd}^{\prime}}{\Sigma \mathrm{f}} \times \mathrm{C} \\ &=125+\frac{19}{100} \times 50 \\ &=125+9.5=134.5 \end{aligned}\)

मानक विचलन 

\(\begin{aligned} &=\sqrt{\frac{\Sigma \mathrm{fd}^{\prime 2}}{\Sigma \mathrm{f}}-\left(\frac{\Sigma \mathrm{fd}^{\prime}}{\Sigma \mathrm{f}}\right)^{2}} \times \mathrm{C} \\ &=\sqrt{\frac{193}{100}-\left(\frac{19}{100}\right)^{2}} \times 50 \\ &=\sqrt{1.93-0.0361} \times 50 \end{aligned}\)

= 13.76 x 50 = 68.81

विचरण गुणांक 
\(=\frac{\sigma}{\bar{X}} \times 100=\frac{68.81}{134.5} \times 100=51.16\)

अतः (क) ब्रांड 'ख' का जीवनकाल अधिक है क्योंकि ब्रांड 'ख' का समान्तर माध्य 'क' से अधिक है।

(ख) ब्रांड 'ख' बल्ब अधिक भरोसेमंद है क्योंकि इसका विचरण गुणांक 'क' से कम है जो कि अधिक संगतता को दर्शाता है।

प्रश्न 9. 
एक कारखाने के 50 मजदूरों की औसत दैनिक मजदूरी 200 रुपये तथा मानक विचलन 40 रुपये था। प्रत्येक मजदूर की मजदूरी में 20 रुपये की वृद्धि की गई। अब मजदूरों की औसत दैनिक मजदूरी एवं मानक विचलन क्या है? क्या मजदूरी में समानता आई है? 
उत्तर:
प्रश्नानुसार N = 50
\(\begin{aligned} &\bar{X}=200 \\ &\sigma=40 \end{aligned}\)
मजदूरी में वृद्धि से पूर्व की कुल मजदूरी
\(\begin{aligned} &\bar{X}=\frac{\Sigma X}{N} \\ &\Sigma X=\bar{X} \times N \end{aligned}\)
= 50 X 20 = 10,000
मजदूरी में वृद्धि = 50 X 20 = 100
अतः मजदूरी में वृद्धि के पश्चात् कुल मजदूरी
= 10,000+ 1000
= 11,000 
वृद्धि के पश्चात् समान्तर माध्य \(\bar{X}=\frac{\Sigma X}{N}\)
\(=\frac{11000}{50}=220\)
वृद्धि से पूर्व का विचरण गुणांक \(=\frac{\sigma}{\bar{X}} \times 100\)
\(\text { C.V. }=\frac{40}{200} \times 100=20\)

वृद्धि के पश्चात् का विचरण गुणांक
\(\text { C. V. }=\frac{\sigma}{\overline{\mathbf{X}}} \times 100\)
यहाँ C.V. = 20, X = 220 दिया हुआ है अतः   σ = ?
\(20=\frac{\sigma}{220} \times 100\)
\(\begin{aligned} 100 \sigma &=4400 \\ \sigma &=\frac{4400}{100}=44 \end{aligned}\)

प्रश्न 10. 
पूर्ववर्ती प्रश्न में यदि प्रत्येक मजदूर की मजदूरी में 10% की वृद्धि की जाए तो माध्य एवं मानक विचलन पर क्या प्रभाव पड़ेगा?
उत्तर:
पूर्ववर्ती प्रश्न में मजदूरों की संख्या = 50 है औसत दैनिक मजदूरी = 200 रुपये है।
औसत दैनिक मजदूरी में 10 प्रतिशत वृद्धि का तात्पर्य है।
\(\begin{aligned} &=200+\frac{200 \times 10}{100} \\ &=200+20 \\ &=220 \end{aligned}\)

हमने पूर्व प्रश्न में भी 20 रुपये वृद्धि के पश्चात् औसत मजदूरी 220 के आधार पर माध्य एवं मानक विचलन निकाला था तथा इस प्रश्न में भी औसत दैनिक मजदूरी 220 के आधार पर माध्य एवं मानक विचलन निकालेंगे तो दोनों मान पूर्व प्रश्न के समान अर्थात् X = 220 व = 44 ही आएगा।