RBSE Solutions for Class 11 Economics Chapter 5 केंद्रीय प्रवृत्ति की माप

Rajasthan Board RBSE Solutions for Class 11 Economics Chapter 5 केंद्रीय प्रवृत्ति की माप Textbook Exercise Questions and Answers.

RBSE Class 11 Economics Solutions Chapter 5 केंद्रीय प्रवृत्ति की माप

RBSE Class 11 Economics केंद्रीय प्रवृत्ति की माप InText Questions and Answers

पृष्ठ: 62.

प्रश्न 1. 
पद विचलन तथा कल्पित माध्य विधि का प्रयोग करते हुए उदाहरण - 3 में दिए गए आंकड़ों के लिए जोत का माध्य आकार ज्ञात करें।
उदाहरण 3. एक आवासीय कॉलोनी में भूखण्ड केवल तीन आकारों में मिलते हैं: 100 वर्ग मीटर, 200 वर्ग मीटर एवं 300 वर्ग मीटर तथा भूखण्डों की संख्या क्रमश: 200, 50 एवं 10 है। 
उत्तर:
कल्पित माध्य विधि से माध्य की गणना सारणी 

भूखण्डों का आकार (X)	भूखण्डों की संख्या (f)	कल्पित माध्य  (A =200)	Fd (f x d)
100	200	- 100	- 20000
200	50	0	0
300	10	+ 100	1000
	∑ f = 260	∑ d = 0	∑ d = - 1500

समान्तर माध्य
  \( \begin{aligned} (\bar{X}) &=A+\frac{\sum f d}{\Sigma f} \\ &=200+\frac{-19000}{260} \\ &=200-73.08 \\ &=126.92 \end{aligned} \)
 

नोट - पद विचलन विधि में विचलनों को समापवर्तक C द्वारा विभाजित किया जाता है अर्थात् d को वर्ग विस्तार अथवा समापवर्तक C द्वारा विभाजित किया जाता है, जिससे परिकलन को सरल बनाया जाता है। उदाहरण 3 में कल्पित माध्य विधि द्वारा कल्पित माध्य से विचलन काफी सरल आ रहा है अतः उसे अधिक आसान बनाने की जरूरत नहीं है, अतः यहाँ पद - विचलन रीति की कोई आवश्यकता नहीं है।

 

पृष्ठ: 64

प्रश्न 2. 
(क) निम्नलिखित उदाहरण से समान्तर माध्य की उपर्युक्त विशेषता की जाँच करें:
x : 4 6 8 10 12
(ख) उपर्युक्त उदाहरण में यदि माध्य के मूल्य में 2 की वृद्धि की जाए, तब व्यष्टिगत प्रेक्षणों में क्या परिवर्तन होता है?
(ग) यदि पहले तीन मदों में 2 की वृद्धि होती है, तब बाद के दो मदों का मान क्या होना चाहिए, ताकि माध्य पूर्ववत् बना रहे।
(घ) यदि मान 12 के स्थान पर 96 का प्रयोग करें, तब समान्तर माध्य क्या होगा? टिप्पणी करें। 
उत्तर:
(क) समान्तर माध्य की रोचक विशेषता

\(\Sigma(\mathbf{X}-\overline{\mathbf{X}})=0\)

अर्थात् समान्तर माध्य से मदों के विचल ∵ का जोड़ सदैव शून्य होता है।
सर्वप्रथम समान्तर माध्य \((\overline{\mathrm{X}})\) ज्ञात करेंगे।
x = 4 6 8 10 12

∑X = 4 + 6 + 8 + 10 + 12
N = 5
\(\overline{\mathrm{X}}=\frac{\sum \mathrm{X}}{\mathrm{N}}=\frac{40}{5}=8\)

समान्तर माध्य की विशेषता की जाँच:

X	\(X-\bar{X}\)
4	4 – 8 = 4
6	6 – 8 = 2
7	8 – 8 = 0
8	10 – 8 = 2
9	12 – 8 = 4
12	\(\Sigma(\mathbf{X}-\mathbf{X})=0\)

(ख) यदि सभी माध्य के मूल्य में 2 जोड़ा जाए तो \((\overline{\mathrm{X}})\) का मान निम्न प्रकार होगा:
X = 6 8 10 12
∑ X = 6 + 8 + 10 + 12 + 14 = 50
N = 5
\(\overline{\mathrm{X}}=\frac{\Sigma \mathrm{X}}{\mathrm{N}}=\frac{50}{5}=10\)

संमान्तर माध्य की विशेषता की जाँच:
​

X	\(X-\bar{X}\)
4	4 – 8 = 4
6	6 – 8 = 2
7	8 – 8 = 0
8	10 – 8 = 2
9	12 – 8 = 4
12	\(\Sigma(\mathbf{X}-\mathbf{X})=0\)

​
(ग) X = 4 6 8 10 12
∑X = 4 + 6 + 8 + 10 + 12 = 40
N = 5
\(\bar{X}=\frac{\Sigma X}{N}=\frac{40}{5}=8\)
यदि X की पहली तीन मदों में 2 जोड़ा जाए तथा बाद की दोनों मदों में से हमें कोई मान y घटाना पड़ेगा ताकि \((\overline{\mathrm{X}})\) = 8 समान रहे, अतः y का मान निम्न प्रकार निकालेंगे:
X = 4+2 6+2 8+2 10-Y 12-Y
∑X = 6+8+10+10-Y+12-Y
= 46 - 2Y
\(\overline{\mathrm{X}}=\frac{\Sigma \mathrm{X}}{\mathrm{N}}\)
\(​​​​​​​8=\frac{46-2 y}{5}\)

46 - 2Y = 40
- 2Y = 40 -46
2Y = 6
Y = 3
अतः बाद की दोनों संख्याओं का मान 10 - 3 = 7 तथा 12 - 3 = 9 होगा।

(घ) यदि मदों में 12 के स्थान पर 96 हो तो समान्तर माध्य निम्न प्रकार निकाला जाएग।
X = 4 6 8 10 96
∑X = 4 + 6 + 8 + 10 + 96 = 124
N = 5
\(\bar{X}=\frac{\Sigma X}{N}=\frac{124}{5}=24.8\)

प्रश्न 3. 
शृंखला के सभी चारों मानों के लिए समान्तर माध्य एवं मध्यिका ज्ञात करें। आप क्या देखते हैं?
सारणी
विभिन्न शृंखलाओं के समान्तर माध्य एवं मध्यिका

श्रृखलाएँ	X (चर मान)	समान्तर	माध्य मध्यिका
(क) (ख) (ग) (घ)	1, 2, 3 1, 2, 30 1, 2, 300 1, 2, 3000	? ? ? ?	? ? ? ?

उत्तर:
(क) X = 1, 2, 3
समान्तर माध्य \(=\frac{\Sigma \mathrm{X}}{\mathrm{N}}=\frac{1+2+3}{3}=\frac{6}{3}=2\)
मध्यिका = \(\left(\frac{\mathrm{N}+1}{2}\right)\) वें पद का मूल्य
\(=\left(\frac{3+1}{2}\right)\) वाँ पद
= 4/2 वाँ पद  = 2  पद
= 2

(ख) \(\mathrm{X}=1,2,30\)
समान्तर माध्य का मूल्य \(=\frac{\Sigma X}{N}\)

\(=\frac{1+2+3000}{3}=\frac{3003}{3}=1001\)
माध्य का मूल्य \(=\left(\frac{N+1}{2}\right)\) वाँ पद
\(=\left(\frac{3+1}{2}\right)\)  वाँ पद = 2पद
मध्यिका = 2

(ग) \(\mathrm{X}=1,2,30\)
समान्तर माध्य का मूल्य \(=\frac{\Sigma X}{N}\)
\(=\frac{1+2+3000}{3}=\frac{3003}{3}=1001\)
माध्य का मूल्य \(=\left(\frac{N+1}{2}\right)\) वाँ पद
\(=\left(\frac{3+1}{2}\right)\) वाँ पद = 2पद
मध्यिका = 2

RBSE Class 11 Economics केंद्रीय प्रवृत्ति की माप Textbook Questions and Answers

प्रश्न 1. 
निम्नलिखित स्थितियों में कौनसा औसत उपयुक्त होगा?
(क) तैयार वस्त्रों के औसत आकार।
(ख) एक कक्षा में छात्रों की औसत बौद्धिक प्रतिभा।
(ग) एक कारखाने में प्रति पाली औसत उत्पादन ।
(घ) एक कारखाने में औसत मजदूरी।
(ङ) जब औसत से निरपेक्ष विचलनों का योग न्यूनतम हो।
(च) जब चरों की मात्रा अनुपात में हो।
(छ) मुक्तांत बारम्बारता बंटन के मामले में।
उत्तर:
(क) बहुलक
(ख) मध्यिका
(ग) समान्तर माध्य
(घ) समान्तर माध्य
(ङ) समान्तर माध्य
(च) मध्यिका
(छ) मध्यिका।

प्रश्न 2.
प्रत्येक प्रश्न के सामने दिए गए बहुविकल्पों में से सर्वाधिक उचित विकल्प को चिह्नित करें:
(i) गुणात्मक मापन के लिए सर्वाधिक उपयुक्त औसत है:
(क) समान्तर माध्य
(ख) मध्यिका
(ग) बहुलक
(घ) ज्यामितीय माध्य
(ङ) उपर्युक्त में से कोई नहीं।

(ii) चरम पदों की उपस्थिति से कौनसा औसत सर्वाधिक प्र भावित होता है:
(क) मध्यिका
(ख) बहुलक
(ग) समान्तर माध्य
(घ) उपर्युक्त में से कोई नहीं

(iii) समान्तर माध्य से मूल्यों के किसी समुच्चय के विचलन का बीजगणितीय योग है:
(क) द
(ख) 0
(ग) 1
(घ) उपर्युक्त कोई भी नहीं।
उत्तर:
(i) (ख)
(ii) (ग)
(iii) (ख)

प्रश्न 3. 
बताइए कि निम्नलिखित कथन सही है या गलत-
(क) मध्यिका से मदों के विचलनों का योग्य शून्य होता है।
(ख) श्रृंखलाओं की तुलना के लिए मात्र औसत ही पर्याप्त नहीं है।
(ग) समान्तर माध्य एक स्थैतिक मूल्य है।
(घ) उच्च चतुर्थक शीर्ष 25 प्रतिशत मदों का निम्नतम मान है।
(ङ) मध्यिका चरम प्रेक्षणों द्वारा अनुचित रूप से प्रभावित होती है।
उत्तर:
(क) गलत  
(ख) सही 
(ग) गलत
(घ) सही 
(ङ) गलत।

प्रश्न 4. 
यदि नीचे दिए गए आँकड़ों का समान्तर माध्य 28 है, तो 
( क) लुप्त आवृत्ति का पता करें, और 
(ख ) शृंखला की मध्यिका ज्ञात करें।
प्रति खुदरा 0 - 10 10 -20 20 -30 30 - 40 40 -50 50 - 60

उत्तर:
( क ) लुप्त आवृत्ति का पता लगानासारणी

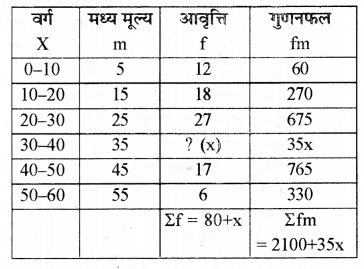
\(\begin{aligned} \bar{X} &=\frac{\sum f m}{\Sigma f} \\ 28 &=\frac{2100+35 x}{80+x} \end{aligned}\)
2240 + 28X = 2100 + 35X
2240 - 2100 = 35X - 28X
7X = 140
X = 140/7
X = 20
अतः अज्ञात आवृत्ति का मूल्य = 20

(ख) शृंखला की मधियिका:

प्रति खुदरा दुकान लाभ	खुदरा दुकानों की संख्या (f)	संचयी बारम्बारता
0 – 10	12	12
10 – 20	18	30 (c.f)
20 – 30	27 (f)	57
30 – 40	20	77
40 – 50	17	94
50 - 60	6	100
	\(\Sigma f \text { or } \mathrm{N}=100\)

सर्वप्रथम मध्यिका वर्ग निकालेंगे:
मध्यिका वर्ग = \(\left(\frac{\mathrm{N}}{2}\right)\) वाँ मद
मध्यिका = \(\left(\frac{100}{2}\right)\) वाँ मद  = 50 वाँ मद
50 वीं मध्यिका मद ऊपर से संचयी आवृत्ति (c.f.) 57 में आता है, अतः उसके सामने वाला वर्ग 20 - 30 मध्यिका वर्ग होगा।
मध्यिका का मूल्य = \(\mathrm{L}+\frac{\left(\frac{N}{2}-\text { c.f. }\right)}{\mathrm{f}} \times \mathrm{h}\)
यहाँ L = 20 N/2 = 50 c.f = 30 f = 27 एवं  h = 20 
\(\begin{aligned} &=20+\frac{50-30}{27} \times 10 \\ &=20+\frac{20}{27} \times 10 \end{aligned}\)
= 20  + 7.04
= 27.074
= 27. 401

प्रश्न 5. 
निम्नलिखित सारणी में एक कारखाने के 10 मजदूरों की दैनिक आय दी गई है। इनका समान्तर माध्य ज्ञात कीजिए।

उत्तर:
समान्तर माध्य की गणना
\(​​​​​​​\overline{\mathbf{X}}=\frac{\sum \mathbf{X}}{\mathrm{N}}\)

\(\Sigma \bar{X}\) = 120 + 150 + 180 + 200 + 250 + 300 + 220 + 350 + 370 + 450
\(\begin{aligned} \Sigma \bar{X} &=2,400 \\ N &=10 \\ \bar{X} &=\frac{2400}{10}=240 \end{aligned}\)

प्रश्न 6. 
निम्नलिखित सूचना 150 परिवारों की दैनिक आय से सम्बद्ध है। समान्तर माध्य का परिकलन कीजिए।

आय (रु. में)	परिवारों की संख्या
75 से अधिक	150
85	140
95	115
105	95
115	70
125	60
135	45
145	40
150	25

उत्तर:
सर्वप्रथम हम वर्ग एवं आवृत्तियों की गणना करेंगे:

आय (रु. में)	परिवारों की संख्या
75 से अधिक	150 – 140 = 10
85 - 95	140 – 115 = 25
95-105	115 – 95 = 20
105-115	95 – 70 = 25
115-125	70 – 60 = 10
125-135	60 – 45 = 15
135-145	45 – 40 = 20
145-155	40 – 25 = 10
155 - 160	25 – 0 = 25

प्रत्यक्ष विधि के द्वारा समान्तर माध्य की गणना:
\(\begin{aligned} \overline{\mathrm{X}} &=\frac{\Sigma \mathrm{fm}}{\Sigma \mathrm{f}} \\ &=\frac{17450}{150} \end{aligned}\)

= 116.33

प्रश्न 7. 
नीचे एक गाँव के 380 परिवारों की जोतों का आकार दिया गया है। जोत का मध्यिका आकार ज्ञात कीजिए।
जोतों का आकार (एकड़ में ) 100 से कम 100 - 200 200 - 300 300 - 400 400 तथा उससे अधिक परिवारों की संख्या 40 
उत्तर:
मध्यिका की गणना:

जोतों का आकार (एकड़ में )	परिवारों की संख्या (f)	संचयी आवृत्ति (c.f.)
0 - 100	40	40
100 - 200	89	129
200 - 300	148	277
300 - 400	64	341
400 - 500	39	380
	N = 380

सर्वप्रथम मध्यिका वर्ग की गणना करेंगे, जो निम्न प्रकार है:
मध्यिका वर्ग = \(=\left(\frac{N}{2}\right)\)वाँ मद
\(=\left(\frac{380}{2}\right) \text { }=190 \text { }\)
190 वाँ मद ऊपर से संचयी आवृत्ति में 277 के अन्तर्गत आता है, अतः इसके सामने वाला मध्यिका वर्ग 200 - 300 होगा।
मध्यिका = \(\mathbf{L}+\frac{\left(\frac{N}{2}-\text { c.f. }\right)}{f} \times h\)
यहाँ  L = 200 N/2 = 190 c.f = 129 
\(\begin{aligned} &=200+\frac{190-129}{148} \times 100 \\ &=200+\frac{61}{148} \times 100 \end{aligned}\)
= 200 + 41.22
= 21.42

प्रश्न 8.
निम्न शृंखला किसी कम्पनी में नियोजित मजदूरों की दैनिक आय से सम्बद्ध है। अभिकलन कीजिए:
(क) निम्नतम 50 प्रतिशत मजदूरों की उच्चतम आय
(ख) शीर्ष 25 प्रतिशत मजदूरों द्वारा अर्जित न्यूनतम आय और
(ग) निम्नतम 25 प्रतिशत मजदूरों द्वारा अर्जित अधिकतम आय।

उत्तर:
सर्वप्रथम समायोजित वर्गान्तराल बनाएँगे।

आय	कर्मचारी (f)	संचयी आवृत्ति (c.f.)
9.5 - 14.5	5	40
14.5 - 19.5	10	129
19.5 - 24.5	15	277
24.5 - 29.5	20	341
29.5 - 30.5	10	380
	N = 35

(क) 
निम्नतम 50 प्रतिशत मजदूरों की उच्चतम आय ज्ञात करने का तात्पर्य है मध्यिका की गणना करनाअतः सर्वप्रथम मध्यिका वर्ग की गणना की जाएगी
मध्यिका वर्ग \(=\left(\frac{N}{2}\right)\) वाँ मद
\(=\frac{65}{2} \text { }=32.5 \text { }\)
32.5 वाँ मद ऊपर से संचयी आवृत्ति 50 में आएगा तथा इसके सामने का वर्ग 24.5 - 29.5
मध्यिका = \(=L+\frac{\left(\frac{N}{2}-c . f .\right)}{f} \times h\)

\(\begin{aligned} &=24.5+\frac{32.5-30}{20} \times 5 \\ &=24.5+\frac{2.5}{20} \times 5 \\ &=24.5+\frac{12.5}{20}=24.5+0.625 \end{aligned}\)

= 21.25

(ख) शीर्ष 25 प्रतिशत मजदूरों द्वारा अर्जित न्यूनतम आय ज्ञात करने हेतु निम्न चतुर्थक अर्थात् Q₁ की गणना की जाएगी। इस हेतु सर्वप्रथम Q₁ का वर्ग ज्ञात होगा जो निम्न प्रकार ज्ञात होगा:
\(=\left(\frac{\mathrm{N}}{4}\right)\)वाँ मद
= 64 / 4 वाँ मद

16.25 वाँ मद संचयी आवृत्ति में ऊपर से 30 के अन्तर्गत शामिल होगा तथा इसके सामने का वर्ग अर्थात् 19.5 - 24.5 निम्न चतुर्थक का वर्ग होगा। अब हम  Q₁ की गणना करेंगे।
\(Q_{1}=L+\frac{\left(\frac{N}{4}-c . f .\right)}{f} \times h\)

\(\begin{aligned} &=19.5+\frac{16.25-15}{15} \times 5 \\ &=19.5+\frac{1.25}{15} \times 5 \\ &=19.5+\frac{6.25}{15} \end{aligned}\)

= 19.5 + 0.42 
= 19.92 

(ग) निम्नतम 25 प्रतिशत मजदूरों द्वारा अर्जित अधिकतम आय ज्ञात करने हेतु उच्च चतुर्थक अर्थात् Q3  की गणना की जाएगी। इस हुतु सर्वप्रथम उच्च चतुर्थक का वर्ग ज्ञात करना होगा जो निम्न प्रकार है।

\(=\frac{3(\mathrm{~N})}{4}\)  वाँ मद

\(=\frac{3(65)}{4}\) वाँ मद
= 195 / 4 वाँ मद = 48.75 वाँ मद
49.5 वाँ मद संचयी आवृत्ति में ऊपर से 50 के अन्तर्गत आएगा अतः इसके सामने वाला वर्ग 24.5 का वर्ग होगा। अब Q₃  की गणना की जाएगी:
\(\begin{aligned} Q_{3} &=L+\frac{\left(\frac{3 N}{4}-\text { c.f. }\right)}{f} \times h \\ &=24.5+\frac{(48.75-30)}{20} \times 5 \end{aligned}\)

= 24.5 + 4.65
= 29.19

प्रश्न 9. 
निम्न सारणी में किसी गाँव के 150 खेतों में गेहूँ की प्रति हेक्टेयर पैदावार दी गई है। समान्तर माध्य, मध्यिका तथा बहुलक के मान की गणना कीजिए। उत्पादित फसल ( प्रति हैक्टेयर कि.ग्रा. में )
50 - 53 53 - 56 56 - 59 59 - 62 62 - 65 65 - 68 68 - 71 71 - 74 74 - 77

उत्तर:
समान्तर माध्य की गणना ( प्रत्यक्ष विधि द्वारा)


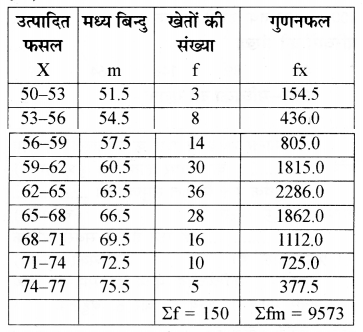
समान्तर माध्य अर्थात् 
\(​​​​​​​\begin{aligned} &=\frac{\Sigma \mathrm{fm}}{\Sigma \mathrm{f}} \\ &=\frac{9573}{150} \end{aligned}\)
= 63.82 किग्रा. प्रति हैक्टेयर
(नोट-अधिक सरलता से समान्तर माध्य ज्ञात करने हेतु कल्पित माध्य रीति का उपयोग भी कर सकते हैं)
मध्यिका की गणना एवं बहलक की गणना:

उत्पादित फसल x	खेतों की संख्या (f)	संचयी आवृत्ति (c.f.)
50 - 53	3	3
53 - 56	8	11
56 - 59	14	25
59 - 60	30	55
60 - 71	36	380
71 - 74	5	91
74 - 77	N = 150	150

मध्यिका की गणना: मध्यिका की गणना करने हेतु सर्वप्रथम हमें मध्यिका वर्ग का पता लगाना है, जो निम्न प्रकार है:
\(=\left(\frac{\mathrm{N}}{2}\right)\)वाँ मद
= 150/2 वाँ मद
= 75 वाँ मद

75 वाँ मद संचयी आवृत्ति में ऊपर से 91 के अन्तर्गत आएगा अतः इसके सामने वाला वर्ग 62 - 65 मध्यिका वर्ग होगा। इसके आधार पर मध्यिका की गणना निम्न प्रकार होगी