RBSE Solutions for Class 11 Economics Chapter 5 Measures of Central Tendency

Rajasthan Board RBSE Solutions for Class 11 Economics Chapter 5 Measures of Central TendencyTextbook Exercise Questions and Answers.

RBSE Class 11 Economics Solutions Chapter 5 Measures of Central Tendency

RBSE Class 11 Economics Measures of Central Tendency Textbook Questions and Answers

1. Which average would be suitable in the following cases

(i) Average size of ready made garments
(ii) Average intelligence of students in a class
(iii) Average production in a factory per shift
(iv) Average wages in an industrial concern
(v) When the sum of absolute deviations from average is least
(vi) When quantities of the variable are in ratios
(vii) In case of open-ended frequency distribution
Answer:
(i) Mode 
(ii) Median 
(iii) Mean 
(iv) Mean
(v) Mean 
(vi) Median 
(vii) Median

2. Indicate the most appropriate alternative from the multiple choices provided against each question.

(i) The most suitable average for qualitative measurement is:
(a) arithmetic mean 
(b) median 
(c) mode
(d) geometric mean 
(e) none of the above
Answer:
(c) The most suitable average for qualitative measurement is mode.

(ii) Which average is affected most by the presence of extreme items?
(a) median 
(b) mode
(c) arithmetic mean 
(d) none of the above
Answer:
(c) Arithmetic mean is most affected by the presence of extreme items.

(iii) The algebraic sum of deviation of a set of n values from AM. is:
(a) n 
(b) O
(c) I 
(d) none of the above
Answer:
(b) The algebraic sum of deviation of a set of n values from A.M.J O.

3. Comment whether the following statements are true or false.

(i) The sum of deviation of items from median is zero.
(ii) An average alone is not enough to compare series.
(iii) Arithmetic mean is a positional value.
(iv) Upper quartile is the lowest value of top 25% of items.
(v) Median is unduly affected by extreme observations.
Answer:
(i) False. The sum of deviation of items from mean is zero. Median is simple the middle-most value of the distribution.
(ii) True. An average alone is not enough to compare series as it hides disparity.
(iii) False. Arithmetic mean is a mathematical value. Median and mode are the positional values.
(iv) True. Upper quartile has 75% of items below it and 25% of items above it.
(v) False. Arithmetic mean, not median, is unduly affected by the presence of extreme items.
Median is a more appropriate measure for data containing extreme values.

Question 4. 
If the arithmetic mean of the data given below is 28. Find (a) the missing frequency and (b) the median of the series.

Answer:
(a) Mean is given as 28. Since it is a frequency distribution, we can solve it by direct method:

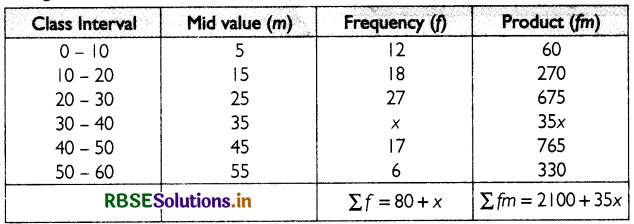
Mean can be calculated by using the formula given below:
\(\bar{x}=\frac{\sum f m}{\sum f}\) ................. (1)
Substituting the appropriate values in (I), we get:

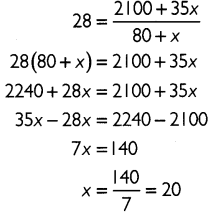
Thus, the missing frequency is 20.

(b) For calculating median, calculate the cumulative frequency for the data:

Thus, the median lies in the class 20 - 30. Median can be calculated by using the formula given below:

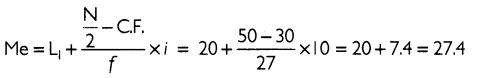
Thus, the median of the series is ₹ 27.4.

Question 5. 
The following table gives the daily income of ten workers in a factory. Find the arithmetic mean.

Answer: 
Arithmetic mean for the given data can be calculated as:

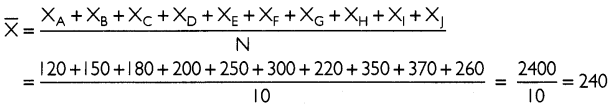
The arithmetic mean of the daily income of ten workers in a factory is ₹ 240. 

Question 6.
Following information pertains to the daily income of the daily income of 150 families.Calculate the arithemic mean:

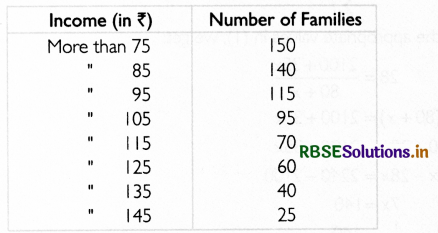
Answer:
First convert the given cumulative frequency series into simple frequency distribution.

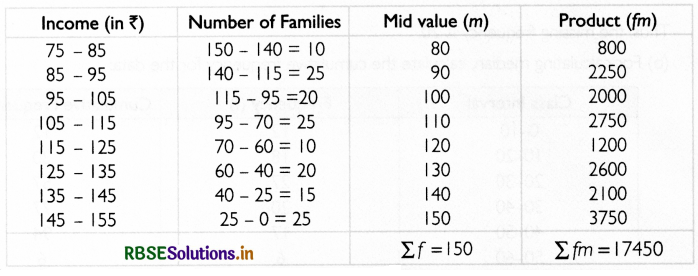
Mean can be calculated by using the formula given below:
\(\bar{x}=\frac{\sum f m}{\sum f}=\frac{17450}{150}=116.33\)
Thus, the arithmetic mean of the daily income of 150 families is ₹ 116.33.

Question 7.
The size of land holdings of 380 families in a village is given below. find the median size of land holdings.

Answer:
For calculating median, calculate the cumulative frequency for the data:

Thus, the median lies in the class 200 - 300.
Median can be calculated by using the formula given below:

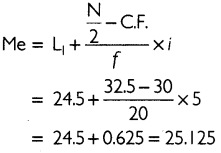
Thus, the median of the series is ₹ 241.22 acres.

Question 8. 
The following series relates to the daily income of workers employed in a firm. Compute
(a) highest income of lowest 50% workers
(b) minimum income earned by the top 25% workers and
(c) maximum income earned by lowest 25% workers.

Answer:
The given series is an inclusive series. Thus, it needs to be converted into exclusive series first as shown below:

(a) The highest income of lowest 50% workers can be determined through the median of the series.
Median = Size of \(\frac{N}{2}\) th item = \(\frac{65}{2}\) = 32.5 th item 
Thus, the median lies in the class 24.5 - 29.5.
Median can be calculated by using the formula given below:

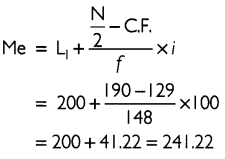
Thus, the highest income of lowest 50% workers is ₹ 25.125.

(b) The minimum income earned by the top 25% workers can be determined through the lower quartile (Q₁) of the series.
Q₁ = Size of \(\frac{N}{4}\)th item
= \(\frac{65}{4}\)= 16. 25 th item
Thus, the Q₁ lies in the class 19.5 - 24.5.
Q₁ can be calculated by using the formula given below:

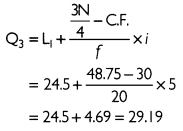
Thus, the minimum income earned by the top 25% workers is ₹ 19.92.

(c) The maximum income earned by lowest 25% workers can be determined through the lower quartile (Q₃) of the senes.

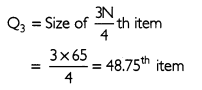
Thus, the Q₃ lies in the class 24.5 - 29.5. Q₃ can be calculated by using the formula given below:

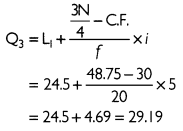
Thus, the maximum income earned by lowest 25% workers is  29.19.

Question 9. 
The following table gives production yield in kg per hectare of wheat of $50 farms in a village. Calculate the mean, median and mode production yield.

Answer:
Let A = 63.5

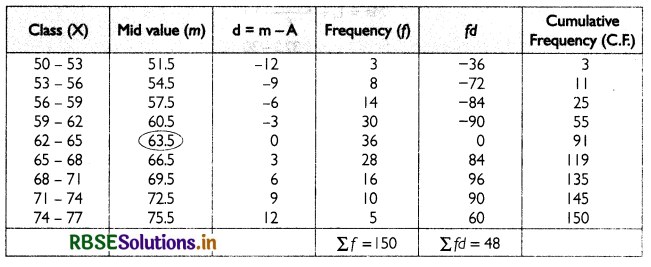
(a) Mean can be calculated by using the formula given below:

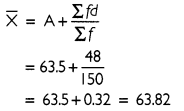
Thus, the arithmetic mean of production yield of wheat in a village is 63.82 kg per hectare. 

(b) Median can be calculated by using the formula given below:

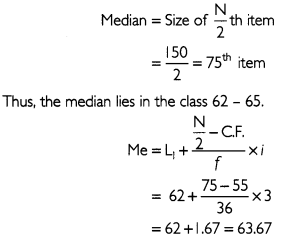
Thus, the median production yield of wheat in a village is 63.67 kg per hectare.

(c) The class with highest frequency, i.e. modal class, is 62 - 65. Mode can be calculated by using the formula given below:

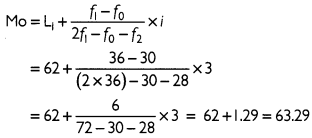
Thus, the mode of production yield of wheat in a village is 63.29 kg per hectare.