RBSE Solutions for Class 11 Economics Chapter 3 आँकड़ों का संगठन

Rajasthan Board RBSE Solutions for Class 11 Economics Chapter 3 आँकड़ों का संगठन Textbook Exercise Questions and Answers.

RBSE Class 11 Economics Solutions Chapter 3 आँकड़ों का संगठन

RBSE Class 11 Economics आँकड़ों का संगठन InText Questions and Answers

पृष्ठ: 26.

प्रश्न 1. 
उदाहरण - 1 में उस वर्ष को बताएं जिसमें भारत की जनसंख्या न्यूनतम और अधिकतम है।
उदाहरण - 1 
भारत की जनसंख्या:

वर्ष	जनसंख्या (करोड़ में )
1951	35.7
1961	43.8
1971	54.6
1981	68.4
1991	81.8
2001	102.7
2011	121.0

उत्तर:
उदाहरण - 1 के अनुसार - भारत की न्यूनतम जनसंख्या वर्ष 1951 में 35.7 करोड़ एवं अधिकतम जनसंख्या 2011 में 121 करोड़ है।

प्रश्न 2. 
उदाहरण 2 में, उस देश का पता लगाइये, जिसकी गेहूँ की उपज भारत से थोड़ी अधिक है। यह प्रतिशत में कितनी होगी?
उदाहरण - 2
विभिन्न देशों में गेहूँ की उपज (2013):

देश	गेहूँ की उपज ( किग्रा./एकड़ )
कनाडा	3594
चीन	5055
फ्रांस	7254
जर्मनी	7998
भारत	3154
पाकिस्तान	2787

उत्तर:
उदाहरण - 2 में विभिन्न देशों की प्रति एकड़ उपज दी गई है। भारत को गेहूँ की प्रति एकड़ उपज 3154 किग्रा. है। तालिका के अनुसार कनाडा की उपज भारत से थोड़ी-सी अधिक है। कनाडा की उपज भारत से कितने प्रतिशत अधिक है यह निम्न सूत्र द्वारा ज्ञात की ज सकती।

\(=\frac{3594-3154}{3154} \times 100=13.95 \%\)

प्रश्न 3. 
उदाहरण - 2 में दिए गए देशों को गेहूँ की उपज के आरोही क्रम में रखिए। ठीक यही अभ्यास उपज को अवरोही क्रम में रखते हुए कीजिए।
उदाहरण - 2 विभिन्न देशों में गेहूँ की उपज (2013) 

देश	गेहूँ की उपज ( किग्रा./एकड़ )
कनाडा	3594
चीन	5055
फ्रांस	7254
जर्मनी	7998
भारत	3154
पाकिस्तान	2787

उत्तर:
(i) विभिन्न देशों को गेहूँ की उपज के आधार पर आरोही क्रम (बढ़ता हुआ क्रम) में निम्न ' तालिका में दर्शाया गया है

देश	गेहूँ की उपज ( किग्रा./एकड़ )
पाकिस्तान	2787
भारत	3154
कनाडा	3594
चीन	5055
फ्रांस	7254
जर्मनी	7998

(ii) विभिन्न देशों को गेहूँ की उपज के आधार पर अवरोही क्रम (घटता हुआ क्रम) में निम्न तालिका में दर्शाया गया है

विभिन्न देशों में गेहूँ की उपज:

देश	गेहूँ की उपज (किग्रा./एकड़ )
जर्मनी	7998
फ्रांस	7254
चीन	5055
कनाडा	3594
भारत	3154
पाकिस्तान	2787

पृष्ठ: 28

प्रश्न 4. 
निम्नलिखित चरों का संतत तथा विविक्त में वर्गीकरण करें:
क्षेत्रफल, आयतन, ताप, पाँसे पर आने वाली संख्या, फसल उपज, जनसंख्या, वर्षा, सड़क पर कारों की संख्या और आयु।
उत्तर:
संतत चर: क्षेत्रफल, आयतन, ताप, फसल उपज, वर्षा, आयु।
विविक्त चर: पाँसे पर आने वाली संख्या, जनसंख्या, सड़क पर कारों की संख्या।

RBSE Class 11 Economics आँकड़ों का संगठन Textbook Questions and Answers

प्रश्न 1. 
निम्नलिखित में से कौनसा विकल्प सही है? 
(i) एक वर्ग मध्य बिन्दु बराबर है।
(क) उच्च वर्ग सीमा तथा निम्न वर्ग सीमा के औसत के 
(ख) उच्च वर्ग सीमा तथा निम्न वर्ग सीमा के गुणनफल के 
(ग) उच्च वर्ग सीमा तथा निम्न वर्ग सीमा के अनुपात के 
(घ) उपरोक्त में से कोई नहीं।

(ii) दो चरों के बारम्बारता वितरण को इस नाम से जानते हैं।
(क) एक विचर वितरण 
(ख) द्विचर वितरण 
(ग) बहुचर वितरण
(घ) उपरोक्त में से कोई नहीं। 

(iii) वर्गीकृत आँकड़ों में सांख्यिकीय परिकलन आधारित होता है।
(क) प्रेक्षणों के वास्तविक मानों पर 
(ख) उच्च वर्ग - सीमाओं पर
(ग) निम्न वर्ग - सीमाओं पर
(घ) वर्ग के मध्य बिन्दुओं पर। 

(iv) अपवर्जी विधि के अन्तर्गत।
(क) किसी वर्ग की उच्च वर्ग - सीमा को वर्ग अन्तराल में समावेशित नहीं करते। 
(ख) किसी वर्ग की उच्च वर्ग - सीमा को वर्ग अन्तराल में समावेशित करते हैं। 
(ग) किसी वर्ग की निम्न वर्ग - सीमा को वर्ग अन्तराल में समावेशित नहीं करते हैं। 
(घ) किसी वर्ग की निम्न वर्ग - सीमा को वर्ग अन्तराल में समावेशित करते हैं। 

(v) परास का अर्थ है।
(क) अधिकतम एवं न्यूनतम प्रेक्षणों के बीच अन्तर 
(ख) न्यूनतम एवं अधिकतम प्रेक्षणों के बीच अन्तर 
(ग) अधिकतम एवं न्यूनतम प्रेक्षणों का औसत 
(घ) अधिकतम एवं न्यूनतम प्रेक्षणों का अनुपात
उत्तर:
(i) (क) 
(ii) (ख) 
(iii) (प) 
(iv) (क) 
(v) (क)।

प्रश्न 2. 
वस्तुओं को वर्गीकृत करने में क्या कोई लाभ हो सकता है? अपने दैनिक जीवन से एक उदाहरण देकर व्याख्या कीजिए।
उत्तर:
वस्तुओं को वर्गीकृत करने में अनेक लाभ होते हैं। पदार्थों अथवा वस्तुओं का वर्गीकरण हमारे श्रम और समय को बचाता है। यदि हमने वस्तुओं को वर्गीकृत करके रखा हुआ है तो उसे खोजने में समय खराब नहीं होता तथा श्रम भी कम लगता है। उदाहरण के लिए हमारे विद्यालय के पुस्तकालय को देखें तो वहाँ पर पुस्तकें एक विशेष क्रम में रखी जाती हैं अर्थात् पुस्तकों का विषय के अनुसार वर्गीकरण किया हुआ होता है, विषय के अनुसार पुस्तकें अलग-अलग रखी जाती हैं। यदि हमें कोई अर्थशास्त्र की पुस्तक चाहिए तो हम केवल अर्थशास्त्र समूह में पुस्तक को खोज लेते हैं। इससे हमारे समय तथा श्रम दोनों की बचत होती है।

प्रश्न 3. 
चर क्या है? एक संतत तथा विविक्त चर में भेद कीजिए।
उत्तर:
चर - चर वे तत्त्व होते हैं जिन्हें संख्यात्मक रूप में व्यक्त किया जाता है तथा जिन तथ्यों के मूल्य में परिवर्तन होता रहता है। चरों को दो भागों में वर्गीकृत किया जाता है-संतत चर एवं विविक्त चर। संतत चर-संतत चर वह होता है जिसका कोई भी संख्यात्मक मान हो सकता है। यह पूर्णांक मान (1, 2,3,4 आदि), भिन्नात्मक मान (1/2, 1/3, 2/3 आदि) थे और फिर 1 से 31 में बदलता है तथा वे मान जो यथातथ्य भिन्न नहीं हैं (जैसे √ 2 = 1 . 414, √ 3 = 1 . 732 आदि) हो सकते हैं।

उदाहरण के लिए एक छात्र का कद 80 से 140 सेमी. तक बढ़ता है तो उसके कद के मान इसके बीच आने वाले सभी मान हो सकते हैं। यह सम्पूर्ण संख्या वाले मान को भी प्रकट कर सकता है, जैसे कि 90 सेमी., 95 सेमी., 105 सेमी. आदि । इसके साथ ही यह भिन्नात्मक मान भी हो सकता है जैसे 90.84 सेमी., 97.30 सेमी. आदि।

विविक्त चर: संतत चर के विपरीत विविक्त चर केवल निश्चित मान हो सकते हैं। इसके मान केवल परिमित उछाल से बदलते हैं। यह उछाल एक मान से दूसरे मान के बीच होता है किन्तु इसके बीच में कोई मान नहीं आता है। उदाहरण के लिए किसी कक्षा में छात्रों की संख्या का आकलन करें तो वह पूर्णांक होगी जैसे 45, 55, 60 आदि। यह कोई भी भिन्नात्मक मान नहीं हो सकता है जैसे 45.5, 655 आदि। लेकिन ऐसा नहीं सोचना चाहिए कि किसी विविक्त चर का मान भिन्न में नहीं हो सकता है। इसके मान भिन्नों में हो सकते हैं तथापि ये दो सन्निकट भिन्नों के बीच नहीं हो सकते हैं। यह \(\frac{1}{8}\) से \(\frac{1}{16}\) किन्तु \(\frac{1}{16}\) से \(\frac{1}{32}\) के बीच या \(\frac{1}{16}\) से \(\frac{1}{32}\) के बीच के मान नहीं ले सकते हैं।

अत: संतत चर का कोई भी संख्यात्मक मान हो सकता है जबकि विविक्त चर का केवन निश्चित मान ही हो सकता है।

प्रश्न 4. 
आँकड़ों के वर्गीकरण में प्रयुक्त अपवजी तथा समावेशी विधियों की व्याख्या कीजिए।
उत्तर:
अपवर्जी विधि: अपवर्जी विधि के अन्तर्गत आँकड़ों का वर्गीकरण इस प्रकार किया जाता है कि एक वर्ग की उच्च वर्ग सीमा, अगले वर्ग की निम्न वर्ग - सीमा के बराबर होती है, जैसे - 10 - 20, 20 - 30, 30 - 40 आदि। इस विधि से आँकड़ों की संततता बनी रहती है। यही कारण है कि वर्गीकरण की यह विधि संतत चर के आँकड़ों के लिए अत्यधिक उपयुक्त होती है।

इस विधि के अन्तर्गत उच्च वर्ग - सीमा को छोड़ देते हैं, परन्तु एक वर्ग की निम्न वर्ग - सीमा को अन्तराल में शामिल कर लिया जाता है। इसी प्रकार, इस विधि के अनुसार कोई प्रेक्षण जो उच्च वर्ग-सीमा के बराबर है उसे उस वर्ग में शामिल न कर अगले वर्ग में शामिल किया जाता है।

यदि यह निम्न वर्ग - सीमा के बराबर होता है तब उसे निम्न वर्ग में शामिल कर लिया जाता है। समावेशी विधि - आकड़ों के वर्गीकरण की समावेशी विधि किसी वर्ग अन्तराल में उच्च वर्ग-सीमा को नहीं छोड़ती है। इस विधि में किसी वर्ग में उच्च वर्ग-सीमा को सम्मिलित किया जाता है। अतः दोनों वर्ग सीमाएँ वर्ग अन्तराल का हिस्सा होती हैं। जैसे - 900 999, 1000 - 1099 आदि।

प्रश्न 5. 
निम्न सारणी के आँकड़ों का प्रयोग करें, जो 50 परिवारों के भोजन पर मासिक व्यय (रु. में) को दिखलाती है, और
(क) भोजन पर मासिक परिवार व्यय का प्रसार ज्ञात कीजिए।
(ख) परास को वर्ग अन्तराल की उचित संख्याओं में विभाजित करें तथा व्यय का बारम्बारता वितरण प्राप्त करें। 
उन परिवारों की संख्या पता कीजिए जिनका भोजन पर मासिक व्यय।
(क) 2000/- रु. से कम है। 
(ख) 3000/-रु. से अधिक है। 
(ग) 1500/- रु. और 2500/- के बीच है।

खाद्य पर 50 परिवारों के मासिक पारिवारिक व्यय ( रु. में )

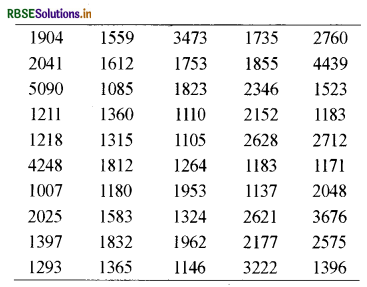
उत्तर:
सर्वप्रथम सारणी को हम आरोही क्रम में लिखेंगे। जिसे नीचे तालिका में लिखा गया है।

(क) भोजन पर मासिक पारिवारिक व्यय का प्रसार
भोजन पर मासिक पारिवारिक व्यय का प्रसार = उच्च सीमा - निम्न सीमा 
= 5090 - 1007 
= 4083 रुपये

(ख) परास का वर्ग अन्तराल की उचित संख्याओं में विभाजन तथा व्यय का बारम्बारता में वितरण निम्न प्रकार है। 

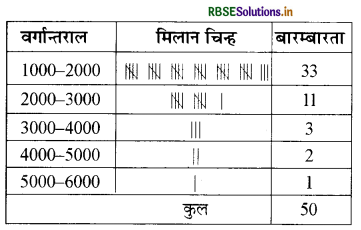
भोजन पर विभिन्न मासिक व्यय करने वाले परिवारों की संख्या
(क) 2000 रु. से कम मासिक व्यय करने वाले परिवारों की संख्या = 33 
(ख) 3000 रुपये से अधिक मासिक व्यय करने वाले परिवारों की संख्या = 06 
(ग) 1500 रुपये तथा 2500 रुपये के बीच मासिक व्यय करने वाले
परिवारों की संख्या - 19 

प्रश्न 6. 
एक शहर में, यह जानने हेतु 45 परिवारों का सर्वेक्षण किया गया कि वे अपने घरों में कितनी संख्या में सेल फोनों का इस्तेमाल करते हैं। नीचे दिए गए उनके उत्तरों के आधार पर एक बारम्बारता सारणी तैयार कीजिए। 

उत्तर:
बारम्बारता सारणी बनाने से पूर्व परिवारों द्वारा दिए गए उत्तर के अंकों को आरोही क्रम में रखना होगा जो निम्न प्रकार है।

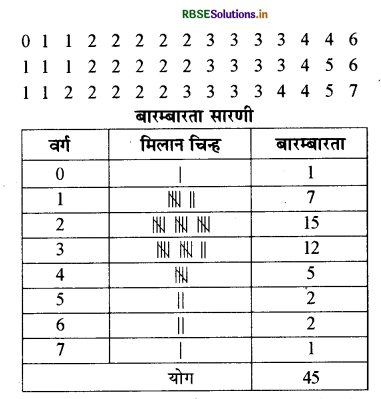
प्रश्न 7. 
वर्गीकृत आँकड़ों में सूचना की क्षति' का क्या तात्पर्य है?
उत्तर:
बारम्बारता वितरण के रूप में आँकड़ों के वर्गीकरण में एक अन्तर्निहित दोष पाया जाता है। यह अपरिष्कृत आँकड़ों का सारांश प्रस्तुत कर उन्हें संक्षिप्त एवं बोधगम्य तो बनाता है, परन्तु इसमें वे विस्तृत विवरण नहीं प्रकट हो पाते जो अपरिष्कृत आँकड़ों में पाए जाते हैं। दूसरे शब्दों में बारम्बारता वितरण में प्रेक्षणों के वास्तविक मान के स्थान पर वर्ग-चिन्हों के प्रयोग को सांख्यिकीय विधियों में शामिल करने पर पर्याप्त मात्रा में सूचनाओं की क्षति होती है। यद्यपि अपरिष्कृत आँकड़ों को वर्गीकृत करने में सूचना की क्षति होती है, तथापि आँकड़ों को वर्गीकरण द्वारा संक्षिप्त करने पर पर्याप्त जानकारी मिल जाती है।

प्रश्न 8. 
क्या आप इस बात से सहमत हैं कि अपरिष्कृत आँकड़ों की अपेक्षा वर्गीकृत आँकड़े बेहतर होते हैं?
उत्तर:
हम इस बात में पूरी तरह सहमत हैं कि अपरिष्कृत आँकड़ों की अपेक्षा वर्गीकृत आँकड़े बेहतर होते हैं। अपरिष्कृत आँकड़े अत्यधिक अव्यवस्थित होते हैं जो प्राय: अति विशाल होते हैं जिस कारण उन्हें संचालना कठिन होता है तथा अपरिष्कृत आँकड़ों के आधार पर सार्थक निष्कर्ष निकालने के लिए अधिक श्रम की आवश्यकता पड़ती है। इसके विपरीत वर्गीकृत आँकड़े अपरिष्कृत आँकड़ों को संक्षिप्त एवं बोधगम्य बनाते हैं। वर्गीकृत आँकड़े आसानी से चिन्हित किए जा सकते हैं। वर्गीकृत आँकड़ों की तुलना करना व निष्कर्ष निकालना आसान रहता है अत: वर्गीकृत आँकड़े अधिक बेहतर हैं।

प्रश्न 9.
एक विचर एवं द्विचर बारम्बारता वितरण के बीच अन्तर बताइए।
उत्तर:
एक विचर बारम्बारता वितरण अकेले चर के बारम्बारता वितरण को प्रस्तुत करता है। उदाहरण के लिए किसी छात्र के प्राप्तांक, एक व्यक्ति की आय इत्यादि एक विचर बारम्बारता वितरण है। द्विचर बारम्बारता वितरण दो चरों का बारम्बारता वितरण होता है। उदाहरण के लिए किसी वस्तु की विभिन्न कीमतों पर उसकी माँग के विभिन्न स्तरों को दर्शाने वाली बारम्बारता द्विचर बारम्बारता वितरण कहलाती है।

प्रश्न 10. 
निम्नलिखित आँकड़ों के आधार पर 7 का वर्ग अन्तराल लेकर समावेशी विधि द्वारा एक बारम्बारता वितरण तैयार कीजिए।

उत्तर:
उपर्युक्त आँकड़ों के आधार पर बारम्बारता वितरण बनाने हेतु सर्वप्रथम आँकड़ों को आरोही क्रम में पुनः लिखना होगा जो निम्न प्रकार हैं1