RBSE Class 11 Physics Notes Chapter 9 ठोसों के यांत्रिक गुण

These comprehensive RBSE Class 11 Physics Notes Chapter 9 ठोसों के यांत्रिक गुण will give a brief overview of all the concepts.

RBSE Class 11 Physics Chapter 9 Notes ठोसों के यांत्रिक गुण

→ किसी वस्तु पर आरोपित वह बाहरी बल जिसके कारण वस्तु के आकार या आकृति या दोनों में परिवर्तन हो जाता है, विरूपक बल (Deforming force) कहलाता है। विरूपक बल को हटाने पर वस्तु फिर अपना प्रारम्भिक आकार अथवा रूप ले लेती है। जिस वस्तु में यह गुण पाया जाता है उसे प्रत्यास्थ (Elastic) वस्तु कहते हैं तथा पदार्थ के इस गुण को प्रत्यास्थता (Elasticity) कहते हैं।

→ प्रतिबल (Stress):
वस्तु के अनुप्रस्थ काट के एकांक क्षेत्रफल पर कार्य करने वाले आंतरिक प्रत्यानयन बल (Restoring force) को प्रतिबल कहते हैं।
प्रतिबल = \(\frac{F}{A}\) न्यूटन/मी.
विमा M¹L¹T^-2 है।
किसी वस्तु में उत्पन्न प्रतिबल इस बात पर निर्भर करता है कि बाह्य बल किस प्रकार लगाया गया है।

प्रतिबल के प्रकार

• अनुदैर्घ्य प्रतिबल
• आयतन प्रतिबल
• अपरूपण प्रतिबल।।

→ विकृति (Strain):
बाहरी बलों के कारण किसी वस्तु की प्रति एकांक लम्बाई में उत्पन्न परिवर्तन को अनुदैर्घ्य विकृति कहते हैं।

→ हुक का नियम (Hooke's Lar)
प्रत्यास्थता की सीमा में
प्रतिबल विकृति
या प्रतिबल = E (विकृति)
E प्रत्यास्थता गुणांक है।

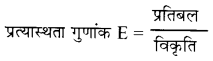
विकृति के आधार पर तीन प्रत्यास्थता गुणांक होते हैं

(i) यंग का प्रत्यास्थता गुणांक

इसका मात्रक न्यूटन/मी. है।।

(ii) आयतन प्रत्यास्थता गुणाक

(iii) अपरूण प्रत्यास्थता गुणांक या दृढ़ता गुणांक

अपरूण प्रत्यास्थता गुणांक सामान्यतः यंग प्रत्यास्थता गुणांक से कम होता है। अधिकतर द्रवों के लिये η = \(\frac{1}{3}\)Y होता है।

→ पार्श्व विकृति और प्वासों अनुपात ( Lateral Strain and Poisson's Ratio)

प्रत्यास्थता सीमा के अन्दर पार्श्व विकृति β तथा तनन विकृति (α) का अनुपात नियत होता है। इसे प्वासों अनुपात (σ) कहते हैं । अतः
σ = \(\frac{-\beta}{\alpha}\)

→ Y, K, η या 6 में सम्बन्ध ( Relation between Y, K, η and σ)
Y = 2η(1 + σ)
Y = 3K(1 - 2σ)
समी. (1) तथा (2) से प्रत्यास्थता के तीनों गुणांकों में सम्बन्ध
\(\frac{9}{Y}=\frac{3}{\eta}+\frac{1}{K}\)

→ यंग प्रत्यास्थता गुणांक ज्ञात करने की सर्ल की विधि (Searl's Method to Determine Young's Modulus)
इस विधि में लम्बाई L व त्रिज्या के निलंबित तार में यदि Mg भार से लम्बाई में वृद्धि l है
तो Y = \(\frac{M g L}{\pi r^2 l}\)

→ ठोसों के प्रत्यास्थ व्यवहार में यह देखा गया कि किसी पिण्ड में लम्बाई वृद्धि प्रत्यारोपित बल या लोड के अनुक्रमानुपाती होती है। उन्होंने सन् 1676 में प्रत्यास्थता का नियम प्रस्तुत किया जो अब हुक का नियम कहलाता है।

→ प्रत्यास्थता के व्यावहारिक उपयोग

• अवनमन कम करने व धातु की बचत के लिये गर्डर व रेल पटरियों का अनुप्रस्थ काट अंग्रेजी अक्षर I की आकृति का बनाया जाता है ।
• खोखला पाइप उसी द्रव्यमान की ठोस छड़ से अधिक मजबूत होता है। इसी कारण से साइकिलों में ठोस छड़ की जगह खोखला पाइप प्रयोग करते हैं ताकि पाइप की सामर्थ्य भी बढ़े तथा धातु की बचत भी हो ।
• छोटी व खोखली शाफ्ट अधिक मरोड़ी बल युग्म सहन कर सकती है ।
• क्रेन आदि में प्रयुक्त रस्सी पतले तारों को एक साथ बट कर बनाई जाती है।

→ किसी तार की वृद्धि में प्रति इकाई आयतन किया गया कार्य (Work done per unit volume in stretching a wire)
W = \(\frac{1}{2}\) प्रतिबल × विकृति