RBSE Class 11 Physics Notes Chapter 8 गुरुत्वाकर्षण

These comprehensive RBSE Class 11 Physics Notes Chapter 8 गुरुत्वाकर्षण will give a brief overview of all the concepts.

RBSE Class 11 Physics Chapter 8 Notes गुरुत्वाकर्षण

→ न्यूटन के अनुसार, इस विश्व में प्रत्येक वस्तु एक निश्चित बल से प्रत्येक दूसरी वस्तु को आकर्षित करती है। बल जिससे दो वस्तुएँ एक-दूसरे को आकर्षित करती हैं, गुरुत्वीय बल (अथवा गुरुत्व) कहलाता है।

→ केपलर के नियम

• कक्षाओं का नियम–सूर्य के चारों ओर ग्रह की कक्षा (या मार्ग) दीर्घवृत्त (अण्डाकार आकृति) होती है और न कि यथार्थ वृत्त।
• क्षेत्रफलों का नियम-प्रत्येक ग्रह सूर्य के चारों ओर इस तरह परिक्रमा करता है कि ग्रह को सूर्य से मिलाने वाली रेखा समय के समान अन्तरालों में समान क्षेत्रफलों में हट जाती है।
• सूर्य से ग्रह की औसत दूरी का घन, समय के वर्ग के अनुक्रमानुपाती होता है, जिसे वह सूर्य के चारों ओर चक्कर लगाने में लेता है। T² ∝ r³

→ गुरुत्वाकर्षण का सार्वत्रिक नियम-"विश्व में प्रत्येक कण अन्य दूसरे कण से विशेष आकर्षण बल से आकर्षित होता है, जिसे गुरुत्वाकर्षण बल कहते हैं।" ।
F = \(\frac{\mathrm{G} m_1 m_2}{r^2}\)
यहाँ G एक नियतांक है, जिसको हम गुरुत्वाकर्षण का सार्वत्रिक नियतांक कहते हैं।

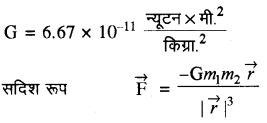
→ बिन्दु द्रव्यमानों के समूह के कारण किसी बिन्दु पर गुरुत्वाकर्षण बल-भिन्न-भिन्न बिन्दुवत् द्रव्यमानों के कारण किसी बिन्दु द्रव्यमान पर गुरुत्वाकर्षण बल उन बिन्दुवत् द्रव्यमानों के कारण उस बिन्दु द्रव्यमान पर कार्यरत अलग-अलग गुरुत्वाकर्षण बलों का सदिश योगफल होता है।

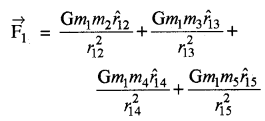
→ न्यूटन के गुरुत्वाकर्षण नियम के अनुसार, “किसी भी पिण्ड द्वारा किसी अन्य पिण्ड पर आरोपित बल

• उस पिण्ड के द्रव्यमान के अनुक्रमानुपाती तथा
• उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।"

 

→ गुरुत्वीय नियतांक G का मापन कैवेन्डिश प्रयोग

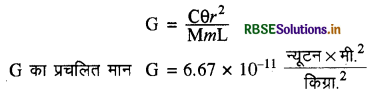
→ g तथा G में सम्बन्ध
g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}=\frac{\mathrm{G}\left(\frac{4}{3} \pi \mathrm{R}^3 \rho\right)}{\mathrm{R}^2}\)
या g = \(\frac{4}{3}\)πRGp यहाँ पृथ्वी का घनत्व p है।

→ पृथ्वी तल के ऊपर जाने पर g के मान में परिवर्तन
g_h ≅ g(1 - \(\frac{2h}{R}\))
(1 - \(\frac{2h}{R}\)) का मान h << R के मानों के लिए सदैव धनात्मक एवं इकाई से कम है।
अतः g_h का मान g से कम होगा अर्थात् पृथ्वी तल से ऊँचाई पर जाने से g का मान सदैव कम होता

→ g के मान में पृथ्वी तल से गहराई के साथ परिवर्तन
g'_h = g(1 - \(\frac{h'}{R}\))
(1 - \(\frac{h'}{R}\)) का.मान भी धनात्मक तथा इकाई से कम है अतः g'_h के मान में भी पृथ्वी की गहराई के साथ कमी होती है।

→ पृथ्वी के आकार के कारण g के मान में परिवर्तन-पृथ्वी दोनों ध्रुवों पर कुछ चपटी है जिससे
R_{भूमध्य} > R_धुव
g_धुव > g_{भूमध्य}

→ पृथ्वी के घूर्णन के कारण g के मान में परिवर्तन ध्रुवों पर-λ = 90°, cos λ = 0 इसलिए g'_λ = g_p, अर्थात् ध्रुवों पर पृथ्वी के घूर्णन का कोई भी प्रभाव नहीं होता है। भूमध्य रेखा पर-भूमध्य रेखा पर पृथ्वी के घूर्णन का अधिकतम प्रभाव होता है।

→ चन्द्रमा पर गुरुत्वीय त्वरण का मान-चन्द्रमा की सतह पर g का मान पृथ्वी सतह पर g के मान का \(\frac{1}{6}\) भाग ही होता है। इसका तात्पर्य यह हुआ कि किसी वस्तु का भार यदि पृथ्वी पर W किग्रा. है तब चन्द्रमा पर उसी वस्तु का भार \(\frac{1}{6}\)w किग्रा होगा।

→ गुरुत्वीय क्षेत्र की तीव्रता-गुरुत्वीय क्षेत्र के किसी बिन्दु पर रखे इकाई द्रव्यमान पर कार्यरत बल (F) को उस बिन्दु पर गुरुत्वीय क्षेत्र की तीव्रता या प्रबलता कहते हैं। इसे \(\overrightarrow{\mathrm{E}}_g\) (या केवल 8) द्वारा प्रदर्शित करते हैं।

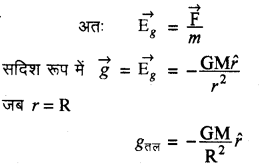
→ ठोस गोलीय पिण्ड के कारण गुरुत्वीय क्षेत्र
(i) गोले के बाहर (> R के लिए)
\(\overrightarrow{\mathrm{E}}_g=-\frac{\mathrm{GM}}{r^2} \hat{r}\)
हाँ बिन्दु की गोले के केन्द्र से दूरी है ।

(ii) गोले के पृष्ठ पर (r = R के लिए)
\(\overrightarrow{\mathrm{E}}_g=-\frac{\mathrm{GM}}{r^2} \hat{r}\)
जहाँ R गोले की त्रिज्या है ।

(iii) गोले के आन्तरिक बिन्दुओं पर (r < R के लिए)
\(\overrightarrow{\mathrm{E}}_g=-\frac{\mathrm{GM}}{r^2} \hat{r}\)
जहाँ M' केवल अन्दर वाले गोले का द्रव्यमान लिया जायेगा जिसकी त्रिज्या है |

→ गुरुत्वीय स्थितिज ऊर्जा
(i) केन्द्र O से r दूरी पर स्थित m द्रव्यमान की स्थितिज ऊर्जा
U_(r) = -\(\frac{\mathrm{GM} m}{r}\)

(ii) गोलाकार पिण्ड के भीतरी बिन्दुओं के लिए स्थितिज
U_Inside = -\(\frac{\mathrm{GM} m}{2 \mathrm{R}^3}\left[3 \mathrm{R}^2-r^2\right]\)

(iii) गोले के केन्द्र पर स्थितिज ऊर्जा का मान - r = 0 लेने पर
U_{केन्द्र पर} = \(-\frac{\mathrm{GM} m}{2 \mathrm{R}^3}\left(3 \mathrm{R}^2-0\right) = -\frac{3}{2} \frac{\mathrm{GM} m}{\mathrm{R}}\)
यह मान गोले के तल पर स्थित कणों की स्थितिज ऊर्जा के मान का 150% है।

(iv) गोले के तल पर - r = R लेने पर
U_surface = -\(\frac{\mathrm{GM} m}{\mathrm{R}}\)
गोले के तल पर स्थित सभी बिन्दुओं के लिए स्थितिज ऊर्जा नियत रहती है।

→ गुरुत्वीय विभव - इकाई द्रव्यमान को अनन्त से गुरुत्वीय क्षेत्र के अन्दर किसी बिन्दु तक लाने में जितना कार्य होता है, उसे उस बिन्दु पर 'गुरुत्वीय विभव' कहते हैं। गुरुत्वीय विभव सदैव ऋणात्मक होता है। इसका मात्रक जूल/ किग्रा. और विमा [M°L²T^-2] होती है।
बिन्दु द्रव्यमान M के कारण r दूरी पर गुरुत्वीय विभव
V_(r) = -\(\frac{\mathrm{GM}}{r}\)

→ किसी ठोस गोलाकार पिण्ड के कारण गुरुत्वीय विभव
(i) गोले के बाहरी बिन्दु A पर (r > R)
V = -\(\frac{\mathrm{GM}}{r}\)

(ii) गोले के पृष्ठीय बिन्दु B पर (r = R)
V = -\(\frac{\mathrm{GM}}{\mathrm{R}}\)

(iii) गोले के बिन्दु C पर (r <R)
V = -\(\frac{\mathrm{GM}}{2 \mathrm{R}^3}\) (3R² - r²)

(iv) गोले के केन्द्र पर (r = 0)
V₀ = -\(\frac{3 \mathrm{GM}}{2 \mathrm{R}}\)

→ गोलीय कोश के कारण गुरुत्वीय विभव
(i) बाहरी बिन्दु A पर (r > R)
V = -\(\frac{\mathrm{GM}}{r}\)

(ii) पृष्ठीय बिन्दु B पर (r = R)
V = -\(\frac{\mathrm{GM}}{\mathrm{R}}\)

(iii) आन्तरिक बिन्दु C पर (r <R)
गोले के अन्दर गुरुत्वीय क्षेत्र का मान शून्य होता है। अतः इकाई द्रव्यमान को पृष्ठ के अन्दर तक ले जाने में कोई अतिरिक्त कार्य नहीं करना पड़ेगा तथा गोले के अन्दर गुरुत्वीय विभव का मान भी पृष्ठ के बराबर ही रहेगा।
अतः V = -\(\frac{\mathrm{GM}}{\mathrm{R}}\)

→ प्रक्षेपण वेग-ऊँचाई त प्राप्त करने के लिए प्रक्षेपण वेग
V = \(\sqrt{\frac{2 g h}{\left(1+\frac{h}{R}\right)}}\)
पिण्ड द्वारा प्राप्त अधिकतम ऊँचाई होगी
h = \(\sqrt{\frac{2 g h}{\left(1+\frac{h}{R}\right)}}\)

यदि v² का मान 2gR की तुलना में नगण्य है तो
h = \(\frac{\mathrm{v}^2 \mathrm{R}}{2 g \mathrm{R}}=\frac{\mathrm{v}^2}{2 g}\)

→ पलायन वेग-पलायन वेग वह न्यूनतम वेग है जिससे किसी | पिण्ड को ऊपर की ओर फेंकने पर वह ग्रह के गुरुत्वीय क्षेत्र को पार कर लेती है तथा उस ग्रह पर कभी वापस नहीं आती है।
पलायन वेग V_e = \(\sqrt{2 g \mathrm{R}}\)
पलायन वेग का मान 11.2 किमी./से. होता है। चन्द्रमा के लिए | पलायन वेग का मान 2.38 किमी./से. होता है अर्थात् यह मान पृथ्वी की तुलना में \(\frac{1}{5}\) गुना है।

h ऊँचाई पर पलायन वेग का मान
V'_e = \(\sqrt{\frac{2 g \mathrm{R}^2}{\mathrm{R}+h}}\)

→ उपग्रह का कक्षीय वेग
v₀ = \(\sqrt{g \mathrm{R}}\)
पलायन वेग व कक्षीय वेग में सम्बन्ध
V_e = √2 v₀
किसी पिण्ड के कक्षीय वेग को √2 गुना कर दिया जाये तो पिण्ड पृथ्वी तल से पलायन कर जायेगा।

→ परिक्रमण काल
T = 2π\(\sqrt{\frac{\mathrm{R}}{\mathrm{g}}}\)
उपग्रह का परिक्रमण काल भी उसकी ग्रह से ऊँचाई पर निर्भर करता है। पृथ्वी के निकट परिक्रमा करने वाले उपग्रह का परिक्रमण काल 84.6 मिनट या लगभग 1.4 घण्टे होता है। पृथ्वी तल के अति निकट परिक्रमा करने वाले उपग्रह की चील V₀ ≈ 7.92 किमी./से. आती है।

→ उपग्रह की कुल ऊर्जा
E = -\(\frac{\mathrm{GM} m}{2 r}\)
उपग्रह की कुल ऊर्जा ऋणात्मक है जिसका अभिप्राय है कि उपग्रह को अनन्त पर भेजने के लिए (अथवा इसकी कुल ऊर्जा को अनन्तीय ऊर्जा के बराबर जो शून्य है, करने के लिए) हमें उपग्रह को ऊर्जा देनी | होगी, इस बाहरी ऊर्जा को बंधन ऊर्जा कहते हैं।

→ उपग्रह की पृथ्वी की सतह से ऊँचाई
h = \(\left(\frac{\mathrm{T}^2 \mathrm{R}^2 g}{4 \pi^2}\right)^{\frac{1}{3}}-\mathrm{R}\)
पृथ्वी तल से लगभग 36000 किमी. ऊपर स्थित उपग्रह भूस्थिर उपग्रह होता है। इस ऊँचाई पर स्थित उपग्रह की कक्षा को पार्किंग कक्षा (Parking Orbit) भी कहते हैं।

→ भू-स्थाई उपग्रह का कक्षीय वेग (v₀) का मान = 3.1 किमी. /से. होता है और कोणीय वेग का मान ω = 7.3 × 10⁵ रेडियन/से. ।

→ भारहीनता-किसी वस्तु का भार वह प्राचल है जो एक कमानी तुला से मापते हैं । पृथ्वी के गुरुत्वाकर्षण क्षेत्र में मुक्त रूप से गिरती हुई वस्तु का भार शून्य होता है । यह स्थिति भारहीनता कहलाती है।