RBSE Class 11 Physics Notes Chapter 7 कणों के निकाय तथा घूर्णी गति

These comprehensive RBSE Class 11 Physics Notes Chapter 7 कणों के निकाय तथा घूर्णी गति will give a brief overview of all the concepts.

RBSE Class 11 Physics Chapter 7 Notes कणों के निकाय तथा घूर्णी गति

→ दृढ़ पिण्ड (Rigid Body):
"ऐसे पिण्ड जिन पर बाह्य बल लगाने पर उनके कणों के मध्य की दूरियाँ अपरिवर्तित रहती हैं, दृढ़ पिण्ड कहलाते हैं"

→ दृढ़ पिण्डों की गति (Motion of Ripitt Body)

• स्थानान्तरण गति
• घूर्णी गति
• लोटनिक गति।।

→ द्रव्यमान केन्द्र (Centre of Mass C.M.):
किसी पिण्ड या निकाय का द्रव्यमान केन्द्र वह बिन्दु होता है जहाँ पिण्ड का सम्पूर्ण द्रव्यमान केन्द्रित माना जा सकता है। दूसरे शब्दों में, “द्रव्यमान केन्द्र वह बिन्दु है जिसके परितः सभी कणों के द्रव्यमान तथा उनके स्थिति सदिशों के गुणनफल अर्थात् द्रव्यमान आघूर्णों का योग शून्य के बराबर होता है।
\(\sum_{i=1}^{i=n} m_i \vec{r}_i\) = 0

→ दो कणों के निकाय का द्रव्यमान केन्द्र
\(\vec{r}_{c m}=\frac{m_1 \overrightarrow{r_1}+m_2 \overrightarrow{r_2}}{m_1+m_2}\)
द्रव्यमान केन्द्र मूल बिन्दु पर स्थित हो तो \(\vec{r}_{c m}\) = 0
\(\therefore m_1 \overrightarrow{r_1}+m_2 \vec{r}\) = 0

→ n-कणों के निकाय का द्रव्यमान केन्द्र
\(\vec{r}_{c m}=\frac{m_1 \overrightarrow{r_1}+m_2 \overrightarrow{r_2}+m_3 \overrightarrow{r_3}+\ldots .+m_n \overrightarrow{r_n}}{m_1+m_2+m_3+\ldots+m_n}\)
द्रव्यमान केन्द्र मूल बिन्दु पर स्थित है तब
\(m_1 \overrightarrow{r_1}+m_2 \overrightarrow{r_2}+m_3 \overrightarrow{r_3}+\ldots .+m_n \overrightarrow{r_n}\) = 0
अर्थात् द्रव्यमान केन्द्र के परितः निकाय के सभी कणों के द्रव्यमान | आघूर्णों का सदिश योग शून्य होता है। यदि द्रव्यमान केन्द्र के कार्तीय | निर्देशांक (x_cm, Y_cm Z_cm) हैं, तो

 

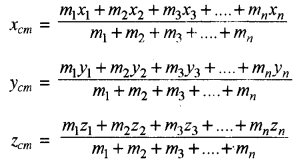
→ दृढ़ पिण्ड का द्रव्यमान केन्द्र
\(\overrightarrow{r_{c m}}=\frac{1}{\mathrm{M}}\)∫r.dm

→ नियमित दृढ़ पिण्डों का द्रव्यमान केन्द्र

• एकसमान पतली छड़ का द्रव्यमान केन्द्र उसके ज्यामिति केन्द्र पर होगा। जो एक सिरे से (\(\frac{L}{2}\)) दूरी पर स्थित है।
• अर्धगोलीय पिण्ड का द्रव्यमान केन्द्र आधार पर स्थित केन्द्र से \(\frac{3R}{8}\) ऊँचाई पर होता है।
• शंकु का द्रव्यमान केन्द्र शीर्ष से \(\frac{3}{4}\)h दूरी पर तथा धरातल से h - \(\frac{3 h}{4}=\frac{h}{4}\) दूरी पर स्थित होता है।

→ द्रव्यमान केन्द्र की गति
\(\mathrm{M} \overrightarrow{a c m}_{c m}=\overrightarrow{\mathrm{F}}=\overrightarrow{\mathrm{F}}_{\mathrm{ext}}\)
कणों के किसी भी निकाय का द्रव्यमान केन्द्र इस प्रकार गति करता है कि मानो निकाय का पूरा द्रव्यमान केन्द्र पर संकेन्द्रित हो तथा सभी बाह्य बल इसी पर लगाये गये हों।

→ कणों के निकाय का रेखीय संवेग-किसी निकाय पर आरोपित बाह्य बलों का योग शून्य होता है। तब उस निकाय का वेग नियत रहता है अर्थात् V_cm = नियतांक
अतः कहा जा सकता है कि किसी निकाय का आन्तरिक बलों के कारण स्वतः त्वरित होना सम्भव नहीं है।

→ द्रव्यमान केन्द्र की गति के उदाहरण

• हवा में विस्फोटित पटाखे के द्रव्यमान केन्द्र की गति
• रेडियोएक्टिव क्षय
• युग्म तारे
• पृथ्वी चन्द्रमा निकाय

→ दो सदिशों का सदिश गुणनफल
\(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}=|\overrightarrow{\mathrm{A}}||\overrightarrow{\mathrm{B}}|\)sin θ. n̂
यहाँ n̂, परिणामी सदिश की दिशा में एकांक सदिश है।

→ सदिश गुणनफल का भौतिकी में अनुप्रयोग
(i) रेखीय वेग तथा रेखीय त्वरण
\(\vec{a}=\vec{\alpha} \times \vec{r}\)
(ii) बल आघूर्ण \(\vec{a}=\vec{\alpha} \times \vec{r}\)
(iii) लॉरेन्ज बल F = q\((\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})=q|\overrightarrow{\mathrm{v}}||\overrightarrow{\mathrm{B}}|\)sin θ. n̂
यहाँ n̂, आवेश पर कार्यरत बल F के अनुदिश एकांक सदिश है।
(iv) सदिश क्षेत्रफल S = \(\frac{1}{2}|\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}|\)

→ घूर्णन गति-ऐसी गति जिसमें पिण्ड अपने स्थानों पर किसी स्थिर अक्ष के चारों ओर घूर्णन करे, घूर्णन गति कहलाती है।

→ कोणीय विस्थापन-कोणीय विस्थापन Δθ = \(\frac{\Delta s}{t}\)

→ कोणीय वेग-कोणीय विस्थापन की दर को कोणीय वेग कहते हैं । अर्थात् एकांक समय में कोई पिण्ड जितने कोण से घूम जाता है, उसे पिण्ड का कोणीय वेग कहते हैं। इसे O (उमैगा) से व्यक्त करते हैं।
ω = \(\lim _{\Delta t \rightarrow 0}\left(\frac{\Delta \theta}{\Delta t}\right)=\frac{d \theta}{d t}\)

→ कोणीय त्वरण-किसी पिण्ड के कोणीय वेग में परिवर्तन की दर को कोणीय त्वरण कहते हैं। इसे & से प्रदर्शित किया जाता है।
α = \(\frac{d \omega}{d t}=\frac{d}{d t}\left(\frac{d \theta}{d t}\right)=\frac{d^2 \theta}{d t^2}\)
इसका मात्रक रेडियन/सेकण्ड होता है।

→ रेखीय व घूर्णन चरों में सम्बन्ध
(i) v = rω
सदिश रूप \(\overrightarrow{\mathrm{v}}=\vec{\omega} \times \overrightarrow{\mathrm{R}}\)
(ii) कोणीय त्वरण \(\vec{α}\) तथा रेखीय त्वरण \(\vec{a}\) में सम्बन्ध
a = rα
सदिश रूप \(\vec{a}=\vec{\alpha} \times \vec{R}\)

→ घूर्णन गति के समीकरण

• ω = ω₀ + αt
• θ = ω₀t + \(\frac{1}{2}\)αt²
• ω = ω₀ + 2αθ

जहाँ पर ω₀ = प्रारम्भिक कोणीय वेग, ω, t समय बाद अन्तिम कोणीय वेग, α = नियत कोणीय त्वरण तथा θ = कोणीय विस्थापन है।

→ बल आघूर्ण-“घूर्णन गति में दिये गये घूर्णन अक्ष के सापेक्ष किसी कण पर कार्यरत बल का आघूर्ण ही बल आघूर्ण कहलाता है।” इसे \(\vec{\tau}\)(tau) से व्यक्त करते हैं। उदाहरण-

• दरवाजे व खिड़कियों में हैंडिल कब्जों से दूर लगाये जाते हैं।
• पेचकस का हत्था चौड़ा बनाया जाता है।

→ कोणीय संवेग (L)-दृढ़ पिण्ड के किसी कण का किसी घूर्णन अक्ष के सापेक्ष कोणीय संवेग (L) का मान उस कण के रेखीय संवेग का आघूर्ण होता है। इसे \(\overrightarrow{\mathrm{J}} \)या \(\overrightarrow{\mathrm{L}}\) से प्रदर्शित करते हैं।
\(\overrightarrow{\mathrm{J}}=\vec{r} \times \overrightarrow{\mathrm{P}}\)
स्थितियाँ-
(i) \(\vec{r}\) व \(\vec{P}\) के मध्य कोण θ = 0° या 180° हो तो
J = rP sin 0° = 0 = न्यूनतम
(ii) r व P लम्बवत् हों तो θ = 90° होने पर
J = rP sin 90°
= rP = अधिकतम मान
J = r (mv) = mvr

→ बल आघूर्ण एवं कोणीय संवेग में सम्बन्ध
\(\vec{\tau}=\frac{d \overrightarrow{\mathrm{J}}}{d t}\)
अर्थात् किसी कण के कोणीय संवेग में परिवर्तन की दर उस पर लगने वाले बल आघूर्ण के बराबर होती है। यही घूर्णन गति की प्रधान समीकरण है। यह कथन रैखिक गति के लिए न्यूटन के द्वितीय नियम \(\overrightarrow{{F}}=\frac{d \overrightarrow{\mathrm{p}}}{d t}\) के तुल्य है।

→ दृढ़ पिण्डों का सन्तुलन
(i) \(\Sigma \overrightarrow{\mathrm{F}_i}\) = 0 कोई दृढ़ पिण्ड रेखीय साम्यावस्था में होगा यदि इस पर आरोपित परिणामी बल या सभी बाह्य बलों का सदिश योग शून्य हो।
(ii) \(\Sigma \vec{\tau}_i\) = 0 कोई दृढ़ पिण्ड घूर्णन साम्यावस्था में होगा यदि इस पर आरोपित परिणामी बल आघूर्ण या सभी बाह्य बल आघूर्णों का सदिश योग शून्य हो।

→ आघूर्णों का सिद्धान्त
F₁d₁ = F₂d₂ भार × भार की भुजा = प्रयास × प्रयास की भुजा

→ गुरुत्व केन्द्र-गुरुत्व केन्द्र पिण्ड का वह बिन्दु होता है जिसके परितः पिण्ड या निकाय की रचना करने वाले विभिन्न कणों पर लगे गुरुत्वीय बलों के आघूर्णों का बीजगणितीय योग शून्य होता है।
\(\sum_{i=1}^n m_i \vec{r}_i\) = 0

→ दृढ़ पिण्ड का जड़त्व आघूर्ण-पिण्ड के किसी कण की दी गई घूर्णन अक्ष के प्रति जड़त्व आघूर्ण (I), उस कण के द्रव्यमान (m) तथा कण की घूर्णन अक्ष से लम्बवत् दूरी r के वर्ग (r) के गुणनफल के बराबर होता है।
I = mr²

→ बल आघूर्ण (τ), जड़त्व आघूर्ण (I) तथा कोणीय त्वरण (a) में सम्बन्ध
τ = Ia
सदिश रूप में \(\vec{\tau}=I \vec{\alpha}\)
किसी पिण्ड का किसी अक्ष के सापेक्ष बल आघूर्ण, उस अक्ष के सापेक्ष जड़त्व आघूर्ण तथा उसमें उत्पन्न कोणीय त्वरण के गुणनफल के बराबर होता है।

→ कोणीय संवेग (L), जड़त्व आघूर्ण (I) तथा कोणीय वेग (a) में सम्बन्ध
L = Iω
जहाँ पर I = m₁r₁² + m₂r₂² + m₃r₃² + ..... + m_nr_n² जो कि पिण्ड का जड़त्व आघूर्ण है।
किसी पिण्ड का किसी घूर्णन अक्ष के सापेक्ष कोणीय संवेग उसके उसी अक्ष के सापेक्ष जड़त्व आघूर्ण एवं उसके कोणीय वेग के गुणनफल के बराबर होता है।

→ घूर्णन गतिज ऊर्जा
E_r = \(\frac{1}{2}\)Iω
यदि ω = 1 रेडियन/से. हो तो
I = 2 E_r,
किसी अक्ष के परितः एकांक कोणीय वेग से घूमने वाले दृढ़ वस्तु का जड़त्व आघूर्ण, दी हुई अक्ष के परितः वस्तु की घूर्णन गतिज ऊर्जा के दुगुने के बराबर होता है।
कुल गतिज ऊर्जा K.E. = \(\frac{1}{2}\)Iω² + \(\frac{1}{2}\)mv²

→ घूर्णन गति में कार्य तथा शक्ति
P=\(\tau \vec{\omega}\)
यहाँ पर \(\vec{\omega}\) = औसत कोणीय वेग, τ = बल आघूर्ण, P = शक्ति

→ कोणीय संवेग संरक्षण नियम-कोणीय संवेग संरक्षण के सिद्धान्त के अनुसार बाह्य बल आघूर्ण की अनुपस्थिति में प्रत्येक कण, निकाय अथवा पिण्ड का कोणीय संवेग नियत रहता है।
किसी पिण्ड के लिए यदि बल आघू \(\vec{\tau}=\frac{d \overrightarrow{\mathrm{L}}}{d t}\)
अतः यदि \(\vec{\tau}\) = 0 तो \(\frac{d \overrightarrow{\mathrm{L}}}{d t}\) = 0 जिससे \(\overrightarrow{\mathrm{L}}\) = नियतांक
यदि कोई पिण्डं कोणीय वेग से घूर्णी गति कर रहा है तथा घूर्णन अक्ष के सापेक्ष उसका जड़त्व आघूर्ण I है तो L = I_o होता है।

→ घूर्णन त्रिज्या-किसी घूर्णन अक्ष के सापेक्ष वस्तु का जड़त्व आघूर्ण (I) तथा वस्तु के कुल द्रव्यमान (M) के अनुपात का वर्गमूल उस घूर्णन अक्ष के सापेक्ष घूर्णन त्रिज्या कहलाती है।
K = \(\sqrt{\frac{I}{M}}\)

→ लम्बवत् एवं समान्तर अक्षों के प्रमेय
(i) लम्बवत् अक्षों का प्रमेय-किसी पिण्ड का किसी तल के लम्बवत् अक्ष के परितः किसी फलक का जड़त्व आघूर्ण फलक के तल में स्थित दो लम्बवत संगामी अक्षों के परितः ज्ञात जड़त्व आघूर्णों के योग के बराबर होगा।
I_z = I_x + I_y

(ii) समान्तर अक्षों का प्रमेय-किसी पिण्ड का किसी अक्ष के परितः जड़त्व आघूर्ण, उस योग के बराबर है जो पिण्ड के द्रव्यमान केन्द्र से गुजरने वाली समानान्तर अक्ष के परितः लिए गए जड़त्व आघूर्ण और पिण्ड के द्रव्यमान तथा दोनों अक्षों के बीच की दूरी के वर्ग के गुणनफल को जोड़ने से प्राप्त होता है।
I_z' = I_z + Md²
जहाँ I_z एवं I_z' क्रमशः z एवं z' अक्ष के परितः जड़त्व आघूर्ण हैं, M पिण्ड का द्रव्यमान है और d दोनों अक्षों के बीच की लम्बवत् दूरी है।

→ नत तल पर दृढ़ पिण्ड की लोटनी गति

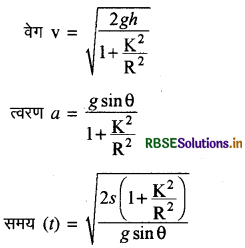
नत तल पर फिसलते हुए पिण्ड की स्थिति में लगा समय
t = \(\sqrt{\frac{2 s}{g \sin \theta}}\)