RBSE Class 11 Physics Notes Chapter 7 System of Particles and Rotational Motion

These comprehensive RBSE Class 11 Physics Notes Chapter 7 System of Particles and Rotational Motion will give a brief overview of all the concepts.

RBSE Class 11 Physics Chapter 7 Notes System of Particles and Rotational Motion

Rigid body:
A body or system of particles on which on applying external force or torque, there is no relative change in the positions of the particle, it is called a rigid body.

Centre of mass:
Centre of mass of a body is that selected point at which the whole mass of the body is supposed to be centered and all external forces are active at this point.

Vector product of two vector quantities:
This product of two vectors is a vector quantity, therefore it is called vector product and it is represented by sign of cross (×), hence it is also known as cross-product. It is obtained by following relation:
\(\vec{A} \times \vec{B}=|\vec{A}||\vec{B}|\). sinθ. n̂ = ABsinθ n̂
Where θ is the angle between the vectors and n̂ is the unit vector at right angle to the plane of \(\vec{A}\) and \(\vec{B}\), in direction decided by right hand screw law.

Couple of forces:
When two equal and opposite forces act on a body such that their line of action be different, then it is called couple of forces. Torque of couple of forces is obtained by
τ = Fr
where r is the normal distance between lines of action of forces.

Moment of force or torque:
Product of magnitude of force and normal distance between line of action of force and axis of rotation, is called moment of force or torque i.e.,
τ = Fr
In vector form, \(\vec{\tau}=\vec{r} \times \vec{F}\)

 

Angular momentum:
Moment of linear momentum about the axis of rotation is called angular momentum and it is denoted by L.
L = pr
or \(\vec{L}=\vec{r} \times \vec{p}\)

Principle of conservation of angular momentum:
In absence of external toruqe, the angular momentum of a body or system of particles remains unchanged i.e, remains conserved.

Centre of gravity:
The point in the body about which the net torque of gravitational force is zero, is called the centre of gravity of the body. The weight of the body is centered at this point.

Moment of inertia:
Inertia of body in rotation motion is called its moment. It is measured by product of mass and square of its distance from the axis of rotation i. e.,
I = mr²

Radius of gyration:
Mass of all particles of a body is supposed to be centralised at a point', the square of its distance of which when multiplied by net mass of the body, then moment of inertia of the body is obtained. This distance is called the radius of gyration which is represented by K.
∴ I = MK² ⇒ K = \(\sqrt{\frac{I}{M}}\)

Important theorems regarding moment of inertia:
(i) Theorem of perpendicular axes: According to this theorem, “The moment of inertia of a plane lamina about an axis passing through it at right angles to its plane is equal to sum of moments of inertia of the lamina about two perpendicular axes lying in the plane of the lamina and meeting at the desired axis. i.e. “If lamina is in X-Y-plane, then its moment of inertia is about Z-axis”
I_z = I_x + I_y

(ii) Theorem of parallel axes: According to this theorem, “The moment of inertia of a body about an axis is equal to the sum of moment of inertia of the body about the parallel axes passing through the centre of mass and product of mass of the body and square of distance between the axes.” i. e.,
I = I_cm + Mh²

Rotational kinetic energy:
Kinetic energy of the particle in rotational motion is called rotational kinetic energy i. e., E_R = \frac{1}{2} Iω².

Rolling motion:
Such motion of a rigid body in which the body moves rotating about the moving axis is called rolling motion. This motion is sum of translational and rotational motion.

Kinetic energy in rolling motion:
As the rolling motion is sum of translational and rotational motions therefore energy is rolling motion
E_rolling = E_{translational} + E_rotational

→ Position vector of the centre of mass of two particle system,
\(\overrightarrow{r_{c m}}=\frac{m_1 \overrightarrow{r_1}+m_2 \overrightarrow{r_2}}{m_1+m_2}\)

→ Position vector of the centre of mass of n-particle system.

→ Co-ordinates of the centre of mass,

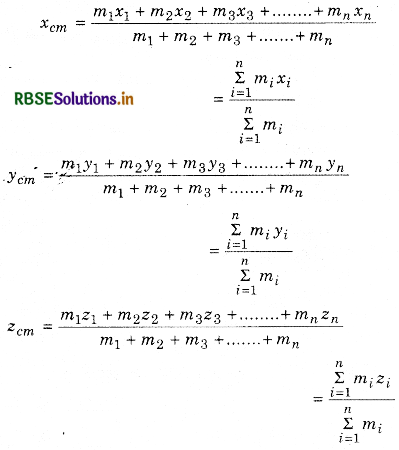
→ Position vector of the centre of mass continuous body,
\(\overrightarrow{r_{c m}}=\frac{\int \vec{r} \cdot d m}{\int d m}=\frac{1}{m} \int \vec{r} \cdot d m\)

→ Motion of the centre of mass,

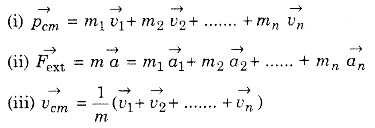
→ Vector product of two vectors
\(\vec{A} \times \vec{B}=|\vec{A}| .|\vec{B}|\) sin θ, n̂ = A. B sin θ, n̂

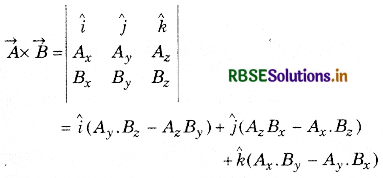
→ Moment of force or torque, \(\vec{\tau}=\frac{d \vec{L}}{d t}\)

→ Moment of couple of force \(\vec{\tau}=\vec{r} \times \vec{F}\)

→ Angular momentum,
\(\vec{L}=\vec{r} \times \vec{p}\)

For three dimensional motion,
L_x = y.p_z - zp_y
L_y = z.p_x - xp_z
L_z = x.p_y - yp_x

→ Principle of Torques
F₁d₁ = F₂d₂

→ Equations of rotational motion,
ω = ω₀ + αt
θ = ω₀t + \(\frac{1}{2}\)αt²
ω² = ω₀² + 2αθ

→ Moment of inertia, I = \(\sum_{i=1}^n\) m₁r_i² or I = Σmr²

→ Radius of gyration

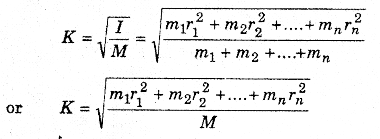
→ Theorem of perpendicular axes regarding moment of inertia.
I_z = I_x + I_y

→ Theorem of parallel axes regarding moment of inertia
I = I_cm + Mh²

→ Relation between torque and moment of inertia,
τ = I.α

→ Angualr momentum, L = I.ω

→ Rotational energy, E_R = Iω²

→ Principle of conservation of angular momentum,
I₁ω₁ = I₂ω₂

→ Effect on length of day,
\(\frac{T_1}{T_2}=\frac{R_1^2}{R_2^2}=\left(\frac{R_1}{R_2}\right)^2\)

→ Total energy of body in rolling motion,
E = \(\frac{1}{2} m v^2\left(1+\frac{K^2}{R^2}\right)\)

→ In rolling motion on inclined plane the velocity of the body at the base of the plane,
v = \(\sqrt{\frac{2 g h}{\left(1+\frac{K^2}{R^2}\right)}}\)

→ Acceleration of the body
a = \(\frac{g \sin \theta}{\left(1+\frac{R^2}{R^2}\right)}\)

→ Couple of forces:
When two equal and opposite forces act on a body such that their lines of action be different, then it is called the couple of forces

→ Centre of gravity:
The point at which the weight of the body is effective and about which the moment of total gravitational force is zero, is called the centre of gravity of the body.

→ Moment of inertia: Inertia of body in rotational motion is called the moment of inertia.

→ Rotation energy: Kinetic energy of the body in rotational motion is called the rotational energy.