RBSE Class 11 Physics Notes Chapter 6 कार्य, ऊर्जा और शक्ति

These comprehensive RBSE Class 11 Physics Notes Chapter 6 कार्य, ऊर्जा और शक्ति will give a brief overview of all the concepts.

RBSE Class 11 Physics Chapter 6 Notes कार्य, ऊर्जा और शक्ति

→ अदिश गुणनफल-किन्हीं दो सदिशों \(\overrightarrow{\mathrm{A}}\) तथा \(\overrightarrow{\mathrm{B}}\) के अदिश या बिन्दु गुणनफल (डॉट गुणनफल) को हम \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}} (\overrightarrow{\mathrm{A}})\) डॉट \((\overrightarrow{\mathrm{B}})\) के रूप में लिखते हैं। इसको निम्न प्रकार से परिभाषित कर सकते हैं
\(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}\) = AB cos θ
यहाँ θ दो सदिशों \(\overrightarrow{\mathrm{A}}\) तथा \(\overrightarrow{\mathrm{B}}\) के बीच का कोण है।
\(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}\) = A (B cos θ)
= B (A cos θ)
ज्यामिति के अनुसार B cos θ सदिश \(\overrightarrow{\mathrm{B}}\) का सदिश A पर प्रक्षेप है। इसी प्रकार (A cos θ) सदिश \(\overrightarrow{\mathrm{A}}\) का सदिश \(\overrightarrow{\mathrm{B}}\) पर प्रक्षेप है।
गुणनफल क्रम विनिमेय नियम का पालन करता है।
\(\vec{A} \cdot \vec{B}=\vec{B} \cdot \vec{A}\)

यह अदिश गुणनफल वितरण-नियम का भी पालन करता है।
A . (B + ) = A . B + A. हे
î.î = ĵ.ĵ = k̂.k̂ = 1
î.ĵ = ĵk̂= k̂î = 0
यहाँ पर î, ĵ तथा k̂ एकांक सदिश हैं।
दो सदिशों \(\vec{A}\) = A_xi + A_yj + A_zk
तथा B = B_xi +B_yj + B_zk का अदिश गुणनफल

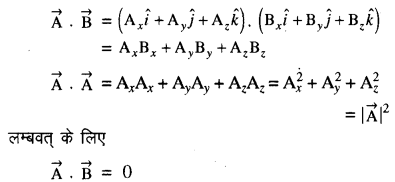
→ कार्य-किसी बल द्वारा किया गया कार्य “बल के विस्थापन की दिशा के अनुदिश घटक और विस्थापन के परिमाण के गुणनफल" के रूप में परिभाषित किया जाता है।
w = (F cos θ) S = \(\vec{F} \cdot \vec{s}\)
कोई भी कार्य सम्पन्न हुआ नहीं माना जाता है यदि

• वस्तु का विस्थापन शून्य है।
• बल शून्य है।
• बल और विस्थापन परस्पर लम्बवत् हैं।

→ कार्य धनात्मक व ऋणात्मक दोनों प्रकार का हो सकता है। यदि ए का मान 0° और 90° के बीच है तो कार्य धनात्मक होगा। यदि θ का मान 90° और 180° के बीच है तो कार्य का मान ऋणात्मक होगा।
ऐसे अनेक उदाहरण देखने को मिलते हैं जिसमें बल, विस्थापन का विरोध करता है और θ = 180° होता है। ऐसी दशा में घर्षण बल द्वारा किया गया कार्य ऋणात्मक होता है। ∵ cos180° = -1
ऋणात्मक कार्य वस्तु की गति में मंदन उत्पन्न करता है। कार्य समय पर निर्भर नहीं करता है।

→ यद्यपि किसी पिण्ड B द्वारा A पर आरोपित बल, पिण्ड A द्वारा पिण्ड B पर आरोपित बल के बराबर तथा विपरीत दिशा में होता है (गति का तृतीय नियम) परन्तु यह आवश्यक नहीं है कि पिण्ड B द्वारा पिण्ड A पर किया गया कार्य पिण्ड A द्वारा पिण्ड B पर किये गये कार्य के बराबर तथा विपरीत हो।

→ परिवर्ती बल द्वारा किया गया कार्य-यदि परिवर्ती बल \(\vec{F}\) के प्रभाव में वस्तु x₁ से x₂ दूरी चले तो
कार्य w = \(\int_{x_1}^{x_2} \overrightarrow{\mathrm{F}} \cdot \overrightarrow{d x}\)
W = बल विस्थापन लेखाचित्र व विस्थापन अक्ष के मध्य क्षेत्रफल

→ ऊर्जा-वस्तु द्वारा कार्य करने की क्षमता को ऊर्जा कहते हैं। ऊर्जा का मात्रक भी जूल होता है।
अन्य मात्रक 1 kwh = 3.6 × 10⁶ जूल
1 eV = 1.6 × 10^-19 जूल

→ ऊर्जा के विभिन्न रूप-प्रकृति में ऊर्जा के कई स्वरूप पाये जाते हैं। जैसे ध्वनि ऊर्जा, प्रकाश ऊर्जा, रासायनिक ऊर्जा, वैद्युत ऊर्जा, यांत्रिक ऊर्जा आदि । ऊर्जा के कुछ स्वरूप निम्न प्रकार के होते हैं

• आन्तरिक ऊर्जा
• ऊष्मा ऊर्जा
• रासायनिक ऊर्जा
• विद्युत ऊर्जा
• नाभिकीय ऊर्जा
• यांत्रिक ऊर्जा।

→ गतिज ऊर्जा-यदि किसी पिण्ड का द्रव्यमान (m) और वेग 1 है तो इसकी गतिज ऊर्जा ।
K = \(\frac{1}{2} m(\overrightarrow{\mathrm{v}} \cdot \overrightarrow{\mathrm{v}})=\frac{1}{2}\)mv²
गतिज ऊर्जा एक अदिश राशि है।
किसी पिण्ड की गतिज ऊर्जा उस पिण्ड द्वारा किये गये कार्य की माप होती है जो अपनी गति के कारण कर सकता है।

→ m द्रव्यमान के किसी कण की पृथ्वी की सतह से h ऊँचाई पर गुरुत्वीय स्थितिज ऊर्जा U = mgh होती है। जहाँ ऊँचाई के साथ g के मान में परिवर्तन उपेक्षणीय है।

→ किसी स्प्रिंग की स्थितिज ऊर्जा-K बल-नियतांक वाले स्प्रिंग जिसमें खिंचाव x है, की प्रत्यास्थ स्थितिज ऊर्जा होती है।
U = \(\frac{1}{2}\)kx²

→ कार्य-ऊर्जा प्रमेय-इस प्रमेय के अनुसार किसी पिण्ड की गतिज ऊर्जा में परिवर्तन उस पर आरोपित कुल बल द्वारा किया गया कार्य है।
K_f - K_i = W_net

→ कोई बल संरक्षी कहलाता है। यदि (i) उसके द्वारा किसी पिण्ड पर किया गया कार्य पथ पर निर्भर न करके केवल सिरे के बिन्दुओं {x_i, x_j} पर निर्भर करता है, अथवा
(ii) बल द्वारा किया गया कार्य शून्य होता है। जब पिण्ड के लिए जो स्वेच्छा से किसी ऐसे बंद पथ में स्वतः अपनी प्रारम्भिक स्थिति पर वापस आ जाता है।

→ एक विमीय संरक्षी बल के लिए हम स्थितिज ऊर्जा फलन U_(x) को इस प्रकार परिभाषित कर सकते हैं
F (x) = \(\frac{\mathrm{U}_{(x)}}{d x}\)
अथवा U_i - U_f = \(\int_{x_i}^{x_f}\) F(x) d x

→ ऊर्जा संरक्षण का सिद्धान्त-संरक्षी बलों की उपस्थिति में किसी विलगित निकाय की यांत्रिक ऊर्जा संरक्षित रहती है। यानी स्थितिज और गतिज ऊर्जा का योग सदैव नियत रहता है।
K.E. + PE. = E
स्थिरांक असंरक्षी बलों की उपस्थिति में निकाय की कुल ऊर्जा (यांत्रिक ऊष्मा आदि) का मान संरक्षित रहता है।

→ द्रव्यमान ऊर्जा तुल्यता-अल्बर्ट आइन्सटीन के अनुसार ऊर्जा व द्रव्यमान तुल्य राशियाँ होती हैं। द्रव्यमान का ऊर्जा में एवं ऊर्जा का द्रव्यमान में रूपान्तरण संभव है। स्थिर द्रव्यमान m से सम्बन्धित ऊर्जा निम्न समीकरण द्वारा दी जाती है
E = mc²
यहाँ पर c निर्वात में प्रकाश की चाल है और इसका मान c = 3 × 10⁸ मी./से. होता है।

→ शक्ति-कार्य करने की दर को शक्ति कहते हैं।
किसी बल की औसत शक्ति उस बल द्वारा किये गये कार्य W और उसमें लगे समय t के अनुपात से परिभाषित करते हैं अतः
P_av = \(\frac{W}{t}\)
P = \(\frac{d \mathrm{~W}}{d t}=\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{v}}\)
जहाँ \(\vec{v}\) तात्क्षणिक वेग है जबकि बल \(\vec{F}\) है। कार्य और ऊर्जा की भाँति शक्ति भी एक अदिश राशि है।
इसका मात्रक वॉट होता है।
अन्य मात्रक 1 अश्व शक्ति = 746 वॉट
1 वॉट = 1 जूल/सेकण्ड
1 kwh = 3.6 × 10⁶ जूल

→ पिण्डों में टक्कर-जब एक पिण्ड दूसरे पिण्ड से टकराता है तो अन्योन्य क्रिया के कारण पिण्डों की गति एवं संवेग में परिवर्तन आ जाता है। इस प्रक्रिया को टक्कर कहते हैं। यह दो प्रकार की होती है

• प्रत्यास्थ टक्कर-इसमें रेखीय संवेग संरक्षण के साथ-साथ गतिज ऊर्जा भी संरक्षित रहती है। उदाहरण-नाभिकीय मूल कणों के मध्य अन्योन्य क्रिया।
• अप्रत्यास्थ टक्कर-ऐसी टक्करों में रेखीय संवेग संरक्षित रहता है तथा गतिज ऊर्जा संरक्षित नहीं रहती है और टक्कर के पश्चात् गतिज ऊर्जा का मान कम हो जाता है। उदाहरण के लिये, सामान्य वस्तुओं की टक्कर।

→ सरल रेखीय या एकविमीय प्रत्यास्थ टक्कर
u₁ - u₂ = - (v₁ - v₂)
Δu = - Δv
अतः टक्कर से पूर्व पास आने की सापेक्ष गति तथा टक्कर के पश्चात् दूर हटने की सापेक्ष गति बराबर होती है।
टक्कर के पश्चात् वेग v₁ व v₂ के मान निम्नलिखित होते हैं

→ प्रत्यवस्थान गुणांक-टक्कर के पश्चात् और टक्कर के पूर्व कणों के आपेक्षिक वेगों का अनुपात नियत होता है। इस नियत अनुपात को - e द्वारा प्रदर्शित किया जाता है। ए को प्रत्यवस्थान गुणांक कहते
हैं।
-e = \(\frac{\overrightarrow{\mathrm{v}_1}-\overrightarrow{\mathrm{v}_2}}{\overrightarrow{u_1}-\overrightarrow{u_2}}\)
पूर्णतः प्रत्यास्थी टक्कर के लिये e = 1
पूर्णतया अप्रत्यास्थी टक्कर के लिये e = 0
आंशिक प्रत्यास्थी टक्कर के लिये 0 < e < 1

→ द्विविमीय टक्कर अथवा तिर्यक टक्कर-यदि टक्कर के पश्चात् वस्तुयें केन्द्रों को जोड़ने वाली रेखा की दिशा में न चलें तो टक्कर तिर्यक टक्कर कहलाती है। इस स्थिति में हमको निम्न समीकरण प्राप्त होते हैं
(i) x-अक्ष की दिशा में संवेग संरक्षण से
m₁u₁cos α₁ + m₂u₂cos α₂

(ii) y-अक्ष की दिशा में संवेग संरक्षण से
m₁u₁sin α₁ + m₂u₂sin α₂ = m₁v₁sin β₁ + m₂v₂sin β₂