RBSE Class 11 Physics Notes Chapter 5 गति के नियम

These comprehensive RBSE Class 11 Physics Notes Chapter 5 गति के नियम will give a brief overview of all the concepts.

RBSE Class 11 Physics Chapter 5 Notes गति के नियम

→ अरस्तू का यह दृष्टिकोण, कि किसी पिण्ड की एकसमान गति रखने के लिए बल आवश्यक है, गलत है। व्यवहार में विरोधी घर्षण बल को प्रभावहीन करने के लिए कोई बल आवश्यक होता है।

→ जड़त्व (Inertia)-यदि कोई पिण्ड स्थिर है तो वह स्थिर रहना चाहता है तथा यदि गतिशील है तो गतिशील रहना चाहता है। पदार्थ के इस गुण को जड़त्व का गुण कहते हैं | . किसी पिण्ड के जड़त्व का गुण निम्न तीन रूपों में दर्शाया जा सकता है

• स्थिरता का जड़त्व
• गतिशीलता का जड़त्व
• दिशा का जड़त्व।

→ जड़त्व एक भौतिक राशि नहीं है। यह तो वस्तु का अंतर्निहित गुण है जो कि वस्तु के द्रव्य भाग पर निर्भर करता है।

→ इसका कोई मात्रक अथवा विमा नहीं होती है।

→ समान द्रव्यमान की दो वस्तुओं (जिसमें से एक गतिमान है और दूसरी स्थिर है) का जड़त्व समान होता है चूंकि जड़त्व केवल द्रव्यमान पर निर्भर करता है। यह वस्तु के वेग व आकार पर निर्भर नहीं करता।

→ रेखीय संवेग-किसी गतिशील वस्तु के वेग तथा द्रव्यमान के गुणनफल को वस्तु का रेखीय संवेग कहते हैं। इसे P से प्रकट करते हैं। रेखीय संवेग
\(\overrightarrow{\mathrm{P}}\) = द्रव्यमान × वेग = m \(\overrightarrow{\mathrm{v}}\)

→ गति का प्रथम नियम (First Law of Motion)
“इस नियम के अनुसार यदि कोई पिण्ड स्थिर है तो वह स्थिर ही रहेगा तथा गतिशील है तो नियत वेग से गतिशील रहेगा, जब तक उस पर कोई बाह्य असंतुलित बल कार्य नहीं करता है।" प्रत्येक पिण्ड सरल रेखा में नियत चाल से गतिमान रहेगा जब तक कोई बाह्य बल उसकी गति को परिवर्तित नहीं करता है।

→ गति का द्वितीय नियम (Second Law of Motion)
किसी वस्तु के संवेग में परिवर्तन की दर उस वस्तु पर आरोपित असंतुलित बल के अनुक्रमानुपाती होती है तथा संवेग में यह परिवर्तन बल की दिशा में होता है। इसको दो भागों में विभाजित किया गया है

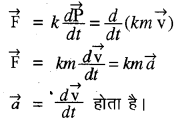
यहाँ F पिण्ड पर आरोपित नेट बाह्य बल है तथा \(\vec{a}\) पिण्ड में

उत्पन्न त्वरण है। SI मात्रकों में राशियों के मात्रकों का चयन कर आनुपातिकता स्थिरांक k = 1 आता है। तब \(\overrightarrow{\mathrm{F}}=\frac{\overrightarrow{d \mathrm{P}}}{d t}=m \vec{a}\) बल का मात्रक न्यूटन होता है।
1N = 1kg m/s²

• किसी पिण्ड के संवेग में परिवर्तन की दर उस पर आरोपित बल के अनुक्रमानुपाती होती है।
• पिण्ड के संवेग में परिवर्तन आरोपित बल की दिशा में होता

→ आवेग (Impulse):
बल तथा समय का गुणनफल आवेग कहलाता है जो संवेग परिवर्तन के बराबर होता है। अतः आवेग
\(\vec{J}=\vec{P} \Delta t\)
आवेग की धारणा उसी स्थिति में लाभदायक होती है जब कोई वृहत् बल अल्पकाल के लिये कार्य करके संवेग में मापने योग्य परिवर्तन उत्पन्न कर देता है क्योंकि बल का क्रिया समय अत्यंत अल्प है इसलिए यह कहा जा सकता है कि आवेगी बल लगने के समय वस्तु की स्थिति में पर्याप्त परिवर्तन नहीं होगा।

→ आवेग का मान धनात्मक, ऋणात्मक या शून्य हो सकता है। यह बल के सम्पूर्ण प्रभाव का मापन है।

→ आवेग संवेग प्रमेय के अनुसार यदि किसी पिण्ड के संवेग में परिवर्तन नियत है तो उसका आवेग भी नियत होगा।

→ आवेगी बल का मान नियत नहीं रहता है बल्कि प्रारम्भ में यह शून्य से अधिकतम उसके पश्चात् अधिकतम से शून्य तक परिवर्तित होता है अर्थात् आवेग का मान समय पर निर्भर रहता है।
एक नियत संवेग परिवर्तन जो यदि कम समय में करना हो तो अधिक बल लगाना पड़ेगा और वही संवेग परिवर्तन के लिए कम बल लगाना पड़ेगा। अतः समान आवेग की स्थिति में
\(\overrightarrow{F_1} t_1=\vec{F}_2 t_2\)
यदि t₁ < t₂ तो \(\overrightarrow{F_1}>\overrightarrow{F_2}\)

→ न्यूटन का तृतीय नियम-इस नियम के अनुसार प्रत्येक क्रिया की समान परिमाण की तथा विपरीत दिशा में प्रतिक्रिया होती है एवं क्रिया तथा प्रतिक्रिया बल भिन्न-भिन्न पिण्डों पर लगते हैं। जब किसी स्प्रिंग को हथेली से दबाते हैं तो हाथ द्वारा लगाया गया क्रिया (action) बल \(\overrightarrow{\mathrm{F}}_{\mathrm{H}}\) है और स्प्रिंग द्वारा लगाया गया प्रतिक्रिया (reaction) बल \(\overrightarrow{\mathrm{F}}_{\mathrm{S}}\) है। न्यूटन के तृतीय नियम से
\(\overrightarrow{\mathrm{F}}_{\mathrm{H}}=\overrightarrow{\mathrm{F}}_{\mathrm{S}}\)
होगा। दोनों बलों की दिशायें विपरीत होंगी।

→ रॉकेट, प्रतिक्रिया टरबाइन, तोप का प्रतिक्षेप वेग आदि क्रिया और प्रतिक्रिया के सिद्धान्त पर आधारित हैं।

→ रैखिक संवेग संरक्षण का नियम (Law of Conservation of Linear Momentum)-न्यूटन के द्वितीय नियम से किसी निकाय के रेखीय संवेग में परिवर्तन की दर उस पर लग रहे कुल बाह्य बल के बराबर होती है।
अतः है \(\vec{F}=\frac{\overrightarrow{d P}}{d t}\)
यदि कुल बाह्य बल \(\vec{F}\) के अनुपस्थित हो तो \(\vec{F}\) = 0
\(\frac{\overrightarrow{d P}}{d t}\) = 0
\(\vec{P}\) = स्थिरांक
अर्थात् कुल बाह्य बल की अनुपस्थिति में किसी निकाय का कुल रेखीय संवेग नियतं रहता है । यही रेखीय संवेग संरक्षण का नियम है।
दो कणों की स्थिति में \(\vec{P}_1+\vec{P}_2\) नियतांक आन्तरिक बलों की उपस्थिति से इस नियम पर प्रभाव नहीं पड़ता है क्योंकि अन्योन्य क्रिया के कारण लगने वाले आन्तरिक बल न्यूटन के तृतीय नियम का पालन करते हैं।

→ संगामी बलों का सन्तुलन (Equilibrium of Concurrent Forces):
यदि किसी वस्तु पर लगने वाले बलों की क्रिया रेखायें (lines of action) एक उभयनिष्ठ बिन्दु से गुजरती हैं तब केवल संगामी बल कहलाते हैं। तीन संगामी बलों के संतुलन के लिये आवश्यक शर्त

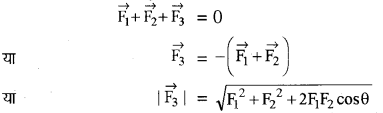
यानी कि सन्तुलन की स्थिति में तीसरा बल पहले और दूसरे बल के परिणामी प्रभाव के बराबर तथा विपरीत दिशा में कार्यरत होना चाहिये।

→ जब दो धरातलों के बीच आपेक्षिक गति हो तो उनके बीच दिशा में एक बल लगता है, जिसे घर्षण बल कहते हैं। घर्षण दो प्रकार के होते हैं-पिण्ड की स्थिर अवस्था में स्थैतिक घर्षण व गतिमान अवस्था में गतिक घर्षण।

→ घर्षण कोण (λ)-सीमान्त घर्षण की अवस्था में वस्तु पर कार्यरत कुल' प्रतिक्रिया बल और अभिलम्ब के मध्य बनने वाला कोण
tan λ = μ_s

→ विश्राम कोण (θ₀)-नत तल का क्षैतिज से वह अधिकतम कोण जिस पर रखा पिण्ड स्थिर रहता है।
tan θ₀ = μ_s

→ लोटनी घर्षण-जब कोई वस्तु लुढ़कती है तो एक बल लुढ़कने का विरोध करता है। वह बल लोटनी घर्षण बल कहलाता है। लोटनी घर्षण बल का मान स्थैतिक और गतिक घर्षण की अपेक्षा बहुत कम होता है।

→ घर्षण गुणांक

• μ_r < μ_k < μ_s
• घर्षण गुणांक पदार्थ की प्रकृति तथा पृष्ठों के खुरदरेपन पर निर्भर करते हैं।

→ घर्षण कम करने की विधियाँ

• स्नेहक (Lubricant)-दो ठोस सतहों के बीच घर्षण को कम करने के लिये काम में लाये जाने वाले पदार्थ; जैसे-तेल, ग्रीस आदि स्नेहक कहलाते हैं।
• बॉल बियरिंग द्वारा तथा
• पॉलिश द्वारा।

→ वर्तुल (वृत्तीय) गति में अभिकेन्द्र बल-r त्रिज्या के किसी वृत्त में एकसमान चाल v से गतिमान किसी पिण्ड का त्वरण \(\left(\frac{\mathrm{V}^2}{r}\right)\) वृत्त के केन्द्र की ओर निर्दिष्ट होता है। द्वितीय नियम के अनुसार इस त्वरण को प्रदान करने वाला बल है
f_c = \(\frac{\mathrm{mv}^2}{\mathrm{r}}\)
जहाँ पर m पिण्ड की संहति है। केन्द्र की ओर निर्दिष्ट इस बल को अभिकेन्द्र बल कहते हैं ।

→ समतल वृत्ताकार पथ पर वाहन की गति- समतल वृत्ताकार पथ पर नियत चाल से गति करने के लिए चाल की एक अधिकतम सीमा निम्न समीकरण द्वारा दी जाती है
V_max = \(\sqrt{\mu r g}\)
यदि वाहन इससे अधिक चाल से गति करे तो वह वृत्ताकार पथ के केन्द्र 0 से दूर (सड़क के बाहर) की ओर फिसल जायेगा।

→ करवट वाली सड़क पर इष्टतम चाल
v = \(\sqrt{r g \tan \theta}\)
इस चाल पर वाहन के टायरों पर त्रिज्यीय दाब नहीं होगा और टायरों में जीर्ण-शीर्ण न्यूनतम रहेगा v = \(\sqrt{r g \tan \theta}\) से प्राप्त होने वाली चाल आदर्श चाल कहलाती है।

→ करवट वाली वृत्ताकार सड़क पर सुरक्षित चाल
(i) अधिकतम सुरक्षित चाल
V_max = \(\sqrt{\frac{r g(\tan \theta+\mu)}{(1-\mu \tan \theta)}}\)
यह करवट कोण θ वाली r त्रिज्या की वृत्ताकार मोड़ पर किसी वाहन की अधिकतम सुरक्षित चाल का व्यंजक है, जहाँ μ टायरों और सड़कं के मध्य घर्षण गुणांक है।

(ii) न्यूनतम सुरक्षित चाल
V_min = \(\sqrt{\frac{r g(\tan \theta-\mu)}{(1+\mu \tan \theta)}}\)
यहाँ पर करवट कोण θ इस प्रकार रखा जाता है कि अपेक्षित चाल सुरक्षित अधिकतम चाल V_max और सुरक्षित न्यूनतम चाल V_min के मध्य रहे।