RBSE Class 11 Physics Notes Chapter 4 समतल में गति

These comprehensive RBSE Class 11 Physics Notes Chapter 4 समतल में गति will give a brief overview of all the concepts.

RBSE Class 11 Physics Chapter 4 Notes समतल में गति

→ भौतिक राशियाँ-वे राशियाँ जिनका मापन किया जा सकता है, उन राशियों को भौतिक राशियाँ कहते हैं । भौतिक राशियों को उनके मान व मात्रक से व्यक्त किया जाता है।

→ अदिश राशियाँ-ऐसी भौतिक राशियाँ जिन्हें पूर्णतया व्यक्त करने के लिए केवल परिमाण व मात्रक की ही आवश्यकता होती है, अदिश राशियाँ कहलाती हैं। उदाहरण-व्यमान, दूरी, चाल, कार्य, ऊर्जा, घनत्व, आयतन, ताप आदि।

→ सदिश राशियाँ-ऐसी भौतिक राशियाँ जिन्हें पूर्णतया व्यक्त करने के लिए परिमाण व मात्रक के साथ दिशा का उल्लेख भी आवश्यक होता है, सदिश राशियाँ कहलाती हैं।
उदाहरण-विस्थापन, वेग, त्वरण, बल, संवेग आदि सदिश राशियाँ हैं।

→ सदिशों का निरूपण-किसी सदिश राशि को एक सरल रेखा द्वारा निरूपित किया जा सकता है, जिसके अन्तिम सिरे पर एक तीर लगाया जाता है। तीर का प्रारम्भिक बिन्दु A पुच्छ (Tail) व अन्तिम बिन्दु B शीर्ष (Head) कहलाता है। इसे हम AB से व्यक्त करते हैं।

→ स्थिति एवं विस्थापन सदिशस्थिति सदिश-बिन्दु P पर स्थित कण का स्थिति सदिश
$\vec{r}$ = xî + yĵ + zk̂ और
$|\vec{r}|=\sqrt{\left(x^2+y^2+z^2\right)}$
r² = x² + y² + z²
cos²α + cos²β + cos²γ = 1 होता है।

→ विस्थापन सदिश-जब कोई कण P (x₁, y₁, z₁) से Q (x₂, y₂, z₂) तक विस्थापित होता है, तब कण का विस्थापन सदिश
$|\overrightarrow{\Delta r}|$ = (x₂ - x₁)î + (y₂ - y₁) ĵ + (z₂ - z₁) k̂
विस्थापन सदिश $\overrightarrow{\Delta r}$ का परिमाण
$|\overrightarrow{\Delta r}|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}$

→ एकांक सदिश-वह सदिश जिसका परिमाण एकांक (1) तथा दिशा दिये गये सदिश के समान्तर हो, एकांक सदिश कहलाता है। X, Y व Z अक्षों की दिशाओं में एकांक सदिश क्रमशः î, ĵ व k̂ होते हैं।
किसी सदिश $\vec{A}$ का एकांक सदिश
n̂ = $\frac{\overrightarrow{\mathrm{A}}}{|\overrightarrow{\mathrm{A}}|}$

→ सदिशों का संयोजन-दो सदिशों का संयोजन निम्न विधियों द्वारा किया जा सकता है
(i) सदिश संयोजन का त्रिभुज नियम-इस नियम के अनुसार, “यदि किसी त्रिभुज की दो भुजाएँ एक ही क्रम में दो सदिशों को व्यक्त करें तो तीसरी भुजा विपरीत क्रम में उनके योग को व्यक्त करती है।"
$\overrightarrow{\mathrm{P}}+\overrightarrow{\mathrm{Q}}=\overrightarrow{\mathrm{R}}$

(ii) सदिश संयोजन का समान्तर चतुर्भुज का नियम-“जब किसी समान्तर चतुर्भुज की दो आसन्न भुजाओं को क्रमशः दो सदिशों के परिमाण व दिशा के रूप में व्यक्त किया जाये, तब उनके कटान बिन्दु से होकर गुजरने वाला विकर्ण परिणामी सदिश के परिमाण व दिशा को व्यक्त करता है।"

यदि दो सदिशों $\overrightarrow{\mathrm{P}}$ व $\overrightarrow{\mathrm{Q}}$ के मध्य कोण 0 हो तो परिणामी सदिश R होगा।
R = $\sqrt{\mathrm{P}^2+\mathrm{Q}^2+2 \mathrm{PQ} \cos \theta}$
एवं सदिश परिणामी $\overrightarrow{\mathrm{R}}$ व $\overrightarrow{\mathrm{P}}$ के मध्य कोण
α = tan^-1$\left(\frac{\mathrm{Q} \sin \theta}{\mathrm{P}+\mathrm{Q} \cos \theta}\right)$

(iii) सदिश संयोजन का बहुभुज का नियम-इस नियम के अनुसार दो से अधिक सदिशों को क्रमशः विस्थापित कर किसी बहुभुज की क्रमिक भुजाओं द्वारा निरूपित किया जाये तो बहुभुज को बन्द करने वाली अन्तिम भुजा, परिमाण व दिशा में परिणामी सदिश को विपरीत क्रम में प्रदर्शित करती है।

→ सदिश योग के गुणधर्म
(i) क्रम विनिमेय का नियम
$\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}=\overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{A}}$

(ii) साहचर्य नियम
$(\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}})+\overrightarrow{\mathrm{C}}=\overrightarrow{\mathrm{A}}+(\overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{C}})$

(iii) वितरण नियम
$n(\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}})=\mathrm{n} \cdot \overrightarrow{\mathrm{A}}+\mathrm{n} \cdot \overrightarrow{\mathrm{B}}$

→ सदिशों का व्यवकलन-सदिश A से सदिश B को घटाने के लिए सदिश A तथा सदिश B के विपरीत (ऋणात्मक) सदिश का योग करना होता है। अर्थात्
$\overrightarrow{\mathrm{A}}-\overrightarrow{\mathrm{B}}=\overrightarrow{\mathrm{A}}+(-\overrightarrow{\mathrm{B}})$

→ संदिशों का वियोजन-सदिशों का वियोजन सदिशों के संयोजन का उल्टा होता है। यदि किसी सदिश $\overrightarrow{\mathrm{A}}$ के x,y व z अक्षों की दिशाओं में घटक क्रमशः A_x, A_y, व A_z, हों तो
A = A_xî + A_yĵ + A_zk̂
$|\overrightarrow{\mathrm{A}}|=\sqrt{\mathrm{A}_x^2+\mathrm{A}_y^2+\mathrm{A}_z^2}$
किसी सदिश के तीनों दिक्कोज्या के वर्गों का योग एक होता है।

→ समतल में गति-जब कोई वस्तु या कण एक तल में गति करता है तब इसे द्विविमा में गति कहते हैं, जैसे

• किसी कागज पर चींटी की गति
• क्षैतिज या ऊर्ध्वाधर तल में वृत्ताकार गति ।

→ द्विविमीय गति में कण के विस्थापन, वेग तथा त्वरण का सदिश निरूपणविस्थापन
$\overrightarrow{\Delta r}$ = Δxi + Δyj
अर्थात् द्विविमीय गति में विस्थापन Δr, x-अक्ष के अनुदिश विस्थापन के घटक Δxi और y-अक्ष के अनुदिश विस्थापन घटक Δx j के सदिश योग के बराबर होता है। वेग

→ द्विविमीय समत्वरित गति के लिए गति के समीकरण

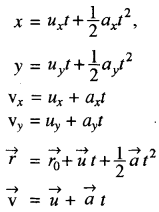
→ द्विविमीय गति में आपेक्षिक वेग-"किसी गतिशील कण या वस्तु का किसी अन्य गतिशील कण या वस्तु के सापेक्ष आपेक्षिक वेग उनके मध्य विस्थापन की समय के साथ परिवर्तन की दर के तुल्य होता है।"
वस्तु B के सापेक्ष वस्तु A का वेग
$\overrightarrow{\mathrm{v}}_{\mathrm{BA}}=\overrightarrow{\mathrm{v}_{\mathrm{B}}}-\overrightarrow{\mathrm{v}_{\mathrm{A}}}$
इसी तरह वस्तु A के सापेक्ष वस्तु B का वेग
$\overrightarrow{\mathrm{v}}_{\mathrm{AB}}=\overrightarrow{\mathrm{v}_{\mathrm{A}}}-\overrightarrow{\mathrm{v}_{\mathrm{B}}}$
$\overrightarrow{\mathbf{v}}_{\mathrm{AB}}=-\overrightarrow{\mathbf{v}}_{\mathrm{BA}}\left|\overrightarrow{\mathrm{v}}_{\mathrm{AB}}\right|=\left|\overrightarrow{\mathbf{v}}_{\mathrm{BA}}\right|$

→ प्रक्षेप्य गति-जब किसी वस्तु या कण को प्रारम्भिक वेग देकर पृथ्वी के गुरुत्वीय बल के प्रभाव में गति करने देते हैं, तब इस वस्तु को प्रक्षेप्य (Projectile) और इसकी गति को प्रक्षेप्य गति कहते हैं। एक प्रक्षेप्य का पथ परवलयाकार होता है। प्रक्षेप्य के पथ का समीकरण निम्न होता है
y = (tan θ)x - $\left(\frac{g}{2 u^2 \cos ^2 \theta}\right)$x²
प्रक्षेप्य की क्षैतिज परास
R = $\frac{u^2 \sin 2 \theta}{g}$
अधिकतम परास R_max = $\frac{u^2}{g}$
जब θ = 45°

प्रक्षेप्य की अधिकतम ऊँचाई
H = $\frac{u^2 \sin ^2 \theta}{2 g}$
एक नियत प्रारम्भिक चाल से फेंके गये प्रक्षेप द्वारा अधिकतम ऊँचाई तब प्राप्त हो सकती है जबकि प्रक्षेप कोण θ = 90° हो। जब प्रक्षेप्य को अधिकतम परास R के लिए θ = 45° पर फेंका जाता है तब अधिकतम ऊँचाई H_max = $\frac{1}{2}$R_max होती है।
प्रक्षेप्य का उड्डयन काल
T = $\frac{2 u \sin \theta}{g}$
एक प्रक्षेप्य को ऊर्ध्वाधर ऊपर की ओर (θ = 90° पर) फेंकने पर यह अधिकतम समय T_max = $\frac{2 u}{g}$ तक हवा में रहता है । स्पष्ट है कि अन्य किसी कोण पर फेंकने पर इसका उड्डयन काल ($\frac{2 u}{g}$) से कम प्राप्त होगा ।

→ एक समान वृत्तीय गति
अभिकेन्द्री त्वरण a_r =$\frac{\mathrm{v}^2}{\mathrm{R}}$
R त्रिज्या के एक वृत्ताकार पथ में नियत चाल से गति कर रहे कण का स्पर्शरेखीय त्वरण शून्य और अभिकेन्द्री त्वरण $\frac{\mathrm{v}^2}{\mathrm{R}}$ होता है। ऐसे कण का कुल त्वरण $\frac{\mathrm{v}^2}{\mathrm{R}}$ ही होता है, क्योंकि
a = $\frac{\mathrm{v}^2}{\mathrm{R}}$
a = ar = $\frac{v^2}{R}$