RBSE Class 11 Physics Notes Chapter 15 Waves

These comprehensive RBSE Class 11 Physics Notes Chapter 15 Waves will give a brief overview of all the concepts.

RBSE Class 11 Physics Chapter 15 Notes Waves

→ Wave motion:
It is a kind of disturbance which travels through a medium due to the repeated vibrations of the particles of the medium about their mean positions, the disturbance being handed over from one particle to the next.

Types:

• Mechanical waves: The waves which have required a mechanical medium for their propagation are called mechanical waves.
• Electromagnetic waves: The waves which travel in the form of oscillating electric and magnetic fields are called electromagnetic waves.
• Matter waves: The waves associated with microscopic particles, such as electrons, protons, neutrons, atoms, molecules, etc. when they are in motion, are called matter waves or De-Broglie waves.

→ Types of mechanical waves:

• Transverse waves: These are the waves in which,particles of the medium vibrate about their mean positions in a direction perpendicular to the direction of propagation of the disturbance.
• Longitudinal waves: These are the waves in which particles of the medium vibrate about their mean positions along the direction of propagation of the disturbance.

→ Progressive wave:
A wave that moves from one point of medium to another is called a progressive wave.

→ Amplitude: It is the maximum displacement suffered by the particles of the medium from the mean position during the propagation of a wave.

→ Time period: It is the time in which a particle of the medium completes one vibration about its mean position.

 

→ Frequency: It is the number of waves produced per second in a given medium.

→ Wavelength: It is the distance covered by a wave during the time a particle of the medium completes one vibration about its mean position. It is the distance between two nearest particles of the medium which are vibrating in the same phase.

→ Propagation constant: It represents the phase change per unit distance. It is equal to 271/X.

→ Wave velocity: It is the distance travelled by a wave in one second.

→ Relation between wave velocity, frequency and wavelength
Wave velocity = Frequency x Wavelength v = v × λ

→ Relation between wave velocity, time period and wavelength
Wave velocity = \(\frac{\text { Wavelength }}{\text { Timeperiod }}\)

→ Velocity of the transverse waves
(i) Velocity of the transverse waves in a solid of modulus of rigidity η and density ρ is given by
v = \(\sqrt{\frac{\eta}{\rho}}\)

(ii) Velocity of the transverse waves in a string of mass per unit length and stretched under tension T is given by
v = \(\sqrt{\frac{T}{m}}\)

→ Velocity of the longitudinal waves
(i) Velocity of the longitudinal Waves in an extended solid (earth’s crust) of bulk modulus β, modulus of rigidity η and density ρ is given by
v = \(\sqrt{\frac{\beta+\frac{4}{3} \eta}{\rho}}\)
The factor (β + (4/3)η is called elongational elasticity.

(ii) Velocity of the longitudinal waves in a long rod of Young’s modulus Y and density ρ is given by
v = \(\sqrt{\frac{Y}{\rho}}\)

(iii) Velocity of the longitudinal waves in a liquid of bulk modulus β and density ρ is given by
v = \(\sqrt{\frac{\beta}{\rho}}\)

(iv) Velocity of the longitudinal waves in a gaseous medium of bulk modulus k and density ρ is given by
v = \(\sqrt{\frac{\beta}{\rho}}\)
According to Newton, when sound travels through gas. the changes taking place in the medium are isothermal in nature. So Newton’s formula for the-speed of sound is
u = \(\sqrt{\frac{\beta_{\text {iso }}}{\rho}}=\sqrt{\frac{P}{\rho}}\), where P = pressure of the gas.

According to Laplace, when sound travels in a gas, the changes taking place in the medium are adiabatic. So Laplace formula for the speed of sound is
v = \(\sqrt{\frac{\beta_{\text {adia }}}{\rho}}=\sqrt{\frac{\gamma P}{\rho}}\)
where γ = \(\frac{C_p}{C_v}\) = specific heat ratio.

→ Factors affecting velocity through gases

• Effect of pressure: No effect on the speed of sound in a gas.
• Effect of density: v ∝ \(\frac{1}{\sqrt{\rho}}\) or \(\frac{v_1}{v_2}=\sqrt{\frac{\rho_2}{\rho_1}}\)
• Effect of temperature. As v = \(\sqrt{\frac{\gamma R T}{M}}\)
  ∴ v ∝ \(\sqrt{T}\) or \(\frac{v_1}{v_2}=\sqrt{\frac{T_1}{T_2}}\)
• Temperature coefficient of velocity of sound is given by
  α = \(\frac{v_t-v_0}{t}\)
  For air, a = 0.61 m s^-1°C^-1
• Effect of humidity: Sound travels faster in moist air.
• Effect of wind: If the wind blows with velocity mina direction making an angle 0 with the direction of sound, then the resultant velocity of sound will be v'= v + w COS0

→ Wave equation: A plane progressive harmonic wave travelling along positive x-direction may be represented as
y = A sin (ωt ∓ kx)
Where a = Amplitude
and ω = 2πv
K = \(\frac{2 \pi}{\lambda}\)
- = Indicate + direction
+ = Indicate (-) direction

→ Phase and phase difference:
Phase is the argument of the sine of cosine function representing the wave. Thus phase,
Φ = 2π\(\left(\frac{t}{T}-\frac{x}{\lambda}\right)\)
The relation between phase difference (ΔΦ) and time interval Δt is
ΔΦ = \(\frac{2 \pi}{T}\)Δt
Thus, in time period T, the phase of a particle changes by 2π

The relation between phase difference (ΔΦ) and path difference (Δx) is
ΔΦ = \(\frac{2 \pi}{T}\)Δt
The negative sign indicates that farther the particle is located from the origin in the positive x-direction, the more it lags behind in phase. Hence between two particles located at separation λ is 2π.

→ Principle of superposition of waves:
When a number of waves travel through a medium simultaneously, the resultant displacement at any point of the medium is equal to the vector sum of the displacements of the individual waves. If \(\overrightarrow{y_1}, \overrightarrow{y_2}, \overrightarrow{y_3}, \ldots, \overrightarrow{y_n}\) the displacements of n waves superposing each over at a point then the resultant displacement at that point will be
\(\vec{y}=\overrightarrow{y_1}+\overrightarrow{y_2}+\overrightarrow{y_3}+\ldots+\overrightarrow{y_n}\)

→ Reflection of a wave:
When a wave is reflected from a rigid boundary or a closed end, it is reflected back with a phase reversal or phase difference of n radians but reflection at an open boundary takes place without any phase change.

→ Stationary waves:
When two progressive waves of equal amplitude and frequency, travelling in opposite directions along a straight line superpose each other, the resultant wave does not travel in either direction and is called a stationary or standing wave. At some points, the particles of the medium always remain at rest. These are called nodes. At some other points, the amplitude of oscillation is maximum. These are called antinodes.

→ Organ pipe:
It is the simplest musical instrument in which sound is produced by setting an air column into vibrations. Longitudinal stationary waves are formed on account of superposition of the incident and the reflected longitudinal waves.

→ Beats:
The periodic variations in the intensity of sound due to the superposition of two sound waves of slightly different frequencies are called beats. One rise and one fall of intensity constitute one beat. The number of beats produced per second is called the beat frequency.
Beat frequency, v_beat = v₁ - v₂

Beats may be used to determine the frequency of a tuning fork. It must be noted here that:

• When the prong of a tuning fork is slightly loaded with wax, its frequency of vibration decreases.
• When the prong of a tuning fork is filed slightly, its frequency of vibration increases.

→ Doppler Effect in Sound:
The phenomenon of the change in apparent pitch of sound due to the relative motion between the source of sound and the observer is called the Doppler effect. If v, v₀, v_s and v_m are the velocities of sound, observer, source and medium (in the direction of sound) respectively then the apparent frequency is always changed;

→ Frequency v = \(\frac{1}{T}\) or time period T = \(\frac{1}{v}\)

→ Wave velocity v = vλ

→ Wave number \(\bar{v}=\frac{1}{\lambda}\)

→ Propagation constant k = \(\frac{2 \pi}{\lambda}\)

→ Wave velocity v = \(\frac{\omega}{k}\) where ω = 2πv = \(\frac{2 \pi}{T}\) and k = \(\frac{2 \pi}{\lambda}\)

→ Wave speed in a stretched string v = \(\sqrt{\left(\frac{T}{m}\right)}\)

→ Speed of longitudinal wave v = \(\sqrt{\left(\frac{E}{\rho}\right)}\)
For solids v = \(\sqrt{\left(\frac{Y}{\rho}\right)}\)
For liquids v = \(\sqrt{\left(\frac{B}{\rho}\right)}\)

→ Equation of a progressive wave:

• y = a sin(ωt - kx)
• y = a sin\(\frac{2 \pi}{\lambda}\)
• y = asin2π\(\left(\frac{t}{T}-\frac{x}{\lambda}\right)\)

→ Intensity of the wave, I = 2π²v² a²ρv

→ Energy density = 2π²v² a²ρ

→ Superposition.principle \(\vec{y}=\vec{y}_1+\vec{y}_2+\vec{y}_3 \ldots \vec{y}_n\)

→ Amplitude of the resultant wave
r = \(\sqrt{a^2+b^2+2 a b \cos \theta}\)
where θ =(β - α),β and α are the initial phase of wave

→ Equation of the standing wave:

• y = -2αsinkx cosωt = -2acos\(\frac{2 \pi x}{\lambda}cos\frac{2 \pi t}{T}\)
• y = 2a cos kx sin ωt = 2a cos\(\frac{2 \pi x}{\lambda}cos\frac{2 \pi t}{T}\)

→ Frequency of the fundamental tone in the stretched string
v = \(\frac{1}{2 l} \sqrt{\left(\frac{T}{m}\right)}\)

→ Laws of transverse vibration in a stretched string:

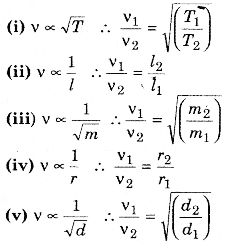
→ Fundamental frequency of a closed air column
v₁ = \(\frac{v}{4 l}\)

→ Fundamental frequency of an open air column
v₁ = \(\frac{v}{2 l}\)

→ Speed of sound from a resonance tube
u = 2v(l₂ - l₁)
and end-correction x =\( \frac{1}{2}\)(l₂ - l₁)

→ Velocity of sound in a gaseous medium (Newton)
v = \(\sqrt{\left(\frac{E_T}{\rho}\right)}=\sqrt{\left(\frac{P}{\rho}\right)}\)

→ Velocity of sound in a gaseous medium by Laplace
v = \(\sqrt{\left(\frac{E_s}{\rho}\right)}=\sqrt{\frac{\gamma P}{\rho}}\)

→ Effect of temperature on the velocity of sound

• v ∝ √T
• v_t = v₀ + 0.61t

→ Beat frequency, b = (v₁ - v₂)

→ Apparent frequency due to Doppler Effect:
(i) When only source is in motion then
v' = \(\left(\frac{v}{v \pm v_s}\right)\)v

(ii) When only observer is in motion, then
v' = \(\left(\frac{v \pm v_0}{v}\right)\)v

(iii) When both are in motion, then
v' = \(\frac{v \pm v_0}{v \pm v_s}\).v

(iv) Effect of air flow, v" = \(\left[\frac{\left(v \pm v_m\right) \pm v_0}{\left(v \pm v_m\right) \pm v_s}\right]\)v

→ Phase:
Phase is the argument of the sine or cosine function representing the wave.

→ Organ pipe:
It is the simplest musical instrument in which sound is produced by setting an air column into vibrations.

→ Resonance tube:
It is an organ pipe closed at one end.

→ Beats:
The periodic variations in the intensity of sound due to the superposition of two sound waves of slightly different frequencies are called beats.

→ Intensity of sound:
The intensity of sound at any point may be defined as the amount of sound energy passing per unit time per unit area around that point in a perpendicular direction.

→ Particle velocity:
It is the velocity with which the particle of the medium vibrate about their mean positions.

→ Phase velocity:
The distance covered by a wave in the direction of its propagation per unit time is called the wave velocity.

→ Node:
A node is formed at the boundary i. e., net displacement is zero.

→ Antinode:
An antinode is formed at the boundary where displacement is maximum.