RBSE Class 11 Physics Notes Chapter 14 दोलन

These comprehensive RBSE Class 11 Physics Notes Chapter 14 दोलन will give a brief overview of all the concepts.

RBSE Class 11 Physics Chapter 14 Notes दोलन

→ नदी में डूबती-उतरती हुई नाव, वाष्प इंजन में अग्र और पश्च चलता हुआ पिस्टन आदि इस प्रकार की गति को दोलन गति कहते हैं।

→ आवर्त गति-जब कोई गतिमान वस्तु एक निश्चित समय के पश्चात् अपनी पुरानी अवस्था में आ जाती है तथा वह फिर इसी प्रकार की गति बार-बार करती है तो उस गति को आवर्त गति कहते हैं।

→ प्रत्येक दोलनी गति आवर्त गति होती है क्योंकि प्रत्येक दोलनी गति निश्चित समय-अन्तराल के बाद दोहरायी जाती है। परन्तु प्रत्येक आवर्त गति दोलनी गति नहीं होती है, जैसे पृथ्वी की सूर्य के चारों ओर परिक्रमण की गति और अपने अक्ष पर घूर्णन की गति, आवर्त गतियाँ तो हैं परन्तु दोलनी गतियाँ नहीं हैं, क्योंकि वे किसी माध्य स्थिति के दोनों ओर नहीं होती हैं।

→ आवर्तकाल-"एक दोलन को पूरा करने में वस्तु जितना समय लेती है उसे उसका आवर्तकाल कहते हैं।" इसको T से प्रदर्शित किया जाता है।

→ आवृत्ति-"एक सेकण्ड में होने वाली आवर्ती गतियों की संख्या को अर्थात् पूरे किये गये दोलनों की संख्या को आवृत्ति कहते हैं।"

→ आवृत्ति तथा आवर्तकाल में सम्बन्ध

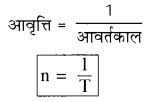
→ प्रत्यानयन बल
प्रत्यानयन बल (F) ∝ y
या F = - ky
यहाँ y = साम्यावस्था में वस्तु का विस्थापन यहाँ पर ऋण चिन्ह इस बात का प्रतीक है कि I तथा y की दिशा परस्पर विपरीत है तथा k एक नियतांक है, जिसे बल नियतांक कहते हैं।

→ विस्थापन तथा आयाम-दोलन करते हुए किसी कण द्वारा किसी क्षण माध्य स्थिति से तय की गयी दूरी को उसका विस्थापन कहते हैं। कण के विस्थापन के अधिकतम मान को आयाम कहते हैं।

→ आवर्ती फलन-वह फलन जिसकी निश्चित समयान्तराल पश्चात् पुनरावृत्ति होती है, आवर्ती फलन कहलाता है। या आवर्ती फलन के वे फलन जो आवर्ती गति को प्रदर्शित करने के लिए उपयोग में लाये जाते हैं।

→ सरल आवर्त गति-जब किसी कण को स्थायी साम्यावस्था की स्थिति से अल्प-सा विस्थापित कर छोड़ दिया जाता है तो वह साम्यावस्था की स्थिति के इर्द-गिर्द आवर्ती गति करती है। इस प्रकार की गति को सरल आवर्त गति कहते हैं। यह गति एक रेखा में हो सकती है। जैसे सरल लोलक अथवा भारित कमानी का पिण्ड । इस गति में प्रत्यानयन बल कण के माध्य स्थिति से विस्थापन के अनुक्रमानुपाती तथा विपरीत दिशा में होता है, अतः
F = - ky
किसी वृत्त की परिधि पर होने वाली एकसमान गति का वृत्त के व्यास पर प्रक्षेप की गति सरल आवर्त गति होती है। रैखिक सरल आवर्त गति का अवकल समीकरण
\(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dt}^2}\) + ω²y = 0
जहाँ ω² = \(\frac{k}{m}\)

→ कोणीय सरल आवर्त गति का अवकल समीकरण
\(\frac{\mathrm{d}^2 \theta}{\mathrm{dt}^2}\) + ω²θ = 0
जहाँ ω² = \(\frac{C}{I}\)
यदि किसी वस्तु का कोणीय त्वरण कोणीय विस्थापन के समानुपाती हो और सदा माध्य स्थिति की ओर कार्य करे तो वह वस्तु कोणीय सरल आवर्त गति करेगी।

→ सरल आवर्त गति का विस्थापन समीकरण
y = A sin (ωt + Φ)
यहाँ y = विस्थापन,
A = आयाम
ω = कोणीय आवृत्ति = 2πn = \(\frac{2 \pi}{T}\)
Φ = प्रारम्भिक कला कोण

→ एक दोलन में लगने वाले समय को आवर्तकाल (T) कहते हैं।

→ आयाम-माध्य स्थिति से अधिकतम विस्थापन आयाम (A) कहलाता है।

→ सरल आवर्त गति में वेग का मान
v = \(\frac{\mathrm{dy}}{\mathrm{dt}}=\frac{\mathrm{d}}{\mathrm{dt}}\) (A sin ωt) = Aω sin ωt
तथा v = ω\(\sqrt{\mathrm{A}^2-\mathrm{y}^2}\)

→ सरल आवर्त गति में त्वरण का मान
a = \(\frac{\mathrm{dv}}{\mathrm{dt}}=\frac{\mathrm{d}}{\mathrm{dt}}\) (aω cos ωt)
a = – aω sin ot = - ω²y
a = -ω²y

→ सरल आवर्ती दोलक की गतिज ऊर्जा
KE = \(\frac{1}{2}\)mω²(A² - y²)
= \(\frac{1}{2}\)mω² A² cos² ωt

→ सरल आवर्ती दोलक की स्थितिज ऊर्जा
PE = U = \(\frac{1}{2}\)ky² = \(\frac{1}{2}\)mω²y²
= \(\frac{1}{2}\)mω²a²sin²ωt

→ औसत गतिज ऊर्जा तथा स्थितिज ऊर्जा का मान
KE = K = \(\overline{\mathrm{U}}=\frac{1}{4}\) kA² =\( \frac{1}{4}\)mω²A²

→ सरल आवर्ती दोलक की कुल ऊर्जा का मान
E = \(\frac{1}{2}\)mω²A² = नियतांक
समय या विस्थापन पर निर्भर नहीं करती है
E = \(\frac{1}{2}\)m(2πn)²A² = 2π² mn² A²
सरल आवर्त गति में कण की सम्पूर्ण ऊर्जा कण के आयाम के वर्ग (A²) तथा आवृत्ति के वर्ग (n²) के समानुपाती होती है।

→ भारित स्प्रिंग
T = 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\)
T = 2π\(\sqrt{\frac{l}{g}}\)
समान्तर स्प्रिंग संयोजन
k = k₁ + k₂
श्रेणी क्रम स्प्रिंग संयोजन
k = \(\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_1+\mathrm{k}_2}\)

→ सरल लोलक का आवर्त काल
T = 2π\(\sqrt{\frac{l}{g}}\)
लोलक का आवर्तकाल लोलक की प्रभावी लम्बाई (l) के वर्गमूल के समानुपाती तथा गुरुत्वीय त्वरण (g) के वर्गमूल के व्युत्क्रमानुपाती होता है एवं गोलक के द्रव्यमान पर निर्भर नहीं करता है। चूंकि g का मान पृथ्वी की सतह से ऊँचाई, गहराई तथा घूर्णन गति पर निर्भर करता है, अतः आवर्तकाल भी परिवर्तित होगा।

→ सेकण्ड लोलक की प्रभावी लम्बाई l = 99.3 सेमी. प्राप्त होती है।

→ पिण्ड लोलक-जब एक दृढ़ पिण्ड क्षैतिज अक्ष के सापेक्ष ऊर्ध्वाधर तल में दोलनी गति करे तो इस व्यवस्था को पिण्ड लोलक कहते हैं।
T = 2π\(\sqrt{\frac{\frac{\mathrm{k}^2}{l}+l}{\mathrm{~g}}}\)
T = 2π\(\sqrt{\frac{L}{g}}\)
यहाँ l = \(\frac{\mathrm{k}^2}{l}\) + 1 = तुल्य सरल लोलक की लम्बाई है।
यहाँ पर k पिण्ड की परिभ्रमण त्रिज्या है।

→ U-नली में द्रव के दोलन का आवर्तकाल
T = 2π\(\sqrt{\frac{h}{g}}\)

→ तैरते हुए लकड़ी के आयताकार गट्टे का आवर्तकाल
T = 2π\(\sqrt{\frac{\mathrm{c} \sigma}{\mathrm{g} \rho}}\)
यहाँ c = गट्टे की गहराई
σ = गट्टे के पदार्थ का घनत्व
p= द्रव का घनत्व

→ मुक्त सरल आवर्ती दोलन-जब किसी कम्पन कर सकने वाली वस्तु, उदाहरणार्थ सरल लोलक, या स्वरित्र पर केवल प्रत्यानयन बल का कार्य करता है तो वह वस्तु अनन्त काल तक कम्पन कर सकती है। इस प्रकार के कम्पनों को मुक्त कम्पन कहते हैं तथा इस प्रकार के दोलक को मुक्त दोलन कहते हैं।

→ अवमंदित सरल आवर्त गति-जब कोई वस्तु वायु या किसी द्रव माध्यम में दोलन गति करती है तो उस पर प्रत्यानयन बल के साथ-साथ घर्षण या श्यान बल भी कार्य करता है जिसके कारण दोलक के आयाम तथा ऊर्जा में लगातार कमी होती है। इस प्रकार के दोलनों की अवमंदित दोलन तथा क्षयकारी बलों को अवमंदन बल कहते हैं और लोलक की गति को अवमंदित सरल आवर्त गति कहते हैं। अवमंदित सरल आवर्त गति का अवकल समीकरण
m\(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dt}^2}\) + b \(\frac{\mathrm{dy}}{\mathrm{dt}}\) +ky = 0

कण के विस्थापन का समीकरण
y = a\(e^{\frac{-b t}{2 m}}\) cos(ω't + Φ)
जहाँ a व Φ नियतांक है तथा कोणीय आवृत्ति
ω' = \(\sqrt{\frac{\mathrm{k}}{\mathrm{m}}-\frac{\mathrm{b}^2}{4 \mathrm{~m}^2}}\)