RBSE Class 11 Physics Notes Chapter 11 द्रव्य के तापीय गुण

These comprehensive RBSE Class 11 Physics Notes Chapter 11 द्रव्य के तापीय गुण will give a brief overview of all the concepts.

RBSE Class 11 Physics Chapter 11 Notes द्रव्य के तापीय गुण

→ ऊष्मा-ऊष्मा, ऊर्जा का ही एक स्वरूप है जो हमें गर्मी अथवा ठण्डक का अनुभव कराती है। पदार्थ के अणुओं की गतिज ऊर्जा और स्थितिज ऊर्जा ही ऊष्मा के रूप में प्रकट होती है।
1 कैलोरी = 4.186 जूल, 1 किलो कैलोरी = 4.186 × 10³ जूल
एक ग्राम पानी का ताप 14.5°C से 15.5°C तक बढ़ाने के लिये आवश्यक ऊष्मीय ऊर्जा का मान एक कैलोरी के तुल्य होता है।

→ ताप-"किसी पदार्थ का ताप वह भौतिक गुण है जो ऊष्मा संचरण (Transfer of heat) की दिशा का बोध कराता है, जब एक ऊष्मीय निकाय दूसरे निकाय के सम्पर्क में लाया जाता है।" ऊष्मा ऊँचे ताप से नीचे ताप की ओर बहती है।
ताप किसी वस्तु का वह गुण है जो यह बताता है कि कोई वस्तु अन्य वस्तु के साथ तापीय साम्य में है या नहीं। .

→ ताप का मापक्रम तथा ताप के विभिन्न पैमाने-ऐसे यन्त्र जिनमें ताप का मापक्रम निर्धारित होता है तापमापी (Thermometer) कहलाते हैं।
भौतिक विज्ञान की वह शाखा जिसके अन्तर्गत ताप को मापा जाता है तापमिति (Thermometry) कहलाती है।

साधारणतः निम्न पैमाने प्रयुक्त किये जाते हैं

• सेण्टीग्रेड अथवा सेल्सियस पैमाना
• फारेनहाइट पैमाना
• केल्विन या परम ताप पैमाना
• यूमर (Reaumer) ताप पैमाना।

→ विभिन्न ताप पैमानों में सम्बन्ध
\(\frac{\mathrm{C}}{5}=\frac{\mathrm{F}-32}{9}=\frac{\mathrm{K}-273}{5}=\frac{\mathrm{R}}{4}\)
K = C + 273

→ आदर्श गैस समीकरण तथा परम ताप-किसी आदर्श गैस के दाब P, आयतन V तथा परमताप T के आपस के सम्बन्ध को ही आदर्श गैस समीकरण कहते हैं।
PV = nRT
यदि किसी गैस में एक मोल है तो n = 1 अतः
PV = RT से गैस समीकरण दर्शाया जाता है।
वह ताप जिस पर गैस का दाब शून्य हो जाता है, उस ताप को परम शून्य ताप कहते हैं। इसका मान -273.15°C होता है तथा इसे OK से प्रदर्शित करते हैं। परम ताप तथा सेल्सियस ताप पैमानों पर तापमानों में निम्न संबंध होता है-TK = T°C + 273
या t°C = T K - 273

 

→ तापमापी का अंशांकन
T = 273.16\(\left(\frac{x}{x_{t_r}}\right)\)
उपर्युक्त समी. तापमापन के सिद्धान्त को बताता है तथा साथ ही ताप पैमाने को निश्चित करता है। X कोई भी प्राचल हो सकता है जैसे कि तापमापी में पारे की लम्बाई, किसी तार का प्रतिरोध, गैस का दाब, गैस का आयतन, ताप वैद्युत युग्म का विद्युत वाहक बल इत्यादि।

→ ताप t = \(\left(\frac{X_t-X_0}{X_{100}-X_0}\right)\) × 100
जहाँ X = कोई ताप मापक गुण
उपरोक्त सूत्र से प्राप्त ताप प्लैटिनम ताप' कहलाता है। इस सूत्र की सहायता से अज्ञात ताप t का मान गणना करके ज्ञात कर सकते हैं। यदि हमें R₀ व R₁₀₀, ज्ञात हो और अज्ञात ताप (t°C) पर प्रतिरोध R. ज्ञात हो।

→ ऊष्मीय प्रसार-किसी वस्तु के ताप में वृद्धि होने पर उसकी विमाओं में वृद्धि होने को ऊष्मीय प्रसार कहते हैं। वस्तु के लम्बाई प्रसार को रेखीय प्रसार, क्षेत्रफल में प्रसार को क्षेत्रीय प्रसार तथा आयतन में प्रसार को आयतन प्रसार कहते हैं।

→ रेखीय प्रसार गुणांक (α)

यदि L = 1 मीटर तथा ΔT = 1°C हो तब
α = ΔL
"किसी पदार्थ का रेखीय प्रसार गुणांक, लम्बाई में उस वृद्धि के बराबर होता है, जब उसकी एकांक लम्बाई का ताप 1°C बढ़ाते हैं ।

→ क्षेत्रीय प्रसार गुणांक (β)

क्षेत्रफल में वृद्धि
यदि A = 1 मीटर², AT = 1°C हो तब
β = ΔA
किसी पदार्थ के पटल के एकांक क्षेत्रफल का ताप 1°C बढ़ाने पर उसके क्षेत्रफल में जो वृद्धि होती है उसे उस पदार्थ का क्षेत्रीय प्रसार गुणांक कहते हैं ।

→ आयतन प्रसार गुणांक (γ)

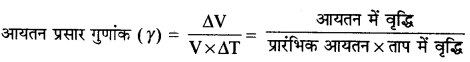
यदि γ = 1 मीटर³ तथा ΔV = 1°C तब γ = ΔV
अतः किसी वस्तु का आयतन प्रसार गुणांक उसके आयतन में वृद्धि के बराबर होता है जब उसके एकांक आयतन का ताप 1°C बढ़ाया जाता है ।

→ ठोसों के प्रसार गुणांक में पारस्परिक सम्बन्ध
α तथा β में सम्बन्ध β = 2α
α तथा β में सम्बन्ध γ = 3α
α, β तथा γ में सम्बन्ध α: β: γ = 1 : 2 : 3

→ तापीय प्रतिबल - जब किसी छड़ के दोनों सिरों को दृढ़ता से जोड़कर इसके तापीय प्रसार को रोका जाता है । स्पष्ट है कि सिरों के दृढ़ अवलंबों द्वारा प्रदत्त बाह्य बलों के कारण छड़ में संपीडन विकृति उत्पन्न हो जाती है जिसके तदनुरूपी छड़ में एक प्रतिबल उत्पन्न होता है जिसे तापीय प्रतिबल कहते हैं ।
तापीय प्रतिबल = YαΔT
तापीय प्रतिबल के कारण छड़ में उत्पन्न तनाव बल
F = YAαΔT

→ जल का असंगत प्रसार - जल को 0°C के 4°C तक गर्म करने पर यह संकुचित होता है । यह व्यवहार जल का असंगत प्रसार कहलाता है
जल के असामान्य प्रसार के दैनिक जीवन के उदाहरण

• सर्दी के दिनों में जल के पाइप फट जाते हैं ।
• ठण्डे प्रदेशों में तालाबों के जम जाने पर भी उनमें मछलियाँ जीवित रहती हैं ।

→ गैसों का तापीय प्रसार

• स्थिर दाब पर आयतन गुणांक तथा
• स्थिर आयतन पर दाब प्रसार गुणांक

सभी आदर्श गैसों का स्थिर दाब पर आयतन गुणांक सदैव समान होता है और वह (\(\frac{1}{273}\)) के बराबर होता है ।
सभी आदर्श गैसों का स्थिर आयतन पर दाब प्रसार गुणांक समान होता है और वह (\(\frac{1}{273}\)) के बराबर होता है ।

→ विशिष्ट ऊष्माधारिता - किसी वस्तु या पदार्थ के एकांक द्रव्यमान का तापमान 1K या 1°C बढ़ाने के लिये आवश्यक ऊष्मा की मात्रा को पदार्थ की विशिष्ट ऊष्माधारिता या विशिष्ट ऊष्मा कहते हैं ।
इसका मान पदार्थ की प्रकृति पर निर्भर करता है ।
S = \(\frac{\Delta Q}{\mathrm{~m} \Delta \mathrm{T}}\)
इसका मात्रक कैलोरी / °C अथवा किलो कैलोरी / °C होता है । SI पद्धति में इसे जूल / °C अथवा जूल / K से व्यक्त करते हैं ।

→ मोलर विशिष्ट ऊष्माधारिता-किसी पदार्थ के मोलर विशिष्ट ऊष्माधारिता का मान उस पदार्थ के द्रव्यमान तथा पदार्थ की विशिष्ट ऊष्मा के गुणनफल के बराबर होता है। इसे C से प्रदर्शित करते हैं।
C = SM

→ गैसों की विशिष्ट ऊष्माधारिता-गैसों की दो विशिष्ट ऊष्माधारितायें होती हैं

• स्थिर आयतन पर विशिष्ट ऊष्माधारिता (c_v)-"स्थिर आयतन पर किसी गैस के 1 ग्राम द्रव्यमान का ताप 1°C बढ़ाने के लिये आवश्यक ऊष्मा की मात्रा को उस गैस की स्थिर आयतन पर विशिष्ट ऊष्माधारिता कहते हैं।" इसे (c_v) से प्रदर्शित करते हैं। .
• स्थिर दाब पर विशिष्ट ऊष्माधारिता-"स्थिर दाब पर किसी गैस के एक ग्राम द्रव्यमान का ताप 1°C बढ़ाने के लिये आवश्यक ऊष्मा की मात्रा को उस गैस की स्थिर दाब पर विशिष्ट ऊष्माधारिता कहते हैं।" इसे c_p से प्रदर्शित करते हैं।

c_v तथा c_p के मात्रक कैलोरी/ग्राम °C होते हैं।
c_p का मान c_v से अधिक होता है अर्थात् c_p > c_v
C_p - C_v = R [यह संबंध 1 मोल गैस के लिये है।]
C_p = \(\left(\frac{f+2}{2}\right)\)
R और C_v = \(\left(\frac{f}{2}\right)\)R
यहाँ पर f = गैस के अणुओं की स्वतंत्रता कोटि

→ ऊष्मामिति-"किसी वस्तु के दूसरी वस्तु को स्थानान्तरित ऊष्मा के मापन को ऊष्मामिति अथवा कैलोरीमिति कहते हैं।"

→ मिश्रण का नियम-दी गई ऊष्मा = ली गई ऊष्मा
m₁S₁(T₁ - T_mix) = m₂S₂ (T_mix - T₂)
या T₂ = \(\frac{m_1 S_1 T_1+m_2 S_2 T_2}{m_1 S_1+m_2 S_2}\)

→ ऊष्मामापी या कैलोरीमापी-ऐसी युक्ति जिससे ऊष्मा का मापन किया जा सके उसे ऊष्मामापी कहते हैं । यह प्रायः तांबे का बना होता है।

→ अवस्था परिवर्तन-"वह परिवर्तन जिसमें पदार्थ अपनी भौतिक अवस्था को परिवर्तित करता है, अवस्था परिवर्तन कहलाता है।" पदार्थ की अवस्था परिवर्तन की निम्न दो सामान्य अवस्थायें होती हैं

• ठोस से द्रव या द्रव से ठोस
• द्रव से गैस या गैस से द्रव ।

→ गलन तथा गलनांक-ठोस अवस्था से द्रव अवस्था में परिवर्तन को गलन कहते हैं । यह क्रिया जिस निश्चित ताप पर होती है, वह गलनांक कहलाता है।

→ वाष्पन तथा क्वथनांक-जब कोई पदार्थ पूर्णतः किसी निश्चित ताप पर द्रव अवस्था से गैस अवस्था में आता है तो इस परिवर्तन को क्वथन कहते हैं। यह क्रिया जिस निश्चित ताप पर होती है, वह क्वथनांक कहलाता है। ऊपरी सतह से द्रव प्रत्येक ताप पर गैसीय अवस्था में परिवर्तित होता रहता है। यह क्रिया वाष्पन कहलाती है।

→ ऊर्ध्वपातन-किसी पदार्थ का ठोस अवस्था से वाष्प अवस्था में बिना द्रव अवस्था से गुजरे, बदलना ऊर्ध्वपातन कहलाता है। जैसेनौसादर, कपूर।

→ प्रावस्था आरेख तथा त्रिक बिन्दु"किसी पदार्थ के दाब तथा ताप के बीच खींचे गये ग्राफ को उसका दाब-ताप प्रावस्था आरेख कहते हैं।"
"किसी पदार्थ के दाब-ताप प्रावस्था आरेख में वह बिन्दु जिसके संगत दाब (P₀) तथा ताप (T₀) पर पदार्थ एक साथ ही ठोस, द्रव तथा वाष्प तीनों प्रावस्थाओं में रह सकता है, उस पदार्थ का त्रिक बिन्दु कहलाता है।

→ गुप्त ऊष्मा-गुप्त ऊष्मा, वह ऊष्मा की मात्रा है जो पदार्थ की अवस्था को बिना ताप परिवर्तित किये बदलने के लिये आवश्यक होती है। गुप्त ऊष्मा दो प्रकार की होती है

• गलन की गुप्त ऊष्मा (L_f)
• वाष्प की गुप्त ऊष्मा (L_v)

(i) गलन की गुप्त ऊष्मा (L_f):
यह ऊष्मा की वह मात्रा है जो किसी पदार्थ के एक मात्रक द्रव्यमान को उसके गलनांक पर ठोस से द्रव अवस्था में लाने के लिये पदार्थ ग्रहण करता है। इसे L_f से प्रदर्शित करते हैं। इसका मात्रक कैलोरी/ग्राम, किलो कैलोरी/किग्रा. अथवा जूल/किग्रा. होते हैं।
L_f = \(\frac{Q}{m}\)

(ii) वाष्य की गुप्त ऊष्मा (L_v):
यह ऊष्मा की वह मात्रा होती है जो कि पदार्थ के एक मात्रक द्रव्यमान को उसके क्वथनांक पर द्रव से गैस अवस्था में लाने के लिये आवश्यक होती है। इसका मात्रक भी कैलोरी/ग्राम, किलो कैलोरी/किग्रा. अथवा जूल/किग्रा. है।
L_v = \(\frac{Q}{m}\)

→ ऊष्मीय ग्राफ:
जब m द्रव्यमान के दिये गये ठोस को नियत दर पर ऊष्मा दी जाती है तथा ताप व समय के बीच ग्राफ खींचा जाता है तब इस ग्राफ को ऊष्मीय ग्राफ कहते हैं।

→ ऊष्मीय संचरण की विधियाँ-ऊष्मीय ऊर्जा के एक स्थान से दूसरे स्थान तक संचरण की तीन विधियाँ होती हैं-चालन. (Conduction), संवहन (Convection) एवं विकिरण (Radiation)। इनमें चालन एवं संवहन के लिए माध्यम की आवश्यकता होती है जबकि विकिरण के लिये नहीं।

• चालन-जब वस्तु में उच्च ताप क्षेत्र से निम्न ताप क्षेत्र की ओर ऊष्मा का संचरण इस प्रकार से हो कि एक कण अपनी साम्यावस्था के इर्दगिर्द कम्पन करते हुये अपने पड़ोसी कण को ऊर्जा स्थानान्तरित करे, तो ऊर्जा संचरण की इस विधि को चालन कहते हैं।
• संवहन-इस विधि में पदार्थ के कण स्वयं ऊष्मा लेकर एक स्थान से दूसरे स्थान तक ऊष्मा को पहुंचाते हैं तथा उनके स्थान पर दूसरे कण ऊष्मा लेने पहुँच जाते हैं। साधारणतया द्रवों तथा गैसों में ऊष्मा का संचरण संवहन प्रक्रिया द्वारा होता है।
• विकिरण-ऊर्जा संचरण की वह विधि जिसके द्वारा ऊर्जा का बिना माध्यम की सहायता से संचरण होता है। इस विधि में ऊर्जा विद्युत चुम्बकीय तरंगों के रूप में संचारित होती है।

→ ऊष्मा चालकता गुणांक-किसी ठोस के एकांक क्षेत्रफल से एकांक ताप प्रवणता की स्थिति में ऊष्मा प्रवाह की दर को ठोस का ऊष्मीय चालकता गुणांक (K) कहते हैं। K का मान जितना अधिक होता है पदार्थ उतना ही अच्छा चालक कहलाता है। एक आदर्श सुचालक के लिये K का मान अनन्त तथा एक पूर्ण कुचालक के लिये K का मान शून्य होता है।

→ न्यूटन का शीतलन का नियम-"यदि वस्तु एवं वातावरण में ताप का अन्तर (ताप आधिक्य) अधिक नहीं हो तो वस्तु के शीतलन की दर, ताप आधिक्य के समानुपाती होती है।"
R = \(\frac{\mathrm{dQ}}{\mathrm{dt}}\) = - K (T – T₀), T = वस्तु का ताप, T₀ = परिवेश का ताप यहाँ पर K शीतलन नियतांक है जो वस्तु के पृष्ठ के क्षेत्रफल तथा उसकी प्रकृति पर निर्भर करता है तथा R शीतलन की दर है। (-) चिन्ह बताता है कि समय के साथ वस्तु की कुल ऊष्मा घट रही है अर्थात् जैसे-जैसे वस्तु ठण्डी होती जाती है उससे ऊष्मा हानि की दर भी घटती जाती है।

सीमा बंधन

• T – T₀ < < T₀ (T₀ = परिवेश का परमताप)
• ऊष्मा का संचरण केवल विकिरण विधि से होना चाहिये।
• ऊष्मा उत्सर्जन के लिये कृष्णिका (काले पृष्ठ) का उपयोग होना चाहिये।

→ स्टीफन का नियम-"किसी कृष्णिका के एकांक पृष्ठीय क्षेत्रफल से प्रति सेकण्ड उत्सर्जित विकिरण ऊर्जा उसके परमताप की चतुर्थ घात के अनुक्रमानुपाती होती है।"
E ∝ T⁴
⇒ E = σ T⁴
यहाँ σ एक समानुपाती नियतांक है जिसे स्टीफन का नियतांक कहते हैं। इसका मान 5.67 × 10^-8 जूल/मी² से.K⁴ होता है।

→ शीतलन की दर-वस्तु द्वारा उत्सर्जित विकिरण ऊर्जा की दर अर्थात् वस्तु के शीतलन की दर
R = \(\frac{\mathrm{dQ}}{\mathrm{dt}}=\frac{\sigma \mathrm{e}_{\mathrm{r}} \mathrm{A}}{\mathrm{J}}\) (T⁴ - T⁴₀) कैलोरी/से.
यह नियम स्टीफन का शीतलन नियम कहलाता है।
यदि वस्तु का द्रव्यमान m तथा विशिष्ट ऊष्मा S हो तो शीतलन की दर
\(\frac{\mathrm{dQ}}{\mathrm{dt}}= mS\frac{\mathrm{dT}}{\mathrm{dt}}\)
∴ ताप गिरने की दर
\(\frac{\mathrm{dT}}{\mathrm{dt}}=\frac{\sigma \mathrm{e}_{\mathrm{r}} \mathrm{A}}{\mathrm{mSJ}}\) (T⁴ - T⁴₀) डिग्री से.

→ न्यूटन का शीतलन नियम
R = स्थिरांक (T - T₀)
तापान्तर अल्प होने पर शीतलन की दर तापान्तर (ताप आधिक्य) के समानुपाती होती है। यही न्यूटन का शीतलन का नियम भी है।

→ कृष्णिका विकिरण का स्पेक्ट्रमी वितरण-किसी निश्चित ताप पर किसी कृष्णिका से उत्सर्जित विभिन्न तरंगदैर्घ्य के संगत ऊर्जा E_λ तथा तरंगदैर्घ्य λ के बीच खींचा गया वक्र स्पेक्ट्रमी वितरण वक्र कहलाता है। यह नियत ताप पर λ बढ़ाने से E, का मान पहले बढ़ता है तथा एक महत्तम मान (E_λ)_m को प्राप्त होकर फिर घटने लगता है। (E_λ)_m के महत्तम मान के संगत तरंगदैर्घ्य λ_m कहलाती है। इस पर वक्र में शिखर प्राप्त होता है।

→ वीन का विस्थापन नियम-"अधिकतम उत्सर्जन क्षमता के लिये तरंगदैर्घ्य (λ_m) का मान कृष्णिका के परम ताप (T) के व्युत्क्रमानुपाती होता है।" अर्थात्
λ_m ∝ \(\frac{1}{T}\)
या λ_m = b या λ_mT = b
यहाँ b वीन नियतांक कहलाता है एवं कृष्णिका के लिये इसका मान 2.898 × 10^-3 मी. K होता है।