RBSE Class 11 Physics Notes Chapter 10 तरलों के यांत्रिकी गुण

These comprehensive RBSE Class 11 Physics Notes Chapter 10 तरलों के यांत्रिकी गुण will give a brief overview of all the concepts.

RBSE Class 11 Physics Chapter 10 Notes तरलों के यांत्रिकी गुण

→ तरल दाब–तरल वे पदार्थ कहलाते हैं जो बहते हैं अर्थात् द्रव व गैस (वायु)।

→ दाब-किसी पृष्ठ के एकांक क्षेत्रफल पर आरोपित लम्बवत् बल को दाब कहते हैं । यदि पृष्ठ क्षेत्रफल A पर कार्यरत लम्बवत् बल F हो
तो दाब P = \(\frac{F}{A}\)
इसका SI मात्रक न्यूटन/मीटर तथा विमा सूत्र | ML^-1T^-2 यह एक अदिश राशि होती है।
1 डाइन/सेमी.² =10^-1 न्यूटन/मी.²
क्षेत्रफल कम होने पर दाब अधिक और क्षेत्रफल अधिक होने पर दाब कम होता है।

→ घनत्व—पदार्थ का घनत्व ρ = \(\frac{M}{V}\)
इसका SI मात्रक Kgm^-3 है।
4°C पर पानी का घनत्व अधिकतम तथा इसका मान 1.0x10 Kgm- होता है।

 

→ आपेक्षिक घनत्व-किसी पदार्थ का आपेक्षिक घनत्व उस पदार्थ के घनत्व तथा पानी के 4°C पर घनत्व का अनुपात होता है अर्थात्

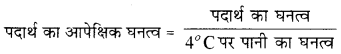
→ द्रव-स्तम्भ के कारण दाब-"द्रव के भीतर किसी बिन्दु पर द्रव के कारण दाब द्रव की सतह से उस बिन्दु तक की गहराई द्रव के घनत्व तथा गुरुत्वीय त्वरण के गुणनफल के बराबर होता है।" किसी तरल (द्रव अथवा गैस) के h ऊँचाई के स्तम्भ के कारण दाब का सूत्र है
p = hρg
इस सूत्र में एक ही द्रव के लिये घनत्व (ρ) तथा स्थान विशेष के लिये g नियत होता है।
अतः P ∝ h
यदि द्रव के मुक्त पृष्ठ पर वायुमण्डलीय दाब Pa हो तब द्रव के मुक्त पृष्ठ से h गहराई पर कुल दाब
P¹ = P_a + hρg

→ वायुमण्डलीय दाब तथा गेज दाब 1 वायुमण्डलीय दाब = 1.013 × 10⁵ Pa - 10⁵ Pa (लगभग)
दाब का मात्रक टॉर भी होता है 1 टॉर = 1 मिमी. पारादाब
1 टॉर (torr) = 133N / m² = 133Pa
1 बार (bar) = 10⁵N/m² = 10⁵ पास्कल (P_a)
गेजदाब P₂ - P₁ = hρg

• P₂ > P₁ अर्थात् द्रव के भीतर द्रव की खुली सतह की अपेक्षा दाब अधिक होता है।
• यदि g = 0 अर्थात् गुरुत्व प्रभाव अनुपस्थित हो तो P₂ - P₁ = 0 अर्थात् P₂ = P₁ द्रव के भीतर, ऊर्ध्वाधर रेखा में किन्हीं दो बिन्दुओं का दाबान्तर केवल गुरुत्व प्रभाव के कारण होता है।

→ पास्कल का नियम:
"किसी पात्र में रखे द्रव की सन्तुलन अवस्था में द्रव के किसी भाग पर आरोपित दाब (बिना क्षय हुये) द्रव द्वारा सभी दिशाओं में समान रूप से (परिमाण में) संचरित कर दिया जाता है।"

→ पास्कल के नियम के अनुप्रयोग

• द्रव चालित लिफ्ट
• हाइड्रोलिक ब्रेक।

→ द्रव चालित लिफ्ट-इसका कार्य सिद्धान्त पास्कल के नियम पर आधारित है, अतः कम परिमाण के दाब को अपेक्षाकृत बहुत बड़े क्षेत्रफल पर संचरित करके उस क्षेत्रफल पर कार्यरत अधिक बल प्राप्त किया जा सकता है।
यदि A₁ अनुप्रस्थ काट के क्षेत्रफल पर F₁ बल आरोपित किया जाये तथा यह A₂, अनुप्रस्थ परिच्छेद क्षेत्रफल पर F₂, बल के रूप में संचरित हो जाये तो
\(\left(\frac{F_2}{F_1}\right)=\left(\frac{A_2}{A_1}\right)\)

→ हाइड्रोलिक ब्रेक-हाइड्रोलिक ब्रेक का कार्य सिद्धान्त भी हाइड्रोलिक लिफ्ट की तरह ही है अर्थात् यह भी पास्कल नियम पर ही आधारित है। इसके द्वारा गाड़ी के सभी पहियों पर एक साथ अवमन्दक बल लगाया जाता है।

→ उत्प्लावक बल-किसी द्रव अथवा तरल में जब एक वस्तु को पूर्णतया अथवा आंशिक रूप से डुबोते हैं तो वह ऊपर की दिशा में एक बल अनुभव करती है। इस बल को उत्प्लावक बल एवं द्रव अथवा तरल के इस गुण को उत्प्लावक़ता कहते हैं।

→ आर्किमिडीज का सिद्धान्त-"जब कोई वस्तु किसी द्रव में पूरी अथवा आंशिक रूप से डुबोई जाती है तो उसके भार में कमी प्रतीत होती है। भार में यह आभासी कमी उस वस्तु द्वारा हटाये गये द्रव के भार के बराबर होती है।"
(W₁ - W₂) = V × ρ × g

→ धारा रेखीय प्रवाह तथा प्रक्षुब्ध प्रवाह-जब कोई तरल इस प्रकार बहता है कि किस बिन्दु पर उसका कोई भी कण ठीक उसी मार्ग पर गति करता है, जिस मार्ग पर उसके पहले वाला कण गुजर चुका है तो द्रव के प्रवाह को धारा रेखीय प्रवाह कहते हैं। किसी तरल का प्रवाह तब तक धारा-रेखी बना रहता है, जब तक कि उसका वेग एक सुपरिभाषित निश्चित वेग से कम रहता है । इस निश्चित वेग को क्रान्तिक वेग कहते हैं । इसके विपरीत जब तरल का वेग क्रान्ति वेग से अधिक हो जाता है तो प्रवाह, धारा-रेखी नहीं रहता और तरल की गति टेढ़ी-मेढ़ी एक अनियमित हो जाती है। इस प्रकार के प्रवाह को प्रक्षुब्ध प्रवाह कहते हैं।

→ श्यानता-द्रव का वह गुण जिसके कारण द्रव अपनी परतों के मध्य होने वाली आपेक्षिक गति का विरोध करता है, श्यानता कहलाता है। ताप बढ़ने से द्रवों की श्यानता घट जाती है परन्तु गैसों की श्यानता बढ़ जाती है।

→ आदर्श द्रव-इसमें दो गुण होते हैं--शून्य सम्पीड्यता तथा शून्य श्यानता।

→ वेग प्रवणता-द्रव की प्रवाह की दिशा के अभिलम्बवत् एकांक दूरी पर स्थित द्रव की दो परतों के बीच वेग परिवर्तन को वेग प्रवणता कहते हैं।

→ श्यानता गुणांक (न्यूटन का सूत्र )

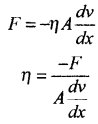
यदि A = 1 ( एकांक) तथा \(\frac{d v}{d x}\) (एकांक) तब η = |F|
अर्थात् किसी द्रव का श्यानता गुणांक उस द्रव के अन्दर एकांक पृष्ठ क्षेत्रफल वाली दो परतों के बीच आवश्यक उस बाह्य बल के बराबर होता है, जो परतों के मध्य एकांक वेग प्रवणता बनाये रखे।
MKS पद्धति में इसका मात्रक किग्रा./ मीटर सेकण्ड होता है। श्यानता गुणांक का एक अन्य (CGS) मात्रक प्वाइज (Poise) भी होता है ।
1 किग्रा./मी. से. = 10 (प्वाइज)

→ श्यानता गुणांक का मान ज्ञात करना: प्वाइज नियम (Poiseuille's Law) के अनुसार
श्यानता गुणांक η = \(\frac{\pi P a^4}{8 \rho Q}\)
जहाँ P = hρg, पानी के लिये ρ = 1 (CGS प्रणाली में )
a = T नली की त्रिज्या (देखें पृष्ठ 74 का चित्र)
l = T नली की लम्बाई एवं Q प्रति सेकण्ड एकत्रित पानी का आयतन है।

→ स्टोक्स का नियम या स्टोक्स का सूत्र - स्टोक्स ने यह सिद्ध किया कि जब एक छोटी गोली जिसकी त्रिज्या है जो अनन्त विस्तार वाले पूर्णत: समांग (homogeneous) तरल (द्रव या गैस) माध्यम में स्वतंत्रतापूर्वक अन्तिम वेग v_t, से गति कर रही हो, तब गोली पर कार्य करने वाला श्यान बल का मान होगा
अतः
F = 6πηrv,
यहाँ η तरल माध्यम का श्यानता गुणांक है। उपरोक्त सूत्र को ही स्टोक्स का नियम या स्टोक्स सूत्र कहते हैं ।

→ द्रव में गोली का गिरना - किसी श्यान माध्यम में नीचे गिरती गोली का वेग गोले की त्रिज्या के वर्ग के समानुपाती, गोली तथा माध्यम के घनत्व के अन्तर के समानुपाती तथा माध्यम के श्यानता गुणांक के व्युत्क्रमानुपाती होता है, अतः
v_t = \(\frac{2}{9} \frac{r^2(\rho-\sigma) g}{\eta}\)

→ क्रान्तिक वेग व रेनॉल्ड संख्या:
क्रान्तिक वेग तरल के श्यानता गुणांक (η) के समानुपाती घनत्व (ρ) के व्युत्क्रमानुपाती एवं नली के
अत: v_c = \(\frac{R \eta}{\rho D}\)
रेनाल्ड्स संख्या R = \(\frac{\nu_c \rho D}{\eta}\) जहाँ R ≈ 2000 रेनाल्ड्स संख्या है।
संकीर्ण बेलनाकार नलियों के लिये R < 2000 हो तो द्रव का प्रवाह धारारेखीय होता है ।

→ अविरतता का सिद्धान्त
A × v = नियतांक
इसको ही अविरतता का सिद्धान्त कहते हैं ।
अत: A₁ × v₁ = A₂ × v₂
⇒ r₁²v₁ = r₂² × v₂

→ बहते हुये द्रव में तीन प्रकार की ऊर्जा हो सकती है

• गतिज ऊर्जा
• स्थितिज ऊर्जा
• दाब ऊर्जा।

→ बरनूली (बरनौली का सिद्धान्त):
जब कोई असंपीड्य तथा अश्यान द्रव अथवा गैस एक स्थान से दूसरे स्थान तक धारा रेखीय प्रवाह में बहता है तो इसके मार्ग के प्रत्येक बिन्दु पर इसके एकांक आयतन की कुल ऊर्जा अर्थात् दाब ऊर्जा, गतिज ऊर्जा तथा स्थितिज ऊर्जा का योग एक नियतांक होता है ।
दाब ऊर्जा + गतिज ऊर्जा + स्थितिज ऊर्जा = स्थिरांक
\(\frac{P}{\rho}+\frac{1}{2}\)v² + gh = स्थिरांक (इकाई द्रव्यमान के लिये)
अथवा
P + \(\frac{1}{2}\)ρv² + ρgh = स्थिरांक (इकाई आयतन के लिये)
बरनौली प्रमेय एक प्रकार से बहते हुए द्रव (अथवा गैस) के लिये ऊर्जा संरक्षण का सिद्धान्त ही है ।

→ बरनूली (बरनौली) सिद्धान्त के अनुप्रयोग
(i) क्षैतिज नली में द्रव का प्रवाह
P + \(\frac{1}{2}\)ρv² = नियमांक ⇒ P₁ + \(\frac{1}{2}\)ρv₁ = P + ρv₂²
जहाँ नली का अनुप्रस्थ काट कम होगा, वहाँ द्रव का वेग अधिक और दाब कम होगा तथा जहाँ नली का अनुप्रस्थ काट अधिक होगा, वहाँ द्रव का वेग कम और दाब अधिक होगा ।

(ii) वेन्ट्यूरी प्रवाहमापी
Q = A₁A₂ \(\sqrt{\frac{2 h g}{A_1^2-A_2^2}}\)
अत: h,A₁, तथा A₂, का मान ज्ञात होने पर द्रव के प्रवाह की दर ज्ञात की जा सकती है ।
फिल्टर पम्प, बुन्सन बर्नर, कणित्र तथा स्प्रेयर इसी सिद्धान्त पर कार्य करते हैं ।

(iii) पिटोट नली
किसी नली में प्रवाहित द्रव का वेग v = \(\sqrt{2 h g}\)
h नापकर नली में प्रवाहित द्रव का वेग ज्ञात किया जा सकता है

(iv) बहिः स्राव वेग - किसी छिद्र से किसी द्रव का बहिःस्राव वेग उस वेग के बराबर होता है, जो कि द्रव अपने स्वतन्त्र तल से छिद्र तक स्वतन्त्रतापूर्वक गिरने में प्राप्त कर लेता है ।
v = \(\sqrt{2 h g}\)
इसे टॉरिसेली प्रमेय भी कहते हैं ।

(v) वायुयान के पंख - ऐयरोफॉयल आकृति

(vi) मैगनस प्रभाव

(vii) आँधी के समय टिन की चद्दरों का उड़ना

(viii) रेलगाड़ी आने पर प्लेटफॉर्म पर पटरियों के नजदीक खड़ा व्यक्ति पटरी से दूर हट जाता है अन्यथा वह पटरी / रेल की ओर गिर जायेगा

(ix) कणित्र

(x) रक्त प्रवाह और हार्ट-अटैक ।

→ पृष्ठ तनाव की परिभाषा
(1) किसी भी द्रव के मुक्त पृष्ठ की इकाई क्षेत्रफल से विस्तृत करने के लिये आवश्यक कार्य अर्थात् पृष्ठ ऊर्जा में वृद्धि को पृष्ठ तनाव कहते हैं।
पृष्ठ तनाव T = \(\frac{W}{A}\) जूल / मी²

(2) किसी द्रव का पृष्ठ तनाव वह बल है जो द्रव के मुक्त पृष्ठ पर खींची गयी काल्पनिक रेखा की एकांक लम्बाई के लम्बवत् तथा पृष्ठ के
तल में कार्य करता है । अर्थात् पृष्ठ तनाव T = \(\frac{F}{L}\)
यदि L हो तो T = F
अर्थात् द्रव के मुक्त पृष्ठ पर एकांक लम्बाई की काल्पनिक रेखा के लम्बवत् तथा पृष्ठ के तल में कार्य करने वाले बल को पृष्ठ तनाव कहते हैं । पृष्ठ तनाव को न्यूटन / मी. से भी व्यक्त करते हैं ।

→ पृष्ठ तनाव व पृष्ठ ऊर्जा में सम्बन्ध
T = \(\frac{W}{\Delta A}\)
किसी द्रव के क्षेत्रफल में नियत ताप पर इकाई वृद्धि करने के लिये आवश्यक कार्य की मात्रा को पृष्ठ तनाव कहते हैं।

→ पानी की बड़ी बूंद को छोटी-छोटी बूंदों में फुहारने पर पृष्ठ ऊर्जा में वृद्धि W = T.47R³\(\left[\frac{1}{r}-\frac{1}{R}\right]\)
यह कार्य छोटी बूंदों में पृष्ठ ऊर्जा के रूप में संग्रहित हो जाता है।
इस कार्य के कारण आन्तरिक ऊर्जा में कमी.
Q = \(\frac{W}{J}=\frac{T .4 \pi R^3}{J}\left(\frac{1}{r}-\frac{1}{R}\right)\) कैलोरी

→ ससंजक बल—एक ही पदार्थ के अणुओं के बीच लगने वाले आकर्षण बल को ससंजक बल कहते हैं । जैसे जल के अणुओं के मध्य लगने वाला बल।

→ आसंजक बल-दो भिन्न प्रकार के पदार्थों के अणुओं के बीच लगने वाले आकर्षण बल को आसंजक बल कहते हैं। जैसे-जल व काँच के अणुओं के मध्य लगने वाला बल।

→ ससंजक तथा आसंजक बलों के प्रभाव

• काँच की प्लेट पर जल डालने पर गीली हो जाती है।
• स्याही का कागज पर चिपक जाना।
• पारा काँच को गीला नहीं करता है।

→ पृष्ठ तनाव पर आधारित दैनिक घटनायें

• साधारण जल की तुलना में साबुन मिले पानी से अधिक बड़े बुलबुले बनाये जा सकते हैं।
• जल के पृष्ठ पर कपूर के टुकड़े नाचने लगते हैं।
• काँच की छड़ को गर्म करने पर उसका सिरा गोल हो जाता है।
• गर्म सूप ठण्डे सूप की अपेक्षा अधिक स्वादिष्ट लगता है।
• फुहारने से ठंडक उत्पन्न होती है।
• पारे की छोटी बूंद गोल तथा बड़ी बूंद चपटी होती है।

→ स्पर्श कोण या सम्पर्क कोण-"द्रव व ठोस के स्पर्श बिन्दु से द्रव के पृष्ठ पर खींची गयी स्पर्श रेखा तथा ठोस के पृष्ठ पर द्रव के अन्दर ओर खींची गई स्पर्श रेखा के बीच बने कोण को उस ठोस व द्रव के लिये स्पर्श कोण कहते हैं।" शुद्ध जल व काँच के लिए सम्पर्क कोण शून्य तथा कारण जल व काँच के लिये 8° होता है। पारे व काँच के लिये सम्पर्क कोण=135° होता है। जल तथा चाँदी के लिये सम्पर्क कोण 90° होता है।

→ गोल बूंद के अन्दर दाब आधिक्य
दाब (P) = \(\frac{2T}{r}\)

→ साबुन के बुलबुले के अन्दर दाब आधिक्य
दाब आधिक्य P = \(\frac{2 T}{r}+\frac{2 T}{r}=\frac{4 T}{r}\)
सभी स्थितियों में दाब आधिक्य (P) का मान पृष्ठ तनाव (T) के समानुपाती तथा त्रिज्या r के व्युत्क्रमानुपाती होता है।

→ केशिकत्व-केशनली को द्रव में खड़ा करने पर उसमें तली के बाहर द्रव तल की अपेक्षा द्रव का नली में ऊपर चढ़ना अथवा नीचे उतरना केशिकत्व कहलाता है।
केशनली में चढ़े द्रव स्तम्भ की ऊँचाई
h = \(\frac{2 T \cos \theta}{r \rho g}\)
जहाँ T = द्रव का पृष्ठ तनाव, r = केशनली की त्रिज्या, ρ = द्रव का घनत्व, g = गुरुत्वीय त्वरण,
= द्रव-ठोस के बीच स्पर्श कोण
अत: h ∝ \(\frac{1}{r}\), अथवा hr = नियतांक
⇒ h₁r₁ = h₂r₂
अर्थात् केशनली में चढ़े द्रव स्तम्भ की ऊँचाई तथा केशनली की त्रिज्या का गुणनफल नियत रहता है।
अथवा केशिका नली में कोई द्रव जितना चढ़ता या उतरता है वह ऊँचाई या गहराई, केशिका नली की त्रिज्या के व्युत्क्रमानुपाती होती है। इसे ही जूरिन का नियम कहते हैं।

→ यदि किसी केशनली में द्रव / ऊँचाई तक चढ़ता है तो यदि इससे कम लम्बाई की तली इसी द्रव में खड़ी की जाये तो द्रव ऊपरी सिरे तक चढ़कर केशनली के किनारों पर फैलकर द्रव पृष्ठ की वक्रता त्रिज्या बढ़ा लेता है तथा सम्बन्ध h'R' = h'R' सन्तुष्ट हो जाता है। अत: अपर्याप्त लम्बाई की केशनली में द्रव बाहर फुहार के रूप में या अन्य किसी रूप में नहीं निकलता है।

→ केशनली को द्रव में तिरछा करने पर (ऊर्ध्वाधर से α कोण पर झुकाने पर) केशनली में द्रव - स्तम्भ की लम्बाई l = \(\frac{h}{\cos \alpha}\) जहाँ h → केशनली में द्रव स्तम्भ की ऊर्ध्वाधर ऊँचाई

→ पृष्ठ तनाव पर विभिन्न कारकों का प्रभाव

• ताप का प्रभाव
• संदूषण का प्रभाव
• विलेय का प्रभाव
• विद्युतीकरण पर प्रभाव