RBSE Class 11 Physics Important Questions Chapter 9 Mechanical Properties of Solids

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 9 Mechanical Properties of Solids Important Questions and Answers.

RBSE Class 11 Physics Chapter 9 Important Questions Mechanical Properties of Solids

Multiple Choice Questions

Question 1.
What is the Young's modulus of elasticity for a perfectly rigid body?
(a) infinity
(b) zero
(c) 1
(d) -1
Asnwer:
(a) infinity

Question 2.
A wire is fixed at the upper end stretches by length l when a force F is applied. The work done in stretching is:
(a) F/2l
(b) Fl
(c) 2Fl
(d) Fl/2
Answer:
(d) Fl/2

Question 3.
A metal rod of Young's modulus 2 x 10¹⁰ Nm^-2 undergoes an elastic strain of 0.06%. The energy per unit volume stored in Jm^-3 is:
(a) 3600
(b) 7200
(c) 10800
(d) 14400
(e) 17600
Answer:
(a) 3600

Question 4.
Two wires of the same radius and material and having lengths in the ratio 8.9 : 7.6 are stretched by the same force. The strains produced in the two cases will be in the ratio:
(a) 1 : 1
(b) 1 : 7.6
(c) 8.9 : 1
(d) 1 : 3.2
Answer:
(a) 1 : 1

Question 5.
Consider the statements A and B, identify the correct answer given below:
A : If the volume of a body remains unchanged, when subjected to tensile strain, the volume of Poisson’s ratio is 1/2.
B : Phosphor bronze has low Young’s modulus and high rigidity modulus:
(a) A and B both are correct
(b) A and B both are wrong
(c) A is correct and B is wrong.
(d) A is wrong and B is right.
Answer:
(c) A is correct and B is wrong.

Question 6.
A wire suspended vertically from one of its ends is stretched by attaching a weight of 200 N to the lower end. The weight stretches the wire by 1 mm. Then the elastic energy stored'in the wire is:
(a) 20 J
(b) 0.1 J
(c) 0.2 J
(d) 10 J
Answer:
(b) 0.1 J

Question 7.
A wire elongates by l mm, when a load W is hung from it. If the wire goes over a pulley and two weights W each are hung at the two ends, the elongation of the wire will be (in mm):
(a) zero
(b) l/2
(c) l
(d) 2l
Answer:
(c) l

Question 8.
An aluminium rod, whose Young’s modulus is 7.0 x 10⁹ Nm^-2, has a breaking strain of 0.2%. The minimum cross sectional area (in m²) of the rod in order to support a load of 10⁴ N is:
(a) 1 x 10^-2
(b) 1.4 x 10^-3
(c) 1.0 x 10^-3
(d) 7.1 x 10^-4
(e) 1 x 10^-4
Answer:
(d) 7.1 x 10^-4

Question 9.
An iron rod of length 2 m and cross-sectional area, of 50 mm² is stretched by 0.5 mm, when a mass of 250 kg is hung from its lower end. Young’s modulus of iron rod is:
(a) 19.6 x 10²⁰ Nm^-2
(b) 19.6 x 10¹⁸ Nm^-2
(c) 19.6 x 10¹⁰ Nm^-2
(d) 19.6 x 10¹⁵ Nm^-2
Answer:
(c) 19.6 x 10¹⁰ Nm^-2

Question 10.
A cube is subjected to a uniform volume compression. If the side of the cube decreases by 2%, the bulk strain is:
(a) 0.02
(b) 0.03
(c) 0.04
(d) 0.06
Answer:
(d) 0.06

Question 11.
A steel wire of cross sectional area 3 x 10^-6 m can withstand a maximum strain of 10^-3. Young’s modulus of steel is 2 x 10¹¹ Nm^-2. The maximum mass the wire can hold is: (Take g = 10 m s^-2)
(a) 40 kg
(b) 60 kg
(c) 80 kg
(d) 100 kg
Answer:
(b) 60 kg

Question 12.
The graph shows the extension (∆l) of a wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 10^-6 m², calculate the Young’s modulus of the material of the wire:

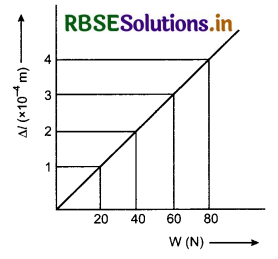
(a) 2 x 10¹¹ Nm^-2
(b) 2 x 10^-11 Nm^-2
(c) 3 x 10^-12 Nm^-2
(d) 2 x 10¹³ Nm^-2
Answer:
(a) 2 x 10¹¹ Nm^-2

Fill in the blanks

Question 1.
The value of bulk modulus for an ideal liquid is ............................
Answer:
infinity.

Question 2.
A material is more elastic. If its value of modulus of elasticity is ............................
Answer:
large.

Question 3.
A wire can support a load Mg wthout breaking. It is cut into two equal parts. The maximum load that each part an support is ............................
Answer:
Mg.

Question 4.
Young’s modulus is the property of ............................
Answer:
material.

Question 5.
The dimensional formula of strain is ............................
Answer:
[M⁰L⁰T⁰]

Very Short Answer Questions

Question 1.
Define elasticity.
Answer:
The property of the material of a body due to which it regains its original size and shape back, after the removed of the deforming force, is called elasticity.

Question 2.
What is a deforming force?
Answer:
Deforming force is a force which when applied changes the shape and size of the body.

Question 3.
Give two examples each of perfectly elastic bodies and perfectly plastic bodies.
Answer:
Examples of:
Perfectly elastic bodies: Phosphor-bronze and quartz.
Perfectly plastic bodies: Paraffin wax and much.

Question 4.
Give the formula for stress.
Answer:
Stress = \(\frac{\text { Restoring force }}{\text { Area }}=\frac{F}{A}\)

Question 5.
Name the three types of stress.
Answer:
The three types erf stress are as following:

• Normal stress
• Bulk stress
• Tangential stress

Question 6.
Give the Young’s modulus for a perfectly rigid body.
Answer:
The Young’s modulus for a perfectly rigid body is infinity.

Question 7.
Define compressibility.
Answer:
Compressibility is defined as the reciprocal of the bulk modulus.

Question 8.
Why is steel used for making heavy duty machines and structural designs?
Answer:
Steel is more elastic than other metals like copper and aluminium. Hence, it is used for making heavy duty machines and structural designs.

Question 9.
Write the dimensional formula and SI unit of Young’s modulus.
Answer:
The dimensional formula for Young’s modulus is [ML^-1T^-2] and the SI unit is Nm^-2 or pascal (Pa).

Question 10.
What is elastic hysteresis?
Answer:
Elastic hysteresis is defined as the lagging of strain behind the stress, when a deforming force is applied.

Short Answer Questions

Question 1.
What are elastomers?
Answer:
Elastomers are those materials for which the strain and stress variation is non-linear or not a straight line within the limits of elasticity.

Question 2.
According to Hooke’s law of elasticity, what happens to the ratio of stress to strain when the stress is increased?
Answer:
According, to Hooke’s law of elasticity, the ratio of stress to strain remains constant. If the stress is increased.
Since, \(\frac{\text { Stress }}{\text { Strain }}\) = Y = Young’s modulus Strain
and Young’s modulus remains constant for same material of the wire.

Question 3.
What affects the elasticity of a substance?
Answer:
Answer:
The elasticity of a substance is affected by change in temperature, impurity in the substance, hammering and annealing.

Question 4.
In pendulum clocks, invar steel is used instead of any other solid body. Given reasons.
Answer:
Pendulum clocks due to the change in the elasticity of the material with the change in the temperature runs slower in summers than in winters. Due to this reason invar steel is used in the pendulums of the pendulum clock as it remains practically unaffected by the change in temperature and thus gives accurate time in all the seasons. 

Match the following:

Question 1.

Column ‘A’	Column 'B'
(a) Stress	(p) θ = \(\frac{x}{L}\)
(b) Strain	(q) Y = \(\frac{F l}{A \Delta l}\)
(c) Energy density	(r) ß = -\(\frac{P V}{\Delta V}\)
(d) Force	(s) η  = \(\frac{F l}{A x}\)

Answer:

Column ‘A’	Column 'B'
(a) Stress	(q) Y = \(\frac{F l}{A \Delta l}\)
(b) Strain	(r) ß = -\(\frac{P V}{\Delta V}\)
(c) Energy density	(s) η  = \(\frac{F l}{A x}\)
(d) Force	(p) θ = \(\frac{x}{L}\)

Question 2.

Column ‘A’	Column 'B'
(a) Young modulus	(p) No unit
(b) Bulk modulus	(q) N/m2
(c) Modulus of rigidity	(r) Newton
(d) Shearing strain	(s) Joule/m3

Answer:

Column ‘A’	Column 'B'
(a) Young modulus	(q) N/m2
(b) Bulk modulus	(p) No unit
(c) Modulus of rigidity	(s) Joule/m3
(d) Shearing strain	(r) Newton

Conceptual Questions

Question 1.
Why does a wire get heated when it is bent hack and forth?
Answer:
When a wire bent and forth, it’s deformations are beyond elastic limit. The work done against interatomic forces is no longer stored totally in the form of potential energy. The crystalline structure of wire gets affected and work done converted into heat energy.

Question 2.
The ratio stress/strain remains constant for a small deformation. What happens to this ratio. It deformation is made very large?
Answer:
When the deforming force exceeds the elastic limit, the strain increases more rapidly than stress. Hence the ratio of stress/strain decrease.

Question 3.
Why is the longer side of cross-section of girder used as depth?
Answer:
Depression δ = \(\frac{W L^3}{4 b d^3}\)
Clearly, the depression of the girder will be small when depth (d) is large, because
δ ∝ d^-3

Question 4.
A wire is cut to half its original length,
(a) How would it affect the elongation under a given load?
(b) How does it effect the maximum load it can support without exceeding the elastic limit?
Answer:
Young’s modulus Y = \(\frac{F \times l}{A \times \Delta l}\)
(a) ∆l = \(\frac{F}{A} \times \frac{l}{Y}\)
i.e., ∆l ∝ l
So when the wire is cut half to it’s original length then extension is halved.
(b) Maximum load (F) = \(\frac{Y A \Delta l}{l}\)
Here Y and A are constant. Whenthe wire is cut to half its original length, there is no charge on the value of \(\frac{\Delta l}{l}\). Hence there is no effect on the maximum load.

Question 5.
The breaking force for a wire is F. What will be the breaking force for (a) two parallel wires of the same size, (b) for a single wire of double the thickness?
Answer:
(a) When two wires of same size are suspended in parallel a force F equal to the breaking force will act on each wire of a breaking force 2F is applied on the parallel combination.
(b) F = \(\frac{Y A \Delta l}{l}=\frac{Y \pi r^2 \Delta l}{l}\)
∴ F ∝ ∆l
Thus for a single wire of double the thickness, the breaking force will be 4F.

Question 6.
Why does modulus of elasticity of most of the materials decrease with the increase of temperature?
Answer:
As the temperature increases, the inter atomic forces of attraction becomes weaker. For given stress, a large strain or deformation is produced at a higher temperature. Hence the modulus of elasticity decreases with increase of temperature.

Long Answer Questions

Question 1.
Differentiate between the following:
(a) Ductile material and brittle material
(b) Perfectly elastic body and perfectly plastic body. Also give examples of them.
Answer:
(a)

Ductile material	Brittle material
A ductile material is a material that can be plastically twisted with no crack. If tensile force is applied to these materials they canbe stretched into a wire. But if compressive force is applied, they can be deformed into sheets.	A brittle material is a material that will break when it is bent. When an external force is applied these materials tend to break, as they have small range of plastic extension.
Examples: Coppers, aluminium, steel, etc.	Examples: Glass, ceramics, etc.

(b)

Perfectly elastic body	Perfectly plastic body
A body that regains its original size and shape immediately and completely after the removal of the deforming force is called perfectly elastic body.	A body that does not regain its original size and shape after the deforming force is removed and remains in the deformed configuration is called perfectly plastic body.
Examples: Phosphor bronze and quartz.	Examples: Paraffin wax and mud.

Question 2.
Explain the stress and strain curve for a metallic wire.
Answer:
Stress-strain curve is a relationship between stress and strain for a given material and it can be calculated experimentally. A graph is plotted between the stress and the strain for a given material and the changes are noted. This could be tested if a wire of any material is stretched by an external force. The wire is stretched with an applied external force and the fractional changes in length are noted. This force is increased gradually and the corresponding changes in the length are noted down. A graph is plotted which clearly depicts the relationship between stress and strain. A typical stress-strain curve for a metallic wire is shown in figure 9.2.
From the graph, we can study that in the region between O to A, the curve is linear. In this region, it is very clear that the Hooke’s law is followed.

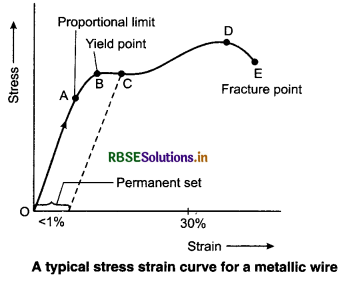
When the external force is removed, the body regains its original size and shape. Hence, in this region the body (wire) behaves as an elastic body and obeys Hooke’s law. In the region from A to B, after removal of the external force the body regains its original dimensions back, but the stress and strain are not proportional. The point B in the curve is known as the field point also called as the elastic limit, and the stress corresponding to this point is known as the yield strength.
Beyond point B, the strain increases more rapidly than the stress. Suppose at some point C, the load is removed, the body does not regain its original dimensions. In this situation, even if the stress is reduced to zero, the strain is not equal to zero. In this case, the material is set to have a permanent set. The wire gets thinner and thinner and develops weaker portion and finally the wire breaks at point E.

The point E is known as the fracture point or the breaking point, and the corresponding stress is called as the breaking stress. At point D, it is known as the ultimate stress point and the corresponding stress is called as ultimate tensile stress.
The region OAB is known as the elastic region, as it shows the elastic behaviour of the wire because the wire regains its original shape. The region CDE shows the plastic behaviour of the wire, as the wire cannot regain its shape. Since, the point D (ultimate stress point) and the point E (breaking point) are close, hence the material is said to be brittle. If these points were far apart then the material would have been ductile. The stress-strain curves would vary from material to material. These curves help us to understand, how a given material deforms with the increasing loads.

Question 3.
A bob of mass 10 kg is attached to a wire 0.3 m long. Its breaking stress is 4.8 x 10⁷ Nm^-2. The area of cross section of the wire is 10^-6 m². What is the maximum angular velocity with which it can be rotated in a horizontal circle?
Answer:
Since, breaking stress = maximum force applied per unit area.
Given, breaking stress = 4.8 x 10⁷ Nm^-2 and cross-sectional area = 10^-6 m².
Putting the values in above equation we get;
4.8 x 10⁷ = \(\frac{F_{\max }}{10^6 \mathrm{~m}^2}\) ∴ F_max = 48 N
In the case of horizontal rotation
F_max = mrω²
or 48N = (10 kg)(0.3 m) ω²
ω = 4 rad/s

Question 4.
Explain Poisson’s ratio.
Answer:
We have observed many times that stretching, applying load or applying an external force causes deformations in the dimensions of a material such as if a rubber band is stretched, the shape changes and so the dimensions. Similarly if a wire is stretched or is loaded with a mass there is change in the dimensions of the wire. The length increases but the diameter decreases and thus decreases the area of cross section of the wire. This also gives rise to two types of strains-longitudinal strain and lateral strain. Longitudinal strain is the strain produced in the direction of the applied force; whereas the strain produced in the perpendicular direction is called lateral strain.

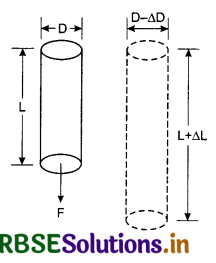
Hence, poisson's ratio is defined as:
"The ratio of lateral strain to longitudinal strain within the elastic limit."
Suppose, the length of the wire increases from L to L + ∆L and its diameter decreases from D to D - ∆D.

The negative sign here indicates that longitudinal and lateral strains are opposite.
Poisson's ratio has no units and dimensions.
The theoretical value of possion's ratio is -1 to \(\frac{1}{2}\).
The experimental value of possion's ratio is 0 to \(\frac{1}{2}\).

Question 5.
What is shear modulus? How do we calculate shear modulus? Explain with the help of a diagram.
Answer:
Shear modulus is defined as the ratio of tangential stress strain, within the elastic limit.
It is also called as the modulus of rigidity and is represented by η or G.
Suppose, we take into consideration a rectangular block or a cuboid whose lower face is fixed and a tangential force F acts on the upper face of area A as shown in the figure below.

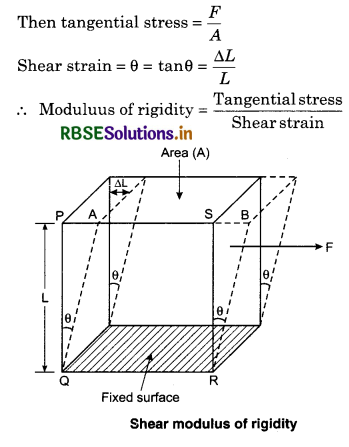
∴ η = \(\frac{F / A}{\theta}=\frac{F}{A \theta}=\frac{F}{A} \frac{L}{\Delta L}\)
Here, θ = ∠PQA and PA = ∆L and PQ = SR = L
The SI unit of modulus of rigidity is Nm^-2 and its CGs unit is dyne cm^-2. The dimensional formula is [ML^-1T^-2].

Question 6.
‘Bulk modulus’ is involved in all the three states of matter? Explain what is bulk modulus and how it is calculated?
Answer:
Bulk modulus of elasticity is defined as the ratio of normal, hydraulic or bulk (volumetric) stress to the volumetric strain, within the elastic limit.

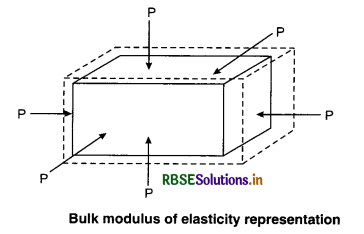
Suppose there is a body of volume V and surface area A as shown in the above figure. A uniform force F acts over the whole surface area of the body and it decreases the volume of the body by V.
Then, bulk modulus = \(\frac{\text { Hydraulic or Bulk (volumetric) stress }}{\text { Volumetric strain }}\)
Bulk modulus (K) = \(\frac{F / A}{-\Delta V / V}=-\frac{F V}{A \Delta V}\) ........................(1)
Hence negative sign indicate that when pressure is increased then volume is decreased.
Bulk modulus is represented by K or B.
The SI unit of bulk modulus is Nm^-2 or Pa and the dimensional formula is [ML^-1T^-2].

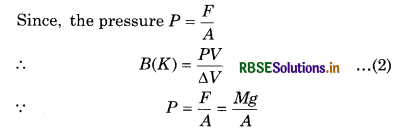
Mass of body = Volume x Density
= Area of cross section x Height x Density
= Ahρ
∴ P = \(\frac{A h \rho g}{A}\) = hρg
Put in equation (2)
∴ K = \(\frac{h \rho g}{-\frac{\Delta V}{V}}\)
Compressibility: Compressibility is defined as the reciprocal of the bulk modulus.
∴ Compressibility = \(\frac{1}{K}\)
The SI unit of compressibility is N^-1m² or Pa^-1; and the dimensional formula is [M¹LT²].
Bulk modulus is involved in all the three states of matter solid, liquid and gas respectively. The bulk modulus of solids is much greater than that of liquids and bulk modulus of liquids is much greater than that of gases.

Question 7.
What is strain? Also explain the various types of strain.
Answer:
When a deforming force acts on a body, the body experiences a change in its dimensions (i.e., shape and size).
The ratio of the change ¡n dimension of the body to its original dimension is known as strain.
Strain = \(\frac{\text { Changeindimension }}{\text { Original dimension }}\)
Since, strain is a ratio of two similar quantities. Therefore, it has no units and dimensions. Strain is thus a dimensionless physical quantity.

Types of Strain
Under the influence of a deforming force, a body experiences change in its dimensions. It could be change in length, volume or shape of the body. Hence, there are three types of strains as classified below:

(a) Longitudinal strain: As the name suggests, under the influence of a deforming force, if there is a change in the length of the body, then the ratio of the change in length to the original length is called the longitudinal strain.
Longitudinal strain = \(\frac{\text { Change in length }}{\text { Original length }}\)
= \(\frac{\Delta L}{L}\)
Where, ∆L is change in length and; L is the original length of the body

(b) Volumetric strain: If a deforming force is applied, due to which there is change in the volume of the body, then the ratio of the change in volume to the original volume is called as the volumetric strain.
Volumetric strain = \(\frac{\text { Change in volume }}{\text { Original volume }}\)
= \(\frac{\Delta V}{V}\)
where, ∆V is change in volume and; V is the original volume of the body.

(c) Shear strain: Shearing strain is defined as the angle θ (in radian) through which a face originally perpendicular to the fixed face gets turned on applying tangential deforming force.
Shear strain = θ = tanθ
= \(\frac{\text { Relative displacement between two parallel planes }}{\text { Distance between parallel planes }}\)

Numerical Questions

Based on Young Modulus

Question 1.
A metal wire of length L₁ and area of cross section A is attached to a rigid support. Another metal wire of length L₂ and of the same cross-sectional area is attached to free end of the first wire. A body of mass M is suspended from the free end of the second wire. Calculate the effective force constant of the system of two wires if Y₁ and Y₂ are the Young’s moduli of the wires respectively.
Solution:
As the Young’s modulus for the force constant for a wire is K = \(\frac{F}{\Delta l}=\frac{Y A}{L}\), where the symbols have their usual meanings.
So, the two wires together will have an effective force constant [\(\frac{K_1 K_2}{K_1+K_2}\)].
Substitute the values.

Question 2.
Calculate the percentage increase in length of a wire of diameter 1 mm stretched by a force of half kilogram weight Young’s modulus of elasticity of wire is 12 x 10¹¹ dyne/cm².
Solution:
d = 1 mm = 0.1 cm
Force applied (F) = \(\frac{1}{2}\) kg wt.
= \(\frac{1}{2}\) x 1000 x 980 dyne
but Y = 12 x 10¹¹ dyne/cm²

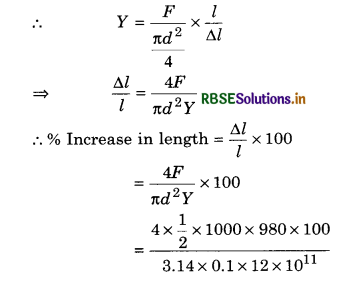
= 5.2 x 10^-3 = 0.0052%

Question 3.
A mass of 100 gm is attached to end of rubber string 49 cm long and having an area of cross section 20 square mm. The string is whirled round horizontally at a constant speed of 40 r.p.s. in circle of radius 51 cm. Find the Young modulus of rubber?
Solution:
When the mass attached at the end of rubber string is whirled into a horizontal circle, the restoring force in the rubber string is equal to centripetal force.
F = mrω² = 100 x 51 x (2π x 40)² dyne
∴ Y = \(\frac{F \times l}{A \times \Delta l}=\frac{100 \times 51 \times 4 \pi^2 \times 40 \times 40 \times 49}{20 \times 10^{-2}(51-49)}\)
= 3.95 x 10¹¹ dyne/cm²
= 3.95 x 10⁹ N/m²

Bulk Modulus of Elasticity

Question 4.
The compressibility of water is 6 x 10^-10 N^-1m². If one litre is subjected to a pressure of 4 x 10⁷ Nm^-2. What is the decrease is the volume?
Solution:
ß = \(\frac{\frac{P}{\Delta V}}{V}\)
∆V = \(\frac{P V}{\beta}\) = PVK
= 4 x 10⁷ x 1 x 10³ x 6 x 10^-10 cm³
= 24 cm³

Question 5.
By how much the pressure on one litre of water be changed to compress it 0.2%? The bulk modulus of water = 2.2 x 10⁹ Pa.
Solution:
\(\frac{\Delta V}{v}\) = 0.2% = \(\frac{0.2}{100}\) = 0.002, ß = 2.2 x 10⁹ Pa
As ß = \(\frac{\frac{P}{\Delta V}}{V}\)
∴ P = ß x \(\frac{\Delta V}{V}\) = 2.2 x 10⁹ x 0.002
= (4.6 x 10⁶ Pa)

Question 6.
A sphere contracts in volume by 0.02% when taken to the bottom of sea 2 km deep. Find the value of bulk modulus of the material of sphere. Density of sea water = 1 g/cc, g = 10m/s^-2
Solution:
\(\frac{\Delta V}{V}\) = 0.02% = -\(\frac{0.02}{100}\)
h = 2 km = 2 x 1000 m = 2000 m
Density of sea water (ρ) = 1 g/cc = 1000 kg/m³
Pressure applied:
P = hρg
= 2000 x 10³ x 10
= 2 x 10⁷ N/m²
Bulk modulus ß = -\(\frac{P}{\frac{\Delta V}{V}}\)
= \(\frac{2 \times 10^7}{-\frac{0.02}{100}}\) = 10¹¹ N/m²

Modulus of Rigidity

Question 7.
Two parallel and opposite forces earth 5000 N are applied tangentially to the upper and lower faces of a cubical metal block 30 cm on a side. Find the angle of shear and the displacement of upper surface relative to the lower surface. The shear modulus for the metal is 8 x 10¹¹ N/m².
Solution:
F = 5000 N, L = 30 cm = 0.30 m, G = 8 x 10¹⁰ N/m²

= 6.94 x 10^-7 rad
∴ ∆L = Lθ = 0.30 x 6.94 x 10^-7
= 2.1 x 10^-7 m

Question 8.
A metallic cube of side 8 cm is under a tangential force. The top face of the cube is sheared through 0.15 mm with respect to the bottom face. Find (a) shearing strain, (b) Shearing stress (and), (c) shearing force.
Given modulus of rigidity of metal = 2.08 x 10¹¹ dyne/cm²
Solution:
Length of each side of cube (L) = 8 cm
Lateral displacement (∆L) = 0.15 mm = 0.015 cm
(a) Shearing strain (θ) = \(\frac{\Delta L}{L}=\frac{0.015}{8}\)
= 0.001875
(b) Shearing stress = \(\frac{F}{A}\) = Gθ
= (2.08 x 10¹¹) x 0.001875
= 3.9 x 10⁸ dyne/cm²
(c) Area of face (A) = 8 x 8 cm² = 64 cm²
G = \(\frac{F}{A \theta}\)
∴ F = GAθ
= 2.08 x 10¹¹ x 64 x 0.001875
= 0.25 x 10¹¹ dyne = 2.5 x 10¹⁰ dyne

Possion’s Ratio

Question 9.
The Poisson’s ratio of a material is 0.5. If a force is applied to a wire of this material there is a decrease in the cross sectional area by 4%. Calculate the percentage increase in the length.
Solution:
4%

Question 10.
A material has Poisson’s ratio 0.50. If a uniform rod of it suffers a longitudinal strain of 2 x 10^-3. Then calculate the percentage change in its volume.
Solution:

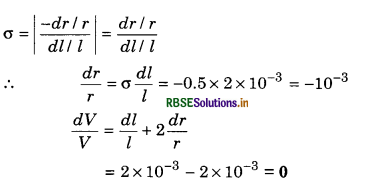
Question 11.
Two wires of the same material and same length but diameters in the ratio 1 : 2 are stretched by the same force. Calculate the ratio of the potential energy per unit volume of the two wires.
Solution:

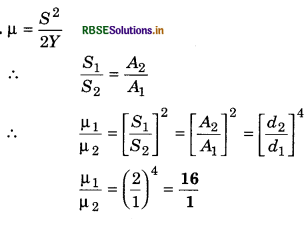
Question 12.
Calculate the increase in energy of a brass bar of length 0.4 m and cross-sectional area 1 cm². When compressed with a load of 4 kg wt. along its length. Young’s modulus of brass is 1.0x 10¹¹ N/m² and g = 10m/S^-2.
Solution:
l = 0.4 m, A = 1 cm² = 10^-4 m²
F = 4 kg wt. = 4 x 10 = 40 N
Y = 1.0 x 10¹¹ N/m²
Increase in energy of brass bar is

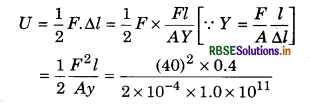
= 3.2 x 10^-5 J

Question 13.
A 45 kg boy whose leg bones are 5 cm² in area and 50 cm long falls through a height of 2 cm without breaking his leg bones. If bones can stand a stress of 0.9 x 10⁸ N/m². Calculate the Young’s modulus for the material of bone. (Use g = 10 m/S^-2)
Solution:
m = 45 kg boy, h = 2 m, L = 0.50 m
A = 5 x 10^-4 m²
Loss in gravitational energy = Gain in elastic energy in both leg bones
∴ mgh = 2 x [\(\frac{1}{2}\) x Stress x Strain x Volume]
45 x 10 x 2 = 2 x \(\frac{1}{2}\) x 0.9 x 10⁸ x Strain x 2.5 x 10^-4
Strain = \(\frac{45 \times 10 \times 2}{0.9 \times 2.5 \times 10^4}\) = 0.04
Young modulus = \(\frac{\text { Stress }}{\text { Strain }}\)
Y = \(\frac{0.9 \times 10^8}{0.04}\) = 2.25 x 10⁹ N/m²

Question 14.
When the load of a wire is increased from 3 kg wt to 5 kg wt, the elongation increases from 0.61 mm to 1.02 mm. How much work is done during this extension of the wire.
Solution:
F₁ = 3 kgf = 3 x 9.8 N, ∆l₁ = 0.61 x 10^-3 m
F₂ = 5 kgf = 5 x 9.8 N, ∆l₂ = 1.02 x 10^-3 m
Work done (W) = \(\frac{1}{2}\)F₂∆l₂ - \(\frac{1}{2}\)F₁∆l₁
= \(\frac{1}{2}\)[5 x 9.8 x 1.02 x 10^-3 - 3 x 9.8 x 0.61 x 10^-3]
= 16.023 x 10^-3 Joule

Question 15.
A wire suspended vertically from one of its ends is stretched by attaching a weight of 200 N to the lower end. The weight attached stretches the wire by 1 mm. What is the elastic potential energy stored in the wire?
Solution:
Elastic potential energy U = \(\frac{1}{2}\) x Stress x Strain x Volume
U = \(\frac{1}{2}\) x \(\frac{F}{A} \times \frac{\Delta l}{l}\) x Al = \(\frac{1}{2}\)F∆l
U = \(\frac{1}{2}\) x 200 x 10^-3
= 0.1 Joule

Hots Questions

Question 1.
A copper wire of negligible mass, length l and cross-section A is kept on a smooth horizontal table with one end fixed. A ball of mass m is attached to the other end. The wire and the ball are rotating with an angular velocity ω. if elongation in the wire is ∆l, obtain the expression for the Young’s modulus.
Solution:
When the ball attached at one end of wire is rotating, then the restoring force in the wire is equal to the centripetal force on the ball.
Centripetal force (F) = mrω² = mlω² ..........................(1)

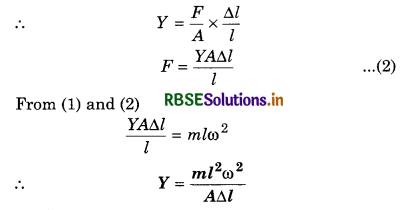
Question 2.
A metallic wire is stretched by suspending weight from it. If α is longitudinal strain and Y is the Young’s modulus. Show that elastic potential energy per unit volume is given by \(\frac{1}{2}\)Yα².
Solution:
Electric potential energy per unit volume

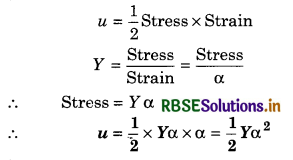
Question 3.
Two rods of different materials but of equal cross-sections and lengths (1.0 m each) are joined to make a rod of legth 2.0 m. The metal of one rod has coefficient of linear thermal expansion 10^-5 °C^-1 and Young’s modulus 3 x 10¹⁰ N/m^-2. The other metal has values 2 x 10^-5 °C^-1 and 10 N/m² respectively. How much pressure must be applied to the ends of composite rod to prevent its expension when the temperature raised by 100°C.
Solution:
When the temperature is raised by 100°C, the extension in the two rods are
∆l₁ = α₁l∆T = 10^-5 x 1.0 x 100 = 10^-3 m
∆l₂ = α₂l∆T = 2 x 10^-5 x 1.0 x 100 = 2 x 10^-3 m
Tension produced in the rods are
T₁ = Y₁\(\frac{A \Delta l_1}{l}=\frac{3 \times 10^{10} \times A \times 10^{-3}}{1.0}\)
= 3 x 10^-7 A newton
T₂ = \(\frac{Y_2 A \Delta l_2}{l}=\frac{10^{10} \times A \times 2 \times 10^{-3}}{1}\)
= 2 x 10⁷ A newton
Total force needed to be applied at the ends to prevent expansion
= T₁ + T₂
= 3 x 10⁷ A + 2 x 10⁷ A
= 5 x 10⁷ A newton
∴ Pressure = \(\frac{\text { Force }}{\text { Area }}=\frac{5 \times 10^7 A}{A}\)
= 5 x 10⁷ N/m^-2

Question 4.
The length of a metal wire is l₁ when the tension in it is T₁ and is l₂ when the tension is T₂. What is the natural length of wire?
Solution:
Let L be the original length and A the area of cross-section of wire.
The charge in length, when tension is T₁ = ∆l₁ = l₁ - L
The charge inlength, when tension is T₂ = ∆l₂ = l₂ - L
Young modulus in btoh case:

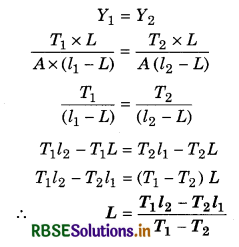
Question 5.
The density of metal at normal pressure is P. Its density when it is subjected to an excess pressue is P'. It B is the bulk modulus of metal. Find the ratio of \(\frac{\rho^{\prime}}{\rho}\).
Solution:
Bulk modulus (ß) = \(\frac{\rho}{d V / V}=\frac{P \times V}{d V}\)
∴ dV = \(\frac{P V}{\beta}\)
When pressure is increased, the volume will decrease.

Questions for Competitive Examinations 

Objective Type Questions

Question 1.
One end of horizontal thick copper wire of length 2L and radius 2R is welded to an end of another horizontal thin copper wire of length L and radius R. When the arrangement is stretched by applying forces at two ends, the ratio of the elongation in the thin wire to that in the thick wire is:
(a) 0.25
(b) 0.50
(c) 2.00
(d) 4.00
Solution:
(c) Force F will be same.
Elongation in the thin wire, l₁ = \(\frac{F L}{A Y}=\frac{F L}{\pi R^2 Y}\)

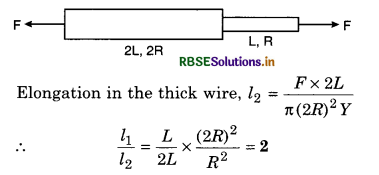
Question 2.
The pressure of a medium is changed from 1.01 x 10⁵ Pa to 1.65 x 10⁵ Pa and change in volume is 10% keeping the temperature constant. The bulk
modulus of the medium is:
(a) 204.8 x 10⁵ Pa
(b) 102.4 x 10⁵ Pa
(c) 51.2 x 10⁵ Pa
(d) 1.55 x 10⁵ Pa
Solution:
(d) Bulk modulus = \(\frac{\Delta P}{\Delta V / V}\)
= \(\frac{(1.165-1.01) \times 10^5}{10 / 100}\) = 1.55 x 10⁵ Pa

Question 3.
In plotting stress versus strain curves for two materials P and Q, a student by mistake puts strain on the y-axis and stress on the x-axis as shown in the figure.

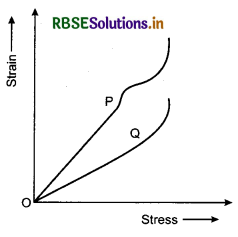
Then the correct statement (s) is (are):
(a) P has more tensile strength than Q
(b) P is more ductile than Q
(c) P is more brittle than Q
(d) The Young’s modulus of P is more than that of Q.
Solution:
(a) (b) Breaking stress of P > Breaking stress of Q
∴ P is more tensile than Q.
∴ option (a) is correct.
But P is also more ductile than Q.
∴ Option (b) is correct.
But P is less brittle than Q.
∴ Option (c) is not correct.
Young's modulus, Y = \(\frac{\text { Stress }}{\text { Strain }}\)
For any given value of stress, strain in P is more than in Q.
∴ Y_P < Y_Q

Question 4.
In designing a beam for its use to-support a load, the depression at the centre (where, Y is Young’s modulus) is proportional to:
(a) Y²
(b) Y
(c) 1/Y
(d) 1/Y²
Solution:
(c) Depression, δ = \(\frac{W l^3}{4 Y b d^3}\)
⇒ δ ∝ \(\frac{1}{Y}\)

Question 5.
The compressibility of water is 4 x 10^-5 per unit atmospheric pressure. The decrease in volume of 100 cm³ of water under a pressure of 100 atmosphere will be:
(a) 0.4 cm³
(b) 4 x 10^-5 cm³
(c) 0.025 cm³
(d) 0.004 cm³
Solution:
(a) Compressibility = \(\frac{\Delta V}{P V}\)
4 x 10^-5 = \(\frac{\Delta V}{100 \times 100}\)
∆V = 0.4 cm³

Question 6.
The breaking stress of a wire depends upon:
(a) length of the wire
(b) radius of the wire
(c) material of the wire
(d) shape of the cross-section
Solution:
(c) The stress at which rupture of the wire occurs is called its breaking stress. Its value depends on the material of the wire.

Question 7.
The relation between Young’s modulus (Y), bulk modulus (K) and modulus of elasticity (η) is: 

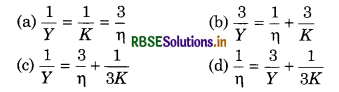
Solution:
(b) \(\frac{3}{Y}=\frac{1}{\eta}+\frac{1}{3 K}\)

Question 8.
In solids interatomic forces are:
(a) Totally repulsive
(b) Totally attractive
(c) Both (a) and (b)
(d) None of these
Solution:
(c) The interatomic forces in solids are both attractive and repulsive.

Question 9.
The breaking force for a wire of diameter D of a material is F. The breaking force for a wire of the same material of radius D is:
(a) F
(b) 2F
(c) \(\frac{F}{4}\)
(d) 4F
Solution:
(d) Breaking force αr²
\(\frac{F^{\prime}}{F}=\frac{D^2}{(D / 2)^2}=4\)
F' = 4F

Question 10.
If longitudinal strain for a wire is 0.03 and its Poisson’s ratio is 0.5, then its lateral strain is: 
(a) 0.003
(b) 0.0075
(c) 0.015
(d) 0.4
Solution:
(c) \(\sigma=\frac{\text { Lateral strain }}{\text { Longitudinal strain }}\)
0.5 = \(\frac{\text { Lateral strain }}{0.03}\)
Lateral strain = 0.5 x 0.03  = 0.015

Question 11.
If the work done in stretching a wire by 1 mm is 2J, the work necessary for stretching another wire of same material but with double radius of cross section and half the length by 1 mm is:
(a) 16 J
(b) 8 J
(c) \(\frac{1}{16}\) J
(d) \(\frac{1}{8}\) J
Solution:
(a) W = \(\frac{1}{2}Y\frac{\left(\Delta l^2\right) A}{l}\)
For same Y and ∆l.W ∝ \(\frac{\pi r^2}{l}\)
∴ \(\frac{W_2}{W_1}=\frac{(2 r)^2}{r^2} \cdot \frac{l}{l / 2}\) = 8
⇒ W₂ = 8W₁ = 8 x 2 = 16 J

Question 12.
A pendulum made of a uniform wire of cross-sectional area A has time period T. When an additional mass M is added to its bob, the time period changes to TM. If the Young’s modulus of the material of the wire is Y then \(\frac{1}{Y}\) [g = gravitational acceleration] is equal to:

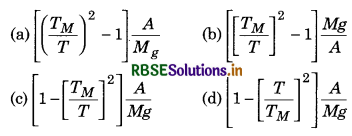
Solution: