RBSE Class 11 Physics Important Questions Chapter 8 Gravitation

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 8 Gravitation Important Questions and Answers.

RBSE Class 11 Physics Chapter 8 Important Questions Gravitation

Multiple Choice Questions

Question 1.
Suppose a light planet is revolving in circular orbit of radius R about a heavy star and its time period is T. Gravitational force between the planet and the star is directly proportional to R^-5/2, then:
(a) T² ∝ R³
(b) T² ∝ R^7/2
(c) T² ∝ R^3/2
(d) T² ∝ r^3.75
[Hint: F = mRω²

Answer:
(b) T² ∝ R^7/2

Question 2.
A body of mass m is taken at a height h = \(\frac{R}{5}\) from the earth’s surface, where R is radius of the earth. If g be the acceleration diie to gravity at the surface of the earth, then change in the potential energy of the body with ∆P:
(a) mgh
(b) \(\frac{4}{5}\) mgh
(c) \(\frac{5}{6}\) mgh
(d) \(\frac{6}{5}\) mgh
Answer:
(c) \(\frac{5}{6}\) mgh

Question 3.
Two identical solid gold spheres are kept in contact, gravitational force between them will be:
(a) Directly proportional to square of radius
(b) Directly proportional to cube of radius
(c) Directly proportional to fourth power of radius
(d) Inversely proportional to square of radius
[Hint: F = \(\frac{G M m}{r^2}=\frac{G M^2}{(2 R)^2}=\frac{G\left(\frac{4}{3} \pi R^3 \rho\right)^2}{4 R^2}\)
or F = \(\frac{4 \pi^2 \rho^2 G}{3} R^4\)
∴ F ∝ R⁴]
Answer:
(c) Directly proportional to fourth power of radius

Question 4.
Reason of absence of atmosphere on moon is:
(a) Moon is much light in weight.
(b) Moon revolves around the earth.
(c) Root mean square velocity of gas molecules is greater than escape velocity.
(d) All above
Answer:
(c) Root mean square velocity of gas molecules is greater than escape velocity.

Question 5.
Mean radius of a planet around the Sun is given by:
(a) Equal to Sun major axis (a) of ellipse
(b) Equal to semi minor axis (b) of the ellipse
(c) Average of semi major and semi minor axis \(\frac{(a+b)}{2}\).
(d) Geometrical mean of semi-major and semi-minor axis i.e., \(\sqrt{ab}\)
Answer:
(a) Equal to Sun major axis (a) of ellipse

Question 6.
What will be height of projectile projected with velocity \(\sqrt{gR_e}\) from the earth’s surface?
(a) 2R_e
(b) \(\frac{R_e}{2}\)
(c) R_e
(d) Infinity

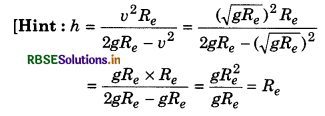
Answer:
(c) R_e

Question 7.
Gravitational acceleration is maximum:
(a) At equator of the earth
(b) At poles of the earth
(c) At top of a hill
(d) At deep mine inside the earth
Answer:
(b) At poles of the earth

Question 8.
Dimensional formula of universal constant of gravity is:
(a) [M¹L³T^-2]
(b) [M^-1L¹T^-2]
(c) [M^-1L³T^-2]
(d) [M^-1L³T^-1]
Answer:
(c) [M^-1L³T^-2]

Question 9.
If the rotational motion of the earth increases, then weight of an object at latitude λ:
(a) Will increase
(b) Will decrease
(c) Will remain unchanged
(d) Nothing can be said certainly
[Hint: g' = g - Rω² cos²λ On increasing the value of ω, g' will decrease]
Answer:
(b) Will decrease

Question 10.
Orbital velocity of satellite revolving near the. surface of the earth will be approximately:
(a) 8 km/s
(b) 11.2 km/s
(c) 4 km/s
(d) 6 km/s
Answer:
(a) 8 km/s

Question 11.
Escape velocity on moon is nearly:
(a) 11.2 km/s
(b) 5 km/s
(c) 10 km/s
(d) 2.4 km/s
Answer:
(d) 2.4 km/s

Question 12.
Masses and radius of the earth and moon are M₁, R₁ and M₂, R₂ respectively. The distance between their centres is d. With what velocity an object of mass m should be projected from the mid-point between them so that it may escape?

Answer:
(a) 2 \(\sqrt{\frac{G}{d}\left(M_1+M_2\right)}\)

Question 13.
Newton’s law of gravitation is universal law because:
(a) It is always attractive.
(b) It is applicable on all members of solar system and particles.
(c) It is applicale on all masses for all distances and it 4s not effected with mean.
(d) All of the above
Answer:
(c) It is applicale on all masses for all distances and it 4s not effected with mean.

Question 14.
Time period of an artificial satellite revolving near the surface of the earth, is:
(a) 24 hours
(b) 84 min
(c) 48 min
(d) 12 hours
Answer:
(b) 84 min

Question 15.
Intensity of gravitational field at the centre of a hollow sphere is:
(a) \(\frac{G M}{r^2}\)
(b) g
(c) 0 (zero)
(d) \(\frac{2G M}{r^2}\)
Answer:
(c) 0 (zero)

Question 16.
A boy of mass 50 kg is standing on a lift moving downwards with acceleration of 9.8 m/s². Apparent weight of the boy is:
(a) 0 (zero)
(b) 50 N
(c) 50 x 9.8 N
(d) \(\frac{50}{9.8}\) N
Answer:
(a) 0 (zero)

Question 17.
If earth stops rotating, then value of 'g' on equator:
(a) will increase
(b) will remain unchanged
(c) will decrease
(d) none of these
Answer:
(a) will increase

Question 18.
Weight of a body at the centre of the earth will be:
(a) zero
(b) infinite
(c) same as that on the earth’s surface
(d) none of these
Answer:
(a) zero

Question 19.
Unit of gravitational potential is:
(a) \(\frac{\mathrm{J}}{\mathrm{kg}} \)
(b) J
(c) J x kg
(d) \(\frac{\text { volt }}{\mathrm{m}}\)
Answer:
(a) \(\frac{\mathrm{J}}{\mathrm{kg}} \)

Question 20.
If the radius of the earth decreases by 1% without, changing its mass, then gravitational acceleration on the earth’s surface:
(a) will increase 1%
(b) will decrease 2%
(c) will decrease 1%
(d) will increase 2%
Answer:
(d) will increase 2%

Question 21.
A person can jump upto more height than on the earth, because:
(a) Value of g on moon is less than that on the earth.
(b) There is no atmosphere on moon.
(c) Moon is cold than earth.
(d) Surface of moon is rough.
Answer:
(a) Value of g on moon is less than that on the earth.

Question 22.
The height from the earth surface, where gravitational acceleration is \(\frac{1}{4}\) of that on the earth's surface, will be:
(a) \(\frac{R}{4}\)
(b) \(\frac{R}{2}\)
(c) \(\frac{3R}{4}\)
(d) R
Answer:
(d) R

Question 23.
Weight of a body of mass m height h from the earth’s surface decreases by 1%. If the body is taken at depth h in mine, then change in weight will be:
(a) decrease of 2%
(b) decrease of 1%
(c) decrease of 0.5%
(d) decrease of 1.5%
Answer:
(c) decrease of 0.5%

Question 24.
The distance between two electrons is 10 cm, gravitational and electric forces are F_g and F_e. Order of ratio F_g and F_e will be:
(a) 10³⁶
(b) 10
(c) 10^-36
(d) 10^-43
Answer:
(d) 10^-43

Question 25.
The value of depth 'd' of where value of g is \(\frac{1}{n}\) of that on the earth's surface, is:

Answer:
(b) R(\(\frac{n-1}{n}\))

Question 26.
Time period of a communication satellite INSAT-IIB around the earth is:
(a) 12 hrs
(b) 24 hrs
(c) 48 hrs
(d) 30 days
Answer:
(b) 24 hrs

Question 27.
Kepler's third law relating to planetary motion is:
(a) T ∝ r
(b) T ∝ r²
(c) T ∝ r³
(d) T ∝ r^3/2
Answer:
(d) T ∝ r^3/2

Very Short Answer Questions

Question 1.
What is the reason of tail of comet being away from the Sun?
Answer:
Due to radiant pressure of Sun, the gases present in comet make a tail away from Sun.

Question 2.
Gravitational attraction acts on moon by the earth, even then moon does not fall on the earth, why?
Answer:
Since moon revolves around earth, in circular orbit, therefore the gravitational force of attraction is consumed in providing required centripetal force. Hence, moon does not fall on the earth.

Question 3.
How does depend the orbital velocity of a satellite on its mass?
Answer:
It does not depend on its mass.

Question 4.
What is main reason of tide in sea?
Answer:
Gravitational attraction of moon on the earth.

Question 5.
If an object is taken from earth towards moon, what will be change in value of g?
Answer:
First the value of g will go on decreasing after attuning zero value, it will start increasing and on moon it will become \(\frac{1}{6}\) of its value on the earth, i.e., \(\frac{g}{6}\).

Question 6.
What is geostationary satellite?
Answer:
The satellite, which appears stationary to an observer on earth, is called geostationary satellite.

Question 7.
What will happen on opening the cap of bottle filled with water at 10°C, on moon?
Answer:
Water will start boiling because atmosphere pressure on moon is zero, hence boiling point decreases.

Question 8. 
In which manner, the value of g decreases on going inside the earth?
Answer:
Value of g will decrease, linearly as shown in the figure.

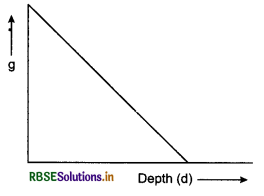
Question 9.
What do you mean by binding energy of a satellite?
Answer:
The energy required for a satellite to escape from its orbit, is called its binding energy i.e.,
E_b = 0 - E_t = \(-\left(-\frac{1}{2} \frac{G M_e m}{r}\right)\)
or E_b = \(\frac{1}{2} \frac{G M_e m}{r}\)

Question 10.
Generally, the rockets are launched directing west to east, why?
Answer:
Earth itself rotates from west to east. Therefore to obtain maximum benefit of earth’s motion, the rockets are launched from west to east.

Question 11.
Why the clock based on pendulum motion is not used in artificial satellite?
Answer:
In satellite the bodies are in situation of weightlessness, i.e., g = 0 and pendulum base clock functions on the basis of g. Therefore it will not work in a satellite.

Question 12.
In an artificial satellite a person experiences weightlessness but not on moon. Why?
Answer:
Moon has its own gravitational field due to its sufficient mass. This is why on moon weightlessness is not experienced.

Question 13.
How the value of g changes with height. Make a graph.
Answer:
Value of g at height h,

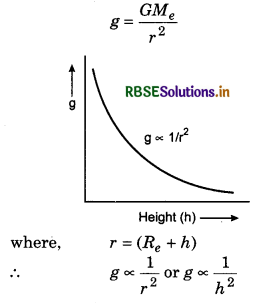
This variation is shown in the figure.

Question 14.
Why it is difficult to walk, to jump and drink water by tumbler, in an artificial satellite?
Answer:
It is due to weightlessness in an artificial satellite. 

Question 15.
If the distance between two objects is decreased by x%, what will be the percentage increase in gravitational force between them?
Answer:
∵ F = \(\frac{G m_1 m_2}{r^2}\) or F = \(\frac{K}{r^2}\)
∴ \(\frac{\Delta F}{F}\) x 100 = 2\(\frac{\Delta r}{r}\) x 100 = 2 x x% = 2x%
i.e., gravitational force will increase by 2x%.

Question 16. 
What will be value of g at the centre of the earth?
Answer:
Zero.

Question 17.
At what height from the earth’s surface, revolve the communication satellites around the earth?
Answer:
At the height of 36000 km.

Question 18.
What is called polar satellite?
Answer:
The satellite, having plane of its orbit passes through north and south poles of earth is called a polar satellite.

Question 19.
How many geostationary satellites will be needed to link the whole earth with communication?
Answer:
Three.

Question 20. 
What is parking orbit?
Answer:
If the centre of orbit of a satellite coincides the centre of earth, then it is called parking orbit.

Question 21.
Find the angular velocity of geostationary satellite.
Answer:
Angular velocity,
ω = \(\frac{2 \pi}{T}=\frac{2 \pi}{24 \times 3600}\) = 7.3 x 10^-5 rad.s^-1

Question 22.
What is value of gravitational potential energy at the centre of a solid sphere? What is its percentage of its value at the surface of the sphere?
Answer:
Gravitational potential energy at the centre and its value on the surface = \(-\frac{3 G M m}{R}\) and its value on the surface = \(-\frac{G M m}{R}\)
Therefore its value at the centre is 150% of its value on its surface.

Question 23.
On conservation of which quantity is based Kepler’s second law of planetary motion?
Answer:
It is based on law of conservation of angular momentum.

Question 24.
A ball is thrown out of satellite by an astronaut, will it rech the ground? 
Answer:
No, the ball will start revolution around the earth with the orbital speed as that of satellite.

Question 25.
When a body falls towards the earth, then does the earth also fall towards the body? If yes, why do we not see it?
Answer:
Because the mass of the earth is very much in comparison to that of the body, therefore acceleration of the earth towards the body is negligible.

Question 26.
When an astronaut lands on moon then he loads a heavy weight on his back, why?
Answer:
Because, the value of g is very small, therefore to maintain the balance he does so.

Question 27.
If the earth stops rotating, what will be its effect on value of g? Will it be same at all places on earth?
Answer:
Value of g will increase at all places on earth except on poles. This change will be maximum on equator and zero on poles.

Question 28.
Gravitational potential energy of a body on venus is -7.5 x 10⁶ J. What amount of energy will be required to throw the body out of venus?
Answer:
Required energy = 7.5 x 10⁶ J.

Question 29.
Centripetal force acting on a satellite revolving around the earth is F. What will be gravitational force applied by the earth on the satellite. What will be work done on satellite by this force?
Answer:
Gravitational force = Centripetal force.
∴ Gravitational force applied by earth on satellite = F
Work done by this force W = 0 because the direction of motion of satellite is normal to this force.

Question 30.
What will be the reading of spring balance on hanging an object of mass m, in an artificial satellite.
Answer:
Zero.

Question 31.
Write the relation between escape velocity (v_e) and orbital velocity of satellite revolving near the surface of earth.
Answer:
Escape velocity = \(\sqrt{2}\) x Orbital velocity
or v_e = v₀\(\sqrt{2}\)

Question 32.
At what projection angle, will the escape velocity be less?
Answer:
Escape velocity does not depend on angle of projection.

Question 33.
Does the friction force increase due to gravitational attraction?
Answer:
No, its origin is of electrical nature.

Question 34.
Can the gravitational mass be determined in an artificial satellite?
Answer:
No, because the artificial satellite is equivalent to freely falling body.

Question 35.
If the orbital velocity of an artificial satellite is changed upto some extent by an obstacle, what will be its effect?
Answer:
It will fall on the earth.

Question 36.
Why the orbit of artificial satellite is kept outside the earth’s atmosphere?
Answer:
So, that its energy may not decay due to friction of the atmosphere.

Question 37.
How many times is electrostatic force of gravitational force between two electrons?
Answer:
1043 times.

Question 38.
Name the scientist who first obtained the practical value G?
Answer:
Cavendish.

Question 39.
What will be the weight of a body at the centre of earth?
Answer:
Zero.

Question 40.
Give the name of first Indian astronaut.
Answer:
Mr. Rakesh Sharma.

Fill in the blanks:
Question 1.
When a stone of mass (m) is falling on the earth of mass M, then the acceleration of earth is ........................
Answer:
\(\frac{m g}{M}\)

Question 2.
The time period of revolution of geostationary satellite, is ........................
Answer:
24 H

Question 3.
Mass of a body is more ........................ than it’s weight.
Answer:
fundamental

Question 4.
The value of acceleration due to gravity is ........................ every where on the surface of earth.
Answer:
same

Question 5.
The magnitude of external force required to produce unit acceleration in the body is equal to ........................ of the body.
Answer:
inertial mass.

Short Answer Questions

Question 1.
If a body is projected from the earth’s surface with velocity v (v > v_e), then find its velocity outside the earth’s gravitational field.
Answer:
Total energy on the earth
E₁ = \(+\frac{1}{2} m v^2-\frac{G M_e m}{R_e}\)
Total energy outside the gravitational potential energy becomes zero.
∴ From the law of conservation of energy,
E₂ = E₁

Question 2.
Gravitational force between two bodies is F. If the distance between them is doubled, what will become the gravitational attraction between them?
Answer:
The gravitational force between two bodies of masses m₁, m₂ situated at distance r,
F = \(\frac{G m_1 m_2}{r^2}\)
If the distance  is doubled, then force
F' = \(\frac{G m_1 m_2}{(2 r)^2}=\frac{1}{4} \frac{G m_1 m_2}{r^2}\) or F' = \(\frac{F}{4}\)
i.e., force will now become one fourth of previous one.

Question 3.
Distance between two bodies, A and B is r. Taking gravitational force according to inverse square law, the acceleration of A is ‘a’. If the mutual interaction obeys the inverse of fourth power of distance, what will be acceleration of A now?
Answer:
Gravitaional force on A due to B,
F_A = \(\frac{G M_A M_B}{r^2}\)
∴ Acceleration of body A, a = \(\frac{F_A}{M_A}\) (according to Newton's second law)

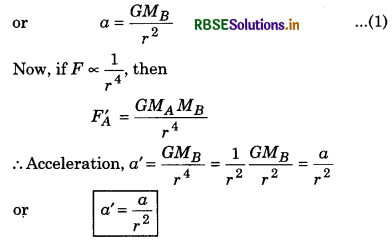
Question 4.
Atmosphere on jupiter contains light gases (generally hydrogen) while the contribution of hydrogen gas in the atmosphere of earth is very less, why?
Answer:
Escape velocity on jupiter is very high than that on earth. This is why to escape from jupiter’s surface, the required velocity is very high. Since thermal velocity of hydrogen gas is less than escape velocity, therefore it can not escape from jupiter surface.

Question 5.
Two bodies on earth attract each other but they do not move towards each other, why?
Answer:
Gravitational force acting between two bodies on earth is very small i.e., negligible in comparison to that due to the earth. Therefore, acceleration produced by this force is also negligible. This is why the bodies do not move towards each other.

Question 6.
When a falling satellite enters the earth’s atmosphere, it becomes hot i.e., its mechanical energy decays. Even then the satellite falls with increasing velocity adopting helical path, why?
Answer:
Total energy of satellite, revolving in orbit, is negative. When it enters the earth’s atmosphere, then its mechanical energy (which is negative) decays i.e., it becomes more negative. But orbital speed v₀ = \(\sqrt{\frac{G M_e}{\left(R_e+h\right)}}\) will increase only when value of h will decrease. Therefore, the satellite falls with increasing velocity adopting helical path.

Question 7.
Establish the relation between g and G.
Answer:
According to Newton's second law,
Force = Mass x Acceleration
∴ Gravitational force = Mass x Gravitational acceleration
i.e., F_g = mg .....................(1)
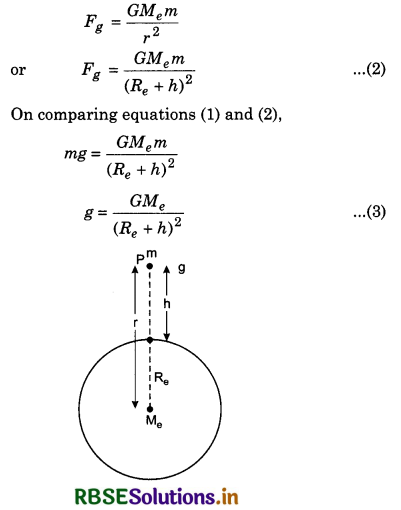
Suppose an object of mass m is situated at P i.e., at height h from the earth's surface, then its distance from the centre of earth,
r = (R_e + h)
∴ Gravitational force acting on the object,

This is the relation between g and G
For earth surface,
r = R_e
Acceleration due to gravity at the earth's surface

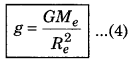
Given G = 6.67 x 10^-11 Nm²/kg²
M = 6.0 x 10²⁴ kg
R_e = 6.4 x 10⁶ m
∴ g_e = \(\frac{6.67 \times 10^{-11} \times 6.0 \times 10^{24}}{\left(6.4 \times 10^6\right)^2}\)
= 9.8 m/sec²
From equations (3) and (4), it is clear that the value of g does not depend on the mass of the body. Therefore, if the bodies of different masses are dropped freely from any height, then they will fall with the same acceleration.

Question 8.
Establish the relation between gravitational potential and intensity of gravitational field.
Answer:
Suppose the intensity of gravitational field at point P, which is at a distance r from the centre of the earth, is I_g and gravitational potential at this point is V_g then

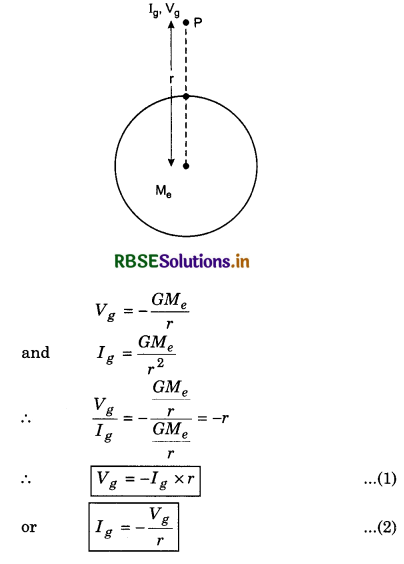
For change in distance ∆r, the change in I_g and V_g is ∆I_g and ∆V_g respectively, then

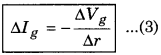
Question 9.
Establish the relation between escape velocity and orbital velocity of satellite revolving near the earth’s surface.
Answer:
Orbital velocity of satellite revolving near the surface of the earth,

Question 10.
Write the uses of artificial satellite.
Answer:
We know that orbital velocity of a satellite, revolving near the earth surface, is nearly 8 km s^-1. If an object is projected from the top of a tower of height nearly 300 km, with velocity less than v₀ in a horizontal direction, then it falls under gravity and adopting a parabolic path it reaches any point on the earth, but if it is projected with velocity equal to v₀ in horizontal direction, then it never strikes the earth. Therefore, we can say that the object tries to strike the ground falling freely under gravity but remains fail to do so. As a result, the object will start moving in a circular path and it becomes an artificial satellite. This is the principle of establishing an artificial satellite.

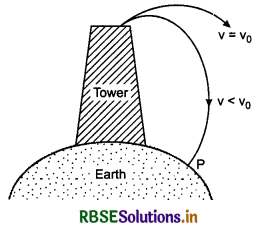
To establish an artificial satellite in orbit, it is projected vertically upward by multistage rocket so that it may cross the dense atmosphere of the earth in minimum time. There is automatic arrangement in rocket due to which the rocket takes turn in horizontal direction just after crossing the earth’s atmosphere and the satellite is left in horizontal direction with the help of a spring and the rocket gets established in its orbit. Thus the rocket starts revolving around the earth. It is important to remember that the rocket should remain out of the earth’s atmosphere otherwise due to high friction in atmosphere the rocket will get destroyed due to heat.

Uses of Artificial Satellites:

1. These satellites are used for investigation of other countries and to know the location of enemy during war.
2. These are used to study the radiations coming from the Sun and cosome.
3. These are used to know about the weather.
4. Information regarding the size of planets is obtained with the help of these satellites.
5. Pilots get guidance of direction with the help of these satellites.
6. Study of various layers of atmosphere is done by these satellites.

Match the following:

Question 1.
A satellite of mass (m) is orbiting around the earth of mass (M) and radius R:

Column-I	Column-II
(a) Gravitational potential energy of satellite close to the earth.	(p) \(\frac{G M m}{2 R}\)
(b) Kinetic energy of orbiting satellite close to the earth is.	(q) \(-\frac{G M m}{2 R}\)
(c) Kinetic energy of orbiting satellite orbiting close to the earth.	(r) \(\frac{G M m}{4 R}\)
(d) Total mechanical energy of satellite orbiting close to the earth.	(s) \(-\frac{G M m}{R}\)

Answer:

Column-I	Column-II
(a) Gravitational potential energy of satellite close to the earth.	(s) \(-\frac{G M m}{R}\)
(b) Kinetic energy of orbiting satellite close to the earth is.	(p) \(\frac{G M m}{2 R}\)
(c) Kinetic energy of orbiting satellite orbiting close to the earth.	(r) \(\frac{G M m}{4 R}\)
(d) Total mechanical energy of satellite orbiting close to the earth.	(q) \(-\frac{G M m}{2 R}\)

Question 2.
A body of mass (m) is to be escaped from the different positions with respect to the earth as given below, M is the mass of the earth, R is the radius of the earth (R) and the gravitational constant (G).

Column-I	Column-II
(a) Escape speed of a body from the surface of the earth.	(p) \(\sqrt{\frac{8}{5} \frac{G M}{R}}\)
(b) Escape speed of a body from the atmosphere at height (R) from the surface of the earth.	(q) \(\sqrt{\frac{2 G M}{1}}\)
(c) Escape speed of a body from satellite orbiting at a height (R) from the surface of the earth.	(r) \(\sqrt{\frac{G M}{R}}\)
(d) Escape speed of a body from the atmosphere at height(\(\frac{R}{4}\)) from the surface of the earth.	(s) \(\sqrt{\frac{G M}{2 R}}\)

Answer:

Column-I	Column-II
(a) Escape speed of a body from the surface of the earth.	(q) \(\sqrt{\frac{2 G M}{1}}\)
(b) Escape speed of a body from the atmosphere at height (R) from the surface of the earth.	(r) \(\sqrt{\frac{G M}{R}}\)
(c) Escape speed of a body from satellite orbiting at a height (R) from the surface of the earth.	(s) \(\sqrt{\frac{G M}{2 R}}\)
(d) Escape speed of a body from the atmosphere at height(\(\frac{R}{4}\)) from the surface of the earth.	(p) \(\sqrt{\frac{8}{5} \frac{G M}{R}}\)

Conceptual Questions

Question 1.
Can an artificial satellite be established in such an orbit so that it may be seen always over Lucknow? Give reason.
Answer:
No; because Lucknow is not in equatorial plane and the satellite can be seen over a particular place only when the plane of orbit coincides the equatorial plane and its time period be 24 hours, i.e., angular velocity of satellite should be equal to that of earth.

Question 2.
Tide is more effected by the attraction of moon than the attraction of Sun while the attraction of Sun is greater than that of moon. Explain why.
Answer:
Tide is inversely proportional to cube of distance and gravitational attraction is inversely proportional to square of distance.

Question 3.
Escape velocity from the earth will be greater for elephant or ant? For which will the escape energy be more?
Answer:
Escape velocity is obtained by following relation
v_e = \(\sqrt{\frac{2 G M_e}{R_e}}\)
This expression does not contain the mass m of the body, therefore escape velocity does not depend on the mass of the body. Therefore escape velocity for both will be same.
∴ Escape energy E_esc = \(\frac{1}{2}\) mv_e²
∴ Escape energy of elephant will be very very greater than that of ant.

Question 4.
Why the tennis ball jumps more on hill than on plane? Explain.
Answer:
Value of g is less on hill than that on plane, therefore the weight of the tennis ball will be less than that on plane. In other words, the force of attraction in ball toward the earth will be less on hill than that on plane. This is why the tennis ball jumps more on hill than on earth.

Question 5.
At mid night, Sun attracts us towards the earth but at mid day it attracts in opposite direction, therefore should our weight be more at mid-night than at mid day? Explain.
Answer:
No, because every body situated on earth revolves in circular orbit of radius equal to radius of earth. Therefore the force acting on us is consumed in providing centripetal force. This is why this force does not change our weight.

Question 6.
A particle of mass m is moving on a circular path of radius r under centripetal force \(\frac{K}{r^2}\), where K is a constant. What is the amount of total energy the particle?
Solution:
Kinetic energy.
E_K = \(\frac{1}{2}\) mv²
Centripetal force,

Question 7.
Find the angular velocity of earth so that the weight of a man on equator may become 3/5 of his weight in situation of not rotating the earth. Radius of earth on equator is 6400 km.
Solution:
The apparent value of gravitational acceleration due to rotation of earth,
g' = g - Rω² cos²λ
For equation λ = 0 ∴ cos²λ = 1
Hence, g' = g - Rω²

Question 8.
Centripetal force on a satellite revolving around the earth is F. What is gravitational force of the earth on the satellite and resultant force on it?
Answer:
Since gravitational attraction of earth on satellite provides the required centripetal force for satellite. Hence the gravitational force and resultant force both will be F.

Question 9.
Weight of 1 kg silver on poles is more than that on equator, why?
Answer:
The weight of any body W = mg.
Since the value of g is maximum at poles and minimum at equator. This is why the weight of 1 kg on poles is more than that on equator.

Question 10.
Do the frictional and other contact forces produce due to gravitational attraction?
Answer:
No, the friction and other contact forces are produced due to electrical forces.

Question 11.
Radius of a sphere of uniform density is R. It applies a force F₁ on an object placed at A which is at a distance of 2R from its centre O. If a small globule of radius \(\frac{R}{2}\) is removed from the sphere, figure then it applies the force F₂ on the same object placed at A. Find the ratio \(\frac{F_2}{F_1}\).
Solution:
If ρ be the density of sphere, then its mass
M = \(\frac{4}{3}\)πR³ρ

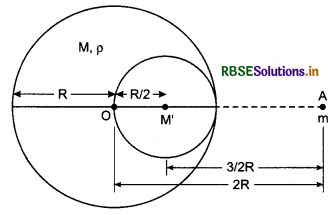
and the mass of removed globule,

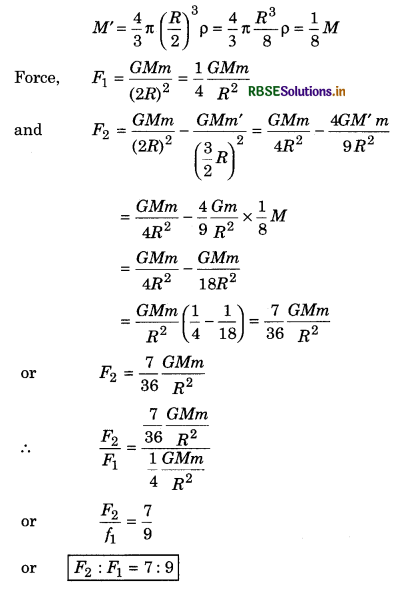
Question 12.
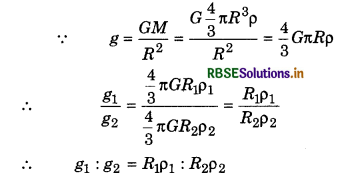
If radii of two planets be R₁ and R₂ and their mean densities be ρ₁ and ρ₂, then prove that the ratio of gravitation accelerations on the planets will be R₁ρ₁ : R₂ρ₂.
Solution:

Question 13.
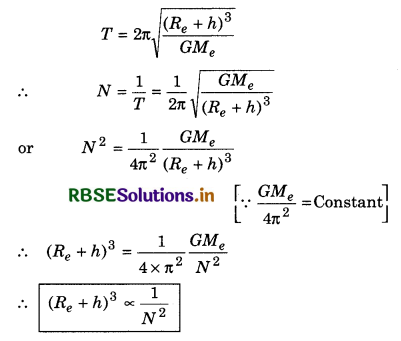
If the rotational frequency of a satellite be N, then prove that (R_e + h)³ ∝ \(\frac{1}{N^2}\).
Solution:
Time period of revolution of a satellite,

Question 14.
Two metallic solid spheres are placed touching each other. How the force acting between them is related with their radius?
Solution:

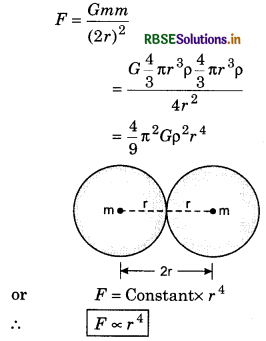
Question 15.
If a body is taken from the centre of earth upto the surface of moon, what will be change in the weight of the body?
Answer:
At the centre of the earth, the value of g is zero, therefore the weight of the body at the centre of earth will be zero. Value of g increases upto the surface of earth, therefore weight will also increase and will become maximum at earth’s surface. On going upward over the earth’s surface value of g starts decreasing, hence weight will also start decreasing and at a certain height where the boundaries of earth’s gravitational field and moon’s gravitational field, g becomes zero and hence weight also becomes zero. Later on the body enters the gravitational field of moon. Therefore weight again starts increasing and increases upto moon’s surface.

Question 16.
If force acting on a body at height h from earth’s surface is \(\frac{1}{2}\) of force acting on the earth’s surface. Find the relation between h and R_e.
Solution:
Given: Force at h height = \(\frac{1}{2}\) x force on earth's surface

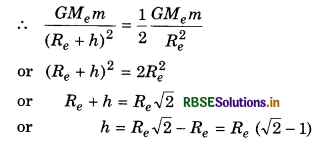
or h = R_e (1.44 - 1)
or h = 0.44R_e

Question 17.
A satellite is revolving near a planet. If the time period of satellite is T and the mean density of planet be ρ, then prove that T x \(\sqrt{\rho}\) is universal constant.
Solution:
Time period of a satellite,
T = 2π\(\frac{(R+h)^{3 / 2}}{\sqrt{G M}}\)
∵ The satellite is revolving near the surface of the planet.
∴ h = 0

Question 18.
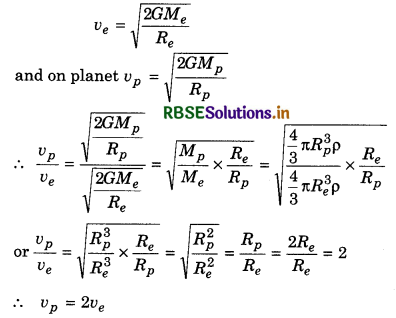
Radius of a planet is two times that of earth. Average densities of both are same. Escape velocities on planet and earth are respectively v_p and v_e. Prove that v_p = 2v_e.
Solution:
Escape velocity on earth,

Question 19.
A planet completes one revolution around the Sun in time T with orbital velocity v. Show that the acceleration of planet towards Sun will be \(\frac{2 \pi v}{T}\).
Solution:
Centripetal acceleration,
a_c = \(\frac{v^2}{r}=\left(\frac{v}{r}\right) v=\omega v=\frac{2 \pi}{T} v\)

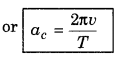
Question 20.
If you shake even your small finger, then whole universe is disturbed, why?
Solution:
According to Newton’s law of gravitation, every particle attract each other and this attraction force is inversely proportional to square of distance between them. When the finger is shaked, then distance between particles changes, hence whole universe gets disturbed.

Question 21.
Two bodies of mass m₁ and m₂ are initially situated at infinity. Later on both bodies move towards each other due to gravitational force what will be relative velocity of approach at distance r between them?
Solution:
Suppose the velocities of bodies at distance r are v₁ and r₂.
∴ According to the principle of conservation of momentum,
m₁v₁ - m₂v₂ = 0
⇒ m₁v₁ = m₂v₂ ......................(1)
According to the law of conservation of energy,

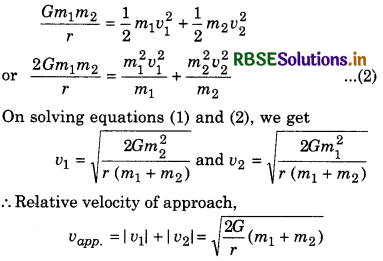
Question 22.
If the ice on the poles melts, how the length of the day will be effected?
Answer:
On melting the ice on poles, it is converted in water which goes away from the axis of rotation. Therefore the moment of inertia increases, as a result the angular velocity decreases. Therefore length of the day increases.

Question 23.
There is no fuel in artificial satellite even then it keeps on revolving around the earth in its orbit, why?
Solution:
The gravitational force acting between the earth and the satellite provides the required centripetal force for satellite to revolve in circular orbit around the earth. Thus the satellite keeps on revolving in its orbit. 

Question 24.
A projectile is projected vertically from the earth’s surface with velocity Kv_e, where K < 1 and ve is escape velocity. Calculate the maximum height of the projectile from the centre of earth.
Solution:
From the law conservation of energy
\(\frac{1}{2} m v^2=\frac{m g h}{\left(1+\frac{h}{R_e}\right)}\) .................(1)
Given, v = Kv_e = K\(\sqrt{2 g R_e}\)
and height from earth's surface
h = r - R_e
Substituting this values in equation (1)

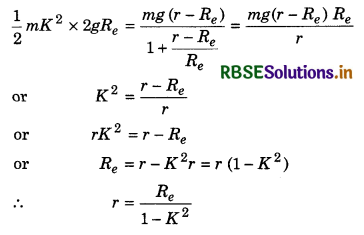
Question 25.
A satellite of mass m is moving in a circular orbit of radius r. Find the angular momentum of satellite about the centre of the orbit in terms of mass of earth.
Solution:
Angular momentum of satellite with respect to the centre of the orbit.
\(\vec{L}=\vec{r} \times m \vec{v}\)
where, \vec{r} is the radius vector of satellite with respect to centre of the orbit and \vec{v} and \vec{r} are perpendicular to each other i.e., angle between them is 90°.
∴ L rmv sin 90° = mvr
as L = mvr ....................(1)
Its direction will be at right angle to plane of the orbit. Now the gravitational force between earth and the satellite
F = \(\frac{G M_e m}{r^2}\)
This force provides provides the required centripetal froce to satellites, therefore,
F = \(\frac{m v^2}{r}\)
∴ \(\frac{G M_e m}{r^2}=\frac{m v^2}{r} \text { or } \frac{G M_e m^2}{r^2}=\frac{m^2 v^2}{r}\)
or (mvr)² = GM_em²r
or mvr = (GM_em²r)^1/2
∴ From equations (1) and (2)
L = (GM_em²r)^1/2

Question 26.
Explain that viscous forces accelerate the satellite.
Solution:
Since the gravitational force between earth and satellite provides centripetal force for orbital motion of satellite.

Satellite does work against viscous forces, therefore it losses its energy. As a result its total energy becomes more negative and it is possible on decreasing tide value of r according to above relation for total energy of satellite.

Question 27.
Earth is supposed to be the sphere of radius R. A platform is placed at h height from earth’s surface. Escape velocity of a body from this platform is fv where v is escape velocity from earth's sufrace. Find the value of f.
Answer:
Escape velocity from the earth's surface,
v = \(\sqrt{2 g R}\)
If v_p be the escape velocity from platform, then

Long Answer Questions

Question 1.
Write Kepler’s laws of planetary motion. What conclusions obtained by Newton from these laws?
Answer:
Following three laws were presented by Kepler:
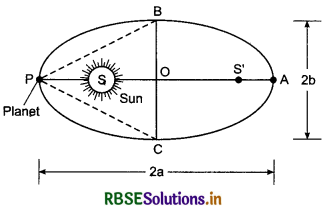
1. Law of Orbits: All the planets revolve around the Sun in an elliptical orbits and Sun is situated at one focus of the orbit.
(This law is different from the copernican model according to which planet can revolve around the sun only in circular orbits.)
Here θ is the centre of the elliptical orbit and PO = AO is called the half major axis. Sun is at its one focus S and planet is shown at P.

2. Law of Areas: According to this law, the line joining planet and Sun sweeps equal area in equal time. It is clear from this law, as the distance of planet increases from sun, its orbital velocity goes on decreasing and vice-versa.

Derivation: Suppose at any time, the position vector and linear moment of the planet are \(\vec{r}\) and \(\vec{p}\) respectively.

∴ Distance travelled by the planet on its orbit in time interval ∆t will be \(\vec{v}\) x ∆t, where \(\vec{v}\) is orbital velocity of the planet.
Therefore area sweeped by line joining the planet and Sun in time interval ∆t,

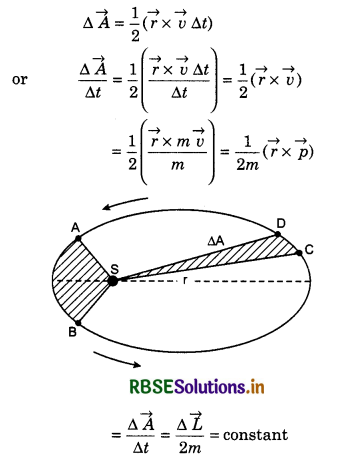
(Because angular momentum remains constant under influence of central force)
i.e., Areal velocity of the planet = Constant
This is the law of areas.

3. Law of Time Periods: Square of time period of planet is directly proportional to cube of radius of semi-major axis of an ellipse traced by the planet, i.e.,
T² ∝ a²
Derivation: Suppose radius of major axis of ellipse is ‘a’ and radius of minor axis is 'b', then the area of the ellipse will be πab.
∴ Time period of the planet

From the denfinition of an ellipse, it latus rectum be l, then,
l = \(\frac{b^2}{a}\) ⇒ b² = la
∴ Substituting this value of b² in equation (1), we get

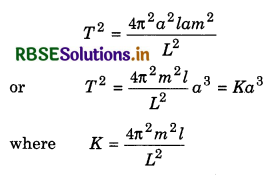
If average distance between Sun and planet be r, then
r ≈ a

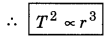
According to Newton, mostly the planets revolve around the Sun in nearly circular orbits and according to Kepler’s second law, the areal velocity of radius vector of planet remains constant, therefore the orbital velocity v of the planet and its angular velocity ω will remain constant. If r be the average distance between the planet and the Sun and m its mass, then the centripetal force acting on the planet towards the Sun,
F = mrω² = mr\(\frac{4 \pi^2}{T^2}\)
Where, T is the time period of the planet around the Sun.
According to Kepler's third law,
T² ∝ r³
or T² = Kr³

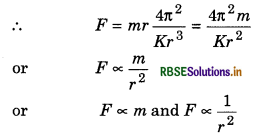
Thus Newton obtained following three conclusions from Kepler’s law:
(i) A force acts on the planet towards the Sun.
(ii) This force is directly proportional to the mass of the planet.
(iii) This force is inversely proportional to the square of the average distance between the planet and the Sun.
On the basis of above conclusions, Newton presented his law of gravitational attraction as, “The gravitation applied by a body on another body is:
(i) Directly propotional to the mass of that body, and
(ii) Inversely proportional to the square of the distance between them.”

Question 2.
Obtain the expression for g in terms of gravitational constant G.
Answer:
According to Newton's second law,
Force = Mass x Acceleration
∴ Gravitational force = Mass x Gravitational acceleration
i.e., Fg = mg .....................(1)
Suppose an object of mass m is situated at P i.e., at height h from the earth's surface, then its distance from the centre of earth,
r = (R_e + h)
∴ Gravitational force acting on the object,

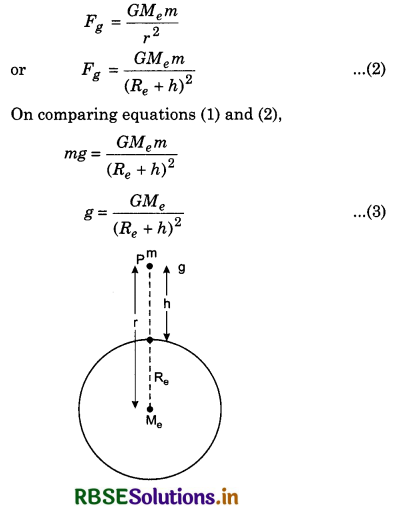
This is the relation between g and G
For earth surface,
r = R_e
Acceleration due to gravity at the earth's surface

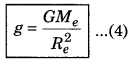
Given G = 6.67 x 10^-11 Nm²/kg²
M = 6.0 x 10²⁴ kg
R_e = 6.4 x 10⁶ m
∴ g_e = \(\frac{6.67 \times 10^{-11} \times 6.0 \times 10^{24}}{\left(6.4 \times 10^6\right)^2}\)
= 9.8 m/sec²
From equations (3) and (4), it is clear that the value of g does not depend on the mass of the body. Therefore, if the bodies of different masses are dropped freely from any height, then they will fall with the same acceleration.

Question 3.
What is meaning of gravitational acceleration? Obtain the expression for g at height h from earth’s surface in terns of gravitational acceleration on earth’s surface R_e = radius of earth.
Answer:
The force acting between two bodies is called the gravitational attraction force. When among two bodies ne is earth, then this force is called ‘Gravitational force’ i.e. gravitational force is the force by which the earth attracts the body towards its centre. For example, the mango plucked from the tree branch, falls down towards the ground due to this force. Any object dropped from a height falls down due to gravitational force. The veiocity of a falling body keeps in increasing with certain acceleration which is called ‘gravitational acceleration.’

“Thus, the acceleration produced by the gravitational force is called gravitational acceleration i.e., rate of increase of velocity of freely falling body with time, is called gravitational acceleration.” It is denoted by g and its value is 9.8 m/s^-2. Its value does not depend upon the mass, shape and size of the falling body.

Variation in the value of g is pioduced due to the following situations:
1. Value of g decreases with the increasing height.
2. Value of g decreases with the increasing depth.
3. Value of g changes with changing place on earth’s surface due to its elliptical shape.
4. Value of g is maximum at poles and minimum at equator due to its rotation about its own axis.
1. Variation of acceleration due to gravity with height: Value of gravitational acceleration on the earth’s surface,

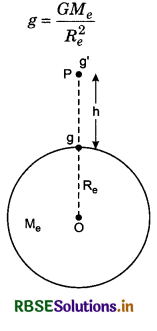
and its value at height h from the earth's surface i.e., at point P.

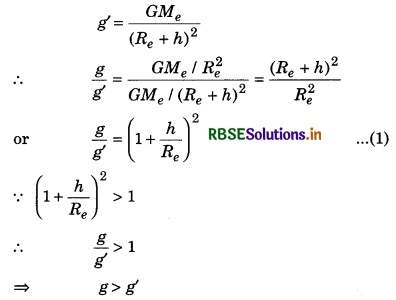
Therefore, acceleration due to gravity decreases with increasing height from the earth's surface.
∴ From equation (1),


2. Variation in the value of gravitational acceleration with depth: Gravitational acceleration on the surface of earth,

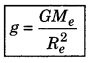
and the value of gravitational acceleration at depth d from earth's surface

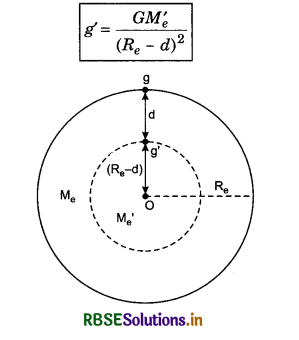
where, M'_e is the mass of earth's part of radius (R_e - d).

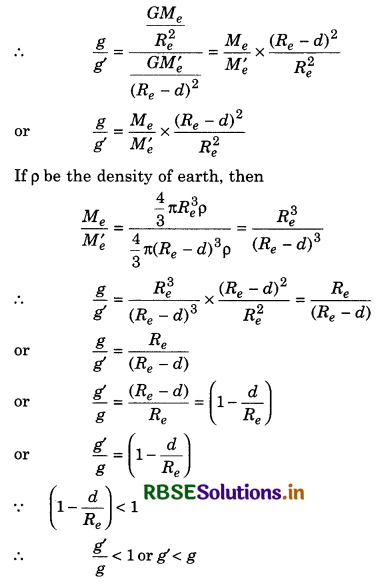
Therefore, gravitational acceleration decreases with the increasing depth.

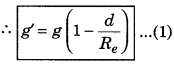
Special situation: To know the value of gravitational acceleration at the centre of earth, we have to substitute R_e in place of d in equation (1),
∴ g' = g(1 - \(\frac{R_e}{R_e}\)) = g(1 - 1) = g x 0

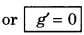
i.e., gravitational acceleration will be zero at the centre of the earth.

Question 4.
What do mean by gravitational potential? Derive an expression for gravitational potential due to mass m at distance r.
Answer:
Work done in bringing the unit mass from infinity a point in gravitational field is called the ‘Gravitational potential’ at that point. It is represented by V_g. Gravitational potential of small mass is taken zero at infinity.
∴ V_G = Work done in bring unit mass from infinity to a point in the gravitational field m.
= Work done in bringing mass m from infinity to a point in the gravitational field

Derivation of formula for gravitational potential in Earth’s gravitational field: Suppose we have to find the gravitational potential at point P situated at distance r from the centre of the earth. For this purpose we have to find the work done in bringing unit mass from infinity to point P. To estimate this work, let us consider another point P' situated at a distance x from the centre of the earth, in the same direction (fig. 8.16).

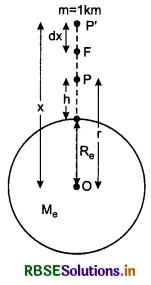
The force acting on m = 1 kg at P'
F = \(\frac{G M_e 1}{x^2}\)
If dx displacement is given to unit mass in direction of above force i.e., towards O the centre of the earth, then work done,
dW = \(\vec{F} \cdot \vec{d} x\) = F dx cos 0° = Fdx
∴ Work done in bringing unit mass from infinity to point P i.e., gravitational potential at P,

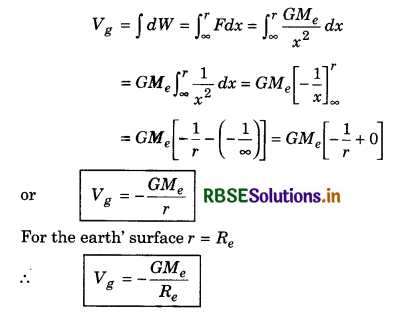
Question 5.
What do you understand by gravitational potential energy? Find the expression for gravitational potential energy of a body of mass m at distance r from the centre of earth.
Answer:
Gravitational potential energy of an object at a point in gravitational field is equal to the work done in bringing the object from infinity to that point. The gravitational potential energy is found to be negative because work is done in bringing the object from infinity to the gravitational field. It is denoted by U.
∴ Unit of U = Joule
Dimensional formula of U = [M¹L²T^-2]
(i) Derivation of gravitational potential energy: To find the gravitational potential energy of an object of mass m at point P situated at a distance r from the centre of the earth, we have to estimate the work done in bringing the object from infinity to point P. For this purpose, let us consider another point ‘P'’ in the same direction situated a distance x from the earth’s centre. The force acting on the object at P',
F = \(\frac{G M_e m}{x^2}\)
If the object is given small displacement dx towards O, then work done,
dW = \(\vec{F} \overrightarrow{d x}\) = F dx cos 0° = F dx

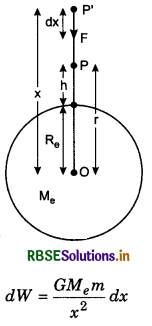
∴ Work done in bringing the object from infinity to point P i.e., gravtitational potential energy of the objcet at P

(ii) Gravitational potential energy of a body near the earth’s surface: Gravitational potential energy of a body of mass m,

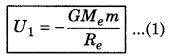
and that at point P', which is at height h from the earth's surface,


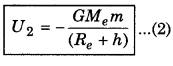
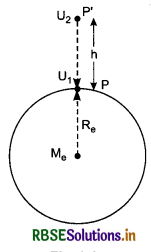
∴ Change in potential enegy of the body in displacing from the earth's surface upto a height h,

Idf point P'is near the earth's surface, then,
h << R_e ⇒ \(\frac{h}{R_e}\) << 1
Therefore, neglecting \(\frac{h}{R_e}\), we have

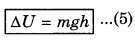
Thus, the potential energy of a body of mass m increases by mgh in displacing it upto small height h from the earth’s surface.
(iii) Maximum height attained by a body projected vertically upward: Suppose the body of mass m is projected with velocity v vertically upwards, then its kinetic energy is changed in potential energy at the highest point.

To find the value of maximum height, from equation (6),

This is maximum height attained by the projectile projected with velocity v.

Question 6.
An artificial satellite is revolving near the earth’s surface in circular orbit. Prove that its time period will be T = \(\sqrt{\frac{3 \pi}{\rho G}}\), where ρ is the density of earth and G is gravitational constant.
Answer:
Period of revolution of the satellite: The time taken by satellite in completing one revolution around the planet, is called the time period of the satellite. It is denoted by T.

For satellite revolving near the surface of the planet,
h << R ⇒ \(\frac{h}{R}\) << 1
∴ On neglecting \(\frac{h}{R}\)

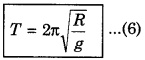
Again from equation (5),
T = 2π\(\sqrt{\frac{(R+h)^3}{G M}}\)
For satellite revolving near the surface of the planet.
h << R
∴ On neglecting h, T = 2π\(\sqrt{\frac{R^3}{G M}}\)
∵ M = \(\frac{4}{3} \pi R^3 \rho\)

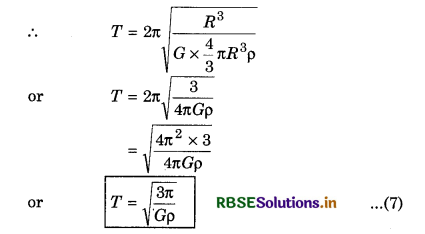
Thus there are following three formula for time period of satellite revolving near the surface of the planet

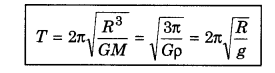
Time period of satellite revolving near the Earth's surface.
∵ Time period T = 2π\(\sqrt{\frac{R_e}{g}}\)
∴ R_e = 6400 km = 64 x 10⁶ m; g = 9.8 m/s²
∴ T = 2 x 3.14\(\sqrt{\frac{6.4 \times 10^6}{9.8}}\)
= 5067 seconds = 86.6 minute
or T = 84.6 min. 

Question 7.
What is the meaning of binding energy of a satellite? Find the expression for binding of a satellite revolving the earth the circular orbit.
Answer:
There are kinetic as well as potential both types of energies in a satellites revolving around the planets. Potential energy of satellites is due to its situation in the gravitational field of the planet while its kinetic energy is due to its motion. Suppose the mass of a planet (earth) is M and its radius is R_e. A satellite of mass m is revolving around the planet with orbital speed u₀ at the height h from the surface of the planet. Therfore, distance of the satellite from the centre of the planet i.e., the radius of the orbit of the satellite.
r = (R_e + h)
∴ Gravitational potential energy of the satellite,
U = \(-\frac{G M_e m}{r}\) .........................(1)
And kinetic energy of the satellite,

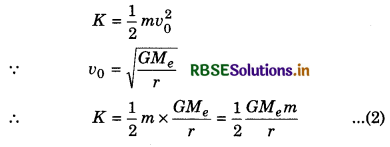
∴ Total energy of the satellite = Gravitational potential energy + Kinetic energy
⇒ E_t = U + K
or E_t = \(-\frac{G M_e m}{r}+\frac{1}{2} \frac{G M_e m}{r}\)

Negative total energy of the satellite indicates that the satellite remains in effective area i.e., gravitational fields of planets and remains moving in circular orbits.
Binding energy: The minimum energy given to a satellite, due to which it may escape from its orbit forever, is called the binding energy of the satellite.
If the satellite escapes, it will reach to infinity where its total energy becomes zero. Thus the binding energy of the satellite,
E_b = E_∞ - E_t = 0 - [-\(\frac{1}{2} \frac{G M_e m}{r}\)]
or E_b = \(\frac{1}{2} \frac{G M_e m}{r}\) ............................(5)
where, r = (R_e + h)

Question 8.
Derive the expressions for orbital velocity and time period of satellite.
Answer:
A celestial body which revolves around a planet is called a satellite. Moon is the only natural satellite of the earth.

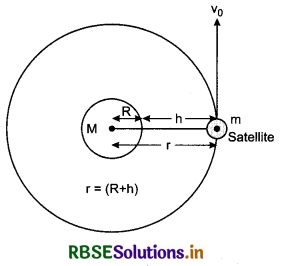
(i) Orbit speed of a satellite: Suppose a satellite of mass m is revolving around a planet of mass M and radius R, at height of h from the surface of the planet with orbital speed v₀.
∴ Radius of the orbit of satellite
r = (R + h)
The gravitational attraction acting between the planet and the satellite provides the required centripetal force for circular motion of the satellite.
i.e.,
Centripetal force = Gravitational force between the planet and satellite

∵ r = (R + h)

If g we the value of gravitational acceleration on the surface of the planet, then

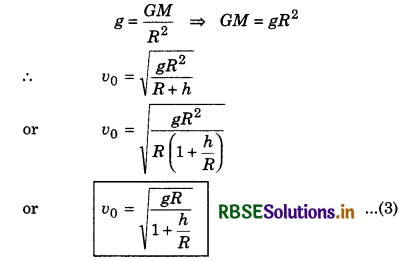
If the satellite is revolving near the surface of the planet then,
h << R ⇒ \(\frac{h}{R}\) << 1
Hence, \(\frac{h}{R}\) can be neglected.
∴ v₀ = \(\sqrt{g R}\) ......................(4)
Calculation of orbital velocity of satellite revolving near the earth's surface:
v₀ = \(\sqrt{g R}\)
For earth, R_e = 6.4 x 10⁶ m; g = 9.8 m/s²
∵ v₀ = \(\sqrt{9.8 \times 6.4 \times 10^6}=\sqrt{98 \times 64 \times 10^4}\)
= \(\sqrt{2 \times 49 \times 64 \times 10^4}=7 \times 8 \times 10^2 \sqrt{2}\)
= 56 x 1.44 x 10²
= 7.9184 x 10³ m/s = 7.9 km s^-1

Period of revolution of the satellite: The time taken by satellite in completing one revolution around the planet, is called the time period of the satellite. It is denoted by T.

For satellite revolving near the surface of the planet,
h << R ⇒ \(\frac{h}{R}\) << 1
∴ On neglecting \(\frac{h}{R}\)

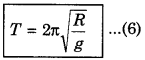
Again from equation (5),
T = 2π\(\sqrt{\frac{(R+h)^3}{G M}}\)
For satellite revolving near the surface of the planet.
h << R
∴ On neglecting h, T = 2π\(\sqrt{\frac{R^3}{G M}}\)
∵ M = \(\frac{4}{3} \pi R^3 \rho\)

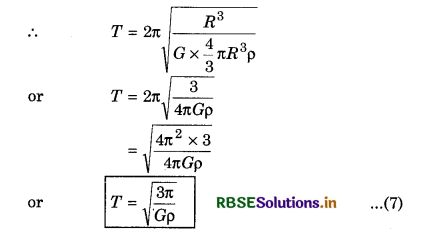
Thus there are following three formula for time period of satellite revolving near the surface of the planet

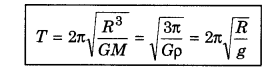
Time period of satellite revolving near the Earth's surface.
∵ Time period T = 2π\(\sqrt{\frac{R_e}{g}}\)
∴ R_e = 6400 km = 64 x 10⁶ m; g = 9.8 m/s²
∴ T = 2 x 3.14\(\sqrt{\frac{6.4 \times 10^6}{9.8}}\)
= 5067 seconds = 86.6 minute
or T = 84.6 min. 

Question 9.
Give the definition of escape velocity. Obtain the expression for escape velocity from earth’s surface.
Answer:
The minimum velocity of projection of the object for which it escapes i.e., it leaves the gravitational field of the earth forever and never returns back, is called the escape velocity. It is denoted by U. When an object is projected vertically from earth’s surface, then its kinetic energy goes on decreasing and potential energy goes an increasing, when complete kinetic energy is converted into the potential energy, from there the object returns back to earth’s surface. Thus, if the object is given kinetic energy equal to magnitude of gravitational, energy, the object will reach to infinity i.e., it will escape.
Hence,
Escape energy = |Gravitational potential energy|

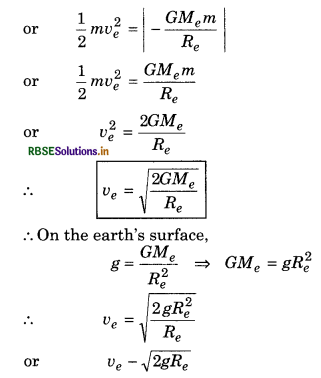
Escape Velocity on the Earth Surface:
∴ g = 9.8 ms^-2
∴ R_e = 6400 km = 64 x 10⁶ m;
∴ v_e = \(\sqrt{2 \times 9.8 \times 6.4 \times 10^6}\)
or v_e = 11.2 km-s^-1

Escape Velocity on Moon:
For moon, g_m = 1.63 ms^-2;
R_m = 1.74 x 10⁶ m
∴ v_e on moon = \(\sqrt{2 \times 1.63 \times 1.76 \times 10^6}\)
= 2.3 km-s^-1

Question 10.
Prove that escape velocity does not depend upon the mass of the body.
Answer:
The minimum velocity of projection of the object for which it escapes i.e., it leaves the gravitational field of the earth forever and never returns back, is called the escape velocity. It is denoted by U. When an object is projected vertically from earth’s surface, then its kinetic energy goes on decreasing and potential energy goes an increasing, when complete kinetic energy is converted into the potential energy, from there the object returns back to earth’s surface. Thus, if the object is given kinetic energy equal to magnitude of gravitational, energy, the object will reach to infinity i.e., it will escape.
Hence,
Escape energy = |Gravitational potential energy|

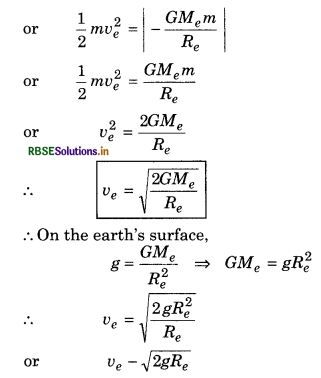
Escape Velocity on the Earth Surface:
∴ g = 9.8 ms^-2
∴ R_e = 6400 km = 64 x 106 m;
∴ v_e = \(\sqrt{2 \times 9.8 \times 6.4 \times 10^6}\)
or v_e = 11.2 km-s^-1

Escape Velocity on Moon:
For moon, g_m = 1.63 ms^-2;
R_m = 1.74 x 10⁶ m
∴ v_e on moon = \(\sqrt{2 \times 1.63 \times 1.76 \times 10^6}\)
= 2.3 km-s^-1

Question 11.
What is the meaning of weightlessness. Clarify it in various circumstances.
Answer:
We know that gravitational force acting on a body towards the centre of the earth is called its weight.
i.e., W = Mg
Where M is the mass of the body and g is the acceleration due to gravity.

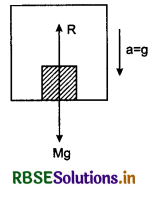
Since M can never be zero, therefore for weight lessness (W = 0) 'g' must be zero. This is possible in following situations:
1. By accelerated system: The apparent weight of a body is freely following lift is zero.
Equation of motion of a body in downward motion,
Mg - R = Ma
or R = Mg - Ma
For freely following lift, a = g
∴ R = Mg - Mg
or R = 0
i.e., the apparent weight (R) of the body is zero.
2. At the centre of the earth: Since the acceleration due to gravity (g) is zero at the centre of earth. Therefore weightlessness is experienced at the centre of earth.
3. At infinite distance from the earth: Value of 'g' decreases with increasing height and becomes zero at infinity. Therefore weight of a body will be zero at infinity.
4. Weightlessness in artifical satellite: Suppose an artifical satellite is revolving in a circular orbit of radius r around the earth wiht orbit speed v0 and object of mass m is placed on the floor of the satellite. Mass of satellite is M and that of the earth is Me.
The equation of motion of satellite,
\(\frac{M v_0^2}{r}=\frac{G M_e M}{r^2}\)
or \(\frac{v_0^2}{r}=\frac{G M_e}{r^2}\) ..........................(1)
If W be the weight of the object placed inside the satellite and R be the reaction of floor on the object, then equation of motion of the object.

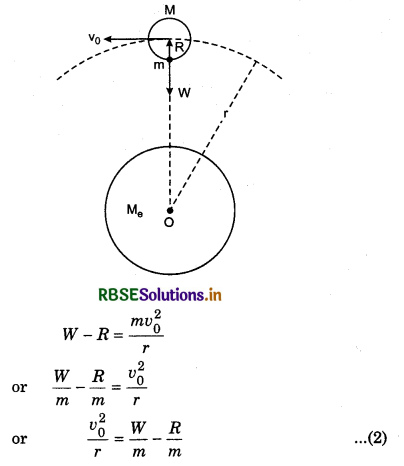
On comparing equations (1) and (2), we have

∵ R is the reaction of weight W, therefore when reaction is zero, then action i.e., weight of the object will be zero. Hence the objects in artificial satellites are in situation of weightiessnes. This is why-
(i) if an astronaut is standing on a spring balance inside an artificial satellite, the reading of balance will be zero.
(ii) If an object is hung through a string in an artificial satellite, then tension in string will be zero.
(iii) An astronaut cannot drink water or milk through tumbler as the tumbler does not pore the liquid content due to weightlessness. To remove this problem, the astronauts suck the liquid through a pipe.

Question 12.
(a) Write Newton’s law of gravitation, (b) Give the definition of universal constant of gravity G and its unit and dimensions.
Answer:
It states that everybody in this universe attracts every another body with force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
Fig. 8.3 shows two bodies A and B of masses m₁ and m₂ situated at distance r apart. Let F be the force of attraction between them, then according to
Newton’s law of Gravitation,
F ∝ m₁m₂
and F ∝ \(\frac{1}{r^2}\)

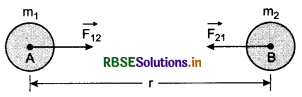
on combining above statements,
F ∝ \(\frac{m_1 m_2}{r^2}\)
or F = \(\frac{G m_1 m_2}{r^2}\) ........................(1)
Where, G is constant of proportionality which is called ‘Universal Constant of Gravity’ or ‘Universal Gravitational Constant’.

Numerical Questions

Based on Gravitational Law

Question 1.
Two spheres of mass 10 kg each, are situated at a distance of 50 cm apart. Find the force acting between them.
Answer:
Given: m₁ = m₂ = 10 kg, r = 50 cm = 0.50 m, F = ?
∴ F = \(\frac{G m_1 m_2}{r^2}=\frac{6.67 \times 10^{-11} \times 10 \times 10}{0.50 \times 0.50}\)
= 2.68 x 10^-8 N

Question 2.
Three identical spheres of mass M and radius R, are placed such that one sphere touches rest two spheres. Find the gravitational force on one sphere due to two others.
Answer:
According to question, the centres of spheres make an equilateral trinagle ABC (as shown in the figure) of arm 2R. Gravitational froce acting between spheres A and C.
F₁ = \(\frac{G M M}{(2 R)^2}=\frac{G M^2}{4 R^2}\) (in direction AC)
Similarly that between A and B
F₂ = \(\frac{G M^2}{4 R^2}\) (in direction AB)

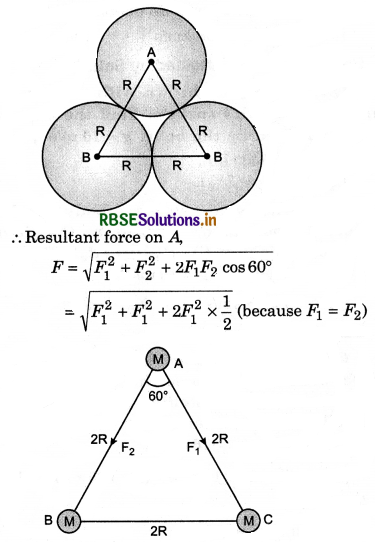
= F₁\(\sqrt{3}\)
∴ F = \(\sqrt{3} \frac{G M^2}{4 R^2}\)

Question 3.
Masses of two spheres are 60 kg and 50 kg. Distance between their centres of gravity is 0.50 m. What is the gravitational attraction between them?
Answer:
F = \(\frac{G m_1 m_2}{r^2}=\frac{6.67 \times 10^{-11} \times 60 \times 50}{0.5 \times 0.5}\)
or F = 8.0 x 10^-7 N

Question 4.
A uniform sphere of mass M and a uniform rod of length L and mass m are situated such that the near end of the rod is at a distance r from the centre of the sphere. Calculate the gravitational force acting at the centre of the rod.
Answer:
Mass per unit length of rod = \(\frac{m}{L}\)
Let there be an element of length dx at a distance x from the centre of the sphere.

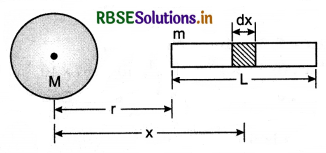
∴ Mass of element dm = \(\frac{m}{L}\)dx .......................(1)
Force acting between sphere and element of length dx,

Based on Gravitational Acceleration

Question 5.
The weight of a man on the earth is 80 kg. What will be its weight on moon? Mass of moon is 7.34 x 10²³ kg; its radius is 1.75 x 10⁶ m; Gravitational constant = 6.67 x 10^-11 Nm²/kg². What will be the mass of the person on moon?
Answer:
Mass of the person m = 80 kg
The value of gravitational acceleration on moon,
g_m = \(\frac{G M_m}{R_m^2}\)
∴ Weight of the person on moon,
W_m = mg_m = m x \(\frac{G M_m}{R_m^2}\)
= 80 x \(\frac{6.67 \times 10^{-11} 7.34 \times 10^{22}}{1.75 \times 10^6 \times 1.75 \times 10^6}\)
or W_m = 128 N
Since the mass does not change, therefore mass of the person on moon = 80 kg

Question 6.
If the diameter of earth becomes half of its present diameter but its density remains unchanged, then what will be the value of g on the surface of new size of the earth?
Answer:

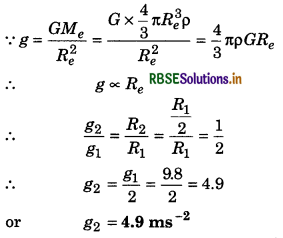
Question 7.
Weight of a person on earth’s surface is 490 N. Gravitational acceleration on the earth’s surface is g = 9.8 m/s² and its value on moon’s surface is \(\frac{g}{6}\). Find:
(i) Weight of the person on the surface of moon.
(ii) Mass of the person on the earth and moon.
(iii) If the person walks 150 m in 1 min on earth, how long will he walk on moon in 1 min?
(iv) If the person jumps upto height of 2 m on earth, how high will he jump on moon?
Answer:
(i) Weight of the person on the earth
W_e = 490 N
But W_e = mg_e
∴ m = \(\frac{W_e}{g_e}=\frac{490}{9.8}\) = 50 kg
∵ g_m = \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\frac{g_e}{6}\)
∴ Weight of the person on moon
W_m = mg_m = m x \(\frac{g_e}{6}\)
or W_m = \(\frac{50 \times 9.8}{6}\) = 81.66 N

(ii) ∵ Mass does not change.
∴ Mass of the person on earth = Mass on moon
= 50 kg

(iii) There is no effect of g in horizontal motion.
∴ On moon also the person will walk 150 min/ 1 min.

(iv) ∵ Height of jump,
H = \(\frac{u^2}{2 g}\)
∴ \(\frac{H_m}{H_e}=\frac{g_e}{g_m}=\frac{g_e}{\frac{g_e}{6}}\) = 6
∴ H_m = H_e x 6
= 2 x 6 = 12 m

Based on Change in Gravitational Acceleration

Question 8.
The weight of a body decreases by 1% on going upto height of h. If the body is taken upto depth of h, what will be change in its weight?
Answer:
At small height

Similarly, on going at depth h,
\(\frac{\Delta g}{g} \times 100=\frac{h}{R} \times 100=\frac{2 h}{2 R} \times 100=\frac{1}{2}\left(\frac{2 h}{R} \times 100\right)\)
= \(\frac{1}{2}\) x 1% = 0.5%

Question 9.
At what height the gravitational acceleration will be (i) half, (ii) one fourth, of that on the earth?
(Radius of the earth = 6400 km).
Answer:

∴ h = 0.414 x R = 0.414 x 6400 km
= 2650 km
(ii) Similarly when, g' = \(\frac{g}{4}\)

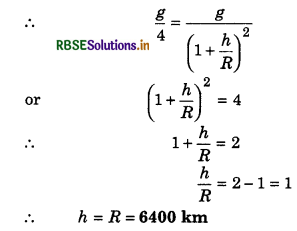
Question 10.
At what height the gravitaional acceleration will remain, (i) 4% and (ii) 5%, of that on earth? Radius of the earth is 6400 km.
Answer:
(i) At height h

or 5 = 1 + \(\frac{h}{R}\)
∴ \(\frac{h}{R}\) = 5 - 1 = 4
∴ h = 4R = 4 x 6400
or h = 25600 km
(ii) When g' = \(\frac{50}{100}\)g = \(\frac{g}{2}\)

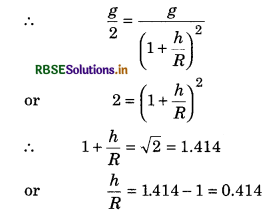
∴ h = 0.414 x R = 0.414 x 6400
= 2649.6 km

Based on Gravitational Field and Gravitational Potential

Question 11.
Average distance between the earth and moon is 3.85 x 10⁸ m. At what place between them, gravitational field will be zero? (Given: mass of earth = 5.96 x 10²⁴ kg, mass of moon = 7.36 x 10²² kg)
Answer:
Solve as solved example 5 of the textbook.

Question 12.
Intensity of gravitational field at a point situated at distance 10000 km from the centre of earth, is 4.8 N.kg. Find the potential difference at that point.
Answer:
V_G = -I x r = -4.8 x 10000 x 10³
or V_G = -4.8 x 10⁷ J/kg

Question 13.
Two bodies of masses 200 kg and 500 kg are situated at distance 2 m apart. Find at mid-point on the line joining them:
(i) Intensity of gravitational field
(ii) Gravitational potential.
(G = 6.67 x 10^-11 Nm²/kg²)
Answer:
(i) Intensity of gravitational field at P
I = I₂ - I₁
= \(\frac{G M_2}{r^2}-\frac{G M_1}{r^2}\)
= G[\(\frac{500}{1 \times 1}-\frac{200}{1 \times 1}\)] = G x 300
= 6.67 x 10^-11 x 300

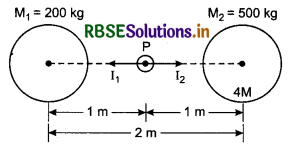
= 20.01 x 10^-9
= 2.001 x 10^-8 ≈ 2.0 x 10^-8 N/kg
(ii) Gravitational potential at P,
V_G = V_G1 + V_G2 = \(-\frac{G M_1}{r}-\frac{G M_2}{r}\)
= \(-\frac{G}{1}\left[M_1+M_2\right]=-\frac{6.67 \times 10^{-11}}{1}\)[200 + 500]
= -6.67 x 10^-11 x 700
= -46.69 x 10^-9
= -4669 x 10^-8 J/kg
= -4.67 x 10^-8 J/kg

Based on Gravitational Potential Energy

Question 14.
Mass of the earth is 6.0 x 10²⁴ kg and its radius is 6.4 x 10⁶ m.
(i) How much work will be done in carrying a body of mass 4 kg from the earth’s surface to intensity?
(ii) What will be gravitational potential energy of a body of mass 4 kg on the surface of earth?
(iii) What will be gravitational potential on earth’s surface?
(iv) If this body falls from infinity to the earth surface, what will be its velocity when its strikes the earth?
(G = 6.66 x 10¹¹ Nm²/kg²)
Answer:
(i) W = \(\frac{G M m}{R_e}=\frac{6.67 \times 10^{-11} \times 6 \times 10^{24} \times 4}{6.4 \times 10^6}\)
= 25.01 x 10⁷ = 2.501 x 10⁸ J
(ii) Gravitational potential energy on the surface of the earth
U = \(-\frac{G M_e m}{R_e}\)
= -2.501 x 10⁸ J
(iii) Gravitational potential on the earth's surface,
V_G = \(-\frac{G M_e}{R_e}=-\frac{U}{m}=\frac{-2.50 \times 10^8}{4}\)
= -0.625 x 10⁸
= -6.25 x 10⁷ J/kg
(iv) \(\frac{1}{2}\)mv² = U
⇒ v = \(\sqrt{\frac{2 U}{m}}=\sqrt{\frac{2 \times 2.5 \times 10^8}{4}}\)
= 1.118 x 10⁴ m/s

Question 15.
A body of mass m starts falling from a height of 4R from earth’s surface. When it will be at height of 2R, what will be its kinetic energy?
Answer:
When a body falls under gravity, then its potential energy decreases and kinetic energy increases.
Therefore, increase in kinetic energy = Decrease in potential energy
∴ Final kinetic energy - Initial kinetic energy = (Initial potential - Final potential) energy

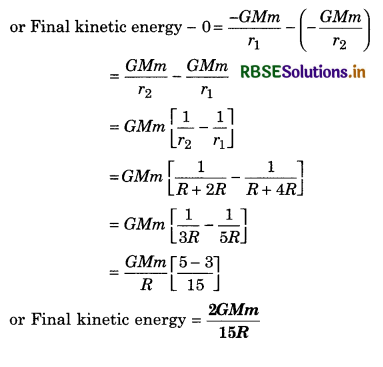
Question 16.
Three particles of masses 200 g are brought from infinity and placed on an equilateral triangle of arm 40 cm, what will be work done?
Answer:
M₁ = M₂ = M₃ = 200 g = 0.2 kg,
r = 40 cm = 0.4 m

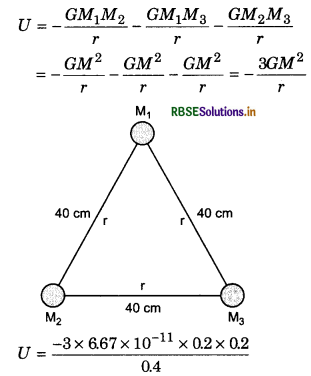
= -2.001 x 10^-11 J

Based Orbital Velocity of Satellite, Escape Velocity and Time of Revolution

Question 17.
If mass and radius of the earth respectively 9 times and double those of a planet then calculate the required escape velocity of a rocket on this planet. Escape velocity on the earth is 11.2 km/s.
Answer:
For earth's surface, escape velocity
v_e = \(\sqrt{\frac{2 G M_e}{R_e}}\)
and for the surface of planet,

Question 18.
A body of mass m is situated at a height of 4R_e from earth surface where R_e is radius of earth. What minimum velocity will be required to escape it?
Answer:
Potential energy of a body at distance 4R_e from earth surface,

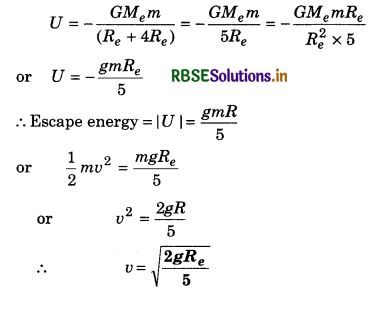
Question 19.
An artificial satellite is revolving around the earth at a distance of 2630 km from earth’s surface. If radius of earth be 6370 km, its mass be 6 x 10²⁴ kg and G = 6.67 x 10^-11 Nm²/kg², then find the orbital speed and revolution time of the satellite.
Answer:
(i) Orbital velocity of satellite,

= 6.67 km/s
(ii) Time period of satellite,
T = \(\frac{2 \pi r}{v_0}=\frac{2 \times 3.14 \times 9 \times 10^6}{6.67 \times 10^3}\)
(because r = R_e + h = 6370 + 2630 = 9000 km)
= 8.4737 x 10³
= 8473.7 s = 8474 s

Question 20.
Calculate the orbital speed of a satellite revolving near the surface of the earth, if radius of the earth be 6.4 x 10⁶ m and gravitational acceleration be 10 m/s². If the satellite remains at a height of 2000 km from earth’ surface. What will be orbital velocity?
Answer:
(i) ∵ v₀ = \(\sqrt{\frac{G M_e}{\left(R_e+h\right)}}\)
For satellite revolving near the earth's surface,

Based on Height Attained by Satellite

Question 21.
A body is thrown with velocity of 10 km/s¹ from earth’s surface. Find the maximum height attained by the body, g = 10 m/s²; radius of earth R_e = 6400 km.
Answer:
Maximum height attained by a body,
h = \(\frac{v^2 R_e}{2 g R_e-v^2}\)
v = 10 km/s = 10⁴ m/s
R_e = 6400 km = 64 x 10⁶ m
g = 10 m/s²
∴ h = \(\frac{10^4 \times 10^4 \times 6.4 \times 10^6}{2 \times 10 \times 6.4 \times 10^6-10^4 \times 10^4}\)
= 2.28 x 10⁷ m

Question 22.
With what velocity a body should be projected from earth’s surface, so that it may attain the height of (i) 2R_e, (ii) 4R_e? (Radius of earth R_e = 6400 km, g = 10m/s²)
Answer:
(i) Velocity of projection

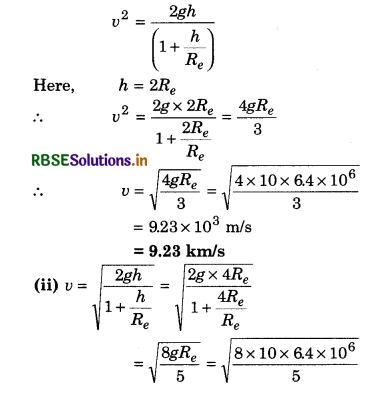
= \(\sqrt{16 \times 6.4 \times 10^6}\)
= 4 x 10³ x \(\sqrt{6.4}\) = 4 x 10³ x 2.5298
= 10.11 x 10³ ms^-1 = 10.11 km/s

Based of Enegy of Satellite

Question 23.
A satellite of 500 kg is revolving at the height of 1800 km from earth’s surface. Find: (i) potential energy of satellite, (ii) kinetic energy of satellite, (iii) its total energy. Given: radius of earth = 6400 km, g = 10 m/s².
Answer:

Based on Kepler’s Laws

Question 24.
Distance of planet Neptune is 30 times that of the earth from the Sun. Time period of revolution of earth is 1 year. Calculate the time period of revolution of Neptune.
Answer:
\(\frac{T_1}{T_2}=\left(\frac{R_1}{R_2}\right)^{3 / 2}=\left(\frac{30 R}{R}\right)^{3 / 2}\) = 164.3
∴ T₁ = T₂ x 164.3 = 1 year x 164.3
or T = 164.3 years

Higher Order Thinking Skills or HOTS

Question 1.
Two satellites S₁ and S₂ are revolving around a planet in plane orbits in same direction. Their time period of revolution are respectively 1 hour and 8 hours. Radius of orbit of S₁ is 10⁴ km. When S₂ is closest to S₁, then find:
(a) Speed of S₂ with respect to S₁.
(b) The observed angular speed of S₂ by an astronaut sitting is S₁.
Solution:
From Kepler's third law of planetary motion,
T² ∝ r³
or r³ ∝ T²
∴ r ∝ T^2/3

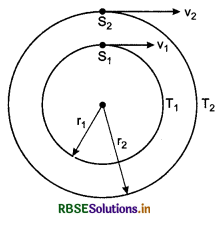
Therefore, \(\frac{r_2}{r_1}=\left(\frac{T_2}{T_1}\right)^{2 / 2}=\left(\frac{8}{1}\right)^{2 / 3}\)
or \(\frac{r_2}{r_1}\) = (2³)^2/3 = 2² = 4
⇒ r₂ = r₁ x 4
∵ r₂ = 4 x 10⁴ km
∵ Time period of satellite,

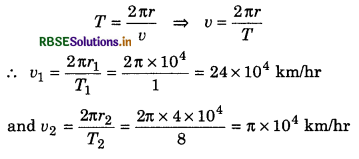
(a) Speed of S₂ with respect to S_1,
v₂₁ = v₂ - v₁ = π x 10⁴ - 2π x 10⁴
or v₂₁ = -π x 10⁴ km/hr
(b) Observed angular speed of S₂ by astronaut sitting in S₁,

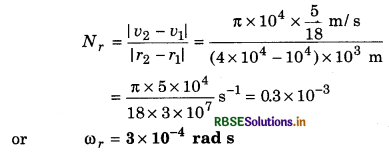
Question 2.
A satellite is revolving around the earth orbital velocity equal to half of escape velocity from the earth.
(a) Find the height of satellite from the earth’s surface with.
(b) If the satellite suddenly stops its revolution in orbit and starts falling freely on the earth, what will be its speed on reaching earth’s surface?
Solution:
(a) Orbital speed of satellite.

∴ R_e + h = 2R_e
or h = R_e = 6400 km
(b) Change in gravitational potential energy on reaching the surface of the earth,
∆U = \(\frac{m g h}{1+\frac{h}{R_e}}=\frac{m g R_e}{1+\frac{R_e}{R_e}}=\frac{1}{2} m g R_e\)
If v be the velocity of satellite on reaching the earth's surface, then
\(\frac{1}{2}\)mv² = ∆U = \(\frac{1}{2}\) mgR_e
or v² = gR_e
∴ v = \sqrt{g R_e}=\sqrt{9.8 \times 6.4 \times 10^6}
or v = 7.919 x 10³ ms^-1
or v = 7.919 km s^-1

Question 3.
Distance between centres of two stars is 10 a. Masses of these stars are M and 16M and their radii are respectively a and 2a. A body of mass m is projected from the surface of big star towards body so that it may reach the surface of small star? Find this speed in terms of G, M and a.

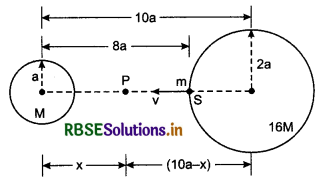
Solution:
Suppose at point P between the stars, resultant force is zero. Therefore, the body will have to be given a minimum velocity so that it may reach upto point P only. After that the body will automatically reach the surface of small star due its attraction.
Therefore at point P,

Gravitational potential energy at point S, due to both stars,

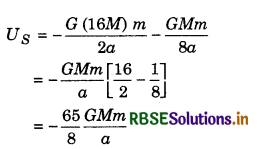
Similarly, gravitational potential energy at point P,

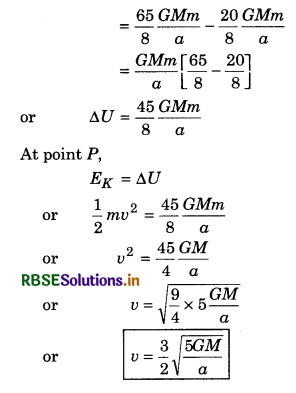
∴ Increase in gravitational potential energy.
∆U = U_P - U_S = \(-\frac{20}{8} \frac{G M m}{a}-\left\lceil\left(-\frac{65}{8}\right) \frac{G M m}{a}\right\rfloor\)

Questions for Competitive Examinations

Objective Type Questions

Question 1.
A satellite is revolving with a constant speed v in a circular orbit around the earth. A body of mass m is projected from the satellite such that it may just escape from the earth’s gravitational field. Kinetic energy of the body of the time of projection will be:
(a) \(\frac{1}{2}\)mv²
(b) mv²
(c) \(\frac{3}{2}\)mv²
(d) 2mv²
Solution:
Potential energy of body placed in satellite in its orbit
= -2 x Kinetic energy
U = -2 x \(\frac{1}{2}\) mv²
or U = -mv²
∴ Escape energy = U_∞ - U = 0 - (-mv²)
or E_escape = mv²
Hence, option (b) is correct.

Question 2.
Two bodies of mass m and 4 m are placed at a distance r apart. Gravitational potential at the point on line joining them, where gravitational field is zero, will be:
(a) zero
(b) \(-\frac{4 G m}{r}\)
(c) \(-\frac{6 G m}{r}\)
(d) \(-\frac{9 G m}{r}\)
Solution:
At P, gravitational field will be zero, if

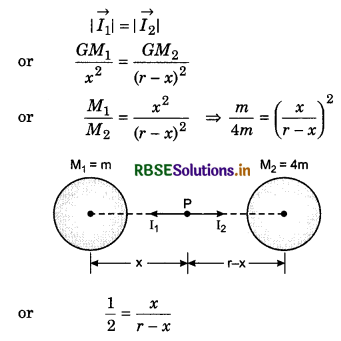
or 2x = r - x

Hence, option (d) is correct.

Question 3.
Two particles of mass m each are moving on a circular path of radius R under mutual gravitation. Speed of each particle, with respect to their centre of mass, is:

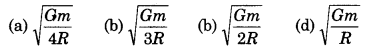
Solution:
For circular motion required centripetal force is obtained by gravitational attraction between the particles.
∴ \(\frac{m V^2}{R}=\frac{G m^2}{(2 R)^2} ⇒ \frac{V^2}{R}=\frac{G m}{4 R^2}\)
∴ V = \(\sqrt{\frac{G M}{4 R}}\)
Thus option (a) is correct.

Question 4.
Mass of moon is \(\frac{1}{81}\) that of earth and gravitational force is \(\frac{1}{6}\) of earth's gravitational force. It means that:
(a) Radius of moon is \(\frac{81}{6}\) of radius of earth
(b) Radius of the earth is \(\frac{9}{\sqrt{6}}\) that of moon
(c) Moon is a satellite of the earth
(d) None of above
Solution:

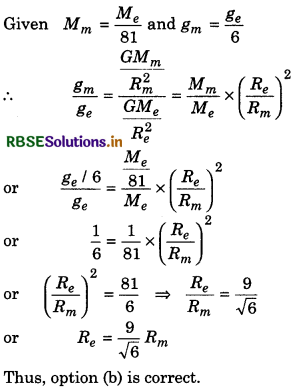
Question 5.
Ratio of diameters of two planets is 4 : 1 and that of their densities is 1 : 2. Ratio of gravitational accelerations on the planets will be:
(a) 1 : 2
(b) 2 : 3
(c) 2 : 1
(d) 4 : 1
Solution:
Gravitational acceleration,
g = \(\frac{4}{3}\)GπRρ
∴ Ratio of gravitational accelerations on the planets,
\(\frac{g_1}{g_2}=\frac{\rho_1 R_1}{\rho_2 R_2}=\frac{1}{2} \times \frac{4}{1}=\frac{2}{1}\)
or g₁ : g₂ = 2 : 1
Hence, option (c) is correct.

Question 6.
Height of the point in terms of radius of the earth R, where gravitational acceleration is \(\frac{g}{9}\) (where g = gravitational acceleration on earth’s surface) is:
(a) \(\frac{R}{\sqrt{2}}\)
(b) \(\frac{R}{2}\)
(c) R\(\sqrt{2}\)
(d) 2R
Solution:
Value of gravitational acceleration at height h,

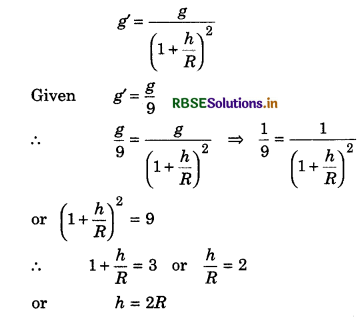
Thus, option (d) is correct.

Question 7.
Gravitational acceleration on a planet is one fourth of that on the earth’s surface. If a brass ball is taken on that planet, which of the following statements is false?
(a) Mass of the brass ball on the planet is one fourth of its mass measured on the earth.
(b) Weight of this ball on the planet is one fourth of its weight measured on the earth.
(c) Mass of this ball on the planet is equal to its mass measured on the earth.
(d) Volume of this ball on this planet is same as that on the earth.
Solution:
Mass of a body does not depend on the value of g. It remains constant.
∴ Option (c) is correct.

Question 8.
A satellite is revolving around the earth in circular orbit of radius r with speed v. If the mass of satellite is M, then its total energy will be:
(a) \(-\frac{1}{2}\) Mv²
(b) \(\frac{1}{2}\) Mv²
(c) \(\frac{3}{2}\) Mv²
(d) Mv²
Solution:
Kinetic energy of a satellite,
K.E. = \(\frac{1}{2}\) mv²
and potential energy
P.E. = \(-\frac{G M_e M}{R}\) = -MgR - Mv² [because v₀ = \(\sqrt{g R}\)]
∴ Total energy = K.E + P.E. = \(\frac{1}{2}\)Mv² - Mv²
= -\(\frac{1}{2}\)Mv²
Hence, option (a) is correct.

Question 9.
If escape velocity for a monkey from the earth’s surface is 11.2 km/s, then escape velocity for elephant will be:
(a) Less than 11.2 km/s
(b) More than 11.2 km/s
(c) 11.2 km/s
(d) None of these
Solution:
Escape velocity v_e = \(\sqrt{2 g r}\) does not depend upon the mass of the body. Therefore, escape velocity for elephant also will be 11.2 km/s.
Hence, option (c) is correct.

Question 10.
In a distant solar system, there is a such planet, the mass of which is 10 times the mass of the earth. Escape velocity from the earth surface is 11 km/s. Escape velocity from the surface of the planet will be:
(a) 11 km/s
(b) 110 km/s
(c) 0.11 km/s
(d) 11.1 km/s
Solution:
Escape velocity
v_e = \(\sqrt{\frac{2 G M}{R}}\)
∴ v_p = \(\sqrt{\frac{2 G .10 M}{\frac{R}{10}}}=\sqrt{100 \times \frac{2 G M}{R}}\) = 10 v_e
= 10 x 10 = 110 km/s
or v_p = 110 km/s
Thus, option (b) is correct.

Question 11.
Two satellites A and B are revolving around the earth in same orbit. Mass of A is 10 times that of B. Ratio of their revolution times will be:
(a) 10
(b) 1
(c) \(\frac{1}{5}\)
(d) \(\frac{1}{10}\)
Solution:
Time period of revolution of a satellite.
T = 2π\(\sqrt{\frac{\left(R_e+h\right)^3}{g R_e^2}}\)
where, R_e is the radius of the earth and h is height from the earth's surface.
It is clear from the above formula that time period does not depend on the mass of a satellite. Hence the time period of both satellites revolving in same orbit will be same.
i.e., T_A = T_B or \(\frac{T_A}{T_B}\) = 1
Hence, option (b) is correct.

Question 12.
If earth stops its rotation about its polar axis, what will be its effect on weight of a body situated at south pole?
(a) It will remain unchanged
(b) It will increase
(c) It will decrease but not zero
(d) It will decrease upto zero
Solution:
Value of g is maximum at the poles because
g'  = g - Rω² cos λ
For pole λ = 90° ⇒ cos λ = 0
∴ g' = g
Thus there is no change in value of g to with rotation of the earth. Therefore there will be no change in weight of body situated at south pole.
Hence, option (a) is correct.

Question 13.
Two bodies of masses 2 kg and 4 kg are approaching each other under mutual gravitational attraction with speeds of 2 m/s and 10 m/s. What will be speed of their centre of mass?
(a) 5 m/s
(b) 6 m/s
(c) 8 m/s
(d) zero
Solution:
Centre of gravity i.e., centre of mass is not affected by mutual gravitational force. Therefore velocity of centre of mass will be zero. Thus, option (d) is correct.

Question 14.
Time period of an earth’s satellite is 5 hours. If the distance between earth and satellite becomes 4 times, what will be new time period of the satellite?
(a) 10 hours
(b) 80 hours
(c) 40 hours
(d) 20 hours
Solution:
From Kepler's law,
T² ∝ r³
∵ \(\left(\frac{T_2}{T_1}\right)^2=\left(\frac{r_2}{r_1}\right)^3=\left(\frac{4 r}{r}\right)^3\) = 4³
or \(\frac{T_2}{T_1}\) = (4)^3/2 = (2²)^3/2 = 2^2x3/2 = 2³ = 8
∴ T₂ = 8 x T₁ = 8 x 5 = 40 hours
Hence, option (c) is correct.

Quesiton 15.
Two satellites of earth S₁ and S₂ are revolving in same orbit. Mass of S₁ is 4 times that of S₂. Which of following statements is correct?
(a) Time period of S₁ is four times that of S₂
(b) Potential energies of the earth and satellite for both satellites are same.
(c) Both satellites S₁ and S₂ are revolving with same speeds.
(d) Kinetic energies of both satellites are same.
Solution:
Since both satellites S₁ and S₂ ae revolving in same orbit. Therefore orbital speed of both satellites will be same. Hence, option (c) is correct.

Question 16.
Two bodies of mass m₁ and m₂ are situated at infinity initially at rest. They start approaching each other due to mutual gravitational attraction. Relative velocity between them when they are at distancer is:

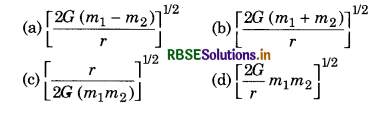
Solution:
Kinetic energy = |Gravitational potenital energy|

Hence, option (b) is correct.

Question 17.
Binary stars of masses M_A and M_B are moving in circular orbits of radius r_A and r_B. If T_A and T_B be the time periods of masses M_A and M_B respectively, then:
(a) \(\frac{T_A}{T_B}=\left(\frac{r_A}{r_B}\right)^{1 / 2}\)
(b) T_A > T_B (if r_A > r_B)
(c) T_A > T_B (if M_A > M_B)
(d) T_A = T_B
Solution:
When two binary stars rotate about their common centre of mass, then they continuously rotate on same orbit for the whole time; otherwise their centres of mass may change. Therfore, angular speed of binary stars remains same.
∵ ω = \(\frac{2 \pi}{T}\)
∵ ω is same for both, therefore T will also be same.
or T_A = T_B
Hence, option (d) is correct.

Question 18.
Ratio of kinetic energy and potential energy of a satellite revolving around the earth will be:
(a) \(\frac{1}{\sqrt{2}}\)
(b) \(\sqrt{2}\)
(c) \(\frac{1}{2}\)
(d) 2
Solution:

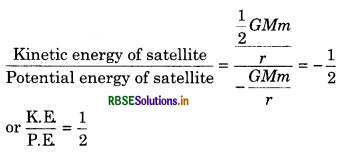
Hence, option (c) is correct.

Question 19.
Effect on gravitational acceleration g due to location on the earth is:
(a) Value of g on equator is maximum and minimum on poles.
(b) Value of g is minimum at equator and maximum at poles.
(c) Value of g is maximum at both places.
(d) Value of g is minimum at both places.
Solution:
Gravitational acceleration at latitude λ,
g' = g - ω²R cos λ
At equation λ = 0
∴ cos λ = 1
∴ g' = g_equation = g - Rω² ......................(1)
For poles λ = 90° ∴ cos λ = 0
∴ g' = g_poles = g ........................(2)
It is clear from equaitons (1) and (2),
g_equator < g_poles
Thus, option (b) is correct.

Question 20.
Time period of a satellite revolving in circular orbits around the earth, does not depend on which of following?
(a) On mass of a satellite
(b) Neither on mass of a satellite nor on the radius of orbit.
(c) On mass of a satellite and radius of a orbit
(d) On the radius of orbit of a satellite.
Solution:
Time period of a satellite,
T = 2π\(\sqrt{\frac{r^3}{G M_e}}\)
This formula does not contain the mass of satellite. Therefore time period of satellite does not depend on its mass.
Hence, option (a) is correct.

Question 21.
If gravitational acceleration on earth is g, then gain in potential energy of the body of mass m in carrying it upto the height equal to radius of earth R is:
(a) 2mgR
(b) mgR
(c) \(\frac{1}{4}\)mgR
(d) \(\frac{1}{2}\)mgR
Solution:
Change in gravitational energy of a body when it is taken from the earth's surface to height h.
∆U = \(\frac{m g h}{1+\frac{h}{R_e}}\)
When h = R_e, then
∆U = \(\frac{m g R_e}{1+\frac{R_e}{R_e}}=\frac{m g R_e}{2}=\frac{1}{2} m g R_e\)
Hence, option (d) is correct.

Question 22.
Suppose the gravitational force is inversely proportional to nth power of distance, then the time period of a planet revolving around the Sun in circular orbit of radius R will be directly proportional to:

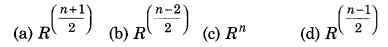
Solution:
For revolving around the Sun, Gravitational force on planet = Required centripetal force to planet

Hence, option (a) is correct.

Question 23.
Velocity of a satellite revolving near the earth surface (R = Radius of earth, r = radius of orbit of satellite) will be:

Solution:
Orbital speed of the satellite,
v₀ = \(\sqrt{\frac{G M_e}{R+h}}\)
For satellite revolving near the earth's surface, h = 0
∴ v₀ = \(\sqrt{\frac{G M_e}{R_e}}=\sqrt{g R_e}\)
Thus, option (b) is correct.

Question 24.
Planetary motion m solar system is an example in which, what remains conserved in this?
(a) mass
(b) linear momentum
(c) angular momentum
(d) kinetic energy
Solution:
According to Kepler’s second law, angular momentum will remain constant. Hence, option (c) is correct.

Question 25.
Mass and diameter of a spherical planet are M_p and D_p. Gravitational acceleration on its surface for freely falling body of mass m, will be:

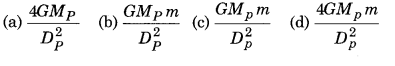
Solution:
∵ Gravitaitonal force

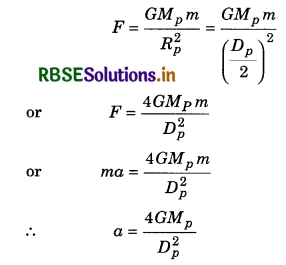
Therefore, option (a) is correct.

Question 26.
An artificial geostationary satellite is revolving around the earth at height of 5R from the earth’s surface, where R is the radius of the earth. Time period of another satellites (in hours) revolving at height of 2R from the earth’s surface, will be:
(a) 5
(b) 10
(c) 6\(\sqrt{2}\)
(d) \(\frac{6}{\sqrt{2}}\)
Solution:
According to Kepler's third law,
T² ∝ r³

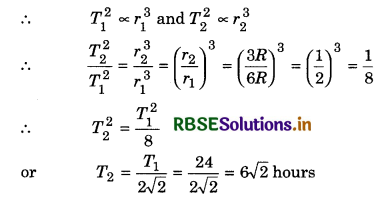
Hence, option (c) is correct.

Question 27.
A body of mass m is taken from the earth’s surface equal to twice the radius of the earth. Change in potential energy of the body will be:
(a) mg2R
(b) \(\frac{2}{3}\)mgR
(c) 3mgR
(d) \(\frac{1}{3}\)mgR
Solution:
Change in gravitational potential energy.

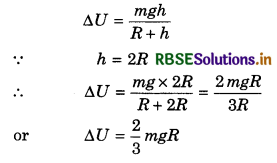
Hence, option (b) is correct.