RBSE Class 11 Physics Important Questions Chapter 7 कणों के निकाय तथा घूर्णी गति

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 7 कणों के निकाय तथा घूर्णी गति Important Questions and Answers.

RBSE Class 11 Physics Chapter 7 Important Questions कणों के निकाय तथा घूर्णी गति

बहुचयनात्मक प्रश्न:

प्रश्न 1. 
बाह्य बल की अनुपस्थिति में द्रव्यमान केन्द्र का वेग:
(अ) शून्य
(ब) नियत
(स) बढ़ेगा
(द) घटेगा
संकेत: बाह्य बल की अनुपस्थिति में द्रव्यमान केन्द्र का वेग नियत रहता है।
उत्तर:
(ब) नियत

प्रश्न 2. 
द्रव्यमान केन्द्र वह बिन्दु है जिसके परितः तंत्र के लिए शून्य होता है-
(अ) द्रव्यमान
(ब) गुरुत्वाकर्षण
(स) द्रव्यमान आघूर्ण
(द) गुरुत्वीय त्वरण
संकेत: द्रव्यमान आघूर्ण ∴  \(\sum_{i=n}^{n^*} m_i r_i=0\)
उत्तर:
(स) द्रव्यमान आघूर्ण

 

प्रश्न 3. 
द्रव्यमान केन्द्र की गति का मुख्य कारण है:
(अ) पारस्परिक बल
(ब) नाभिकीय बल
(स) बाह्य बल
(द) उपर्युक्त में से कोई नहीं
संकेत: द्रव्यमान केन्द्र की गति का कारण बाह्य बल होता है।
उत्तर:
(स) बाह्य बल

प्रश्न 4. 
दिये गये पदार्थ के गोले के लिए उसके व्यास के प्रति जड़त्व आघूर्ण I का मान उसकी त्रिज्या R पर निर्भर करता है:
(अ) α R²
(ब) α R⁵
(स) α R⁴
(द) α R³
संकेत : गोले का व्यास के प्रति जड़त्व आघूर्ण
I = 2/5MR²
द्रव्यमान M = आयतन x घनत्व 
= 4/3πR² x p
\(I=\frac{2}{5} \times \frac{4}{3} \pi R^3 \rho \times R^2=\frac{8}{15} \pi \rho R^5\)
उत्तर:
(ब) α R⁵

प्रश्न 5.
यदि एक चकती को ढालकर गोले में परिवर्तित कर दिया जावे तो:
(अ) दोनों के जड़त्व समान होंगे।
(ब) चकती का जड़त्व अधिक व गोले का कम होगा।
(स) दोनों के जड़त्व आघूर्ण समान होंगे।
(द) उपर्युक्त में से कोई नहीं।
संकेत: हम जानते हैं कि द्रव्यमान, जड़त्व का माप होता है। चूँकि चकती तथा गोले के द्रव्यमान समान हैं, अतः दोनों के जड़त्व समान होंगे।
उत्तर:
(अ) दोनों के जड़त्व समान होंगे।

प्रश्न 6. 
किसी ठोस गोले का उसके व्यास के सापेक्ष जड़त्व आघूर्ण का मान I है, तो गोले का उसकी स्पर्श रेखा के सापेक्ष जड़त्व आघूर्ण होगा:
(अ) 7/2I
(ब) 5/2I
(स) 2/5I
(द) 1/2I
संकेत: I = 2/5MR²
MR² = 5/2I
Ir = I + MR²
= I + 5/2I = 7/2I
उत्तर:
(अ) 7/2I

प्रश्न 7. 
1 मीटर व 5 मीटर त्रिज्या की दो वलय एक नत तल पर एक साथ बिना फिसले लुढ़कना प्रारम्भ करती हैं। पृथ्वी तल पर कौनसी वलय पहले पहुँचेगी?
(अ) बड़ी वलय
(ब) छोटी वलय
(स) दोनों एक साथ
(द) कुछ नहीं कहा जा सकता
संकेत: हम जानते हैं कि पृथ्वी तल पर पहुँचने में लगा समय (K²/R²) पर निर्भर करता है। वलय के लिए I का मान 1 होता है। अतः दोनों वलय एक साथ पृथ्वी तल पर पहुँचेंगी। 
उत्तर:
(स) दोनों एक साथ

प्रश्न 8. 
एक व्यक्ति घूमती मेज पर भुजायें फैलाये बैठा है, अगर वह भुजायें सिकोड़ ले तो:
(अ) कोणीय वेग घट जाता है।
(ब) जड़त्व आघूर्ण घट जायेगा
(स) कोणीय वेग नहीं रहेगा
(द) कोणीय संवेग बढ़ जायेगा
उत्तर:
(ब) जड़त्व आघूर्ण घट जायेगा

प्रश्न 9. 
किसी वस्तु का जड़त्व आघूर्ण निर्भर नहीं करता है:
(अ) द्रव्यमान पर
(ब) कोणीय वेग पर
(स) द्रव्यमान वितरण पर
(द) घूर्णन अक्ष पर
उत्तर:
(ब) कोणीय वेग पर

प्रश्न 10. 
किसी वस्तु की घूर्णन त्रिज्या निर्भर करती है:
(अ) वस्तु के द्रव्यमान व आकृति एवं आकार पर 
(ब) वस्तु के द्रव्यमान व अक्ष की स्थिति पर
(स) वस्तु की बनावट व अक्ष की स्थिति पर
(द) वस्तु के द्रव्यमान व अक्ष की स्थिति एवं बनावट पर
उत्तर:
(ब) वस्तु के द्रव्यमान व अक्ष की स्थिति पर

प्रश्न 11. 
किसी पिण्ड की घूर्णन त्रिज्या का मान निर्भर नहीं करता है:
(अ) घूर्णन अक्ष पर
(ब) द्रव्यमान वितरण पर
(स) पिण्ड के द्रव्यमान पर
(द) उपर्युक्त में से किसी पर भी
उत्तर:
(स) पिण्ड के द्रव्यमान पर

प्रश्न 12. 
h की ऊँचाई तथा क्षैतिज साथ θ कोण बनाते नत तल के पेंदे पर लुढ़कते गोलाकार पिण्ड का वेग होता है:

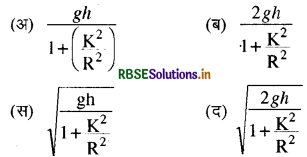
उत्तर:
\(\text { (द) } \sqrt{\frac{2 g h}{1+\frac{\mathrm{K}^2}{\mathrm{R}^2}}}\)

प्रश्न 13. 
एक छल्ला 30° के झुकाव कोण वाले नत तल पर फिसलता है।
उसका त्वरण होगा:
(अ) 8
(ब) 1/2g
(स) 1/4 g
\(\text { (द) } \frac{g}{\sqrt{2}}\)
संकेत: छल्ला फिसलता है 
∴ K²/R² = 0 होगा।
अतः
\(\begin{aligned} a & =\frac{g \sin \theta}{1+\frac{\mathbf{K}^2}{\mathbf{R}^2}}=\frac{g \sin 30^{\circ}}{1+0} \\ & \end{aligned}\)
= g x 1/2 = 1/2g
उत्तर:
(ब) 1/2g

प्रश्न 14. 
यदि दो द्रव्यमान m₁ तथा m₂ की द्रव्यमान केन्द्र से दूरी क्रमशः
r₁ तथा r₂ हो तो r₁/r₂ का मान होगा:

संकेत द्रव्यमान केन्द्र को मूल बिन्दु लेने पर
- m₁r₁ + m₂r₂ = 0

उत्तर:
\(\text { (स) } \frac{m_2}{m_1}\)

प्रश्न 15. 
कोणीय संवेग का 2 घटक रैखिक संवेग के घटकों रूप में अग्र है:
(अ) J_z = xP_y - yP_x
(ब) J_z = yP_y - xP_x
(स) J_z = yP_x - xP_y
(2) J_z = xP_x - yP_y,
उत्तर:
(अ) J_z = xP_y - yP_x

प्रश्न 16. 
शंकु का द्रव्यमान केन्द्र स्थित होता है आधार से-
(अ) h/3 ऊँचाई पर
(ब) h/2 ऊँचाई पर
(स) h/4ऊँचाई पर
(द) 2h/3 ऊँचाई पर
उत्तर:
(स) h/4ऊँचाई पर

प्रश्न 17. 
वृत्तीय गति में किसी कण के रैखिक त्वरण तथा कोणीय त्वरण में सम्बन्ध होता है:

उत्तर:

\(\text { (अ) } \vec{a}=\vec{\alpha} \times \vec{R}\)

प्रश्न 18. 
घूर्णन गति में किया गया कार्य होता है:

उत्तर:
\(\text { (ब) } \vec{\tau} \cdot \overrightarrow{\Delta \theta}\)

प्रश्न 19. 
समकोणीय अक्षों की प्रमेय में यदि पटल X Y तल में हो तो
(अ) I_x + I_y = I.
(ब) I_x + I_z = l_y
(स) I_y + I_z = I_x
(द) I_x - I_z = I_y
उत्तर:
(अ) I_x + I_y = I.

प्रश्न 20. 
समान त्रिज्या के एक रिंग, ठोस गोला, चकती तथा ठोस बेलन. किसी नत तल पर एक साथ लुढ़काये जाते हैं तो नत तल के नीचे सबसे बाद में पहुँचेगा-
(अ) रिंग
(ब) ठोस गोला
(स) चकती
(द) ठोस बेलन
संकेत रिंग के लिए: K²/R² का मान अधिकतम होता है अर्थात् 1 होता है। इस कारण से नीचे पहुँचने में सर्वाधिक समय लेगी।
उत्तर:
(अ) रिंग

रिक्त स्थानों की पूर्ति कीजिए:

प्रश्न 1. 
ऐसे पिण्ड जिन पर बाह्य बल लगाने पर उनके कणों के मध्य की दूरियाँ अपरिवर्तित रहती हों, ........................ कहलाते है।
उत्तर:
दृढ़ पिण्ड

प्रश्न 2.
द्रव्यमान केन्द्र के परितः सभी द्रव्यमान आघूर्णों का सदिश योग .................. होता है।
उत्तर:
शून्य

प्रश्न 3.
समान द्रव्यमान वाले कणों का द्रव्यमान केन्द्र उनके .......................... में स्थित होता है।
उत्तर:
मध्य

प्रश्न 4.
घन, चकती, वलय, गोला आदि का द्रव्यमान केन्द्र उसका .....................  होता है।
उत्तर:
केन्द्र बिन्दु

प्रश्न 5.
अर्ध गोलाई पिण्ड का द्रव्यमान केन्द्र आधार पर स्थित केन्द्र से ....................... ऊँचाई पर होता है।
उत्तर:
3R/8

प्रश्न 6.
शंकु का द्रव्यमान केन्द्र धरातल से ........................ दूरी पर स्थित होता है।
उत्तर:
1/4h

प्रश्न 7.
घूर्णन गति में दिये गये घूर्णन अक्ष के सापेक्ष किसी कण पर कार्यरत बल का आघूर्ण ही ........................  कहलाता है। 
उत्तर:
बल आघूर्ण

प्रश्न 8.
किसी कण के कोणीय संवेग में परिवर्तन की दर उस पर लगने वाले ........................ के बराबर होती है।
उत्तर:
बल आघूर्ण

प्रश्न 9.
यदि कोई वस्तु घूर्णन गति के साथ-साथ रेखीय गति भी करती हो, तब KE. = ...........................
उत्तर:
1/2Iw² + 1/2mv²

प्रश्न 10.
किसी नत तल पर लुढ़कने वाली वस्तु में उत्पन्न त्वरण का मान .......................... पर निर्भर करता है।
उत्तर:
K²/R²

नीचे दिये गये वाक्यों में सत्य / असत्य कथन का चयन कीजिए:

प्रश्न 1. 
द्रव्यमान आघूर्णो का योग शून्य के बराबर होता है।
उत्तर:
सत्य

प्रश्न 2.
शंकु का द्रव्यमान केन्द्र शीर्ष से h दूरी पर स्थित होता है।
उत्तर:
असत्य

प्रश्न 3.
किसी निकाय पर आरोपित बाह्य बलों का योग शून्य होता है। तब उस निकाय का वेग नियत नहीं रहता है।
उत्तर:
असत्य

प्रश्न 4.
कोणीय त्वरण \(\vec{\alpha}\) तथा रेखीय त्वरण \(\vec{a}\) में सदिश सम्बन्ध
a = rα 
उत्तर:
असत्य

प्रश्न 5.
किसी कण के कोणीय संवेग में परिवर्तन की दर उस पर लगने वाले बल आघूर्ण के बराबर होती है।
उत्तर:
सत्य

प्रश्न 6.
पिण्ड के किसी कण की दी गई घूर्णन अक्ष के प्रति जड़त्व आघूर्ण (I), उस कण के द्रव्यमान m तथा कण की घूर्णन अक्ष से लम्बवत् दूरी r के गुणनफल के बराबर होता है।
उत्तर:
असत्य

प्रश्न 7.
I = 2Er
उत्तर:
असत्य

प्रश्न 8.
किसी घूर्णन अक्ष के सापेक्ष वस्तु का जड़त्व आघूर्ण (I) तथा वस्तु के कुल द्रव्यमान (M) के अनुपात का वर्गमूल उस घूर्णन अक्ष के सापेक्ष घूर्णन त्रिज्या कहलाती है।
उत्तर:
सत्य

प्रश्न 9.
ठोस गोले का स्पर्श रेखीय अक्ष के सापेक्ष जड़त्व आघूर्ण का मान = 5/7MR² होता है।
उत्तर:
असत्य

प्रश्न 10.
यदि पिण्डों के द्रव्यमान समान हों तो नत तल की तली में पहुँचने पर गोले पिण्ड की गतिज ऊर्जा सबसे अधिक होगी।
उत्तर:
सत्य

कॉलम - A से कॉलम B का सही मिलान कीजिए:

प्रश्न 1.

 

कॉलम-A	कॉलम-B
1. किसी दृढ़ पिण्ड के समस्त कणों के कोणीय वेग होते हैं।	(A) शून्य
2. आयताकार छड़ चकती एवं गोला आदि के द्रव्यमान केन्द्र की स्थिति होती है।	(B) एक समान
3. यदि बल की क्रिया-रेखा उसी बिन्दु से गुजर रही होती है, जिसके सापेक्ष उसका आघूर्ण निकालना हो तो बल आघूर्ण का मान होता है।	(C) τ = Iα का मान, I का मान कम होने से
4. किस अक्ष के सापेक्ष पिण्ड का जइत्व आघूर्ण न्यूनतम होता है?	(D) g sin θ
5. किसी डोरी के सिरे से पत्थर बाँधकर बड़ी लम्बाई के सिरे से पत्थर बाँधकर घुमाने की अपेक्षा सरल क्यों होता है?	(E) न्यूनतम
6. गतिशील वाहनों के पहिये को बीच से खोखले तथा परिधि पर मोटे बनाये जाते हैं, क्योंकि	(F) कम जड़त्व आघूर्ण वाली वस्तु की
7. जब कोई वस्तु क्षैतिज से θ कोण पर झुके तल पर फिसलती है तो उसका त्वरण होगा	(G) द्रव्यमान पर
8. किसी पिण्ड का जड़त्व आघूर्ण उसके द्रव्यमान केन्द्र से गुजरने वाली अक्ष के सापेक्ष होता है?	(H) समाज्तर अक्षों की प्रमेय
9. दो असमान जड़त्व आघूर्ण वाली वर्तुओं के कोणीय संवेग समान हैं तो कौनसी वस्तु की घूर्णन गतिज ऊर्जा अधिक होगी?	(I) ज्यामिति केन्द्रबिन्दु होता है
10. जड़त्व केवल निर्भर करता है।	(J) द्रव्यमान वही रहता है तथा जड़त्व आघूर्ण बढ़ जाता है।

उत्तर:

कॉलम-A	कॉलम-B
1. किसी दृढ़ पिण्ड के समस्त कणों के कोणीय वेग होते हैं।	(B) एक समान
2. आयताकार छड़ चकती एवं गोला आदि के द्रव्यमान केन्द्र की स्थिति होती है।	(A) शून्य
3. यदि बल की क्रिया-रेखा उसी बिन्दु से गुजर रही होती है, जिसके सापेक्ष उसका आघूर्ण निकालना हो तो बल आघूर्ण का मान होता है।	(I) ज्यामिति केन्द्रबिन्दु होता है
4. किस अक्ष के सापेक्ष पिण्ड का जइत्व आघूर्ण न्यूनतम होता है?	(H) समाज्तर अक्षों की प्रमेय
5. किसी डोरी के सिरे से पत्थर बाँधकर बड़ी लम्बाई के सिरे से पत्थर बाँधकर घुमाने की अपेक्षा सरल क्यों होता है?	(C) τ = Iα का मान, I का मान कम होने से
6. गतिशील वाहनों के पहिये को बीच से खोखले तथा परिधि पर मोटे बनाये जाते हैं, क्योंकि	(J) द्रव्यमान वही रहता है तथा जड़त्व आघूर्ण बढ़ जाता है।
7. जब कोई वस्तु क्षैतिज से θ कोण पर झुके तल पर फिसलती है तो उसका त्वरण होगा	(D) g sin θ
8. किसी पिण्ड का जड़त्व आघूर्ण उसके द्रव्यमान केन्द्र से गुजरने वाली अक्ष के सापेक्ष होता है?	(E) न्यूनतम
9. दो असमान जड़त्व आघूर्ण वाली वर्तुओं के कोणीय संवेग समान हैं तो कौनसी वस्तु की घूर्णन गतिज ऊर्जा अधिक होगी?	(F) कम जड़त्व आघूर्ण वाली वस्तु की
10. जड़त्व केवल निर्भर करता है।	(G) द्रव्यमान पर

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
क्या द्रव्यमान केन्द्र की गति घूर्णन गति हो सकती है? 
उत्तर:
नहीं। चूँकि द्रव्यमान केन्द्र की गति हमेशा स्थानान्तरीय होती है।

प्रश्न 2. 
यदि कण तंत्र उसके विभिन्न कणों के वेग द्रव्यमान केन्द्र का वेग शून्य हो तो क्या आवश्यक रूप से शून्य होंगे?
उत्तर:
आवश्यक नहीं निकाय के कणों का कुल रेखीय संवेग शून्य होगा निकाय के कणों का कुछ भी वेग हो सकता है। 

प्रश्न 3. 
क्या कण तंत्र के द्रव्यमान केन्द्र का संवेग आंतरिक बलों के कारण परिवर्तित सकता है?
उत्तर:
नहीं। चूँकि आन्तरिक बलों का परिणामी बल शून्य होता है। 

प्रश्न 4. 
किसी दृढ़ पिण्ड के समस्त कणों के कोणीय वेग एकसमान होते हैं या भिन्न-भिन्न?
उत्तर:
एकसमान।

प्रश्न 5. 
यदि बल की क्रिया रेखा उसी बिन्दु से गुजर रही होती है जिसके सापेक्ष उसका आघूर्ण निकालना हो तो बल-आघूर्ण का मान क्या होगा?
उत्तर:
शून्य। चूँकि बल भुजा की लम्बाई शून्य है।

प्रश्न 6. 
यदि घूर्णन अक्ष पर निर्देश बिन्दु की स्थिति परिवर्तित कर दी जाती है तो क्या बल-आघूर्ण का मान परिवर्तित हो जायेगा?
उत्तर:
नहीं।

प्रश्न 7. 
R त्रिज्या के वृत्तीय पथ में गति करते m द्रव्यमान व v वेग वाले कण का वृत्त के केन्द्र के सापेक्ष कोणीय संवेग क्या होगा?
उत्तर:
कोणीय संवेग
\(\overrightarrow{\mathrm{L}}=\overrightarrow{\mathrm{R}} \times \overrightarrow{\mathrm{P}}=\mathrm{R} \operatorname{Psin} \theta \cdot \hat{n}\)
यहाँ पर θ = 90° है
लेकिन P = mv होता है।
∴ कोणीय संवेग का परिमाण = mvR होगा।

प्रश्न 8. 
आयताकार छड़ चकती एवं गोला आदि के द्रव्यमान केन्द्र की स्थिति बताइये।
उत्तर:
इन सभी का द्रव्यमान केन्द्र उनका ज्यामिति केन्द्र बिन्दु होता है।

प्रश्न 9. 
क्या वस्तु का द्रव्यमान केन्द्र बाहर हो सकता है? 
उत्तर:
हाँ; वलय, अर्द्धवलय, खोखला बेलन, खोखला गोला आदि के द्रव्यमान केन्द्र पिण्ड पर नहीं होते हैं।

प्रश्न 10. 
यदि कोई वस्तु घूर्णन कर रही है तो क्या निश्चित रूप से उस पर कोई बल आघूर्ण लग रहा है?
उत्तर:
आवश्यक नहीं है। चूँकि बल आघूर्ण केवल कोणीय त्वरण उत्पन्न करने के लिये लगता है।

प्रश्न 11. 
चकती, खोखली चकती, घन, ठोस गोला, खोखला गोला आदि के द्रव्यमान केन्द्र की स्थिति बताइये।
उत्तर:
सभी उपर्युक्त पिण्डों के द्रव्यमान केन्द्र की स्थिति उनके केन्द्र होते हैं।

प्रश्न 12. 
क्या सभी ठोस पिण्ड दृढ़ होते हैं?
उत्तर:
नहीं, जैसे रबड़।

प्रश्न 13. 
एक सीढ़ी दीवार के सहारे तिरछी लगी है। यदि वह फिसले तो उसका तात्क्षणिक घूर्णन केन्द्र कहाँ होगा?
उत्तर:
ऊपर के स्पर्श बिन्दु पर दीवार के लम्ब व नीचे के स्पर्श बिन्दु पर जमीन के लम्ब के काट बिन्दु पर।

प्रश्न 14. 
यदि एक सीढ़ी पर आदमी ऊपर के सिरे पर खड़ा हो अथवा नीचे के सिरे पर खड़ा हो तो सीढ़ी के फिसलने की सम्भावना कब अधिक होगी?
उत्तर:
जब आदमी ऊपर के सिरे पर हो, तब घूर्णी केन्द्र के प्रति बल आघूर्ण अधिक होगा।

प्रश्न 15. 
मोम की एक चकती को पिघला कर ठोस गोले के रूप में ढाल दिया जाता है। केन्द्र से गुजरने वाली उभयनिष्ठ अक्ष के प्रति जड़त्व आघूर्ण पर क्या प्रभाव पड़ेगा?
उत्तर:
जड़त्व आघूर्ण घट जायेगा।

प्रश्न 16. 
किस अक्ष के सापेक्ष पिण्ड का जड़त्व आघूर्ण न्यूनतम होता है?
उत्तर:
समान्तर अक्षों की प्रमेय।
1 = Ig + Md² से स्पष्ट है कि द्रव्यमान केन्द्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण न्यूनतम होता है।

प्रश्न 17. 
ω कोणीय वेग से घूर्णन करती वस्तु के लिये यदि घूर्णन अक्ष से किसी कण की लम्बवत् दूरी अधिक हो तो उसका कोणीय वेग क्या होगा?
उत्तर:
ही रहेगा। कोणीय वेग नियम रहता है।

प्रश्न 18. 
समान द्रव्यमान त्रिज्या तथा आकृति की खोखली तथा ठोस वस्तुओं में से किसका जड़त्व आघूर्ण अधिक होगा?
उत्तर:
खोखली का  चूँकि खोखली वस्तुओं में ठोस वस्तुओं की  अपेक्षा द्रव्यमान का वितरण घूर्णन अक्ष से अधिक दूरी पर होता है।

प्रश्न 19. 
यदि कण तंत्र पर बाह्य बल-आघूर्णो का मान शून्य होता है तो क्या ऐसा संभव है कि उसके विभिन्न कणों के कोणीय संवेग परिवर्तित हो रहे हों लेकिन उनका सदिश योग परिवर्तित न हो?
उत्तर:
हीं।
∵ τ = dL/dt
यदि = 0 L = नियत तो [L + L2 + ...... = नियत ] 

प्रश्न 20. 
किसी डोरी के सिरे से पत्थर बाँधकर बड़ी लम्बाई के सिरे से पत्थर बाँधकर घुमाने की अपेक्षा सरल क्यों होता है?
उत्तर:
τ = To का मान, I का मान कम होने से कम होता है।

प्रश्न 21. 
एक कण मूल बिन्दु से गुजरने वाली सीधी रेखा पर गतिशील है तो मूल बिन्दु के सापेक्ष उसका कोणीय संवेग क्या होगा?
उत्तर:
शून्य।

प्रश्न 22. 
लोटनी गति में सम्पर्क बिन्दु का तात्क्षणिक वेग सतह के सापेक्ष क्या होता है?
उत्तर:
शून्य।

प्रश्न 23. 
जब कोई वस्तु क्षैतिज से 9 कोण पर झुके तल पर फिसलती है तो उसका त्वरण होगा:
उत्तर:
g sin θ

प्रश्न 24. 
गतिशील वाहनों के पहिये के बीच से खोखले तथा परिधि पर मोटे बनाये जाते हैं, क्योंकि:
उत्तर:
द्रव्यमान वही रहता है तथा जड़त्व आघूर्ण बढ़ जाता है। 

प्रश्न 25. 
दो असमान जड़त्व आघूर्ण वाली वस्तुओं के कोणीय संवेग समान हैं, तो कौनसी वस्तु की घूर्णन गतिज ऊर्जा अधिक होगी? 
उत्तर:
कम जड़त्व आघूर्ण वाली वस्तु की।

प्रश्न 26. 
किसी वस्तु के किस कण का जड़त्व आघूर्ण सबसे कम होता है?
उत्तर:
घूर्णन अक्ष पर स्थित कण का जड़त्व आघूर्ण सबसे कम होता है।

प्रश्न 27. 
किसी पिण्ड का जड़त्व आघूर्ण उसके द्रव्यमान केन्द्र से गुजरने वाली अक्ष के सापेक्ष कितना होता है?
उत्तर:
न्यूनतम होता है।

प्रश्न 28. 
दो समान ज्यामितीय आकृति की वस्तुएँ जिनमें से एक ऐलुमिनियम की है तथा दूसरी लोहे की है, किसका जड़त्व आघूर्ण ज्यामितीय अक्ष के सापेक्ष अधिक होगा और क्यों?
उत्तर:
लोहे का जड़त्व आघूर्ण ज्यामितीय अक्ष के सापेक्ष अधिक होगा। चूँकि लोहे की वस्तु का द्रव्यमान अधिक है।

प्रश्न 29. 
एक बन्द बॉक्स में गैस भरी है तथा बॉक्स प्रारम्भ में स्थिर अवस्था में है। गैस के अणुओं की गति और आपसी टक्कर में बॉक्स के द्रव्यमान केन्द्र की गति पर क्या प्रभाव होगा?
उत्तर:
द्रव्यमान केन्द्र की गति स्थिर रहेगी चूँकि बॉक्स और उसमें गैस एक विगलित निकाय है और बॉक्स पर कोई बाह्य बल कार्य नहीं कर रहा है।

प्रश्न 30.
0.2 मीटर त्रिज्या और 2 किग्रा द्रव्यमान की एक चकती स्वयं के अक्ष के परितः परिभ्रमण कर रही है। चकती का जड़त्व आघूर्ण क्या होगा?
उत्तर:
स्वयं के अक्ष के परितः चकती का जड़त्व आघूर्ण
I = 1/2 MR²
I = 1/2 × 2 × 0.2 x 0.2
 ∵ M= 2 किग्रा.
R = 0.2 मीटर
= 0.04 किग्रा.- मीटर² 

लघुत्तरात्मक प्रश्न:

प्रश्न 1. 
द्रव्यमान केन्द्र क्या है? क्या किसी वस्तु के द्रव्यमान केन्द्र पर द्रव्यमान का होना आवश्यक है?
उत्तर:
(i) किसी कण तंत्र का द्रव्यमान केन्द्र वह बिन्दु होता है। जिस पर उस कण तंत्र के कणों का सम्पूर्ण द्रव्यमान इसकी स्थानान्तरीय गति के अध्ययन के लिये प्रभावी रूप से केन्द्रित हुआ माना जा सकता है।
(ii) द्रव्यमान केन्द्र वह बिन्दु है जिसके परितः कण तंत्र के समस्त कणों के द्रव्यमान आघूर्णो का सदिश योग शून्य होता है अर्थात्
\(\sum_{i=1}^{i=n} m_i \vec{r}_i=0\)
जहाँ द्रव्यमान केन्द्र के सापेक्ष वें कण का स्थिति सदिश है। द्रव्यमान केन्द्र पर भौतिक रूप से कोई द्रव्यमान उपस्थित होना आवश्यक नहीं है।

प्रश्न 2. 
दो द्रव्यमान m₁ तथा m₂,r दूरी पर रखे हों तो उनके द्रव्यमान केन्द्र की स्थिति क्या होगी?
उत्तर:
माना कि द्रव्यमान केन्द्र की स्थिति m₁ से x दूरी है। से यह दूरी (x) होगी।
तब 

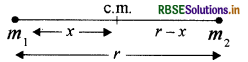
m₁x = (r - x) m₂
m₁x = rm₂ – xm₂
m₁x + m₂x = rm₂
x(m₁ + m₂) = rm₂
\(x=\frac{r m_2}{m_1+m_2}\)
अत: m1 से द्रव्यमान केन्द्र की दूरी \(\left(\frac{r m_2}{m_1+m_2}\right)\) होगी तथा m₂
द्रव्यमान से \(\left(r-\frac{r m_2}{m_1+m_2}\right)=\left(\frac{r m_1}{m_1+m_2}\right)\) दूरी पर होगा।

प्रश्न 3. 
सिद्ध करो कि द्रव्यमान केन्द्र के सापेक्ष कण तंत्र के कणों का कुल द्रव्यमान आघूर्ण शून्य होता है।
उत्तर:
दो कणों के निकाय के द्रव्यमान केन्द्र का स्थिति सदिश का व्यंजक निम्न होता है
\(\vec{r}_{c m}=\frac{m_1 \overrightarrow{r_1}+m_2 \overrightarrow{r_2}+\ldots \ldots+m_n \overrightarrow{r_n}}{m_1+m_2+\ldots \ldots+m_n}\)
यदि द्रव्यमान केन्द्र को मूल बिन्दु मानें तो
\(\begin{aligned} \vec{r}_{c m} & =0 \\ 0 & =\frac{m_1 \overrightarrow{r_1}+m_2 \overrightarrow{r_2}+\ldots \ldots+m_n \overrightarrow{r_n}}{m_1+m_2+\ldots \ldots+m_n} \end{aligned}\)
ऊपर वाले व्यंजक से स्पष्ट है कि सभी कणों के द्रव्यमान आघूर्णी का योग शून्य होता है। अतः समीकरण (1) से स्पष्ट है कि द्रव्यमान केन्द्र के सापेक्ष निकाय के सभी कणों के द्रव्यमानों के आघूर्णो का योग सदैव शून्य होता है।

प्रश्न 4. 
जड़त्व और जड़त्व आघूर्ण में क्या अन्तर है?
उत्तर:

जड़त्व	जड़त्व आघूर्ण
1. जड़त्व केवल द्रव्यमान पर निर्भर करता है।	जड़त्व आघूर्ण पिण्ड के द्रव्यमान तथा घूर्णन अक्ष के सापेक्ष द्रव्यमानवितरण पर निर्भर करता है। इसका मात्रक किग्रा. मी2 होता है।
2. इसका मात्रक किग्रा. होता है।	यह घूर्णन गति का गुण है।
3. यह रेखीय गति का गुण होता है।	यह गुण अक्ष के प्रति गति में परिवर्तन का विरोध करता है।
4. यह गुण रैखिक गति में परिवर्तन का विरोध करता है।	जड़त्व आघूर्ण पिण्ड के द्रव्यमान तथा घूर्णन अक्ष के सापेक्ष द्रव्यमानवितरण पर निर्भर करता है। इसका मात्रक किग्रा.  मी2  होता है।

प्रश्न 5. 
कोणीय त्वरण को परिभाषित कीजिए।
उत्तर:
समय के सापेक्ष कोणीय वेग परिवर्तन की दर के रूप में कर सकते हैं। यानी
α = dω/dt
यदि घूर्णन अक्ष स्थिर है तो के की दिशा और इसलिए  ँ की दिशा भी स्थिर होगी। इस स्थिति में तब सदिश समीकरण अदिश समीकरण में बदल जाती है और हम इसको निम्न प्रकार से लिख सकते हैं
α = dω/dt

प्रश्न 6. 
हैण्डपम्प का हत्था लम्बा एवं पेंचकस का हत्था चौड़ा बनाया जाता है। क्यों?
उत्तर:
हैण्डपम्प का हत्था एवं पेंचकस का हत्था दोनों घूर्णन गति करते हैं और घूर्णन गति बल आघूर्ण पर निर्भर करती है तथा बल-आघूर्ण या बल-युग्म का आघूर्ण τ = F x r होता है।
यदि घूर्णन अक्ष से बल की दूरी को बढ़ा दें तो बल आघूर्ण का मान भी बढ़ जाता है और घूर्णन गति आसानी से हो सकेगी इसलिये हैण्डपम्प का हत्था लम्बा और पेंचकस का हत्था चौड़ा बनाया जाता है।

प्रश्न 7. 
बिना किसी बल आघूर्ण के एक वस्तु का कोणीय वेग 1 चक्कर प्रति 25 सेकण्ड से बदल कर 1 चक्कर प्रति सेकण्ड हो जाता है। इन दो स्थितियों में वस्तु की घूर्णन त्रिज्याओं का अनुपात ज्ञात करो।
उत्तर:
हम जानते हैं।
कोणीय संवेग संरक्षण के नियम से
या
या
कोणीय संवेग संरक्षण के नियम से-
I₁ω₁ = I₂ω₂
यहाँ पर n₁ तथा n₂ आवृत्तियाँ हैं।
I₁n₁ = I₂n₂
यदि पिण्ड की दोनों स्थितियों में घूर्णन त्रिज्यायें K₁ व K₂ हैं। उस स्थिति में
MK₁²n₁ = MK₂²n₂
∴ K₁²n₁ = K₂²n₂
∴ \(\frac{\mathrm{K}_1^2}{\mathrm{~K}_2^2}=\frac{n_2}{n_1}\)
दिया गया है: n₁ = 1/25
n₂ = 1
\(\begin{aligned} & \frac{\mathrm{K}_1^2}{\mathrm{~K}_2^2}=\frac{1}{\frac{1}{25}}=\frac{25}{1} \\ & \frac{\mathrm{K}_1}{\mathrm{~K}_2}=\sqrt{\frac{25}{1}}=\frac{5}{1} \end{aligned}\)
\(\frac{\mathrm{K}_1}{\mathrm{~K}_2}=\frac{5}{1}\)

प्रश्न 8. 
एक वस्तु एक समान कोणीय त्वरण से घूर्णन कर रही है। यदि घूर्णन विराम अवस्था से प्रारम्भ किये गये हों तब समय पश्चात् कोणीय विस्थापन समय की किस घात के समानुपाती होगी? 
उत्तर:
घूर्णन गति के दूसरे समीकरण से
θ = ω₀t + 1/2αt²
यहाँ पर ω₀ = शून्य है।
θ = 0 × t + 1/2αt²
θ = 1/2αt²
यहाँ पर α समान कोणीय त्वरण है।

प्रश्न 9 
समान बनाये जाते हैं। द्रव्यमान के ठोस गोले भिन्न-भिन्न पदार्थों के के जड़त्व आघूर्ण का उनके घनत्व (d) के साथ गोलों क्या सम्बन्ध होगा?
उत्तर:
ठोस गोले का जड़त्व आघूर्ण
I = 2/5MR²
I ∞ R² ................ (1)
लेकिन
4/3πR³ x d = M
∴ R³ ∞ 1/d
य \(\mathrm{R} \propto \frac{1}{(d)^{\frac{1}{3}}}\) ............ (2)
समी (2) से R का मान समी (1) में रखने पर
\(\begin{aligned} & I \propto\left(\frac{1}{(d)^{\frac{1}{3}}}\right)^2 \\ & I \propto \frac{1}{d^{\frac{2}{3}}} \end{aligned}\)

प्रश्न 10.
क्षैतिज तल पर लुढ़कते गोलीय कोश के घूर्णन गतिज ऊर्जा कुल ऊर्जा के कितने प्रतिशत होती है?
उत्तर:
कुल ऊर्जा
E = 1⁄2MV²  + 1/2Iω²
=  1⁄2 MV² + 1/2 × 2/ MR² x V²/R²
= 1⁄2MV² + 1/3MV²
= 5/6MV²
अतः प्रतिशत घूर्णन गतिज ऊर्जा
\(=\frac{\frac{1}{3} \mathrm{MV}^2}{\frac{5}{6} \mathrm{MV}^2} \times 100\)
= 40% 

आंकिक प्रश्न:

प्रश्न 1. 
त्रिज्या R के एक ठोस गोले में से त्रिज्या (R/2) का गोला काट कर चित्रानुसार निकाल दिया गया है। शेष गोले के द्रव्यमान केन्द्र की स्थिति ज्ञात कीजिये।
उत्तर:
यदि गोले के पदार्थ का घनत्व है ρ तो त्रिज्या R के गोले का
द्रव्यमान  M = 4/3 πR³ρ
त्रिज्या (R/2) के गोले का द्रव्यमान

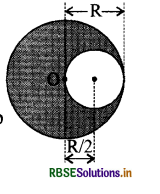
\(\begin{aligned} \mathbf{M}_1 & =\frac{4}{3} \pi\left(\frac{\mathrm{R}}{2}\right)^3 \rho \\ & =\frac{4}{3} \frac{\pi R^3 \rho}{8} \\ & =\frac{M}{8} \end{aligned}\)

शेष गोले का द्रव्यमान M₂ = M - M/8 = 7M/8

शेष गोले के द्रव्यमान केन्द्र के गोले के केन्द्र O से दूरी x है तो पूर्ण गोले का द्रव्यमान केन्द्र मूल बिन्दु पर लेने पर
M₁ (R/2) + M₂x = 0
M₁ (R/2) = -M₂x
x = -M₁/M₂(R/2)
= - M/8 x 8/7M(R/2)
x = - R/14

प्रश्न 2. 
एक कार का पहिया 20 चक्कर / सेकण्ड की गति से घूम रहा है। यदि त्वरण के कारण 10 सेकण्ड में इसकी घूर्णन गति 75 चक्कर / सेकण्ड हो जावे तो इस समय पश्चात् कोणीय त्वरण एवं कोणीय विस्थापन ज्ञात कीजिये ।
उत्तर:
दिया गया है:
n1 = 20 चक्कर / सेकण्ड
t = 10 सेकण्ड
n₂ = 75 चक्कर / सेकण्ड
हम जानते हैं:
ω₀ = 2π n₁
= 2 x 3.14 x 20
= 125.6 रेडियन / सेकण्ड
ω₁ = 2πn₂
= 2 x 3.14 x 75
= 150 × 3.14
= 471.00
= 471 रेडियन / सेकण्ड
10 सेकण्ड के बाद कोणीय त्वरण का मान होगा-
\(\begin{aligned} & =\frac{\omega_1-\omega_0}{t} \\ & =\frac{471-125.6}{10} \end{aligned}\)
\(=\frac{345.4}{10}\)
= 34.54 रेडियन / सेकण्ड
कोणीय गति के दूसरे समीकरण से
कोणीय विस्थापन
θ = ω₀t + 1/2αt²
θ = 125.6 x 10 + 1/2 x 34.54 x 100
= 1256 + 50 x 34.54
= 1256 + 1727.00 = 2983
= 950π

प्रश्न 3. 
एक गतिपालक चक्र की रिम पर स्थित एक बिन्दु की कोणीय स्थिति निम्न सूत्र से प्रदर्शित है-
θ = 4t - 3t² + t³
यहाँ θ रेडियन में और t सेकण्ड में है। समय t = 2 सेकण्ड से प्रारम्भ होकर t = 4 सेकण्ड पर समाप्त होने वाले समयान्तराल के लिये औसत त्वरण ज्ञात कीजिये।
उत्तर:
दिया गया है:
θ = 4t - 3t² + t3
∴ ω  = dθ/dt = 4 - 6 + 3t²
t = 2 सेकण्ड के लिये
ω₂ = 4 - 6 x 2 + 3 x (2)²
= 4 - 12 + 12 = 4
t = 4 सेकण्ड के लिये
ω₄ = 4 - 6 x 4 + 3 x (4)²
= 4 - 24 + 48 = 28
औसत कोणीय त्वरण 
\(\begin{aligned} & =\frac{\omega_4-\omega_2}{t_4-t_2} \\ & =\frac{28-4}{4-2}=\frac{24}{2} \end{aligned}\)
= 12 रेडियन/से.²

प्रश्न 4. 
सिद्ध कीजिए कि अचर वेग से चलते एकल कण का किसी बिन्दु के परितः कोणीय संवेग उसकी समस्त गति के दौरान अचर रहता है।
उत्तर:
माना कि कोई कण P किसी क्षण t पर, v वेग से चल रहा है। इस कण का कोणीय संवेग L स्वेच्छ बिन्दु O के परितः ज्ञात करना चाहते हैं।

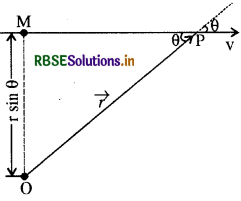
कोणीय संवेग \(\overrightarrow{\mathrm{L}}=\vec{r} \times m \overrightarrow{\mathrm{v}}\) है। इसका परिमाण mVR sinθ है। जहाँ θ \(\vec{r}\) और \(\overrightarrow{\mathrm{v}}\) के बीच का कोण है। यद्यपि कण समय के साथ अपनी स्थिति बदल रहा है, फिर भी \(\overrightarrow{\mathrm{v}}\) की दिशा रेखा वही बनी रहती है और इसलिए OM = r sinθ अचर है।

\(\overrightarrow{\mathrm{L}}\) की दिशा \(\vec{r}\) एवं \(\overrightarrow{\mathrm{v}}\) के तल के अभिलम्बवत् पृष्ठ के अन्दर की ओर जाती हुई है। यह दिशा भी नहीं बदलती अतः \(\overrightarrow{\mathrm{v}}\) का परिमाण एवं दिशा वही रहती है। इति सिद्धम्

प्रश्न 5. 
एक वृत्ताकार चकती का जड़त्व आघूर्ण इसके किसी व्यास के परितः क्या होगा?
उत्तर:
हम जानते हैं कि किसी चकती का जड़त्व आघूर्ण, उसके केन्द्र से गुजरती और इसके तल के लम्बवत् अक्ष के परितः I = MR²/2 होता है।
जहाँ पर M चकती का द्रव्यमान और R इसकी त्रिज्या है। लम्बवत् अक्षों के प्रमेय के अनुसार
Iz = I + ly
अब, x और y अ चकती के दो व्यासों के अनुदिश हैं और सममिति के विचार से प्रत्येक व्यास के परितः जड़त्व आघूर्ण का मान समान होना चाहिए। अतः
अतः
Ix = ly Iz = 2Ix

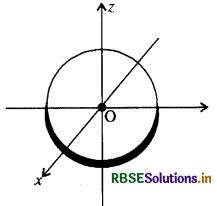
लेकिन
Iz = MR²
∴ Ix = 1/2Iz = 1/2 × MR²/2
⇒ Ix = 1/4MR²
अतः किसी व्यास के परितः चकती का जड़त्व आघूर्ण MR²/4 है।

प्रश्न 6. 
द्रव्यमान M और लम्बाई l वाली छड़ का उस अक्ष के परितः जड़त्व आघूर्ण क्या होगा जो इसके लम्बवत् किसी एक सिरे से गुजरती हो? 
उत्तर:
M द्रव्यमान और l लम्बाई की छड़ का इसके द्रव्यमान केन्द्र से लम्बाई के लम्बवत् गुजरने वाली अक्ष के परितः जड़त्व आघूर्ण I = Ml²/12 है।
समान्तर अक्ष का प्रमेय लगाने पर
I = I + Ma²
यहाँ पर
d = 1/2
\(\mathrm{I}^{\prime}=\frac{\mathrm{M} l^2}{12}+\mathrm{M}\left(\frac{l}{2}\right)^2=\frac{\mathrm{M} l^2}{12}+\frac{\mathrm{M} l^2}{4}\)
∴ \(=\frac{\mathrm{M} l^2+3 \mathrm{M} l^2}{12}=\frac{4 \mathrm{M} l^2}{12}=\frac{\mathrm{M} l^2}{3}\)

प्रश्न 7. 
किसी पतले वलय की परिधि पर स्पर्श रेखा बनाती हुई और इसके तल में ही स्थित अक्ष के परितः इसका जड़त्व आघूर्ण क्या है?
उत्तर:
वलय की परिधि पर स्पर्श रेखा इसके व्यास के समान्तर है। इन समान्तर अक्षों के बीच की दूरी R है यानी वलय की त्रिज्या समान्तर अक्षों का प्रमेय से

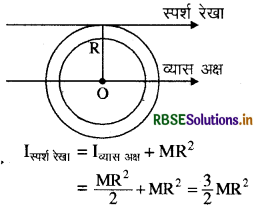
प्रश्न 8. 
M द्रव्यमान तथा R त्रिज्या वाली चकतियाँ किसी द्रव्यमान रहित 2R लम्बाई की छड़ के किनारों पर लगी हुई हैं। इस तंत्र का छड़ के लम्बवत् तथा उसके केन्द्र से गुजर रही अक्ष के सापेक्ष जड़त्व आघूर्ण ज्ञात कीजिये।
उत्तर:
दोनों चकतियों का जड़त्व आघूर्ण व्यास के सापेक्ष बराबर है,
जिसका मान

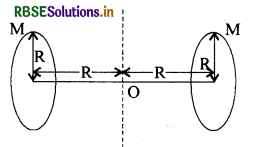
चूँकि जिस अक्ष के सापेक्ष जड़त्व आघूर्ण प्राप्त करना है वह दोनों से R दूरी पर है और दोनों के व्यासों के समानान्तर है।
∴ समानान्तर अक्ष प्रमेय से अभीष्ट अक्ष के सापेक्ष एक का जड़त्व
= 1/4MR² + MR² = 5/4MR²
∴ दोनों चकतियों का जड़त्व आघूर्ण अभीष्ट अक्ष के सापेक्ष
\(=\frac{2 \times 5}{4} \mathrm{MR}^2=\frac{5}{2} \mathrm{MR}^2\)

प्रश्न 9 
तीन कण जिनके द्रव्यमान समान हैं, a भुजा वाले समबाहु त्रिभुज के तीनों कोनों पर रखे जाते हैं। किसी एक कण से होकर जाने वाली तथा त्रिभुज के तल के लम्बवत् अक्ष के सापेक्ष निकाय का जड़त्व आघूर्ण ज्ञात कीजिये।
उत्तर: 
माना कि समबाहु त्रिभुज के शीर्ष पर रखे प्रत्येक कण का द्रव्यमान m है।

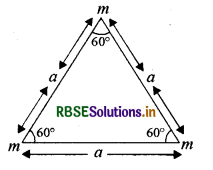
अभीष्ट अक्ष जिस शीर्ष से गुजर रहा है उस पर रखे कण का जड़त्व आघूर्ण शून्य होगा क्योंकि अक्ष से उसकी दूरी शून्य है। और बाकी दो शीषों पर रखे कणों के कारण जड़त्व आघूर्ण होगा। चूँकि अन्य दो शीर्षो पर रखे कण बराबर द्रव्यमान के हैं और अक्ष से बराबर दूरी पर हैं इसलिये दोनों कणों का जड़त्व आघूर्ण बराबर होगा। एक कण का जड़त्व आघूर्ण = m(a)²
= ma²
दोनों कणों का जड़त्व आघूर्ण = 2 x ma² = 2ma² 
अतः निकाय का जड़त्व आघूर्ण = 0 + 2ma²
= 2ma² 

गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न:

प्रश्न 1. 
किसी एकसमान ठोस शंकु के द्रव्यमान केन्द्र की उसके शीर्ष से दूरी 20 हैं। यदि शंकु के आधार की त्रिज्या R तथा शंकु की ऊँचाई h हो तो 26 का मान निम्नांकित में से किसके बराबर होगा:
(a) h²/4R
(b) 3h/R
(c) 5h/8
(d) 3h²/8R
उत्तर: 
(b) 3h/R

प्रश्न 2. 
विभिन्न द्रव्यमानों के तीन पिण्ड X- अक्ष पर इस प्रकार रखते हैं कि 300g का पिण्ड मूल बिन्दु पर, 500g का x = 40 cm पर तथा 400g का x = 70 cm पर हो तो मूलबिन्दु से द्रव्यमान केन्द्र की दूरी होगी:
(a) 40 cm
(b) 45 cm
(c) 50 cm
(d) 30 cm
उत्तर: 
(a) 40 cm

प्रश्न 3. 
चित्र द्वारा दर्शाये समबहुभुजों की भुजाओं की संख्या n = 3, 4, 5........ है। सभी बहुभुजों का संहति केन्द्र अनुभूमिक तल से h ऊँचाई पर है। ये बिना फिसले क्षैतिज तल पर प्रतिगामी शीर्ष के चारों ओर घूर्णन कर अग्रसरित हो रहे हैं। प्रत्येक बहुभुज के संहति केन्द्र के रेखापथ की ऊँचाई की अधिकतम वृद्धि 4 है। तब A की है और 1 पर निर्भरता निम्न में से दी जाएगी

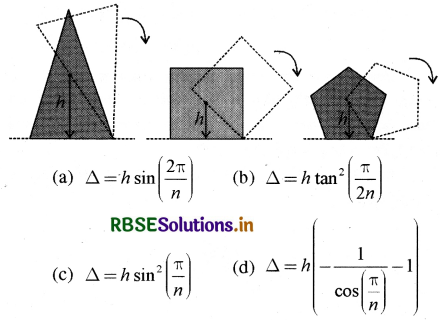
उत्तर: 
\(\text { (a) } \Delta=h \sin \left(\frac{2 \pi}{n}\right)\)
 

प्रश्न 4. 
एक हल्की छड़ की लम्बाई है। इसके दो सिरों से क्रमश: m₁ तथा m₂ द्रव्यमान के पिण्ड संलग्न हैं। इस छड़ के लम्बवत् तथा इसके द्रव्यमान केन्द्र से गुजरते हुए अक्ष के परितः इस निकाय का जड़त्व आघूर्ण होगा:

उत्तर: 
\(\text { (b) } \frac{m_1 m_2}{m_1+m_2} l^2\)

प्रश्न 5. 
 त्रिज्या R तथा लम्बाई के एक समान बेलन का उसके अभिलम्ब द्विभाजक के सापेक्ष जड़त्व आघूर्ण I है जड़त्व आघूर्ण के निम्नतम मान के लिए अनुपात I/R क्या होगा:

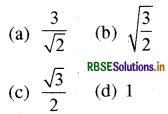
उत्तर:
\(\text { (b) } \sqrt{\frac{3}{2}}\)

प्रश्न 6. 
चित्रानुसार सात एक जैसी वृत्ताकार समतल डिस्कों, जिनमें प्रत्येक का द्रव्यमान M तथा त्रिज्या R है, को सममित रूप से जोड़ा जाता है। समतल के लम्बवत् तथा P से गुजरने वाली अक्ष के सापेक्ष, इस संयोजन का जड़त्व आघूर्ण है:

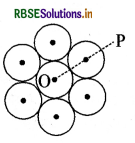
(a) 55/2 MR²
(b) 73/2 MR2
(c) 181/2 MR²
(d) 19/2 MR²
उत्तर:
(c) 181/2 MR²
 

प्रश्न 7. 
R त्रिज्या तथा 9 M द्रव्यमान की एक वृत्तीय चकती से R/3 त्रिज्या की एक छोटी चकती काटी जाती है। चकती के तल के लम्बवत् तथा O से गुजरने वाली अक्ष के परितः शेष चकती का जड़त्व आघूर्ण होगा:

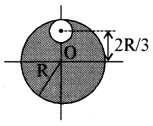
(a) 4MR²
(b) 40/9 MR²
(c) 10MR²
(d) 37/9 MR²
उत्तर:
(a) 4MR²

प्रश्न 8. 
किसी दृढ़ छड़ की लम्बाई I है और उसका द्रव्यमान नगण्य है। इसके दो विपरीत सिरों पर क्रमशः m1 तथा m2 द्रव्यमान के दो बिन्दु पिण्ड रखे गये हैं। इस छड़ को उसके स्वयं के लम्बवत् अक्ष के परितः घूर्णन कराना है, जो छड़ पर स्थित किसी बिन्दु P से होकर गुजरती है (आरेख देखिये) । तो बिन्दु P की वह स्थिति जिसके लिये छड़ को कोणीय वेग 00 से घूर्णन कराने के लिए आवश्यक कार्य न्यूनतम होगा, कौनसी है:


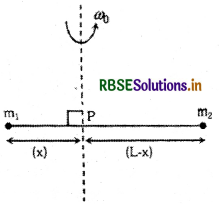
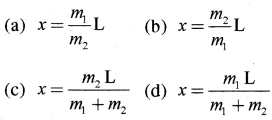
उत्तर:
\(\text { (c) } x=\frac{m_2 \mathrm{~L}}{m_1+m_2}\)

प्रश्न  9. 
किसी ठोस गोले का द्रव्यमान M तथा इसकी त्रिज्या R है। इसमें से अधिकतम सम्भव आयतन का एक क्यूब (घन) काट लिया जाता है। इस क्यूब का जडत्व आघूर्ण कितना होगा, यदि इसका घूर्णन अक्ष इसके केन्द्र से होकर गुजरता है तथा इसके किसी एक फलक के लम्बवत् है:

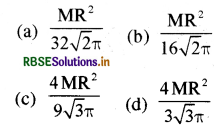
उत्तर:
\(\text { (a) } \frac{\mathrm{MR}^2}{32 \sqrt{2} \pi}\)

प्रश्न 10. 
एक घर्षणहीन बेयरिंग पर एक घिरनी के चारों ओर एक डोरी को लपेट कर द्रव्यमान m लटकाया गया है। घिरनी का द्रव्यमान और त्रिज्या R है। यह मान लें कि घिरनी एक पूर्ण एकसमान वृत्तीय चकती है। यदि डोरी घिरनी पर फिसलती नहीं है, तब द्रव्यमान 1 का त्वरण है:
(a) 3/2g
(b) g
(c) 2/3g
(d) g/3

उत्तर:
(c) 2/3g

प्रश्न 11. 
एक मोटर वाहन किसी सड़क पर 54 kmh की चाल से चल रहा है। इसके पहियों की त्रिज्या 0.45m और घूर्णन अक्ष के परितः का जड़त्व आघूर्ण 3 kgm² है। यदि वाहन 155 में विराम अवस्था में आए तब ब्रेक द्वारा पहिए पर लगा औसत बल आघूर्ण
का मान होगा:
(a) 8.58 kg m²s^-2
(b) 10.86 kg m²s^-2
(c) 2.86 kg m²s²
(d) 6.66 kg m²s²

उत्तर:
(d) 6.66 kg m²s²

प्रश्न 12. 
एक समरूप छड़ AB की लम्बाई । तथा द्रव्यमान 1m है, यह बिन्दु A के परितः घूर्णन के लिए स्वतंत्र है। क्षैतिज स्थिति में विराम से छड़ को छोड़ा जाता है। छड़ का A के परितः जड़त्व आघूर्ण ml²/3 हो तब छड़ का प्रारम्भिक कोणीय त्वरण होगा:

(a) 2g/3l
(b) mg l/2
(c) 3/2gl
(d) 3g/2l
उत्तर:
(d) 3g/2l

प्रश्न 13. 
एक छल्ला जिसका द्रव्यमान M तथा त्रिज्या R है केन्द्र O से होकर जाने वाले स्थिर ऊर्ध्वाधर अक्ष के चारों ओर ω कोणीय गति से घूम रहा है। इस समय पर M/8 द्रव्यमान के दो बिन्दु O द्रव्यमान छल्ले के केन्द्र पर विराम स्थिति में हैं। वे चित्र में दर्शाए अनुसार छल्ले पर लगी द्रव्यमान रहित दो छड़ों के त्रिज्यतः बाहर की ओर गति कर सकते हैं। किसी एक क्षण पर निकाय की कोणीय गति 8/9ω  है तथा एक बिन्दु द्रव्यमान O से 3/5 R की दूरी पर है। इस क्षण दूसरे बिन्दु द्रव्यमान की O से दूरी होगी:

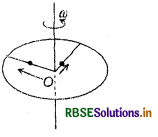
(a) 2/3R
(b) 1/3R
(c) 3/5R
(d) 4/5R
उत्तर:
(d) 4/5R

प्रश्न 14. 
लम्बाई की एक अवितान्य डोरी से बँधे द्रव्यमान 11 के एक बांब को एक ऊर्ध्वाधर आधार से लटकाया जाता है। बाब ऊर्ध्वाधर पर कोणीय चाल ωrad/s से एक क्षैतिज वृत्त में घूर्णन करता है। निलम्बन बिन्दु पर:
(a) कोणीय संवेग संरक्षित रहता है।
(b) कोणीय संवेग परिमाण में परिवर्तनशील है परन्तु दिशा में नहीं
(c) कोणीय संवेग दिशा में परिवर्तनशील है परन्तु परिमाण में नहीं
(d) कोणीय संवेग दोनों दिशा एवं परिमाण में परिवर्तनशील है। 
उत्तर:
(c) कोणीय संवेग दिशा में परिवर्तनशील है परन्तु परिमाण में नहीं

प्रश्न 15. 
घूर्णन करते हुए दो पिण्डों A तथा B के द्रव्यमान क्रमशः m तथा 2m और जड़त्व आघूर्ण क्रमशः IA तथा IB(IB > IA) है। दोनों की घूर्णन गतिज ऊर्जाएँ बराबर हैं। यदि इनके कोणीय संवेग क्रमशः LA तथा LB हों, तब:
(a) LA > LB
(b) LA = LB/2
(c) LA = 2LB
(d) LB > LA
उत्तर:
(d) LB > LA

प्रश्न 16. 
द्रव्यमान M तथा त्रिज्या R का एक ठोस गोला अपने व्यास के परितः घूर्णन कर रहा है। उसी द्रव्यमान तथा उसी त्रिज्या का एक ठोस बेलन (सिलिण्डर) भी अपने ज्यामितीय अक्ष के परितः घूर्णन कर रहा है। बेलन के घूर्णन की कोणीय चाल गोले से दोगुना है। इन दोनों की घूर्णन गतिज ऊर्जाओं का अनुपात 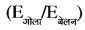होगा:
(a) 3 : 1
(b) 2 : 3
(c) 1 : 5
(d) 1 : 4
उत्तर:
(c) 1 : 5

प्रश्न 17. 
कोई डिरक और कोई गोला, जिनकी त्रिज्याएँ समान परन्तु द्रव्यमान भिन्न हैं, समान उन्नतांश और लम्बाई के दो आनत समतलों पर लुढ़कते हैं। इन दोनों पिण्डों में से तली तक पहले कौन पहुँचेगा:
(a) डिस्क
(b) गोला
(c) दोनों एक ही समय पहुँचेंगे
(d) इनके द्रव्यमानों पर निर्भर करता है।
उत्तर:
(b) गोला

प्रश्न 18. 
एक ठोस गोला लोटन गति में है। लोटन गति में वस्तु की स्थानान्तरीय गति ऊर्जा (Kt) के साथ-साथ घूर्णी गतिज ऊर्जा (Kr) भी होती है। गोले के लिए K t : (Kf + Kr) का अनुपात होगा:
(a) 7 : 10
(b) 5 : 7
(c) 10 :  7
(d) 2 : 5
उत्तर:
(b) 5 : 7

प्रश्न 19. 
एक समतल को पोंछे से साफ करने की एक मशीन द्वारा R त्रिज्या के पोंछे को कुल ऊर्ध्वाधर बल F से दबाकर उसे उसकी अक्ष के परितः एक नियत कोणीय गति से घुमाया जाता है। यदि बल F पोंछे पर एकसमान वितरित है तथा पोंछे तथा समतल के बीच घर्षण गुणांक है, तो मशीन द्वारा पोंछे पर लगाया गया बल आघूर्ण होगा:
(a) 2/3 μ FR
(b) μ FR/3
(c) μ FR/2
(d) μ. FR/6
उत्तर:
(a) 2/3 μ FR

प्रश्न 20. 
एक द्रव्यमान रहित तथा 3l की छड़ पर दो द्रव्यमान चित्रानुसार उसके सिरों पर लगाये हैं तथा उसे एक क्षैतिज अक्ष पर बिन्दु P से कीलकित किया जाता है। जब इस छड़ को क्षैतिज अवस्था से छोड़ा जाता है तो उसका तात्क्षणिक कोणीय त्वरण होगा:

(a) g/2l
(b) 7g/3l
(c) g/13l
(d) g/3l
उत्तर:
(c) g/13l

प्रश्न 21. 
चित्रानुसार 20g द्रव्यमान के एक कण को 5 m/s व वक्र के अनुगत प्रारम्भिक वेग से बिन्दु A से छोड़ा जाता है। बिन्दु A की बिन्दु B से ऊँचाई /1⁄2 है। यह कण घर्षणहीन पृष्ठ पर सरकता है। जब कण बिन्दु B पर पहुँचता है, तो इसका बिन्दु O के सापेक्ष कोणीय संवेग क्या होगा:

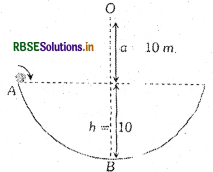
(a) 8kgm/s
(b) 6kgm²/s
(c) 3kgm²/s
(d) 2kgm²/s
उत्तर:
(b) 6kgm²/s

प्रश्न 22. 
द्रव्यमान M तथा लम्बाई L की एक पतली छड़ कोणीय चाल ω₀ से छड़ के लम्बवत् तथा उसके केन्द्र से जाने वाली अक्ष के परितः स्वतंत्र रूप से घूम रही है। द्रव्यमान m तथा नगण्य आकार की दो मणिकायें आरम्भ में छड़ के केन्द्र पर है। यह मणिकायें छड़ पर चलने को स्वतंत्र हैं। मणिकायें जब छड़ के विपरीत सिरों पर पहुँचती है, तो इस विन्यास की कोणीय चाल होगी:

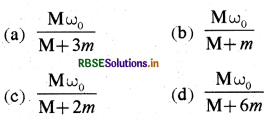
उत्तर:
\(\text { (a) } \frac{\mathbf{M} \omega_0}{\mathbf{M}+3 m}\)

प्रश्न 23. 
द्रव्यमान M तथा त्रिज्या R के एक ठोस गोले को दो असमान हिस्सों में बाँटा जाता है। 7M/8 द्रव्यमान के पहले हिस्से को एक 2R त्रिज्या की एकसमान डिस्क में बदला जाता हैं। बचे हुए हिस्से से एक एकसमान ठोस गोला बनाया जाता है। मानाकि l1, डिस्क का उसकी अक्ष के परितः जड़त्व आघूर्ण है तथा l2 नये गोले का उसके अक्ष के परितः जड़त्व आघूर्ण है। अनुपात I1/I2 होगा:
(a) 185
(b) 65
(c) 285
(d) 140
उत्तर:
(d) 140

प्रश्न  24. 
द्रव्यमान (mass) mm के एक कण की स्थितिज ऊर्जा (potential energy) V(r) = kr²2 है, जहाँ point) O से कण की दूरी है एक नियत बिन्दु (fixed और k उचित विमाओं (dimensions) वाला एक धनात्मक नियतांक (positive constant) है। यह कण बिन्दु O के सापेक्ष R त्रिज्या वाली एक वृत्तीय कक्षा (circular orbit) में घूम रहा है। यदि कण की चाल है और L बिन्दु Q के सापेक्ष इसके कोणीय संवेग (angular momentum) का परिमाण (magnitude) है, तो निम्नलिखित कथनों में से कौनसा (से) सही हैं (हैं):

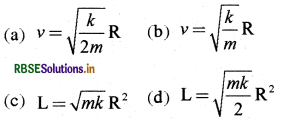
उत्तर:
\(\text { (b) } v=\sqrt{\frac{k}{m}} \mathrm{R}\)

प्रश्न  25. 
10 kg द्रव्यमान ( mass) की एक वस्तु समय t = 0 पर मूल बिन्दु (origin) पर विरामावस्था में हैं। इस वस्तु पर एक बल \(\overrightarrow{\mathrm{F}}=(\alpha t \hat{i}+\beta \hat{j})\) लगाया जाता है, जहाँ α = 1.0 Ns^-1 और β = 1.0 N हैं। समय t = 1.05 पर मूलबिन्दु के सापेक्ष वस्तु पर लगने वाला बल आघूर्ण (torque) T है। निम्नलिखित कथनों F में से कौनसा (से) सही हैं (हैं):
\(\text { (a) } \vec{\tau}=\frac{1}{3} \mathrm{Nm}\)
(b) बल आघूर्ण \(\vec{\tau}\) मात्रक सदिश (unit vector) + दिशा में है
(c) समय t = 1s पर वस्तु का वेग v = imm\(\vec{v}=\frac{1}{2}(\hat{i}+2 \hat{j}) \mathrm{ms}^{-1}\) है
(d) समय t = 1s पर वस्तु के विस्थापन का परिमाण 1/6cm है
उत्तर:
\(\text { (a) } \vec{\tau}=\frac{1}{3} \mathrm{Nm}\)

प्रश्न  26. 
एक वृत्ताकार वलय (ring) और एक वृत्ताकार चकती (disc), एक आनत तल (inclined plane) के शीर्ष पर अगल-बगल (side by side) विरामावस्था में हैं। आनत तल, क्षैतिज तल (horizontal plane) से 60° का कोण बनाता है। दोनों वस्तुएँ एक ही पल; न्यूनतम दूरी वाले पथ पर बिना फिसले लोटना (rolling without slipping) आरम्भ करती हैं। यदि दोनों वस्तुओं का क्षैतिज तल पर पहुँचने का समयान्तर imm हो, तो आनंत तल के शीर्ष की ऊँचाई मीटर है। (g = 10ms2 लें।  
उत्तर:
6.0

प्रश्न  27. 
एक I लम्बाई का दृढ़ दंड AB अपनी ऊर्ध्वाधर स्थिति से घर्षणहीन अनुभूमिक तल पर चित्रानुसार फिसल रहा है। समय के किसी क्षण पर दंड ऊर्ध्वाधर से बनाया कोण θ है। निम्न में से कौनसा (से) प्रकथन सही है/हैं

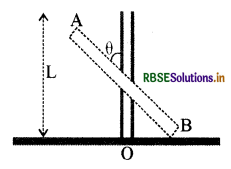
(a) बिन्दु A का प्रपथ परवलयिक है
(b) दंड और भूतल के स्पर्श बिन्दु के चारों तरफ तात्क्षणिक बल आघूर्ण sin 9 के समानुपाती हैं
(c) जब दंड ऊर्ध्वाधर से 0 कोण बनाता है तब दंड के मध्य बिन्दु का विस्थापन उसके आरम्भिक स्थिति (1 समानुपाती है)
(d) दंड का मध्य बिन्दु ऊर्ध्वाधर की ओर गिरेगा
उत्तर:
(c) जब दंड ऊर्ध्वाधर से 0 कोण बनाता है तब दंड के मध्य बिन्दु का विस्थापन उसके आरम्भिक स्थिति (1 समानुपाती है)

Passage-I
ऊर्ध्वाधर धुरी पर दो चकती A तथा B को समाक्ष रूप से लगाया गया है। चकती के जड़त्व आघूर्ण, उभयनिष्ठ अक्ष के परितः क्रमशः I तथा 2I है। स्प्रिंग को x दूरी तक सम्पीड़ित करने से प्राप्त सम्पूर्ण स्थितिज ऊर्जा से चकती A प्रारम्भिक कोणीय वेग 20 प्राप्त करती है। समान स्प्रिंग नियतांक की स्प्रिंग को x दूरी तक सम्पीड़ित करने से चकती B कोणीय वेग 0 प्राप्त करती है। दोनों चकतियाँ दक्षिणावर्त दिशा में घूर्णन करती है।
प्रश्न  28. 
उपरोक्त प्रक्रम में गतिज ऊर्जा का क्षय है:

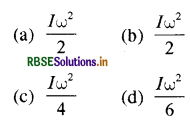
उत्तर:
\(\text { (b) } \frac{I \omega^2}{2}\)

प्रश्न  29. 
जब चकती B को चकती A के सम्पर्क में किया जाता है, तब वे समय t में उभयनिष्ठ कोणीय वेग प्राप्त कर लेती है। इस समय 1 अन्तराल में एक चकती द्वारा दूसरी से प्राप्त औसत घर्षण बल आघूर्ण है:

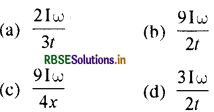
उत्तर:
\(\text { (a) } \frac{2 \mathrm{I} \omega}{3 t}\)

प्रश्न  30. 
अनुपात x1/x2 है:
(a) 2
(b) 1/2
(c) √2
(d) 1/√2
उत्तर:
(c) √2