RBSE Class 11 Physics Important Questions Chapter 7 System of Particles and Rotational Motion

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 7 System of Particles and Rotational Motion Important Questions and Answers.

RBSE Class 11 Physics Chapter 7 Important Questions System of Particles and Rotational Motion

Multiple Choice Questions

Question 1.
Main cause of motion of the centre of mass is
(a) mutual force
(b) nuclear force
(c) external force
(d) none of these
Answer:
(c) external force

Question 2.
Length of a wire is L and its mass is M. It is coverted in a circular ring. Its moment of inertia about its geometric axis is
(a) \(\frac{M L^2}{8 \pi^2} \)
(b) 8π² ML²
(c) \(\frac{M L^2}{4 \pi^2}\)
(d) π² ML²
Answer:
(c) \(\frac{M L^2}{4 \pi^2}\)

Question 3.
Centre of mass is the point with respect to which the following quantity is zero?
(a) moment of angle
(b) moment of force
(c) moment of mass
(d) weight
Answer:
(c) moment of mass

Question 4.
Centre of mass is always the point:
(a) which is geometrical centre of the body
(b) distance of all particles from where is same
(c) where the whole mass of the body is supposed to be centralised
(d) which is the origin of frame of reference
Answer:
(c) where the whole mass of the body is supposed to be centralised

Question 5.
Distance of H atom in HCl molecule is x from the centre of mass, then distance of Cl³⁵ atom from the centre of mass will be:
(a) 35x
(b) x
(c) \(\frac{36 x}{35}\)
(d) \(\frac{x}{35}\)
Answer:
(d) \(\frac{x}{35}\)

Question 6.
In absence of external force, the quantity attached with the centre of mass remains constant is:
(a) velocity
(b) acceleration
(c) position
(d) none of these
Answer:
(a) velocity

Question 7.
Radius of a rotating disc is suddenly halved but mass remains unchanged, then its angular velocity will be:
(a) two times
(b) half
(c) four times
(d) unchanged
Answer:
(c) four times

Question 8.
z-component of the angular momentum will be in form:
(a) L_z = xp_y - yp_x
(b) L_z = yp_y - xp_x
(c) L_z = yp_x - xp_y
(d) L_z = x.p_x - yp_x
Answer:
(a) L_z = xp_y - yp_x

Question 9.
In revolution of planets, the quantity which remains constant, is:
(a) gravitational force
(b) centripetal force
(c) angular momentum 
(d) angular acceleration
Answer:
(c) angular momentum 

Question 10.
Work done in rotational motion, is:

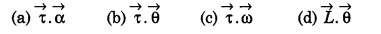
Answer:
(b) \(\vec{\tau} \cdot \vec{\theta}\)

Question 11.
The quantity which remains constant in central force, is:
(a) linear momentum
(b) angular momentum
(c) kinetic energy
(d) potential energy
Answer:
(b) angular momentum

Question 12.
Two point masses m₁ and m₂ under influence of mutual gravitational attraction. If there is no other force in action, then which of following will remain conserved?
(a) only linear momentum
(b) only angular momentum
(c) both linear and angular momentum
(d) none of above
Answer:
(c) both linear and angular momentum

Question 13.
If the distances of two masses m₁ and m₂ from centre of mass are r₁ and r₂, then value of \(\frac{r_1}{r_2}\) will be:

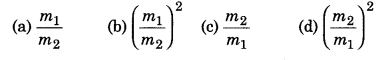
Answer:
(c) \(\frac{m_2}{m_1}\)

Question 14.
If the position vectors of two masses of 10 kg and 30 kg are (\(\hat{i} + \hat{j} + \hat{k}\)) and (\(-\hat{i} -\hat{j} -\hat{k}\)), then the centre of mass will be:

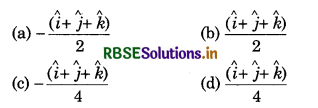
Answer:
(a) \(-\frac{(\hat{i}+\hat{j}+\hat{k})}{2}\)

Question 15.
Product of moment of inertia and angular acceleration is called:
(a) angular momentum
(b) moment of force
(c) force
(d) work
Answer:
(b) moment of force

Question 16.
J.s is unit of:
(a) power
(b) angular momentum
(c) torque
(d) linear momentum
Answer:
(b) angular momentum

Question 17.
Radius of gyration of disc about its own axis is:
(a) R/2
(b) R/\(\sqrt{2}\)
(c) R
(d) R\(\sqrt{2}\)
Answer:
(b) R/\(\sqrt{2}\)

Question 18.
A wire of length l and mass m is bent in form of semi-circle. Moment of inertia of this semi-circle about the line (axis) joining its free ends will be:

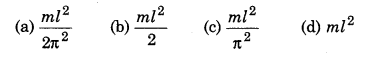
Answer:
(a) \(\frac{m l^2}{2 \pi^2}\)

Question 19.
First time a ring slips without rolling on an inclined plane and second time it rolls down without slipping. The ratio of accelerations produced in both situations will be:
(a) 1:1
(b) 2:1
(c) 1:2
(d) 4:1
[Hint: Ratio of accelerations in given situations:
\(\frac{a_1}{a_2}=\frac{\frac{g \sin \theta}{g \sin \theta}}{1+\frac{K^2}{R^2}}=1+\frac{K^2}{R^2}\)
For ring I = MK² = MR² ⇒ \(\frac{K^2}{R^2}\) = 1
∴ \(\frac{a_1}{a_2}\) = 1 + 1 = 2
∴ a₁ : a₂ = 2 : 1
Thus option (b) is correct.]
Answer:
(b) 2:1

Question 20.
Diameter of a thin hollow cylinder is 0.3 m and is allowed to roll freely on an inclined plane of height 2 m. Its linear velocity at the bottom of the plane will be:
(a) 2g
(b) \(\sqrt{2g}\)
(c) g/2
(d) \(\frac{3g}{10}\)
Answer:
(b) \(\sqrt{2g}\)

Question 21.
In absence of external force, velocity of the centre of mass:
(a) is zero
(b) will remain constant
(c) will increase
(d) will decrease
Answer:
(b) will remain constant

Question 22.
Which of following quantities remains constant in planetary motion?
(a) kinetic energy
(b) potential enrgy
(c) linear momentum
(d) angular momentum
Answer:
(d) angular momentum

Question 23.
Moment of inertia of a solid sphere about its diameter is I, then its moment of inertia about its tangent will be:

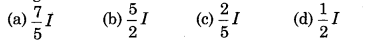
Answer:
(a) \(\frac{7}{5}\) I

Question 24.
Two rings of radii 1 m and 5 m start rolling on an inclined plane without slipping. Which ring will reach on ground first?
(a) big ring
(b) small ring
(c) both at the same time
(d) nothing can be said.
Answer:
(c) both at the same time

Fill in the blanks:

Question 1.
The moment of inertia of a solid cylinder of mass m, length (l) and radius r is ........................
Answer:
\(\frac{1}{2}\)mr²

Question 2.
The radius of gyration of a uniform circular disc of radius R., about any diameter of the disc is ........................
Answer:
K = \(\frac{R}{2}\)

Question 3.
The rotational angular of force is ........................
Answer:
torque

Question 4.
The moment of linear momentum called is ........................
Answer:
Angular momentum

Question 5.
Angular velocity of minute hand of a clock in radian/sec is ........................
Answer:
π/1800

Very Short Answer Questions

Question 1.
Is the radius of gyration of a body constant quantity?
Answer:
No; on changing the axis of rotation, radius of gyration also changes.

Question 2.
A disc is made by melting a sphere. Moment of inertia of which will be more?
Answer:
Moment of inertia of disc will be more.

Question 3.
Write the conditions for equilibrium of a body.
Answer:
∑F = 0 and ∑τ = 0

Question 4.
Write the expression of a diatomic molecule.
Answer:
I = \(\frac{m_1 m_2}{m_1+m_2}\).r²

Question 5.
What is the meaning of positive torque and negative torque?
Answer:
If the force tends to rotate the body about the axis of rotation in anticlockwise direction, then torque is called positive. On the other hand if the force tends to rotate the body about the axis of rotation in clockwise direction, then torque is called negative.

Question 6.
Does the centre of mass and centre of gravity coincide?
Answer:
Both coincide in body of uniform mass density.

Question 7.
If \(\vec{A}.\vec{B}\) = |\(\vec{A}\) x \(\vec{B}\)|, find the angle between \(\vec{A}\) and \(\vec{B}\).
Answer:
∵ \(\vec{A}.\vec{B}\) = |\(\vec{A}\) x \(\vec{B}\)|
∴ ABcosθ = ABsinθ
⇒ tanθ = 1 ⇒ θ = 45° or π/4 rad

Question 8.
Why the handle of screw driver is made wide?
Answer:
Moment of force τ = F x r. When r is more then for small value of F, τ can be obtained more. This is why the handle of screw driver is made wide.

Question 9. 
Whether the angular welocity of particles of a rotating body is same or different?
Answer:
Angular velocity of all particles is same.

Question 10.
Can a body roll on a smooth surface?
Answer:
No; the body will slip. For rolling motion friction is must.

Question 11.
Among the solid and hollow bodies of same mass, same radius and same size, which will have more moment of inertia?
Answer:
Hollow body will have more moment of inertia.

Question 12.
A body is rotating. Is certainly acting a torque on it?
Answer:
Not necessary; because no torque is required for angular acceleration.

Question 13.
On what factors depends the moment of inertia of a body?
Answer:
(i) On axis of rotation
(ii) On the distance of mass from axis of rotation.

Question 14.
Is the centre of mass a reality?
Answer:
No; it is only a mathematical concept.

Question 15.
Can angular momentum be in linear motion?
Answer:
Yes.

Question 16.
If the radius of earth be reduced, what will be its effect on the duration of day?
Answer:
On reducing the radius of earth, its moment of inertia will decrease. Therefore according to L = Iω, the value of ω will increase, hence T = \(\frac{2 \pi}{\omega}\) will decrease. Therefore duration of the day will decrease.

Question 17.
About which axis, the moment of inertia of a body is minimum?
Answer:
The moment of inertia of a body is minimum about the axis passing through its centre of mass.

Question 18.
When a body is rotating, then in which situation, there will be no torque in action?
Answer:
When the line of action of force passes through axis of rotation, then no torque act on the rotating body.

Question 19.
A person is sitting on a rotating chair with his arms extended what will happen if he closes his arms?
Answer:
On closing his arms, his moment of inertia will decrease, therefore according the of conservation of angular momentum (L = I.ω = constant), his angular velocity of rotation will increase.

Question 20.
Cap of a pen is opened easily with the help two fingers, not by only one finger, why?
Answer:
Forces applied by two fingers form a couple of forces, which is required for opening the cap of a pen. On the other hand one finger can not produce couple of forces.

Question 21.
Can the location of centre of mass be outside the body?
Answer:
Yes; for example the centres of mass of a ring, hollow cylinder; hollow sphere etc. are not on the body.

Question 22.
The wheels of vehicles are made hollow at centre and thick at circumference; why?
Answer:
On doing so, the moment of inertia of the wheel increase and hence amount of rotational energy ER = \(\frac{1}{2}\) Iω² increases and it behaves as flywheel.

Question 23.
Does the value of moment of inertia of a body depend on its angular velocity?
Answer:
No.

Question 24.
Internal and external radii of a hollow cylinder of mass m and length l are R₁ and R₂. Write the expression for its moment of inertia about an axis passing through its centre and normal to its length.
Answer:
I = m[\(\frac{l^2}{12}+\frac{R_1^2+R_2^2}{4}\)]

Question 25.
Moment of inertia of a homogeneous square shaped plate about axis AB is I. What will be its moment of inertia about axis CD lying in its plane?

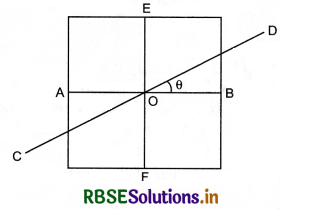
Answer:
Moment of inertia about axis CD will also remain I because moment of inertia of a plate about all axes lying in its plane remains same.

Question 26.
What type of motion is produced by torque?
Answer:
Only rotational motion is produced by torque.

Question 27.
Why the spokes are used in bicycle wheels?
Answer:
Spokes are used in bicycle wheels to increase the moment of inertia of the wheels.

Question 28.
A man is sitting at the circumference of a rotating table. Suddenly he starts moving to the centre what will be its effect?
Answer:
Due his motion, the moment of inertia will decrease, hence angular velocity will increase according to conservation law of angular momentum.

Question 29.
What is the situation of centre of mass of a triangular lamina?
Answer:
Centre of mass of a triangular lamina is the piont of intersection medians of the arms of the lamina.

Question 30.
Mass of a rectangular lamina is M; its length is l and width is b. What will be its moment of inertia about the axis passing through the centre of lamina and normal to its plane?
Answer:
I = M[\(\frac{l^2+b^2}{12}\)]

Question 31.
Match the following question:
The following bodies are rolling without slipping with a velocity (v). Each has a mass m. Their total K.E. is:

Column-I	Column-II
(a) Hollow cylinder	(p) \(\frac{7}{10}\)mv2
(b) Solid cylinder	(q) \(\frac{5}{6}\)mv2
(c) Hollow sphere	(r) mv2
(d) Solid sphere	(s) \(\frac{3}{4}\)mv2

Answer:

Column-I	Column-II
(a) Hollow cylinder	(r) mv2
(b) Solid cylinder	(s) \(\frac{3}{4}\)mv2
(c) Hollow sphere	(q) \(\frac{5}{6}\)mv2
(d) Solid sphere	(p) \(\frac{7}{10}\)mv2

Question 32.
Match the following:

Column-I	Column-II
(a) Moment of inertia	(p) Mass
(b) Radius of gyration	(q) Size and shape
(c) Angular momentum	(r) Angular velocity
(d) Kinetic energy of rotation	(s) Position of axis of rotation

Answer:

Column-I	Column-II
(a) Moment of inertia	(p) Mass (q) Size and shape (s) Position of axis of rotation
(b) Radius of gyration	(q) Size and shape (s) Position of axis of rotation
(c) Angular momentum	(p) Mass (q) Size and shape (r) Angular velocity (s) Position of axis of rotation
(d) Kinetic energy of rotation	(p) Mass (q) Size and shape (r) Angular velocity (s) Position of axis of rotation

Short Answer Questions

Question 1.
A solid sphere is rolling on an inclined plane. What will be the percentage of its rotational energy in its total energy?
Answer:
Rotational energy of the sphere
E_R = \(\frac{1}{2}\)Iω²
Total energy:

Question 2.
Thickness and mass of two circular discs A and B are same. Density of A is two times that of B. What will be ratio of moment of inertia of A and B about their own axes?
Answer:
Moment of inertia of a disc is

Question 3.
Three rings of mass M and radius R each, are arranged in triangular shape. Find the moment of inertia of this system about axis YY'.
Answer:
Moment of inertia of ring 1 about YY' axis = moment of inertia of ring about tangential axis lying in the plane of the ring

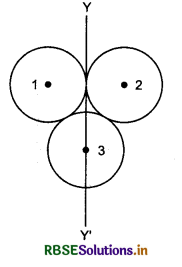
∴ I₁ = \(\frac{3}{2}\)MR²
Similarly that of ring 2,
I₂ = \(\frac{3}{2}\) MR²
Moment of inertia of ring -3 about YY' axis = Moment of inertia about the diameter of the ring
or I₃ = \(\frac{1}{2}\) MR²
∴ Moment of inertia of the whole system
I = I₁ + I₂ + I₃
= \(\frac{3}{2}\)MR² + \(\frac{3}{2}\)MR² + \(\frac{1}{2}\)MR²

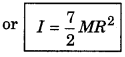
Question 4.
A particle of mass m is moving with velocity v in x-direction. When the particle is at point (x, y, z), then find the components of angular momentum about origin.
Answer:
Position vector of the particle,
\(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\)
and velocity vector,
\(\vec{b}=v \hat{i}\)
∴ Angular momentum

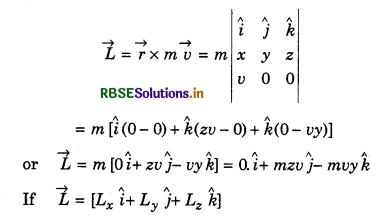
Then L_x = 0; L_y = mzv; L_z = -mvy

Question 5. 
What is relation between moment of inertia and radius of spheres of same substance?
Answer:
Moment of inertia of a solid sphere

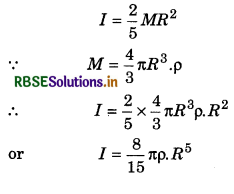
∵ \(\frac{8}{15}\) πρ = Constant
∴ I ∝ R⁵

Question 6.
Solid spheres of same mass are made of different substances. What will be relation between their moment of inertia and their density d?
Answer:
Moment of inertia of solid sphere

Question 7.
Two masses m₁ and m₂ are placed at the ends of a weightless rod of length r. Find the moment of inertia of this system about the axis passing through the centre of mass and perpendicular to length of the rod.
Answer:
Suppose the distance of masses m₁ and m₂ from centre of mass are r₁ and r₂. Therefore from the definition of centre of mass,

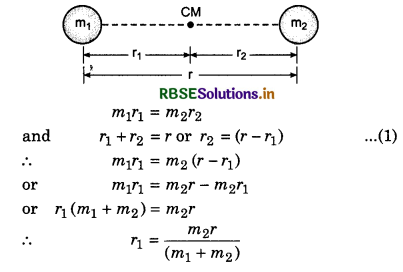
Substituting this value of x₁ in equation (1)
r₂ = r₁ - \(\frac{m_2 r}{\left(m_1+m_2\right)}=\frac{m_1 r+m_2 r}{m_1+m_2}-m_2 r\)
or r₂ = \(\frac{m_1 r}{m_1+m_2}\)
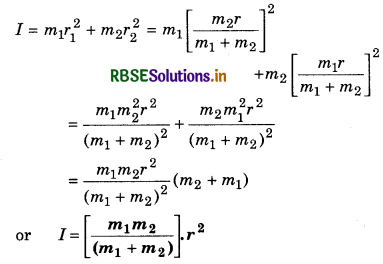
∴ Moment of inertia about axis passing through CM. at right angles to the length of the rod

Question 8.
Why two propellers are used in helicopter?
Answer:
On using only propeller in helicopter, it will not raise up and it will start rotating in opposite direction to that of propeller. This is why two propellers are used in helicopter.

Question 9.
A disc of wax is melted and is given a shape of solid sphere. What will be its effect on moment of inertia about common axis?
Answer:
Moment of inertia will decrease.

Question 10.
Two spheres one solid and other hollow of same mass and same radius, are rotated with same angular velocities. Which sphere will come at rest first?
Answer:
Solid sphere; because its moment of inertia will be less than that of hollow sphere, there it will oppose rotational motion less than that by hollow sphere.

Question 11.
A symmetrical lamina of mass M is made of a square of side 2a and a semi-circular construction on each arm figure. Moment of inertia of lamina about an axis passing through its centre of mass and at right angles to its plane is 1.6 Ma². What will be its moment of inertia about tangential axis AB lying in plane of the lamina?
Answer:
Given: Moment of inertia about an axis passing through centre of mass and normal to plane

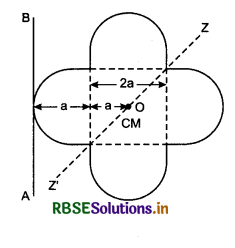
I_zz' = 1.6 Ma²
According to the theorem of perpendicular axes,
I_zz' = I_cm + I_cm = 2I_cm
where I_cm is moment of inertia of lamina about two perpendicular axes passing through the centre of mass and lying in plane of lamina.
∴ I_cm = \(\frac{1}{2}\)I = \(\frac{1.6 M a^2}{2}\) = 0.8 Ma²
Now according to theorem of parallel axes,
I_AB = I_cm + M(2a)²
= 0.8 Ma² + 4 Ma²
I_AB = 4.8 Ma²

Question 12.
Three masses m₁, m₂ and m₃ are situated at the vertexes of a equilateral triangle of arm a. Find the moment of inertia of this system about the median passing through m₁.
Answer:
In figure, ABC is an equilateral triangle of arm length ‘a’. We have to find the moment of inertia of the system about median AD.
∴ Distance of m₁ from AD, r₁ = O
Distance of m₂ and m₃ from AD,
r₂ = a/2 and r₃ = \(\frac{a}{2}\)

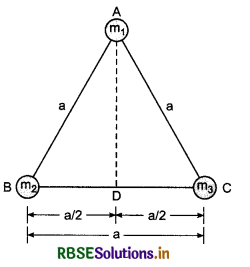
∴ Moment of inertia of the system,

Question 13.
Give the definition of angular momentum and write its unit. Prove that the rate of change of angualr momentum is equal to torque applied.
Answer:
Continuous body can be supposed to be made of nfinite small mass particles. In this reference, mass ecomes very small and can be represented by dm. If m be the total mass of the body then:
\(\sum_{i=1}^{\infty} m_i=M \text { and } \sum_{i=1}^{\infty}\left(m_i x_i\right)=\int x d m\)
Thus, the co-ordinates of the centre of mass can be written as under

In terms of position vector, these relations can be written by:
\(\vec{r}_{c m}=\frac{1}{M} \int \vec{r}_1 d m \text { or } \frac{\int \vec{r}_1 d m}{\int d m}\)

Torque and angular momentum for system of particles: To determine the angualr momentum of system of prtic1es we take the vector sum of angular momentums of the individual particles i.e.,

Total torque acting on a particle is sum of torques due to internal and external forces.
∴ \(\vec{\tau}=\vec{\tau}_{\mathrm{int}}+\vec{\tau}_{\mathrm{ext}}\)
where \(\overrightarrow{\tau_{\text {int }}}=\Sigma \overrightarrow{r_i} \times \vec{F}_{\text {int }}\)
and \(\vec{\tau}_{\mathrm{ext}}=\Sigma \overrightarrow{r_i} \times \vec{F}_{\mathrm{ext}}\)
According to Newton's third law, the contribution of torque due to the internal forces will be zero i.e.,
\(\vec{F}_{\text {int }}=0 \text { therefore } \vec{\tau}_{\text {int }}=0\)
∴\(\vec{\tau}=\overrightarrow{\tau_{\mathrm{ext}}} \text { or } \frac{\overrightarrow{d L}}{d t}=\vec{\tau}_{\mathrm{ext}}\)
Thus, rate of change of angular momentum of a system of particles is equal to vector sum of torques due to the external forces.

Question 14.
Prove that θ = ω₀t + \(\frac{1}{2}\)αt²
Answer:
Pure rotation dynamics around static axis: The quantities which are used in pure rotational dynamics are angular displacement θ, angular velocity ω, angular acceleration α. These quantities are corresponding to linear displacement x, linear velocity v and linear acceleration a in the translatory motion.
Therefore equations of motion in rotational motion corresponding to equations of motion in translatory motion are:
ω = ω₀ + α.t .......................(1)
θ = θ₀ + ω₀t + \(\frac{1}{2}\)α.t .....................(2)
ω² = ω₀² + 2α(θ - θ₀) ......................(3)
Proof: First equation:
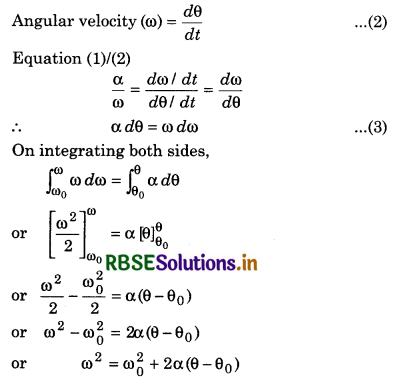
Angular acceleration, α = \frac{d \omega}{d t}
or dω = αdt
On integrating both the sides,
\(\int_{\omega_0}^\omega d \omega=\int_0^t \alpha d t\)
or \([\omega]_{\omega_0}^\omega=\alpha[t]_0^t\)
or ω - ω₀ = α(t - 0)
or ω = ω₀ + αt
Second equation: Angular velocity
ω = \(\frac{d \theta}{d t}\)
or dθ = ωdt
On integrating both sides

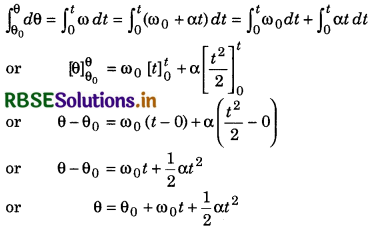
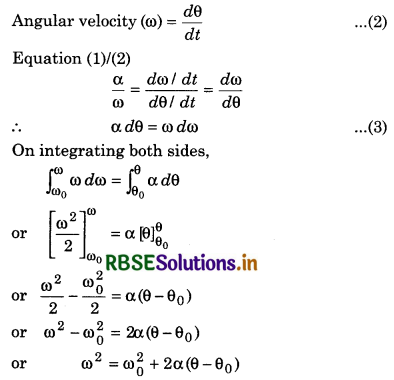
Third equation: Angular acceleration
(α) = \(\frac{d \omega}{d t}\) ..........................(1)

Question 15.
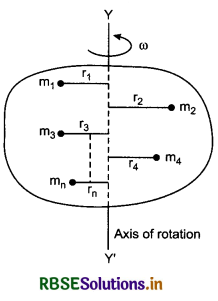
Find the expression for moment of inertia of a body and its radius of gyration.
Answer:
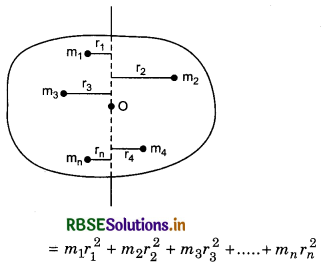
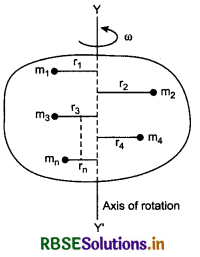
A rigid body can be supposed to be made of many small particles. The moment of inertia of the rigid body is obtained by the sum of moment of inertias of indivdual particles i.e.,
I = I₁ + I₂ + I₃ + ............... + I_n

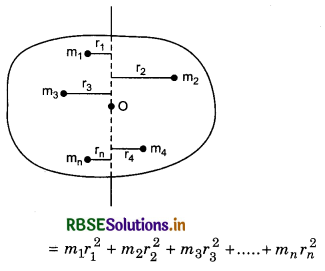
where m₁, m₂, m₃, ......................., m_n are the masses of the particles of rigid body and their distances from the axis of rotation are r₁, r₂, r₃, ....................., r_n respectivley as shown in fig. 7.28

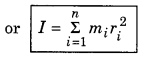
Moment of inertia of a rigid body can be obtained by
I = m₁r₁² + m₂r₂² + m₃r₃² + .................... + m_nr_n²
This method is pure theoretical but practically it is very difficult, say rather impossible. Therefore to obtain moment of inertia of a rigid body, we consider a point in the body where all the mass of the body is considered centralised such that the square of its distance from the axis of rotation when multiplied with the mass of the body, then moment of inertia is obtained. This distance is called the ‘radius of gyration’ and it is denoted by K.
∴ I = MK²
or K = \(\sqrt{\frac{I}{M}}\) ........................(1)
If the body is supposed to be made of n particles, then
I = m₁r₁² + m₂r₂² + m₃r₃² + ..................... + m_nr_n²
And M = m₁ + m₂ + m₃ + .................. + m_n
∴ K = \(\sqrt{\frac{m_1 r_1^2+m_2 r_2^2+\ldots \ldots+m_n r_n^2}{m_1+m_2+\ldots . .+m_n}}\) ........................(2)
If mass of each particle be m, i.e.,
m₁ = m₂ = m₃ = ....................... = m_n
Then M = m + m + ........................... + m(n times)
or M = mn ........................(3)

Question 16.
Write the principle of conservation of angular moment giving one example.
Answer:
We know that rate of change of angular momentum is equal to the torque applied i.e.,
\(\frac{d L}{d t}\) = τ
If external torque is zero, i.e., τ = 0
the \(\frac{d L}{d t}\) = 0
or L = constant

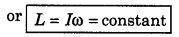
i.e., "In absence of external torque the angular momentum of a body remains unchanged or constant." This is the principle of conservation of angular momentum.

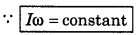
Therefore on decreasing the value of I, angular velocity increases and vice-versa.
∴ I₁ω₁ = I₂ω₂
Example:
When a person rotates sitting on a rotating stool, then as he opens his hands away from his body his angular velocity decreases and as he starts closing his hands again, his angular velocity of rotation goes on increasing. Above fact can be explained on the basis of law of conservation of angular momentum according to which,

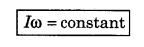
As the person opens his hands his moment of inertia increases, hence angular velocity ω decreases and hence vice-versa.

Question 17.
Give the statement and proof of theorem of perpendicular axes relating moment of inertia.
Answer:
Suppose, we have a circularring of radius R and mass M. We have to find its moment of inertia about axis YY' which is normal to the plane of the ring and passes through the centre O. This axis is also known as the geometric axis of the ring.
Circumference of the ring = 2πR

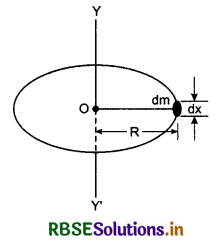
∴ Mass of the ring per unit length = \(\frac{M}{2 \pi R}\)
∴ Mass of a small element of the circle of length dx,
dm = \(\frac{M}{2 \pi R}\) dx
∴ Moment of inertia of this element about the axis YY',
dI = dmR² = \(\frac{M}{2 \pi R}\) dx R²
or dI = \(\frac{M R}{2 \pi}\) dx
∴ Moment of inertia of the whole ring about the axis YY',

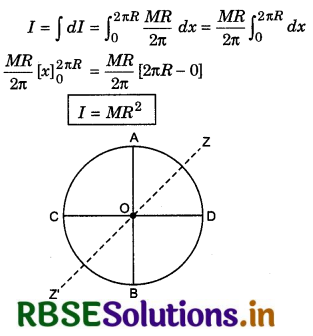
1. Moment of inertia about the diameter of the ring:
In fig. 7.33, two cross diameters AB and CD are shown. We have to find the moment of inertia of the ring about the diameter AB or CD. Moment of inertia of the ring about ZZ' axis
I_z = MR² ..........................(1)
Now according to the theorem of the perpendicular axes of moment of inertia,
I_z = I_AB + I_CD = I_d + I_d
or I_z = 2I_d
∴ I_d = \(\frac{I_z}{2}\)
or I_d = \(\frac{1}{2}\) MR²

2. Moment of inertia of the ring about the tangential axis lying in the plane of the ring:
Suppose we have to find the moment of inertia of the ring about the tangential axis PQ.
∴ According to the theorem of parallel axes of the moment of inertia,
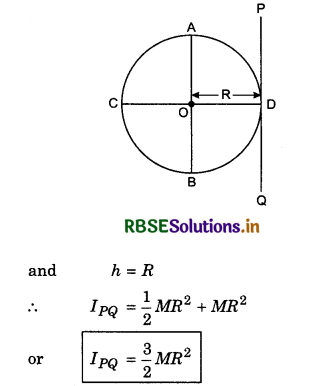
I_PQ = I_cm + Mh²
Here I_cm = I_AB = \(\frac{1}{2}\)MR²

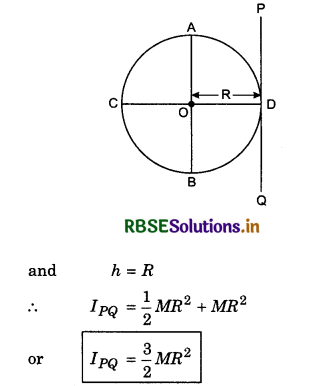
3. Moment of inertia of the ring about the tangential axis at right angles to plane of the ring: We have to find the moment of inertia about the axis PQ which is tangent of the ring at right angles to plane of the ring. Again applying the theorem of parallel axes,

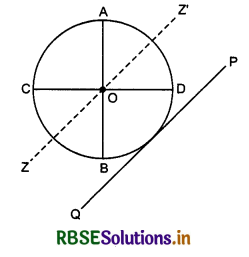
I_PQ = I_cm + Mh²
Here I_cm = I_zz' = MR²
and h = R
∴ I_PQ = MR² + MR²

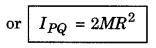
Question 18. 
Given the statement and proof of theorem of parallel axes of moment of inertia.
Answer:
Moment of inertia of the disc about the tangential axis in the plane of the disc: We have to find the moment of inerita of the disc about the tangential axis PQ parallel to the diameter AB. From the theorem of parallel axes,
I_PQ = I_cm + Mh²

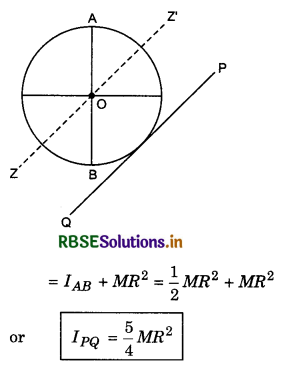
Question 19.
Write the expression for angular momentum and define moment of inertia with the help of this relation.
Answer:
Suppose a rigid body is rotating about an axis YY' with angular velocity ω.

Moment of linear momentum about the axis of rotation is called the angular momentum and it is denoted by L.
∴ L = Moment of linear momentum
= p x r
= mv x r
= mrωr

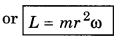
A body can be supposed to be made of n small particles of masses m₁, m₂, m₃, ........................, m_n and distant r₁, r₂, r₃, ....................., r_n from the axis of rotation. Then
L = L₁ + L₂ + ................... + L_n
= m₁r₁²ω + µ₂r₂²ω + .......................... + m_nr_n²ω
= (m₁r₁² + m₂r₂² + ........................ + m_nrn²) ω
= \(\sum_{i=1}^n\) m_iri² ω

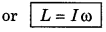
i.e., Angular momentum = Moment of inertia x Angular velocity.
If ω = 1 rads^-1, then L = I
i.e., "moment of inertia of a body about a given axis of rotation is equivalent to its angular momentum which is in the equation of unit angular velocity."

Question 20.
Give the definition of moment of inertia in terms of rotation energy.
Answer:
Work is done to rotate a wheel and rotating wheel can do the work. It means there is kinetic energy in same manner as it is in body under linear motion. Thus the kinetic energy of the body in rotational motion is called the “Rotational kinetic energy” and it is represented by K_rotational or simply K_r.

∴ Rotational kinetic energy
K_r = kinetic energy in rotational motion

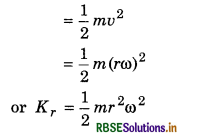
For a big rigid body it can be supposed to be made of n small particles of masses m₁, m₂, m₃, ..........................., m_n situated at distances r₁, r₂, r₃, ................, r_n from the axis of rotation.
Angular velocity of all the particles will be same and in same direction. Therefore sum of rotational kinetic energies of all particles will provide the rotational kinetic energy of the body i.e.,
K_r = K₁ + K₂ + .................... + K_n

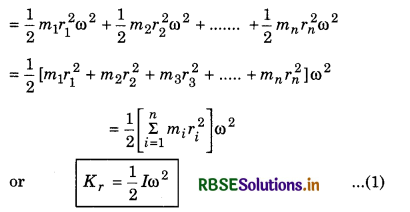
Similarly in translational motion, kinetic energy
K_{translational} = \(\frac{1}{2}\)MV² ..........................(2)
If ω = 1 rad.s^-1, then from equation (1),

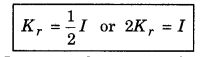
i.e., "Moment of inertia of a body about a given axis of rotation is equivalent to double of its rotational energy which is in equation of unit angular velocity."

Conceptual Questions

Question 1.
A cubical block of arm a is moving on smooth surface with velocity v figure. It strikes a ridge at O. What will be angular velocity of the block after striking the ridge? 

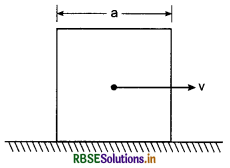
Answer:
From conservation of angular momentum about O,
p x \(\frac{a}{2}\) = I₀ω ........................(1)
Where ω is angular velocity of the block after striking the ridge and I is moment of inertia of the block about axis passing through O and normal to plane of paper.

Question 2.
A solid circular disc of mass m and radius r is lolling on a horizontal plane with anguair velocity ω figure. What will be angular momentum of the disc about origin O?
Answer:
Moment of inertia of the disc about the axis OX. According to the theorem of parallel axes:

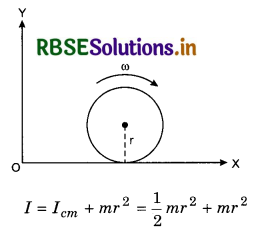
= \(\frac{3}{2}\) mr²
∴ Angular momenutm of the disc about the origin:
L = Iω = \(\frac{3}{2}\) mr²ω

Question 3.
Two circular discs A and B of same mass and sanie thickness, are made of different substances of densities ρ_A and ρ_B (ρ_A > ρ_B). Their moment of inertia about their geometric axes are I_A and I_B respectively. Which will be greater whether I_A or I_B?
Answer:
Moment of inertia of a disc about geometric axis
I = \(\frac{1}{2}\)MR² .....................(1)
If the thickness of the disc be t, then mass of the disc,

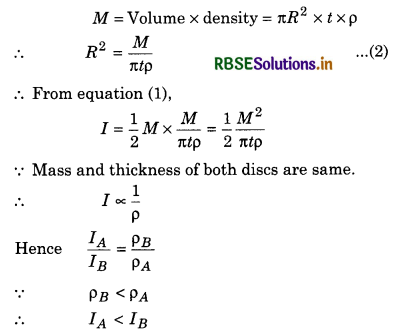
i.e., moment of inertia of disc B will be greater than that of A.

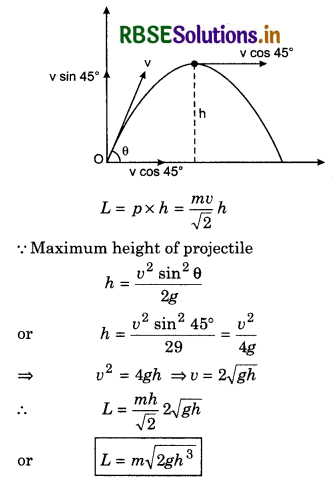
Question 4.
A particle of mass m is projected with velocity v at cm angle of projection 45°. When the particle is at highest point of height h. Then what will be its angular momentum about projection point?
Answer:
At highest point, there will be only horizontal velocity (v cos45°) which does not change.
∴ Momentum of the particle at highest point
p = mv cos45° = \(\frac{m v}{\sqrt{2}}\)
∴ Angular momentum of the particle about projection point O,

Question 5.
Moon revolves around the earth while earth revolves around the sun in elliptical orbit. Is the orbit of moon around the sun elliptical?
Answer:
Moon does not revolve around the sun in elliptical orbit but the centre of mass of earth-moon system revolves around the sun in elliptical orbit.

Question 6.
Newton’s laws are applicable for individual particles of a system, even the motion of a system of particles is not described by Newton’s laws. Explain.
Answer:
Total mass of the system is supposed to be centeralised at the centre of mass and all forces are also supposed to be centered at centre of mass. Then motion of centre of mass will represent the motion under Newton’s laws.

Question 7.
A cat falls safely on her feet, why?
Answer:
According to law of conservation of momentum,
L = Iω = constant
∴ ω ∝ \(\frac{L}{I}\)
When cat jumps downwards, then it stretches her body and tail due to which the moment of inertia increases. Hence her angular velocity ω decreases. Thus a falling cat comes on earth safely on her feet.

Question 8.
Clarify the difference between centre of mass and centre of gravity. Do they coincided each other?
Answer:
Centre of mass and centre of gravity are given by:
\(\overrightarrow{r_{c m}}=\frac{\Sigma m_i \overrightarrow{r_1}}{\Sigma m_i} \text { and } \overrightarrow{r_{c g}}=\frac{\Sigma m_i g_i \cdot \overrightarrow{r_i}}{\Sigma m_i g_i}\)
For small bodies value of g will he same at points of the body. Therefore centre of mass and centre of gravity will coincide each other. For big bodies, due to different values of g at various points of the body. Therefore centre of gravity will differ from centre of mass. In this situation centre of gravity is same what below the centre of mass.

Question 9.
Moment of inertia of two rotating bodies A and B are I_A and I_B. If their angular momentum s are euqal, which will have more rotational energy J? Given I_A > I_B.
Answer:
Angular momentum of both are same,

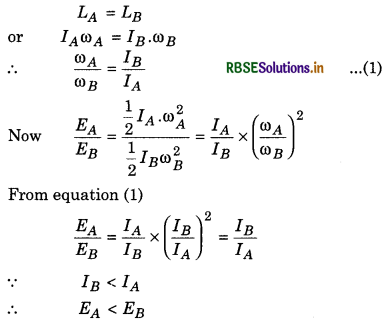
i.e., rotational energy of B will be greater than that of A.

Question 10.
It is easy to rotate a stone with the help of small string in comparison to long string, why?
Answer:
Moment of inertia of stone, I = mr², where r is the length of the string for small string (i.e., r), the moment of inertia will be less than that for long string. Therefore according to formula τ = Iα, for same value of a more torque will be required to rotate a stone with the help of long string. In other words, it is easy to rotate a stone with the help of small string.

Question 11.
A thin ring of mass m and radius r is rotating about its axis with angular velocity ω. Four particles of mass m are placed on the ends of two perpendicular diameters of the ring. Find the new angular velocity of the ring.
Answer:
Initial moment of inertia of the ring,
I₁ = Mr²
and ω₁ = ω
Moment of inertia of the ring after placing the masses (m)
I₂ = I₁ + 4 mr² = (Mr² + 4 mr²)
ω₂ = ?
Now according to the principle of conservation of angular momentum
L₂ = L₁

Question 12.
Four rods of same mass m and same length l make a square as shown in figure. What will be moment of inertia of this system about an axis passing through O and normal to plane of the square?
Answer:
Moment of inertia of rod AB about axis passing through P and normal to its length.
I₁ = \(\frac{M l^2}{12}\)

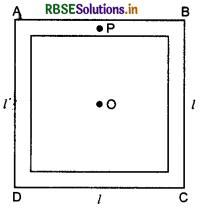
Moment of inertia of the rod AB about the axis passing through O at right angles to plane of square:
I' = I_cm + M(\(\frac{l}{2}\))² (according to theorem of parallel axes)
or I' = I₁ + M\(\frac{l^2}{4}=\frac{M l^2}{12}+\frac{M l^2}{4}=\frac{4 M l^2}{12}=\frac{M l^2}{3}\)
∴ Moment of inertia of the system about given axis passing through O,

Question 13.
A body of mass m is slipping on an inclined plane and reaches the end of the plane with velocity v. If the body be in form of a ring and roll on the plane, then what would be the velocity at the end of the plane?
Answer:
If the body slips on the plane, then
v = \(\sqrt{2 g h}\)
In case rolling of ring on the plane

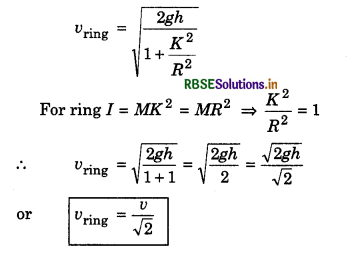
Question 14.
Mass of the bob of simple pendulum is m, is left from horizontal position. This bob strikes a body of mass 2m elastically and rebounds. What will be maximum angle with vertical after rebound?
Answer:
When the bob reaches the mean position, its velocity before striking the body of mass 2m,
u = \(\sqrt{2gl}\)

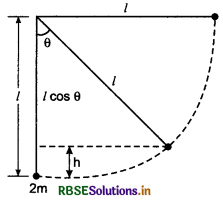
Its velocity after elastic collision,
v₁ = \(\frac{\left(m_1-m_2\right) u}{m_1+m_2}=\frac{(m-2 m) u}{m+2 m}=\frac{-m u}{3 m}=-\frac{u}{3}\)
or v₁ = -\(\frac{\sqrt{2 g l}}{3}\)
When the bob reaches its maximum height h, then

Question 15.
Two particles of masses m₁ and m₂, move towards each other from rest under influence of mutual attraction. what will be speed of their centre of mass at time t when distance between them is r?
Answer:
Since, the particles are initially at rest, therefore the velocity of their centre of mass will be zero. Here no external force is acting on the system, hence the speed of centre of mass will remain zero.

Question 16.
Moment of inertia of a solid cylinder about its axis is the same as that about an axis passing through its centre at right angles to its length. Find the relation between the length L and radius R of the cylinder.
Answer:
Moment of inertia of cylinder about its own axis
I₁ = \(\frac{1}{2}\) MR²
and its moment of inertia about axis passing through its centre at right angles to its length.
I₂ = M(\(\frac{L^2}{12}+\frac{R^2}{4}\))
∵ I₁ = I₂
∴ \(\frac{1}{2}\) MR² = M[\(\frac{L^2}{12}+\frac{R^2}{4}\)]

Long Answer Questions

Question 1.
Find the expression for position vector of centre of mass of a system of n particles.
Answer:
Let us consider a system of two particles of masses m₁ and m₂ and their position vectors with respect to reference point O, are \(\vec{r_1}\) and \(\vec{r_2}\) respectively then the position vector of their centre of mass will be

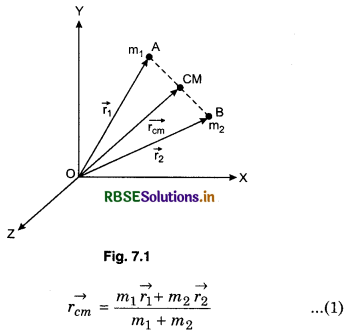
Proof:
Suppose the external forces acting on the particles are \(\overrightarrow{F_1^{\mathrm{ext}}}\) and \(\overrightarrow{F_2^{\mathrm{ext}}}\) and internal forces due to mutual interaction are \(\overrightarrow{F_{12}}\) and \(\overrightarrow{F_{21}}\) respectively. Therefore, net force on particle A,
\(\overrightarrow{F_1}=\overrightarrow{F_1^{\mathrm{ext}}}+\overrightarrow{F_{12}}\) ....................(2)
and net force on B,
\(\overrightarrow{F_2}=\overrightarrow{F_2^{\mathrm{ext}}}+\overrightarrow{F_{21}}\) .....................(3)

Suppose, at any instant the position vector, velocity and acceleration of centre of mass are \(\overrightarrow{r_{c m}}\), \(\overrightarrow{v_{c m}}\) and \overrightarrow{a_{c m}} respectively and total mass of the system is supposed to be centred at the centre of mass. Therefore, from Newton's second law of motion,
\(\vec{F}=\vec{F}_1+\vec{F}_2=\vec{F}_1^{\mathrm{ext}}+\vec{F}_2^{\mathrm{ext}}=M \overrightarrow{a_{c m}}\) ........................(9)
where M = (m₁ + m₂) and \(\vec{F}=\vec{F}_1^{\mathrm{ext}}+\vec{F}_2^{\mathrm{ext}}\) = Net force acting on the system.
∴ From equation (8) and (9)

Here \(\overrightarrow{v_{c m}}\) is the velocity of centre of mass.
On writing equation (11) in terms of position vectors,

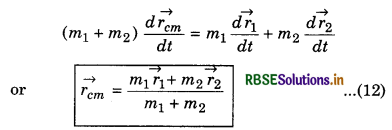
Special Situation
(i) When masses of both the particles are same, i.e.,
m₁ = m₂ = m

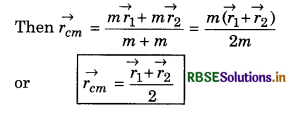
(ii) When the centre of mass is at the origin, then \(\overrightarrow{r_{c m}}\) = 0
∴ \(\frac{m_1 \vec{r}_1+m_2 \vec{r}_2}{\left(m_1+m_2\right)}\) = 0
or m₁\(\vec{r_1}\) + m₂\(\vec{r_2}\) = 0
i.e., "The point inside the body or system of particles, with respect to which the sum of moments of mass of all particles is zero, is called the centre of mass."
(iii) Position vector of the centre of mass of n-particle system,

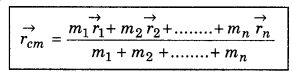
(iv) Co-ordinates of the centre of mass
Let us consider a system of n particles of masses m₁, m₂, m₃, ......................, mn having position vectors \(\vec{r}_1, \vec{r}_2, \vec{r}_3, ...................., \vec{r}_n\) respectively. If \(\vec{r}_{c m}\) be the position vector of the centre of mass, then
\(\overrightarrow{r_{c m}}=\frac{m_1 \vec{r}_1+m_2 \vec{r}_2+\ldots .+m_n \vec{r}_n}{m_1+m_2+\ldots . .+m_n}=\frac{\sum_{i=1}^n m_i \vec{r}_i}{\sum_{i=1}^n m_i}\) .......................(13)
Here we take \(\sum_{i=1}^n m_i\) = M
If (x₁, y₁, z₁); (x₂, y₂, z₂); ......................; (x_n, y_n, z_n) be the co-ordinates of different mass-particles, then

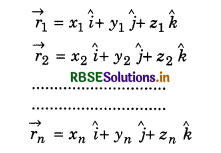
If (x_cm, y_cm, z_cm) be the co-ordinates of the centre of mass, then
\(\vec{r}_{c m}=x_{c m} \hat{i}+y_{c m} \hat{j}+z_{c m} \hat{k}\)
On substituting the values in equation (13), we have

Question 2.
Write the theorem of perpendicular axes of moment of inertia and prove it.
Answer:
Suppose, we have a circularring of radius R and mass M. We have to find its moment of inertia about axis YY' which is normal to the plane of the ring and passes through the centre O. This axis is also known as the geometric axis of the ring.
Circumference of the ring = 2πR

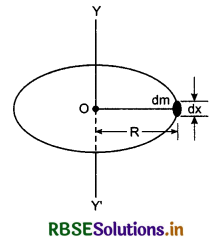
∴ Mass of the ring per unit length = \(\frac{M}{2 \pi R}\)
∴ Mass of a small element of the circle of length dx,
dm = \(\frac{M}{2 \pi R}\) dx
∴ Moment of inertia of this element about the axis YY',
dI = dmR² = \(\frac{M}{2 \pi R}\) dx R²
or dI = \(\frac{M R}{2 \pi}\) dx
∴ Moment of inertia of the whole ring about the axis YY',

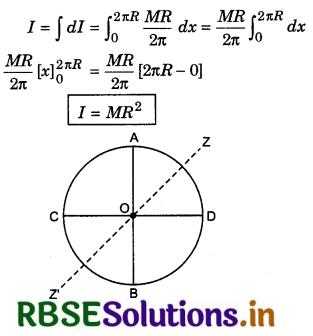
1. Moment of inertia about the diameter of the ring:
In fig. 7.33, two cross diameters AB and CD are shown. We have to find the moment of inertia of the ring about the diameter AB or CD. Moment of inertia of the ring about ZZ' axis
I_z = MR² ..........................(1)
Now according to the theorem of the perpendicular axes of moment of inertia,
I_z = I_AB + I_CD = I_d + I_d
or I_z = 2I_d
∴ I_d = \(\frac{I_z}{2}\)
or I_d = \(\frac{1}{2}\) MR²
2. Moment of inertia of the ring about the tangential axis lying in the plane of the ring:
Suppose we have to find the moment of inertia of the ring about the tangential axis PQ.
∴ According to the theorem of parallel axes of the moment of inertia,
I_PQ = I_cm + Mh²
Here I_cm = I_AB = \(\frac{1}{2}\)MR²

3. Moment of inertia of the ring about the tangential axis at right angles to plane of the ring: We have to find the moment of inertia about the axis PQ which is tangent of the ring at right angles to plane of the ring. Again applying the theorem of parallel axes,

I_PQ = I_cm + Mh²
Here I_cm = I_zz' = MR²
and h = R
∴ I_PQ = MR² + MR²

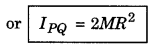
Question 3.
Write the theorem of perpendicular axes of moment of inertia and prove it.
Answer:
Moment of inertia of the disc about the tangential axis in the plane of the disc: We have to find the moment of inerita of the disc about the tangential axis PQ parallel to the diameter AB. From the theorem of parallel axes,
I_PQ = I_cm + Mh²

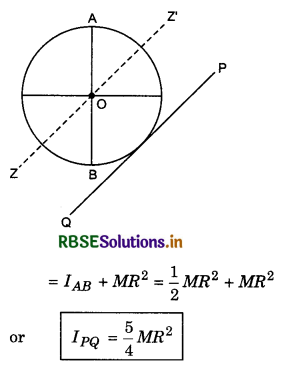
Question 4.
Give the derivation of equations of rotational motion.
Answer:
Pure rotation dynamics around static axis: The quantities which are used in pure rotational dynamics are angular displacement θ, angular velocity
ω, angular acceleration α. These quantities are corresponding to linear displacement x, linear velocity v and linear acceleration a in the translatory motion.
Therefore equations of motion in rotational motion corresponding to equations of motion in translatory motion are:
ω = ω₀ + α.t .......................(1)
θ = θ₀ + ω₀t + \(\frac{1}{2}\)α.t .....................(2)
ω² = ω₀² + 2α(θ - θ₀) ......................(3)
Proof: First equation:
Angular acceleration, α = \(\frac{d \omega}{d t}\)
or dω = αdt
On integrating both the sides,
\(\int_{\omega_0}^\omega d \omega=\int_0^t \alpha d t\)
or \([\omega]_{\omega_0}^\omega=\alpha[t]_0^t\)
or ω - ω₀ = α(t - 0)
or ω = ω₀ + αt
Second equation: Angular velocity
ω = \(\frac{d \theta}{d t}\)
or dθ = ωdt
On integrating both sides

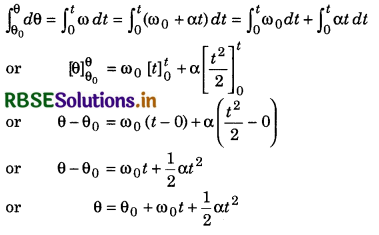
Third equation: Angular acceleration
(α) = \(\frac{d \omega}{d t}\) ..........................(1)

Question 5.
What is moment of inertia? Obtain expression for it.
Answer:
As in translatory motion, the objects oppose any change in their state of rest and state of motion. The property due to which this behaviour is observed, is called ‘Inertia’. Inertia depends on the mass of the body. Therefore the mass of the body is the measure of inertia. Similarly, in rotational motion also, the rotating body about an axis or resting body free to rotate about the axis, opposes any change in their state. This tendency of opposing the change in rotatory motion is called ‘moment of inertia’ or ‘Rotational inertia’ i.e., ‘Rotational inertia of a body about the axis of rotation is called moment of inertia of the body about the axis of rotation,’ It is denoted by I. 
Measurement of moment of inertia: Measurement of moment of inertia of a body is done by the product of the mass of the body and square of its distance from the axis of rotation.
∴ Moment of inertia (I) = mass (m) x (normal distance)² from the axis

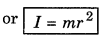
∴ Unit of moment of inertia in M.K.S. system = kg m²
Unit of moment of inertia in C.G.S. system = g cm²
Dimensional formula of I = [M¹L²T⁰]

Question 6.
What is radius of gyration? Obtain expression for it.
Answer:
A rigid body can be supposed to be made of many small particles. The moment of inertia of the rigid body is obtained by the sum of moment of inertias of indivdual particles i.e., I = I₁ + I₂ + I₃ + ............... + I_n

where m₁, m₂, m₃, ......................., m_n are the masses of the particles of rigid body and their distances from the axis of rotation are r₁, r₂, r₃, ....................., r_n respectivley as shown in fig. 7.28

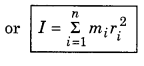
Question 7.
Establish the expressions of moment of inertia of ring about various axes.
Answer:
Suppose, we have a circularring of radius R and mass M. We have to find its moment of inertia about axis YY' which is normal to the plane of the ring and passes through the centre O. This axis is also known as the geometric axis of the ring.
Circumference of the ring = 2πR

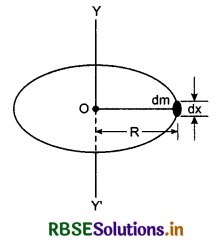
∴ Mass of the ring per unit length = \(\frac{M}{2 \pi R}\)
∴ Mass of a small element of the circle of length dx,
d_m = \(\frac{M}{2 \pi R}\) dx
∴ Moment of inertia of this element about the axis YY',
dI = dmR² = \(\frac{M}{2 \pi R}\) dx R²
or dI = \(\frac{M R}{2 \pi}\) dx
∴ Moment of inertia of the whole ring about the axis YY',

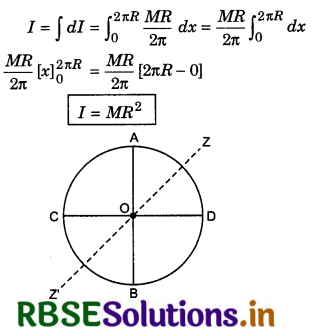
1. Moment of inertia about the diameter of the ring:
In fig. 7.33, two cross diameters AB and CD are shown. We have to find the moment of inertia of the ring about the diameter AB or CD. Moment of inertia of the ring about ZZ' axis
I_z = MR² ..........................(1)
Now according to the theorem of the perpendicular axes of moment of inertia,
I_z = I_AB + I_CD = I_d + I_d
or I_z = 2I_d
∴ I_d = \(\frac{I_z}{2}\)
or I_d = \(\frac{1}{2}\) MR²
2. Moment of inertia of the ring about the tangential axis lying in the plane of the ring:
Suppose we have to find the moment of inertia of the ring about the tangential axis PQ.
∴ According to the theorem of parallel axes of the moment of inertia,
I_PQ = I_cm + Mh²
Here I_cm = I_AB = \(\frac{1}{2}\)MR²

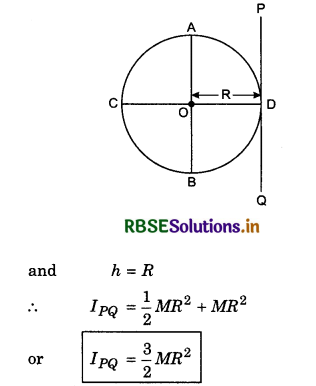
3. Moment of inertia of the ring about the tangential axis at right angles to plane of the ring: We have to find the moment of inertia about the axis PQ which is tangent of the ring at right angles to plane of the ring. Again applying the theorem of parallel axes,

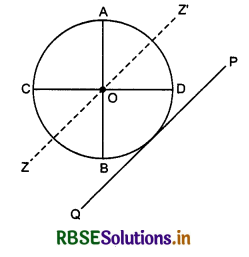
I_PQ = I_cm + Mh²
Here I_cm = I_zz' = MR²
and h = R
∴ IPQ = MR² + MR²

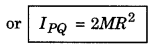
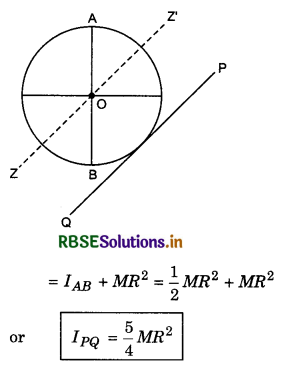
Question 8.
Establish the expressions of moment of inertia of disc about various axes.
Answer:
Moment of inertia of the disc about the tangential axis in the plane of the disc: We have to find the moment of inerita of the disc about the tangential axis PQ parallel to the diameter AB. From the theorem of parallel axes,
I_PQ = I_cm + Mh²

Question 9.
Establish the relation between moment of inertia, torque, angular acceleration and define moment of inertia on the basis of this relation.
Answer:
Suppose a rigid body is made of n particles of masses m₁, m₂, m₃, ............., m_n and their distances from the axes of rotation YY' are r₁, r₂, r₃, .................., r_n respectively. If a₁, a₂, a₃, .................., a_n are linear accelerations of the particles, then forces acting on the particles,

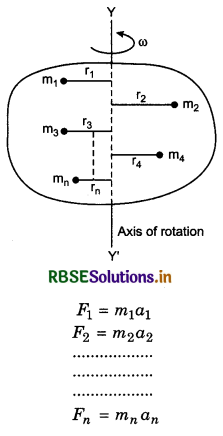
If the body is rotating with the angular acceleration α, then
F₁ = m₁a = m₁r₁α (because a₁ = r₁α)

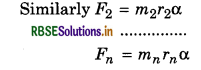
∵ Torque = force x normal distance from the axis of rotation
or τ = F x r
or τ = mrα x r = mr²α
∴ τ₁ = m₁r₁²α; τ₂ = m₂r₂²α; ................., τ_n = m_nr_n²α
∴ If all these torque are in the same direction then net torque acting on the body,
τ = τ₁ + τ₂ + τ₃ + ...................... + τ_n
= m₁r₁²α + m₂r₂²α + m₃r₃²α + .................... + m_nr_n²α
= (m₁r₁² + m₂r₂² + m₃r₃² + ................... + m_nr_n²)α
= \(\sum_{i=1}^n m_i r_i^2 \cdot \alpha\)

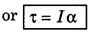
i.e., Torque = Moment of inertia x Angular acceleration,
If α = 1 rad.s^-1, then τ = I
i.e., "Momentum of inertia of a body about a given axis of rotation is equivalent to torque which can produce unit angular acceleration in the body."

Question 10. 
Establish the relation between angular momentum (L), moment of inertia (I) and angular velocity (ω) and give the definition of I on the basis of this relation.
Answer:
Suppose a rigid body is rotating about an axis YY' with angular velocity ω.

Moment of linear momentum about the axis of rotation is called the angular momentum and it is denoted by L.
∴ L = Moment of linear momentum
= p x r
= mv x r
= mrωr

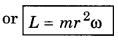
A body can be supposed to be made of n small particles of masses m₁, m₂, m₃, ........................, mn and distant r₁, r₂, r₃, ....................., r_n from the axis of rotation. Then
L = L₁ + L₂ + ................... + L_n
= m₁r₁²ω + µ₂r₂²ω + .......................... + m_nr_n²ω
= (m₁r₁² + m₂r₂² + ........................ + m_nr_n²) ω
= \(\sum_{i=1}^n\) m_ir_i² ω

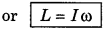
i.e., Angular momentum = Moment of inertia x Angular velocity.
If ω = 1 rads^-1, then L = I
i.e., "moment of inertia of a body about a given axis of rotation is equivalent to its angular momentum which is in the equation of unit angular velocity."

Question 11.
What is principle of conservation of angular momentum and explain it by giving two examles.
Answer:
We know that rate of change of angular momentum is equal to the torque applied i.e.,
\(\frac{d L}{d t}\) = τ
If external torque is zero, i.e., τ = 0
the \(\frac{d L}{d t}\) = 0
or L = constant

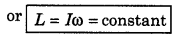
i.e., "In absence of external torque the angular momentum of a body remains unchanged or constant." This is the principle of conservation of angular momentum.

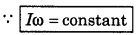
Therefore on decreasing the value of I, angular velocity increases and vice-versa.
∴ I₁ω₁ = I₂ω₂
Example:
When a person rotates sitting on a rotating stool, then as he opens his hands away from his body his angular velocity decreases and as he starts closing his hands again, his angular velocity of rotation goes on increasing.
Above fact can be explained on the basis of law of conservation of angular momentum according to which,

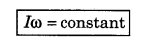
As the person opens his hands his moment of inertia increases, hence angular velocity ω decreases and hence vice-versa.

Question 12.
What do you mean by rolling motion. Obtain the expression for total energy in volling motion.
Answer:
The motion of a rigid body in which the body rotates about a moving axis of rotation, is called the rolling motion. Rolling motion is the combination of translatory and rotatory motions. e.g., the motion of the wheels of the vehicles, i.e.,
Rolling motion = translational motion + rotational motion
Condition of Rolling Motion:
A disc of radius R is shown in the fig. 7.44 which is under rolling motion. Here C is its the centre of mass (or geometrical centre).
Velocity of point C is vcm. There are two components of velocities of other point P₀ ,P₁ and P₂ of the disc, one cqmponent is translatory velocity v_cm and the other is linear velocity v_r. due to rotation.
∵ v_r = rω
where, r is the distance of the point from the axis of rotation.

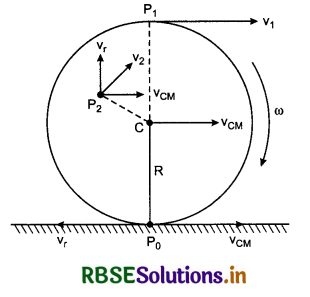
Velocity v_r is at right angles to the line joining point P₂ and C i.e., normal to radius vector.
Point P₀ is at rest with respect to the surface.
∴ v_r = Rω (where R is radius of the disc)
∵ Direction of v_r is opposite to v_cm, therefore,
v_cm = Rω
∴ Condition of rolling of disc without slipping is the same. Similarly, the direction of v_r is same as that of v_cm at highest point P₁. Therefore
v₁ = v_cm + Rω = v_cm + v_cm
or v₁ = 2v_cm
Its direction is parallel to surface.

Question 13.
Find the expressions for velocity and acceleration of a rolling body on inclined plane.
Answer:
Suppose the inclination of a inclined smooth plane AB is a and its height is ‘h’. Length of the plane is S. A body of mass M and radius R is left free from the top A from rest i.e., u = 0. When it reaches to the lowest point B, its linear velocity becomes u. Thus both type of kinetic energy (translational and rotation) is there in rolling motion between A and B.

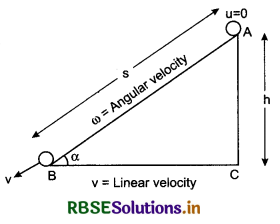
At highest point, total energy E_A = mgh ........................(1)
(because the body starts rolling from rest.)
At lowest point total energy,
E_B = E_T + E_R

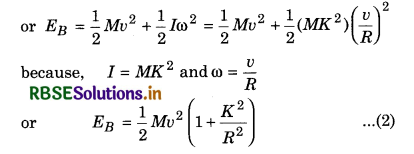
From law of conservation of energy at A and B
E_A = E_B

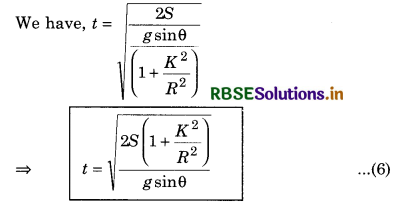
If the acceleration produced in the motion be 'a', then from equation of motion v² = u² + 2as
v² = (0)² + 2aS = 2aS

If the rolling body takes time 't' in rolling from A to B, then from equation S = ut + \(\frac{1}{2}\)at²
S = 0 + \(\frac{1}{2}\)at² ⇒ t² = \(\frac{2S}{a}\)
or t = \(\sqrt{\frac{2 S}{a}}\)
On substituting the value of 'a' from equation (5),

Numerical Questions

Based on Centre of Mass

Question 1.
Two particles of masses 1 kg and 3 kg are moving with velocities (\(2\hat{i} + 3\hat{j}\)) ms^-1 and (\(3\hat{i} - 4\hat{k}\))ms^-1 respectively. What will be velocity of centre of mass?
Solution:
Given: m₁ = 1 kg; m₂ = kg; v₁ = (\(2\hat{i} + 3\hat{j}\)) ms^-1; v₂ = (\(3\hat{i} - 4\hat{k}\)); v_cm = ?

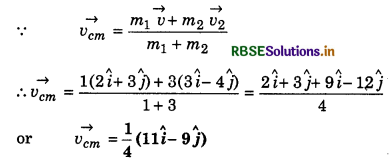
Question 2.
Two block of mass 10 kg and 4 kg, connected with a light spring, are placed on a smooth horizontal plane. An impulse provides a velocity of 14 m s^-1 to heavy block towards light block. Find the velocity of centre of mass of this system.
Solution:
m₁ = 10 kg; m₂ = 4 kg; v₁ = 14 ms^-1; v₂ = 0
v_cm = 0

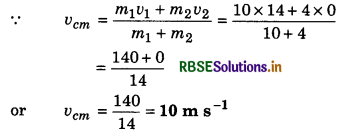
Question 3.
In a two particle system, the masses of particles are 2 and 5 kg and at t = 0 their positions are respectively (\(4\hat{i} + 3\hat{j}\)) and (\(6\hat{i} - 7\hat{j} + 7\hat{k}\)) m and their velocities are respectively (\(10\hat{i} - 6\hat{k}\)) and (\(3\hat{i} + 6\hat{j}\)) ms^-1. Find the velocity of the centre of mass of this system. What will the positions of centre of piass at t = 0 and t = 4 s?
Solution:
m₁ = 2 kg; m₂ = 5 kg

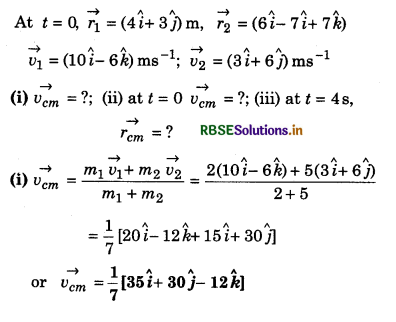
(ii) At t = 0

Question 4.
In molecule of carbon mono-oxide the distance between carbon and oxygen atoms is 1.150 Å. Give the situation of centre of mass of CO molecule with respect to carbon atom.
Solution:
m₁r₁ = m₂r₂

∴ 12 x x = 16(1.15 - x)
3x = 4(1.15 - x)
or 3x = 4.60 - 4x
7x = 4.60
∴ x = \(\frac{460}{7}\) = 0.6571 Å
or x = 0.6571 Å

Based on Torque, Angular Momentum and Laws of Rotational Motion

Question 5.
An electric fan is rotating with angular speed of 600 cycle min^-1. When electric flow is cut, then the fan stops after 60 revolutions. How much time will the fan take before coming at rest?
Solution:
Initial frequency n₀ = 600 c.min^-1 = \(\frac{600}{60}\) c.s^-1 = 10 c.s^-1
and final frequency n = 0
∴ ω₀ = 2πn₀ = 2π x 10 = 20π rad.s^-1
and ω = 2πn = 2π x 0 = 0 rad.s^-1
Angular displacement θ = 60 revolution
= 60 x 2π rad = 120π rad
Now, from equation,
ω² = ω₀² + 2αθ
We have, 0 = (20π)² + 2α x 120π
∴ α = -\(\frac{20 \pi \times 20 \pi}{2 \times 120 \pi}\)
= -\(\frac{5}{3}\)π rad.s^-2
Now applying first equation
ω = ω⁰ + αt
∴ 0 = 20π - \(\frac{5 \pi t}{3} \Rightarrow \frac{5 \pi t}{3}\) = 20π
∴ t = 3 x 4 = 12 s

Question 6.
A body of mass 20 kg is moving on a circular path of diameter 0.20 m at the rate of 100 revolutions in 3 s. Find:
(i) rotational energy of the body
(ii) angular momentum of the body, π² = 9.86.
Solution:
m = 20 kg; R = \(\frac{D}{2}=\frac{0.20}{2}\) = 0.10 m; frequency n = \(\frac{100}{3}\) c.s^-1
∴ ω = 2πn = \(\frac{2 \pi \times 100}{3}=\frac{200}{3}\)π rad.s^-1
∴ I = MR² = 20 x 0.1 x 0.1 = 0.2 kg.m²
(i) Rotational energy,

Question 7.
Moment of inertia of a resting body is 3 kg m². It is rotated upto 20 s by a torque of 6 Nm. Find the angualr displacement of the body.
Solution:
ω₀ = 0; I = 3 kg.m²; τ = 6 Nm; t = 20 s; θ = ?

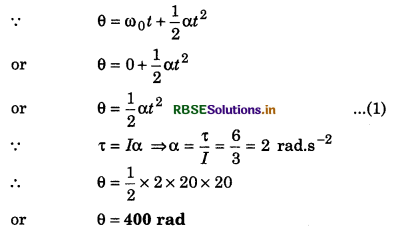
Question 8.
A man, holding spheres of 10 kg each in his hands, is standing on a rotating table completing 1 cycle in 2 s. His arms are extended and each sphere is at a distance of 3 m from axis of rotation. If the person through away spheres, what will be new angular velocity of the table? Moment of inertia of man with table is 15 kgm².
Solution:
Moment of inertia of man with extended arms,
I₁ = I_man + mr² + mr²
or I₁ = 15 + 2 x 10 x (3)² = 15 + 10 x 9
= 195 kgm²
ω = \(\frac{2 \pi n}{t}=\frac{2 \pi \times 1}{2}\) = π rad.s^-1
After throwing the spheres from hands, its moment of inertia
I₂ = 15 kgm²
ω₂ = 2πn²
From principle of conservation of angular momentum,
L₁ = L₂
or I₁ω₁ = I₂ω₂
∴ 195 x π = 15 x 2π x n²
∴ n² = \(\frac{195}{30}\) = 6.5 c.s^-1.

Question 9.
A disc of moment of inertia 5 x 10^-4 kg m², is rotating about its axis at the rate of 40 c min^-1. If a wax ball of mass 0.02 kg is gently placed on the disc at a distance of 0.08 m from the axis of rotation, how many rounds per minute will it complete now?
Solution:
I₁ = 5 x 10^-4 kgm²; ω₁ = 2πn₁ = 2π x \(\frac{40}{60}=\frac{4 \pi}{3}\) rad.s^-1;
I₂ = I₁ + mr² = 5 x 10^-4 + 0.02 x 0.08 x 0.08
= 5 x 10^-4 + 1.28 x 10^-4
= 6.28 x 10^-4 kgm²
ω₂ = ?
From the law of conservation of angular momentum,
L₂ω₂ = L₁ω₁

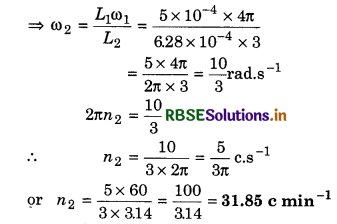
Question 10.
A vertical solid wheel of radius 25 cm and mass 5000 g is free to rotate on its horizontal axle. A cord is wound on the wheel. Cord is drawn for 5 seconds by a force of 2 N. Calculate the angular velocity of the wheel. (Axle is frictionless).
Solution:
Given: r = 25 cm = 0.25 m
m = 5000 g = 5 kg; f = 2 N; t = 5 s
Moment of inertia of wheel,
I = \(\frac{1}{2}\) mr² = \(\frac{1}{2}\) x 5 x 0.25 x 0.25
= 0.156 kgm²
Torque acting on the wheel,
τ = F x r = 2 x 0.25 = 0.50 Nm
∴ Angular acceleration,
α = \(\frac{\tau}{I}=\frac{0.50}{0.156}\) = 3.20 rad s^-2
From equation,
ω = ω₀ + αt = 0 + 3.205 x 5
= 16.025
= 16 rad s^-1

Based on Equilibrium

Question 11.
A homogenous rod of length 1 m is pivoted at the sign of 40 cm. A block of 10 g is suspended at sign of 10 cm. If the rod is in equilibrium then find its mass.

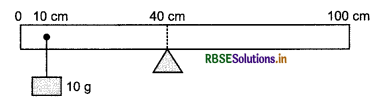
Solution:
In equation
∑τ = 0

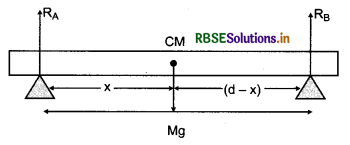
∴ Anticlockwise torque = Clockwise torque
or 10g x 30 = Mg x 10
or M = \(\frac{10 \times 30}{10}\) = 30g
or M = 30 g

Based on Moment of Inertia, Rotational Energy and Conservation Laws

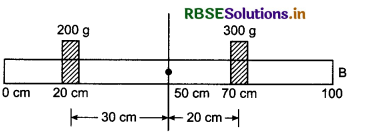
Question 12.
Two weights of 200 g and 300 g are placed on .20 cm and 70 cm signs of a light metre scale figure. Find the moment of inertia of this system about axis passing normally through (i) 0 cm sign, (ii) 50 cm sign and (iii) 100 cm sign.

Solution:
(i) Moment of inerita about the axis passing through the sign of 0 cm.
I = m₁r₁² + m₂r₂²

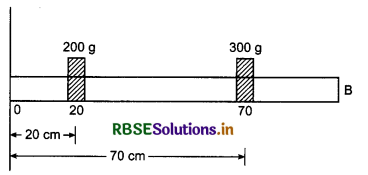
or I = 200 x (20)² + 300 x (70)²
= 200 x 400 + 300 x 4900
= 80000 + 1470000
= 8 x 10⁴ + 147 x 10⁴
= (8 + 147) x 10⁴ = 155 x 10⁴
= 15.5 x 10⁵ g cm²
(ii) Moment of inertia about the axis passing through sign of 50 cm.

I = m₁r₁² + m₂r₂²
= 200 x (30)² + 300 x (20)²
= 200 x 900 + 300 x 400
= 180000 + 120000
= 300000
= 3.0 x 10⁵ g cm²
(iii) Moment of inertia about axis passing through sign of 100 cm.

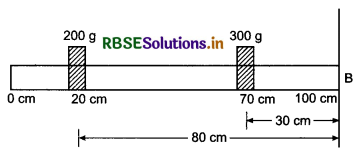
I = m₁r₁² + m₂r₂²
= 200 x (80)² + 300 x (30)²
= 200 x 6400 + 300 x 900
= 1280000 + 270000 = 155 x 10⁴
= 15.5 x 10⁵ g cm²

Question 13.
A circular disc of mass 49 kg and radius 50 cm, is rotating about its own axis at the rate of 20 revolution for minute. Calculate the rotational energy of the disc.
Solution:
M = 49 kg; R = 50 cm = 0.50 m
n = 120 rev.min^-1 = \(\frac{120}{60}\) rev.s^-1 = 2 rev.s^-1
∴ I = \(\frac{1}{2}\) MR² = \(\frac{1}{2}\) x 49 x (0.5)² = \(\frac{1}{2}\) x 49 x 0.25
= \(\frac{49}{8}\) kg.m²
ω = 2πn = 2π x 2 = 4π rad.s^-1
∴ Rotational energy
E_R = \(\frac{1}{2}\)Iω² = \(\frac{1}{2}\) x \(\frac{49}{8}\) x 16π² = 49 x 9.86
or E_R = 483.1204 J
≈ 484 J

Question 14.
Five point particles of equal mass 1 kg are placed at points A, B, C, D, E which are situated at equal distance on a thin rod of length 1 m. figure. Mass of the rod is 0.5 kg which is centered at the centre of the rod. Find the moment of inertia of the system about an axis passing through A right angles to the rod.

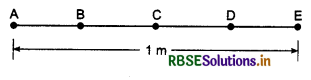
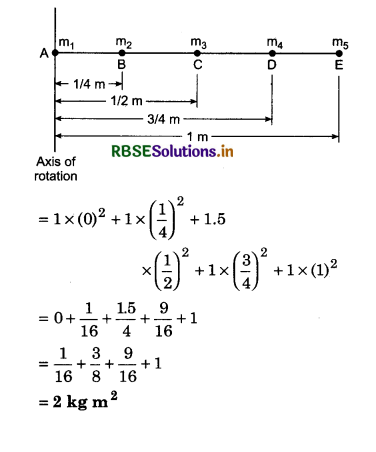
Solution:
m₁ = 1 kg; r₁ = 0
m₂ = 1 kg; r₂ = \(\frac{1}{4}\) m
m₃ = (1 + 0.5) = 1.5 kg; r₃ = \(\frac{1}{2}\) m
m₄ = 1 kg; r₄ = \(\frac{3}{4}\) m
m₅ = 1 kg; r₅ = 1 m
∴ Moment of inertia about axis passing through A,
I = m₁r₁² + m₂r₂² + m₃r₃² + m₄r₄² + m₅r₅²

Question 15.
Two blocks of same mass 50 g are placed on a hanging rod in three different situations as shown in figure. Moment of inertia of the rod about axis of rotation is I₀ = 5000 g.cm². Find the moment of inertia of the system in each situation.

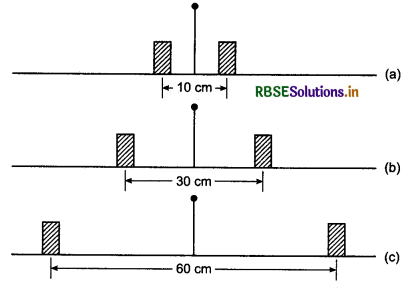
Solution:
(a) I₁ = I₀ + mr₁² + m₂r₂²
= 5000 + 50 x (5)² + 50 x (5)²
= 5000 + 1250 + 1250
= 7500 g cm²
(b) I₂ = I₀ + m₁r₁² + m₂r₂²
= 5000 + 50 x (15)² + 50 x (15)²
= 5000 + 50 x 225 + 50 x 225
= 5000 + 11250 + 11250
= 27500 g cm²
(c) I₃ = I₀ + m₁r₁² + m₂r₂²
= 5000 + 50 x (30)² + 50 x (30)²
= 5000 + 50 x 900 + 50 x 900
= 5000 + 45000 + 45000
= 95000 g cm²

Question 16.
If earth suddenly contracts such that its radius becomes one third of radius of gyration. How much will decrease the duration of the day now? Suppose that the mass of earth remains unchanged.
Solution:
According the law of conservation of angular momentum,
L₁ = L₂
or I₁ω₁ = I₂ω₂ .......................(1)

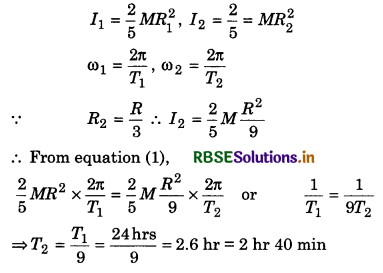
∴ Decrease in duration of days,
∆T = T₁ - T₂ = 24hr - 2 hr. 40 min
= 21 hr 20 min

Question 17.
Maximum and minimum distances of a comet from sun are 1.4 x 10¹² m and 7 x 10¹⁰ m respectively. If its velocity closer to sun is 6 x 10⁴ m s^-1, what will be its velocity in position of maximum distance?
Solution:
According to the principle of conservation of momentum
L₁ = L₂
m₁v₁r₁ = m₂v₂r₂ [because L = mvr]
here m₁ = m₂ = m
∴ r₁v₁ = r₂v₂
∴ v₁ = \(\frac{r_2 v_2}{r_1}=\frac{6 \times 10^4 \times 7 \times 10^{10}}{1.4 \times 10^{12}}\)
v = 3 x 10³ m s^-1

High Order Thinking Skills or HOTS

Question 1.
Diameter of a disc is 0.5 m and its mass is 16 kg. What torque will be required to increase the angular velocity from 0 (zero) to 120 c min^-1 in 8 s? At what rate the work will done after 8s?
Solution:
Given: Mass of the disc M = 16 kg
Radius R = \(\frac{0.5}{2}\) = 0.25 m; t = 8 s
ω₁ = 0; ω₂ = 2πn² = 2π x \(\frac{120}{60}\) = 4π rad.s^-1
From first equation of rotational motion,
ω = ω₀ + α.t
ω₂ = ω₁ + αt
or ω₂ = 0 + α.t
∴ α = \(\frac{\omega_2}{t}=\frac{4 \pi}{8}=\frac{\pi}{2}=\frac{3.14}{2}\) = 1.57 rad.s^-1
Moment of inertia of the disc,
I = \(\frac{1}{2}\)MR² = \(\frac{1}{2}\) x 16 x (0.25)² = 8 x 0.0625
= 0.5 kgm²
∴ τ = Iα = 0.5\(\frac{\pi}{2}=\frac{\pi}{4}\) Nm
Rate of doing work i.e., power
P = τω = \(\frac{\pi}{4}\) x 4π = π²
or P = π² watt

Question 2.
A uniform rod of mass 40 kg and length 10 m is situated at inclination of 30° with vertical. Find the reaction forces acting on the ends of the rod by friction force (f) and the plane.

Solution:
Condition of equation,
∑F = 0 and ∑τ = 0
In horizontal direction i.e., X-direction,

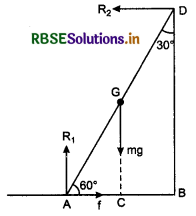
∑F_x = 0
∴ R₂ - f = 0
R₂ = f ........................(1)
In Y-direction,
∑F_y = 0
∴ R₁ - Mg = 0 or R₁ = Mg
or R₁ = 40 x 10 = 400 N ..........................(2)
Taking torque about point A for application of ∑τ = 0
R₂ x BD - mg x AC = 0
or R₂ = \(\frac{m g \times A C}{B D}\)
From diagram, \(\frac{BD}{AD}\) = sin 60° or BD = AD sin 60

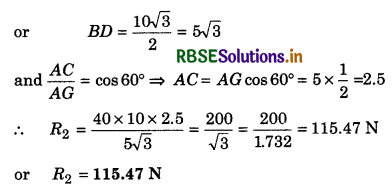
Question 3.
A rod of mass M and length L is suspended from a base figure. A bullet of mass m strikes the rod as shown in figure and gets embeded in the rod. Find the angular velocity of the system just after the collision.

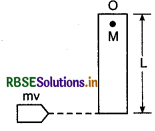
Solution:
By the theorem of parallel axes, the moment of inertia of the rod about O

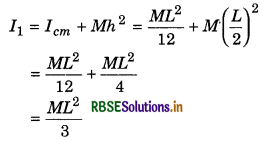
Moment of inertia after collision of bullet
I = I₁ + mL²
= \(\frac{M L^2}{3}\) + mL²
∴ I = L²(\frac{M}{3} + m)
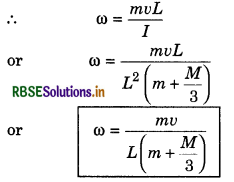
Angular momentum of the system will remain conserved about O.
∴ L₁ = L₂
or mvL = Iω

Question 4.
A person holding 2 spheres of mass 2 kg each in his hands is standing on a rotating table with angular velocity of 10 rad s. His arms are extendedand each sphere is at a distance of 1 m from axis of rotation. If moment of inertia of the person about axis of rotation be 1 kgm 2, what will be rotational energy of the system? If the person closes his arms such that each sphere becomes at a distance of 0.3 m from axis of rotation, what will be rotational energy now? Describe the change in this energy.
Solution:
I₀ = 1 kgm²; ω₁ = 10 rad.s^-1
I₁ = I₀ + mr₁² + mr₁² = I₀ + 2mr₁²
= 1 + 2 x 2 x (1)² = 1 + 4
= 5 kgm²
∴ K₁ = \(\frac{1}{2}\)I₁ω₁² = \(\frac{1}{2}\) x 5 x 10 x 10
or K₁ = 250 J
I₂ = I₀ x 2mr₂² = 1 + 2 x 2 x (0.3)² = 1 + 0.36
= 1.36 kgm²
From conservation of angular momentum
I₂ω₂ = I₁ω₁
or ω₂ = \(\frac{I_1 \omega_1}{I_2}=\frac{5 \times 10}{1.36}=\frac{50}{1.36}\) rad.s^-1
∴ K₂ = \(\frac{1}{2} I_2 \omega_2^2=\frac{1}{2} \times 1.36 \times\left(\frac{50}{1.36}\right)^2\)
or K₂ = 919 J

Question 5.
A small disc of radius R/3 is cut from a disc of mass 9 M and radius R. Find the moment of inertia of rest disc about centre O of the disc and normal to plane.
Solution:

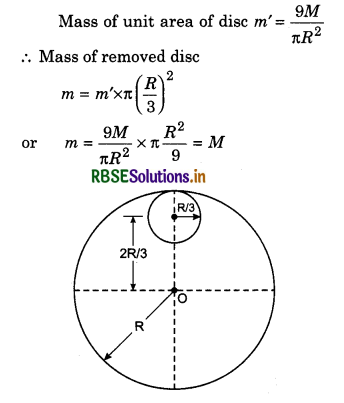
Moment of inertia of the disc about the axis passing through O normal to plane of the disc
I₁ = \(\frac{1}{2}\)(9M)R² = \(\frac{9 M R^2}{2}\)
Moment of inertia of removed disc about the same axis,
I₂ = I_cm + Mh²

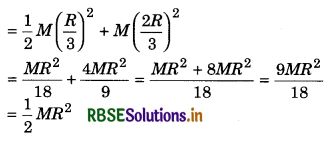
∴ Moment of inertia of rest disc about the same axis
I = I₁ - I₂ = \(\frac{1}{2} \times 9 M R^2-\frac{1}{2} M R^2=\frac{1}{2} 8 M R^2\)
or I = 4MR²

Questions for Competitive Examinations

Objective Type Questions

Question 1.
A uniform thin rod of length l and mass m is oscillating freely on axis passing through one end of the rod. If maximum angular velocity ω. Upto what maximum height will its centre of mass rise?

Solution:
\(\frac{1}{2}\)Iω² = mgh
or \(\frac{1}{2}\left(\frac{m l^2}{3}\right) \omega^2\) = mgh
∴ h = \(\frac{l^2 \omega^2}{6 g}\)
∴ Option (c) is correct.

Question 2.
A ball of mass 0.2 kg is situated on the top of a pillar of height 5 m. A bullet of mass 0.01 kg moving horizontally with velocity of v m s-1 strikes the ball at its centre, the ball strikes the ground at a distance of 20 m and bullet at 100 m. The initial velocity v of the bullet is:

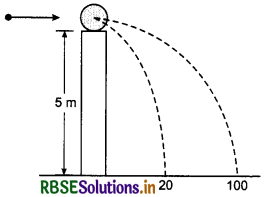
(a) 250 ms^-1
(b) 250\(\sqrt{2}\) ms^-1
(c) 400 ms^-1
(d) 500 ms^-1
Solution:
Time taken by the bullet and ball in reaching the ground

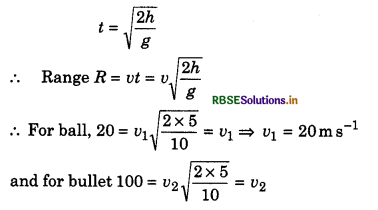
⇒ v₂ = 100 ms^-1
Now according to the principle of conservation of linear momentum
m x v = mv₁ + mv₂
or 0.01 x v = 0.2 x 0.2 + 0.01 x 100 = 4 + 1 = 5
∴ v = \(\frac{5}{0.01}\) = 500 ms^-1
∴ Option (d) is correct.

Question 3.
Two balls of linear momentum\( \vec{p_1} = p\hat{i}\) and \(\vec{p_2} = -p\hat{i}\) strike in free space. No external force is acting on the balls. Suppose their final momentum are \(\overrightarrow{p_1^{\prime}}\) and \(\overrightarrow{p_2^{\prime}}\). Which option/options is/are not permissible for non zero values of p, a₁, a₂, b₁, b₂, c₁ and c₂:

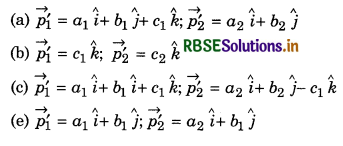
Solution:
Initial momentum of the system, \(\vec{p_1} + \vec{p_2}\) = 0 since no external force is acting on the system, therefore final momentum will also be zero.
∴ \(\overrightarrow{p_1^{\prime}}+\overrightarrow{p_2^{\prime}}\) = 0
Option (b) is permissible because if C₁ = C₂ ≠ 0 is substituted, then \(\vec{p_1} + \vec{p}\) = 0.Similarly (c) can also be checked.
∴ Options (a) and (d) are correct.

Question 4.
A thin horizontal circular disc is rotating about vertical axis passing through the centre of the disc. An insect is at rest at any point near the axle. Now the insect starts moving on a diameter from its one end to other end. The angular speed of the disc during the journey of the insect:
(a) remains unchanged
(b) continuously decreases
(c) continuously increases
(d) increases first and then decreases
Solution:
According to the principle of angular momentum I.ω = constant. In first situation when insect moves from circumference to centre, then moment of inertia I will decrease, hence ω will increase. Similarly in second situation (from centre to circumference) I will increase, hence ω will decrease.
∴ Option (d) is correct.

Question 5.
The reason of being constant the angular momentum of a particle rotated by the central force is:
(a) zero torque
(b) constant torque
(c) constant force
(d) constant linear momentum
Solution:
According to the principle torque will be zero
∴ Option (a) is correct.

Question 6.
A drawing design is given in figure in which each line is made of same width with ink. Mass of ink of each inner line and circle is m. Mass of ink of
outer circle is 6 m. Coordinate of centres of various parts are as follows:

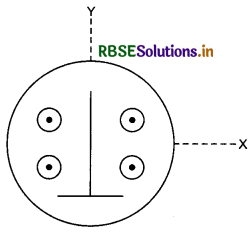
Outer circle = (0,0); right inner circle = (a, a); inner vertical line = (0,0); horizontal line = (0, -a) and left inner circle = (-a,a). Y-coordinate of the centre of mass is:

Solution:

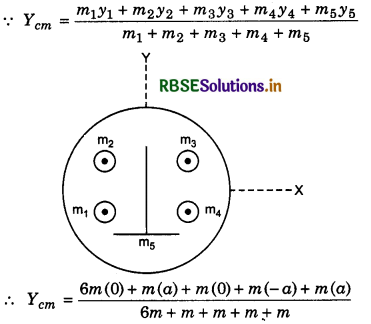
Option (a) is correct.

Question 7.
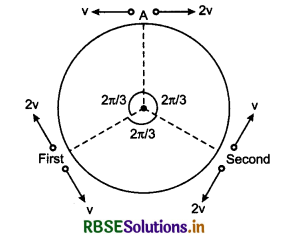
Two small particles of same mass, start moving in a horizontal circle from point A in opposite directions. Their tangential velocities are respectively V and 2V figure. Between collisions, the particles move with constant speed. After how many collisions, they again meet at point A?

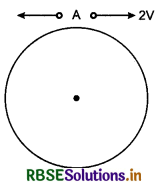
(a) 4
(b) 3
(c) 2
(d) 1
Solution:
In first collision the particle of velocity 2v will rotate by \(\frac{4 \pi}{3}\) rad and that of velocity v will rotate by \(\frac{2 \pi}{3}\) rad. Similarly after first collision at, second collision figure. After this collision i.e., after two collisions, they will again meet at point A.
Option (c) is correct.

Question 8.
A wheel is moving with the speed of 1200 cycle/min^-1, and its speed is slowed down with retardation of 4 rad s^-2. The rounds completed by the wheel before coming at rest, is:
(a) 143
(b) 272
(c) 314
(d) 722
Solution:
n₀ = 1200 cycle min^-1 = \(\frac{1200}{60}\) cs^-1 = 20 cs^-1
∴ ω₀ = 2πn₀ = 2π x 20 = 40π rad s^-1

α = -4 rad.s^-2
ω = 0
∵ ω² = ω₀² + 2αθ ∴ 0 = (40π)² - 2 x 4 x θ

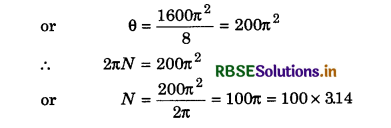
or N = 314
∴ Option (c) is correct.

Question 9.
A sphere and a disc of same mass and same radius, start rolling on a smooth inclined plane upto the same distance. The ratio of times taken by them will be:
(a) 15 : 14
(b) 15¹ : 14²
(c) \(\sqrt{14}\) : \(\sqrt{15}\)
(d) 14 : 15
Solution:
Time taken by a rolling body on an inclined plane

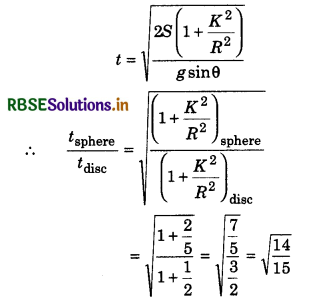
Thus option (c) is correct.

Question 10.
If moment of inertia of disc about a tangential axis lying in its plane is I, then its moment of inertia about the tangent perpendicular to its plane will be.

Solution:
Given: The moment of inertia of a disc about tangent in the plane of the disc,
I = \(\frac{5}{4}\) MR²
and that about tangent perpendicular to the plane of the disc

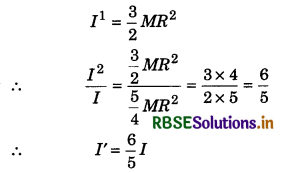
Thus option (a) is correct.

Question 11.
A uniform solid sphere is rolling on floor without slipping. Ratio of  its rotational energy and its total energy is:

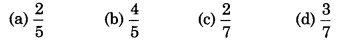
Solution:
Total kinetic energy of a rolling sphere

∴ Option (c) is correct.

Question 12.
Moment of inertia of a solid sphere of mass m and radius R about its tangent is:

Solution:
I_AB = I_d = I_cm = \(\frac{2}{5}\)MR²
Applying therorem of parallel axes,

I_CD = I_cm + \(\frac{2}{5}\) MR² + MR²
or I_CD = \(\frac{7}{5}\)MR²
∴ Option (a) is correct.

Question 13.
A force -F\(\hat{k}\) is acting at the origin O of a co-ordinate system. Torque at point (1, -1) is:

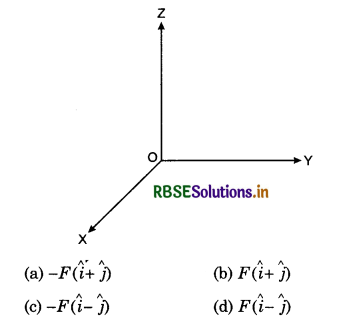
Solution:

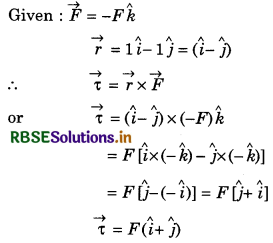
∴ Option (b) is correct.

Question 14.
Consider square shaped uniform plate of side 'a' and mass 'm'. Its moment of inertia about axis passing through its one corner and perpendicular to its plane is:

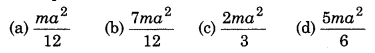
Solution:
Moment of inertia of square-plate passing through its centre O and normal to its plane.

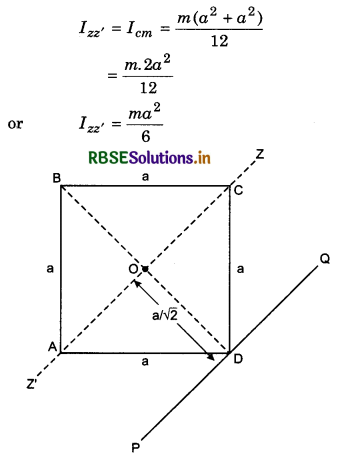
On applying the theorem of parallel axes,
I_PQ = I_cm + Mh² = I_zz' + m(\(\frac{a}{\sqrt{2}}\))²
= \(\frac{m a^2}{6}+\frac{m a^2}{2}=\frac{4 m a^2}{6}\)
or I_PQ = \(\frac{2}{3}\) ma²
∴ Option (c) is correct.

Question 15.
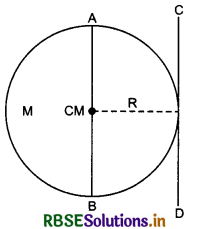
Moment of inertia of a ring of radius R and mass M about an axis parallel to horizontal diameter and situated at distance of R/2 from axis of rotation is:
(a) MR²
(b) \(\frac{1}{2}\)MR²
(c) 2MR²
(d) \(\frac{3}{4}\)MR²
Solution:
From theorem of parallel axes:
I = I_cm + mh² = \(\frac{1}{2} M R^2+M\left(\frac{R}{2}\right)^2\)
= \(\frac{1}{2} M R^2+\frac{M R^2}{4}=\frac{3}{4} M R^2\)
∴ Option (d) is correct.

Question 16.
Earth revolues around the sun in an elliptical orbit shown in figure. Sun is situated at its one focus S. At which point will the rotational kinetic energy of earth maximum?

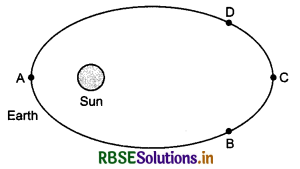
(a) A
(b) B
(c) C
(d) D
Solution:
Rotational energy E_R = \(\frac{1}{2}\)Iω² and principle of conservation of anguair momentum
L = Iω = constant.
Angular momentum remains constant in planetary motion. Moment of inetia at A will be minimum (Imin), therefore anguair velocity (ω) at A will be maximum. Hence rotational kinetic energy at A will be maximum. Hence option (a) is correct.

Question 17.
Moment of inertia of a ring about its diameter is I. Its moment of inertia about axis passing through its centre and normal to its plane is:
(a) 2I
(b) \(\frac{I}{2}\)
(c) \(\frac{3}{2}\)I
(d) I
Solution:
Given: I_AB = I_CD = I_d = I
I_zz = ?
On applying theorem of perpendicular axes
I_zz' = I_AB + I_CD = I + I = 2I
I_zz' = 2I
∴ Option (a) is correct.

Question 18.
Angular momentum of a particle executing uniform circular motion is L If its angular frequency is doubled and kinetic energy is halved, then its new angular momentum will be:
(a) \(\frac{L}{4}\)
(b) 2L
(c) 4L
(d) \(\frac{L}{2}\)
Solution:
Angular momentum L = Iω and kinetic energy K = \(\frac{1}{2}\) Iω²

When angular velocity is doubled and kinetic energy is halved, then angular momentum,
L' = \(\frac{2\left(\frac{K}{2}\right)}{2 \omega}=\frac{K}{2 \omega}=\frac{2 K}{4 \omega}=\frac{L}{4} \quad \text { or } \quad L^{\prime}=\frac{L}{4}\)
∴ Option (a) is correct.

Question 19.
A hot sphere is rotating about is diameter with the angular velocity w. If on cooling its radius becomes \(\frac{1}{n}\) of its initial radius, then its angular
velocity will become:
(a) \(\frac{\omega}{n}\)
(b) \(\frac{\omega}{n^2}\)
(c) nω
(d) n²ω
Solution:
No external torque is acting on the sphere, therefore its angular momentum will remain constant i.e.,

∴ Option (d) is correct.

Question 20.
A solid cylinder of mass 3kg is rolling on a horizontal plane with velocity of 4 ms^-1. It strikes with a spring of force constant 200 Nm^-1, what will be maximum compression in the spring?
(a) 0.5 m
(b) 0.6 m
(c) 0.7 m
(d) 0.2 m
Solution:
The rolling cylinder strike a spring,
∴ Loss in kinetic energy = Increase in potential energy of spring
or \(\frac{1}{2} m v^2\left(1+\frac{K^2}{R^2}\right)=\frac{1}{2} K x_{\max }^2\)

or x_max = 0.6 m
∴ Option (b) is correct.

Question 21.
ABC is an equilateral triangle, and forces F₁ ,F₂ and F₃ are acting in direction AB, BC and AC. If net torque about O is zero, then value of F₃ will be:

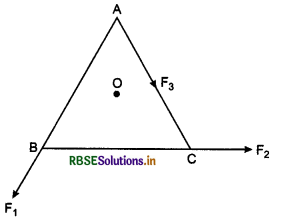
(a) F₁ + F₂
(b) F₁ - F₂
(c) \(\frac{F_1+F_2}{2}\)
(d) 2(F₁ + F₂)
Solution:
On taking clockwise torque,
τ = τF₁ + τF₂ + τF₃
Since net torque is zero,
∴ 0 = F₁ x r + F₂ x r + F₃ x r
or F₃ x r = F₁ x r + F₂ x r
or F₃ = F₁ + F₂
∴ Option (a) is correct.

Question 22.
A rod PQ of mass M and length L is joined at P. Rod is kept horizontal with the help of a massless string joined at Q figure. When string is cut, then initial angular acceleration of the rod is:

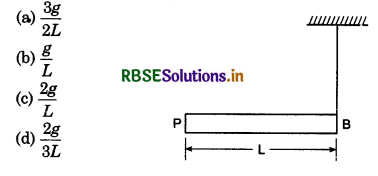
Solution:
When the string attached with end Q is cut, then torque acting on the rod,
τ = mg x \(\frac{L}{2}\)
Moment of inertia of the rod, about P,

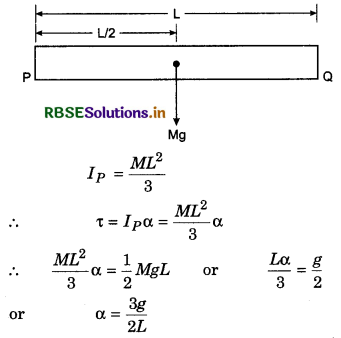
∴ Option (a) is correct.