RBSE Class 11 Physics Important Questions Chapter 6 कार्य, ऊर्जा और शक्ति

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 6 कार्य, ऊर्जा और शक्ति Important Questions and Answers.

RBSE Class 11 Physics Chapter 6 Important Questions कार्य, ऊर्जा और शक्ति

बहुचयनात्मक प्रश्न:

प्रश्न 1. 
किसी निकाय पर संरक्षी आंतरिक बल द्वारा किये गये कार्य का ऋणात्मक मान तुल्य होता है:
(अ) कुल ऊर्जा में परिवर्तन के
(ब) गतिज ऊर्जा में परिवर्तन के
(स) स्थितिज ऊर्जा में परिवर्तन के
(द) उपर्युक्त में से कोई नहीं
उत्तर:
(स) स्थितिज ऊर्जा में परिवर्तन के

प्रश्न 2. 
सभी प्रकार के बलों (बाह्य तथा आंतरिक) द्वारा निकाय पर किये गये कार्य का मान तुल्य होता है:
(अ) कुल ऊर्जा में परिवर्तन के
(ब) गतिज ऊर्जा में परिवर्तन के
(स) स्थितिज ऊर्जा में परिवर्तन के
(द) उपर्युक्त में से कोई नहीं
उत्तर:
(ब) गतिज ऊर्जा में परिवर्तन के

 

प्रश्न 3. 
दो पिण्डों की गतिज ऊर्जा बराबर है एवं उनके द्रव्यमानों का अनुपात 12 हो तो उनके रेखीय संवेगों का अनुपात होगा:
(अ) 1
(ब) 4
(स) 0.707
(द) 2
उत्तर:
(स) 0.707

प्रश्न 4. 
एक कण बल F = - kx के प्रभाव में x = 0 से x = x1 तक गति करता है। इसमें किया गया कार्य होगा:
(अ) kx³₁
(ब) kx₁²/2
(स) शून्य
(द) kx²₁
उत्तर:
(ब) kx₁²/2

प्रश्न 5. 
क्षमता अथवा शक्ति का SI मात्रक वाट तुल्य है:
(अ) किग्रा.- मीटर/सेकण्ड²
(ब) किग्रा.- मीटर/सेकण्ड²
(स) किग्रा.- मीटर/सेकण्ड³ 
(द) किग्रा.-मीटर
उत्तर:
(स) किग्रा.- मीटर/सेकण्ड³ 

प्रश्न 6. 
ऊर्जा संरक्षण नियम का अभिप्राय है:
(अ) कुल यांत्रिक ऊर्जा संरक्षित रहती है। 
(ब) कुल गतिज ऊर्जा संरक्षित रहती है
(स) कुल स्थितिज ऊर्जा संरक्षित रहती है
(द) सभी प्रकार की ऊर्जाओं का योग संरक्षित रहता है। 
उत्तर:
(द) सभी प्रकार की ऊर्जाओं का योग संरक्षित रहता है। 

प्रश्न 7. 
यदि किसी वस्तु का वेग दोगुना कर दिया जाये तो उसकी गतिज ऊर्जा:
(अ) वही रहेगी
(ब) आधी हो जायेगी
(स) दुगुनी हो जायेगी
(द) चार गुनी हो जायेगी
संकेत K α v2
अतः सही विकल्प (द) है।
उत्तर:
(द) चार गुनी हो जायेगी

प्रश्न 8. 
m द्रव्यमान के एक कण का संवेग P है उसकी गतिज ऊर्जा होगी:
(अ) p²/2m
(ब) P²/m
(स) p²m
(द) mP
उत्तर:
(अ) p²/2m

प्रश्न 9. 
एक मनुष्य एक दीवार को धकेलता है तथा इसको विस्थापित नहीं कर पाता है, वह दर:
(अ) ऋणात्मक कार्य करता है।
(ब) धनात्मक कार्य करता है, परन्तु अधिकतम नहीं
(स) कोई कार्य नहीं करता है।
(द) अधिकतम कार्य करता है।
उत्तर:
(स) कोई कार्य नहीं करता है।

प्रश्न 10. 
ऐसी कौनसी राशि है जो कि प्रत्यास्थ तथा अप्रत्यास्थ दोनों टक्करों में संरक्षित रहती है:
(अ) रेखीय ऊर्जा
(ब) कुल यान्त्रिक ऊर्जा
(स) स्थितिज ऊर्जा
(द) गतिज ऊर्जा
उत्तर:
(अ) रेखीय ऊर्जा

प्रश्न 11. 
एक प्लेटफॉर्म पर बॉक्स को उठाने में किया गया कार्य निम्न में से किस पर निर्भर करता है:
(अ) इसे कितनी तेजी से उठाया गया है।
(ब) आदमी की शक्ति पर
(स) ऊँचाई, जिस तक इसे उठाया गया है
(द) बॉक्स के क्षेत्रफल पर
उत्तर:
(स) ऊँचाई, जिस तक इसे उठाया गया है

प्रश्न 12. 
दो स्प्रिंगों के बल नियतांक k₁ तथा k₂ हैं। उनमें समान खिंचाव x उत्पन्न किया जाता है। इनकी प्रत्यास्थ ऊर्जा E₁ व E₂ हो तो E₁ तथा E₂ का अनुपात होगा:
\(\text { (अ) } \frac{k_1}{k_2}\)
\(\text { (ब) } \frac{k_2}{k_1}\)
\(\text { (स) } \sqrt{\frac{k_2}{k_1}}\)
(द) उपर्युक्त में से कोई नहीं
संकेत: \(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{\frac{1}{2} k_1 x^2}{\frac{1}{2} k_2 x^2}=\frac{k_1}{k_2}\)
अतः सही विकल्प (अ) है।
उत्तर:
\(\text { (अ) } \frac{k_1}{k_2}\)

प्रश्न 13. 
राशियाँ (Quantities) जो किसी टक्कर में नियत रहती हैं:
(अ) संवेग, गतिज ऊर्जा तथा ताप
(ब) संवेग लेकिन गतिज ऊर्जा तथा ताप नहीं
(स) संवेग, गतिज ऊर्जा तथा ताप में से कोई नियत नहीं रहती 
(द) उपर्युक्त में से कोई नहीं
उत्तर:
(ब) संवेग लेकिन गतिज ऊर्जा तथा ताप नहीं

प्रश्न 14. 
यदि एक बल F को किसी पिण्ड पर लगाने से उस पिण्ड को v वेग प्राप्त होता है तो शक्ति का मान होगा:
((अ) v/F
(ब) Fv²
(स) Fv
(द) F/v²
उत्तर:
(स) Fv

प्रश्न 15. 
किसी पिण्ड पर किया गया कार्य निर्भर नहीं करता
(अ) पिण्ड की प्रारम्भिक चाल पर
(ब) बल व विस्थापन के मध्य कोण पर
(स) विस्थापन पर
(द) आरोपित बल पर
उत्तर:
(अ) पिण्ड की प्रारम्भिक चाल पर

प्रश्न 16. 
एक व्यक्ति दूरी तक सिर पर वजन रखकर ढोता है। उसे अधिकतम कार्य करना पड़ता है जब वह वस्तु को लेकर:
(अ) खुरदरे क्षैतिज सतह पर चलता है।
(ब) चिकनी क्षैतिज सतह पर चलता है। 
(स) ऊर्ध्व तल पर ऊपर चलता है। 
(द) नत तल पर चलता है।
उत्तर:
(स) ऊर्ध्व तल पर ऊपर चलता है। 

प्रश्न 17. 
यदि \(\overrightarrow{\mathrm{F}}=(20 \hat{i}+15 \hat{j}-5 \hat{k})\) तथा \(\overrightarrow{\mathrm{v}}=(6 \hat{i}-4 \hat{j}+3 \hat{k})\) m/s है तो तात्क्षणिक शक्ति होगी:
(अ) 35 W
(ब) 25 W
(स) 90 W
(द) 45 W
संकेत: तात्क्षणिक शक्ति
\(\begin{aligned} & =\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{v}} \\ & =(20 \hat{i}+15 \hat{j}-5 \hat{k}) \cdot(6 \hat{i}-4 \hat{j}+3 \hat{k}) \end{aligned}\)
= 20 × 6 + 15 × (-4 ) + (-5) × 3 
= 120 - 60 - 15 = 45 W
अतः सही विकल्प (द) है।
उत्तर:
(द) 45 W

प्रश्न 18. 
पूर्णतः प्रत्यास्थ टक्कर के लिए प्रत्यावस्थापन गुणांक ९ का मान होता है:
(अ) 1
(ब) 0
(स) ∞
(द) - 1
उत्तर:
(अ) 1

रिक्त स्थानों की पूर्ति कीजिए:

प्रश्न 1.
यदि \(\overrightarrow{\mathrm{A}}\) और \(\overrightarrow{\mathrm{B}}\) दो सदिश राशियाँ हैं और इनके बीच का θ कोण है, तब\(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}\) = ........................
उत्तर:
AB cosθ

प्रश्न 2. 
तब दो सदिश आपस में लम्बवत् हैं तब \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}\) = .........................
उत्तर:
शून्य

प्रश्न 3.
जब विस्थापन बल की दिशा में हो तो बल द्वारा किया गया। कार्य ............................. होता है।
उत्तर:
अधिकतम

प्रश्न 4.
1 kwh = .................. जूल
उत्तर:
3.6 x 100 जूल

प्रश्न 5.
किसी पिण्ड की गतिज ऊर्जा में परिवर्तन उस पर आरोपित कुल बल द्वारा किया गया कार्य है। Kf - Ki = .....................
उत्तर:
Wnet

प्रश्न 6.
संरक्षी बलों की उपस्थिति में किसी विलगित निकाय की यांत्रिक ऊर्जा ........................  रहती है।
उत्तर:
संरक्षित
 
प्रश्न 7. 
अल्बर्ट आइंस्टीन के अनुसार ऊर्जा व द्रव्यमान तुल्य राशियाँ होती हैं। अर्थात् E = .........................
उत्तर:
mc²

प्रश्न 8.
1 अश्व शक्ति = ....................... वॉट
उत्तर:
746

प्रश्न 9.
आंशिक प्रत्यास्थी टक्कर के लिए .....................
उत्तर:
0 < e < 1 

प्रश्न 10.
टक्कर से पूर्व पास आने की सापेक्ष गति तथा टक्कर के पश्चात् दूर हटने की सापेक्ष गति ........................... होती है।
उत्तर:
बराबर

नीचे दिये गये वाक्यों में सत्य / असत्य कथन का चयन कीजिए:

प्रश्न 1.
ज्यामिति के अनुसार B cos θ सदिश \(\overrightarrow{\mathrm{B}}\) का सदिश A पर प्रक्षेप है।
उत्तर:
सत्य

प्रश्न 2.
ऋणात्मक कार्य वस्तु की गति में मंदन कार्य समय पर निर्भर नहीं करता है।
उत्तर:
सत्य

प्रश्न 3.
1 eV = 16 x 10^-19 जूल।
उत्तर:
असत्य

प्रश्न 4.
K बल - नियतांक वाले स्प्रिंग जिसमें खिंचाव x है, की प्रत्यास्थ स्थितिज ऊर्जा U = mgx होती है।
उत्तर:
असत्य

प्रश्न 5.
बल द्वारा किया गया कार्य शून्य होता है। जब पिण्ड के लिए जो स्वेच्छा से किसी ऐसे बन्द पथ प्रारम्भिक स्थिति पर वापस आ जाता है।
उत्तर:
सत्य

प्रश्न 6. 
ऊर्जा संरक्षण सिद्धान्त के लिए K.E. + P.E. = E स्थिरांक
उत्तर:
सत्य

प्रश्न 7. 
सरल रेखीय या एकविमीय प्रत्यास्थ टक्कर के लिए में स्वतः अपनी u₁ - u₂ = -(v² - v¹)
उत्तर:
असत्य

प्रश्न 8.
स्थितिज ऊर्जा जो कि प्रत्यास्थ तथा अप्रत्यास्थ दोनों टक्करों में संरक्षित रहती है।
उत्तर:
असत्य

प्रश्न 9.
पिण्ड की प्रारम्भिक चाल पर किया गया कार्य निर्भर नहीं करता है।
उत्तर:
सत्य

प्रश्न 10.
यदि किसी वस्तु का वेग दुगुना कर दिया जाये तो उसकी गतिज ऊर्जा भी दुगुनी हो जायेगी।
उत्तर:
असत्य

कॉलम - A से कॉलम B का सही मिलान कीजिए:

प्रश्न 1.

 

कॉलम-A	कॉलम-B
\(\text { 1. } \hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=\)	(A) 16
\(\text { 2. }|\hat{i}|=|\hat{j}|=|\hat{k}|\)	(B) शून्य
\(\text { 3. }(3 \hat{i}+4 \hat{j}-5 \hat{k}) \cdot(5 \hat{i}+4 \hat{j}+3 \hat{k})=\)	(C) 4.2 जूल/ कैलोरी
4. विस्थापन के लम्बवत् लगने वाले बल द्वारा किया गया कार्य सदैव होता है।	(D) विद्युत ऊर्जा
5. किसी निकाय पर किया गया कार्य (W) तथा उत्पन्न ऊष्मा (H) परस्पर होते हैं।	(E) असंरक्षी बल
6. ऊष्मा का यांत्रिक तुल्यांक का मान होता है।	(F) 1/2Iω2
7. एक शुष्क सेल में रासायनिक ऊर्जा का रूपान्तरण होता है।	(G) न्यूटन/मीटर
8. पिण्ड की घूर्णन गतिज ऊर्जा का मान होता है।	(H) समानुपाती
9. स्प्रिंग नियतांक का मात्रक है।	(I) 1
10. घर्षण बल तथा श्यान बल होते हैं।	(A) 16

उत्तर:

कॉलम-A	कॉलम-B
\(\text { 1. } \hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=\)	(B) शून्य
\(\text { 2. }|\hat{i}|=|\hat{j}|=|\hat{k}|\)	(I) 1
\(\text { 3. }(3 \hat{i}+4 \hat{j}-5 \hat{k}) \cdot(5 \hat{i}+4 \hat{j}+3 \hat{k})=\)	(A) 16
4. विस्थापन के लम्बवत् लगने वाले बल द्वारा किया गया कार्य सदैव होता है।	(H) समानुपाती
5. किसी निकाय पर किया गया कार्य (W) तथा उत्पन्न ऊष्मा (H) परस्पर होते हैं।	(C) 4.2 जूल/ कैलोरी
6. ऊष्मा का यांत्रिक तुल्यांक का मान होता है।	(D) विद्युत ऊर्जा
7. एक शुष्क सेल में रासायनिक ऊर्जा का रूपान्तरण होता है।	(F) 1/2Iω2
8. पिण्ड की घूर्णन गतिज ऊर्जा का मान होता है।	(G) न्यूटन/मीटर
9. स्प्रिंग नियतांक का मात्रक है।	(E) असंरक्षी बल
10. घर्षण बल तथा श्यान बल होते हैं।	(B) शून्य

 

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
गुरुत्व के विरुद्ध किसी मनुष्य द्वारा किया गया कार्य कितना होगा यदि वह समतल में चल रहा है?
उत्तर:
शून्य। चूँकि वह गुरुत्व बल के लम्बवत् चल रहा है।

प्रश्न 2. 
एक ट्रक तथा एक कार समान गतिज ऊर्जा से सीधी सड़क पर चल रहे हैं। दोनों के इंजन एक साथ बंद कर देने पर कौनसा कम दूरी पर रुकेगा?
उत्तर:
∵ 1/2m₁v₁² = 1/2m₂v₂²
यहाँ पर M₁. V₁ट्रक का द्रव्यमान और वेग है और M₂. V₂ कार का द्रव्यमान और वेग है।
∵ m₁  > m₂
∴ ट्रक का वेग कम होने के कारण ट्रक कम दूरी तय करेगा।

प्रश्न 3. 
एक कुली ने एक बॉक्स को बस की छत पर 5 मिनट में चढ़ा दिया। दूसरे कुली ने उसी बॉक्स को 2 मिनट में चढ़ा दिया। कौनसे कुली ने अधिक कार्य किया?
उत्तर:
दोनों ने बराबर कार्य किया। चूँकि दोनों का विस्थापन बराबर है।

प्रश्न 4. 
एक कुली बॉक्स को पृथ्वी से ऊँचाई पर एक बस की छत पर रख देता है। बॉक्स पर कुली तथा गुरुत्वीय क्षेत्र द्वारा किया गया कुल कार्य क्या होगा?
उत्तर:
शून्य चूँकि कुली के द्वारा किया गया कार्य गुरुत्वीय बल के द्वारा किये गये कार्य के बराबर व विपरीत है।

प्रश्न 5. 
घड़ी में चाबी भरने पर स्प्रिंग में कौनसी ऊर्जा संचित होती है? घड़ी के चलते रहने पर यह ऊर्जा कौनसी ऊर्जा में परिवर्तित होती है?
उत्तर:
स्थितिज ऊर्जा, गतिज ऊर्जा।

प्रश्न 6. 
क्या यांत्रिक ऊर्जा हमेशा संरक्षित रहती है?
उत्तर:
नहीं, सिर्फ विलगित निकाय की जबकि आंतरिक असंरक्षी बल शून्य है।

प्रश्न 7. 
10 किग्रा द्रव्यमान को ऊपर की ओर 10 मी. उठाने में गुरुत्वीय बल द्वारा किया गया कार्य कितना होगा?
उत्तर:
गुरुत्वीय बल द्वारा किया गया कार्य
W = m(-g)h 
= - mgh
= - 10 × 10 × 10 = 1000 जूल

प्रश्न 8. 
क्या किसी निकाय के संवेग में परिवर्तित किये बिना, गतिज ऊर्जा परिवर्तित की जा सकती है?
उत्तर:
हाँ चूँकि ऐसा अप्रत्यास्थ टक्कर में होता है।

प्रश्न 9. 
क्या किसी कण की गतिज ऊर्जा परिवर्तित किये बिना, उसका संवेग परिवर्तित किया जा सकता है?
उत्तर:
हाँ, एक समान वृत्तीय गति में।

प्रश्न 10. 
क्या किसी पूर्णतः अप्रत्यास्थ टक्कर में सम्पूर्ण गतिज ऊर्जा क्षय हो सकती है?
उत्तर:
हाँ, जबकि टक्कर से पूर्व कणों का कुल संवेग शून्य हो। 

प्रश्न 11. 
इलेक्ट्रोन वोल्ट किस भौतिक राशि का मात्रक होता है? 
उत्तर:
ऊर्जा का।

प्रश्न 12. 
जब तीर को छोड़ा जाता है तो उसे गतिज ऊर्जा कहाँ से प्राप्त होती है?
उत्तर:
धनुष की स्थितिज ऊर्जा से।

प्रश्न 13. 
चन्द्रमा को अपनी कक्षा में (कक्षा को वृत्तीय माना गया है) बनाये रखने में पृथ्वी के गुरुत्वाकर्षण बल द्वारा किया गया कार्य, यदि दीर्घवृत्तीय कक्षा हो तब।
उत्तर:
कार्य W = 0 क्योंकि विस्थापन हमेशा लगाये गये बल के लम्बवत् है। दीर्घवृत्तीय कक्षा में पूर्ण कक्षा के लिये W = 0 होगा। 

प्रश्न 14. 
एक हल्के व भारी पिण्ड की गतिज ऊर्जायें समान हैं। किसका संवेग अधिक होगा?
उत्तर:
भारी पिण्ड का संवेग अधिक होगा क्योंकि संवेग
\(\mathrm{P}=\sqrt{2 m \mathrm{E}}\)

प्रश्न 15. 
क्या किसी वस्तु में बिना संवेग के ऊर्जा संभव है? 
उत्तर:
स्थितिज ऊर्जा संभव है।

प्रश्न 16. 
क्या सदिशों का अदिश गुणनफल (Scalar Product) ऋणात्मक हो सकता है?
उत्तर:
सदिशों \(\overrightarrow{\mathbf{A}}\) व \(\overrightarrow{\mathrm{B}}\) का अदिश गुणनफल \(\vec{A} \cdot \vec{B}=A B\) cos θ होता है। यदि θ का मान 90° से अधिक हो तो cosθ का मान ऋणात्मक होगा, जिसके अनुरूप A. B का मान भी ऋणात्मक होगा। 

प्रश्न 17. 
किसी पिण्ड की चाल कितनी कर दी जाये जिससे उसकी गतिज ऊर्जा प्रारम्भिक गतिज ऊर्जा की आधी रह जाये ?
उत्तर:
प्रारम्भिक चाल की \(\frac{1}{\sqrt{2}}\) गुना।

प्रश्न 18. 
पृथ्वी के चारों ओर घूमने वाले उपग्रह पर अभिकेन्द्रीय बल द्वारा किया गया कार्य शून्य होता है। कारण लिखिये।
उत्तर:
अभिकेन्द्रीय बल व उपग्रह का विस्थापन परस्पर सदैव लम्बवत होता है।

प्रश्न 19. 
वृत्ताकार पथ में गतिमान कण पर अभिकेन्द्रीय बल द्वारा किया गया कार्य शून्य क्यों होता है?
उत्तर:
यह बल केवल कण की गति की दिशा में परिवर्तन करता है एवं चाल का मान समान रहता है एवं गतिज ऊर्जा भी समान रहती है। 

प्रश्न 20. 
एक किलोवाट घण्टा में जूल की संख्या ज्ञात कीजिये। 
उत्तर:
1 किलोवाट घण्टा = 1000 x 1 वाट घण्टा
= 1000 x 3600
1 किलोवाट घण्टा = 36 x 105 जूल
= 3.6 x 106 जूल।

प्रश्न 21. 
शक्ति किसे कहते हैं?
उत्तर:
कार्य करने की दर को शक्ति कहते हैं।

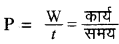
इसका मात्रक जूल / से होता है।

प्रश्न 22. 
अधिकतम तथा न्यूनतम कार्य के लिये बल तथा विस्थापन के बीच कितना कोण होना चाहिये?
उत्तर:
कार्य W= FS cos θ
जब कोण का मान शून्य होता है तो कार्य अधिकतम होता है। जब कोण 90° का हो तो कार्य W= FS cos 90° होगा। अर्थात् कार्य W= शून्य होगा।

प्रश्न 23 
वस्तु की पृथ्वी की सतह से ऊँचाई अधिक होने पर स्थितिज ऊर्जा के मान पर क्या प्रभाव पड़ता है?
उत्तर:
स्थितिज ऊर्जा का मान अधिक होगा।

प्रश्न 24. 
क्या यह सम्भव है कि गति नहीं होने पर भी किसी बल से कार्य किया जा सकता है?
उत्तर:
हाँ, कमानी को दबाने अथवा खींचने पर।

प्रश्न 25. 
क्या किसी पिण्ड में बिना संवेग के ऊर्जा हो सकती है? 
उत्तर:
हाँ, पिण्ड के कणों की ऊष्मीय गति के कारण आन्तरिक ऊर्जा होती है, जबकि गतिमान कणों के संवेगों का सदिश योग शून्य हो सकता है।

प्रश्न 26. 
किसी कण पर कार्यरत असमान बलों की न्यूनतम संख्या कितनी होनी चाहिये जिनका परिणामी बल शून्य 'जाये? 
उत्तर:
किसी भी कण पर कार्य करने वाले बलों की संख्या तीन होनी चाहिये जिनका परिणामी बल शून्य हो जायेगा।

प्रश्न 27. 
एक वस्तु की गतिज ऊर्जा 40 जूल है, यदि उसका द्रव्यमान 5 किग्रा हो तो वस्तु का वेग कितना होगा?
उत्तर-
K.E. = 1/2 mv²
40 = 1/2 x 5 x v²
v² = 16
v = 4 मी./सेकण्ड

प्रश्न 28. 
खींची हुई स्प्रिंग के प्रत्यास्थ स्थितिज ऊर्जा का मान कितना होता है?
उत्तर:
U_(x) = 1/2kx²

प्रश्न 29. 
पूर्णतः प्रत्यास्थ टक्कर में प्रत्यावस्थान गुणांक का मान कितना होता है?
उत्तर:
प्रत्यावस्थान गुणांक e = 1

प्रश्न 30. 
क्या किसी पूर्णतः अप्रत्यास्थी टक्कर में सम्पूर्ण गतिज ऊर्जा का क्षय हो सकता है?
उत्तर:
नहीं।

प्रश्न 31. 
गुरुत्वीय क्षेत्र में स्वतन्त्र रूप से गिरती हुई वस्तु की कुल यान्त्रिक ऊर्जा बढ़ती है। यह कथन सत्य है अथवा असत्य?
उत्तर:
असत्य 

प्रश्न 32. 
सरल रेखीय प्रत्यास्थ टक्कर में यदि कोई कण समान द्रव्यमान के कण से टकराते हैं तो टक्कर के पश्चात् कणों के वेगों में क्या सम्बन्ध होता है?
उत्तर:
टक्कर के पश्चात् कणों के वेग परस्पर आपस में बदल जाते

प्रश्न 33.
जब संघट्ट ऋणात्मक आवेशित पिण्ड तथा धनात्मक आवेशित पिण्डों के बीच हो, तो संघट्ट किस प्रकार का होता है? 
उत्तर:
पूर्णतः अप्रत्यास्थ

प्रश्न 34. 
जब दो क्वाटर्स की गेंदें आपस में संघट्ट करती हैं तो संघट्ट किस प्रकार का होता है?
उत्तर:
पूर्णतः प्रत्यास्थ संघट्ट।

प्रश्न 35. 
दोलनकारी लोलक की चाल कहाँ पर अधिकतम है? 
उत्तर:
लोलक के न्यूनतम बिन्दु पर

प्रश्न 36. 
प्रत्यास्थ संघट्ट में कब ऊर्जा विनिमय अधिकतम होता हैं।
उत्तर:
जब दो संघटनकारी पिण्ड समान द्रव्यमान के हों।

प्रश्न 37. 
किसी पिण्ड की प्रत्यास्थता के उस प्राचल का नाम लिखिए जिसको इसके मापन का अंश कहते हैं।
उत्तर:
प्रत्यावस्थान गुणांक।

प्रश्न 38. 
क्या किसी सम्पूर्ण प्रत्यास्थ संघट्ट में पूर्ण गतिज ऊर्जा का क्षय हो जाता है?
उत्तर:
नहीं, केवल उतनी ही गतिज ऊर्जा का हास होता है, जितनी रैखिक संवेग संरक्षण के लिए आवश्यक है।

प्रश्न 39. 
एक हवाई जहाज का वेग तिगुना किया जाता है। संवेग क्या होगा? क्या संवेग संरक्षित रहेगा?
उत्तर:
हवाई जहाज का संवेग तिगुना हो जायेगा। जहाज + वायु का संवेग संरक्षित रहेगा क्योंकि जहाज के संवेग में जितनी वृद्धि होगी उतनी ही वृद्धि वायु के संवेग में उल्टी दिशा में हो जायेगी।

प्रश्न 40. 
एक तोप से गोला दागा जाता है और वह ऊपर जाकर फट जाता है। इसके संवेग तथा गतिज ऊर्जा में क्या परिवर्तन होगा? 
उत्तर:
संवेग नियत रहेगा। गतिज ऊर्जा बढ़ेगी क्योंकि बारूद की रासायनिक ऊर्जा गतिज ऊर्जा में बदलती है।

लघुत्तरात्मक प्रश्न:

प्रश्न 1. 
दो सदिश \(\overrightarrow{\mathbf{A}}\) व \(\overrightarrow{\mathbf{B}}\) का योग व अन्तर परस्पर लम्बवत् हो तो सिद्ध कीजिए कि दोनों सदिश परिमाण में बराबर हैं।
उत्तर:
सदिशों \(\overrightarrow{\mathrm{A}}\) व \(\overrightarrow{\mathbf{B}}\) का योग = \(\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\)
अन्तर = \(\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\)
∵ दिया गया है कि दोनों लम्बवत् है अतः इनका अदिश गुणनफल शून्य होगा।

या
A² - B² = 0
A = B
अर्थात् दोनों सदिश परिमाण में बराबर हैं।

प्रश्न 2. 
जब एक गेंद को ऊपर फेंका जाता है तो पहले उसके संवेग का परिमाण घटता है तत्पश्चात् बढ़ता है। क्या यह संवेग संरक्षण के सिद्धान्त का उल्लंघन करता है?
उत्तर:
नहीं, क्योंकि निकाय (गेंद तथा वायु के अणु) का संवेग हमेशा नियत रहता है जब गेंद का संवेग घटता है तब वायु के कणों का संवेग बढ़ता है तथा गेंद का संवेग बढ़ने पर वायु के कणों का संवेग घटता है।

प्रश्न 3. 
चित्र में दो चिकने नत तल प्रदर्शित हैं। इन पर समान द्रव्यमान के दो पिण्ड A व B बिन्दु P से स्थिरावस्था से फिसलना प्रारम्भ करते हैं। कौनसा पिण्ड अधिक वेग से जमीन पर पहुँचेगा ?

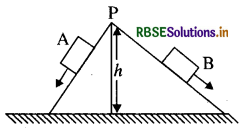
उत्तर:
गतिज ऊर्जा में वृद्धि स्थितिज ऊर्जा में हानि
या 1/2mv² = mgh
∴ \(\mathrm{v}=\sqrt{2 g h}\)
∵ दोनों गेंदें एक ही ऊँचाई से गिरती हैं, अतः दोनों धरती पर समान चाल से पहुँचेंगी।

प्रश्न 4. 
कार्य किसे कहते हैं और साथ ही निम्न के उदाहरण दीजिए:
(i) शून्य कार्य 
(ii) धनात्मक कार्य 
(iii) ऋणात्मक कार्य।
उत्तर:
माना कि एक अचर बल F, किसी m द्रव्यमान के पिण्ड पर लग रहा है, जिसके कारण पिण्ड का धनात्मक x-दिशा में होने वाला
विस्थापन \(\overrightarrow{\mathrm{s}}\) है। जैसा कि चित्र में दिखाया गया है।

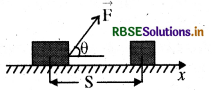
अतः किसी बल द्वारा किया गया कार्य "बल के विस्थापन की दिशा के अनुदिश घटक और विस्थापन के परिमाण के गुणनफल" के रूप में - परिभाषित किया जाता है। अतः
W = (Fcos 6) s = \(\vec{F} \cdot \vec{S}\) .....(1) 
(i) शून्य कार्य-समीकरण (1) से स्पष्ट है कि यदि वस्तु का विस्थापन शून्य है, तो बल का परिमाण कितना ही अधिक क्यों न हो, वस्तु द्वारा किया गया कार्य शून्य होता है। कोई भी कार्य संपन्न हुआ नहीं माना जाता है यदि
(i) वस्तु का विस्थापन शून्य है, (ii) बल शून्य है, (iii) बल और विस्थापन परस्पर लम्बवत् हैं। चूँकि θ = π/2 पर cosπ⁄2 = 0 होता है। नियत चाल से वृत्ताकार पथ में गतिशील पिण्ड पर अभिकेन्द्रीय बल, विस्थापन के लम्बवत् है इसलिए अभिकेन्द्रीय बल के द्वारा किया गया कार्य शून्य होता है।
(ii) धनात्मक कार्य - यदि θ > 0° और θ < 90° होता है तो cose का मान धनात्मक होता है। ऐसी स्थिति में कार्य धनात्मक होता है। जैसे जब कोई आदमी किसी रोलर को खींचता है, तो कार्य का मान धनात्मक होता है।
(iii) ऋणात्मक कार्य जब 90° < θ < 180° तो cos θ का मान ऋणात्मक (Negative) होता है अतः कार्य ऋणात्मक होता है। जैसे जब किसी रोलर को खुरदरी सतह (Rough Surface) पर खींचा जाता है तो घर्षण बल तथा विस्थापन परस्पर विपरीत दिशा में होते हैं अतः घर्षण बल के द्वारा किया गया कार्य ऋणात्मक होता है।

प्रश्न 5. 
गतिज ऊर्जा किसे कहते हैं? सिद्ध कीजिए कि किसी पिण्ड की गतिज ऊर्जा का मान 1/2 mv2 होता है।
उत्तर:
गतिज ऊर्जा किसी पिण्ड की गति के कारण उसमें कार्य करने की क्षमता को गतिज ऊर्जा कहा जाता है।
जैसे- बन्दूक से गोली का निकलना, नदी का बहता हुआ पानी, चलती हुई साइकिल में गतिज ऊर्जा होती है।
गतिज ऊर्जा का मापन कार्य के उस परिमाण से किया जाता है, जो कोई गतिशील पिण्ड गति विरोधी बलों के विरुद्ध विराम अवस्था में आने तक कर सकता है। इसको हम साधारणतः K से प्रदर्शित करते हैं।
माना कोई पिण्ड जिसका द्रव्यमान । है, वह वेग v मी./से. के वेग से चल रहा है जिस पर कोई नियत बल F लग रहा है। विरोधी बल के कारण पिण्ड का वेग लगातार घट रहा है तथा वह अन्त में आकर स्थिर अवस्था प्राप्त कर लेता है। माना पिण्ड S दूरी तय करने के बाद स्थिर अवस्था में आ जाता है।
अतः पिण्ड की गतिज ऊर्जा
K = W = F x S
K = W = ma x S
∵ F = ma
∴ K = mas .............. (1)
न्यूटन के तीसरे समीकरण से
v² = u² - 2as
O = v² - 2as
(∵ मंदन हो रहा है)
( ∵ यहाँ पर अन्तिम वेग शून्य है)
∵ a = v²/2s
समी. (1) मेंa का मान रखने पर
\(\mathrm{K}=m\left(\frac{\mathrm{v}^2}{2 \mathrm{~S}}\right) \times \mathrm{S}=\frac{1}{2} m \mathrm{v}^2\)
K = 1/2 mv²

प्रश्न 6. 
स्थितिज ऊर्जा की प्रमुख विशेषताएँ लिखिए। 
उत्तर:
(i) स्थितिज ऊर्जा स्थिति का अदिश फलन है।
(ii) स्थितिज ऊर्जा का स्थिति के सापेक्ष अवकलन का ऋणात्मक मान बल का निर्धारण करता है।
\(\overrightarrow{\mathrm{F}}=-\frac{d}{d t} \mathrm{U}_{(x)}\)
(iii) स्थितिज ऊर्जा का मान निर्देश तन्त्र पर निर्भर करता है। 
(iv) स्थितिज ऊर्जा की अभिधारणा केवल आन्तरिक संरक्षी बलों के लिए परिभाषित होती है, असंरक्षी बलों के लिए नहीं।
(v) किसी दृढ़ पिण्ड की गति में स्थितिज ऊर्जा में परिवर्तन जारी रहता है क्योंकि दृढ़ पिण्ड की गति में बाह्य बल लगाने पर भी इसके कणों के मध्य की दूरी परिवर्तित नहीं होती।

प्रश्न 7. 
संरक्षी व असंरक्षी बलों को परिभाषित कीजिए। इनके उदाहरण भी दीजिए।
उत्तर:
संरक्षी बल-यदि बल द्वारा सम्पन्न कार्य, विस्थापन के पथ पर निर्भर न कर केवल प्रारम्भिक व अन्तिम स्थितियों पर निर्भर करे तो बल संरक्षी कहलाते हैं। संरक्षी बल के प्रभाव में पूर्ण चक्र में किया गया कार्य शून्य होता है।
उदाहरणार्थ: प्रत्यानयन बल, केन्द्रीय बल, गुरुत्वीय बल आदि। असंरक्षी बल-यदि बल द्वारा सम्पन्न कार्य पथ पर निर्भर करता है। तो बल असंरक्षी कहलाते हैं। इसके पूर्ण चक्र में किया गया कार्य शून्य नहीं होता है।
उदाहरणार्थ: श्यान बल, घर्षण बल अवमन्दन बल आदि।

प्रश्न 8. 
दो स्प्रिंग A व B सभी प्रकार से समान हैं। परन्तु स्प्रिंग A स्प्रिंग B से कठोर है यानी KA > KB किस स्प्रिंग पर अधिक कार्य करना पड़ेगा यदि:
(a) दोनों समान लम्बाई तक खींची जायें
(b) दोनों समान बल से खींची जायें।
उत्तर:
(a) यदि स्प्रिंगों के खिंचाव x₁ व x₂ हों, तो किये गये कार्य W₁ = 1/2k₁x₁²
तथा W₂ = 1/2k₂x₂²
∵ x₁ = x₂ तथा k₁ > k₂ 
अतःW₁ > W₂
अतः स्प्रिंग A पर अधिक कार्य जायेगा।

(b) F₁ = k₁x₁ तथा F₂ = k₂x₂ हो तो
W₁ = 1/2F₁x₁ ............ (1)
तथा
W₂ = 1/2F₂x₂ ................ (2)
∵दिया गया है - F₁ = F₂
अतः
k₁x₁ = k₂x₂
∵ k₁ > k₂
अतः x₁ < x₂
समीकरण (1) तथा (2) से स्पष्ट है कि
W₁ < W₂ अतः स्प्रिंग B पर अधिक कार्य किया जायेगा 

प्रश्न 9. 
दोलन करता हुआ एक लोलक कुछ समय पश्चात् रुक जाता है क्या यह यांत्रिक ऊर्जा के संरक्षण के नियम का उल्लंघन है ?
उत्तर:
दोलन करते हुए लोलक की गतिज ऊर्जा तथा स्थितिज ऊर्जा में परस्पर रूपान्तरण होता रहता है तथा पिण्ड की सम्पूर्ण ऊर्जा नियत रहती है तथा यांत्रिक ऊर्जा के संरक्षण के नियम का पालन होता है परन्तु यह स्थिति तभी सम्भव है जब घर्षण बल उपस्थित न हो लेकिन वास्तव में दोलन करते लोलक में कुछ न कुछ घर्षण बल अवश्य होता है जिसके कारण लोलक कुछ समय बाद रुक जाता है।

प्रश्न 10. 
सिद्ध कीजिये कि वस्तु ऊँचाई से जैसे-जैसे धरातल की ओर आती है, स्थितिज ऊर्जा घटती है एवं समान मात्रा में गतिज ऊर्जा बढ़ती है।
उत्तर:
माना m द्रव्यमान की वस्तु पृथ्वी की सतह से / ऊँचाई पर चित्र में बिन्दु A पर स्थिर अवस्था में है। बिन्दु A पर वस्तु में केवल स्थितिज ऊर्जा होगी और गतिज ऊर्जा शून्य होगी। बिन्दु A पर स्थितिज ऊर्जा का मान = mgh माना वस्तु स्वतन्त्रतापूर्वक गिरती है और जब वस्तु धरातल पर पहुँचती है तब उसकी चाल v है, अतः बिन्दु B पर गतिज ऊर्जा का
मान 1⁄2mv² होगा। यहाँ पर h = 0 इसलिए स्थितिज ऊर्जा u = 0 होगा।

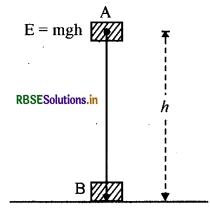
गति के तीसरे समीकरण से बिन्दु B पर वस्तु की चाल
v² = u² + 2as
v² = 0 + 2gh
∴ v² = 2gh बिन्दु 13 पर वस्तु की गतिज ऊर्जा
K = 1⁄2mv²
∴ K = 1⁄2m x 2gh = mgh
K = mgh
अर्थात् पृथ्वी के धरातल पर वस्तु की गतिज ऊर्जा का मान बिन्दु A पर स्थितिज ऊर्जा के तुल्य होता है। स्वतन्त्रतापूर्वक गिरती हुई वस्तु की स्थितिज ऊर्जा में कमी, उसकी गतिज ऊर्जा में वृद्धि के तुल्य होती है। वस्तु ऊँचाई से जैसे-जैसे धरातल की ओर आती है, स्थितिज ऊर्जा घटती है एवं समान मात्रा में गतिज ऊर्जा बढ़ती है।
ΔΚ = -ΔU

प्रश्न 11. 
यदि दो स्प्रिंगों के बल नियतांक क्रमश: k₁ तथा k₂ हों तथा k₁ = 2k₂ है तो उन स्प्रिंगों को समान बल लगाकर खींचने पर किये गये कार्यों का अनुपात ज्ञात कीजिये ।
उत्तर:
यहाँ
k₁ = 2k₂ 
F₁ = F₂
-k₁x₁ = - k₂x₂

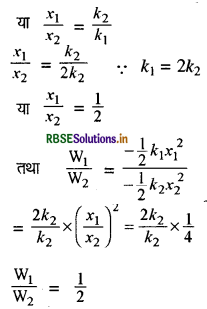
W₁ : W₂ = 1 : 2

प्रश्न 12. 
एक आदर्श स्प्रिंग में \(\overrightarrow{\mathrm{F}}=-k \vec{x}\) नियम का पालन किया जाता है। यहाँ स्प्रिंग नियतांक है। स्प्रिंग को उसकी साम्यावस्था से x दूरी तक खींचने में स्प्रिंग द्वारा किये गये कार्य की गणना समाकलन विधि एवं ग्राफीय विधि से कीजिये।
उत्तर:
समाकलन विधि:

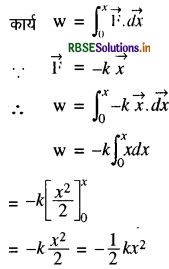
ग्राफी विधि: यदि स्प्रिंग की लम्बाई में वृद्धि तथा बल F के मध्य ग्राफ खींचें तो यह चित्रानुसार एक सरल रेखा प्राप्त होती है।

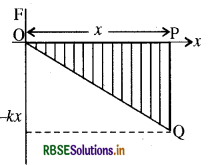
प्रत्यानयन बल के द्वारा किया गया कार्य
w = त्रिभुज OPQ का क्षेत्रफल
w = 1/2 × OP × PQ
= 1/2x x (-kx)
= 1/2kx²
अतः दोनों ही विधियों द्वारा प्राप्त कार्य का मान समान प्राप्त होता है।

आंकिक प्रश्न:

प्रश्न 1. 
एक मनुष्य 2 किग्रा. के बॉक्स को अपने हाथ में लेकर एक समतल पर गति कर रहा है। यदि वह 0.5 मी./से. ² के त्वरण से 40 मी. चलता है तो गति के दौरान मनुष्य द्वारा बॉक्स पर किया गया कार्य कितना होगा?
उत्तर:
दिया गया है:
m = 2 किग्रा.
a = 0.5 मी./से.²
s = 40 मीटर
यहाँ पर बल तथा विस्थापन एक ही दिशा में हो रहे हैं।
∵ θ = शून्य होगा
कार्य (W) = mas cos∵
= 2 x 0.5 x 40 cos 
= 2 x 0.5 x 40
W = 40 जूल
∴ cos ()  = 1

प्रश्न 2. 
दो एक समान 2 किग्रा. के गुटके एक समान चाल (2 मी./से.) से एक घर्षण रहित क्षैतिज तल पर एक-दूसरे की ओर गतिशील होते हैं। वे आपस में टक्कर करके एक-दूसरे से सम्बद्ध हो जाते हैं तथा स्थिरावस्था में आ जाते हैं। दोनों कणों के निकाय पर बाह्य बलों तथा आन्तरिक बलों द्वारा किये गये कार्य का परिकलन
करो।
उत्तर:
चूँकि गुटकों पर कोई भी बाह्य बल नहीं लग रहा है। 
∴ बाह्य बलों द्वारा किया गया कार्य = शून्य होगा
दो गुटकों की टक्कर से पहले की कुल गतिज ऊर्जा
= 1/2 × 2 × (2)² + 2 × 2 × (2)²
= 4 + 4 = 8 जूल
टक्कर होने पर दोनों गुटके सम्बद्ध होकर स्थिरावस्था में आ जाते हैं, अतः उनकी कुल ऊर्जा = शून्य 
∴ आन्तरिक बलों द्वारा किया गया कार्य
= kf - ki
= 0 - 8 = - 8 जूल 

प्रश्न 3. 
एक स्टील के तार से 2.5 किग्रा भार लटकाने से वृद्धि हो जाती है। उसकी लम्बाई में 25 सेमी. की में किया गया कार्य ज्ञात करो (g = 10 मी./से.)
उत्तर:
दिया गया है:
M = 2.5 किग्रा. भार
∴ Mg = 2.5 × 10 = 25 x = 0.25 सेमी.
= 0.25/100 मीटर
सूत्र Mg = kx से
= \(\begin{aligned} & \frac{25}{0.25} \\ & 100 \\ & \end{aligned}\)

= \(\frac{25 \times 100}{0.25}\)
= 10000 
N/m = 10⁴ N/m
तार को खींचने में किया गया कार्य
w = 1⁄2 kx²
W = 1/2 × 10⁴ x (0.25/100)²
W = 1/2 × (0.25)² = 2 ×0.0625
= 0.03125 जूल 

प्रश्न 4. 
एक 2 किग्रा. द्रव्यमान का पिण्ड 10 मी. की ऊँचाई से रेती में गिरता है। पिण्ड विरामावस्था में आने से पहले रेती में 2 सेमी. तक गति करता है तो औसत प्रतिरोध बल क्या होगा ? (g = 10 मीटर / से. ²)
उत्तर:
दिया गया है:
m = 2 किग्रा.
h = 10 मीटर
g = 9.8 मी./से.²
विस्थापन s = 2 सेमी. = 2/100 मीटर
2 किग्रा. पिण्ड की रेती पर गिरने पर स्थितिज ऊर्जा = mgh
= 2 × 9.8 × 10
= 196 जूल
माना कि प्रतिरोध बल F न्यूटन है।
इस स्थिति में
F x s = mgh
F x 2/100 = 196
⇒  \(\mathrm{F}=\frac{196 \times 100}{2}\)
= 196 × 50
= 9800 न्यूटन

प्रश्न 5. 
एक पम्प इंजन 100 किग्रा. पानी को 10 मी. की ऊँचाई पर 10 सेकण्ड में पहुँचाता है, जबकि इंजन की दक्षता 60 प्रतिशत है। इंजन की वास्तविक शक्ति कितनी होगी? (g10 मी./से. ²)
उत्तर:
दिया गया है:
m = 100 किग्रा.
8 = 10 मी./से.²
h = 10 मीटर 1 = 10 सेकण्ड
पम्प इंजन की शक्ति = mgh/t
\(=\frac{100 \times 10 \times 10}{10}\)
= 1 किलोवाट
माना कि इंजन की वास्तविक शक्ति= x किलोवाट है।
\(\frac{x \times 60}{100}=1\) किलोवाट
\(x=\frac{100 \times 1}{60}\) किलोवाट
= 1.67 किलोवाट

प्रश्न 6. 
1000 किग्रा. द्रव्यमान की एक कार 32 मीटर / सेकण्ड के वेग से आती हुई 4 मीटर / सेकण्ड के वेग से उसी दिशा में जाती हुई 8000 किग्रा. के ट्रक से पीछे से टकराती है। टक्कर के पश्चात् कार विपरीत दिशा में 8 मीटर/सेकण्ड के वेग से लौटती है, तो टक्कर के पश्चात् ट्रक का वेग ज्ञात कीजिये।
उत्तर:
कार व ट्रक का कुल संवेग
= 1000 × 32 + 8000 × 4
= 32000 + 32000
= 64000 किग्रा. x मी./से.
कार व ट्रक का कुल संवेग टक्कर के पश्चात् वही रहेगा जितना टक्कर से पहले था। यदि टक्कर होने पर ट्रक का वेग v हो, तब
8000 v 1000 (-8) = 64000
या
8000 v = 64000 + 8000
8000 v = 72000
v = 72000/8000
= 9 मी./से.
अतः टक्कर के पश्चात् ट्रक का वेग 9 मी./सेकण्ड होगा। 

प्रश्न 7. 
एक नियत बल के प्रभाव में कण की स्थिति एवं समय में सम्बन्ध x = (t - 4)² से दिया जाता है। जहाँ पर x मीटर में तथा समयt सेकण्ड में है तो बल द्वारा प्रथम 8 सेकण्ड में किये गये कार्य की गणना कीजिये।
उत्तर:
कार्य ऊर्जा प्रमेय से,
सम्पन्न कार्य = गतिज ऊर्जा परिवर्तन
\(=\left(\frac{1}{2} m \mathrm{v}_{t=8}^2-\frac{1}{2} m \mathrm{v}_{t=0}^2\right)\)
यहाँ x = (t - 4)² से
वेग v = dx/dt = d/dt(t - 4)²
v = 2(t - 4)
अतः
vt = 0 = 2(0 - 4) = -8 मी. /से.
vt = 8 = 2(8 - 4) = 8 मी. /से.
W = 1/2 m[(8)² - (-8)²]
= 1/2m [64 - 64] = 0
या
W = 0

प्रश्न 8. 
एक ट्यूबवेल का पम्प 2400 किग्रा. पानी प्रति मिनट ऊपर फेंकता है। यदि पानी के बाहर आने की चाल 3 मी./से. हो तो पम्प की शक्ति ज्ञात कीजिये। यदि पम्प 5 घंटे तक चले तो पम्प द्वारा किये गये कार्य का मान ज्ञात करिये।
उत्तर:
दिया गया है:
m = 2400 किग्रा.
t = 1 मिनट = 60 सेकण्ड
v = 3 मीटर / सेकण्ड
∴ पम्प की शक्ति = 1/2 mv²/t
\(=\frac{2400 \times 3 \times 3}{2 \times 60}\)
= 180 वाट
यदि पम्प 5 घंटे चलता है तब किया गया कार्य
W = P × t
= 180 × 5 × 60 x 60
= 18 × 5 × 6 × 6 × 10³ जूल
= 3240 × 10³
या W = 3.24 x 10⁶ जूल

प्रश्न 9. 
एक स्प्रिंग जिसका बल नियतांक है, हुक के नियम का पालन करती है। उसको मूल लम्बाई से 10 सेमी. खींचने हेतु 4 जूल कार्य की आवश्यकता होती है। गणना करें:
(i) k का मान
(ii) इसे अतिरिक्त 10 सेमी. लम्बाई तक खींचने हेतु अतिरिक्त कार्यै।
उत्तर:
(i) W = 1/2kx²
∴ k = 2w/x²
दिया गया है।
w = 4 जूल
x = 10 सेमी = 0.1 मीटर
\(k=\frac{2 \times 4}{(0.1)^2}=\frac{8}{0.01}\) = 800 न्यूटन/मी.
(ii) कुल 20 सेमी खींचने में किया गया कार्य
W = 1/2kx²
= 1⁄2 × 800 × (0.2)²
w = 400 x 0.04
= 16 जूल
अतिरिक्त कार्य = 16 - 4 = 12 जूल
= 8000 न्यूटन/मी.

प्रश्न 10. 
एक घोड़ा क्षैतिज से 60° के कोण पर 40 न्यूटन का बल लगाता हुआ पीछे बंधी गाड़ी को 7.2 किमी. प्रति घंटे की चाल से खींचता है:
(i) इस घोड़े ने 10 मिनट में कुल कितना कार्य किया? 
(ii) घोड़े की शक्ति क्या है?
उत्तर:
दिया गया है:
F = 40 न्यूटन
v = 7.2 किमी./ घण्टा
\(=\frac{7.2 \times 1000}{60 \times 60}\)
= 2 मी./सेकण्ड
1 मिनट में तय की गई दूरी,
दूरी = वेग x समय = 2 x 60 = 120 मी.
(i) घोड़े द्वारा 10 मिनट में किया गया कार्य
कार्य W = FS cos θ
= 40 x 120 cos 60° x 10
= 40 × 120 × 1⁄2 × 10 = 40 x 120 x 5
कार्य W = 24000 जूल उत्तर
(ii) शक्ति (P) = \(\frac{\mathrm{W}}{t}=\frac{24000}{10 \times 60}\)
= 40 वाट

प्रश्न 11. 
एक गोला समान द्रव्यमान वाले एक अन्य स्थिर गोले से टकराता है। प्रत्यावस्थान गुणांक e हो तो टक्कर के पश्चात् गोलों के वेगों का द्रव्यमान क्या होगा?
उत्तर:
माना दोनों गोलों का द्रव्यमान m है तथा प्रथम गोले का प्रारम्भिक वेग u है। टक्कर के पश्चात् प्रथम तथा द्वितीय गोले का वेग है।  क्रमश: V₁ तथा V₂ है। दूसरा दूसरा गोला स्थिर है।
संवेग संरक्षण नियम के अनुसार
mu = mv₁ + mv₂
V₁ + V₂ = u .............. (1)
प्रत्यावस्थान गुणांक e = -(v₁ - v₂/u)
(V₁ - V₂) = - eu ................ (2)
समी. (1) तथा (2) को जोड़ने पर
2V₁ = = en = (1 - e)u
V₁ = 1 - e/2u ................ (3)
समी. (1) तथा (2) को घटाने पर
2V₂ = u + eu
2V₂ = (1 + e)u
⇒ \(\mathrm{v}_2=\left(\frac{1+e}{2}\right) u\)
समी (3) तथा (4) से
\(\frac{v_1}{v_2}=\frac{1-e}{1+e}\)

गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न:

प्रश्न 1. 
किसी कण पर \((4 \hat{i}+3 \hat{j})\) N बल लगाने पर वह बिन्दु \((-2 \hat{i}+5 \hat{j})\) से बिन्दु \((4 \hat{j}+3 \hat{k})\) तक विस्थापित हो जाता है। इस प्रक्रिया में बल द्वारा किया गया कार्य:
(a) 2 J
(b) 8 J
(c) 11 J
(d) 5 J
उत्तर:
(d) 5 J

प्रश्न 2. 
जब एक रबड़ के छल्ले को x दूरी तक तानित किया जाता है, तब परिमाण F = ax + bx² एक प्रत्ययन बल लगता है, वहाँ a तथा स्थिरांक है। बिना तानित रबड़ के छल्ले की L से तानित करने में किया गया कार्य है:
(a) aL² + bL³
(b) 1/2(aL² + bL³)
(c) aL²/2 + bL³/3
\(\text { (d) } \frac{1}{2}\left(\frac{a \mathrm{~L}^2}{2}+\frac{b \mathrm{~L}^3}{3}\right)\)
उत्तर:
(c) aL²/2 + bL³/3

प्रश्न 3. 
m द्रव्यमान का एक बिन्दु कण एक खुरदरे पथ PQR (चित्र देखिये पर चल रहा है। कण और पथ के बीच घर्षण गुणांक है। कण, P से छोड़े जाने के बाद R पर पहुँच कर रूक जाता है। पथ के भाग PQ और QR पर चलने में कण द्वारा खर्च की गई। ऊर्जाएँ बराबर हैं। PQ से QR पर होने वाले दिशा बदलाव में कोई ऊर्जा खर्च नहीं होती तब और दूरी x( = QR) के मान
लगभग हैं क्रमश:

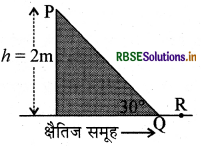
(a) 0.2 एवं 3.5m
(b) 0.29 एवं 3.5m
(c) 0.29 एवं 6.5m
(d) 0.2 एवं 6.5 m
उत्तर:
(b) 0.29 एवं 3.5m

प्रश्न 4. 
किसी बल क्षेत्र में कण की स्थितिज ऊर्जा निम्नलिखित हैं:
\(\mathrm{U}=\frac{\mathrm{A}}{r^2}-\frac{\mathrm{B}}{r}\)
जहाँ A तथा B धनात्मक नियतांक है तथा कण की बल क्षेत्र के केन्द्र से दूरी है। स्थायी सन्तुलन की दशा में कण की दूरी होगी:
(a) B/2A 
(b) 2A/B
(c) A/B
(d) B/A
उत्तर:
(b) 2A/B

प्रश्न 5. 
एक तार जो एक छोटे मोती के मध्य में स्थित छिद्र से गुजरता है, को एक चतुर्थांश वृत्त के अनुरूप मोड़ा गया है। तार को भूमि पर ऊर्ध्व तल में स्थित किया गया है जैसा चित्र में दर्शाया गया है। मोती को तार के ऊपरी सिरे से छोड़ा जाता है, जिससे यह तार के अनुदिश बिना किसी घर्षण से सरकता है। जब मोती A से B तक सरकता है, तब इसके द्वारा तार पर लगने वाला बल है:

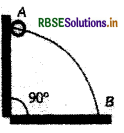
(a) हमेशा त्रिज्या दिशा में बहिर्मुखी
(b) हमेशा त्रिज्या अन्तर्मुखी
(c) प्रारम्भ में त्रिज्या दिशा में बहिर्मुखी तत्पश्चात् त्रिज्या दिशा में अन्तर्मुखी
(d) प्रारम्भ में त्रिज्या दिशा में अन्तर्मुखी तत्पश्चात् त्रिज्या दिशा में बहिर्मुखी
उत्तर:
(d) प्रारम्भ में त्रिज्या दिशा में अन्तर्मुखी तत्पश्चात् त्रिज्या दिशा में बहिर्मुखी

प्रश्न 6. 
400ms^-1 के क्षैतिज वेग से चलती हुई 10g द्रव्यमान की एक गोली 2 kg द्रव्यमान के लकड़ी के एक गुटके से टकराती है। यह गुटका एक 5m लम्बी हल्की अवितान्य डोरी से लटका है। यदि गोली के टकराने के परिणामस्वरूप गुटके का गुरुत्व केन्द्र 10 cm ऊर्ध्वाधर ऊपर उठ जाता है, तो गुटके से क्षैतिज दिशा में बाहर निकलने पर गोली की चाल होगी:
(a) 160 ms^-1
(b) 100ms^-1
(c) 80ms^-1
(d) 120ms^-1
उत्तर:
(d) 120ms^-1

प्रश्न 7. 
एक कण किसी एक आकर्षण विभव U = k/2r² के अन्तर्गत त्रिज्या a के एक गोलाकार पथ में चल रहा है, उसकी कुल ऊर्जा होगी:
(a) k/2a²
(b) Zero
(c) - 3k/2a²
(d) - k/4a²
उत्तर:
(b) Zero

प्रश्न 8. 
1 kg द्रव्यमान का कोई पिण्ड किसी कालाश्रित बल \(\overrightarrow{\mathrm{F}}=\left(2 t \hat{i}+3 t^2 \hat{j}\right) N\), यहाँ \(\hat{i}\) और \(\hat{j}\) x और y अक्ष के अदिश मात्र सदिश है, के अधीन गति आरम्भ करता है, तो समय t पर इस बल द्वारा विकसित शक्ति क्या होगी:
(a) (2t² + 3t³) W
(b) (2t² + 4t⁴)W
(c) (2t³ + 3t⁴) W
(d) (2t³ + 3t⁵) W
उत्तर:
(d) (2t³ + 3t⁵) W

प्रश्न 9. 
x - दिशा में 2v चाल से चलते हुए । द्रव्यमान के एक कण से, y- दिशा में v वेग से चलता हुआ 2m द्रव्यमान का एक कण टकराता है। यदि यह संघट्ट (टक्कर) पूर्णतः अप्रत्यास्थ है तो टक्कर के दौरान ऊर्जा का क्षय (हानि) होगा:
(a) 44%
(b) 50%
(c) 56%
(d) 62%
उत्तर:
(c) 56%

प्रश्न 10. 
किसी घर्षणहीन पृष्ठ पर v चाल से चलता हुआ M द्रव्यमान का एक ब्लॉक उसी द्रव्यमान M के विरामावस्था में स्थित एक अन्य ब्लॉक से टकराता है। टक्कर के पश्चात् पहला ब्लॉक चाल  v/3 से अपनी प्रारम्भिक गति की दिशा से θ  कोण पर चलने लगता है। तो टक्कर के पश्चात् दूसरे ब्लाक की चाल होगी:

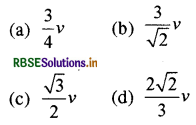
उत्तर:
\(\text { (d) } \frac{2 \sqrt{2}}{3} v\)

प्रश्न 11. 
दो एकसमान गेंदों A तथा B के वेग क्रमश: 0.5m/s तथा 1-0.3 m/s है। ये एक रेखा के अनुदिश चलते हुए टकराती हैं। यदि यह टक्कर प्रत्यास्थ है, इस टक्कर के पश्चात् A तथा B के वेग क्रमशः होंगे:
(a) 0.3 m/s तथा 0.5m/s
(b ) - 0.5m/s तथा 0.3m/s
(c) 0.5m/s तथा 0.3m/s
(d) -0.3m / s तथा 0.5m/s
उत्तर:
(d) -0.3m / s तथा 0.5m/s

प्रश्न 12. 
द्रव्यमान m एवं प्रारम्भिक वेग के एक कण A की टक्कर m/2 द्रव्यमान के स्थिर कण B से होती है। यह टक्कर सम्मुख एवं प्रत्यावस्था है। टक्कर के बाद डि-ब्रॉग्ली तरंगदैयों λA से λB का अनुपात होगा:

उत्तर:
\(\text { (c) } \frac{\lambda_{\mathrm{A}}}{\lambda_{\mathrm{B}}}=2\)

प्रश्न 13. 
द्रव्यमान m का एक गतिशील गुटका 4m द्रव्यमान के किसी दूसरे स्थिर गुटके से संघट्ट करता है। संघट्ट के पश्चात् हल्का गुटका विराम अवस्था में आ जाता है। यदि हल्के गुटके का आरम्भिक वेग है तो प्रत्यानयन गुणांक (e) का मान होगा:
(a) 0.5 
(b) 0.25
(c) 0.8
(d) 0.4
उत्तर:
(b) 0.25

प्रश्न 14. 
1 kg द्रव्यमान का एक कण समय पर निर्भर (time dependent) बल F = 6t का विरामावस्था से चलता है तो पहले 1 सेकण्ड में बल द्वारा किया अनुभव करता है। यदि कण गया कार्य होगा:
(a) 18 J
(b) 4.5 J
(c) 22 J
(d) 9 J
उत्तर:
(b) 4.5 J

प्रश्न 15.
m = 10^-2 kg द्रव्यमान का एक पिण्ड एक माध्यम: गति कर रहा है और एक घर्षण बल F = - kv² का अनुभव करता है पिण्ड का प्रारम्भिक वेग Vo = 10 ms^-1 है यदि 10 के बाद उसकी ऊर्जा 1/8mV₀² है तो k का मान होगा:
(a) 10^-1 Kgm^-1 s^-1
(b) 10^-3 Kgm^-1
(c) 10^-3 Kgs^-1
(d) 10^-4 Kgm^-1
उत्तर:
(d) 10^-4 Kgm^-1

प्रश्न 16. 
द्रव्यमान 'm' का एक कण चाल '2v' से जाते हुए एक द्रव्यमान '2m' के कण जो इसी दिशा में चाल 'V' से जा रहा है, से संघट्ट करता है| संघट्ट के बाद पहला कण स्थिर अवस्था में आ जाता है तथा दूसरा कण एक ही द्रव्यमान 'm' के दो कणों में विभाजित हो जाता है। ये दोनों कण आरम्भिक दिशा से 45° के कोण पर जाते हैं। प्रत्येक चलायमान कण की गति का मान होगा:
(a) v/(2√2)
(b) 2√2v
(c) √2v
(d) 1 √2
उत्तर:
(b) 2√2v

प्रश्न 17. 
M = 4m द्रव्यमान का एक वेज (wedge) आकार का गुटका एक घर्षणहीन सतह पर रखा है। m द्रव्यमान का एक कण गुटके की ओर, V चाल से आता है। कण और सतह या कण और गुटके के बीच कोई घर्षण नहीं है। कण के द्वारा गुटके के ऊपर चढ़ी गयी अधिकतम ऊँचाई होगी:
(a) 2v²/7g
(b) v²/g
(c) 2v²/5g
(d) v²/2g
उत्तर:
(c) 2v²/5g

प्रश्न 18. 
एक टेनिस की गेंद को एक क्षैतिज चिकनी सतह पर गिराया जाता है। गेंद सतह से टकराने के पश्चात् पुनः अपने मूल स्थान पर पहुँच जाती है। संघट्ट के दौरान, गेंद पर लगने वाला बल उसकी संपीडन लम्बाई के अनुक्रमानुपाती है। निम्न में से कौनसा रेखाचित्र, समय के साथ गेंद की गतिज ऊर्जा K के परिवर्तन को सर्वाधिक उचित रूप से प्रदर्शित करता है। (चित्र केवल सांकेतिक है और मापन के अनुरूप नहीं है:

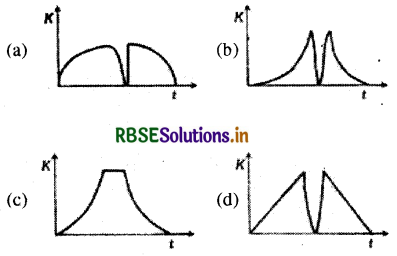
उत्तर:

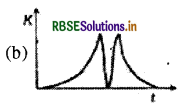
प्रश्न 19. 
वृत्ताकार चाप वाले एक गुटके का द्रव्यमान M है। ये गुटका एक घर्षण रहित मेज पर स्थित है। मेज के सापेक्ष (in a coordinate system fixed to the table) गुटके का दाहिना कोर (right edge ) x = (0 पर स्थित है। द्रव्यमान m वाले एक बिन्दु कण (point mass) को वृत्ताकार चाप के उच्चतम बिन्दु से विरामावस्था से छोड़ा जाता है (released from rest ) है। ये बिन्दु कण वृत्ताकार पथ पर नीचे की ओर सरकता है। जब बिन्दु कण गुटके से सम्पर्क विहीन हो जाता है, तब उसकी तात्क्षणिक स्थिति x और गति है। निम्न में से कौनसा (से) कथन सही है/हैं:

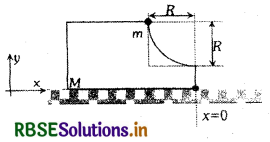
(a) बिन्दु कण (m) का वेग v = \(\sqrt{\frac{2 g \mathrm{R}}{1+\frac{m}{\mathrm{M}}}}\)
(b) गुटके (M) के संहति केन्द्र के विस्थापन का x घटक \(=\frac{m \mathrm{R}}{\mathrm{M}+m}\)
(c) बिन्दु कण (m) का स्थान x = \(-\sqrt{2} \frac{m \mathrm{R}}{\mathrm{M}+m}\)
(d) गुटके (M) का वेग v = \(-\frac{m}{\mathrm{M}} \sqrt{2 g \mathrm{R}}\)
उत्तर:
 (b) गुटके (M) के संहति केन्द्र के विस्थापन का x घटक \(=\frac{m \mathrm{R}}{\mathrm{M}+m}\)

प्रश्न 20. 
1 kg द्रव्यमान का एक कण एक स्थिर 5 kg द्रव्यमान के कण से प्रत्यास्थता टकराता है। टकराने के बाद 1 kg का कण 2 ms^-1 चाल से पहले की विपरीत दिशा में जाने लगता है। इन दो द्रव्यमानों के बारे में निम्न में से कौनसे (कौनसा) प्रक्कथन सही है: 
(a) निकाय का कुल संवेग 3 kg ms^-1 है
(b) टकराने के बाद 5kg द्रव्यमान का संवेग 4 kg ms^-1 है 
(c) द्रव्यमान केन्द्र की गतिज ऊर्जा 0.75J है
(d) निकाय की कुल गतिज ऊर्जा 4J है
Passage-I
m द्रव्यमान का एक छोटा गुटका नत समतल की घर्षण रहित सतह पर गति करता है (चित्रानुसार) । नत समतल का झुकाव कोण अचानक बिन्दु B पर 60° से 30° परिवर्तित हो जाता है। प्रारम्भ में गुटका, A पर विराम में है। मान लीजिये कि गुटके व - समतल के मध्य संघट्ट पूर्णतः अप्रत्यास्थ है। (g = 10 m/s² )

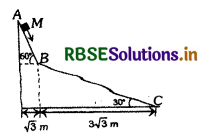
उत्तर:
(b) टकराने के बाद 5kg द्रव्यमान का संवेग 4 kg ms^-1 है 

प्रश्न 21. 
द्वितीय नत तल पर टकराने के तुरन्द बाद गुटके की बिन्दु B पर चाल है:
(a) √60 m/s
(b) √45m/s
(c) √30m/s
(d) √15 m/s
उत्तर:
(b) √45m/s

प्रश्न 22. 
द्वितीय नत - तल को छोड़ने के तुरन्त पूर्व बिन्दु C पर गुटके की चाल है:
(a) √120 m/s
(b) √105m/s
(c) √90m/s
(d) √75 m/s
उत्तर:
(b) √105m/s

प्रश्न 23. 
यदि गुटके व नत-तल के मध्य संघट्ट पूर्णतः प्रत्यास्थ हो, तब द्वितीय नत तल पर टकराने के तुरन्त पश्चात् बिन्दु B पर गुटके के वेग का ऊर्ध्वाधर (ऊपर की दिशा में) घटक होगा:
(a) √30m/s
(b) √15 m/s
(c) 0
(d) - √15 m/s
उत्तर:
(d) - √15 m/s