RBSE Class 11 Physics Important Questions Chapter 6 Work, Energy and Power

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 6 Work, Energy and Power Important Questions and Answers.

RBSE Class 11 Physics Chapter 6 Important Questions Work, Energy and Power

Multiple Choice Questions

Question 1.
Which is not unit of energy?
(a) Watt
(b) Kilowatt hour
(c) Joule
(d) Electron volt
Answer:
(a) Watt

Question 2.
Kinetic energy of a freely falling body:
(a) remains constant
(b) decreases
(c) increases
(d) remains zero
Answer:
(c) increases

Question 3.
Velocity-time graph of moving particle is shown in figure. Work done by force from C to D will be:

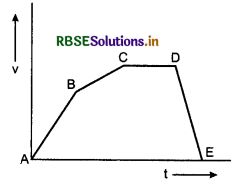
(a) positive
(b) zero
(c) negative
(d) infinite
Answer:
(b) zero

Question 4.
If on applying a force F on a body it attains a velocity v, then power will be:
(a) F/v
(b) Fv²
(c) F. v
(d) F/v²
Answer:
(c) F. v

Question 5.
A boy carries a weight placed on his head. He will have to do maximum work when he:
(a) walks on rough horizontal surface
(b) walks on a smooth horizontal surface
(c) walks on an inclined plane in downward direction
(d) walks upwards on inclined plane
Answer:
(d) walks upwards on inclined plane

Question 6.
A box is raised from floor and placed on a table. Work done by us will depend on: 
(a) On various paths adopted in above process
(b) On place taken by us
(c) On our weight
(d) On the weight of the box
Answer:
(d) On the weight of the box

Question 7.
Negative value of work done by internal conservative force on a system is equvalent to:
(a) change in total energy
(b) change in kinetic energy
(c) change in potential energy
(d) none of these
Answer:
(c) change in potential energy

Question 8.
Kinetic energy of a body increases by 0.1% then percentage increase in its momentum will be:
(a) 0.5%
(b) 0.05%
(c) 1.0%
(d) 10%
[Hint: ∵ p = \(\sqrt{2 m K}\) ∴ p ∝ \(\sqrt{E}\)
∴ \(\frac{\Delta p}{p} \times 100=\frac{1}{2} \frac{\Delta E}{E} \times 100=\frac{1}{2} \times 0.1 \%\) = 0.05%]
Answer:
(b) 0.05%

Question 9.
Quantities which remain constant in a collision:
(a) momentum, kinetic energy and temperature
(b) momentum but not kinetic energy and temperature
(c) momentum, kinetic energy but not temperature
(d) none of above
Answer:
(b) momentum but not kinetic energy and temperature

Question 10.
Force constants of two springs are K₁ and K₂. Same expansion x is produced in both. Their elastic energies are E₁ and E₂, then ratio of E₁ and E₂ will be:

Answer:
(a) \(\frac{K_1}{K_2}\)

Question 11.
Work done on a body does not depend on:
(a) applied force
(b) on initial speed of the body
(c) on angle between force and displacement
(d) on displacement
Answer:
(b) on initial speed of the body

Question 12.
If the momentum of a body is doubled, what will be increase in its kinetic energy?
(a) 400%
(b) 200%
(c) 300%
(d) 50%
Answer:
(b) 200%

Question 13.
Kinetic energy of two molecules of masses m and 4m is same. Ratio of their linear momentum will be:
(a) 1 : 4
(b) 4 : 1
(c) 1 : 2
(d) 1 : 2
[Hint: Use relation E = \(\frac{p^2}{2 m}\)]
Answer:
(c) 1 : 2

Question 14.
A particle moving with uniform velocity creates two dimensional collision with a resting particle of same mass. What will be angle between them after collision?
(a) 45°
(b) 90°
(c) 60°
(d) 30°
Answer:
(b) 90°

Question 15.
A bullet of mass m is fired in horizontal direction with velocity u. This bullet embades in a sand bag of mass M. What will be the velocity of sand bag after collision?

Answer:
(a) \(\frac{m u}{M+m}\)

Question 16.
The value of coefficient of restitution e for perfectly elastic collision is:
(a) 1
(b) 0
(c) ∞
(d) -1
Answer:
(a) 1

Question 17.
A retarding force is applied to stop a train. If speed is doubled then the stopping distance will be:
(a) same
(b) two times
(c) half
(d) 4 times
Answer:
(d) 4 times

Question 18.
Graph between \(\sqrt{E_k}\) and \(\frac{1}{\rho}\) (where E_k is kinetic energy and ρ is linear momentum) will be:

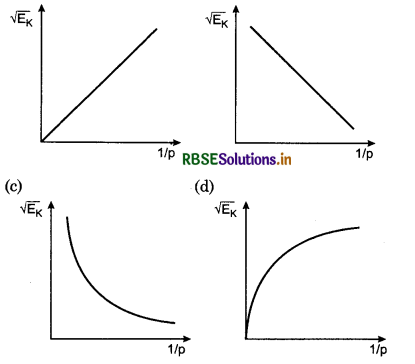
Answer:

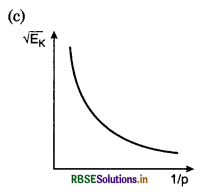
Question 19.
If \(\vec{F}\) = (20\(\hat{i} + 15 \hat{j} - 5\hat{i}\))N and \(\vec{v}\) = (\(6\hat{i} - 4\hat{j} + 3\hat{k}\)) m/s^-1, then instantaneous power will be:
(a) 35 W
(b) 25 W
(c) 90 W
(d) 45 W
Answer:
(d) 45 W

Question 20.
A ball falls from a height of 5 m and rebounds upto 1.8 m. Ratio of velocities before and after the collision will be:

Answer:
\frac{3}{5}

Question 21.
A particle is displaced by (\(3\hat{i} + 5\hat{j} - 7\hat{k}\)) m by applying a force of (\(3\hat{i} + \hat{j} - 2\hat{k}\))N. Work done will be:
(a) 28 J
(b) 10 J
(c) 100 J
(d) 0 J
Answer:
(d) 0 J

Question 22.
Kinetic energies of a truck and a car are same. If the weight of truck is 16 times the weight of car, then ratio of their momentums will be:
(a) 1 : 16
(b) 16 : 1
(c) 1 : 4
(d) 4 : 1
Answer:
(d) 4 : 1

Fill in the Blanks

Question 1.
1 Joule is equal to ........................... erg.
Answer:
10⁷

Question 2.
The coefficient of restitution for perfectly elastic collision is ...........................
Answer:
1

Question 3.
The coefficient of restitution for perfectly in elastic collision is ...........................
Answer:
0

Question 4.
When a body is thrown up, work done by gravity on the body is ...........................
Answer:
Negative

Question 5.
When linear momentum of a body is incresed by 10%, increase in k.E. of the body is ...........................
Answer:
21%

Question 6.
A collision is an isolated event in which ........................... extra ........................... on one another for ...........................
Answer:
Two or more colliding bodies, relatively strong force, relatively short time.

Very Short Answer Questions

Question 1.
If a person is walking with uniform speed on a horizontal plane, what will be work done against gravity?
Answer:
Zero, because angle between gravitational force and displacement is 90°.

Question 2.
A truck and a car are moving on road with same kinetic energy. If the engines of both are stopped simultaneously, then which of them will stop at less distance?
Answer:
∵ E_Truck = E_Car
∴ \(\frac{1}{2}\)m_Truckv²_Truck = \(\frac{1}{2}\)m_Car v²_Car
∵ m_Truck > m_Car ∴ v_Truck < m_Car
Therefore truck will stop at less distance.

Question 3.
On giving energy to a clock by rotating its key, which type of energy is stored? On working the clock, this energy is converted in which energy?
Answer:
Energy will store in form of potential energy of the spring. This energy is converted in kinetic energy when the clock starts working.

Question 4.
Can the momentum of a body be changed without changing its kinetic energy?
Answer:
Yes; in uniform circular motion, the kinetic energy of particle remains unchanged while momentum remains changing at each moment.

Question 5.
A man is operating a boat against the river flow such that the boat remains stationary with respect to river bank. Is the force applied by the man doing any work?
Answer:
Since the boat is stable with respect to river bank, therefore the force and displacement with respect to bank of river will be perpendicular, therefore no work is done by the force.

Question 6.
Can the scalar product of two vectors be negative?
Answer:
Yes; when the angle between the vectors is more than 90° but less than 270°.

Question 7.
If \(\vec{A}.\vec{C} = \vec{B}.\vec{C}\), will A and B be always equal?
Answer:
No; for being equal, \(\vec{A}\) and \(\vec{B}\) should make equal angle with \(\vec{C}\).

Question 8.
Write the mass-energy relation given by Einstein.
Answer:
E = mc², where c is velocity of light equal to 3 x 10⁸ ms^-1.

Question 9.
Can (E - U) for a body be negative? Where E is total energy and U is potential energy.
Answer:
No; because (E - U) represents kinetic energy of the body and it cannot be negative.

Question 10.
Can the kinetic energy of a system be increased without applying the force?
Answer:
Yes; for example in explosion of bomb.

Question 11.
Does linear momentum remain conserved always?
Answer:
No; linear momentum remains conserved only in isolated system.

Question 12.
Can a force be applied on a body without change in kinetic energy?
Answer:
Yes; when a body is pulled on a rough surface with uniform speed or spring is compressed.

Question 13.
An air bubble is rising up in water. What is change in its potential energy?
Answer:
Potential energy will decrease.

Question 14.
How many joules (J) will there be in 1 k?
Answer:
1 kWh = 3.6 x 10⁶ J.

Question 15.
What is the value of elastic energy of a stretched spring?
Answer:
U(x) = \(\frac{1}{2}\)Kx²

Question 16.
Does mechanical energy remains always conserved?
Answer:
No, it is only in isolated system when internal non-conservative forces be zero.

Question 17.
When conservative force does positive work on a body, then what is effect on its potential energy?
Answer:
Potential energy decreases.

Question 18.
A man is standing on platform holding his suitcase in his hand, does he doing any work?
Answer:
No; because displacement is zero.

Question 19.
Does the electron revolving around the nucleus has potential energy?
Answer:
It has negative potential energy.

Question 20.
When match box stick is burnt, then which energy is converted in heat energy?
Answer:
Chemical energy is converted in heat energy.

Question 21.
What is called capacity of doing work of a body?
Answer:
Energy.

Question 22.
When the temperature of a body increases, what change becomes in its internal energy?
Answer:
Internal energy increases.

Question 23.
Which energy decays in doing work against friction force?
Answer:
Kinetic energy decays in doing work against force of friction.

Question 24.
A man pulls a bucket filled with water with the help of rope, whether the work done by the man is positive or negative?
Answer:
Positive.

Question 25.
Arrow released from a bow has kinetic energy. From where this kinetic energy is obtained?
Answer:
Potential energy of arrow-bow system is converted in kinetic energy which is attained by the arrow.

Question 26.
Does the total energy of the system remains conserved in perfectly non-elastic collision?
Answer:
No, only that kinetic energy remains conserved which is required for conservation of momentum.

Question 27.
In elastic and non elastic collision, in which momentum remains conserved and in which mechanical energy remains conserved?
Answer:
In elastic collision, momentum and mechanical energy both remain conserved while in non-elastic collision only momentum remains conserved.

Short Answer Questions

Question 1.
Give the definition of coefficient of restituation 'e'.
Answer:
This law was presented on the basis of experiments. According to this law, “If the bodies collide head on then ratio of relative velocities after the collision and before the collision, remains constant and is equal to negative value of coefficient of restitution.” i.e.,

Here ( v₂ - v₁) is relative velocity of separation

and (u₁ - u₂) is relative velocity of approach.
∴ Relative velocity before collision = u₁ - u₂ and relative velocity after collision = v₁ - v₂
∴ e = \(\frac{v_2-v_1}{u_1-u_2}\)

Question 2.
Establish the relation between kinetic energy and momentum and with the help of this relation answer, if the momentum of a light and heavy body are same then kinetic energy of which body will be greater?
Answer:
Relation between kinetic energy and momentum
K = \(\frac{p^2}{2 m}\)
∴ \(\frac{K_1}{K_2}=\frac{m_2}{m_1}\) because p₁ = p₂ = p
If m₁ > m₂ or m₂ < m₁
The K₁ < K₂
∴ Kinetic energy of light body will be greater.

Question 3.
Explain, how does the work depend on frame of reference?
Answer:
Work depends upon frame of reference because on changing the frame of reference, displacement changes. For example, if a man carries a box of mass m, keeping on his head, to height of h, then displacement of box with respect to man will be zero. Therefore work done with respect to man is zero but for a person standing on platform work will be W mgh because for the person standing on plate form displacement is h.

Question 4.
What do you understand by kinetic energy? State its main properties.
Answer:
There are so many kinds of energy. For examples- mechanical energy; heat energy; light energy; sound energy; magnetic energy; electrical energy; nuclear energy; air energy; chemical energy etc. In this chapter only mechanical energy will be considered in detail. Mainly in mechanical energy, there are two types of energy:
1. Kinetic energy
2. Potential energy.
i.e., The sum of kinetic and potential energy is known as Mechanical energy.
(i) Kinetic energy: The energy possessed due to motion of the body is called its kinetic energy. It means, the energy i.e. work of a moving body is stored in which form, that is called kinetic energy.

Question 5.
If sum and difference of two vectors \(\vec{A}\) and \(\vec{B}\) are perpendicular to each other, then prove that the magnitudes of both vectors will be equal.
Answer:
As given that (\(\vec{A} + \vec{B}\)) and (\(\vec{A} - \vec{B}\)) are at right angles to each other.

Question 6.
Define conservative and non-conservative forces. Give their examples.
Answer:
Conservative forces: The force by which displacing a particle from one point to other point, does not depend on the path adopted, then the force is called conservative force. i.e., W₁ = W₂

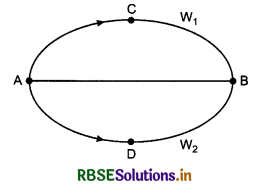
where W₁ = the work done for path ACB and W₂ = the work done for path ADB.
For examples: Central force, gravitational force, elastic force, electrostatic force, Lorentz force and uniform magnetic force etc.
Non conservative force: The force by which displacing a particle from one point to other point depends on path adopted, is called non-conservative force.

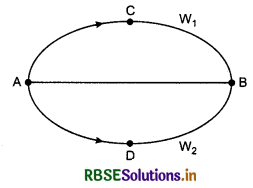
i.e., W₁ ≠ W₂
where W₁ = work done for path ACB
and W₂ = work done for path ADB
For examples: Force of friction, retarding force, magnetic force produced by electric current, viscous force and all forces which depend on velocity.

Question 7.
If the momentum of a particle is increased by 50%, then how many times its kinetic energy will be changed?
Answer:
Suppose initial kinetic energy E₁ = E
and momentum p₁ = p
After increasing the momentum by 50%,
P₂ = p + 50% of p = p + \(\frac{p}{2}=\frac{3 p}{2}\)
∵ Relation between kinetic energy and momentum,

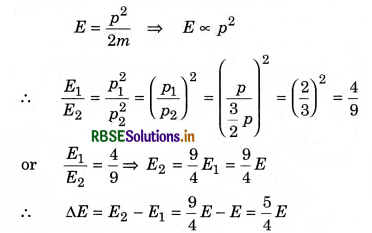
Therefore increase in kinetic energy = \(\frac{5}{4}\) times the inital energy.

Question 8.
Is it possible that a body be acted upon a force and it be accelerated also but even then no work is done by the force? Give an example.
Answer:
Yes, it is possible. For example- gravitational attraction acting on moon as centripetal force is at right angles to velocity of the moon. Therefore no work is done by earth on moon.

Question 9.
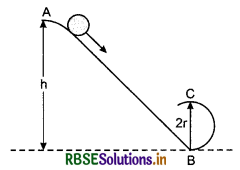
Two smooth inclined planes are shown in figure. Two blocks of same mass start slipping from A Which block will reach the ground with more velocity?
Answer:
Increase in kinetic energy = Loss of potential energy

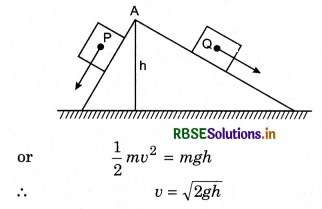
∵ Both the blocks start slipping from same height therefore both will reach the ground with same velocity.

Question 10.
If two protons be brought close to each other, then will the potential energy of this system increase or decrease? If one proton and one electron are brought close to each other then what will happen?
Answer:
In first case, potential energy will increase due to work done against repulsive forces. In second case potential energy will decrease due to force of attraction.
 
Match the Following Questions

Question 1.

Column I	Column II
(A) Work done is maximum	(P) Potential energy is stored
(B) Velocity of a body is doubled	(Q) Spring constant becomes twice
(C) Length of a spring is halved	(R) K.E. becomes four times
(D) On compressing or streching a spring	(S) Angle to between force and displacement ISO

Answer:

Column I	Column II
(A) Work done is maximum	(S) Angle to between force and displacement ISO
(B) Velocity of a body is doubled	(R) K.E. becomes four times
(C) Length of a spring is halved	(Q) Spring constant becomes twice
(D) On compressing or streching a spring	(P) Potential energy is stored

Question 2.

Column I	Column II
(A) Magnetic potential energy	(P) negative
(B) Electrostatic potential energy	(Q) Positive
(C) Elastic potential energy	(R) Zero
(D) Gravitational potential energy	(S) Not defined

Answer:

Column I	Column II
(A) Magnetic potential energy	(P) negative (Q) Positive
(B) Electrostatic potential energy	(P) negative (Q) Positive (R) Zero
(C) Elastic potential energy	(Q) Positive (R) Zero
(D) Gravitational potential energy	(P) negative (R) Zero

Conceptual Questions

Question 1.
A bullet is fired by a gun. Kinetic energy of which bullet or gun will be greater and why?
Answer:
Suppose mass of the bullet is m and that of gun is M. Velocities of bullet and gun are v and V.
According to law of conservation of momentum

∵ M > m ∴ K₁ > K₂
i.e., Kinetic energy of bullet will be greater.

Question 2.
If a machine gun fires n bullets per second and mass of each bullet is m, then what will be the power of machine gun?
Answer:
Change in momentum of machine gun on firing one bullet = Momentum of bullet = mv
Therefore recoil force on gun
F = n\(\frac{m v}{1}\) = mnv
∴ Power of machine gun
P = Fv = mnv v
or P = mnv²

Question 3.
A block of mass m is lowered with acceleration of \(\frac{3 g}{4}\) with the help of rope, from height h, find:
(i) Work done by gravitation force on block.
(ii) Total work done on the block.
(iii) Work done on the block by rope.
Answer:
(i) Work done by gravitational force on the block
W₁ = \(\vec{F}.\vec{S}\)
∵ Gravitational force (F = mg) and displacement (S = h) both are in same direction.
∴ θ = 0
∴ W₁ = FS cos 0° = FS = mgh
or W₁ = mgh
(ii) Net work done on the block,
W₂ = m \(\frac{3}{4}\) g x h
(because acceleration is \(\frac{3}{4}\) g)
or W₂ = \(\frac{3}{4}\) mgh
(iii) Work done on the block by rope
W = W₁ - W₂ = mgh - \(\frac{3}{4}\)mgh
(because rope resists the block from falling with acceleration g)
or W = \(\frac{3}{4}\) mgh

Question 4.
Which energy decays in doing work against the friction?
Answer:
Kinetic energy decays in doing work against friction.

Question 5.
When a ball is thrown vertically upwards, then its momentum decreases first and later on it starts increasing. Is this the violation of principle of conservation of momentum?
Answer:
No; because the momentum of the system (ball and air molecules) remains always conserved. When the momentum of ball decreases then that of air molecules increases and vice-versa.

Question 6.
A particle is displaced from (\(3\hat{i} + 2\hat{j}\))m to (\(14\hat{i} + 13\hat{j}\))m by applying a force of (\(4\hat{i} + \hat{j}\))N. Calculate the work done by the force.
Answer:

Question 7.
A pendulum of length 1 m and mass 100 g is displaced by 60° from mean position. Calculate the work done. (g = 10 ms^-2).
Answer:
Given: l = 1 m; m = 100g = 0.1 kg; g = 10 ms^-2; W = mgh
From the figure
h = l - l cosθ = l - l cos 60°
= l - \(\frac{1}{2}\)l

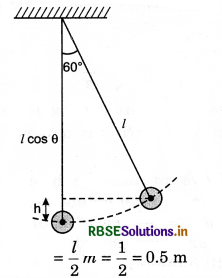
∴ Work done
W = mgh = 0.1 x 10 x 0.5
or W = 0.5 J

Question 8.
A connon ball fired by a cannon vertically upwards, explodes in air. What changes will be in momentum and energy?
Answer:
Momentum will remain conserved but kinetic energy will increase because the chemical energy of explosive changes in to kinetic energy.

Question 9.
A particle of mass m is moving on horizontal circular path, under centripetal force F = \(-\frac{K}{r^2}\), where K is constant. Find the total energy of the particle.
Answer:
If uniform speed of the particle be v, then centripetal force,
\(\frac{m v^2}{r}=-\frac{K}{r^2}\)
or mv² = \(-\frac{K}{r}\)
∴ Kinetic energy of the particle
K = \(\frac{1}{2}\)mv² = \(-\frac{K}{2 r}=\frac{K}{2 r}\) .........................(1)
(Because kinetic energy can never be negative)
Potential energy of the particle,

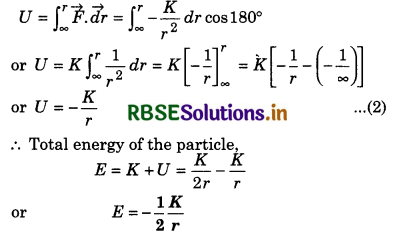
Question 10.
A lump of soil is thrown on a wall, then it sticks with wall. What happens with initial kinetic energy of the lump?
Answer:
Some part of kinetic energy of lump is used to deform the lump and rest part is converted in heat and sound energy.

Question 11.
If for two springs A and B, K_A > K_B, then more work will be done on which spring if:
(i) both are pulled by same length?
(ii) both are stretched by same force?
Answer:
(i) If a spring is expanded by x then work done
W = \(\frac{1}{2}\) Kx²
∴ For same displacement,

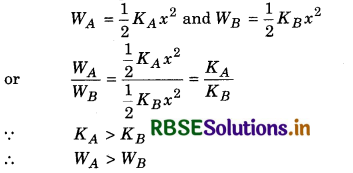
Therefore on spring A, more work will be done.
since F = Kx
∴ F_A = K_Ax_A and F_B = K_Bx_B

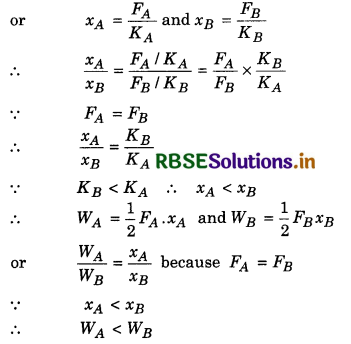
i.e., more work will be done on spring B.

Question 12.
Can there be momentum in a body without energy?
Answer:
Yes; when E = K + U = 0, then either both are zero or K = -U, thus kinetic energy may be zero or non zero.
But p = \(\sqrt{2 m K}\)
Therefore p = 0, only when K = 0 and p ≠ 0 when K = -U

Long Answer Questions

Question 1.
Prove that the relative velocity of approach is equivalent to relative velocity of separation in head on elastic collision. Draw labelled diagram also.
Answer:
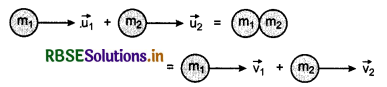
Suppose two bodies of masses m₁ and m₂ moving with velocities \(\overrightarrow{u_1}\) and \(\overrightarrow{u_2}\) respectively collide each other and after collision they move with velocities \(\overrightarrow{v_1}\) and \(\overrightarrow{v_2}\). This collision is perfectly elastic.

From law of conservation of momentum
Total momentum before collision = Total momentum after collision
or m₁ \(\overrightarrow{u_1}\) + m₂ \(\overrightarrow{u_2}\) = m₁ \(\overrightarrow{v_1}\) + m₂ \(\overrightarrow{v_2}\)
The collision is one-dimensional, therefore the direction of all velocities will be same.
Hence on considering only magnitude,
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ ..........................(1)
or m₁u₁ - m₁v₁ = m₂v₂ - m₂u₂
or m₁(u₁ - v₁) = m₂(v₂ - u₂) ..........................(2)
Now from law of conservation of energy,
Total kinetic energy before collision = Total kinetic energy after collision.
or \(\frac{1}{2}\) m₁u₁² + \(\frac{1}{2}\) m₂u₂² = \(\frac{1}{2}\) m₁v₁² + \(\frac{1}{2}\) m₂v₂²
or m₁u₁² + m₂u₂² = m₁v₁² + m₂v₂²
or m₁u₁² - m₁v₁² = m₁v₂² - m₂u₂²
or m₁(u₁ + v₁)(u₁ - v₁) = m₂(v₂ + u₂)(v₂ - u₂) .............................(3)
On dividing equation (3) by (2), we get
u₁ + v₁ = v₂ + u₂
or v₁ = v₂ + u₂ - u₁ ..........................(4)
Substituting this value of v₁ in equation (1),
m₁u₁ + m₂u₂ = m₁(v₂ + u₂ - u₁) + m₂v₂
or m₁u₁ + m₂u₂ = m₁v₂ + m₁u₂ - m₁u₁ + m₂v₂
or m₁u₁ + m₂u₂ - m₁u₂ + m₁u₁ = (m₁ + m₂) v₂
or 2m₁u₁ + u₂(m₂ - m₁) = v₂(m₁ + m₂)
∴ v₂ = \(\frac{2 m_1 u_1+u_2\left(m_2-m_1\right)}{\left(m_1+m_2\right)}\) ...........................(5)
For obtaining the expression for v₁, replace 1 by 2 and 2 by 1 in equation (5),
v₁ = \(\frac{2 m_2 u_2+u_1\left(m_1-m_2\right)}{\left(m_2+m_1\right)}\) ..........................(6)
Special situations: (i) When masses of both bodies are same, i.e., m₁ = m₂ = m
Then v₂ = \(\frac{2 m u_1+(m-m) u_2}{m+m}=\frac{2 m u_1+0}{2 m}\)
or v₂ = u₁ ..........................(7)
and v₁ = \(\frac{2 m u_2+(m-m) u_1}{m+m}=\frac{2 m u_2+0}{2 m}\)
or v₁ = u₂ ......................(8)
Conclusion: Therefore the velocities of the bodies of same mass are interchanged after perfectly head on collision, that is in head on collision, the exchange of momentum is maximum when their masses are equal.
(ii) When second body is at rest i.e., u₂ = 0, then from equation (5),
v₂ = \(\frac{2 m_1 u_1}{m_1+m_2}\)
and from equation (6),
v₁ = \(\frac{u_1\left(m_1-m_2\right)}{m_2+m_1}\)
If m₁ = m₂ = m₁ then
v₂ = \(\frac{2 m u_1}{2 m}\) = u₁
and v₁ = 0
Transfer of energy when m₁ ≠ m₂: The part of energy which is transfered to other body (u₂ = 0)

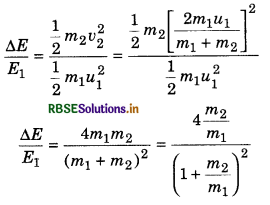
(iii) When m₂ >>> m₁ and u₂ = 0, then from equation (6),
v₁ = \(\frac{-m_2}{m_2} u_1\)
or v₁ = -u₁
and v₂ = \(\frac{2 m_1 u_1}{m_2}\) = 0
For example, if a ball falls from a height on the smooth surface of earth, then the collision of earth and the ball is of this type of collision, and the ball returns back with initial speed.
(iv) If m₂ << m₁ and u₂ = 0, then from equations (5) and (6),
v₁ = \(\frac{m_1}{m_1}\)u₁ = u₁
or v₁ = u₁
and v₂ = \(\frac{2 m_1}{m_1} u_1\)
or v₂ = 2u₁
i.e., when a heavy particle strikes the light particle, then the change in velocity of heavy particle is negligible but light particle moves with double velocity of heavy particle.

Question 2.
What is called energy? What are types of mechanical energy? Explain the law of conservation of energy by giving the example of freely falling body.
Answer:
According to this theorem, "Work done by a force in displacing an object on horizontal surface, is equal to increase in its kinetic energy." i.e.,
W = K_f - K_i
Proof: (i) When force is constant.
According to third equation of motion,
v² = u² + 2\(\vec{a}\vec{s}\)
or v² - u² = 2\(\vec{a}\vec{s}\)
Multiplying the whole equation by \(\frac{m}{2}\), we have,

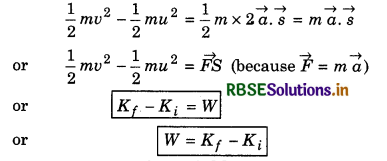
(ii) When force is variable.
∵ Kinetic energy,
K = \(\frac{1}{2}\)mv²
∴ Rate of change of kinetic energy

or dK = F dx
On integrating both sides,

Question 3.
Write work energy theorem and prove it.
Answer:
According to this theorem, "Work done by a force in displacing an object on horizontal surface, is equal to increase in its kinetic energy." i.e.,
W = K_f - K_i
Proof: (i) When force is constant.
According to third equation of motion,
v² = u² + 2\(\vec{a}\vec{s}\)
or v² - u² = 2\(\vec{a}\vec{s}\)
Multiplying the whole equation by \(\frac{m}{2}\), we have,

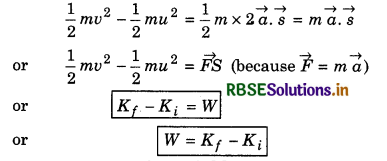
(ii) When force is variable.
∵ Kinetic energy,
K = \(\frac{1}{2}\)mv²
∴ Rate of change of kinetic energy

or dK = F dx
On integrating both sides,

Question 4.
A spring of force constant K is compressed by x Show that its potential energy is \(\frac{1}{2}\)Kx².
Answer:
Spring force is also variable conservative force. In fig. 9.20, a spring of force constant K is shown. One end of spring is attached with a rigid wall and a block of mass m is attached. Here spring is considered massless. In ideal situation, spring force is given by
F_S = -Kx
Where K is spring constant.
(i) When spring is pulled outwards, then displacement in spring is x.
The work done by spring
∴ W_S = \(\int_{x_1}^{x_2} F_S \cdot d x=-\int_{x_1}^{x_2} K x \cdot d x\)
or W_S = \(-\frac{1}{2}\)Kx² ............................(1)
Work done by external force F will be positive.
i.e., W = \(\frac{1}{2}\)Kx² .......................(2)
(ii) If spring is compressed, then also above expressions are obtained but in this situation x is negative and spring force F_S is positive. If the block returns from displacement x₁ to x₁, then
W_S = \(\int_{x_1}^{x_1} K x\)dx = 0

i.e., work done in complete cycle is zero. Therefore spring force is also a conservation force.
∴ Potential energy of the spring under influence of external force

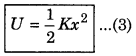
According to law of conservation of energy, the kinetic energy of the block will be maximum in mean position i.e., when x = 0
Therefore \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) Kx²

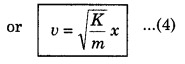
Thus the potential energy of the system remains changing in kinetic energy and kinetic energy in potential energy but the sum of types of energies i.e., the mechanical energy of the system remains constant.

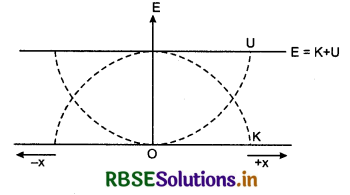
i.e., Total energy = kinetic energy + potential energy.

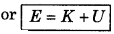
Question 5.
What is non-elastic, elastic and perfectly non-elastic collision? Give their properties.
Answer:
“Mutual interaction between two bodies for short time due to which their momentum and energy are changed, is called collision.”
For examples: Collision of cricket ball with bat; collision of two billiard balls; collision of gas molecules etc. In all these collisions, there is physical contact. When an α-particle moves towards a nucleus, then due Coulomb force (repulsion), the α-particle is scattered without physical contact. This is also, the example of collision.
Kinds of collision:
(i) Perfectly elastic collisons: The collision in which the energy and momentum of the system remain conserved separately, is called perfectly elastic collision. For example: collision of gas molecules.
Properties of perfectly elastic collisions:

1. Total momentum of the system remains conserved.
2. Total energy of the system remains conserved.
3. The forces applied by the bodies on each other are conservative.

(ii) Non-elastic collisions: The collision in which the momentum remains conserved but mechanical energy does not remain conserved, is called non-elastic collision. For example; collision of two vehicles in road accident.
Properties of non-elastic collisions:

1. Total momentum of the system remains conserved.
2. Total energy of the system remains conserved.
3. Mechanical energy of the system does not remain conserved.
4. Some part of mechanical energy is converted in sound, heat and light energy.
5. Internal attractive forces of the system are non-conservative.

(iii) Perfectly non-elastic collisions: The collision in which the momentum of the system remains conserved but mechanical energy does not remain conserved and after collision both bodies move with same velocity in same direction i.e, both bodies get attached with each other. For example, when a bullet is fired on wooden block then it penetrates and remains in it.
Properties of perfectly non-elastic collisions: The properties of these collisions are same as those of non-elastic collision. Only the difference is that after collision the bodies are attached with each other.

(iv) Super elastic Collision: In such type of collision, there is an increase in kinetic energy. This occurs if there is a release of potential energy on an
impact.
Examples: Bomb blasting
The coefficient of restitution is always greater than 1 in super elastic collision.

Question 6.
What do you understand by positive, negative and zero work? Give examples.
Answer:
There are following three types of work:
1. Positive work: When the directions of applied force and displacement are same (0 ≤ θ ≤ 90°), then work done is positive.
i.e., if the angle between F and d is θ = 0°, then
W = \(\vec{F}.\vec{d}\) = Fd cos 0° = Fd
or W = +Fd
This if the value of θ is between 0° and 90° (i.e., 0° ≤ θ ≤ 90°), the work done is positive.

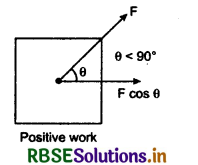
"Meaning of positive work is that external force provides the energy to the system."
Example: 1. When a weight is lifted by a person upwards from earth's surface, the work done by the person is positive (Fig. 6.4)

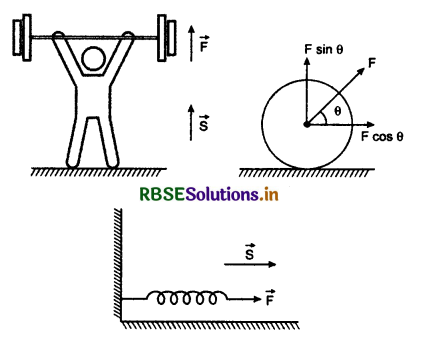
2. When a roller is pulled by applying force on its handle at an acute angle with horizontal, then roller moves in horizontal direction and the work done is positive. (Fig. 6.5).
3. When a spring is pulled, then the work done by external force is positive. (Fig. 6.6).
4. When a gas filled in a cylinder is expanded by pulling the piston, then work done by external force acting on piston is positive.

2. Negative work: When applied force and displacement both are in opposite directions, then work done is negative i.e., for negative work (90° ≤ θ° ≤ 180°)
If θ = 180°, then
W = \(\vec{F}.\vec{d}\) = Fd cos 180° or W = -Fd
"Meaning of negative work is that force takes energy from the system."

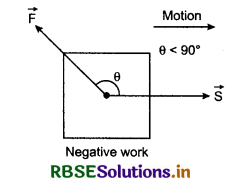
Examples:
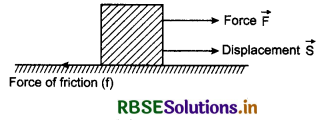
1. When a body moves on a rough surface, on applying the force, then the work done by force of friction is negative. (Fig.6.8)

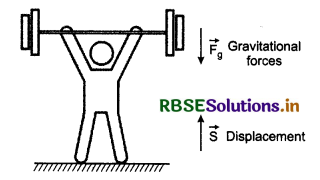
2. When a person lifts a body from earth's surface then the work done by the gravitational force is negative. (Fig.6.9)

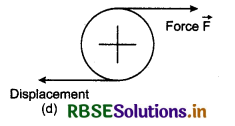
3. When brakes are applied on a moving vehicle, then the work done by retarding force is negative. (Fig6.10)

4. When a position charge goes towards another positive charge, then the work done by electrostatic force (repulsion) is negative.

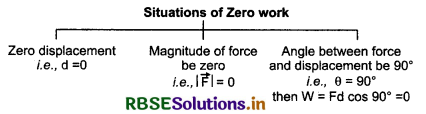
3. Zero work: Zero work is possible in following situations.
When θ = 90°, then
W = \(\vec{F}.\vec{d}\) = Fd cos 90° = Fd x 0
or W = 0

Examples:
1. When a satellite revolves around the eath, then the work done by the centripetal force is zero because the angle between force and displacement is 90°. (Fig. 6.11)

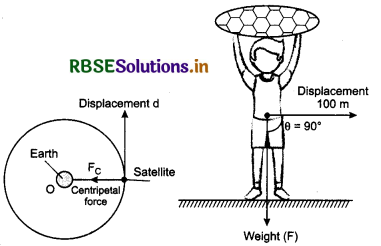
2. When a person covers a distance of 100 m on platform having some load on his head, then the work done by weight (force) is zero because here also angle θ is 90°.

Question 7.
What is called work? Establish the expression for obtaining work by variable force.
Answer:
If the magnitude or direction or both of an applied force force are changing, then the force is called variable force. Suppose a variable force displaces an object in the direction of force, from x₁ to x₂. If the force F displaces the object by very small displacement dx, the work done by the force,
dW = F.dx = area of figure PQRS.
∴ Total work done from displacement x₁ to x₂
W = \(\sum_{x=x_1}^{\substack{x=x_2}} F d x\)

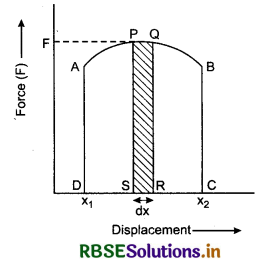
or W = \(\int_{x_1}^{x_2} F d x\) = area of figure ABCD.
Thus work done is obtained by area covered by the graph in fore-displacement graph.

Question 8.
What do you understand by kinetic energy? Establish the expression for kinetic energy of moving object.
Answer:
There are so many kinds of energy. For examples-mechanical energy; heat energy; light energy; sound energy; magnetic energy; electrical energy; nuclear energy; air energy; chemical energy etc. In this chapter only mechanical energy will be considered in detail. Mainly in mechanical energy, there are two types of energy:
1. Kinetic energy
2. Potential energy.
i.e., The sum of kinetic and potential energy is known as Mechanical energy.
(i) Kinetic energy: The energy possessed due to motion of the body is called its kinetic energy. It means, the energy i.e, work of a moving body is stored in which form, that is called kinetic energy.

Examples of kinetic energy:

1. Kinetic energy of flowing water which is used to rotate the turbine for generation of electricity.
2. Energy produced by moving vehicles is kinetic energy.
3. There is kinetic energy in the bullet fired by a gun, due to this energy it can penetrate the target.
4. Wind machines are operated by energy produced by blowing air.

Factors of measurement of kinetic energy

Kinetic energy can be measured by
1. Calculating the work done in bringing a body in the position of particular velocity from its state of rest i.e., the state of zero velocity.
2. Work done in bringing a moving body in its zero velocity position by retarding forces.
Expression for kinetic energy: Suppose a body of mass m starts moving from state of rest. If the force is variable and at any instant its value is F. During short time interval dt the body gets displaced by ds, then work done,
dW = \(\vec{F}.\vec{ds}\) = F ds cos 0°
or dW = F ds
∵ F = ma
∴ dW = ma ds

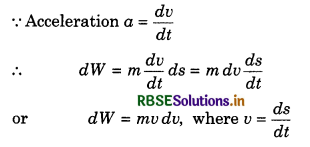
Therefore total work done in providing velocity v i.e., the kinetic energy of the body when its velocity is v,

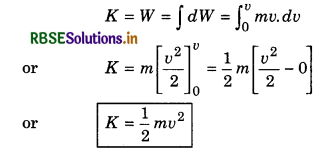
Alternative method: Suppose a body starts moving from rest under influence of a constant force F and the force remains active for time t. During this
time the body travels distance S and attains velocity v.
∴ Work done,
W = Force . distance
or W = F. S ..........................(1)
From Newton’s second law of motion
F = ma .....................(2)
Form third equation of motion,
v² = u² + 2aS
∵ The initial velocity is zero,
∴ u = 0
Hence v² = 2aS
⇒ S = \(\frac{v^2}{2 a}\) .............................(3)
Now from equations (1), (2) and (3),
W = ma x \(\frac{v^2}{2 a}\)
or W = \(\frac{1}{2}\) mv²
This work is stored in the body as its kinetic energy K.

Question 9.
Prove that in head on elastic collision of two balls of same mass, their velocities are interchnged after collision.
Answer:
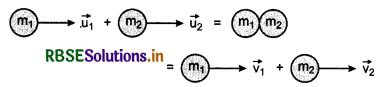
Suppose two bodies of masses m₁ and m₂ moving with velocities \(\overrightarrow{u_1}\) and \(\overrightarrow{u_2}\) respectively collide each other and after collision they move with velocities \(\overrightarrow{v_1}\) and \(\overrightarrow{v_2}\). This collision is perfectly elastic.

From law of conservation of momentum
Total momentum before collision = Total momentum after collision
or m₁ \(\overrightarrow{u_1}\) + m₂ \(\overrightarrow{u_2}\) = m₁ \(\overrightarrow{v_1}\) + m₂ \(\overrightarrow{v_2}\)
The collision is one-dimensional, therefore the direction of all velocities will be same.
Hence on considering only magnitude,
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ ..........................(1)
or m₁u₁ - m₁v₁ = m₂v₂ - m₂u₂
or m₁(u₁ - v₁) = m₂(v₂ - u₂) ..........................(2)
Now from law of conservation of energy,
Total kinetic energy before collision = Total kinetic energy after collision.
or \(\frac{1}{2}\) m₁u₁² + \(\frac{1}{2}\) m₂u₂² = \(\frac{1}{2}\) m₁v₁² + \(\frac{1}{2}\) m₂v₂²
or m₁u₁² + m₂u₂² = m₁v₁² + m₂v₂²
or m₁u₁² - m₁v₁² = m₁v₂² - m₂u₂²
or m₁(u₁ + v₁)(u₁ - v₁) = m₂(v₂ + u₂)(v₂ - u₂) .............................(3)
On dividing equation (3) by (2), we get
u₁ + v₁ = v₂ + u₂
or v₁ = v₂ + u₂ - u₁ ..........................(4)
Substituting this value of v₁ in equation (1),
m₁u₁ + m₂u₂ = m₁(v₂ + u₂ - u₁) + m₂v₂
or m₁u₁ + m₂u₂ = m₁v₂ + m₁u₂ - m₁u₁ + m₂v₂
or m₁u₁ + m₂u₂ - m₁u₂ + m₁u₁ = (m₁ + m₂) v₂
or 2m₁u₁ + u₂(m₂ - m₁) = v₂(m₁ + m₂)
∴ v₂ = \(\frac{2 m_1 u_1+u_2\left(m_2-m_1\right)}{\left(m_1+m_2\right)}\) ...........................(5)
For obtaining the expression for v₁, replace 1 by 2 and 2 by 1 in equation (5),
v₁ = \(\frac{2 m_2 u_2+u_1\left(m_1-m_2\right)}{\left(m_2+m_1\right)}\) ..........................(6)
Special situations: (i) When masses of both bodies are same, i.e., m₁ = m₂ = m
Then v₂ = \(\frac{2 m u_1+(m-m) u_2}{m+m}=\frac{2 m u_1+0}{2 m}\)
or v₂ = u₁ ..........................(7)
and v₁ = \(\frac{2 m u_2+(m-m) u_1}{m+m}=\frac{2 m u_2+0}{2 m}\)
or v₁ = u₂ ......................(8)
Conclusion: Therefore the velocities of the bodies of same mass are interchanged after perfectly head on collision, that is in head on collision, the exchange of momentum is maximum when their masses are equal.

(ii) When second body is at rest i.e., u₂ = 0, then from equation (5),
v₂ = \(\frac{2 m_1 u_1}{m_1+m_2}\)
and from equation (6),
v₁ = \(\frac{u_1\left(m_1-m_2\right)}{m_2+m_1}\)
If m₁ = m₂ = m₁ then
v₂ = \(\frac{2 m u_1}{2 m}\) = u₁
and v₁ = 0
Transfer of energy when m₁ ≠ m₂: The part of energy which is transfered to other body (u₂ = 0)

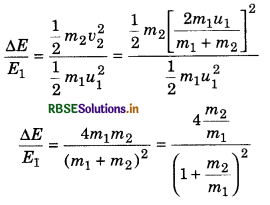
(iii) When m₂ >>> m₁ and u₂ = 0, then from equation (6),
v₁ = \(\frac{-m_2}{m_2} u_1\)
or v₁ = -u₁
and v₂ = \(\frac{2 m_1 u_1}{m_2}\) = 0
For example, if a ball falls from a height on the smooth surface of earth, then the collision of earth and the ball is of this type of collision, and the ball returns back with initial speed.
(iv) If m₂ << m₁ and u₂ = 0, then from equations (5) and (6),
v₁ = \(\frac{m_1}{m_1}\)u₁ = u₁
or v₁ = u₁
and v₂ = \(\frac{2 m_1}{m_1} u_1\)
or v₂ = 2u₁
i.e., when a heavy particle strikes the light particle, then the change in velocity of heavy particle is negligible but light particle moves with double velocity of heavy particle.

Question 10.
Define potential energy. Prove that gravitational potential energy is mgh where parameters are in their usual meaning.
Answer:
Concept of potential energy is related with stored energy. Potential energy of a body possessed is due to its position or configuration. For example, on stretching the string of bow, potential energy is stored in it. Suppose a ball of mass m is raised by height h without providing motion to it, then work done by external agency against gravitational force,
W = mgh
This work is stored in the ball as its potential energy.
U_(h) = mgh
Actually it is not the gravitational potential energy of the ball; it is the energy of earth-ball system. When the object falls from height h, then according to third equation,
v² = u² + 2gh
For freely falling body, u = 0
∴ v² = 2gh
or \(\frac{1}{2}\) mv² = \(\frac{1}{2}\)m x 2gh = mgh
or \(\frac{1}{2}\)mv² = mgh
i.e., the potential energy of the body automatically changes in its kinetic energy on reaching the earth’s surface.
Unit of potential energy is ‘Joule’ (J) and its dimensional formula is [M¹L²T^-2]. Zero value of potential energy is taken arbitrarily. For example, in the case of spring we take U = 0 when displacement x = 0.
For conservative force, the change in potential energy is taken equal to negative value of work done by the force, i.e.,

Question 11.
Describe two dimensional elastic collision. How the velocities of particle are obtained after collision.
Answer:
Suppose a particle A of mass m₁, moving with velcoity u₁ strikes another resting particle B of mass m₂. After collision the motion of particles is in X-Y plane such that particle A moves with velocity v₁ making an angle θ₁ with X-axis and B with velocity v₂ makg an angle θ₂ with X-axis (fig. 6.25).

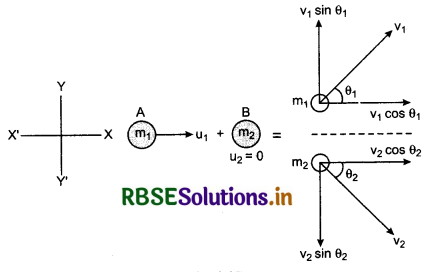
On applying the law of conservation of momentum, along X-axis.
m₁u₁ + m₂ x 0 = m₁v₁ cosθ₁ + m₂v₂ cosθ₂
or m₁u₁ = m₁v₁ cosθ₁ + m₂v₂ cosθ₂ ..............................(1)
and along Y-axis,
Initial momentum = Final momentum
or 0 = m₁v₁ sinθ₁ - m₂v₂ sinθ₂
or m₁v₁ sinθ₁ = m₂v₂ sinθ₂ ...........................(2)
Since the collision is elastic, therefore the kinetic energy of the system will remain conserved.
∴ \(\frac{1}{2}\)m₁u₁² + 0 = \(\frac{1}{2}\)m₁v₁² + \(\frac{1}{2}\)m₂v₂²
or m₁u₁² = m₁v₁² + m₂v₂² ..........................(3)
Equations (1), (2) and (3) are the  basic equations of two dimension elastic collision.
There are four unknown quantities v₁, v₂, θ₁ and θ₂, if one qunatity is measured then rest three quantities can be obtained by solving above three basic equations.
Special situations: When the masses of both particles are same i.e., m₁ = m₂ = m, then from equation (1),
mu₁ = mv₁ cosθ₁ + mv₂ cosθ₂
u₁ = v₁ cosθ₁ + v₂ cosθ₂ ............................(4)
from equation (2),
mv₁ sinθ₁ = mv₂ sinθ₂
or v₁ sinθ₁ = v₂ sinθ₂
or 0 = v₁ sinθ₁ - v₂ sinθ₂ ..........................(5)
From equation (3),
mu₁² = mv₁² + mv₂²
or u₁² = v₁² + v₂² .........................(6)
On adding the squares of equations (4) and (5),
(u₁)² + 0 = (v₁ cosθ₁ + v₂ cosθ₂)² + (v₁ sinθ₁ - v₂ sinθ₂)²
or u₁² = v₁² cos²θ₁ + v₂² cos²θ₂ + 2v₁v₂ cosθ₁ cosθ₂ + v₁² sin²θ₁ + v₂² sin₂θ₂ - 2v₁v₂ sinθ₁ sinθ₂
or u₁² = v₁² (cos² θ₁ + sin² θ₁) + v₂² (cos² θ₂ + sin² θ₂) + 2v₁v₂(cosθ₁ cosθ₂ - sinθ₁ sinθ₂)
or u₁² = v₁² + v₂² + 2v₁v₂ cos(θ₁ + θ₂)
or u₁² = u₁² + 2v₁v₂ cos(θ₁ + θ₂) (from equation (6))
or 2v₁v₂ cos(θ₁ + θ₂) = 0
or cos(θ₁ + θ₂) = 0
⇒ (θ₁ + θ₂) = 90°

Numerical Questions

Based on Scalar Product of Vectors

Question 1.
If \(\vec{A}\) = (\(2\hat{i} - 2\hat{j} + \hat{k}\)) and \(\vec{B}\) = (\(2\hat{i} + 2\hat{j} + 2\hat{k}\)), then find the angle between \(\vec{A}\) and \(\vec{B}\).
Answer:
Given: \(\vec{A}\) = (\(2\hat{i} - 2\hat{j} + \hat{k}\)) and \(\vec{B}\) = (\(2\hat{i} + 2\hat{j} + 2\hat{k}\))
The angle between \(\vec{A}\) and \(\vec{B}\), θ = ?

Based on Work

Question 2.
Three forces \(\vec{F_1}\) = (\(2\hat{i} + 3\hat{j} + 4\hat{k}\)); \(\vec{F_2}\) = (\(\hat{i} + \hat{j} + \hat{k}\)) and \(\vec{F_3}\) = (\(3\hat{i} - 2\hat{j} - \hat{k}\)) are working on a system in same direction. These forces displace the system from (2, 3, 6) to point (5, 3, 8). Calculate the work done by the forces.
Answer:
Given: \(\vec{F_1}\) = (\(2\hat{i} + 3\hat{j} + 4\hat{k}\)); \(\vec{F_2}\) = (\(\hat{i} + \hat{j} + \hat{k}\)); \(\vec{F_3}\) = (\(3\hat{i} - 2\hat{j} - \hat{k}\))
Co-ordinate of initial and find points = (2, 3, 6) and (5, 3, 8).

Question 3.
Relation between displacement x and time t for a moving particle under influence of a force, is t = \(\sqrt{x}\) + 3, where x is in metres and t is in second, find:
(i) Displacement of the particle at the moment when its velocity is zero.
(ii) Work done by the force in first 6 seconds.
Answer:
∵ t = \(\sqrt{x}\) + 3 or \(\sqrt{x}\) = t - 3
or x = (t - 3)² = t² - 6t + 9
∴ Velocity v = \(\frac{d x}{d t}=\frac{d}{d t}\)(t² - 6t + 9)
= 2t - 6
(i) When v = 0,
then 2t - 6 = 0 ⇒ t = 3
∴ Displacement when v = 0
x = t² - 6t + 9 = (3)² - 6 x 3 + 9
= 9 - 18 + 9 = 18 - 18 = 0
or x = 0 (zero)
(ii) ∵ x = t² - 6t + 9
∴ At t = 0, x₀ = 0 = 0 - 0 + 9 = 9
at t = 6s, x₆ = (6)² - 6 x 6 + 9 = 36 - 36 + 9
or x₆ = 9 m
∴ Displacement ∆x = x₆ - x0 = 9 - 9 = 0
Therefore work done
W = F.∆x = F x 0 = 0
or W = 0

Question 4.
Force acting on a body of mass 1 kg is \(\vec{F}\) = -2\(\vec{x}\) N, Where x is in metres. If velocity of the body at x = 3.0 m be 8.0 ms^-1, then what will be its velocity at x = 4 m?
Answer:
u = 8 ms^-1, v = ?, x₁ = 3m, x₂ = 4m, \(\vec{F}\) = -2\(\vec{x}\), m = 1kg
∴ From work energy theorem,
K_f - K_i = W

Question 5.
Force constant of a spring is K and it obeys Hooke’s law. Work done in stretching the spring by 10 cm from its original length, is 4 J, calculate:
(i) Value of K.
(ii) Work done in stretching 10 cm more.
Answer:
W = 4J; x = 10 cm = 10 x 10^-2 m = 0.10 m
(i) ∵ W = \(\frac{1}{2}\)Kx²
⇒ K = \(\frac{2 W}{x^2}=\frac{2 \times 4}{0.1 \times 0.1}\) = 800 N.m^-1
(ii) x₁ = 10 cm = 0.10 m; x₂ = 20 cm = 0.20 m

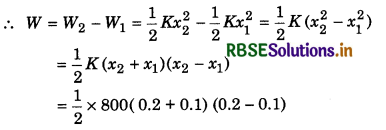
= 400 (0.3)(0.1)
= 400 x0.03 = 4 x 3
= 12J

Question 6.
A chain is placed on a frictionless table figure such that its 1/5 part is hanging from the edge of the table. If length of the chain be l and its mass be m kg, then calcualte the work done in pulling the hanging part of the chain on the table.

Answer:
Solve as example 22.

Question 7.
A rain drop of radius 1 mm falls from the height of 200 m. When it falls with reducing acceleration due to air resistance then it attains maximum speed in half distance of its real height and after that it falls with uniform speed. How much work is done by gravitational force during its first half and second half journey? Density of water = 10³ kgm^-3.
Answer:
r = 1mm = 1 x 10^-3 m, dw = 10³ kgm^-3
∴ Volume of the drop,
V = \(\frac{4}{3}\)πr³ = \(\frac{4}{3}\) x 3.14 x (10^-3)² = 4.189 x 10^-9 m³
∴ Mass of the drop m = Vdw
∴ Force acting on the drop,
F = mg = V dW g = 4.189 x 10^-9 x 10³ x 9.8
= 4.105 x 10^-5 N
Distance of half journey = \(\frac{200}{2}\) = 100 m
∴ Work done in half journey
= F d = 4.105 x 10^-5 x 100
= 4.105 x 10^-3 J
Similarly the work done by gravitational force during rest half journey.
W = 4.105 x 10^-3 J

Question 8.
A stone of mass 6 kg and density 2g. cm^-3 is immersed in water. Calculate the work done in raising this stone from the depth of 4 m to 1 m in water. (g = 10 ms^-2)
Answer:
Mass of the stone m = 6 kg
∴ Weight of the stone W = mg = 6 x 10 = 60 N
Density of the stone d = 2g.cm^-3 = 2 x 10³ kg.m^-3
∴ Volume of stone V = \(\frac{m}{d}=\frac{6}{2 \times 10^3}\) = 3 x 10^-3 m³
∴ Volume of displacement water
V = 3 x 10^-3 m³,
Therefore the force of buoyancy F = V.dw.g
or F' = 3 x 10^-3 x 10³ x 10
= 30N
∴ Resultant force acting on stone
F = W - F' = 60 - 30 = 30N
Displacement of stone = 4 - 1 = 3m
∴ Work done on stone in raising it in water
W = F d = 30 x 3
or W = 90J

Based on Energy

Question 9.
In figure, a smooth curved path ABC is shown. Its path after B is vertical circular path of radius r. From what minimum height, a ball should be released so that it may cross the highest point C remaining in contact the plane?

Answer:
When the ball reaches point B, then potential energy = kinetic energy
or mgh = \(\frac{1}{2}\)mv_B² ⇒ v_B = \(\sqrt{2 g h}\)
For completing vertical circular path i.e., to reach highest point C, the velocity at B should be equal to critical velocity at lowest point of vertical circle.
i.e., v_B = \(\sqrt{5 r g}\)
∴ \(\sqrt{2 g h}=\sqrt{5 r g}=\sqrt{2 h}=\sqrt{5 r}\)
or h = \(\frac{5}{2}\)r

Question 10.
A block of mass 2 kg is allowed to fall from a height of 40 cm on a spring of force constant of 1960 Nm^-1. What will be maximum compression in spring?

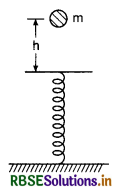
Answer:

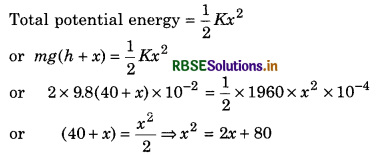
or x² - 2x - 80 = 0
or x² - 10x + 8x - 80 = 0
or x(x - 10) + 8(x - 10) = 0
or x(x - 10)(x + 8) = 0
∴ x = 10 and x = -8
Therefore x = 10 cm (on considering positive value only)

Question 11.
Cross-section of hill feature is shown in figure. A ball of mass 1.0 kg is rolled at A with kinetic energy of 300 J and it reaches to point C passing through point B. Considering ball and the hill frictionless, calculate the following: 

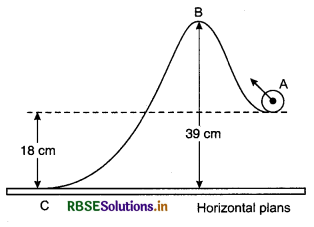
(i) Kinetic energy of the ball at B
(ii) If potential energy of the ball at A be zero, then its potential energy at C.
(iii) Speed of the ball at C.
(iv) Change in potential energy in going from B to C. (g = 10ms^-2)
Answer:
(i) Increase in potential energy from A to B on hill
= mgh = 1 x 10 x (39 - 18) = 10 x 21
= 210J
Kinetic energy of the ball at A = 300 J
∴ Kinetic energy a B = 300 - 210 = 90 J
(ii) Potential energy of the ball at C = Potential energy at A + Decrease in potential energy from A to C
= 0 - 1 x 10 x 18
= -108 J
(iii) Kinetic energy at C = Kinetic energy at A - Potential energy
= 300 - (-180) = 300 + 180
= 480 J
or \(\frac{1}{2}\)mv_c² = 480
or \(\frac{1}{2}\) x 1 x v_c² = 480
or v_c² = 480 x 2 = 960
∴ v_c = \(\sqrt{960}\) = 30.98 ≈ 31 ms^-1
or v_c = 31 ms^-1
(iv) Change in potential energy from B to C
= potential energy at C - potential energy at B
= -180 - 210 = -390 J
= -390 J

Question 12.
A ball is thrown from height of 10 m with initial velocity of u₀. 50% of its energy decays on striking the ground and again raises upto same height. Find:
(i) Initial velocity u₀.
(ii) If it is thrown vertically upward then upto which height the ball will raise?
Answer:
(i) Suppose the mass of the ball = m, then kinetic energy of the ball at the time of throwing it
= \(\frac{1}{2}\)mu₀² ................................(1)
Potential energy of the ball at height h = mgh ...................................(2)
∴ Total energy of the ball = \(\frac{1}{2}\)mu₀² + mgh ...........................(3)

(ii) If the ball is thrown vertically upward with velocity u₀, then during its return journey, the velocity of the ball at projection point will be u₀ in downward direction. Therefore the action of part (i) will be repeated.
∴ The height upto which the ball will reach = 10 m

Question 13.
Force-compression graph for a spring is shown in figure. An object of mass 5 kg, moving with velocity of 8 ms-1, strikes. Find the force constant and compression produced in spring.
Answer:
Gradient of the graph = force constant
or tanθ = K

∵ Kinetic energy of the body = Potential energy of the body

Question 14.
A man of weight 50 kg-wt, taking a load of 15 kg-wt walks 20 m, calculate the work done:
(a) When he walks on plane surface.
(b) When he walks on an inclined plane of 5° to 1°. (g= 10ms^-2)

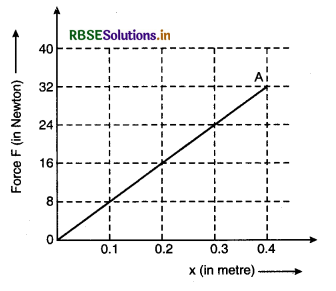
Answer:
(a) On horizontal plane the angle between displacement and gravitational force is 90°.
i.e., θ = 90°
∴ W = Fd cos90°
or W = 0
(b) Note: In such type of question (inclined from 5° to 1°), the value of sinθ is \(\frac{1}{5}\).
i.e., sinθ = \(\frac{1}{5}\)
The force applied by the man = Mg sinθ
∴ Work done
W = Mg sinθ x d
= 65 x 10 x \(\frac{1}{5}\) x 20
= 2600 J

Based on Power

Question 15.
A petrol operated water pump pumps the water from the depth of 30 m at the rate of 0.50 m³. min^-1. If the efficiency of the pump is 70%, then find the power generated by the pump. (g = 9.8 ms^-2; density of water is 10³ kg.m^-3)
Answer:
Mass of water pumped in 1 min = volume x density
= 0.50 x 10³ kg
= 50 kg
h = 30 m
∴ Work done
W = mgh = 50 x 9.8 x 30
= 14700 J
∴ Output power of the pum
P₀ = \(\frac{W}{t}=\frac{14700}{60}\) = 2450 watt
∵ Efficiency of the pump

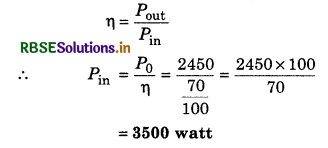
Question 16.
Human heart pumps blood at the rate of 4 litre per minute at pressure of 130 mm of mercury. If density of mercury 13.6 g. cm^-3, then determine the power of the heart.
Answer:
Height of mercury column h = 130 mm = 0.130 m
Density of mercury ρ = 13.6 g.cm^-3
= 13.6 x 10³ kg.m^-3
∴ Pressure P = hρg = 0.130 x 13.6 x 10³ x 9.8
= 17.3 x 10³ N.m^-2
Volume of blood V = 4 liter = 4 x 10^-3 m³
∴ Work done by heart,
W = force x displacement
= \(\frac{\text { force }}{A}\) x A x displacement
= Pressure x volume
= 17.3 x 10³ x 4 x 10^-3
= 69.2 J
Time t = 1 min = 60 s
∴ Power of the heart
P = \(\frac{W}{t}=\frac{69.2}{60}\)
or P = 1.153 J.s^-1
or P = 1.153 watt
or P = 1.15 watt.

Question 17.
A tubewell pumps 2400 kg water per minute. If water comes out of pipe with the velocity of 3 ms^-1, then find the power of the pump. How much work is done by the pump in 10 hrs? (g = 10ms^-2).
Answer:
Mass of pumped water = \(\frac{2400}{60}\) = 40 kg per second
Velocity of water v = 3 ms^-1
∴ Power = \(\frac{\text { Energy }}{\text { time }}=\frac{\frac{1}{2} m v^2}{t}=\frac{\frac{1}{2} m v^2}{1}=\frac{1}{2} m v^2\)
= \(\frac{1}{2}\) x 40 x 3 x 3
= 180 watt
t = 10 hr = 10 x 3600 s
∴ Work done = P x t
= 180 x 10 x 3600
= 6480000
= 6.48 x 106 J

Question 18.
A motor boat is moving with constant speed of 36 km.h^-1. If the resistance of water against the boat is 400 N, then find the power of the engine of the boat.
Answer:
Velocity of motor boat
v = 36 km.h^-1 = 36 x \(\frac{5}{18}\) = 10 ms^-1
F = 4000 N
∴ Power, P = Fv
or P = 4000 x 10 = 40 x 10³ watt
or P = 40 kW

Based on Collision

Question 19.
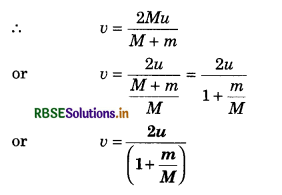
A smooth sphere of mass M and moving with velocity u, strikes another resting sphere of mass m making head on elastic collision. After collision, there velocities are respectively V and v. Prove that v = \(\frac{2 u}{1+\frac{m}{M}}\)
Answer:
According to principle of conservation of momentum,
m₁u₁ + m₂u₂ = m₁v₁ + m₁v₂
or Mu + M x O = MV + mv
or Mu = MV + mv ........................(1)
From Newton's law of collision,
e = \(\frac{v_2-v_1}{u_1-u_2}=\frac{v-V}{u-0}\)
For perfectly elastic collision, e = 1
∴ 1 = \(\frac{v-V}{u}\)
or u = v - V
∴ V = v - u
∴ From equation (1)
Mu = M(v - u) + mv
or Mu = Mv - Mu + mv
or 2Mu = v(M + m)

Question 20.
A body of mass 10 kg moving with velocity of 5 ms^-1, strikes another resting body of mass 10 kg under head on elastic collision. Find the velocities of both the bodies after collision.
Answer:
In perfectly head on elastic collision of bodies of same mass, the velocities are interchanged.
i.e., v₁ = u₂ and v₂ = u₁
Given: u₁ = 5 ms^-1; u₂ = 0
∴ v₁ = u₂ = 0
or v₁ = 0
and v₂ = u₁ = 5 ms^-1

Question 21.
A proton moving with velocity of 500 ms^-1, does head on collision with another resting proton. After collision, first proton scatters at an angle of 60° with initial direction. What will be direction of second proton after collision? Also determine the speed of protons after collision.
Answer:
u₁ = 500 ms^-1; u₂ = 0
m₁ = m₂ = m
From conservation of momentum

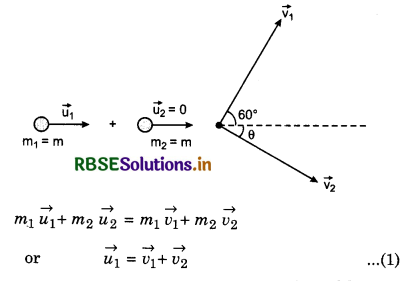
For elastic collision, for conservation of kinetic energy


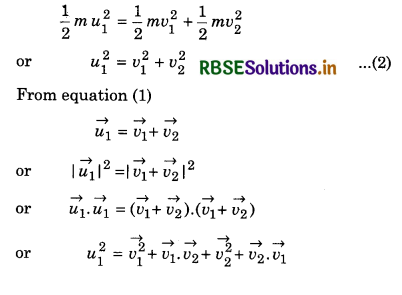
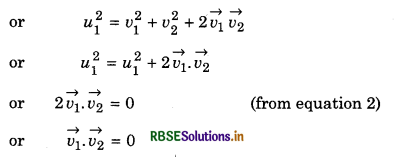
or v₁v₂ cosΦ = 0
or cosΦ = 0
∴ Φ = 90°
or (60° + θ) = 90°
∴ θ = 30°
Now from conservation of moment in horizontal direction
mu₁ = mv₁ cos 60° + mv₂ cos 30°
or u₁ = v₁ cos 60° + v₂ cos 30°
or u₁ = \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2} \)v₂ .....................(3)
For conservation of momentum in vertical direction
0 = v₁ sin 60° - v₂ sin 30°
or 0 = \(\frac{\sqrt{3}}{2} v_1-\frac{v_2}{2}\)
or \(\sqrt{3} \)v₁ = v₂
or v₁ = \(\frac{v_2}{\sqrt{3}}\) ....................(4)
From equation (3),
2u₁ = v₁ + \(\sqrt{3}\)v₂
Substituting the value of v₁ from equation

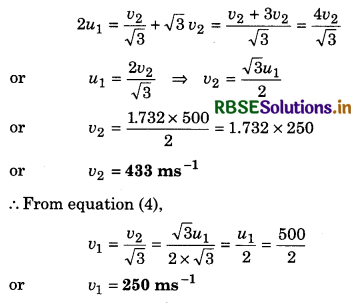
High Order Thinking Skills or HOTs

Question 1.
In figure, two blocks are released from the shown situation. Find the velocity with which the block of 5 kg touches the surface when its initial height from the surface is 4 m. Also show that gain in kinetic energy of the system is equal to loss of its potential energy. (g = 10 ms^-2).

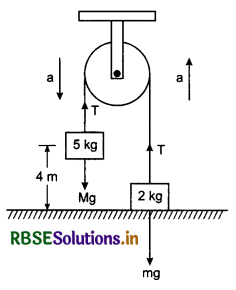
Solution:
Equation of motion block of mass 5 kg,
Mg - T = Ma ...................(1)
and for mass of 2 kg,
T - mg = ma .................(2)
On adding equations (1) and (2),
Mg - mg = a(M + m)

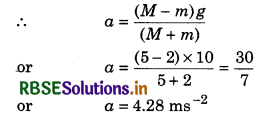
Now if the velocity with which the block of mass M reaches the ground, be v, then using equation v² = u² + 2as
v² = 0 + 2 x 4.28 x 4 = 34.29 (because initially both the blocks are at rest, hence u = 0)
∴ v = \(\sqrt{34.29}\)
or v = 5.85 ms^-1
∵ u = 0
∴ Initial kinetic energy K_i = \(\frac{1}{2}\)(M + m)u₂ = 0
Final kinetic energy
K_f = \(\frac{1}{2}\)(M + m)v₂ = \(\frac{1}{2}\)(5 + 2) x 34.29
or K_f = \(\frac{1}{2}\) x 7 x 34.24
or K_f = 120.015 J
or K_f = 120 J
Initial potential energy of the system
U_i = Mgh₁ + mgh₂ = 5 x 10 + 4 + 2 x 10 x 0
= 200 + 0
or U_i = 200 J
Final potential energy of the system
U_f = Mgh₁ + mgh₂ = 5 x 10 x 0 + 2 x 10 x 4
= 0 + 80
or U_f = 80 J
∴ Loss in potential energy
= U_i - U_f = 200 - 80 = 120J
Thus gain in kinetic energy = Loss in potential of system energy = 120J

Question 2.
A bullet of mass 20 g moving with velocity v, strikes a block of mass 980 g and enters in it. The block is attached with a spring of force constant 100 N.m^-1. The spring gets compressed by 10 cm after collision. Find:

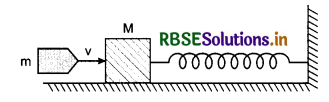
(a) velocity of the block after collision.
(b) value of v, the velocity of bullet.
(c) decay in kinetic energy in collision.
Solution:
(a) Given: Mass of bullet m = 20g = 0.020 kg; Mass of the block M = 980 g = 0.980 kg; Velocity of bullet = v and that of the block = V.
∴ From principle of conservation of momentum,
mv + M x 0 = (M + m)V
∴ V = \(\frac{m v}{(M+m)}\) .....................(1)
Potential energy of spring = Kinetic energy of (block + bullet) system
or \(\frac{1}{2}\)Kx² = \(\frac{1}{2}\)(M + m)V²
or Kx² = (M + m)V²
or 100 x (0.10 x 0.10) = (0.98 + 0.02)V²
or 1 = 1 x V²
or V = 1 ms^-1
(b) From equation (1),

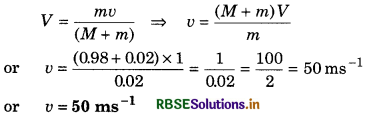
(c) Decay in kinetic energy after collision,

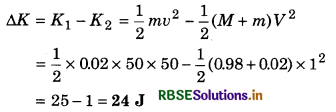
Question 3.
A particle of mass M moving with velocity u does head on elastic collision with another resting particle of mass m. Prove that the ratio of decay in initial energy of particle of mass M and its initial energy will be \(\frac{4 R}{(1+R)^2}\); where R = \(\frac{m}{M}\). For what value of R this ratio will be maximum?
Solution:
In head on elastic collision,


For maximum value of this ratio, denominator (1 + R)² should be minimum.
∵ (1 + R)² = (1 - R)² + 4R
For minimum value of L.H.S.
(1 - R)² = 0 or (1 - R) = 0
or R = 1
∴ Fro R = 1, the given ratio will be maximum

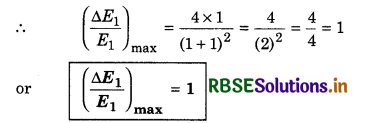
Question 4.
Two bodies of masses m and 2m are placed on a smooth plane and are attached with ends of a spring. A third body C of mass m is moving with velocity u₀ along the line joining A and B as shown in the diagram and collides elastically with A. After time t₀ of collision, instantaneous velocities of A and B are same and compression in spring is x₀. Find:

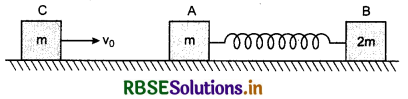
(a) Common velocity of A and B at time t₀,
(b) Spring constant.
Solution:
Masses of bodies A and B are m and 2m which are placed on a smooth plane. Therefore when body C strikes body A elastically, then it transfers it momentum mv₀ and kinetic enrgy \(\frac{1}{2}\)mv₀² to body A. At this moment the spring is in its own shape and B is stationary. Therefore instantaneous momentum of the system is mv₀ and energy \(\frac{1}{2}\)mv₀². Immediately, the spring starts compressing and B also starts moving.
After time t₀ instantaneous velocity of A and B is v, it is supposed. Compression of spring is x₀. Therefore at this moment (at time t₀), the kinetic energies of A and B are respectively \(\frac{1}{2}\)mv² and \(\frac{1}{2}\)(2m)v² and the potntial energy of compressd spring is \(\frac{1}{2}\)Kx₀².
∵ There is no external force in action, therefore from conservation of energy and momentum,
mv₀ = mv + 2mv
or v₀ = v + 2v
or v₀ = 3v ..........................(1)
and \(\frac{1}{2}\)mv₀² = \(\frac{1}{2}\)mv² + \(\frac{1}{2}\)(2m)v² + \(\frac{1}{2}\)Kx₀²
or mv₀² = mv² + 2mv² + Kx₀²
or mv₀² =  3mv² + Kx₀² ..........................(2)
From equation (1),

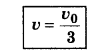
Substituting this value of v in equation (2),

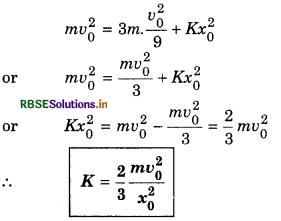
Question 5.
A body of mass 4 m, suddenly explodes in three pieces. If two pieces of mass m move at right angles to each other with velocity t then what will be velocity of third piece of mass 2 m? Calculate the increase in kinetic energy after explosion.

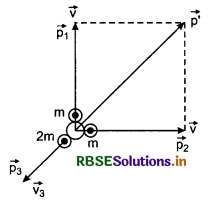
Solution:
On applying the principle of conservation of momentum,

Initally, the big body is at rest, therefore initial kinetic energy K_i = 0
∴ Find kinetic energy

Question 6.
A bullet of mass m moving with velocity v strikes a body of mass M, which is at rest and is hanging from the cord of length L. The bullet enters the body and remains in it. What will be maximum angle of the bullet with vertical after collision?

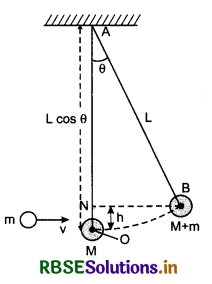
Solution:
In ∆ABN
\(\frac{A N}{A B}\) = cosθ
or AN = AB cosθ
or AN = L cosθ
If h is height, by which the combined body (M + m) rises from horizontal level
h = AO - AN
h = L - L cosθ = L(1 - cosθ) .....................(1)
From conservation of momentum
mv + 0 = (M + m)v'
or v' = \(\frac{m v}{M+m}\) ........................(2)
Now from conservation of energy,
\(\frac{1}{2}\)(M + m)v'² = (M + m)hg
or v'² = 2gh ....................(3)
∴ v' = \(\sqrt{2gh}\)
∴ From equations (2) and (3),

Question 7.
Potential energy of a body of mass 1 kg, free to move along X-axis, is given by U_(x) = \(\left(\frac{x^4}{4}-\frac{x^2}{2}\right)\)J. Net mechanical energy of the body be 2J, then what will be maximum speed in ms-1?
Solution:
Given potential energy of the body of mass m = 1 kg
U_(x) = \(\left(\frac{x^4}{4}-\frac{x^2}{2}\right)\) J
The velocity of the body will be maximum when its potential energy will be minimum. i.e.,
\(\frac{d U}{d x}\) = 0 and \(\frac{d^2 U}{d x^2}\) = Positive

(iii) When x = 1, then \(\frac{d^2 U}{d x^2}\) = 3(1)² - 1 = 3 - 1 = 2
Thus it is clear that the potential energy (U) will be minimum when x = -1 or x = 1

Question 8.
Potential energy function for force between two atoms of a diatomic molecule, is given by U_(x) = \(\frac{a}{x^{12}}-\frac{b}{x^6}\), where a and b are constants and x is distance between the atoms. If dissociation enrgy of atoms is given by D = U_{at x=∞} - U_{at equlibrium}, then find the value of D.
Solution:
Given: Potential energy
U_(x) = \(\frac{a}{x^{12}}-\frac{b}{x^6}\)
∴ Force acting between the atoms,

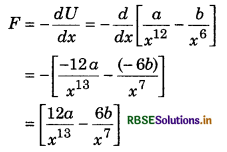
When both the atoms are in equilibrium, then F = 0
∴ \(\frac{12 a}{x^{13}}-\frac{6 b}{x^7}=0 \Rightarrow \frac{12 a}{x^{13}}=\frac{6 b}{x^7}\)
or \(\frac{2 a}{x^6}=b \quad \text { or } \quad x^6=\frac{2 a}{b}\)

Questions for Competitive Examinations

Objective Type Questions

Question 1.
A block of mass 2 kg is free to move along X-axis. It is at rest and a force depending on time F_(t) is applied on the block at t = 0. Force F_(t) depends on time according to diagram. Kinetic enrgy of the block after 4.5 s is:

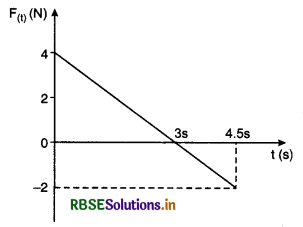
(a) 4.50 J
(b) 7.50 J
(c) 5.06 J
(d) 14.06 J
Solution:
According to impulse momentum theorem,
I = ∫F dt = ∆p
Area of (∆OAB + BCD) = pi - 0

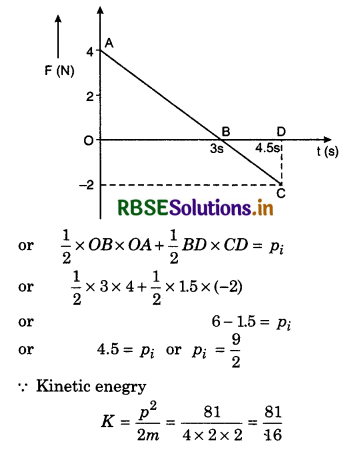
or K = 5.06 J
Thus, option (c) is correct.

Question 2.
Two particles of same mass, start moving from A in opposite directions in a horizontal circular orbit. As is shown in figure, their velocities along a tangent are v and 2v, and they move with uniform velocities between two collisions. After how many elastic collisions, after colliding at A, will they reach their initial plane?

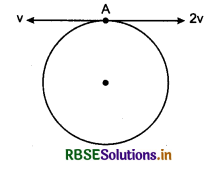
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
Since the masses of the particles are same and collision is elastic, therefore their velocities will interchange after each collision. First collision will take place at P and second at Q. After collidingat Q, they will collide at A which is initial position hence option (c) is correct.

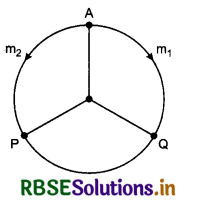
Question 3.
If resulant of external forces acting on a system of particles be zero, then certainly it can be said from an inertial frame of reference that.
(a) linear momentum of the system does not change with time.
(b) kinetic energy of the system does not change with time.
(c) angular momentum of the system does not change with time.
(d) potential enrgy of the system does not change with time.
Solution:
(a) Since there is no resultant external force acting on the system, therefore the linear momentum of the system will remain constant.
(b) In absence of external force, the kinetic energy of the system may change.
(c) Angular momentum of the system may change because in situation of couple of forces, the net force is zero while net torque is not zero. Therefore the angular moment of the system is not constant.
(d) Potential energy also may change.
Thus; option (a) is correct.

Question 4.
When a spring is pulled by 2 cm, then energy stored in it is 100 J. If the spring is pulled 2 cm more, then increase in stored energy will be:
(a) 100 J
(b) 200 J
(c) 300 J
(d) 400 J
Solution:

Question 5.
If the kinetic energy of an object is decreased by 64%, then the decrease in its momentum will be:
(a) 36%
(b) 20%
(c) 32%
(d) 6%
Solution:
∵ Momentum p = \(\sqrt{2mK}\) or p ∝ \(\sqrt{K}\)
∵ Kinetic energy is reduced by 64%.

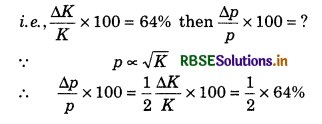
or Change in momentum = 32%
∴ Option (c) is correct.

Question 6.
A machine moves an object in straight line by a certain power. What will be relation between distance travelled and time?
(a) S² ∝ t³
(b) S² ∝ t³
(c) S³ ∝ t²
(d) S ∝ t³
Solution:
Given that power is constant

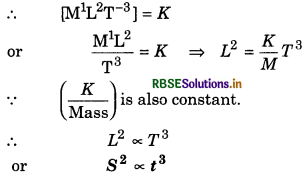
Therefore, option (a) is correct.

Question 7.
When two bodies collide elastically, then
(a) only kinetic energy of the sytem remains conserved.
(b) only momentum of the system remains conserved
(c) kinetic energy and momentum both of the system remain conserved
(d) neither momentum nor kinetic energy of the system remain conserved.
Solution:
In elastic collision kinetic energy and momentum both remain conserved.
Therefore, option (c) is correct.

Question 8.
A particle of mass 20 kg moving with the speed of 10 ms^-1, collides with a resting particle of mass 5 kg. On colliding both particles stick each other. What will be kinetic energy of joint particle?
(a) 600 J
(b) 800 J
(c) 1000 J
(d) 1200 J
Solution:
u₁ = 10 ms^-1, m₁ = 20 kg
u₂ = 0; m₂ = 5 kg
Velocity of combined particle = v
∴ According conservation of momentum,
m₁u₁ + m₂u₂ = (m₁ + m₂)v
∴ v = \(\frac{m_1 u_1}{\left(m_1+m_2\right)}=\frac{20 \times 10}{(20+5)}=\frac{200}{25}\)
or v = 8 ms^-1
∴ Kinetic energy of combined particle.
K = \(\frac{1}{2}\)(m₁ + m₂)v² = \(\frac{1}{2}\) x 25 x 8 x 8
or K = 800 J
∴ Option (b) is correct.

Question 9.
A body is situated on the earth in stable equilibrium. If a light push is applied on the body, what will be initial position of the centre of gravity?
(a) near the earth surface
(b) at some height from earth’s surface
(c) will remain unchanged
(d) will be at same level.
Solution:
In stable equilibrium, centre of gravity is at minimum distance from earth. When the object is slightly pushed, then it becomes in unstable equilibrium, therefore its centre of gravity rises by some extent.
Hence, option (b) is correct.

Question 10.
How much work will be done in accelerating a body of mass 50 kg from rest to speed of 20 ms^-1?
(a) 10³ J
(b) 10⁴ J
(c) 2 x 10³ J
(d) 4 x 10⁴
Solution:
m = 50 kg; u = 0; v = 20 ms^-1; a = ?; t = 10 s
∵ v = u + at
∴ 20 = 0 + a x 10 ⇒ a = \(\frac{20}{10}\) = 2 ms^-2
Now distance travelled
S = ut + \(\frac{1}{2}\)at² = 0 + \(\frac{1}{2}\) x 2 x 10 x 10 = 100 m
∴ Force F = m x a = 50 x 2 = 100 N
∴ Work done W = F x S = 100 x 100 = 10⁴ J
Therefore option (b) is correct.

Question 11.
A particle covers a distance of 10m under influence of a force of 5 N. If work done is 25 J , what will be angle between the direction of motion and force?
(a) 0°
(b) 30°
(c) 60°
(d) 90°
Solution:

Question 12.
A spring of force constant 5 x 10³ N.m^-1 expanded by 5 cm from its initial state. What will be work done in expanding the spring by 5 cm more?
(a) 12.50 Nm
(b) 18.75 Nm
(c) 25 Nm
(d) 6.25 Nm
Solution:
K = 5 x 10³ N.m^-1; x₁ = 5 cm = 5 x 10^-2 m,
∴ W₁ = \(\frac{1}{2}\)Kx₁² = \(\frac{1}{2}\) x 5 x 10³ x 25 x 10^-4 = 6.25 J
Now x₂ = (5 + 5) = 10 cm = 10 x 10^-2 m = 0.1 m
∴ W₂ = \(\frac{1}{2}\)Kx₂² = \(\frac{1}{2}\) x 5 x 10³ x 0.1 x 0.1 = 25 J
∴ Required work done
W = W₂ - W₁ = 25 - 6.25
or W = 18.75 J
Therefore, option (b) is correct.

Question 13.
For elastic collision between two spherical rigid bodies:
(a) total kinetic energy remains conserved
(b) total mechanical energy does not remain conserved
(c) linear momentum does not remain conserved
(d) linear momentum remains conserved.
Solution:
In non-elastic collision, after collision, the bodies do not regain their original shape and size. Therefore some of mechanical energy is not conserved. Howeve, in absence of external force, the momentum remains conserved.
Hence, option (d) is correct.

Question 14.
Kinetic energies of two particles of masses m and 2 m are same, then ratio of their linear moments will be:
(a) 1
(b) 1/2
(c) 1/V²
(d) 2
Solution:
Linear momentum p = \(\sqrt{2mK}\)
∵ K₁ = K₂ = K; m₁ = m; m₂ = 2m
∴ \(\frac{p_1}{p_2}=\sqrt{\frac{2 m_1 K}{2 m_2 K}}=\sqrt{\frac{m_1}{m_2}}=\sqrt{\frac{m}{2 m}}=\frac{1}{\sqrt{2}}\)
p₁ : p₂ = 1 : \(\sqrt{2}\)
Hence, option (c) is correct.

Question 15.
A player covers 100 m in 10s in Olympic games. What may be his kinetic energy range?
(a) 200 - 500 J
(b) 2 x 10⁵ - 3 x 10⁵ J
(c) 20000 - 50000 J
(d) 2000 - 5000 J
Solution:
Answer of this question will be obtained by considering most probable mass of a player i.e. by taking mass m = 65 kg. Velocity of player v = 10 ms^-1
∴ His kinetic energy
K = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) x 65 x 10 x 10
or K = 3250 J
Thus, option (d) is correct.

Question 16.
300 J work is done by a body of 2 kg in slipping on a inclined plane from the height of 10 m. Assuming g = 10 ms^-2, the work done against the force of friction will be:
(a) Zero
(b) 100 J
(c) 200 J
(d) 1000 J
Solution:
h = 10 m; m = 2 kg
W = 300 J; g = 10 ms^-2

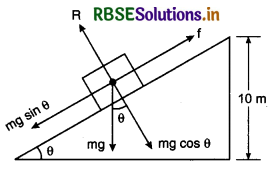
Work done in displacing the block upto top of inclined plane = Work done in slipping + Work done
or mgh = W + W_f
or W_f = mgh - W = 2 x 10 x 10 - 300
or W_f = -100 J
∴ Option (b) is correct.

Question 17.
An object of 2 kg slips on a horizontal plane with the velocity of 4 ms^-1. It strikes with a non-compressed spring and the spring gets compressed till the object does not become at rest. Kinetic force of friction is 15 N and force constant of the spring is 10,000 N.m^-1. The compression of the spring will be:
(a) 8.5 cm
(b) 5.5 cm
(c) 2.7 cm
(d) 11.10 cm
Solution:
Here m = 2kg; u = 4 ms^-1; dynamic friction force f_k = 15 N; force constant K = 10,000 N.m^-1
Suppose the compression in spring is x m, then kinetic energy of the body = Work done against frictional force + Potential energy of the spring
or \(\frac{1}{2}\)mv² = W_x + \(\frac{1}{2}\)Kx²

= 0.055 m
= 5.5 cm
Therefore, option (b) is correct.

Question 18.
A static bomb of 16 kg explode in two parts of masses 16 kg and 4 kg. Velocity of piece of 12 kg is 4 ms^-1. Kinetic energy of second piece is:
(a) 44 J
(b) 288 J
(c) 192 J
(d) 96 J
Solution:
From law of conservation of momentum,
m₁v₁ = m₂v₂
∴ v₁ = \(\frac{m_2 v_2}{m_1}=\frac{12 \times 4}{4}\) = 12 ms^-1
∴ Kinetic energy of piece of mass 4 kg
= \(\frac{1}{2}\)m₁v₁² = \(\frac{1}{2}\) x 4 x 12 x 12
= 288 J
∴ Option (b) is correct.

Question 19.
A block of mass M moving on a frictionless horizontal surface, strikes a spring of force constant K and compresses it by L. Maximum momentum of the block after collision will be:

(a) zero
(b) \(\frac{ML^2}{K}\)
(c) L\(\sqrt{MK}\)
(d) KL²/2M
Solution:
From law of conservation of energy,
Kinetic energy of the block = Potential energy of the spring

Therefore, option (c) is correct.

Question 20.
Two spheres A and B of masses m₁ and m₂ collide each other. Initially sphere A is at rest and B is moving with velocity v along X-axis. After collision, sphere B moves with velocity \(\frac{v}{2}\) in direction perpendicular to initial velocity. What will be direction of motion of A after collision?
(a) Same to B
(b) Opposite to B
(c) at angle θ = tan^-1(\(\frac{1}{2}\)) with X-axis
(d) at angle θ = tan^-1(-\(\frac{1}{2}\)) with X-axis
Solution:

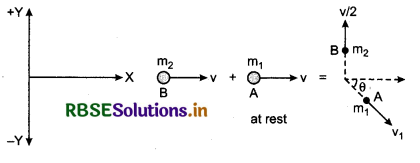
Here initial momentum,

Therefore, option (d) is correct.

Question 21.
A stone explodes in three pieces in horizontal plane. Two pieces move at right angles to each other. Mass of first piece is 1 kg which moves with velocity of 12 ms^-1 and second piece of 2 kg moves with speed of 8 ms^-1. If velocity of third piece be 4 ms^-1, then its mass is:
(a) 3 kg
(b) 5kg
(c) 7 kg
(d) 17 kg
Solution:
From law of conservation of momentum,

Thus, option (b) is correct.