RBSE Class 11 Physics Important Questions Chapter 5 Laws of Motion

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 5 Laws of Motion Important Questions and Answers.

RBSE Class 11 Physics Chapter 5 Important Questions Laws of Motion

Multiple Choice Questions

Question 1.
1 kg wt is equal to:
(a) 9.8 N
(b) 1 N
(c) 980 N
(d) 98 N
Answer:
(a) 9.8 N

Question 2.
Newton's law are applicable:
(a) in acceleration frame
(b) in non-acceleration frame
(c) in rotating frame
(d) in non-inertail frame.
Answer:
(b) in non-acceleration frame

Question 3.
Newton's third law of motion is equivalent to:
(a) law of conservation of linear momentum
(b) law of conservation of energy
(c) law of conservation of angular momentum
(d) law of conservation of mass and energy
Answer:
(a) law of conservation of linear momentum

Question 4.
Newton's third law of motion gives:
(a) measurement of force
(b) definition of inertia 
(c) definition of force
(d) property of force
Answer:
(d) property of force

Question 5.
A car is moving on rough road with uniform velocity then:
(a) the momentum of car is increasing
(b) no force is applied by the engine of car
(c) the force is applied by the engine of the car
(d) it is not possible
Answer:
(c) the force is applied by the engine of the car

Question 6.
To move on a smooth floor, a man requires the help of following law:
(a) Newton's first law 
(b) Newton's second law
(c) Newton's third law
(d) All above laws
Answer:
(c) Newton's third law

Question 7.
A person moves on a rough surface, then the force of friction applied by the surface is:
(a) in the direction of motion of the person
(b) in opposite direction of motion of the person
(c) in perpendicular direction of motion of the person
(d) in downward direction perpendicular to motion of the person.
Answer:
(a) in the direction of motion of the person

Question 8.
A train is moving on straight track with uniform velocity. A boy sitting in the train is holding the string attached with a balloon filled with hydrogen gas. If the drive applies the brakes suddenly, then balloon:
(a) will vertically upward
(b) will remain vertically downward
(c) will move ahead
(d) will move backwards
Answer:
(d) will move backwards

Question 9.
A beaker filled with some water, is placed on the pan of a spring balance. If we dip our finger in water without touching the bottom of the beaker, then the reading of the balance:
(a) will increase in comparison to previous reading
(b) will decrease in comparison to previous reading
(c) will remain unchanged
(d) will (change) depend on the liquid filled in beaker
[Hint: According to Newton's third law of motion, when finger is dipped in the beaker of water, the force applied by water on finger is same as that finger applies on the water i.e, on the bottom of the beaker. Hence the reading of balance will increase]
Answer:
(a) will increase in comparison to previous reading

Question 10.
A horse rider, sitting on the back of horse running on circular path, jumps and again comes on the back of horse; because:
(a) the motion is on circular path
(b) there is inertia of mobility
(c) there is inertia of rest
(d) it is impossible.
Answer:
(b) there is inertia of mobility

Question 11.
A block is placed on a table, reaction force will be:
(a) downwards by the block
(b) downwards by the table
(c) upwards by the block
(d) upwards by the table
Answer:
(d) upwards by the table

Question 12.
A force \(\vec{F}\) = 4t³ is applied on a body for first two second, the increase in linear momentum will be:
(a) 32 Ns
(b) 48 Ns
(c) 16 Ns
(d) 8 Ns
[Hint: Increase in linear momentum = Impulse of force

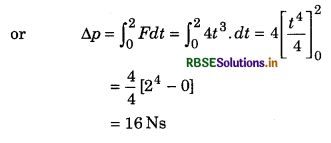
Answer:
(c) 16 Ns
 
Question 13.
Which of following is maximum friction force?
(a) Static friction
(b) Limiting friction
(c) Kinetic friction
(d) Rolling friction
Answer:
(b) Limiting friction

Question 14.
An object is placed on the table, the force of friction acting on the object depends on which of following?
(a) On the nature of the surface of the object
(b) On the area of contact surface
(c) On the weight of the object
(d) On the shape of the table
Answer:
(c) On the weight of the object

Question 15.
A force is applied on a free body for moving it. If the magnitude of force and the mass of the body is known, then we can find the following with the help of Newton’s second law:
(a) position of the body
(b) acceleration of the body
(c) speed of the obect
(d) weight of the body
Answer:
(b) acceleration of the body

Question 16.
Force of friction is:
(a) not self adjusting
(b) is self adjusting
(c) sometimes self adjusting and some times not
(d) nothing can be said
Answer:
(c) sometimes self adjusting and some times not

Question 17.
On polishing a rough surface beyond the limit, the value of frictional force:
(a) will increase
(b) will decrease
(c) Sometimes will increase and sometimes will decrease
(d) nothing can be said
Answer:
(a) will increase

Question 18.
A container filled with gas is moving with some acceleration in horizontal direction. Effect of gravity is negligible. The pressure in the container:
(a) is same every where
(b) is less in front
(c) is less in rear
(d) is less in upper part
Answer:
(b) is less in front

Question 19.
A block of mass m is placed on an inclined plane making an angle θ with horizontal. Coefficient of friction between block and plane is µ then the force of friction acting on the blcok is:
(a) µmg
(b) µmgtanθ
(c) µmg sinθ
(d) µmg cosθ
Answer:
(d) µmg cosθ

Question 20.
Working of rocket propulsion is based on:
(a) Newton’s first law of motion
(b) Principle of conservation of mass
(c) Newton’s third law of motion
(d) Law of conservation of momentum
Answer:
(d) Law of conservation of momentum

Question 21.
Value of \(\frac{\mu_s}{\mu_k}\) is:
(a) zero
(b) less than 1
(c) equal to 1
(d) greater than 1
Answer:
(d) greater than 1

Question 22.
A lift is moving downwards with acceleration ‘a’. A person drops a ball in the lift. What will be acceleration of ball for the person inside the lift and the person standing out side the lift is?
(a) a;g
(b) g;g
(c) (g - a),g
(d) (g - a);(g - a)
Answer:
(c) (g - a),g

Question 23.
Radius of a trun on national highway is R. The width of the road is b. For safe passing of a vehicle with velocity v, what should be the elevation of outer edge in comparision to inner edge be h, then value of h will be:

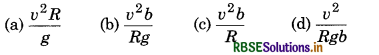
Answer:
(b) \(\frac{v^2 b}{R g}\)

Question 24.
When a particle moves on circular path, then no work is done by the force applied, because:
(a) the displacement of the object is zero
(b) no resultant force is present
(c) force and displacement are at right angles to each other
(d) force always acts away from the centre
Answer:
(c) force and displacement are at right angles to each other

Question 25.
A bottle is filled upto its neck by soda-water and it is rotated fastly in vertical circle. The bubbles will be gathered in which region of the bottle?
(a) Near the bottom
(b) Near the neck of the bottle
(c) At the middle region of the bottle
(d) Bubbles will be uniformly distributed in whole volume of the bottom
Answer:
(b) Near the neck of the bottle

Question 26.
A car is moving on the horizontal road turn of radius 10 m with the speed of 10 ms-1. A solid metallic ball is hanging from the ceiling of the car with the help of light rod of length 1.0 m. The angle made by the rod from vertical will be:
(a) 60°
(b) 45°
(c) 30°
(d) zero
[Hint: tanθ = \(\frac{v^2}{r g}=\frac{10 \times 10}{10 \times 10}\) = 1; θ = 45°]
Answer:
(b) 45°

Question 27.
To provide required centripetal force, the roads on hills are made rounded:
(a) plane
(b) circular
(c) banked
(d) non of these
Answer:
(c) banked

Fill in the Blanks

Question 1.
Friction always ............................
Answer:
Opppose relative motion

Question 2.
Banking of road is the phenomenon of ............................ outer edge of the road ............................ inner edge.
Answer:
Raising, above

Question 3.
1 Newton is equal to ............................ dyne.
Answer:
10⁵

Quesiton 4.
Linear momentum of a body is defined as ............................
Answer:
the product of mass and velocity

Question 5.
The net force on a body is equal to ............................ and ............................
Answer:
product of mass, acceleration

Question 6.
Impulse of a force is ............................ and ............................
Answer:
product of fone, time interval

Question 7.
The dimensional formula of force is ............................
Answer:
[MLT^-2]

Question 8.
Accelerated motion is always due to ............................
Answer:
external force.

Very Short Answer Questions

Question 1.
A body is moving with uniform velocity, will a force be required to keep the velocity uniform?
Answer:
No; according to Newton’s first law of motion, in absence of external force, the velocity of a moving body remains unchanged.

Question 2.
On which conservation principle is based jet engine? Whether conservation of energy or momentum or mass?
Answer:
Jet engine is based on principle of conservation of momentum.

Question 3.
Why a player runs upto some distance before he jumps?
Answer:
The player runs upto some distance to create inertia of motion.

Question 4.
If net force on a body is zero, will it be in state of rest?
Answer:
Not necessary; because net force is also zero on an obect moving with uniform velocity.

Question 5.
When a ball is thrown vertically upward, then its momentum decreases first and then increases. Is there violation of conservation of momentum in this process?
Answer:
No; because the momentum of (ball + Earth) remains conserved.

Question 6.
Can rocket fly in free space?
Answer:
Yes, rocket can fly in free space.

Question 7.
A bomb splits up in equal parts in air, what will be direction of motion of each part?
Answer:
Both parts will move in opposite directions according to law of conservation of momentum.

Question 8.
Air is projected on a sail of a boat by an electric fan situated at boat. Will the boat start moving?
Answer:
No; because the sum of momentum of boat and fan is zero. For moving the boat, reaction should be obtained by boat from external object.

Question 9.
What is the weight of man in freely falling lift?
Answer:
Zero; in freely falling lift the bodies are in position of weightlessness.

Question 10.
If the balls of iron, stone, clay and tennis, having same mass are projected on a wall one by one with same velocity, which ball will apply maximum force on the wall?
Answer:
Maximum force will be applied by tennis ball because it will rebounce with maximum velocity from the wall, therefore maximum change in momentum will be observed for tennis ball.

Question 11.
A man is standing on frictionless ice, how will he reach at the edge?
Answer:
By throwing an object he will move in opposite direction and will reach the edge of ice plateform.

Question 12.
Which one is maximum among coefficient of static friction, kinetic friction and rolling friction?
Answer:
∵ µ_r < µ_k < µ_s
i.e, coefficient of rolling friction < coefficient of kinetic friction < coefficient of static friction.

Question 13.
On what factors does the coefficient of friction depend between two contact surfaces?
Answer:
On humidity, nature of surface, temperature and cleanliness of surfaces.

Question 14.
What type of frame of reference is Earth?
Answer:
Non-inertial frame of reference; because rotating planes do accelerated motion. In this motion, the centripetal force produce acceleration.

Question 15.
Why the wheels are made circular?
Answer:
Because of this shape, they change sliding friction into rolling friction which is very less.

Question 16.
It is easy to maintain the motion than to start the motion; why?
Answer:
It is because the kinetic friction less than the static friction.

Question 17.
Two persons of same mass are standing on a plane surface, with ice skates in their feet; at some distance. A rope is tied round the waist of one person and second end of rope in hands of other person. What will happen when the person pulls the rope?
Answer:
Both persons will move towards each other with same momentum.

Question 18.
The distance travelled by a moving body is directly proportional to time (i.e. S ∝ t). Is any force acting on the body?
Answer:
∵ s ∝ t or s = Kt where K is a constant
∴ velocity v = \(\frac{d s}{d t}=\frac{d}{d t}\)(Kt) = K = constant
which means acceleration a = 0
∴ F = ma = 0 (zero)

Question 19.
What should be minimum number of unequal concurrent forces acting on a body for its equilibrium?
Answer:
For equilibrium of a body, there should be atleast three concurrent unequal forces.

Question 20.
A box of weight W, situated on a plane surface, is pulled by applying a force F on the box making an angle θ with vertical direction. If the box slides horizontally, how much reactional force is obtained to box?

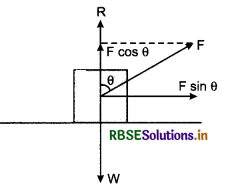
Answer:
On resolving the applied force F in two normal components as shown in fig. For vertical motion,
F cosθ + R = W
∴ R = W - Fcosθ
This is the reactional force acting on the box.

Question 21.
A ball is hanging with the help of a thread from the ceiling of a car. If the car takes turn towards left, then towards which side the ball will turn?
Answer:
When the car turns towards left, then a pseudo force will act in opposite direction. Therefore the ball will turn towards right.

Question 22.
A ball is suspended from the ceiling of a motor car-cart by a string. How will the position of the ball change if
(i) the cart is moving with uniform velocity
(ii) cart is moving with acceleration
(iii) cart is taking turn towards right.
Answer:
(i) The ball will suspend vertically.
(ii) The ball will shift towards rear.
(iii) The ball will shift towards left.

Question 23.
When a heavy train starts moving suddenly, then sometimes, the coupling of the compartments is broken. The breaking of which coupling is most possible?
Answer:
Sudden motion of engine applies sudden pull on the coupling between various compartments. This is why, the coupling may be damaged. Maximum pull is applied on the coupling between engine and first compartment, therefore it is most probable to be damaged.

Question 24.
A person jumps from the roof of his house, having some weight on his head. What weight will he experience during jump?
Answer:
Zero.

Question 25.
A boy is holding a cage in his hand, in which a bird is sitting. If the bird starts flying inside the cage, will the body experience any change in the weight of the cage?
Answer:
He will experience slight less weight of the cage because now the weight of the bird will not he effective on the cage.

Question 26.
A boy has a glass-cage in his hands and a bird is sitting on the floor of the cage. What change in the weight of the cage will be experienced by the boy if the bird (i) starts flying in the cage with constant velocity; (ii) starts flying upwards with acceleration; (iii) starts flying downwards with acceleration?
Answer:
No change, (ii) heavier than previous weight, (iii) lighter than previous weight.

Quesiton 27. 
Action and reaction forces are equal in magnitude and opposite in direction but even then they do not cancel each other, why?
Answer:
Action and reaction forces act on two different bodies, this is why they do not cancel each other.

Question 28.
Why we slip easily in rainy season?
Answer:
It is due to less friction between our shoes and wet surface.

Question 29.
What do you understand by isolated system?
Answer:
The system at which no external force is active, is called isolated system.

Question 30.
On placing a coin of 10 paise on a rotating table, it jumps in tangential direction, explain why?
Answer:
It happens due to inertia of direction.

Quesiton 31.
A small smooth bullet is placed on a smooth disc. On rotating the disc, the bullet rolls down from the disc, why?
Answer:
Since disc and bullet both are smooth, therefore required centripetal force for bullet to move with disc in circle, is not available. This is why the bullet rolls down.

Question 32.
A person sitting in a car strikes the outer window when car gets turn. Explain this event.
Answer:
It happen’s due to centrifugal force experienced by the person.

Question 33.
What is advantage of road banking on turn?
Answer:
Due to banking of road on turn, the safe velocity is increased and the vehicle crosses the turn with good velocity without slipping.

Question 34.
In uniform horizontal circular motion the kinetic energy of the particle remains constant in each position. Does this statement is true for vertical circular motion also?
Answer:
No; because the velocity of particle remains changing with position in vertical circle.

Question 35.
A heavy stone is suspended from a cord. As the stone was oscillated like simple pendulum, then the cord breaks. State the reason of this event.
Answer:
We know that tension in string becomes maximum at lowest point of vertical circle and is given by T = \(\frac{m v_{\max }^2}{r}\) + mg. This is why the cord breaks as the tension exceeds the limit of tolerance of tension.

Question 36.
Does the direction of centripetal force depend on the direction of rotation (i.e. clockwise or anticlockwise)?
Answer:
No; its direction is always towards the centre along the radius, this is why it is also called radial force. 

Question 37.
From where the centripetal force is provided to a car for turning on plane road?
Answer:
The required centripetal force is provided by force of friction between road and tyres of the car for turning on plane road.

Question 38.
Which is real force in centripetal and centrifugal forces and which is psuedo force?
Answer:
Centripetal force is real force while centrifugal force is psuedo force.

Match the following

Question 1.

Column I	Column II
(A) Newton's first law of motion	(p) nature
(B) Netwon's second law of motion	(q) defines force and inertia
(C) Newton's third law of motion	(r) measure of force
(D) Rate of change of linear momentum	(s) real law of motion

Answer:

Column I	Column II
(A) Newton's first law of motion	(q) defines force and inertia
(B) Netwon's second law of motion	(r) measure of force
(C) Newton's third law of motion	(p) nature
(D) Rate of change of linear momentum	(r) measure of force

Question 2.

Column I	Column II
(A) Centipetal force	(p) tanθ = \(\frac{v^2}{r g}\)
(B) Rounding a level curve	(q) \(\frac{m v^2}{r}\)
(C) Bending cyclist	(r) mrw2
(D) Centrifugal force	(s) vmax = \(\sqrt{\mu r g}\)

Short Answer Questions

Question 1.
The driver of a train, after starting the engine, first he pushes the engine backward and later on he takes it forward. Explain why.
Answer:
On pushing the compartments backwards, the coupling joining the compartments, become loose. Therefore, now moving the engine in forward direction, first of all first compartment and then rest compartments, one by one goes on moving. If driver does not do so, then due to stretched coupling, the whole train will start moving simultaneously. Therefore due to large inertia of rest, very high force will be required.

Question 2.
Whether a body moving with uniform velocity, in equilibrium?
Answer:
Yes; in equilibrium in linear motion,
F_net = 0
i.e., ma = 0 ⇒ a = 0
or \(\frac{d v}{d t}\) = 0 ⇒ v = constant or ∆u = 0
i.e., the body is moving with uniform velocity.

Question 3.
Linear momentum of a light and heavy body are same. Kinetic energy of which particle will be more?
Answer:
∵ K = \(\frac{1}{2} m v^2=\frac{1}{2} \frac{m^2 v^2}{m}=\frac{p^2}{2 m}\)
∵ p is constant here
∴ K ∝ \(\frac{1}{m}\)
∴ Kinetic energy of light body will be more than heavy one.

Question 4.
Kinetic energies of one light and one heavy object are same. Linear momentum of which object will be more?
Answer:
∵Kinetic energy K = \(\frac{p^2}{2 m}\) or p² = 2mK
∴ p = \(\sqrt{2 m K}\)
∵ K is constant here
∴ p ∝ \(\sqrt{m}\)
Therefore momentum of heavy object will be more than lighter object.

Question 5.
An object of 0.5 kg is hanging from a spring balance and the similar object is balanced on pan of a physical balance. Both these are placed in a lift which is moving upwards with uniform acceleration. What will be effect on reading of both balances?
Answer:
(i) For spring balance, the reading will show the apparent weight (R) of the object which is given by
R = m(g + a)
Therefore the reading of spring balance will increase.

(ii) Apparent weight will be effective equally on both pans of physical balance. Hence there will be no change in reading of physical balance.

Question 6.
A person is standing in a lift. When he experiences his weight increasing and when decreasing?
Answer:
When lift moves upwards with uniform acceleration then his weight is increased and when the lift moves downwards with acceleration, then his weight is decreased.

Question 7.
Three blocks of equal mass m are placed on a frictionless table (see fig.). The blocks are pushed by applying a force F. Tell that:

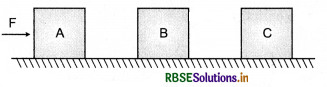
(i) What is acceleration of blocks?
(ii) What is net force on block A?
(iii) What is the force applied by block A on block B?
(iv) What force is applied by block B on block C?
(v) Show the action and reaction forces on the blocks.

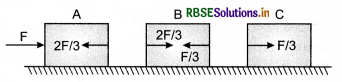
Answer:
(i) Acceleration of each block, a = \(\frac{F}{3 M}\)
(ii) Net force on block A = \(\frac{F}{3}\)
(iii) Force applied by block A on block B = \(\frac{2 F}{3}\)
(iv) Force applied by block B on block C = \(\frac{F}{3}\).
(v) The action and reaction force on the blocks are shown in figure.

Question 8.
Three blocks of same mass m are conne'cted by strings and are placed on a smooth table. The blocks are pulled by force F. Find the tensions in strings.

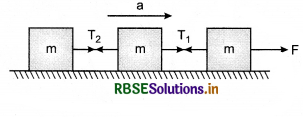
Answer:
Suppose ‘a’ be the acceleration of the system. On applying Newton’s second law of motion:
F - T₁ = ma ⇒ T₁ = F - ma

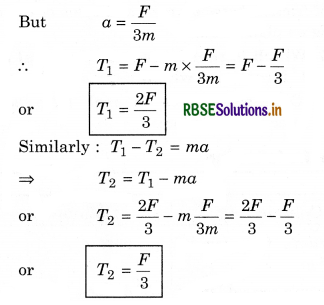
Question 9.
A person falls on cemented floor, he gets injured more than on falling on a sand bag; why?
Answer:
∵ Impulse = F∆t = ∆p
As soon as the person strikes the cemented floor, he comes to rest instantaneously. It is because of cemented floor does not get compressed. This sudden change in momentum of the person gives rise to very large force which is exerted by the floor on the person and hence he receives more injuries.

On the other hand, if the person strikes on the sand-bag, he receives less injuries. It is because sand does get compressed. As a result the time ∆t for change in the momentum (∆p) increases and hence the force applied by sand bag on the person becomes less. As a result he gets less injuries.

Question 10.
Two bodies of mass M and m (M > m) are allowed to fall from same height. Will both the bodies reach the ground simultaneously while air resistance for both the bodies is same?
Answer:
No; because there are two forces acting on the bodies, (i) Their weight and (ii) air resistance F. Net force acting on the mass M,
F_net = Mg - F and that on m, F_net = mg - F
∴ Acceleration of mass M
a₁ = \(\frac{F_{\text {net }}}{M}=\frac{M g-F}{M}=\left(g-\frac{F}{M}\right)\)
and for mass m,
a₂ = \(\frac{m g-F}{m}=\left(g-\frac{F}{m}\right)\)
∵ M > m ∴ \(\frac{F}{M}<\frac{F}{m}\)
Therefore, a₁ > a₂
Hence, body of mass M will reach the ground first.

Question 11.
A rope is tied with a balloon of mass m and a man of mass m is suspending from this balloon by catching the rope in his hands. If the man starts climbing on this rope then the balloon will move with what velocity and in which direction? Velocity of man with respect to rope is v.
Answer:
Initial momentum of man and balloon is zero, therefore on climbing upwards by man, the balloon will move downwards with velocity u such that the combined momentum of balloon and man may remains zero. The velocity of man with respect to Earth will be (v - u), therefore
m(v - u) - Mu = 0 or mv - mu = Mu
or mv = (Mu + mu)
∴ mv = u(M + m)

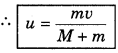
Question 12.
Why we get slipped on a muddy road?
Answer:
On muddy road, there is a thin layer of water between our feet and the road which breakes interlocking. As a result friction becomes very less.

Question 13.
A truck is moving with speed v, its driver looks a wide wall at a distance of r. To avoid the collision, should he apply the brakes or he should take turn on circular path without applying brakes? Give reason also.
Answer:
He should apply the brakes. On doing so, the kinetic energy of the truck will be consumed in doing work against the frictional force. If force of friction be F and the distance travelled before stopping be x, then.

Thus it is obvious that application of brakes is suitable because in this process the force of friction \(\left(\frac{m v^2}{2 r}\right)\) is half of that required for circular motion.

Question 14.
A man is standing in a lift which is moving downwards with uniform velocity. He experiences decrease in his weight in beginning but no change in weight during uniform motion of lift. Explain both these events.
Answer:
In beginning, the lift moves down with acceleration, therefore the man experience decrease in his weight i.e.,
R = (mg - ma). During uniform motion a = 0, therefore
R = mg i.e., no change in weight.

Question 15.
Interlocking of tyres is stronger on plane road than during riding on inclined road, why?
Answer:
On plane road, the force of friction obtained is µmg while on inclined road it is µmg cosθ
∵ cosθ < 1 for inclined road,
∴ µmg> µmgcosθ
This is why the interlocking on plane road is stronger than that on inclined road.

Question 16.
On polishing a surface beyond limit, the friction is increased. Give reason.
Answer:
When a surface is polished beyond a limit, then the moleules of the surface become in range of each other. Therefore intermolecular attraction is increased. As a result the force of friction is increased.

Question 17.
To move a bicycle, initially more force is required on paddles but once bicycle comes in motion, then less force is required to maintain the motion, why?
Answer:
When force is applied on the paddle, the bicycle tends to slip. To move the wheel, the force of friction applies torque on it. Therefore, initially due inertia of rest, more force is required to be applied on the paddle. Once the bicycle comes in motion, less force is required to maintain the speed of the bicycle.

Question 18.
An object of mass 50 g is moving in vacuum with uniform velocity of 10 ms^-1 on a smooth surface, what will be force on the object?
Answer:
Since the object is moving in vacuum with uniform speed on frictionless surface, therefore.
(i) Force of friction f = 0
(ii) Anyother force F = 0 because a = 0
Thus no force is applied on the body.

Question 19.
Electric fan remains rotating for some time even after switching it off, answer with reason.
Answer:
It is due to inertia of motion. If any resisting force is not there (e.g, air friction etc.), then it may remain rotating for infinite time.

Question 20.
If similar bullets are fired by a light and a heavy rifle, with same velocity, which rifle will exert heavy shock?
Answer:
The momentum of bullets fired by both rifles is same, therefore the recoil momentum of both rifles should be same.
i.e., mv = MV
where m and M are masses of light and heavy rifles and v and V are recoil velocity respectively.
∴ v = \(\frac{M V}{m}\)
∵ \(\frac{M}{m}\) > 1 ∴ v > V
Therefore light rifle will exert heavier shock then that by heavy rifle.

Question 21.
Why the pulling of grass cutting roller is easy than pushing it?
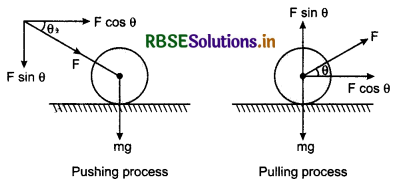
Answer:
The forces acting on the roller are shown in figure in both situations of pushing and pulling. While pushing the roller one component of force applied I sinθ makes the roller more heavy (mg + Fsinθ) and in pulling process it makes lighter (mg - F sinθ). The force which moves the roller is same (F cosθ) in both cases. This it is obvious that pulling of roller is easier than pushing it.

Question 22.
When a ball falls on Earth, then Earth also moves upward for meeting the ball. But the motion of Earth can not be seen, why?
Answer:
Acceleration produced in Earth a = \(\frac{F}{M}\), where M is mass of a Earth. Since mass M is very much, therefore value of a will be negligible. This is why the motion of Earth cannot be seen.

Question 23.
When a stone is moving in horizontal circular path, tied with a string and suddenly the string breaks, then the stone moves in tangential direction, why?
Answer:
It happens so due to inertial of direction. When string suddenly breaks, then the centripetal force due to tension of the string disappears, therefore due to inertia of direction the stone moves in tangential direction.

Question 24.
A nucleus is at rest, suddenly it splits in two equal nuclei. Find the angle between both nuclei, at which they move away.
Answer:
Suppose the mass of initial nucleus is M and it is, at rest.
Initial momentum = M x 0 = 0 (zero)
If m (= \(\frac{M}{2}\)) be the mass of each nucleus after breaking in two equal parts and their velocities are \(\overrightarrow{v_1}\) and \(\overrightarrow{v_2}\) then final momentum = m\(\overrightarrow{v_1}\) + m\(\overrightarrow{v_2}\).
∴ According to law of conservation of momentum,

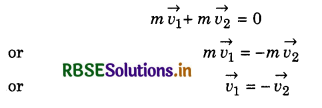
∴ Angle between \(\overrightarrow{v_1}\) and \(\overrightarrow{v_2}\) will be 180°. i.e., both nuclei will move in opposite directions.

Question 25.
Some passengers sitting inside a vehicle, are pushing the vehicle from inside. State with reason, will vehicle move or not?
Answer:
No; because the force applied by passengers is neutralised by reaction force exerted by the wall of the vehicle. Therefore net force on vehicle becomes zero.

Question 26.
Fuel is saved on filling appropriate air in tyres of vehicles, why?
Answer:
On filling the apporpriate air in tyres, they roll without slipping. We know that sliding friction is greater than rolling friction. Therefore loss of energy is reduced due to rolling friction in place of sliding friction and hence, fuel is saved.

Question 27.
In competition of rope stretching, two persons pull a rope in opposite direction. Does the winner person apply more force on rope or on ground?
Answer:
The winner person applies more force on ground than the other person and due reaction obtained from the person wins the competition.

Question 28.
A sphere of weight W is suspended by a cord. The tension in cord is T. Determine:
(i) The weight of sphere is due to which action, where will be the reaction of that action?
(ii) Reaction of tension of the cord will act on what?
(iii) The relation between W and T if upward acceleration is produced in weight and cord.
Answer:
All the pairs of action and reaction are shown in fig.
(i) Reaction of weight W will be at the centre of the earth in upward direction.
(ii) Reaction of tension will act at that point where the cord is tied and it will be in upward direction.

Question 29.
A rope of L length and uniform thickness is spread on a smooth surface. When it is pulled at its one end by a force F, what will be tension in the cord at distance l from pulling end?

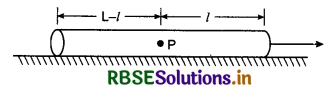
Answer:
Suppose the mass of the rope is M.
∴ Its mass per unit length = \(\frac{M}{L}\)
Acceleration of the system
a = \(\frac{F}{M}\)
∴ Tension at point P,

Question 30.
A force is acting on a particle of mass m at t = 0, which depends on time according to relation F = kt (t' - t), where k is a constant and force acts on the particle up to time t'. Find the momentum of the particle at the moment when force becomes inactive.
Answer:
The direction of force F = kt(t' - t) does not change because k is constnat vector, therefore particle is moving with uniform velocity. Hence motion of particle will be in direction of force.
∴ m.\(\frac{d v}{d t}\) = kt(t' - t) (By Newton's second law)
or m.dv = kt(t' - t)dt
On integrating both sides,

Question 31.
A block is moving downwards on a smooth inclined plane of angle of inclination θ. On reaching the bottom its velocity is v. If it slips on a rough inclined plane, then its velocity at the bottom is \(\frac{v}{n}\) where n is a number greater than zero. What will be coefficient of friction µ?

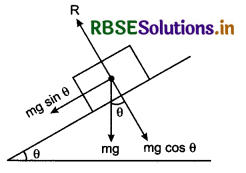
Answer:
On smooth plane,
v² = 2(g sinθ).s ............................(1)
On rough surface, (inclined plane)
(\(\frac{v}{n}\))² = 2(g sinθ - µg cosθ)s .............................(2)
On equating the values of v₂ from equation (1) and (2)
2g sinθ s = 2n² (g sinθ - µg cosθ)s
or g sinθ = n² g sinθ - n² µg cosθ
or n²µg cosθ = n² g sinθ - g sinθ = g sinθ(n² - 1)

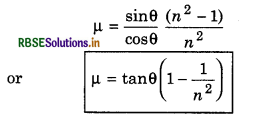
Question 32.
What is the need of banking in path?
Answer:
On horizontal turn, the centripetal force is provided by force of friction between road and the tyres of the vehicle but it is sufficient for low velocity of the vehicle. For velocity more than safe velocity, the vehicle gets slipped on turn. This why to increase safe velocity, the road is made banked on turn. On this road one component of reaction of road on vehicle, provides the required centripetal force.

Question 33.
Why motor cyclist does not fall down while operating motor cycle on inner wall of a death well?
Answer:
Bending of cyclist at circular path: We know that without centripetal force, the path of an object can never be circular. When a cyclist reaches a turn, its path becomes circular. Therefore he requires a centripetal force. To obtain the centripetal force, he bends towards the centre of the turn. On doing so, the force of friction between the tyres and the road provides the required centripetal force and cyclist safely crosses the turn.

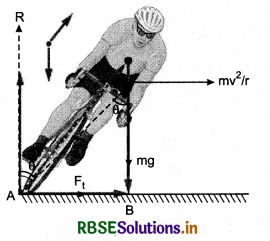
The forces acting the cyclist at turn in fig. 5.69: Cyclist crosses turn in equilibrium of clockwise torque due to mg about point A and anticlockwise torque due to force of friction f_s about centre of gravity (C.G.)
∴ In equilibrium,
Momentum of Force F_f about C.G. = Moment of force mg about A.

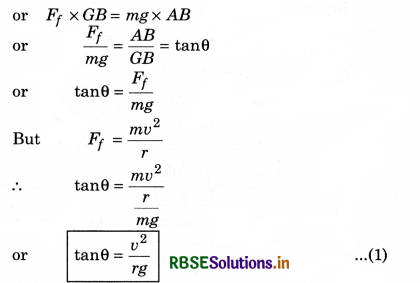
As we have considered here that required centripetal force (\(\frac{m v^2}{r}\)) is provided by force of friction F_f. Therefore for safe passing through the turn,
F_f ≥ F_c
or µ_s R = µ_s mg ≥ F_c
or µ_s mg ≥ \(\frac{m v^2}{r}\)
For optimum speed on turn.

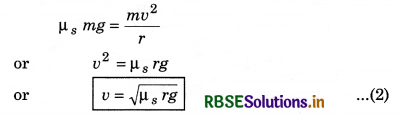
Optimum speed or maximum safe speed on turn can be calculated with the help of above equation (2).
Cyclist slows down the speed at the turn: When a cyclist reaches a circular turn, it requires a centripetal force because without centripetal force circular motion is impossible. To obtain this centripetal force, he bends towards the centre of the turn and O be the angle of inclination with vertical,
then it can be proved, that
tanθ = \(\frac{v^2}{r g}\)
Since the values of r and g are constant for a turn, therefore
tanθ ∝ v²
Thus it is clear, for greater value of v, θ will also be greater and for high value of θ, the possibility of slipping the cycle will increase. This is in ω to avoid this mis-happening, cyclist shows down his speed on the turn.

Question 34.
Two similar trains are moving with same speed but in opposite directions on rail-track along the equator of Earth. Will both the trains exert same pressure on the rails?
Answer:
No; because due to rotational motion of Earth, the relative velocities of both the trains with respect to Earth will be different. Therefore centripetal forces for them will also be different. As a result, their effective weight (mg - \(\frac{m v^2}{R}\)) will also be different. Thus the trains will exert different pressure on the rails.

Question 35.
A stone tied with one end of a string is rotated in horizotnal circle when the string breaks then the stone flies in the tangential direction. Why?
Answer:
Till the string does not break, it keeps on providing centripetal force to stone for circular motion. When string breaks, then centripetal force disappears. As a result the stone flies in tangential direction.

Question 36.
A particle of mass m, tied with one end of a cord, is rotated in horizontal circle (neglect the effect of gravity). Keeping the angular momentum of the particle about the centre constant, the length of the cord is reduced gradually, then the tension of the cord is given by T = Arⁿ, where A is a constant and r is instantaneous radius of the circle. Find the value of n.
Answer:
Suppose instantaneous velocity of the particle is v. Since angular momentum (mvr) remains cosntant, therefore v ∝ \(\frac{1}{r}\) or c = \(\frac{k}{r}\), where k is cosntant. The tension of the cord provides the centripetal force \(\frac{m v^2}{r}\).

Question 37.
Why the centrifugal force is called psuedo force?
Answer:
Centrifugal force is called psuedo force because it is not produced by any real cause and is not related to any object present in environment.

Question 38.
A coin is placed on a record player. On starting the motor, the coin slips from the record player before the player attain full angular velocity. Explain why?
Answer:
The force of friction between coin and record player provides the centripetal force to coin. Which increases with increasing angular velocity (i.e., F = mrω²). Since the static friction does not increase beyond a limit which is called limiting friction, hence after a certain anglular velocity, the coin starts slipping on the record player. 

Conceptual Questions

Question 1.
When a ball is projected upward in a compartment of a moving train. After sometime, the ball returns to projecting hands. Clear its reason.
Answer:
The velocity of train and the ball is same in moving train. When a hall is projected upwards, then due to inertia of motion the ball remains moving in horizontal direction with same velocity, therefore, the ball always remains above the projecting hands. This is why it returns back to these hands.

Question 2.
Why a person jumping out of a moving train need to run for some distance in direction of motion of the train?
Answer:
While jumping out of moving train, the feet of the person come to rest on touching the ground, but the body (remaining part) remains moving due to inertia of motion. If he does not run for some distance in direction of motion of the train, he will fall on the ground and will get injured. To avoid this mishappenning, he runs for some distance and gradually the whole becomes in same situation.

Question 3.
Aeroplanes with wings fly at less altitude than jet-plane, why?
Answer:
The wings of aeroplane push the air in backward direction and move forward by its reaction. At low altitude air is dense, therefore good reaction is obtained for motion of plane. At high altitude the air density is less. This is why aeroplanes with wings fly at low altitude. On the other hand, jet plane moves due to reaction of gases passing through the nozzle. There is no role of air. This is why jet planes fly at high altitude. Also at high altitude the air resistance is too less. Therefore opposition of motion becomes very less.

Question 4.
Walking is difficult in sand or on ice, why?
Answer:
Walking on an ice is difficult due to very less friction between feet and surface of ice. When a person walks on sand, then feet are blocked in the sand, as a result the friction between sand and feet increases. Hence it becomes difficult to walk on sand.

Question 5.
An object of mass m is left from the top of a inclined rough plane (see fig.). If force of friction is F, then prove that the velocity of the object at the bottom will be v = \(\sqrt{2(m g h-F L) / m}\)
Answer:
Loss of potential energy of the object when it reaches the bottom = mgh.

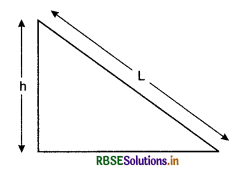
Increase in kinetic energy at the bottom = \(\frac{1}{2}\)mv²
∴ Net loss of energy = mgh - \(\frac{1}{2}\)mv²
Work done against the friction = FL

Question 6.
Why mud-guards are used over the tyres of a vehicle?
Answer:
The mud particles in contact of tyre move in tangential direction and can make the vehicle dirty. Therefore to save the vehicle from mud, mud guards are used over the tyres of vehicle.

Question 7.
It is easy to pull an object than pushing it. Explain why.
Answer:
In action of pushing the normal reaction,
R₁ = (Mg + P sinθ)
If µ_k be coefficient of dynamic friction, then force of friction,
F₁ = µ_k R₁
or F₁ = µ_k(Mg + P sinθ) ............................(1)

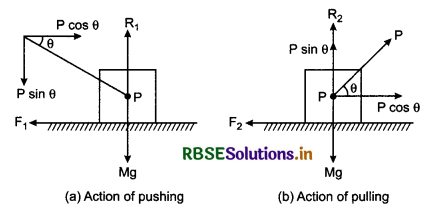
In the action of pulling the object, reaction,
R₂ = (Mg - P sinθ)
∴ Force of friction,
F₂ = µ_kR₂ = µ_k(Mg - P sinθ) .........................(2)
From equations (1) and (2) it is clear that
F₁ > F₂
Therefore it is easy to pull an object than pushing it.

Question 8.
A balloon of mass m is decending with acceleration ‘a’ where a< g. How much mass should be removed from the balloon so that it may start ascending with acceleration ‘a’?
Answer:
Suppose F is the retarding force acting on balloon in upward direction. When the balloon decends with acceleration ‘a’,then the equation of motion,

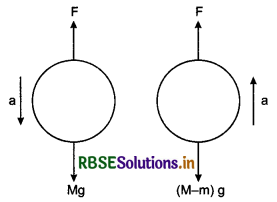
Mg - F = Ma
or F = Mg - Ma ........................(1)
Suppose mass m is removed from the balloon, then it starts ascending with acceleration 'a'. In this situation equation of motion,
F - (M - m)g = (M - m)a
Substituting the value of F from (1)
Mg - Ma = Mg + mg = Ma - ma
or mg + ma = Ma + Ma = 2Ma

Question 9.
Why the lubricant is used in machines?
Answer:
Lubriction: Lubricants like grease, oil, mobile oil etc are put or spread between the two solid surfaces in contact. They form a thin layer between them by filling up the irregularities of the surfaces. This avoids direct contact of solid surfaces. As a result, friction as well as heating of the moving parts get reduced quite effectively. Actually, the lubricants in between the two solid surfaces convert dry friction (without labricants) into wet friction (with lubricants), which is of comparatively less magnitude.

Question 10.
How the cream is separated from the milk?
Answer:
Milk is poured in centrifuge and it is rotated about its axis, then the light cream particles require less centripetal force (F_c = mrω²), therefore they are gathered near the axis while heavy other milk parts require more centripetal force, therefore they are separated at large distances from the axis.

Question 11.
Often the scooter slips on turn in rainy period, why?
Answer:
During rain, the road becomes wet therefore the friction between road and tyres of the scooter decreases. Hence required centripetal force is not obtained at the turn and scooter slips.

Question 12.
On rotating the bottle of coca-cola catching its neck by hand, where will the bubble be in the bottle?
Answer:
Mass of bubble is very less, therefore centrifugal force acting on the bubble will also be very less. Due to this reason the bubble remains near the centre. Therefore it will move towards the narrow part of the bottle.

Question 13.
What is moment of centripetal force about axis of rotation?
Answer:
Moment of force \(\vec{\tau}=\vec{r} \times \vec{F}\) = r. F. sinθ.\(\hat{n}\)
∴ T = F r sinθ
Since θ is the angle between \(\vec{r}\) and \(\vec{F}\). The direction of centripetal force F_c is in opposite direction of \(\vec{r}\).
∴ θ = π or 180°  ∴ sinθ = sin π = 0
Therefore moment of Fc about axis of rotation τ = 0(zero)

Question 14.
A particle of mass m is rotating in horizontal circle of radius r by centripetal force (\(\frac{k}{r^2}\)). What will be its total energu?
Answer:

Question 15.
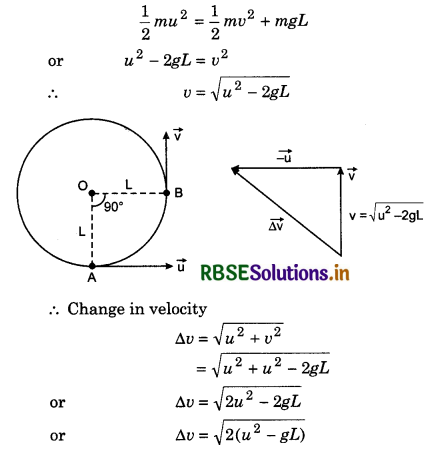
A stone tied with a cord of length L, is rotated in vertical circle while second end of cord remains at the centre of the circle. At any instant the stone is at lowest position and its velocity is u. When the cord becomes horizontal, at that instant, find the change in velocity of the stone.
Answer:
From law of conservation of energy

Long Answer Questions

Question 1. 
What is inertia? Explain with example.
Answer:
Law of inertia is sub-divided in following three forms :
1. Inertia of rest: It is the inability of body to oppose the force that tries to move it.
2. InertIa of motion : It is the inablity of body in unitbrm motion to oppose the force that tries to stop
3. Inertia of direction: It is the inability of a body t oppose the force that tries to change its direction of motion.

Examples of inertia of rest:
(a) Experiencing a backward and forward jerk, if the bus driver suddenly starts and stops the bus: While standing in bus, our feet are in touch with the floor of bus. There 18 some friction between the feet and the floor. Due to friction, our body is supposed to be attached to the floor of bus by the means of feet. If the bus start8 not too suddenly, the jerk will be very minute. Feet as well as the upper part of body will move along the slowly accelerating bus. 

But our body is not strictly a rigid body. It can deform or bend a little. In case suddenly accelerating bus, i.e., if bus driver suddenly starts the bus, our feet will move with the bus as they are attached to the floor of bus, due to the friction. But rest of the body remains where it is, due to the inertia of the upper part of the body (or rest or the body). As a result, we experience a backward jerk, if the driver suddenly starts the bus. 
Similarly, a forward jerk is experienced by U8, if the bus driver suddenly applies the brakes in moving bus.

(b) The dust particles in the carpet fall off with a stick on hitting it: On hitting with a stick, the carpet surface is disturbed and comes into motion. But the inertia of the dust particles does not allow them to move along the carpet. Thus the dust particles tend to remain at rest and hence get removed from the carpet on hitting it with a stick.

(c) When bullet is fired on a glass window, it. makes a hole but on throwing a stone, it breaks in pieces: When a bullet is fired on a glass window, then it strikes the glass with high velocity. Therefore the glass particles move immediately with bullet making a hole in it while the rest part of window remains as it is due to inertia of rest. On the other hand when stone is thrown on glass window, then its speed is very low in comparison to that of the bullet, then the glass breaks up in many pieces due to inertia of rest.

Question 2. 
Write Newton's second law of motion and prove F = ma from this law. Also define S.l. unit of force "Newton" with the help of this relation and find the dimensional formula of force.
Answer:
According to this law, "Rate of change of momntum of a moving body is directly proportional to force applied on the body and in same direction in which force is applied.
Suppose the momentum of a moving body is \(\vec{p}\), then rate of change of momentum = \(\frac{d \vec{p}}{d t}\)
∴ According to second law of motion, the force acting on the body, 
\(\vec{F}\) ∝ \(\frac{d \vec{p}}{d t}\)
or \(\vec{F}\) = K\(\frac{d \vec{p}}{d t}\) .........(1)

where K is constant of proportionality. The value of K depends on the system of chosen unit. We chose the units uch that
K = 1
∴ \(\vec{F} = \frac{d \vec{p}}{d t}\) .........(2)
Second law of motion is known as real law.

Therefore the force applied on a body is defined by the product of mass of body and acceleration produced. 

Case (ii) When Velocity is constant, then
\(\frac{d v}{d t}\) = 0
∴ \(\vec{F} = \vec{v}\frac{d m}{d t}\)

Unit of force : ∵ F = ma
∴ In M.K.S. system, unit of F = kg.ms^-2 = Newton (N)
In C.G.S. system, unit of F= g.cm.s^-2 = dyne

Dimensions: ∵ F = ma
∴ Dimensional formula of F = [M¹L¹T^-2]

Relation between N and dyne:
1 N = 1 kg × \(\frac{1 m}{1 s^2}=\frac{1000 g × 100 cm}{s^2}\)
= 10⁵ g.cm.s^-2
or 1 N = 10⁵ dyne

Definition of N: ∵ F= ma
If m = 1 kg; a = 1 ms^-2; then F = 1 N
Thus, “1 N is the force which can produce an acceleration of 1 ms^-2 in an object of mass 1 kg.”

Question 3. 
Write Newton's second law of motion and prove that the impulse of force is equal to change in momentum. Explain its importance giving examples.
Answer:
According to this law, "Rate of change of momntum of a moving body is directly proportional to force applied on the body and in same direction in which force is applied.
Suppose the momentum of a moving body is \vec{p}, then rate of change of momentum = \(\frac{d \vec{p}}{d t}\)
∴ According to second law of motion, the force acting on the body, 
\(\vec{F}\) ∝ \(\frac{d \vec{p}}{d t}\)
or \(\vec{F} = K\frac{d \vec{p}}{d t}\) .........(1)

where K is constant of proportionality. The value of K depends on the system of chosen unit. We chose the units such that
K = 1
∴ \(\vec{F} = \frac{d \vec{p}}{d t}\) .........(2)
Second law of motion is known as real law.

Therefore the force applied on a body is defined by the product of mass of body and acceleration produced. 

Case (ii) When Velocity is constant, then
\(\frac{d v}{d t}\) = 0
∴ \(\vec{F} = \vec{v}\frac{d m}{d t}\)

Unit of force : ∵ F = ma
∴ In M.K.S. system, unit of F = kg.ms^-2 = Newton (N)
In C.G.S. system, unit of F= g.cm.s^-2 = dyne

Dimensions: ∵ F = ma
∴ Dimensional formula of F = [M¹L¹T^-2]

Relation between N and dyne:
1 N = 1 kg × \(\frac{1 m}{1 s^2}=\frac{1000 g × 100 cm}{s^2}\)
= 10⁵ g.cm.s^-2
or 1 N = 10⁵ dyne

Definition of N: ∵ F= ma
If m = 1 kg; a = 1 ms^-2; then F = 1 N
Thus, “1 N is the force which can produce an acceleration of 1 ms^-2 in an object of mass 1 kg.”

Impulse:
Total effect of force on the motion of a body is called impulse or impulse of force. If a constant force is applied on a body then product of force and ti.rne for which the force is applied provides the impulse i.e.,
Impulse = Force × time interval = F ∆t
Impulse is denoted by I
∴ I = F ∆t
or I = Force × time = \(\frac{\text { Change in momentum }}{\text { time }}\) × time
or I = Change in momentum
or I = ∆p
Impulse is a vector quantity and its direction is the same as that of change in momentum.
∴ In vector form,
\(\vec{I}\) = ∆\(\vec{p}\)
∴ I = F ∆t = ∆p

Therefore for certain change in momentum, if ∆t decreases, the force F increases accordingly i.e., we have to obtain a certain change in momentum in less time, then more force will have to be applied. If I increases, then force F decreases. This is why when a cricketer catches the ball, he draws his hands back to increase the time interval ∆t.
If a force  acts on a body for short time interval dt, then impulse of this force
dI = F dt ........(1)
If force F remains acting for time from t₁ to t₂, then total impulse
I = \(\int_{t_1}^{t_2} F d t\)
If force F is not the function of time, then it will remain constant.
I = F \(\int_{t_1}^{t_2} d t = F [t]_{t_1}^{t_2}\)
or I =F(t₁ - t₂)
or I = F ∆t

Unit of impulse : ∵ I = F ∆t
∴ Unit of I in M.K.S. system = N.s
and unit of I in C.G.S. system = dyne s

Dimensions of impulse: ∵ I = F ∆t
∴ Dimensional formula of I = M¹L¹T^-2T¹
= [M¹L¹T^-2]

Impulse of a force:
I = F ∆t = ∆p
If change in momentum is constant, then
F ∆t = constant
If two forces F₁ and F₂ acting on a body produce same change in momentum, then
F₁ ∆t₁ = F₂ ∆t₂
Thus it is clear that if the time duration of an impulse is increased, the force exerted will be decreased. The following practical examples will make this concept more clear.

(i) Buffers are provided between the bogies of a train : Buffers increase the time of jerk during shunting the train. This decreases the force of impact between the bogies. The bogies are thus prevented from receiving severe jerks. Thus bogies receive slow jerks.

(ii) Automobiles are provided with shockers : When a vehicle, bike, car, bus etc, move on bumpy road, it receives jerk. The shockers increase the time of jerk and hence reduce their force. This makes journey comfortable and saves the automobile from damage due to bumps.

(iii) Chinawares are packed in straw papers: The straw paper between the chinawares increases the time of experiencing the jerk during transportation. Hence, they strike against each other with a lesser force and are less likely to be damaged. 

(iv) A person receive more injuries on falling cemented floor than on a heap of sand : In both the cases, the impulse or total change in momentum is same. On the cemented road floor,the person is stopped abruptly. Due to small duration, cemented floor exerts a greater force of reaction causing him severe injuries. When person falls on a heap of sand, the sandy fields gets depressed under his weight, so the person takes longer time to stop. To make the impulse constant, the force exerted by the sandy floor on the person decreases.

(v) A cricket player lowers his hands while catching a ball : When a player catches the ball, he draws his hands backwards to increase the time of catch. Hence the force exerted on his hands lowers and it does not hurt him.

Question 4. 
What is rocket propulsion? Establish the expression for the velocity of the rocket. 
Answer:
Varying Mass Concept Problems:
(i) Conveyor-belt loading system : If the system moves with constant velocity but its mass changes with time, then it is called varying mass system.

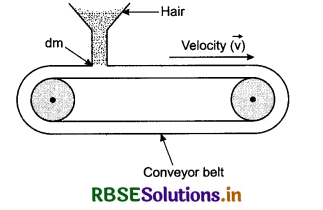
From Newton's second law of motion,
\(\vec{F}=\frac{d \vec{p}}{d t}=\frac{d}{d t}(m \vec{v})\)
or \(\vec{F}=\vec{v} \frac{d m}{d t}\) ......(1) (because u is constant)
Conveyed belt works on this principle. In this the material to be conveyed is allowed to fall at certain rate on the conveyer belt with the help of hair. If the belt moves with constant velocity u, then the force required to maintain the speed, 
\(\vec{F}=\vec{v} \frac{d m}{d t} where \frac{d m}{d t}\) is rate of increase of mass.
This force is provided by the motor used is the system. Therefore required power of the motor.
\(\vec{P} =\vec{F} \cdot \vec{v}=\left(\vec{v} \frac{d m}{d t}\right) \cdot \vec{v}\)
= \(\vec{v} \cdot \vec{v} \frac{d m}{d t}\)
or P = \(v^2 \frac{d m}{d t}\)
because \(\vec{v} \cdot \vec{v}\) = |v| |v| cos 0 = v²

(ii) Rocket propulsion : In rocket, due to combustion ‘of fuel the residual gases pass through the nozzle with high velocity. Due to Newton’s third law of motion, a force of reaction is applied on the rocket in opposite direction, As a result the rocket move ahead in vertical direction.

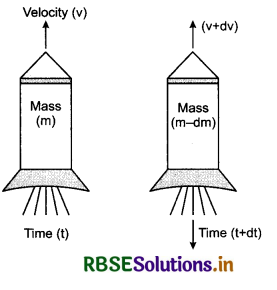
The rocket continuously gets the momentum till the gases keep on passing through the nozzle. 

Velocity of rocket : Suppose the mass of the rocket at any time t is m and its velocity is u. Hot gases produced due to combustion of fuel dm pass in time interval di through the nozzle with velocity u. Here u is the velocity of gas with respect to rocket. The mass of the rocket now remains (m - dm) and its velocity becomes (u + du). 

From Newton’s second law,
\(\vec{F}=\frac{d \vec{p}}{d t}=\frac{d}{d t}(mv)\)
but v = u = constant
∴ \(\vec{F}=-\vec{u} \frac{d m}{d t}\)
Here minus sign (-) indicates the decrease in mass with time.
∵ F = ma
ma = -u \(\frac{d m}{d t}\)
m \(\frac{d u}{d t} = -u \frac{d m}{d t}\)
or m \(\frac{d u}{d t} = -u \frac{d m}{d t}\)
or du = -u dm
or du = \(-\frac{u}{m}dm\) ........(1)

Suppose initial mass of rocket is m_i and initial velocity is u_i. Alter time t these parameters become m_f and u_f. then integrating both sides of equation (1), we get:

Following conclusions are obtained by equation (2),
(i) Final velocity of rocket is directly proportional to velocity of gases (u) passing through the nozzle. 
(ii) Final velocity obtained by the rocket depends upon the ratio of initial mass and final mass of the rocket. Therefore the fuel is arranged in different stages in the rocket. When fuel of one stage is finished, then its case is seperated from the rocket so that the final mass (m₁) may become less.

Question 5. 
Prove that Newton's second law is real Newton's law.
Answer:
Proof of Newton’s Third Law by Newton’s Second Law:
Suppose there are two bodies A and B in an isolated system. When they collide, then at the time of collision, body A applies force \(\vec{F}_{21}\) on body Band body B applies force \(\vec{F}_{21}\) on body A These forces \(\vec{F}_{21}\) and \(\vec{F}_{12}\) are said action and reaction respectively. The time of contact of both particles is ∆t.
∵ Change in linear momentum = Force × time interval
∴ Change in momentum of particle A
\(\overrightarrow{\Delta p_1}=\overrightarrow{F_{12}} \times \Delta t\)
and that of particle B,
\(\overrightarrow{\Delta p_2}=\overrightarrow{F_{21}} \times \Delta t\)
∴ Total change in momentum of the system = \(\overrightarrow{\Delta p_1}+\overrightarrow{\Delta p_2}\). If no external force is acting on the system, then according to law of conservation of momentum,

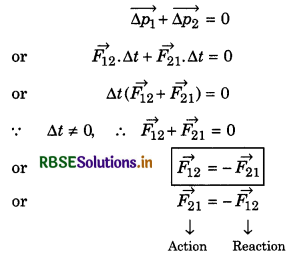
This is Newton's third law of motion.

Question 6. 
Write the law of conservation of momentum and prove it. Derive Newton's law of motion with the help of above law.
Answer:
Law of Conservation of Linear Momentum:
According to Newton’s second law of motion the force acting on an isolated force is equal to rate of change of momentum i.e.,
\(\vec{F}=\frac{d \vec{p}}{d t}\)
If external force is absent i.e. \(\vec {F}\) = 0
\(\frac{d \vec{p}}{d t}\) = 0
or \(\vec p\) = constant (Because differentiation of constant with respect to any quantity is zero)
or p = mu = constant
or m₁u₁ = m₂u₂
i.e., in absence of external force the linear momentum of particle remains unchanged.

Proof of Newton’s Third Law by Newton’s Second Law:
Suppose there are two bodies A and B in an isolated system. When they collide, then at the time of collision, body A applies force \(\vec{F}_{21}\) on body Band body B applies force \(\vec{F}_{21}\) on body A These forces \(\vec{F}_{21}\) and \(\vec{F}_{12}\) are said action and reaction respectively. The time of contact of both particles is ∆t.
∵ Change in linear momentum = Force × time interval
∴ Change in momentum of particle A
\(\overrightarrow{\Delta p_1}=\overrightarrow{F_{12}} \times \Delta t\)
and that of particle B,
\(\overrightarrow{\Delta p_2}=\overrightarrow{F_{21}} \times \Delta t\)
∴ Total change in momentum of the system = \(\overrightarrow{\Delta p_1}+\overrightarrow{\Delta p_2}\). If no external force is acting on the system, then according to law of conservation of momentum,

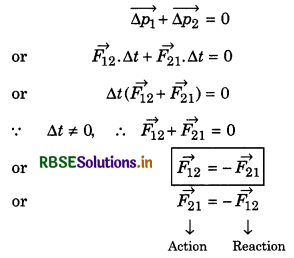
This is Newton's third law of motion.

Question 7. 
What do you mean by concurent forces? What is necessary condition for equilibrium of concurrent forces?
Answer:
EquilIbrium of a Particle Concurrent forces:
If the lines of action of all the forces acting on an object pass through a common point, then these forces are called concurrent forces.
For example, if three forces \(\vec{F_1},\vec{F_2}\) and \(\vec{F_3}\) are acting on an object (fig. 5.16) and their lines of action are passing through common point O, therefore these forces are concurrent forces.

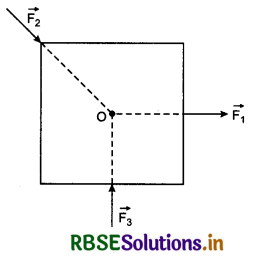
When concurrent forces act on a body, then only linear acceleration is produced in the body. 

Necessary conditions of equilibrium of concurrent forces:
For equilibrium of a body following conditions are necessary:
(i) If two concurrent forces are acting on a body, then for equilibrium of forces, the magnitudes of both the forces should be equal and their directions should be opposite.
(ii) If the lines of action of forces are not along a straight line, then minimum number of forces should be three.
(iii) For equilibrium of three forces,
\(\vec{F_1}+\vec{F_2}+\vec{F_3}=0\)
or \(\vec{F_3}=-(\vec{F_1}+\vec{F_2})\)
or\(|\vec{F_3}|=|-(\vec{F_1}+\vec{F_2)}|\)
or F₃ = \(\sqrt{F_1^2+F_2^2+2 F_1 F_2 \cos \theta}\)
Value of θ varies from 0° to 180°.
When θ = 0°, then F₃ = (F₁ + F₂)
When θ = 180° ,then F₃ = (F₁ - F₂)
i.e., the value of F₃ should be between (F₁ + F₂) and (F₁ - F₂)
∴ (F₁ + F₂) F₃ (F₁ - F₂)
Therefore the equilibrium can be checked with the help of this relation.

(iv) If N forces acting on a body can be represented by N arms of a polygon in a certain pattern, then the forces will be in equilibrium.

Question 8. 
What is friction? Decribe the cause of friction.
Answer:
Friction:
No object in universe is perfectly smooth. When  a body slips on the surface of other body, then an opposing force starts acting between the surfaces in contact and this force opposes the motion. This force is called ‘force of friction’. This force always acts parallel to contact surface and always acts in opposite direction of relative motion of bodies. When a ball rolls on a rough surface, then due to friction only it stops shortly. If surface is smooth, then friction is less and the ball keeps on rolling for long time. Friction 

is of two types :
(i) Static friction and 
(ii) Dynamic or kinetic friction.
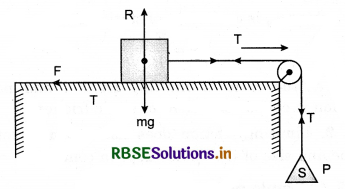
Static friction : The friction acting on the body in state of rest, is called static friction. The maximum value of static friction is called ‘Limiting friction’. It can be understood by an experiment given below:

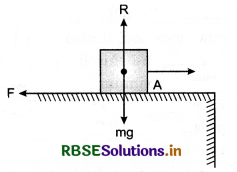
Experiment : Suppose T is a table at one edge of which a julley is ftxed. A block ‘A’ is placed on the table and a cord is attached with the block. The cord passes over the pulley and a pan is attached with the other end of the cord. The mass of the pan is ‘S’. Suppose the weight of the block is mg and R is normal reaction. Weight mg balances the normal reaction R.

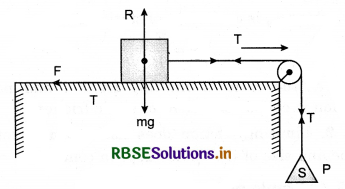
Initially, when there is no weight on the pan, the block does not move. In this situation, the pull acting on the block is sg. The reason of not moving the block is the force of static friction F developed between the table and the block in opposite direction of pull. Thus both forces balance each other. When the weight are placed on the pan, then pulling force increases and the block does not move. On continuously placing the weight on the pan, an situation is reached when block starts moving. “The maximum static friction is called ‘Limiting friction”. When the pulling force increases beyond limiting friction, then only, the block starts moving.
Static friction is self adjusting force. Under limiting friction limit, the force of friction is equal to applied force (in magnitude).

Cause of Friction:
According to modern theory, the cause of friction is the mutual interaction between the atom at contact point. When an object is placed on the surface of other object, then due to irregularity of surfaces at very less points, the atoms of both surfaces come in contact i.e, the area of contact of both surfaces is very small. At points of actual contact, the atoms of both surfaces are very close to each other and attract each other strongly. As a result both surfaces get attached with each other. When one object tries to move on the surface of other, then force of attraction between both surfaces opposes the relative motion between them. This opposing force is called force of friction. This is the reason, the force of friction is measured by that external force which is necessary to break the force of attraction between the surfaces in contact.

For Your Knowledge:
1. The force opposing the relative motion between two surfaces, is called force of friction and maximum static friction is called limiting friction.
2. Friction force produces due to mutual interaction between two surfaces in contact.

Question 9. 
What do you understand by angle of friction and angle of repose? Prove that in the situation of limiting friction the values of both these angles are same.
Answer:
Angle of Friction:
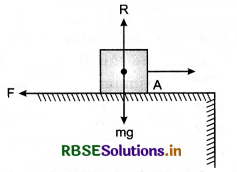
In situation of limiting friction, the angle between normal reaction R and resultant P of normal reaction R and limiting friction f(s), is called the angle of friction. In figure 5.53 it is shown by α. 
In figure 5.53, a block A is shown placed on a rough surface and an external force F is acting on it to move it. As a reaction of F, there will be two forces. 
1. Normal reaction R which balances the weight mg of the block.

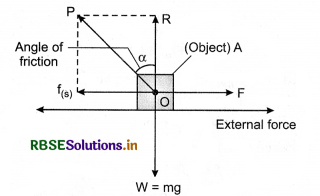
2. Limiting friction force f(s) = µ(s). R parallel to surface of contact which is equal and opposite to applied force \(\vec{F}\). Resultant of both these reactions is P which makes an angle a with normal reaction R.
∴ \(\tan \alpha=\frac{P R}{O R}=\frac{f_{(s)}}{R}=\frac{\mu_s(R)}{R}\)
\(\tan \alpha=\mu_s\)
∴ Angle of friction
α = \(\tan ^{-1}\left(\mu_s\right)\)

Coefficient of Static Friction:
∵ \(\mu_s\) = tan α
Therefore, the tangent of angle of friction is called coefficient of static friction.

Magnitude of resultant force : This force is known as contact force. The value of contact force shown in figure 5.53 is,
It magnitude of resultant force 
P = \(\sqrt{f_{(s)}^2+R^2}\) ∵ \(\vec{R} \perp \overrightarrow{f_{(s)}}\)
= \(\sqrt{\left(\mu_s R\right)^2+R^2}\)
P = R \(\sqrt{1+\mu_s^2}\)

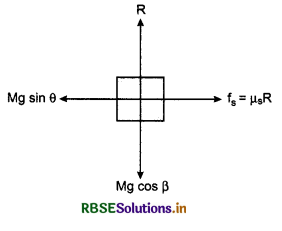
Friction on an Inclined Plane-Angle of Repose:
The angle between inclined plane and horizontal, when any block placed on the plane remains at rest, is called angle of repose.
In figure 5.55, a block of mass M is placed on an inclined plane of anige of inclination f₃. The forces acting on the block are shown in the diagram. 

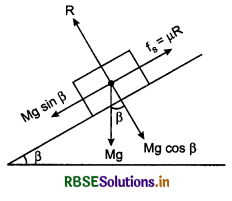
Free body diagram of block
Equations of motion,
Mg cos ß = R .........(1)
and Mg sin ß = µ_s.R .......(2)

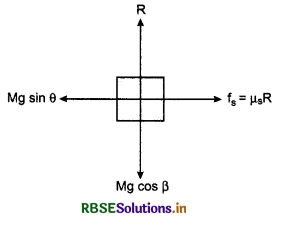
On dividing equation (2) by (1), we have
\(\frac{M g \sin \beta}{M g \cos \beta}=\frac{\mu s R}{R}\)
or tan ß = µ_s ......(3)
but tan α = µ_s ........(4)
where α is angle of friction.
From equations (3) and (4), we have
ß = α
i. e, Angle of repose = Angle of friction
If the angle of inclination of the plane ≤ß, then the block placed on the plane will remain at rest. But when angle of inclination of the plane > ß, then the block will start slipping on the plane in downward direction.

Question 10. 
What do you understant by friction? Describe static friction, limiting friction, dynamic friction and rolling friction.
Answer:
Friction:
No object in universe is perfectly smooth. When  a body slips on the surface of other body, then an opposing force starts acting between the surfaces in contact and this force opposes the motion. This force is called ‘force of friction’. This force always acts parallel to contact surface and always acts in opposite direction of relative motion of bodies. When a ball rolls on a rough surface, then due to friction only it stops shortly. If surface is smooth, then friction is less and the ball keeps on rolling for long time.
Friction is of two types:
(i) Static friction and 
(ii) Dynamic or kinetic friction.
Static friction: The friction acting on the body in state of rest, is called static friction. The maximum value of static friction is called ‘Limiting friction’. It can be understood by an experiment given below:

Experiment : Suppose T is a table at one edge of which a julley is ftxed. A block ‘A’ is placed on the table and a cord is attached with the block. The cord passes over the pulley and a pan is attached with the other end of the cord. The mass of the pan is ‘S’. Suppose the weight of the block is mg and R is normal reaction. Weight mg balances the normal reaction R.

Initially, when there is no weight on the pan, the block does not move. In this situation, the pull acting on the block is sg. The reason of not moving the block is the force of static friction F developed between the table and the block in opposite direction of pull. Thus both forces balance each other. When the weight are placed on the pan, then pulling force increases and the block does not move. On continuously placing the weight on the pan, an situation is reached when block starts moving. “The maximum static friction is called ‘Limiting friction”. When the pulling force increases beyond limiting friction, then only, the block starts moving.
Static friction is self adjusting force. Under limiting friction limit, the force of friction is equal to applied force (in magnitude).

Laws of Limiting Friction:
There are following two laws of limiting friction:
1. Force of limiting friction is directly proportional to normal reaction acting between the contact surfaces and always acts in opposite direction of motion of the object.
i.e., F_s ∝ R

Where Fs is limiting friction,
and R is normal reaction.
or F_s = µ_s R
R = mg
F_s  = µ_s R = µ_s mg ......(1)
where µ_s is coefficient of static friction 
µ_s = \(\frac{F_s}{R}\) ......(2)
i.e., the ratio of limiting friction and normal reaction is called coefficient of static friction.

2. Limiting friction does not depend upon the shape and size of the bodies kept in contact.

Dynamic or Kinetic Friction:
When a body tries to move on the surface of other body, then till it does not move, the force of friction developed between contact surfaces is called static friction. Static friction is equal and opposite to external force and it increases upto a certain limit called limiting friction. After this limit, the body starts moving. In this situation, the force of friction between contact surfaces is called “Dynamic or kinetic friction”. Its value is slightly less than the limiting friction.

Laws of Dynamic Friction:
1. Dynamic friction is directly proportional to normal reaction and always less than limiting friction.
i.e., F_k ∝ R
or F_k ∝ µ_k R = µ_k mg
Where, F_k = Dynamic friction;
R = Normal reaction;
µ_k = Coefficient of dynamic friction.

2. Dynamic friction does not depend on the velocity of the body provided it should neither be very much or very less.

Distinguish between Static and Dynamic Friction:
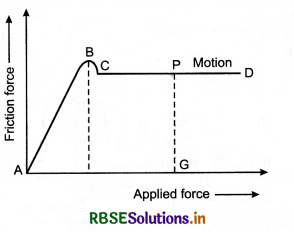
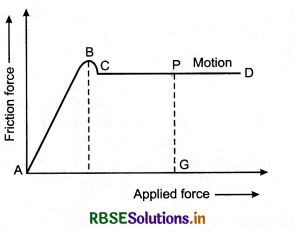
Static friction is self adjusting force. As the external force is increased, it also increases but upto a certain.limit i.e., beyond this limit friction force does not increase. This maximum force of static friction is called limiting friction. In the given diagram, limiting friction is represented by BE. Below limiting friction, the object does not mvoe. As the external froce is increased beyond limiting friction, the body starts moving and force of friction becomes slightly less then limiting friction. In the diagram, this decrease in friction is shown by BC. Now the force of friction is called the dynamic friction which does not change on increasing external force. PQ is the measure of dynamic friction force.

RoIling Friction:
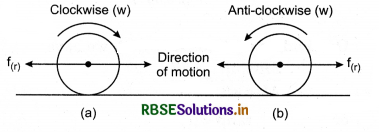
When an object is rolled on a surface, then friction produced due to rolling motion is called rolling friction.
For an object of same weight, the rolling friction is always very less than kinetic friction. At the time of rolling motion momentarily deformation takes place between contact surfaces. One component of contact force appears parallel to contact surface and opposes the motion. Coefficient of rolling friction (µ_r) is very less, therefore the invention of wheel is very important.

For example:
A sphere is rolling on a plane surface. If the angular velocity of the sphere is w in clockwise direction, then its direction of motion will be towards right side and rolling friction force towards left side (fig. 5.54 a). On the other hand when angular velocity is anticlockwise, then direction of motion is towards left and rolling friction force towards right side.

Question 11. 
Which one is greater n static triction and kinetic friction and why? Write the laws of static and kinetic friction.
Answer:
Laws of Limiting Friction:
There are following two laws of limiting friction:
1. Force of limiting friction is directly proportional to normal reaction acting between the contact surfaces and always acts in opposite direction of motion of the object.
i.e., F_s ∝ R

Where F_s is limiting friction,
and R is normal reaction.
or F_s = µ_s R
R = mg
F_s  = µ_s R = µ_s mg ......(1)
where µs is coefficient of static friction 
µ_s = \(\frac{F_s}{R}\) ......(2)
i.e., the ratio of limiting friction and normal reaction is called coefficient of static friction.

2. Limiting friction does not depend upon the shape and size of the bodies kept in contact.

Dynamic or Kinetic Friction:
When a body tries to move on the surface of other body, then till it does not move, the force of friction developed between contact surfaces is called static friction. Static friction is equal and opposite to external force and it increases upto a certain limit called limiting friction. After this limit, the body starts moving. In this situation, the force of friction between contact surfaces is called “Dynamic or kinetic friction”. Its value is slightly less than the limiting friction.

Laws of Dynamic Friction:
1. Dynamic friction is directly proportional to normal reaction and always less than limiting friction.
i.e., F_k ∝ R
or F_k ∝ µ_k R = µ_k mg
Where, F_k = Dynamic friction;
R = Normal reaction;
µ_k = Coefficient of dynamic friction.

2. Dynamic friction does not depend on the velocity of the body provided it should neither be very much or very less.

Distinguish between Static and Dynamic Friction:
Static friction is self adjusting force. As the external force is increased, it also increases but upto a certain.limit i.e., beyond this limit friction force does not increase. This maximum force of static friction is called limiting friction. In the given diagram, limiting friction is represented by BE. Below limiting friction, the object does not mvoe. As the external froce is increased beyond limiting friction, the body starts moving and force of friction becomes slightly less then limiting friction. In the diagram, this decrease in friction is shown by BC. Now the force of friction is called the dynamic friction which does not change on increasing external force. PQ is the measure of dynamic friction force.

Question 12. 
What is the meaning of angle of friction on inclined plane? An object slips down on an inclined plane, establish the expression of acceleration for the object.
Ans. 
Friction on an Inclined Plane-Angle of Repose:
The angle between inclined plane and horizontal, when any block placed on the plane remains at rest, is  called angle of repose.
In figure 5.55, a block of mass M is placed on an inclined plane of anige of inclination f₃. The forces acting on the block are shown in the diagram. 

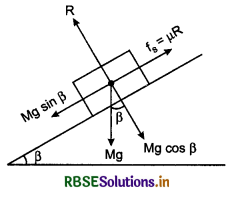
Free body diagram of block
Equations of motion,
Mg cos ß = R .........(1)
and Mg sin ß = µ_s.R .......(2)

On dividing equation (2) by (1), we have
\(\frac{M g \sin \beta}{M g \cos \beta}=\frac{\mu s R}{R}\)
or tan ß = µ_s ......(3)
but tan α = µ_s ........(4)
where α is angle of friction.
From equations (3) and (4), we have
ß = α
i. e, Angle of repose = Angle of friction
If the angle of inclination of the plane ≤ß, then the block placed on the plane will remain at rest. But when angle of inclination of the plane > ß, then the block will start slipping on the plane in downward direction.

Upwards Motion on Inclined Plane:
Suppose a block of mass ‘m’ is placed on a inclined plane having angle of inclination I with horizontal direction. Suppose the block is moved upward with acceleration ‘ci by applying a force P. All the forces acting on the block are shown in the same diagram. In these force f is the force of friction.

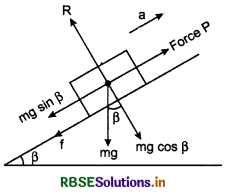
Free body diagram of the block
Equations of motion,
R = mg cosß

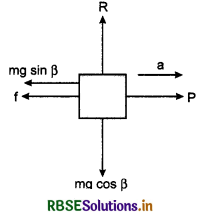
and F_net = P - f - mg sin ß
but F_net = ma
∴ P - f - mg sin ß = ma
∵ Force of friction,
f = µ_R
∴ f = µ mg cos ß
∴ P - µ mg cos ß - mg sin ß = ma ........(2)
If the block is moving upwards with uniform velcoity, then
a = 0
∴ P - µ mg cos ß - mg sin ß = ma
or P = µ mg cos ß + mg sin ß .........(3)
If the block covers a disance S along the plane with uniform velocity,then work done, 
W = force × displacement
= P × S
or W = (µ mg cos ß - mg sin ß) × S

Question 13. 
What are disadvantages of friction? State the methods of minimising the friction.
Ans. 
Friction as a Necessity and as An Evil:
1. Friction as a necessity

1. It is impossible to walk without the presence of friction between the foot and the ground. 
2. Friction helps us to write on a paper or board.
3. Without friction, physical brakes provided in the vehicles cannot work. There are some advanced electromagnetic brakes which do not work on the principle of friction. These are used in advanced high speed trains and sports cars.
4. Friction between the tyres and the surface of road provides the necessary grip of the vehicle on the road,to drive the vehicle safely, even on a slipping road (or wet road).
5. We cannot even hold a pen, if the friction is not there.
6. To tie knot in a string or rope, friction is necessary. Knots will untie readily in the absence of friction. 
7. Motion cannot be transferred in the absence of friction. For example : Transfer of the motion of paddling (by foot), via chain, to the rear wheel of the bicycle.
8. Not only the contact friction, but the air friction (air resistance) is also necessary. In the absence of air friction, rain drops can even cause heavy damage. It is because of extremely high speed, attained by the rain drops in absence of air friction. Air friction or viscous drag keeps the velocity of rain drops constant and comparatively low.

2. Friction as an evil or disadvantages of friction:
(i) Friction causes unnecessary wear and tear of the machinery parts in contact. Thus it decreases the efficiency as well as life of the machines. 
(ii) Friction involves unnecessary production of heat. For example : Brakes of vehicle may get overheated due to firction (if used for a long time), resulting in malfunctioning of brakes, moving parts etc.
(iii) An alarmingly large amount of energy is dissipated in overcoming the friction.

Methods of Reducing Friction:
In order to avoid the wastage of energy, we have to devise some means to reduce friction. Friction can be reduced using the following methods:
1. Lubriction : Lubricants like grease, oil, mobile oil etc are put or spread between the two’ solid surfaces in contact. They form a thin layer between them by filling up the irregularities of the surfaces. This avoids direct contact of solid surfaces. As a result, friction as well as heating of the moving parts get reduced quite effectively.

Actually, the lubricants in between the two solid surfaces convert dry friction (without labricants) into wet friction (with lubricants), which is of comparatively less magnitude.

2. By polishing: Polishing a surface, either by rubbing it or by depositing a ñne layer of suitable material on the surface, makes it smooth. Thus polishing reduces the friction. However it should be noted that the force of friction increases if two highly polished and super smooth surface slide over each other.

3. Ball bearings : The ball bearings arrangement (fig. 5.62), is used to convert the sliding friction into rolling friction between the two moving parts of a machine. Ball bearings are commonly used in bicycles etc.

Inner cylinder (axle) is rolling on the outer cylinder (fixed to the wheel) by means of ball bearings. If the ball bearings are not used, then both the inner and outer cylinders will slide relative to each other. Since, sliding friction is greater than rolling friction, “that is why ball bearings are used to convert the sliding friction into rolling friction. As a result, friction gets reduced quite effectively.

Question 14. 
What do you mean by angle of friction and coefficient of friction? Establish the relation between them.
Answer:
Angle of Friction:
In situation of limiting friction, the angle between normal reaction R and resultant P of normal reaction R and limiting friction f(s), is called the angle of friction. In figure 5.53 it is shown by α. 
In figure 5.53, a block A is shown placed on a rough surface and an external force F is acting on it to move it. As a reaction of F, there will be two forces. 
1. Normal reaction R which balances the weight mg of the block.

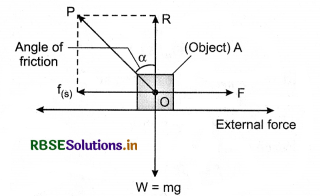
2. Limiting friction force f(s) = µ(s). R parallel to surface of contact which is equal and opposite to applied force \(\vec{F}\). Resultant of both these reactions is P which makes an angle a with normal reaction R.
∴ \(\tan \alpha=\frac{P R}{O R}=\frac{f_{(s)}}{R}=\frac{\mu_s(R)}{R}\)
\(\tan \alpha=\mu_s\)
∴ Angle of friction
α = \(\tan ^{-1}\left(\mu_s\right)\)

Coefficient of Static Friction:
∵ \(\mu_s\) = tan α
Therefore, the tangent of angle of friction is called coefficient of static friction.

Magnitude of resultant force : This force is known as contact force. The value of contact force shown in figure 5.53 is,
It magnitude of resultant force 
P = \(\sqrt{f_{(s)}^2+R^2}\) ∵ \(\vec{R} \perp \overrightarrow{f_{(s)}}\)
= \(\sqrt{\left(\mu_s R\right)^2+R^2}\)
P = R\( \sqrt{1+\mu_s^2}\)

Question 15. 
What do you understand by centripetal force? State its formula and obtain its dimensional formula.
Answer:
Centripetal Force:
We have gone through the fact that when a particle moves on circular path with uniform speed, then an acceleration acts on the particle,  always directed towards the centre of the path. This acceleration is called ‘centripetal acceleration’ (ac). According to Newton’s second law of motion for acceleration a force is necessary. Without force, acceleration is not possible. Therefore in uniform circular motion, a force always acts on the particle toward the centre of the path. This force is called ‘centripetal force’. This force is shown on three points P,Q, and R.

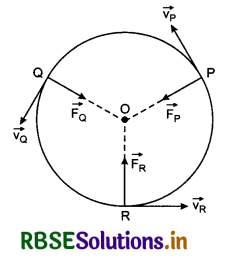
∵Force = mass × acceleration
∴ Centripetal force = mass × centripetal acceleration
or F = m.a_c

In uniform circular motion, the values of centripetal acceleration and centripetal force remain same but their directions always remain changing.

Question 16.
An object of mass m is moving with uniform speed u on circiur path of radius r. Find the centripetal force acting on the particle and give its direction also.
Ans. 
Centripetal Force:
We have gone through the fact that when a particle moves on circular path with uniform speed, then an acceleration acts on the particle,  always directed towards the centre of the path. This acceleration is called ‘centripetal acceleration’ (ac). According to Newton’s second law of motion for acceleration a force is necessary. Without force, acceleration is not possible. Therefore in uniform circular motion, a force always acts on the particle toward the centre of the path. This force is called ‘centripetal force’. This force is shown on three points P,Q, and R.

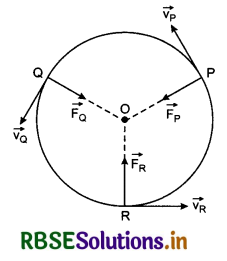
∵Force = mass × acceleration
∴ Centripetal force = mass × centripetal acceleration
or F = m.a_c

In uniform circular motion, the values of centripetal acceleration and centripetal force remain same but their directions always remain changing.

Question 17. 
What is meaning of centripetal force? Derive its formula in terms of angular velocity. State its use in daily life and tell, what will be resultant acceleration in non uniform circular motion?
Ans. 
Centripetal Force:
We have gone through the fact that when a particle moves on circular path with uniform speed, then an acceleration acts on the particle,  always directed towards the centre of the path. This acceleration is called ‘centripetal acceleration’ (ac). According to Newton’s second law of motion for acceleration a force is necessary. Without force, acceleration is not possible. Therefore in uniform circular motion, a force always acts on the particle toward the centre of the path. This force is called ‘centripetal force’. This force is shown on three points P,Q, and R.

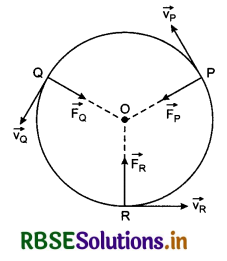
∵Force = mass × acceleration
∴ Centripetal force = mass × centripetal acceleration
or F = m.a_c

In uniform circular motion, the values of centripetal acceleration and centripetal force remain same but their directions always remain changing.
1. Bending of cyclist at circular path: We know that without centripetal force, the path of an object can never be circular. When a cyclist reaches a turn, its path becomes circular. Therefore he requires a centripetal force. To obtain the centripetal force, he bends towards the centre of the turn. On doing so, the force of friction between the tyres and the road provides the required centripetal force and cyclist safely crosses the turn.

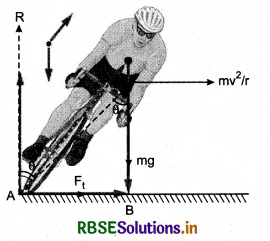
The forces acting the cyclist at turn in fig. 5.69: Cyclist crosses turn in equilibrium of clockwise torque due to mg about point A and anticlockwise torque due to force of friction f_s about centre of gravity (C.G.)
∴ In equilibrium,
Momentum of Force F_f about C.G. = Moment of force mg about A.

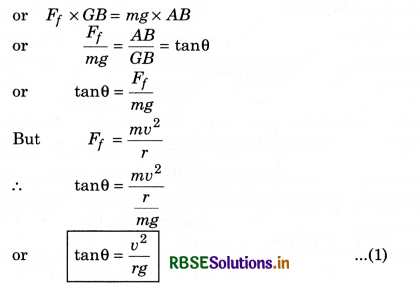
As we have considered here that required centripetal force (\frac{m v^2}{r}) is provided by force of friction F_f. Therefore for safe passing through the turn,
F_f ≥ F_c
or µ_s R = µ_s mg ≥ F_c
or µ_s mg ≥ \frac{m v^2}{r}
For optimum speed on turn.

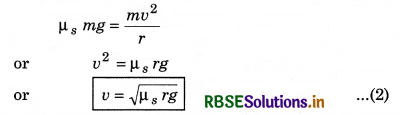
Optimum speed or maximum safe speed on turn can be calculated with the help of above equation (2).
Cyclist slows down the speed at the turn: When a cyclist reaches a circular turn, it requires a centripetal force because without centripetal force circular motion is impossible. To obtain this centripetal force, he bends towards the centre of the turn and O be the angle of inclination with vertical,
then it can be proved, that
tanθ = \(\frac{v^2}{r g}\)
Since the values of r and g are constant for a turn, therefore
tanθ ∝ v²
Thus it is clear, for greater value of v, θ will also be greater and for high value of θ, the possibility of slipping the cycle will increase. This is in ω to avoid this mis-happening, cyclist shows down his speed on the turn.

2. Circular turn of road: At the turn, the roads are, generally, made of circular shape. Therefore the vehicles require centripetal force on turn and this required centripetal force is provided to vehicles by the force of friction between the tyres of the vehicles and the road. But if the friction force is not sufficient, the road is made banked at the turn, due to which the required centripetal force is obtained by following three types:
(i) By friction force or motion of a car on leveled road: Suppose, m be the mass of the vehicle, r be the radius of the turn and u be the velocity of the vehicle on turn, then the forces acting on the vehicle are shown in the fig. 5.70 and these forces are:
(i) Weight of the car (mg)
(ii) Normal reaction (R)
(iii) Force of friction (f)

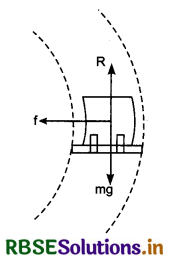
For balancing of vertical forces,
R = mg ........................(1)
For circular motion, the centripetal force is provided by the friction force, therefore,
f ≤ µ_sR or \(\frac{m v^2}{r}\) ≤ µ_s mg
or v² ≤ µ_s rg
∴ v ≤ \(\sqrt{\mu_s r g}\) ...........................(2)
Here the velocity does not depend on the mass of the vehicle. Therefore the optimum speed, i.e., maximum safe speed on the turn,
v_max = \(\sqrt{\mu r g}\)
If the vehicle moves on the turn with more than this safe speed, then either the vehicle will overturn or it will slip.
(ii) By banking of road: In above first part we have studied that if vehicle passes through curved horizontal road on turn, then friction provides the required centripetal force and maximum safe velocity on turn is v_max = \(\sqrt{\mu_s r g}\). If velocity of the vehicle is more than this velocity, the vehicle will slip. To solve this problem, the roads are made banked on the turn so that banking of road may also provide centripetal force. Here we are considering only the banking of road, not the friction.
When a vehicle passes over banked road at turn with obtimum velocity v, then there is no friction between the tyres of the vehicle and road. In this case the required centripetal force is applied by horizontal component of reaction (R₁ + R₂) and its vertical component balances the weight of the vehicle.

Question 18.
The slope of road on turn of radius r, is θ. If µ be the coefficient of friction between road and tyres, then determine:
(i) Ideal velocity the car.
(ii) Formula for maximum safe velocity of car.
Answer:
1. Bending of cyclist at circular path: We know that without centripetal force, the path of an object can never be circular. When a cyclist reaches a turn, its path becomes circular. Therefore he requires a centripetal force. To obtain the centripetal force, he bends towards the centre of the turn. On doing so, the force of friction between the tyres and the road provides the required centripetal force and cyclist safely crosses the turn.

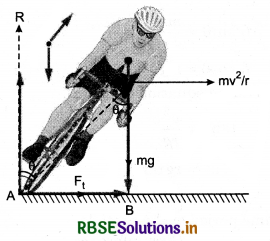
The forces acting the cyclist at turn in fig. 5.69: Cyclist crosses turn in equilibrium of clockwise torque due to mg about point A and anticlockwise torque due to force of friction fs about centre of gravity (C.G.)
∴ In equilibrium,
Momentum of Force F_f about C.G. = Moment of force mg about A.

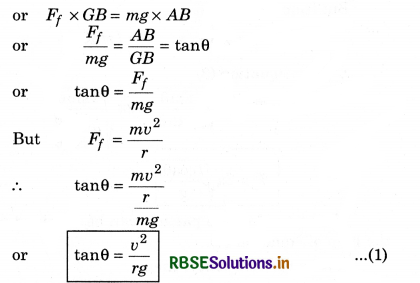
As we have considered here that required centripetal force (\(\frac{m v^2}{r}\)) is provided by force of friction F_f. Therefore for safe passing through the turn,
F_f ≥ F_c
or µ_s R = µ_s mg ≥ F_c
or µ_s mg ≥ \(\frac{m v^2}{r}\)
For optimum speed on turn.

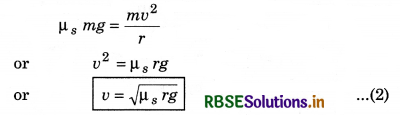
Optimum speed or maximum safe speed on turn can be calculated with the help of above equation (2).
Cyclist slows down the speed at the turn: When a cyclist reaches a circular turn, it requires a centripetal force because without centripetal force circular motion is impossible. To obtain this centripetal force, he bends towards the centre of the turn and O be the angle of inclination with vertical,
then it can be proved, that
tanθ = \(\frac{v^2}{r g}\)
Since the values of r and g are constant for a turn, therefore
tanθ ∝ v²
Thus it is clear, for greater value of v, θ will also be greater and for high value of θ, the possibility of slipping the cycle will increase. This is in ω to avoid this mis-happening, cyclist shows down his speed on the turn.

2. Circular turn of road: At the turn, the roads are, generally, made of circular shape. Therefore the vehicles require centripetal force on turn and this required centripetal force is provided to vehicles by the force of friction between the tyres of the vehicles and the road. But if the friction force is not sufficient, the road is made banked at the turn, due to which the required centripetal force is obtained by following three types:
(i) By friction force or motion of a car on leveled road: Suppose, m be the mass of the vehicle, r be the radius of the turn and u be the velocity of the vehicle on turn, then the forces acting on the vehicle are shown in the fig. 5.70 and these forces are:
(i) Weight of the car (mg)
(ii) Normal reaction (R)
(iii) Force of friction (f)

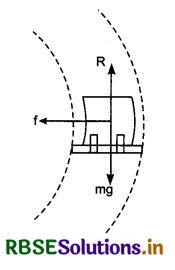
For balancing of vertical forces,
R = mg ........................(1)
For circular motion, the centripetal force is provided by the friction force, therefore,
f ≤ µ_sR or \(\frac{m v^2}{r}\) ≤ µ_s mg
or v² ≤ µ_s rg
∴ v ≤ \(\sqrt{\mu_s r g}\) ...........................(2)
Here the velocity does not depend on the mass of the vehicle. Therefore the optimum speed, i.e., maximum safe speed on the turn,
v_max = \(\sqrt{\mu r g}\)
If the vehicle moves on the turn with more than this safe speed, then either the vehicle will overturn or it will slip.
(ii) By banking of road: In above first part we have studied that if vehicle passes through curved horizontal road on turn, then friction provides the required centripetal force and maximum safe velocity on turn is v_max = \(\sqrt{\mu_s r g}\). If velocity of the vehicle is more than this velocity, the vehicle will slip. To solve this problem, the roads are made banked on the turn so that banking of road may also provide centripetal force. Here we are considering only the banking of road, not the friction.
When a vehicle passes over banked road at turn with obtimum velocity v, then there is no friction between the tyres of the vehicle and road. In this case the required centripetal force is applied by horizontal component of reaction (R₁ + R₂) and its vertical component balances the weight of the vehicle.

Question 19.
Derive the expression for time period of an object rotating in horizontal circle with the help of a cord, when weight of the object is not negligible.
Answer:
Motion of a Particle Attached to String, In Horizontal Circle:
(i) When weight of the particle is negligible: When a particle of negligible weight is tied with a cord and allowed to move on horizontal circular path, then the tension of the cord provides the required centripetal force and the cord remains horizontal. In fig. 5.67, a particle of mass m is allowed to move in horizontal circle of radius r with uniform speed u. If f be the tension in the cord, then

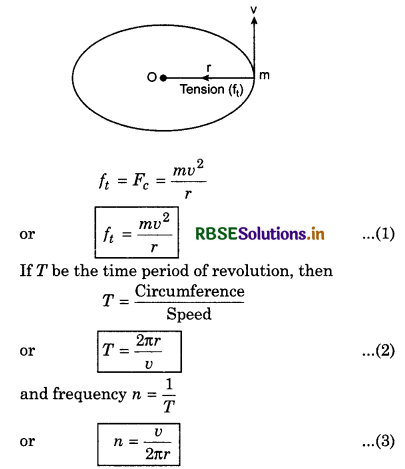
(ii) When weight of the particle is not negligible: When weight of the particle is not negligible and it is moved in horizontal circle with the help of a cord of length l, then due to weight mg of the particle the cord does not remain horizontal and the cord traces the surface of a cone. Therefore this system is called ‘conical pendulum’. (Fig. 5.68).

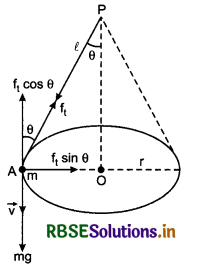
If f_t be the tension in the cord and it makes an angle θ with the axis OP of the cone, then one component f_t cosθ of tension f_t balances the weight mg of the particle and other component ft sinθ provides the required centripetal force \(\frac{m v^2}{r}\).
∴ f_t sinθ = \(\frac{m v^2}{r}\) .......................(1)
and f_t cosθ = mg .....................(2)
On dividing equation (1) by (2),

Time period of the particle can be obtained with the help of equation (4).
If n be the frequency, then

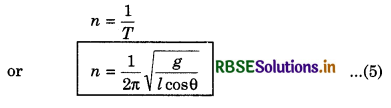
Numerical Questions

Based on Newton’s Laws

Question 1.
Find the force acting on the wall of a tower applied by a water fountain, while area of cross-section of pipe be 10^-2m² and velocity of water is 30 ms^-1. It can be supposed that water does not reflects from the wall. (g = 10ms^-2)
Answer:
Area of cross-section of pipe A = 10^-2 m²
Velocity of water v = 30 ms^-1
Mass of water striking the wall
m = volume x density
= Area x velocity x density
= 10^-2 x 30 x 10³
= 300 kg
Initial velocity v = 30 ms^-1
Final velocity v = 0
∴ Force applied by water
F = \(\frac{\Delta p}{\Delta t}=\frac{p_2-p_1}{\Delta t}=\frac{m v-m u}{1}\)
= \(\frac{300(0-30)}{1}\)
= -300 x 30 = -9000 N

Question 2.
A child pulls two toys on a smooth plane by applying a force of 1.5 N at an angle of 30° with horizontal line, in vertical plane (fig.). What will be acceleration of toy of mass 40 kg and that of 20 kg? Also find the tension in string joining both the boxes.

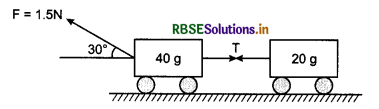
Answer:
Force acting in horizontal direction
= F cos 30°
∴ Acceleration of the system

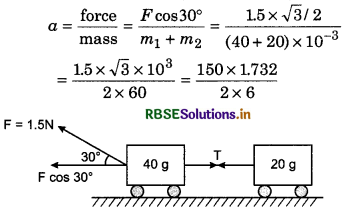
= 21.65 ms^-2
For toy of mass 20 g,
T = m².a = \(\frac{20}{1000}\) x 21.65 = \(\frac{43.30}{100}\)
= 0.433 N

Question 3.
Rescue of a person of 70 kg caught in sea-accident is conducted by a helicopter with the help of a rope. It the rope can bear maximum tension of 100 kg.wt, what should be the maximum acceleration of helicopter in upward direction so that the rope may not break?
Answer:
Suppose the acceleration of helicopter is a.
∴ Equation of motion
F - mg = ma
or 100 x g - 70 x g = 70 x a
or 30g = 70a
∴ a = \(\frac{30 \times g}{70}\)
= \(\frac{30 \times 10}{70}=\frac{30}{7}\)
= 4.2 ms^-2

Question 4.
N bullets of mass m each, are fired on a wall with velocity v ms^-1. If n bullets are fired per second then calculate the force of reaction on bullets by wall.
Answer:
Total mass of bullets = N x m
Time taken in firing these bullets
t = \(\frac{N}{n}\)
Momentum of bullets striking the wall = Nm x v
∴ Rate of change of momentum = Force applied
or Applied force = \(\frac{N m v}{t}=\frac{N m v}{\frac{N}{n}}\)
= mnv

Question 5.
A child hangs a steel plate with the help of a string in vertical plane. The child fires bullet on this plate by a toy-gun. If mass of each bullet be 2 g and it strikes the plate with the velocity of 11 ms^-1 and returns back with same speed, then how much force is acting on the plate? The child is firing the bullets at the rate of 3 bullets per second.
Answer:
Average force applied on the plate,
F = Rate of change of momentum
= 24 x m x n
= 2 x 11 x \(\frac{2}{1000}\) x 3
= 0.132 N

Question 6.
A vehicle of mass 500 kg is moving with the velocity of 6 ms^-1. Sand is being dropped from the vehicle at the rate of 10 kg/min. What force will be required to maintain the speed of the vehicle?
Answer:
F = \(\frac{d p}{d t}=\frac{d}{d t}(m v)\)
= v \(\frac{d m}{d t}=6 \times \frac{10}{60}\)
= 1 N

Based on Impulse

Question 7.
A hammer of mass 500 g is striking a nail with the velocity of 6 ms^-1. As a result, the nail penetrates by 5 cm. If the mass of the nail be negligible, then find:
(a) Acceleration after the strike
(b) time taken in strike
(c) magnitude of impulse.
Answer:
(i) Mass of hammer m = 500 g = 0.5 kg
Initial velocity of hammer, u = 6 ms^-1
Final velocity of hammer v = 0
Distance travelled s = 5 cm = 0.05 m
From equation v² = u² + 2as
or 0.10 a = -36
∴ a = \(\frac{-36}{0.1}\) = -360 ms^-2

(ii) From first equation of motion
v = ut + at
∴ 0 = 6 - 360 x t
or 360t = 6
∴ t = \(\frac{6}{360}=\frac{1}{60}\)s

(iii) Impule I = F ∆t = ∆p = ma x ∆t
= 0.5 x 360 x \(\frac{1}{60}\)
= 3.0 Ns

Question 8.
The mass of a body is 2 kg and its initial velocity is 5 ms^-1. A force is acting on the body for 4 seconds as shown in fig. Calculate the impulse and velocity of the body.

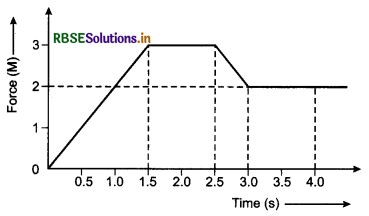
Answer:
(i) Impulse of the force
= Area of figure O ABCDE
= Area of [∆OAH + ☐ HABG + trapezium GBCF + ☐ CDEF]
= \(\frac{3 \times 1.5}{2}\) + (2.5 - 1.5) + \(\frac{3 + 2}{2}\) x (3 - 2.5) + 2 x (4 - 3)
= 2.25 + 3 + 1.25 + 2
= 8.5 Ns
(ii) Mass of the object m = 2 kg
Initial velocity u = 5 ms^-1
Final velocity v = ?
∵ Impulse = ∆p = m(v - u)
8.5 = 2(v - 5)
or v - 5 = \(\frac{8.5}{2}\) = 4.25
∴ v = 5 + 4.25
= 9.25 ms^-1

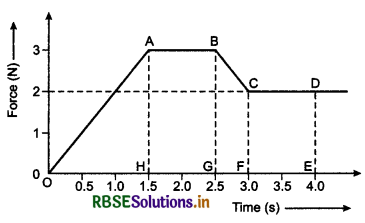
Question 9.
A bullet is fired by a gun. The force acting on the bullet is given by F = (600 - 2 x 10⁵ t). Where F is in ‘N’ and t is in 's'. As the bullet leaves the barrel of the gun, force acting on it becomes zero. What will be average impulse of the bullet?
Answer:
Given: F = 600 - 2 x 10⁵ t
∵ The force becomes zero as the bullet leaves the barrel.
∴ 600 - 2 x 10⁵ t = 0
∴ t = \(\frac{600}{2 \times 10^5}\) = 3 x 10^-3 s

Based on Equilibrium of Concurrent Forces and Pulley

Question 10.
What should be maximum weight of body B so that body A should not slip? Coefficient of static friction is µ.

Answer:
R = Mg
∴ f_s = µ R = µMg
For equilibrium of 0,
T cosθ = fs
or T cosθ = µMg .....................(1)
and T sinθ = mg ......................(2)

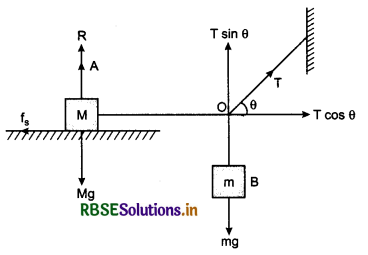
On dividing equation (2) by (1)
\(\frac{\sin \theta}{\cos \theta}=\frac{m g}{M g}\)
or \(\frac{m g}{M g}\) = tanθ
∴ Mg = mg tanθ

Question 11.
A sphere of mass 200 g is hung from a unstretchable cord of length 130 cm. Upper end of this cord is joint with the ceiling of the room. The sphere is moving on circular path of radius 50 cm. Find the time period of this conical pendulum and tension in the cord.
Answer:
T cosθ = mg .......................(1)
and T sinθ = \(\frac{m v^2}{r}\) ............................(2)
∴ On dividing equation (2) by (1),
tanθ = \(\frac{v^2}{r g}\)
∵ tanθ = \(\frac{O B}{O P}=\frac{r}{\sqrt{l^2-r^2}}\)
From equation (1),

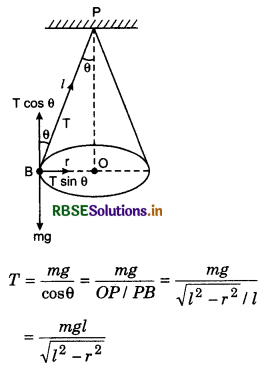
Given: m = 200 g = 0.2 kg
l = 130 cm = 1.30 m
r = 50 cm = 0.5 m
∴ T = \(\frac{0.2 \times 10 \times 1.30}{\sqrt{(1.3)^2-(0.5)^2}}=\frac{2 \times 1.30}{\sqrt{1.69-0.25}}\)
= \(\frac{2 \times 1.3}{\sqrt{1.44}}=\frac{2.6}{1.2}\)
= 2.12 N
Time period of conical pendulum,

Question 12.
A mass M is hung by a unstretchable string as shown in fig. What is tension in horizontal string?

Answer:
For equilibrium of O,
T sin 30° = Mg ..........................(1)
and T cosθ = T₁ .........................(2)
∴ From equations (1) and (2),
tan 30° = \(\frac{M g}{T_1}\)

Question 13.
A block of mass m₁ = 10 kg is placed on a smooth table. A cord is attached with this block and it passes over a frictionless pulley. A mass m₂ of 5 kg is attached with the other end of the cord. What will be tension in string during motion of the masses and what will be tension when masses become at rest? (g = 9.8N.kg^-1)

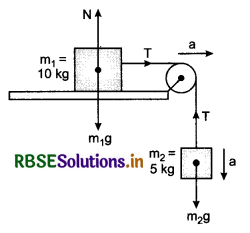
Answer:
Given: m₁ = 10 kg
m₂ = 5 kg
Equations of motion for block m₁,
N = m₁g = m₁ x 9.8 = 9.8 m₁ ...............................(1)
or N = 9.8 x 10 = 98 Newton
T = m₁a
or T = 10a .............................(2)

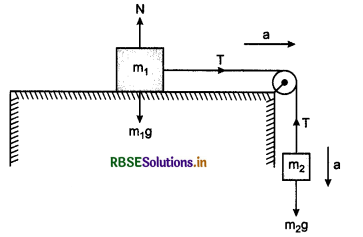
Equation of motion for m₁,
m₁g - T = m₁a
or T = m₁g - m₁a = 5 x 9.8 - 5a
or T = 49 - 5a ..............................(3)
Equating equations (2) and (3).
10a = 49 - 5a
or 15a = 49
∴ a = \(\frac{49}{15}\) = 3.266
or a = 3.27 ms^-2
Substituting the value of a in equation (2)
T = 10 x 3.27 = 32.7 Newton
When the system becomes at rest,
then a = 0
∴ From equation, (3)
T = 49 - 5 x 0 = 49 - 0
or T = 49 N

Question 14.
In fig., the relation in masses is M₁ = 4M₂ and pullies are smooth. At t = 0, the system is at rest. If the system is left free and acceleration of M₁ is a₁; what will be acceleration of M₂?

Answer:
Distance travelled by M₂ will be two times that travelled by M₁. Therefore acceleration of M₂ will be two times the acceleration of M₁.
∴ Acceleration of M₂ = 2a

Question 15.
Two blocks of masses m₁ and m₂ are attached with a string which passes over a pulley as shown in fig. Calculate acceleration of the system. Given: m₁ = 1 kg; m₂ = 2 kg; (g = 10ms^-2)

Answer:
Given: m₁ = 1 kg
m₂ = 2 kg
g = 10 ms^-2
For the motion block of mass m₁ i.e., block A.
T - m₁g sin 30° = m₁a
or T = m₁a + m₁g sin 30° ............................(1)

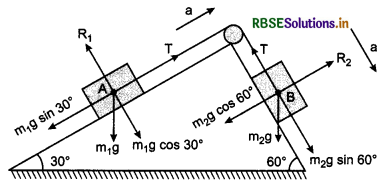
Similarly equation of motion of block B,
m₂g sin 60° - T = m₂a
or T = m₁g sin 60° - m₂a ..............................(2)
Equating equations (1) and (2),
m₁a + m₁g sin 30° = m₂g sin 60° - m₂a
or m₁a + m₂a = m₂g sin 60° - m₁g sin 30°
or a(m₁ + m₂) = 2 x 10 x \(\frac{\sqrt{3}}{2}\) - 1 x 10 x \(\frac{1}{2}\)
or a(1 + 2) = 10\(\sqrt{3}\) - 5
a x 3 = 10 x 1.732 - 5 = 17.32 - 5 = 12.32
∴ a = \(\frac{12.32}{3}\) = 4.1 ms^-2
or a = 4.1 ms^-2

Based on Varying Mass

Question 16.
To project a rocket of mass 200 quintal, a force of 5 x 10⁵ N is applied for 20 s. What will be the velocity of the rocket after this time interval?
Answer:
m = 200 quintal = 200 x 100 kg = 2 x 10⁴ kg
F = 5 x 10⁵ N, t = 20s
∵ F = ma ⇒ a = \(\frac{F}{m}=\frac{5 \times 10^5}{2 \times 10^4}=\frac{50}{2}\) = 25 ms^-1
Now applying first equation of motion,
v = u + at = 0 + at
= 25 x 20
= 500 ms^-1

Question 17.
The combustion of fuel is taking place in a rocket at the rate of 100 kg.s^-1. The gases are rejected with velocity of 4.5 x 10⁴ ms^-1. Calculate the upthrust force on the rocket.
Answer:
Given: \(\frac{d m}{d t}\) = 100 kg.s^-1;
u = 4.5 x 10⁴ ms^-1; F = ?
∴ F = u\(\frac{d m}{d t}\) = 4.5 x 10⁴ x 100
= 4.5 x 10⁶ N

Question 18.
A gun is placed on a car of 2000 kg. standing on frictionless road. At any time a bullet of 10 gm is fired by gun with velocity of 500 ms^-1 with respect to car. Number of bullets fired per second is 10, then find the average force applied on the car.
Answer:
F = mnu
= \(\frac{10}{1000}\) x 10 x 500
= 50 N

Based on Limiting Friction

Question 19.
A block of mass 2 kg is placed on an inclined plane of inclination angle of 60° with horizontal. Coefficient of friction between plane and the block is 0.7. What is the force of friction acting on the block?
Answer:
R = mg cos 60
∴ Force of friction
f_s = µ_s.R°
= µ_s. mg cos 60
= 0.7 x 2 x 9.8 x \(\frac{1}{2}\)
= 6.86 N

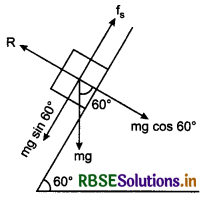
Question 20.
Just to move a block of mass 20 kg on a rough surface, the required force is 98 N. Find the coefficient of friction and angle of friction. (g = 9.8 ms^-2).
Answer:
Given: m = 20 kg; F = 98N; g = 9.8 ms^-2; µ_s = ?; α = ?
∵ F = µ_s mg ⇒ µ_s = \(\frac{F}{m g}=\frac{98}{20 \times 9.8}=\frac{1}{2}\) = 0.5
or µ_s = 0.5
If α is angle of friction, then
tanα = µ_s
∴ α = tan^-1µ_s
or α = tan^-1(0.5)

Based on Coefficient of Friction

Question 21.
A body rolling with speed of 10 ms^-1 on a road, stops after travelling a distance 50 m. Find the coefficient of friction. (g = 10ms^-2)
Answer:
u = 10 ms^-1; S = 50m; v = 0; µ_s = ?; g = 10 ms^-2
F_s = µ_s x R = µ_s. mg
∵ Kinetic energy of the body is coverted in work done against force of friction,

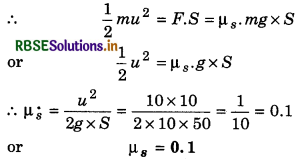
Question 22.
Angle of friction between two surfaces in contact, is 60°. What will be coefficient of friction between them?
Answer:
α = 60°; µ = ?
∵ µ_s = tanα = tan 60° = \(\sqrt{3}\)
∵ µ_s = \(\sqrt{3}\)

Based on Distance

Question 23.
A motor-car is moving on a horizontal road with speed u. Coefficient of friction between road and tyres is (µ_s). Find the minimum distance in which the car will stop.
Answer:
u = 20 ms^-1; µ_s = 0.4
g = 10 ms^-2; S = ?

Force of friction,
F_s = µ_s R = µ_s mg

Question 24.
A car is moving on a straight road with speed of 20 ms^-1. Coefficient of friction between the tyres and road is 0.4. Find the minimum distance in which the car will stop. (g= 10ms^-2)
Answer:
u = 20 ms^-1; µ_s = 0.4; S = ?; g = 10 ms^-2
As we found,
S = \(\frac{u^2}{2 \mu_s \cdot g}=\frac{20 \times 20}{2 \times 0.4 \times 10}\)= 50 m
or S = 50 m
 
Based on Angle of Friction

Question 25.
Coefficient of friction between two surfaces in contact is \(\frac{1}{\sqrt{3}}\), what is angle of  friction between them?
Answer:
Given: µ_s = \(\frac{1}{\sqrt{3}}\); α = ?
∵ α = tan^-1(µ_s)
∴ α = tan^-1(\(\frac{1}{\sqrt{3}}\))
or α = 30°

Question 26.
Just to move a block of mass 25 kg on a rough surface, a force of 98 N is required. Calcualte the angle of friction and coefficient of friction.
Answer:
∵ F_s = µ_s. R = µ_s. mg
Given: m = 25 kg; F_s = 98N, µ_s = ?, α = ?
∴ 98 = µ_s x 25 x 9.8
∴ µ_s = \(\frac{98}{25 \times 9.8}=\frac{10}{25}=\frac{2}{5}\)
or µ_s = 0.4
Angle of friction
α = tan^-1(µ_s)
or α = tan^-1(0.4)

Based on Motion in Vertical Plane and Horitzontal Plane

Question 27.
A man of mass 80 kg slips down along a pole. Force of friction is 720 N. Find the acceleration of the man. (g = 10 ms^-2)
Answer:
Given: F_s = 720N; m = 80 kg; g = 10 ms^-2; a = ?
Equation of motion,
mg - F_f = ma
∴ 80 x 10 - 720 = 80a
or 800 - 720 = 80a
or 80 = 80a
∴ a = \(\frac{80}{80}\) = 1 ms^-2
a = 1 ms^-2

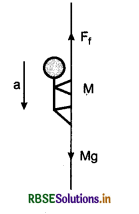
Question 28.
Mass of a body is 5 kg and is placed on a horizontal plane. Coefficient of static friction is 0.4 and coefficient of kinetic friction is 0.3. If the forces (a) 10 N end (b) 30 N are applied horizontally on the body, then find the force of friction on the body.
Answer:
(i) Force of friction available
f_s = µ_s R = µ_s mg
= 0.4 x 5 x 10 = 20N
∵ Force applied F = 10N, and F < f_s
∴ Force of friction = F = 10N

(ii) When F = 30N, then the block will start moving.
∴ Kinetic friction,
f_k = µ_k R = µ_k mg
= 0.3 x 5 x 9.8
= 14.7N

Based on Inclined Plane

Question 29.
Length of an inclined plane is 13 m and its height is 5 m and µ = \(\frac{1}{3}\). With what initial velocity should an object be projected so that it may become at rest at highest point?
Answer:
For upward motions,
mg sinθ + f_s = P
or mg sinθ + µ_s mg cosθ = ma
or g sinθ + µ_s g cosθ = a

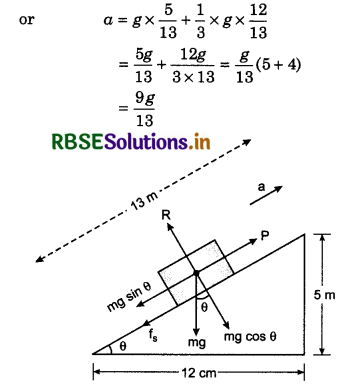
Now on applying third equation of motion,
v² = u² + 2as
∴ 0 = u² - 2 x \(\frac{9 g}{13}\) x 13
u² = 18g = 18 x 9.8
∴ u = \(\sqrt{18 \times 9.8}\)
= 13.28 ms^-1

Question 30.
A metallic block is placed on an metallic inclined plane of inclination angle 30°. If mass of the block is 0.5 kg and coefficient of friction is 0.2, then (i) what force will be required to stop the block from slipping? (ii) What force will be required to just move the block upwards? (iii) The force required to provide the motion of acceleration 20 ms^-2.
Answer:
Given: θ = 30°
M = 0.5 kg
µ = 0.2
(i) Force required to check the block from slipping,
F = mg sin 30° - f_s
or F = mg sin 30° - µ_s. mg cos 30°
= mg(sin 30° - µ_s. cos 30°)
= 0.5 x 9.8(0.5 - 0.2 x \(\frac{\sqrt{3}}{2}\))
= 4.9(0.5 - 0.1732)
= 1.6N

(ii) Force required to just move the block upwards
F = mg sin 30° + f_s = mg sin 30° + µ_s. mg cos 30°
= mg(sin 30° + µ_s. cos 30°)
= 0.5 x 9.8(0.5 + 0.2 x \(\frac{\sqrt{3}}{2}\))
= 4.9(0.5 + 0.1732)
= 4.9 x 0.6732
= 3.299N
(iii) Equation for upwards acceleration motion
F - (mg sin 30° + µ mg cos 30°) = ma
or F - (3.299) = 0.5 x 0.2 = 0.10
∴ F = 3.299 + 0.1
= 3.399 N

Question 31.
Length of a rough inclined plane is 6.4 m and its inclination is 30° with horizontal. An object starts slipping from the top of the plane. Find the time taken in reaching the bottom of the plane. (Given µ_k= 0.2 and g = 9.8ms^-2)
Answer:
For downwards motion, the equation of motion
ma = mg sin 30° - f_s = mg sin 30° - µ_s mg cos 30°
or a = g sin 30° - µ_s g cos 30°
= \(\frac{g}{2}\) - 0.2 x g x \(\frac{\sqrt{3}}{2}=\frac{g}{2}\)(1 - 0.2 x \(\sqrt{3}\))
or a = \(\frac{9.8}{2}\)(1 - 0.2 x 1.732)

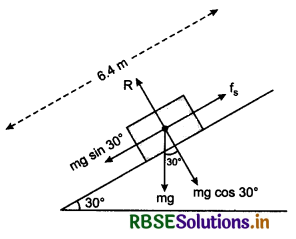
= 4.9(1 - 0.3464)
= 3.2 ms^-2
∴ On applying equation S = ut + \(\frac{1}{2}\)at²
6.4 = 0 + \(\frac{1}{2}\) x 3.2 x t²
∴ 6.4 = 1.6t²
or t² = \(\frac{6.4}{1.6}\) = 4
∴ t = 2s

Based on Centripetal Force and Tangential Force

Question 32.
A goods train is turning at the turn of radius 400 m with the speed of 72 km h^-1. A spring balance is hanging from the ceiling of a compartment and a body of 20 kg is hanging with this balance. What will be reading of the balance?
Answer:
Given: r = 400 m; v = 72 kmh^-1
= 72 x \(\frac{5}{18}\) = 20 ms^-1
m = 20 kg

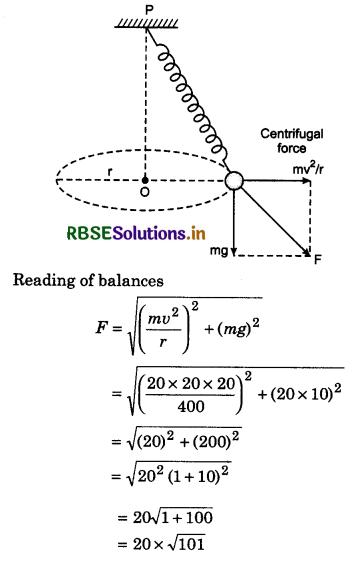
= 10.049 x 20
= 200.99 N
= \(\frac{200.99}{10}\) kgwt = 20.1 kg wt

Question 33.
A particle of mass 5 g is moving on a circular path of radius 25 cm at the rate of half cycle per second. What is acceleration of the particle? Calculate the centripetal force on the particle.
Answer:
Given: m = 5 g = 5 x 10^-3 kg,
r = 25 cm = 25 x 10^-2 m
Frequency n = \(\frac{1}{2}\) cs^-1 = 0.5 cs^-1
∴ Angular velocity, ω = 2πn = 2π x 0.5 = π rads^-1
∴ Acceleration of the particle i.e., centripetal acceleration
a_c = rω² = 25 x 10^-2 x π² = 0.25 π² ms^-2
The force acting on the particle
F_c = ma_c = 5 x 10^-3 x 0.25 x π² N
= 1.25 π² x 10^-3 N

Question 34.
A body of mass 0.10 kg is moving on a circular path of diameter 1.0 M at the rate of 10 cycles in 31.4 s. Calculate force acting on the body.
Answer:
Given: m = 0.10 kg; 2r = 1.0 m ⇒ r = 0.5 m
Frequency n = \(\frac{10}{31.4} \text { c.s }^{-1}=\frac{1}{3.14}=\frac{1}{\pi} c_{.} s^{-1}\)
∴ F_c = mrω² = mr4π²n²
mr x 4 x π² x \(\frac{1}{\pi^2}\)
= 4 mr
= 4 x 0.10 x 0.5
= 0.20 N

Based on Bodies Moving on Banked and Plane Surfaces:

Question 35.
Find the maximum velocity with which a train can be moved on a circular track of radius 100 m. The slope of the rails is 11.31°. [tan 11.31° = 0.2; g = 9.8 ms^-2]
Answer:
Given: r = 100 m, v_max = ?, θ = 11.31°
tan 11.31° = 0.2, g = 9.8 ms^-2

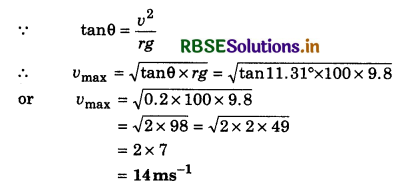
Question 36.
Radius of a road-turn is 500 m and the width of the road is 10 m. Its outer edge is elevated by 0.15 m with respect to inner edge. (g = 10 ms^-2). This inclination of the road is ideal for which dpeed of a running vehicle?
Answer:
Given: r = 500 m; b = 10 m; h = 0.15 m; v = ?; g = 10 ms^-2

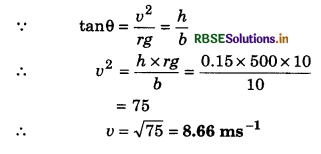
Question 37.
A car is turning on turn of radius 60 m. If the coefficient of friction be 0.8, then find:
(i) With what maximum velocity a car can cross the turn without slipping?
(ii) What should be the slope of the road for this speed?
Answer:
Given: r = 60m; µ = 0.8
(i) v_max = ?

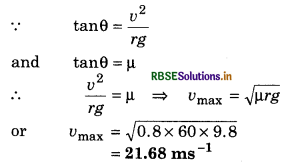
(ii) ∵ tanθ = µ ⇒ θ = tan^-1(µ)
or θ = tan^-1(0.8)

Question 38.
What will be maximum speed of a car on a horizontal road turn of radius 20m? While coefficient of friction between road and the tyres is 0.3.
Answer:
Given: r = 60 m; v_max = ?; µ = 0.3
∵ v_max = \sqrt{\mu r g}=\sqrt{0.3 \times 60 \times 9.8}
= 13.28 ms^-1

Based on Motion on Horizontal Circle

Question 39.
A stone of mass 0.1 kg is rotated in horizotnal circle with the help of a cord of length 1.0 m at the rate of \(\frac{10}{\pi}\) c.s^-1. Find the tension in the cord.
Answer:
Given: m = 0.1 kg; r = 1.0 m; n = \(\frac{10}{\pi}\)cs^-1
∴ ω = 2πn = 2π x \(\frac{10}{\pi}\) = 20 rad s^-1
∴ Tension in starting,
T = F_c = mrω²
= 0.1 x 1.0 x 20 x 20
= 0. x 400
= 40N

Question 40.
A object of mass 1 kg is rotated in horizontal circle of radius 0.1 m at the rate of 3 c.s^-1. Neglecting the effect of gravity, calculate
(i) linear velocity the object
(ii) centripetal acceleration
(iii) tension of the cord
(iv) what will happen it the cord breaks?
Answer:
m = 1 kg; r = 0.1 m; n = 3 cs^-1
(i) v = rω = r.2πn = 0.1 x 6.28 x 3
or v = 1.884 ms^-1
(ii) Centripetal acceleration,
a_c = rω² = r x 4π² n²
= 0.1 x 4 x 9.86 x 9
= 35.34 ms^-2
(iii) Tension in string,
T = F_c = m.a_c = 1 x 35.34
or T = 35.34 N
(iv) If the string breaks, then the tension will disappears. Therefore the particle will move tangentially.

Higher Order Thinking Skills or HOTS

Question 1.
A ball of mass 400 g is dropped from the height of 5 m. A boy standing on ground, attacks on ball by a bat applying a force 100 N vertically upwards. After attack, if the maximum height achieved by the ball is 20 m, then find the time of contact between bat and ball.
Solution:
Mass of the ball m = 400 g = 0.4 kg
h = 5 m, initial velocity u = 0, a = +g = 9.8ms^-2
∴ From equation v² = u² + 2as
v² = 0+ 2 x 9.8 x 5 = 98
∴ v = \(\sqrt{98}=7 \sqrt{2}\)
After collision of ball and bat the ball reaches upto height h = 20 m, a = -g = -9.8 ms^-2, v =0
Again from same relation v² = u² + 2as
or u² = 4 x 98
∴ u = 14\(\sqrt{2}\) ms^-1
∴ Change in momentum

Question 2.
An object of mass m is suspended by two cords which make angles α and ß with the horizontal. Find the tension in each string. 
Solution:
The position of forces is shown in fig. (a)
∵ The object is in equilibrium,
∴ In horizontal direction
∑F_x = 0

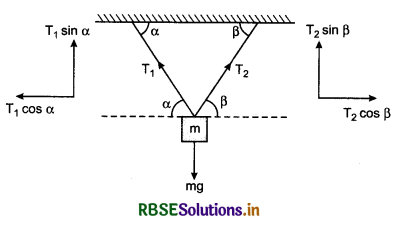
∴ T₁ cos α = T₂ cos ß
or T₁ = \(\frac{T_2 \cos \beta}{\cos \alpha}\) ...........................(1)
For vertical direction, ∑F_y = 0
∴ T₁ sinα + T₂ sin ß = mg
or \(\frac{T_2 \cos \beta}{\cos \alpha}\) x sinα + T₂ sinß = mg
or T₂ [cosß.sinα + cosα sinß] = mg cosα
or T₂. sin(α + ß) = mg cos α

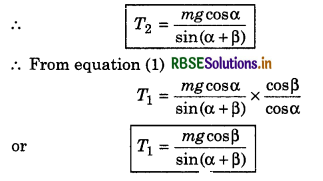
Question 3.
A wire of mass 9.8 x 10^-3 kg m^-1, passes over a pulley. The pulley is at the top of a inclined smooth plane making an angle of 30° with horizontal M₁ and M₂ masses are attached with wire. Mass M₁ is placed on the inclined plane while M₂ is suspending from the other end of the wire. The whole system is in equilibrium. Now a transverse wave is travelling through the wire, then find the value of M₁ and M₂. (g = 9.8 ms^-2)
Solution:
The situation of the given system is shown in fig.(a)

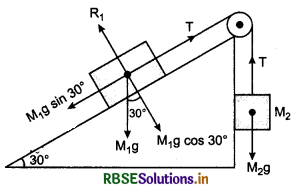
In this diagram, the free body diagrams of m₁ and m₂ are shown.
In equlibrium R₁ = M₁g cos 30° ...............................(1)
and T = M₁g sin 30° ......................(2)
For mass M₂,
T = M₂g ............................(3)
On comparing equations (2) and (3),
M₂g = M₁g sin 30° = \(\frac{M_1 g}{2}\)
∴ M₁ = 2M₂ ............................(4)
Velocity of transverse waves in the wire,
v = \(\sqrt{\frac{T}{m}}\) or v² = \(\frac{T}{m}\)
∴ T = v² . m = 100 x 100 x 9.8 x 10^-3
= 98N
∴ From equation (3),
T = M₂g ⇒ M₂ = \(\frac{T}{g}=\frac{98}{9.8}\) = 10 kg
∴ From equation (4),
M₁ = 2M₂ = 2 x 10 = 20 kg

Question 4.
The pulleys shown in figure (a) are ideal and stable at their own places. Two weightless strings are attached with spring balance and masses M₁ and M₂ are attached with other ends of the string which are passing over the pulleys. Calculate the reading of spring balance.
Solution:
In this problem, the reading of spring balance will be equal to tension of strings. Therefore to estimate the tension, the given diagram can be replaced by figure (b).

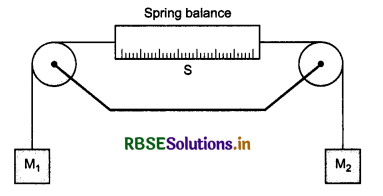
Suppose M₁ > M₂, therefore M₁ will move downwards while M₂ will move upwards. If a be the acceleration of the system,
Equation of motion of m₁,
M₁g - T = M₁a ...........................(1)
and equation of motion of M₂,
T - M₂g = M₂a ..........................(2)
∴ From equation (1),
T = M₁g - M₁a ..........................(3)
From equation (2),
T = M₂g + M₂a .........................(4)
Equating equations (3) and (4),
M₁g - M₁a = M₂g + M₂a
or M₁g - M₂g = M₁a + M₂a = a(M₁ + M₂)
or a = \(\frac{\left(M_1-M_2\right) g}{\left(M_1+M_2\right)}\)

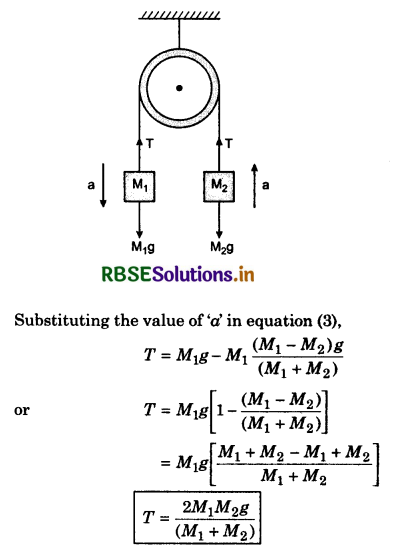
This will be the reading of spring balance.

Question 5.
A block A of mass m is placed on block B of mass M and both of these are placed on a horizontal surface C.A and B are connected with a long cord which passes over a frictionless pulley. Coefficient of kinetic friction is µ_k. Find the force acting on B which may move A and B with uniform speed.

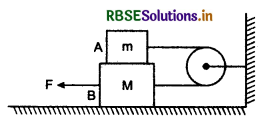
Solution:
For block A,
T - f_k = ma = 0
because a = 0
or T = f_k = µ_k mg
or T = µ_k mg ...........................(1)

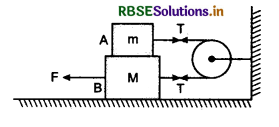
For block B,
F - T - f_SB = Ma
or F - µ_k mg - µ_k mg - µ_k(M + m)g = Ma
or F - 2µ_k.mg - µ_k(M + m)g = Ma
If the blocks move with uniform speed, then a = 0
∴ F - 2µ_k. mg - µ_k(m + M)g = 0
or F = 2µ_k mg + µ_k(m + M)g
= µ_k[2m + m + M]g

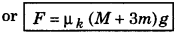
Question 6. 
A car of mass 1000 kg is moving on a horizontal circular path of radius 200 m, with uniform speed of 30 ms^-1. What should be the force of friction to provide centripetal force. What should be coefficient of friction for this? (g = 9.8 ms^-2).
Solution:
Given: m = 1000 kg; r = 200 m; v = 30 ms^-1, µ_s = ?; f_s = ?; g = 9.8ms^-2
Required centripetal force for turning on the turn,
F_c = \(\frac{m v^2}{r}=\frac{1000 \times 30 \times 30}{200}\) = 500 x 3 x 3
= 4500N
∵ Centripetal force is provided by force of friction.
∴ Force of friction f_s = 4500N
∵ f_s = µ_sR = µ_s.mg
∴ µ_s = \(\frac{f_s}{m g}=\frac{4500}{1000 \times 9.8}=\frac{45}{98}\)
or µ_s = 0.459 ≈ 0.46

Question 7.
A particle slips from the top of a big smooth sphere of radius r. The sphere is placed on the ground. At what height from the ground will the particle leave the surface of the sphere?
Solution:
Suppose, the particle leaves the sphere at point P the angle ∠AOP = θ
At point P, the net centripetal force acting on particle,
F_c = mg cosθ - N
But F_c = \(\frac{m v^2}{r}\)
∴ mg cosθ - N = \(\frac{m v^2}{r}\) ..........................(1)
Here v is the velocity of the particle at P.

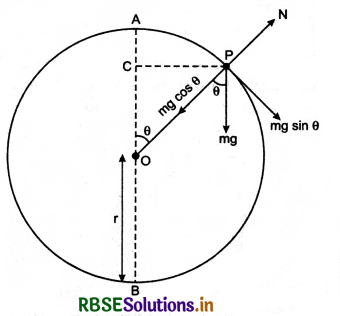
When particle will leave the sphere at P, then N will become zero i.e. N = 0
∴ From equation (1),
mg cosθ = \(\frac{m v^2}{r}\) ....................(2)
or mgr cosθ = mv²
or \(\frac{1}{2}\) mgr cosθ = \(\frac{1}{2}\) mv² .........................(3)
On slipping from A to P, the vertical height covered by the particle,
AC = AO - OC = r - r cosθ
∴ Decrease in potential energy
∆Ep = mg.AC = mg(r - r cosθ)
or ∆Ep = mgr(1 - cosθ) ..........................(4)
This loss in potential energy is converted in kinetic energy.
∴ ∆Ep = \(\frac{1}{2}\)mv²
or mgr(1 - cosθ) = \(\frac{1}{2}\)mgr.cosθ
or 2(1 - cosθ) = cosθ
or 2 - 2cosθ = cosθ
or 2 = cosθ + 2cosθ = 3 cosθ
∴ cosθ = \(\frac{2}{3}\)
∴ Height of point P from the ground,
BC = BO + OC
= r + r cosθ = r(1 + cosθ)

Question 8.
On the surface of a smooth inverted cone, a particle makes a horizontal circle. The height of the plane of the circle from the vertex of the cone is 9.8 cm. Find the speed of the particle. (g = 9.8 ms^-2).
Solution:
Suppose, the particle P is in motion in an inverted cone. Velocity of the particle is v and radius of its circular path is r. In equilibrium, the horizontal component R cosθ of normal reaction R, provides the require centripetal force \(\frac{m v^2}{r}\) and its vertical component Rsinθ balances the weight mg of the particle.

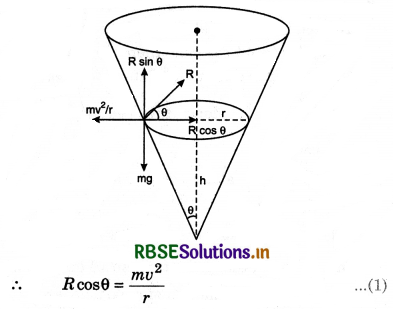
and R cosθ = mg ...........................(2)
on dividing equation (2) by (1), we get
tanθ = \(\frac{r g}{v^2}\) ...........................(3)
If the vertical height of plane of circular path for the vertex of the cone be h, then
tanθ = \(\frac{r}{h}\) ..........................(4)
Now equating equations (3) and (4), we have,

Questions for Competitive Examinations

Objective Type Questions

Question 1.
The maximum value of force F which when applied on the block it does not move is:
(a) 20N
(b) 10N
(c) 12N
(d) 15N

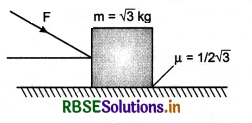
Solution:
Indicator diagram of the bock are given below:
For vertical equilibrium of the block,
N = mg + F sin 60° = \(\sqrt{3}\) g+F \(\frac{\sqrt{3}}{2}\) ............................(1)
For horizontal equilibrium, force of friction,
f ≥ F cos 60°
or µ.N ≥ F cos 60°
or µ(\(\sqrt{3}\) g + \(\frac{\sqrt{3}}{2}\) F) ≥ \(\frac{F}{2}\)

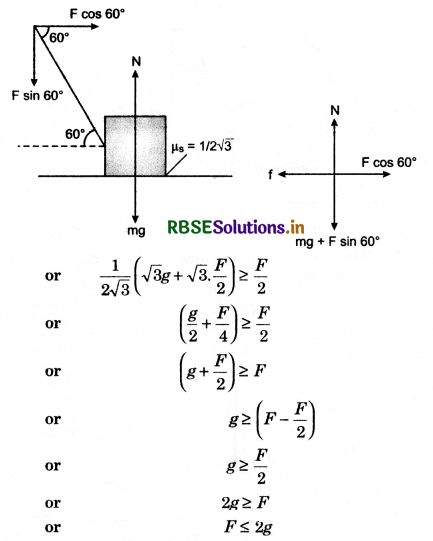
In limiting friction,
F = 2g = 2 x 10 = 20
or F = 20N
Thus option (a) is correct.

Question 2.
A stone, tied to one end of a string of length l, is rotated in horizontal circle. If the stone completes 22 cycles in 44 seconds, then the magnitude and direction of acceleration of stone will be.
(a) \(\frac{\pi^2}{4}\) ms^-2, along the radius towards the centre.
(b) π² ms^-2, along the radius away from the centre.
(c) π² ms^-2, along the radius towards the centre.
(d) π² ms^-2, along the tangential direction.
Solution:
r = 1m, frequency n = \(\frac{22}{44}=\frac{1}{2}\) c.s^-1
∴ Angular velocity ω = 2πn = 2π x \(\frac{1}{2}\) = π rad.s^-1
∴ Centripetal acceleration,
a_c = rω² = 1 x π² = π² ms^-2
or a_c = π² ms^-2 (along the radius towards centre)
Hence option (c) is correct.

Question 3.
Uniform circular motion of a particle is:
(a) Simple harmonic motion but not periodic motion
(b) Simple harmonic motion and periodic motion
(c) Neither periodic motion nor simple harmonic motion
(d) Periodic but not simple harmonic motion.
Solution:
The motion of particle is periodic and simple harmonic.
∴ Option (b) is correct.

Question 4.
On a hemi-spherical surface, an insect crowls upwards (figure). Coefficient of friction between insect and the surface is \(\frac{1}{3}\). If the line joining the centre of spherical surface and insect makes an angle α with vertical direction, then the maximum posiible value of a will be obtained by:

(a) cotα = 3
(b) tanα = 3
(c) secα = 3
(d) cosecα = 3
Solution:
For equilibrium,
N = mg cosα ...........................(1)
and µs.N = mg sinα ......................(2)
On dividing equation (1) by (2), we have,
cot α = \(\frac{1}{\mu_s}=\frac{1}{1 / 3}\) = 3

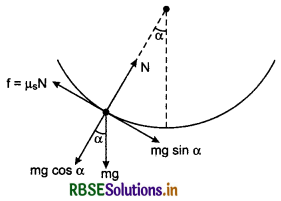
or cot α = 3
Thus option (a) is correct.

Question 5.
A block of mass m is at rest under the action force F against a wall as shown in figure. Which of the following statement is correct?

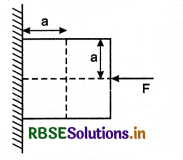
(a) f = mg, where f is a friction al force
(b) F = N, where N is the normal reaction
(c) F will not produce any torque
(d) N will produce a torque
Solution:
This equilibrium of planar equilibrium; therefore
∑F_x = 0
∴ F = N
∑F_y = 0
∴ f = mg
⇒ ∑τ_c = 0
or \(\overrightarrow{\tau_N}+\overrightarrow{\tau_F}\) = 0
∴ \(\overrightarrow{\tau_N}\) ≠ 0 and \(\overrightarrow{\tau_F}\) ≠ 0
Hence option (d) is correct. 

Question 6.
A disc rolling without slipping on horizontal surface (figure) C is the centre of the disc and P and Q are to equidistant point from C. If velocities of P,Q and C are V_P, V_Q and V_C respectively, then

(a) V_Q > V_C > V_P
(b) V_Q < V_C < V_P
(c) V_Q = V_P ,V_C = \(\frac{1}{2}\)V_P
(d) V_Q < V_C < V_P
Solution:
In the given diagram, in the situation of rolling point O will be the point of zero velocity. For any point on disc u = rω where r is distance of the point from O.
∵ r_Q > r_C > r_P
∴ v_Q > v_C > v_P
Hence option (a) is correct.

Question 7.
A particle is moving on circular path with acceleration a. If its velocity is doubled then the ratio of final and initial accelerations will be:
(a) 1 : 4
(b) \(\frac{1}{4}\) : 1
(c) 2 : 1
(d) 4 : 1
Solution:
a₁ = \(\frac{v^2}{r}\) and a₂ = \(\frac{(2 v)^2}{r}=\frac{4 v^2}{r}\) = 4a,
∴ \(\frac{a_2}{a_1}=\frac{4}{1}\) or a₂ : a₁ = 4 : 1
Hence option (d) is correct.

Question 8.
A bucket full of water is rotated in vertical circle of radius 4 m such that even at highest point of the path, water does not fall of the bucket. The maximum time of one revolution is:
(a) 1s
(b) 2s
(c) 3s
(d) 4s

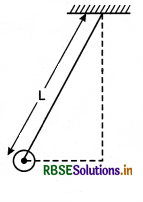
Solution:
T = \(\frac{2 \pi r}{v_c}=\frac{2 \pi r}{\sqrt{r g}}=2 \pi \sqrt{\frac{r}{g}}=6.28 \sqrt{\frac{4}{9.8}}\)
or T = 4.01 = 4 sec
Option (d) is correct.

Question 9.
Mass of a ball is 0.5 kg and it is hanging from one end of a cord of length 0.5 m. The ball is rotated about vertical axis in horizontal circle. If the cord can withstand maximum tension of 324 N, what will be possible maximum angular velocity of the ball?
(a) 9 rad.s^-1
(b) 18 rad.s^-1
(c) 27 rad.s^-1
(d) 36 rad.s^-1
Solution:
As is shown in firgure, vertical component T cosθ of tension balances the weight mg of bob and horizontal component T sinθ provides the required centripetal force.
∴ T cosθ = mg ...........................(1)
and T sinθ = mrω² ........................(2)
∴ ω² = \(\frac{T \sin \theta}{m r}\)

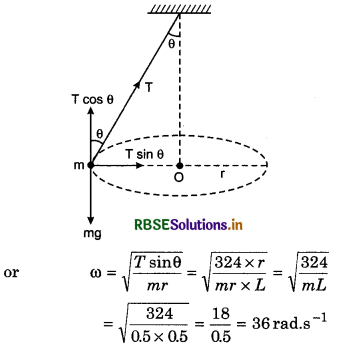
Thus option (d) is correct.

Question 10.
A block of mass m is placed on a inclined plane of inclination angle θ with horizontal. Coefficient of friction between block and plane is µ. tanθ > µ is kept. The block is kept stationary by applying force P parallel to plane. Direction of force P is taken positive in upward direction. When P is changed from P₁ = mg(sinθ - µ cosθ) to P₂ = mg(sinθ + µ cosθ), then the graph between force of friction f and P will represented by:

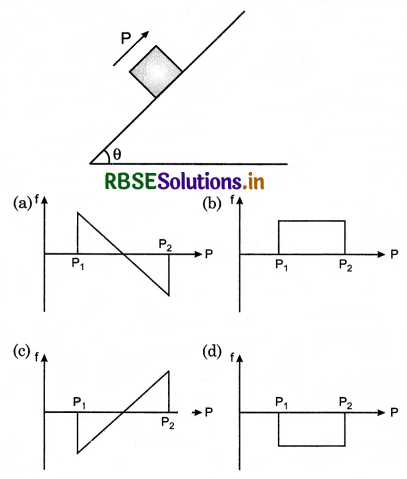
Solution:
Limiting friction on the block,
f = µ.R = µmg cosθ

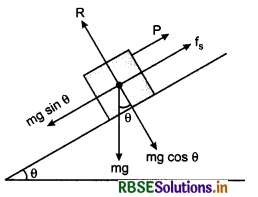
Initially the force of friction is upwards.
∴ P + f = mg sinθ
or f = mg sinθ - P
or µmg cosθ = mg sinθ - P
∴ P = (mg sinθ - µmg cosθ)
As force P changes from (mg sinθ - mgcosθ) to (mgsinθ + µmgcosθ), the value of f changes from µmgcosθ to -µmgcosθ. Therefore graph (a) is correct.

Question 11.
By bending a wire, it is given a shape of parabola y = Kx² (y-axis is vertical). A bead of mass m is on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola, when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the equilibrium position of the bead, where the bead can stay at rest w.r.t. the wire from the Y-axis is:

Solution:
macosθ = mg cos(90° - θ)
or acosθ = g sinθ
or \(\frac{a}{g}\) = tanθ

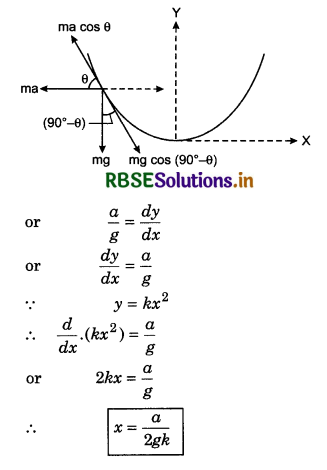
Thus option (b) is correct.

Question 12.
Two particles of mass m each are tied with the ends of light string of length 2a. This whole system is placed on a frictionless table such that the cord held tight and each particle is at a distance ‘a’ from the centre of the cord (figure). Now the mid-point of the cord is pulled vertically upwards with a small but constant force F. As a result the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x is:

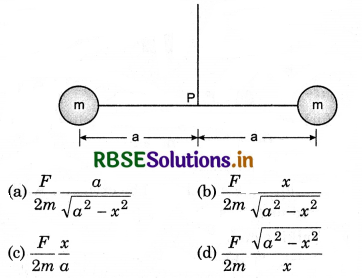
Solution:
Suppose, when the distance between the particles is 2x, then the tension of each string is T.
Therefore
2T sinθ = F ..........................(1)
and T cosθ = max .......................(2)

∴ Vertical acceleration ay is negligible. Therefore acceleration of each particle can be taken as a_x. Thus option (b) is correct.

Question 13.
A mass m is hung by a cord wraped over a pulley on bearing. Mass of pulley is m and its radius is R. Assume that pulley is a uniform circular disc. If the cord does not slip on the pulley then the acceleration of the mass will be:
(a) \(\frac{3g}{2}\)
(b) g
(c) \(\frac{2g}{3}\)
(d) \(\frac{g}{3}\)
Solution:
For the motion of the block
mg - T = ma ....................(1)
For rotation of pulley,
τ = T.R = Iα

Thus option (c) is correct.

Question 14.
A mass M attached with a horizontal spring is executing simple harmonic motion of amplitude A₁. When mass m passes through its mean position, a small mass m is placed on it, then amplitude of vibrations become A₂. Ratio \(\frac{A_1}{A_2}\) is:

Solution:
In mean position F_ext = 0
According to law of conservation of linear momentum
mv₁ = (M + m)v²
∵ v = Aω
∴ MA₁ω₁ = (M + m)A₂ω₂
But ω₁ = \(\sqrt{\frac{K}{M}}\) and ω₂ = \(\sqrt{\frac{K}{(M+m)}}\)

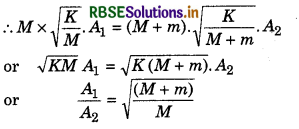
∴ Option (d) is correct.

Question 15.
A pulley of radius 2 m rotates about its axis on applying a tangential force F = (20t - 5t)² N. Where t is measured in seconds. If the moment of inertia of pulley about its axis is 10 kg.m², then on reversing the direction of motion of the pulley, the cycles completed by the pulley is:
(a) less than 3
(b) more than 3 but less than 6
(b) more than 3 but less than 6
(c) more than 6 but less than 9
(d) more than 9
Solution:
Force F = 20t - 5t²
∵ Torque τ = Iα = F.R
∴ α = \(\frac{F \cdot R}{I}=\frac{\left(20 t-5 t^2\right) \times 2}{10}\)
or α = 4t - t²
or \(\frac{d \omega}{d t}\) = 4t - t²
or dω = (4t - t²).dt
On integrating both sides,

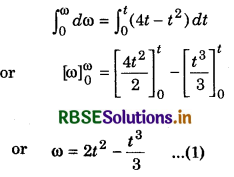
When direction is reversed, then ω = 0

or θ = 144 - 108 = 36 rad
or θ = 36 rad
∴ Number of rotation n = \(\frac{\theta}{2 \pi}=\frac{36}{2 \pi}=\frac{18}{314}\)
or n < 6
Hence option (b) is correct.

Question 16.
The pulley and string shown in figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle θ should be:

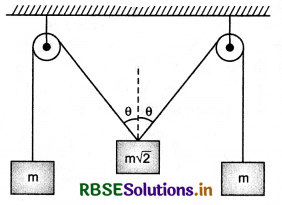
(a) 0°
(b) 30°
(c) 45°
(d) 60°
Solution:
In equilibrium of the system
T = mg
and 2T cosθ = m\(\sqrt{2}\).g

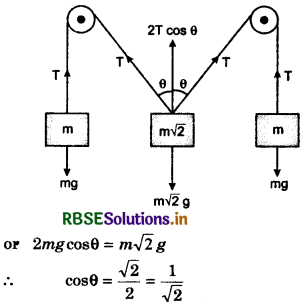
⇒ θ = 45°
Thus option (c) is correct.

Question 17.
Which of the following statements is not based on Newton’s third law of motion?
(a) Flight of jet plane
(b) Taking hands backward by cricketer while holding the catch
(c) Walking on floor
(d) Recoil of rubber ball
Solution:
A cricketer pulls his hands backward while holding the catch to minimise the impulse imapred on hands. On doing so, the     time interval increases, therefore the force on hands decreases.
Thus option (b) is correct.

Question 18.
An object is slipping on a rough inclined plane of inclination angle 45°. The time taken by the object on this plane is n times the time taken by the object in slipping on smooth inclined plane of inclination angle 45°. Coefficient of friction of rough plane its:

Solution:
On smooth inclined plane,
S = \(\frac{1}{2}\)g sinθ.t² ............................(1)
On rough inclined surface,

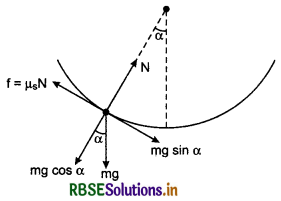
Hence option (a) is correct.

Question 19.
A machine-gun fires the bullet of mass 40 g with velocity of 1200 ms^-1. A man holding the machine-gun can apply maximum force of 144 N on machine. Maximum number of bullets fired by the gun will be:
(a) Only one
(b) Three
(b) Unlimited number of bullets canbe fired
(c) 144 x 48
Solution:
Suppose n bullets can be find per second by machine-gun. Therefore according to Newton's second law of motion:

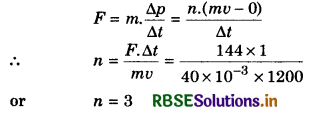
Thus option (b) is correct.

Question 20.
A hall of mass 0.1 kg is thrown vertically upwards by applying force by hand. If hand moves by 0.2 m while applying force, and ball goes upward by 2 m more, then magnitude of force will be:
(a) 16 N
(b) 20 N
(c) 22 N
(d) 4 N
Solution:
The situation of throwing the ball is shown in the figure. Force is applied on the ball by hand from P to A and from A to B. The ball moves under the influence of force applied. The acceleration from P to A is a (supposed to constant) and is in vertical direction. At point A, the velocity is u, then

v² = u² + 2as
or v² = 0 + 2a x 0.2
or v² = 0.4a .........................(1)
For A to B again from same equation
v² = u² + 2as
0 = v² - 2g x 2
or v² = 4g .............................(2)
From equations (1) and (2)
0.4 a = 49
∴ a = \(\frac{4 g}{0.4}\) = 10 x 10 = 100 ms^-2
or a = 100 ms^-2
If F be the force applied by hand on the ball, then equation of motion of the ball,
F - mg = ma
or F = ma + mg = m(a + g)
= 0.2(100 + 10)
= 0.2 x 110
or F = 22N

Thus option (c) is correct.

Question 21.
A particle is moving uniformly on a circular path of radius R. Acceleration \(\vec{a}\) of the particle at point P (R, 0) where θ is the angle of radius vector with X-axis, is:

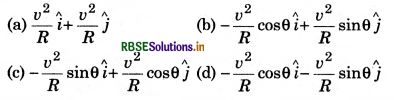
Solution:
Centripetal acceleration at point P,
a_c = _{\(\frac{v^2}{R}\)} (in PO direction)
If we take the co-ordinate system as shown in figure, then on resolving this acceleration in two components a_x and a_y then

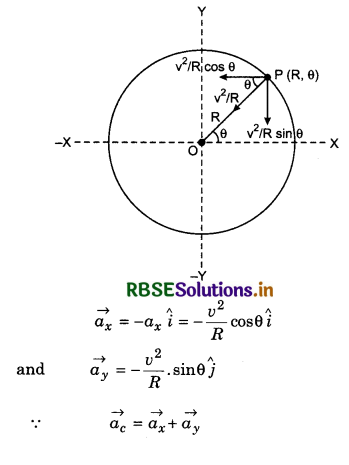
∴ \(\overrightarrow{a_c}=-\frac{v^2}{R} \cos \theta . \hat{i}-\frac{v^2}{R} \sin \theta . \hat{j}\)
Therefore option (d) is correct.

Question 22.
A point P revolves on a circular path of radius 20 m figure. The motion of P covers the distance S = t³ + 5, where S is measured in metres and t in seconds. When t = 2 s, then acceleration of particle P is nearly: 

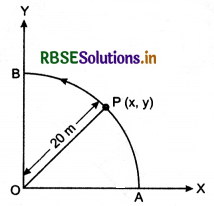
(a) 14 ms^-2
(b) 13 ms^-2
(c) 12 ms^-2
(d) 7.2 ms^-2
Solution:
Distance covered by point P
S = t³ + 5
∴ Speed v = \(\frac{d S}{d t}=\frac{d}{d t}\)[t³ + 5]
or v = 3t²
Speed of point P at t = 2s,
v = 3 x (2)² = 12 ms^-1
∴ Tangential acceleration.

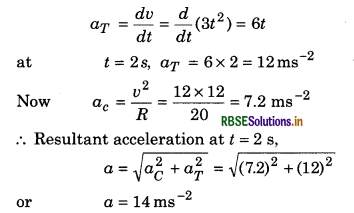
∴ Option (a) is correct.

Question 23.
A bob of mass M is suspended by a massless spring of length L. The horizontal velocity at A is just sufficient to send the bob at B. If the speed of the bob is half of that at A in position of θ deflection, then the relation satisfied will be:

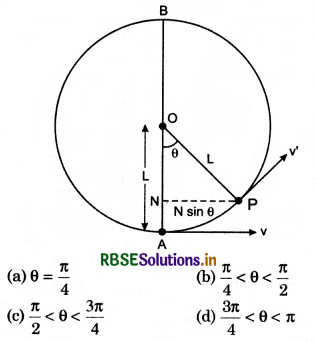
Solution:
According to law of conservation of energy
\(\frac{1}{2} m v^2=\frac{1}{2} m\left(\frac{v}{2}\right)^2\) + mg(L - Lcosθ)
or v² = \(\frac{v^2}{4}\) + 2gL(1 - cosθ)

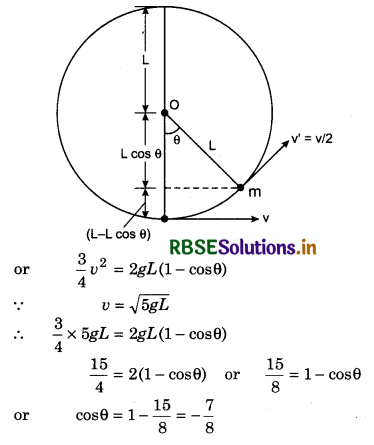
⇒ \(\frac{3 \pi}{4}<\theta<\pi\)
Hence option (d) is correct.

Question 24.
A rocket of mass 500 kg is ready for vertical firing out. Let speed is 800 ms^-1. How much gas per second it should release to obtain thrust to provide initial vertical acceleration of 20 ms^-2?
(g = 10 ms^-2)
(a) 127.5 kg.s^-1
(b) 18.75 kgs^-1
(c) 185.55 kg.s^-1
(d) 137.5 kg.s^-1
Solution:
m = 500 kg; u₀ = 800 ms^-1; a = 20 ms^-2

This option (b) is correct.

Question 25.
A car of mass m is moving on circular plane path. If coefficient of friction between road and tyres is µs, then what will be maximum rotational speed of the care?

Solution:
For safe turn on the circular path, centripetal force = friction force

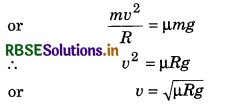
∴ Option (d) is correct.

Question 26.
Two cars of mass m₁ and m₂ are moving on circular path of radii r₁ and r₂ .Their speed is such that they complete circular path in same time t. Ratio of their centripetal acceleration is:
(a) m₁r₁ : m₂r₂
(b) m₁ : m₂
(c) r₁ : r₂ 
(d) 1 : 1
Solution:
Since the time periods of cars are same, therefore their angular velocities will also be same.
∵ Centripetal acceleration a = rω²
∴ \(\frac{a_1}{a_2}=\frac{r_1 \omega^2}{r_2 \omega^2}=\frac{r_1}{r_2} \quad \text { or } \quad \frac{a_1}{a_2}=\frac{r_1}{r_2}\)
∴ Option (c) is correct.

Question 27.
Three bodies of mass m, 2m and 3m are connected with strings as shown in figure. When a force F is applied on mass m in vertical direction, then the system raises up with velocity v. What is magnitude of force acting on mass 2 m?

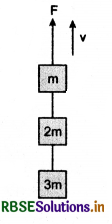
Where g = gravitational acceleration.
(a) Zero
(b) mg
(c) 3 mg
(d) 6 mg
Solution:
The system is moving with uniform velocity. Therefore acceleration will be zero. Hence the apparent force will be zero. Thus option (a) is correct