RBSE Class 11 Physics Important Questions Chapter 4 समतल में गति

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 4 समतल में गति Important Questions and Answers.

RBSE Class 11 Physics Chapter 4 Important Questions समतल में गति

बहुचयनात्मक प्रश्न:

प्रश्न 1. 
यदि सदिश \(\vec{A}\) की दिशा में एकांक सदिश  \(\hat{n}\) है, तो:

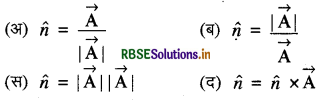
संकेत: एकांक सदिश =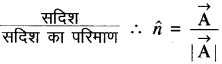
अतः सही विकल्प (अ) है।
उत्तर:
\(\text { (अ) } \hat{n}=\frac{\overrightarrow{\mathrm{A}}}{|\overrightarrow{\mathrm{A}}|}\)

 

प्रश्न 2. 
\(\hat{i}+2 \hat{j}+\hat{k}\) के अनुदिश एकांक सदिश होगा:

अतः सही विकल्प (स) है।
उत्तर:
\(\text { (स) } \frac{\hat{i}+2 \hat{j}+\hat{k}}{\sqrt{6}}\)

प्रश्न 3. 
एक बिन्दु पर तीन बल एक साथ लग रहे हैं। दो बल \(\overrightarrow{\mathrm{P}}, \overrightarrow{\mathrm{Q}}\)
क्रमश: \((2 \hat{i}-3 \hat{j})\) व \((\hat{i}-\hat{j})\) हैं। यदि वस्तु साम्यावस्था में है
तो तीसरा कौन होगा:

अतः सही विकल्प (ब) है।
उत्तर:
\(\text { (ब) }-3 i+4 j\)

प्रश्न 4. 
2 व 3 न्यूटन के दो बल किसी कण पर परस्पर लम्बवत् लग रहे हैं। इनका परिणामी बल 3 न्यूटन के बल के साथ कोण बनायेगा:
(अ) 2/3
(ब) tan^-1 (2/3)
(स) 3/2
(द) tan^-1 (3/2)
संकेत - जब \(\overrightarrow{\mathrm{p}}\) और \(\overrightarrow{\mathrm{Q}}\) परस्पर लम्बवत् दिशा में हों और परिणामी बल \(\overrightarrow{\mathrm{Q}}\) के साथ α कोण बनाता हो, तब

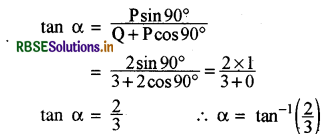
अतः सही विकल्प (ब) है।
उत्तर:
\(\text { (ब) } \tan ^{-1}\left(\frac{2}{3}\right)\)

प्रश्न 5. 
यदि A_x तथा A_y किसी सदिश के घटक हैं तो उस सदिश का परिमाण होगा:
(अ) A_x + A_y
(ब) A_x² + Ay²
(स) (A_x + A_Y)²

\(\text { (द) }\left(\frac{r_1}{r_2}\right)^2\)

संकेत-हम जानते हैं- \(\overrightarrow{\mathrm{A}}=\mathrm{A}_x \hat{i}+\mathrm{A}_y \hat{j}\)
\(|\overrightarrow{\mathrm{A}}|=\sqrt{\mathrm{A}_x^2+\mathrm{A}_y^2}\)
अतः सदिश का परिमाण \(\sqrt{A_x^2+A_y^2}\) होगा।
अतः सही विकल्प (द) है।
उत्तर:
\(\text { (द) }\left(\frac{r_1}{r_2}\right)^2\)

प्रश्न 6. 
एक कण के वेग के घटक निम्न प्रकार हैं:
vx = (5t) मी./से., Vy = (7t) मी./से.
कण के त्वरण का मान है:
(अ) 12
(ब) \(\sqrt{74}\)
(स) 2
(द) शून्य
संकेत:
त्वरण \(a=\sqrt{\left(\frac{d v_x}{d t}\right)^2+\left(\frac{d v_y}{d t}\right)^2}=\sqrt{(5)^2+(7)^2}=\sqrt{74}\)
अतः विकल्प (ब) है।
उत्तर:
 (ब) \(\sqrt{74}\)

प्रश्न 7. 
एक हाथ घड़ी की मिनट वाली सुई का कोणीय वेग (रे/ से.) में है:

हल- मिनट वाली सुई 1 घंटे में अर्थात् 3600 से. में एक चक्कर पूर्ण करती है अर्थात् 2π  कोण से विस्थापित होती है।
∴ कोणीय वेग = 2π/3600
अर्थात् π/1800 रे/से.
अतः सही विकल्प (अ) है।
उत्तर:
\(\text { (अ) } \frac{\pi}{1800}\)

प्रश्न 8. 
समान द्रव्यमान के दो कण r1 व r2 त्रिज्या के वृत्ताकार पथों पर समान चाल से गति कर रहे हैं। उनके अभिकेन्द्रीय बलों का अनुपात होगा:

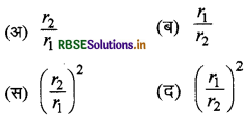
संकेत:
F1 = mv²/r₁ F2 = mv²/r₂
द्रव्यमान व चाल समान हैं।
∴ F1/F2 = r₂/r₁ होगा।
अतः सही विकल्प (अ) होगा।
उत्तर:
\(\text { (अ) } \frac{r_2}{r_1}\)

प्रश्न 9. 
एक प्रक्षेप्य की अधिकतम ऊँचाई पर चाल उसकी प्रारम्भिक चाल u की आधी है। प्रक्षेप्य की क्षैतिज परास है:

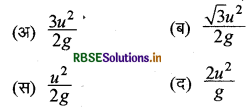
संकेत- अधिकतम ऊँचाई पर प्रक्षेप्य वेग
V = u cos θ
u/2 = u cos θ
1/2 = cos θ
∴ θ = 60°
क्षैतिज परास \(\mathrm{R}=\frac{u^2 \sin 2 \theta}{g}=\frac{u^2 \sin 120^{\circ}}{g}\)

\(\mathrm{R}=\frac{\sqrt{3} u^2}{2 g}\) ∴ \(\sin 120^{\circ}=\frac{\sqrt{3}}{2}\)
अतः सही विकल्प (ब) है।
उत्तर:
\(\text { (ब) } \frac{\sqrt{3} u^2}{2 g}\)

प्रश्न 10. 
किसी प्रक्षेप्य का पथ होता है:
(अ) सरलरेखीय
(ब) परवलयिक
(स) दीर्घवृत्तीय
(द) अतिपरवलयिक
उत्तर:
(ब) परवलयिक

प्रश्न 11. 
समान परास के लिए एक पिण्ड को समान चाल से कितनी दिशाओं में (कोणों पर) प्रक्षेपित किया जा सकता है:
(अ) 2 
(ब) 3
(स) 4
(द) 1
हल:
परास \(\mathrm{R}=\frac{u^2 \sin 2 \theta}{g}\)
sin 2θ = sin (π  - 2θ)
 प्रक्षेपण कोण θ या \(\frac{\pi-2 \theta}{2}=\left(\frac{\pi}{2}-\theta\right)\) पर परास समान होगी।
अतः सही विकल्प (अ) है।
उत्तर:
(अ) 2 

प्रश्न 12. 
एकसमान वर्तुल गति में:
(अ) वेग व त्वरण, दोनों परिवर्तित होते हैं।
(ब) वेग व त्वरण दोनों नियत होते हैं।
(स) वेग नियत रहता हैं व त्वरण परिवर्तित होता है।
(द) त्वरण नियत रहता है व वेग परिवर्तित होता है। 
उत्तर:
(अ) वेग व त्वरण, दोनों परिवर्तित होते हैं।

रिक्त स्थानों की पूर्ति कीजिए: 

प्रश्न 1. 
जड़त्व आघूर्ण प्रतिबल, विद्युतशीलता तथा चुम्बकशीलता .......................... राशियाँ हैं।
उत्तर:
सदिश

प्रश्न 2.
बल आघूर्ण, कोणीय वेग, कोणीय संवेग वे सदिश राशियाँ पेंच नियम द्वारा तय की हैं, जिनकी दिशा .........................  जाती है।
उत्तर:
दक्षिणावर्त 

प्रश्न 3.
cos² α + cos² β + cos² γ = ....................
उत्तर:
1

प्रश्न 4.
तीन असमतलीय सदिशों का परिणामी सदिश ........................... नहीं हो सकता है।
उत्तर:
शून्य

प्रश्न 5.
किसी वस्तु के अधिकतम क्षैतिज परास के लिए प्रक्षेप्य कोण θ ........................ होना चाहिए।
उत्तर:
45°

प्रश्न 6.
अधिकतम ऊँचाई Hmax .....................  होती है।
उत्तर:
1/2 Rmax

प्रश्न 7.
एक प्रक्षेप्य का पथ ......................... होता है।
उत्तर:
परवलयाकार

प्रश्न 8.
प्रक्षेप्य का उड्डयन काल T = ........................
उत्तर:
2 sin 6

प्रश्न 9.
R त्रिज्या के एक वृत्ताकार पथ में नियत चाल से गति कर रहे कण का स्पर्श रेखीय त्वरण .......................... होता है। 
उत्तर:
 शून्य
 
प्रश्न 10.
समान परास के लिए एक पिण्ड को समान चाल से ................. दिशाओं में (कोणों पर प्रक्षेपित किया जा सकता है। 
उत्तर:
2

नीचे दिये गये वाक्यों में सत्य / असत्य कथन का चयन कीजिए:

प्रश्न 1.
विस्थापन सदिश सदैव प्रारम्भिक व अन्तिम स्थितियों के बीच न्यूनतम दूरी वाले पथ की ओर इंगित होता है।
उत्तर:
सत्य

प्रश्न 2.
समान वेग से गतिशील कण का त्वरण सदिश शून्य सदिश नहीं होता है।
उत्तर:
असत्य

प्रश्न 3.
परिणामी सदिश R का परिणाम \(\mathrm{R}=\sqrt{\mathrm{P}+\mathrm{Q}+2 \mathrm{PQ} \cos \theta}\) होता है
उत्तर:
असत्य

प्रश्न 4.
क्षैतिज गति करते हुए हवाई जहाज से गिराये गति प्रक्षेप्य गति का उदाहरण है।
उत्तर:
सत्य

प्रश्न 5.
मूल बिन्दु से गुजरने वाले परवलय का व्यापक समीकरण गये बम की y = ax - bx³ होता है।
उत्तर:
असत्य

प्रश्न 6.
एक समान चाल वाले प्रक्षेप्यों में θ = 40° और θ = 50° दोनों स्थितियों में परास समान प्राप्त नहीं होते हैं।
उत्तर:
असत्य

प्रश्न 7.
अधिकतम परास के लिए θ = 45° होना चाहिए।
उत्तर:
सत्य

प्रश्न 8.
सदिश परिणामी \(\overrightarrow{\mathrm{R}}\) के मध्य कोण \(\alpha=\tan ^{-1}\left(\frac{Q \sin \theta}{P+Q \cos \theta}\right)\) होता है।
उत्तर:
सत्य

प्रश्न 9.
अधिकतम परास R = U/g होता है।
उत्तर:
असत्य

प्रश्न 10.
किसी कागज पर चींटी की गति समतल में गति है।
उत्तर:
सत्य

कॉलम - A से कॉलम B का सही मिलान कीजिए:

प्रश्न 1. 
 

कॉलम-A	कॉलम-B
किसी बिन्दु P पर स्थित कण का रिथति सदिश \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\) तब सदिश का परिणाम \(|\vec{r}|=\)	(A) न्यूनतम
किसी सदिश को उसके परिमाण व एकांक सदिश के गुणनफल के रूप में व्यक्त किया जा सकता है तब \(\overrightarrow{\mathrm{A}}=\)	(B) 45°
के विपरीत दिशा में होने पर \(\overrightarrow{\mathrm{R}}\) का परिमाण होता है	(C) V2/R2
4. किसी सदिश के तीनों दिक्-कोज्या के वर्गों का योग सदैव है।	(D) \(\sqrt{x^2+y^2+z^2}\)
5. प्रक्षेप्य की परास \(\mathrm{R}=\frac{u^2 \sin 2 \theta}{g}\) में अधिकतम परास के लिए θ का मान है	(E) \(\hat{n}|\overrightarrow{\mathrm{A}}|\)
6. अभिकेन्द्री त्वरण का मान होता है।	(F) स्पर्शी
7. \(\overrightarrow{\mathrm{A}}=\mathrm{A}_x \hat{i}+\mathrm{A}_y \hat{j}+\mathrm{A}_z \hat{k}\) तब \(|\mathrm{A}|\) का मान होगा	(G) \(\frac{d v}{d t}\)
8. तात्क्षणिक त्वरण a =	(H)  1
9. प्रक्षेप्य की अधिकतम ऊँचाई व अधिकतम परास में क्या सम्बन्ध है?	(I) \(|\mathrm{A}|=\sqrt{\mathrm{A} x^2+\mathrm{A} y^2+\mathrm{A} z^2}\)
10. वेग सदिश सदैव गति के पथ के होता है।	(J) \(\mathrm{H}_{\max }=\frac{1}{2} \mathrm{R}_{\max }\)

उत्तर:
 

कॉलम-A	कॉलम-B
किसी बिन्दु P पर स्थित कण का रिथति सदिश \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\) तब सदिश का परिणाम \(|\vec{r}|=\)	(D) \(\sqrt{x^2+y^2+z^2}\)
किसी सदिश को उसके परिमाण व एकांक सदिश के गुणनफल के रूप में व्यक्त किया जा सकता है तब \(\overrightarrow{\mathrm{A}}=\)	(E) \(\hat{n}|\overrightarrow{\mathrm{A}}|\)
के विपरीत दिशा में होने पर \(\overrightarrow{\mathrm{R}}\) का परिमाण होता है	(A) न्यूनतम
4. किसी सदिश के तीनों दिक्-कोज्या के वर्गों का योग सदैव है।	(H) 1
5. प्रक्षेप्य की परास \(\mathrm{R}=\frac{u^2 \sin 2 \theta}{g}\) में अधिकतम परास के लिए θ का मान है	(B) 45°
6. अभिकेन्द्री त्वरण का मान होता है।	(C) V2/R2
7. \(\overrightarrow{\mathrm{A}}=\mathrm{A}_x \hat{i}+\mathrm{A}_y \hat{j}+\mathrm{A}_z \hat{k}\) तब \(|\mathrm{A}|\) का मान होगा	(I) \(|\mathrm{A}|=\sqrt{\mathrm{A} x^2+\mathrm{A} y^2+\mathrm{A} z^2}\)
8. तात्क्षणिक त्वरण a =	(J)  \(\mathrm{H}_{\max }=\frac{1}{2} \mathrm{R}_{\max }\)
9. प्रक्षेप्य की अधिकतम ऊँचाई व अधिकतम परास में क्या सम्बन्ध है?	(G) \(\frac{d v}{d t}\)
10. वेग सदिश सदैव गति के पथ के होता है।	(F) स्पर्शी

 

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
क्या सदिशों के घटाने में क्रम विनिमय का नियम लगता है?
उत्तर:
नहीं।

प्रश्न 2. 
सदिश संयोजन का त्रिभुज नियम लिखिये।
उत्तर:
इस नियम के अनुसार यदि दो सदिशों को परिमाण व दिशा त्रिभुज की दो क्रमागत भुजाओं से समान क्रम में निरूपित करें तो त्रिभुज की तीसरी भुजा विपरीत क्रम में परिमाण व दिशा में परिणामी सदिश को प्रदर्शित करती है।
\(\vec{R}=\vec{P}+\vec{Q}\)

प्रश्न 3. 
क्या अदिश राशि का परिमाण चयन किये गये निर्देश तन्त्र पर निर्भर करता है?
उत्तर:
नहीं।

प्रश्न 4. 
क्या सदिश राशि के घटक चयन किये गये निर्देश तन्त्र पर निर्भर करते हैं?
उत्तर:
हाँ।

प्रश्न 5. 
दो सदिशों का योग कब अधिकतम तथा कब न्यूनतम होता है?
उत्तर:
जब दोनों एक ही दिशा में हों, जब दोनों विपरीत दिशाओं में

प्रश्न 6. 
क्या तीन सदिश राशियों को इस प्रकार जोड़ा जा सकता है कि उनका परिणामी सदिश शून्य हो?
उत्तर:
हाँ, यदि उन्हें परिमाण व दिशा में किसी त्रिभुज की चक्रीय क्रम से ली गई भुजाओं द्वारा निरूपित किया जा सके।

प्रश्न 7. 
यदि किसी वेक्टर À को स्केलर m से गुणा किया जाये तो परिणामी वेक्टर क्या होगा?
उत्तर:
mA

प्रश्न 8. 
क्या एक अदिश और एक सदिश राशि को जोड़ा जा सकता
उत्तर:
नहीं। अदिश राशि में दिशा नहीं होती है जबकि सदिश राशि में दिशा होती है। अतः दोनों के जोड़ने की बीजगणित में अन्तर होता है। 

प्रश्न 9. 
यदि किसी सदिश का एक घटक (Component) शून्य हो व अन्य घटक शून्य न हो तो क्या वह सदिश शून्य हो सकता है? 
उत्तर:
नहीं।

प्रश्न 10. 
एक चींटी अपनी प्रारम्भिक स्थिति (-2 मी. 4 मी. - 3 मी.) से रेंगकर अन्तिम स्थिति (6 मी. 2 मी. -3 मी.) पर पहुँचती है। इसका विस्थापन कितना होगा?
उत्तर:

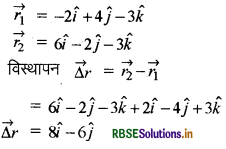
प्रश्न 11. 
क्या दो सदिशों के परिणामी सदिश का मान दिये गये सदिशों में से किसी एक सदिश के मान से कम हो सकता है?
उत्तर:
हाँ, यदि सदिशों के बीच कोण 90° से अधिक है।

प्रश्न 12. 
यदि \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}=\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{C}}\) तो क्या \(\overrightarrow{\mathrm{B}}\) तथा \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\) समान होने चाहिए ?
उत्तर:
सामान्यतः नहीं, लेकिन यदि \(\overrightarrow{\mathrm{A}} \text { व } \overrightarrow{\mathrm{B}}\) के बीच का कोण \(\vec{A} \text { व } \vec{C}\) के बीच के कोण के बराबर हो तो \(\overrightarrow{\mathrm{B}}=\overrightarrow{\mathrm{C}}\) हो सकता है।

प्रश्न 13. 
यदि \(\vec{A}-\vec{B}=\vec{A}+\vec{B}\) तो \(\overrightarrow{\mathrm{B}}\) का मान क्या होगा?
उत्तर:
\(\overrightarrow{\mathrm{A}}-\overrightarrow{\mathrm{B}}=\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\)
\(2 \vec{B}=0\)
\(\overrightarrow{\mathrm{B}}=0\)
अतः उपर्युक्त समीकरण तभी सत्य होगा जब B एक शून्य सदिश

प्रश्न 14. 
क्या यह सम्भव है कि दो सदिशों के योग और अन्तर एक ही दिशा में हों? यदि हाँ तो किस परिस्थिति में?
उत्तर:
हाँ, यह सम्भव है कि दो सदिशों के योग और अन्तर एक ही दिशा में हों। यह तब सम्भव होगा जब दोनों सदिश परिमाण में असमान परन्तु दिशा में समान हों।

प्रश्न 15. 
क्या परिमाण और दिशा दोनों रखने वाली भौतिक राशियाँ सदैव सदिश राशियाँ होती हैं?
उत्तर:
नहीं, परिमाण और दिशा दोनों रखने वाली राशियाँ सदैव सदिश राशियाँ नहीं होतीं। वे सदिश राशियाँ केवल तभी होती हैं जब वे योग के सदिश नियम अर्थात् \(\vec{A}+\vec{B}=\vec{B}+\vec{A}\) का अनुपालन करें। जैसे विद्युत धारा, समय आदि दिशा रखते हुए भी अदिश है।

प्रश्न 16. 
प्रक्षेप्य गति में जब प्रक्षेप्य कोण 6 हो तब तात्क्षणिक वेग और तात्क्षणिक त्वरण में अधिकतम और न्यूनतम कितना कोण हो सकता है?
उत्तर:
\(\frac{\pi}{2}+\theta, \frac{\pi}{2}-\theta\)

प्रश्न 17. 
हाथ की घड़ी की मिनट वाली सूई का कोणीय वेग कितना होता है?
उत्तर:
\(\frac{\pi}{1800}\)  रेडियन / सेकण्ड

प्रश्न 18. 
एक प्रक्षेप्य के तात्क्षणिक वेग के घटक Vx Vy और त्वरण के घटक ax, ay में कौन-कौनसे अवयव नियत रहते हैं? 
उत्तर:
प्रक्षेप्य गति में कोण का क्षैतिज घटक Vx नियत रहता है. जबकि वेग का ऊर्ध्वाधर घटक Vy गुरुत्वीय त्वरण के कारण परिवर्तित रहता है।
Vx = u cos  θ
a = -g और  
∴ ax, ayनियत रहेंगे।

प्रश्न 19. 
नियत चाल से वृत्तीय पथ में गति कर रहे कण के तात्क्षणिक वेग और तात्क्षणिक त्वरण की सदिश स्थिति क्या होती है? 
उत्तर:
परस्पर लम्बवत् होती है। चूंकि वृत्तीय पथ में नियत चाल से गति के कारण अभिकेन्द्रीय त्वरण उत्पन्न होता है जिसकी दिशा केन्द्र की ओर होती है।

प्रश्न 20. 
वृत्ताकार मोड़ पर साइकिल सवार ऊर्ध्वाधर से मोड़ के केन्द्र की ओर क्यों झुक जाता है?
उत्तर:
अभिकेन्द्रीय बल उपलब्ध कराने के लिये।

प्रश्न 21. 
एक फुटबॉल का खिलाड़ी गेंद को क्षैतिज से 30° के कोण पर 50 मी./से. के वेग से उछालता है तो ज्ञात कीजिये- गेंद द्वारा प्राप्त अधिकतम ऊँचाई।
उत्तर:
अधिकतम ऊँचाई H = \(\frac{u^2 \sin ^2 \theta}{2 g}\)

\(=\frac{50 \times 50 \times \frac{1}{2} \times \frac{1}{2}}{2 \times 10}=31.25\)

प्रश्न 22. 
प्रक्षेप पथ के उच्चतम बिन्दु पर प्रक्षेप्य की गति की दिशा क्षैतिज क्यों हो जाती है?
उत्तर:
क्योंकि उच्चतम बिन्दु पर ऊर्ध्वाधर वेग शून्य हो जाता है। 

प्रश्न 23. 
प्रक्षेप पथ के उच्चतम बिन्दु पर वेग व त्वरण की दिशाओं के बीच कितना कोण होता है?
उत्तर:
90°

प्रश्न 24. 
प्रक्षेप पथ के किस बिन्दु पर चाल निम्नतम होती है ? किस बिन्दु पर अधिकतम ?
उत्तर:
उच्चतम बिन्दु पर, प्रक्षेपण बिन्दु पर।

प्रश्न 25. 
एक खिलाड़ी गेंद को क्षैतिज से किस झुकाव पर फेंके कि गेंद अधिकतम दूरी तक जाये ?
उत्तर:
45°

प्रश्न 26. 
प्रक्षेप्य पथ ऋजुरेखीय होने के लिये प्रक्षेप कोण का मान कितने डिग्री के बराबर होना चाहिये ?
उत्तर:
90°

प्रश्न 27. 
एक मीनार की चोटी से एक गेंद क्षैतिज दिशा में फेंकी जाती है तथा उसी मीनार की चोटी से एक दूसरी गेंद गिराई जाती है। दोनों गेंदों के पृथ्वी पर पहुँचने में समयान्तराल क्या होगा ? में
उत्तर:
शून्य दोनों गेंदों के ऊर्ध्वाधर गति हेतु सूत्र s = ut + 1/2 at² में x = 0 और a = g अतः दोनों गेंदों के लिये समान होंगे अर्थात् · दोनों गेंदें एक साथ पृथ्वी पर पहुँचेंगी।

प्रश्न 28. 
मार्ग के उच्चतम बिन्दु पर कण के वेग और त्वरण की दिशाओं के बीच बना कोण क्या होगा?
उत्तर:
90°

प्रश्न 29.
उड्डयन काल आप क्या समझते हैं?
उत्तर:
वह समय अंतराल है, जिसमें प्रक्षेप्य फेंकने के पश्चात् पुनः अपने प्रारम्भिक क्षैतिज तल पर लौट आता है। यह समय, किसी पिण्ड को ऊ र्वाधर ऊपर के समय के बराबर होता है, अतः यदि उड्डयन काल T हो तो
T = 2usineθ

प्रश्न 30. 
महत्तम ऊँचाई का सूत्र लिखिये और यह बताइये कि महत्तम ऊँचाई पर प्रक्षेप्य का वेग कितना होता है?
उत्तर:
महत्तम ऊँचाई
\(\mathrm{H}=\frac{u^2 \sin ^2 \theta}{2 g}\)

महत्तम ऊँचाई पर प्रक्षेप्य का वेग केवल क्षैतिज दिशा में ucosθ  होता है।

प्रश्न 31. 
प्रक्षेप्य का क्षैतिज परास से क्या तात्पर्य है? उदाहरण दीजिए।
उत्तर:
एक ही क्षैतिज तल पर आरम्भ से उड़ान के अन्तिम बिन्दु तक की क्षैतिज दूरी को प्रक्षेप्य का क्षैतिज परास कहते हैं।

प्रश्न 32. 
ऊपर की ओर फेंकी एक गेंद के प्रक्षेप मार्ग के किस बिन्दु पर त्वरण वेग के अभिलम्ब है?
उत्तर:
प्रक्षेप मार्ग के उच्चतम बिन्दु पर।

प्रश्न 33. 
किसी कोण पर एक गेंद को फेंका जाये जिससे इसका क्षैतिज परास अधिकतम हो?
उत्तर:
45°

प्रश्न 34. 
प्रक्षेप मार्ग के कौनसे बिन्दु पर चाल अधिकतम होगी? 
उत्तर:
वह बिन्दु जहाँ पर प्रक्षेप उस स्थान पर वापस आता है, जहाँ से उसे प्रक्षेपित किया गया।

प्रश्न 35. 
एक वस्तु एक तल में अपने प्रारम्भिक वेग की दिशा से भिन्न दिशा में गतिमान है। इसके द्वारा तय किया गया पथ किस प्रकार का होगा?
उत्तर:
उसका पथ परवलीय पथ होगा।

प्रश्न 36. 
एक मीनार की चोटी से एक गेंद क्षैतिज दिशा में 1 वेग से प्रक्षेपित की जाती है व दूसरी गेंद उसी स्थान से नीचे गिराई जाती है। क्या पृथ्वी से टकराते समय दोनों के वेग समान होंगे?
उत्तर:
नहीं, क्योंकि फेंकते समय यद्यपि दोनों गेंदों के ऊर्ध्व वेग शून्य हैं तथापि दोनों के क्षैतिज वेग भिन्न-भिन्न हैं। अतः दोनों गेंदें पृथ्वी पर असमान वेगों से पहुँचेंगी।

प्रश्न 37. 
एक समतल पर क्षैतिज के ऊपर 8 कोण पर एक तोप का निशाना x दूरी पर स्थित एक ऊर्ध्वाधर पहाड़ी पर लेकर v नलिका चाल से एक गोला दागा गया है। तली से पहाड़ी की किस ऊँचाई y पर गोला टकरायेगा?
उत्तर:
\(y=x \tan \theta-\frac{g x^2}{2 v^2 \cos \theta}\)

प्रश्न 38. 
एक प्रक्षेपित वस्तु का अधिकतम क्षैतिज परास R है। उड़ान में कितनी अधिकतम ऊँचाई तक यह पहुँचता है?
उत्तर:
यदि θ = 45° तो

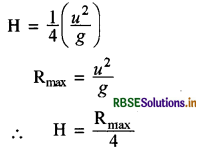
प्रश्न 39. 
क्या वृत्तीय गति स्थिर चाल अथवा स्थिर वेग में सम्भव है? समझाइए।
उत्तर:
वृत्तीय गति स्थिर चाल से सम्भव क्योंकि इसमें वेग का परिमाण या चाल तो स्थिर रहती है परन्तु इस कण की गति दिशा बदलती रहती है।

प्रश्न 40. 
जब एक प्रक्षेप द्वारा प्राप्त अधिकतम ऊँचाई सबसे बड़ी हो तो उन दो राशियों के नाम बताइए जो सबसे बड़ी होंगी।
उत्तर:
उड़ान समय तथा वेग का अर्द्धघटक|

लघुत्तरात्मक प्रश्न:

प्रश्न 1. 
सदिश संयोजन में क्रम-विनिमय और साहचर्य नियम का पालन होता है, समझाइए।
उत्तर:

प्रश्न 2. 
सदिशों के x, y, z अक्षों के अनुदिश घटकों का क्या अर्थ है और सिद्ध कीजिये cos² αt + cos² βt + cos² γt = 1 होता है।
उत्तर:

प्रश्न 3. 
वृत्ताकार पथ में नियत कोणीय चाल 600 से गति कर रहे कण के किसी क्षण पर निर्देशांक x = A cos ωt तथा y = A sin ωt हैं। वृत्तीय पथ की त्रिज्या क्या है?
उत्तर:
दिया गया है:
x = A cos ωt ..(1)
y = Asin  ωt ..(2)
समीकरण (1) तथा (2) का वर्ग करके जोड़ने पर 
x² + y² = A² cos²ωt + A² sin²ωt
=> x² + y² = A² (cos² ωt + sin² ωt) 
=> x² + y² = A² × 1
∴ sin² ωt + cos² ωt = 1 .....(3)
समीकरण (3) वृत्त का समीकरण है अतः इस वृत्त के केन्द्र (0, 0) और इस वृत्तीय पथ की त्रिज्या A है।

प्रश्न 4. 
द्विविमीय और त्रिविमीय गतियों में अन्तर उदाहरण देकर स्पष्ट कीजिये ।
उत्तर:

1. द्विविमीय गति: किसी तल में वक्रीय पथ पर किसी पिण्ड की गति द्विविमीय गति कहलाती है।
2. उदाहरण: किसी समतल में वृत्ताकार पथ पर किसी कण की गति, कागज पर चींटी की गति, पृथ्वी की सतह पर वाहनों की गति, ऊर्ध्वाधर तल में एक प्रक्षेप्य की गति, द्विविमीय गति के वर्णन के लिये, दो निर्देशांक अक्षों की आवश्यकता होती है।
3. त्रिविमीय गति: आकाश (Space) में किसी कण की गति त्रिविमीय गति कहलाती है। इस गति का वर्णन करने के लिये परस्पर लम्बवत् तीन निर्देशांक अक्षों की आवश्यकता होती है; जैसे किसी मक्खी की गति, जब तेज हवा चल रही हो तो पतंग की गति । त्रिविमीय गति के वर्णन के लिये परस्पर लम्बवत् तीन निर्देशांक अक्षों की आवश्यकता होती है।

प्रश्न 5. 
एक प्रक्षेप्य का उड्डयन काल T तथा क्षैतिज परास R है। प्रक्षेप्य कोण \(\theta=\tan ^{-1}\left(\frac{g T^2}{2 R}\right)\) कितना होगा ?
अथवा
एक प्रक्षेप्य का उड्डयन काल T तथा क्षैतिज परास R है।

प्रश्न 6. 
एक प्रक्षेप्य की अधिकतम ऊँचाई H तथा उड्डयन काल T है । दर्शाइये 8H = gT²
अथवा
एक प्रक्षेप्य की अधिकतम ऊँचाई H तथा उड्डयन काल T है। तब सिद्ध कीजिये कि
8H = gT² होगा।
उत्तर:

समीकरण (1) में मान रखने पर
∴ gT² = 8H
L.H.S. = R.H.S.
यही सिद्ध करना था।

प्रश्न 7. 
सिद्ध कीजिये कि प्रक्षेप्य की अधिकतम क्षैतिज परास अधिकतम ऊँचाई की चार गुना होती है।
उत्तर:

प्रश्न 8. 
प्रक्षेप्य पथ पर वलयाकार होने की क्या शर्तें हैं? 
उत्तर:
प्रक्षेप्य पथ पर वलयाकार होने की शर्तें:

1. प्रक्षेप्य का कोण क्षैतिज से 0° से 90° के बीच में होना चाहिये।
2. उसकी अधिकतम ऊँचाई पर g का मान समान रहना चाहिये।
3. प्रक्षेप्य वेग बहुत अधिक नहीं होना चाहिये जिससे वायु घर्षण का मान नगण्य रहे।

प्रश्न 9. 
किसी प्रक्षेप्य का उड्डयन काल उसके क्षैतिज परास से निम्न समीकरण द्वारा सम्बन्धित है-
gT² = 2R
इसके प्रक्षेपण कोण का मान ज्ञात कीजिये।
उत्तर:

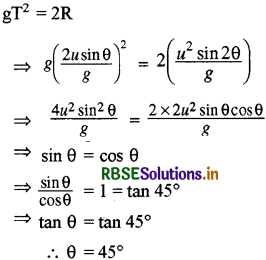
प्रश्न 10. 
एक प्रक्षेप्य की क्षैतिज परास उसकी अधिकतम ऊँचाई की \(4 \sqrt{3}\) गुनी है। इसके प्रक्षेपण कोण का मान ज्ञात कीजिये।
उत्तर:

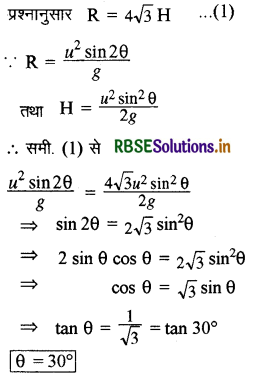
प्रश्न 11. 
सिद्ध कीजिये कि प्रक्षेप्य गति में पिण्ड को क्षैतिज से 6) कोणों से प्रक्षेपित करने पर उनकी क्षैतिज (45° + Φ) एवं ( 45° - Φ) परास समान होती है।
उत्तर:
हम जानते हैं कि किसी वस्तु को 8 कोण पर प्रक्षेपित करने पर उसका परास

आंकिक प्रश्न:

प्रश्न 1. 
5 व 3 न्यूटन के दो सदिश बल एक कण पर कार्यरत हैं। परिणामी बल का परिमाण व दिशा ज्ञात कीजिए:
(अ) जब दोनों बल एक ही दिशा में हैं।
(ब) जब दोनों बल समकोणिक हैं।
(स) जब दोनों बल 60° के कोण पर झुके हुए हैं। 
उत्तर:

प्रश्न 2. 
सिद्ध कीजिये कि दो समान और लम्बवत् सदिश के योग तथा अन्तर सदिश भी समान तथा लम्बवत् होंगे।
उत्तर:

प्रश्न 3.
दो संदिशों P की दिशा विपरीत करने पर परिणामी सदिश ड हो जाता है तब सिद्ध कीजिए:
\(R^2+S^2=2\left(P^2+Q^2\right)\)
उत्तर:

प्रश्न 4 
सिद्ध कीजिये कि जब समान परिमाण के दो सदिशों के मध्य का कोण ग है, तो परिणामी सदिश का परिमाण किसी एक सदिश के परिमाण के तुल्य होगा।
उत्तर:
दिया गया है:
P = Q एवं θ = 2/3π
θ = 2 × 180 = 120°

प्रश्न 5.
एक कण का स्थिति सदिश समय पर निम्न प्रकार निर्भर करता है \(\vec{r}=\left(2+3 t-t^3\right) \hat{i}+\left(-t+t^2\right) \hat{j}+\left(7 t+t^3\right) \hat{k}\) (मीटर में)। ज्ञात कीजिये (i) समय t = 0 सेकण्ड से t = 1 सेकण्ड के मध्य कण का विस्थापन, (ii) समय t = 1 सेकण्ड पर कण का तात्क्षणिक वेग और तात्क्षणिक त्वरण का परिमाण ज्ञात कीजिए।
उत्तर:

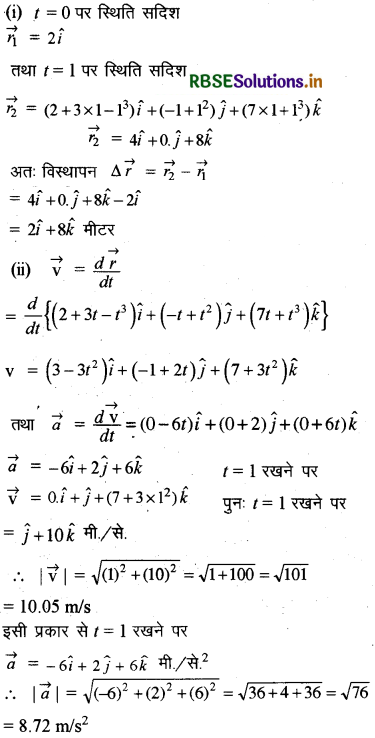
प्रश्न 7. 
एक 20 मीटर ऊँची मीनार से, एक बंदूक से एक गोली क्षैतिज दिशा में दागी जाती है। यदि g = 10 मी./से.2 हो और गोली का प्रारम्भिक वेग 400 मी./से. हो तब गोली, पृथ्वी पर मीनार से कितनी दूरी पर गिरेगी?
उत्तर:
माना गोली का क्षैतिज दिशा में गिरने का समय = t सेकण्ड है।

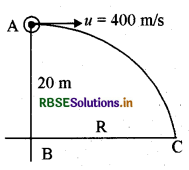
माना गोली का क्षैतिज दिशा में गिरने का समय = t सेकण्ड है।
यहाँ पर u = 0
h = 1/2gt² के सूत्र से
20 = 1/2 x 10 x t²
t² = 4
∴ t = 2
∴ गोली के गिरने की पृथ्वी पर मीनार से दूरी
BC = u x t
= 400 x 2 = 800

प्रश्न 8. 
एक व्यक्ति एक पत्थर को अधिकतम 100 मीटर की क्षैतिज दूरी तक फेंक सकता है। वह खिलाड़ी उसी पत्थर को अधिकतम कितनी ऊर्ध्वाधर ऊँचाई तक फेंक सकता है?
उत्तर:
दिया गया है:
Rmax = 100 मीटर
लेकिन Rmax = u²/g  = 100 मीटर
u² = 100.g
ऊर्ध्वाधर स्थिति के लिये
या
v² = u² + 2gh
O = 100g - 2gH 
2gH = 100g
या H = 100g/2g 
50 मीटर 

प्रश्न 9. 
दो पिण्डों को समान वेग से दो विभिन्न कोणों पर एक ही बिन्दु से फेंका जाता है। यदि दोनों बार एक ही परिसर R हो और उड्डयन काल और हो, तो सिद्ध करो कि R = 1/2gt
उत्तर:
हम जानते हैं कि यदि किसी पिण्ड को θ व (π/2 - θ) कोण पर फेंका जाये तो परिसर बराबर होती है।

प्रश्न 10. 
एक तोप के गोले का क्षैतिज परिसर R है। यदि उन दोनों पथों की, जिनके लिये यह सम्भव है, महत्तम ऊँचाइयाँ हों, तो सिद्ध करो कि:
\(4 \sqrt{h h^{\prime}}=\mathbf{R}\)
उत्तर:
माना गोले को u वेग से θ तथा (π/2 - θ) कोणों से फेंका जाता है, तो परिसर

प्रश्न 11. 
0.1 किग्रा का एक पत्थर 1 मीटर लम्बे धागे से बँधा 2 घूर्णन प्रति सेकण्ड की चाल से क्षैतिज वृत्ताकार पथ में घूम रहा है। धागे पर लगने वाले तनाव की गणना करो।
उत्तर:
दिया गया है:
m = 0.1 
R = 1 मीटर
f = 2 घूर्णन / सेकण्ड
माना धागे पर लगने वाला तनाव T है तब
तनाव
T = mv²/R = mω²R²/R V = Rω
T = mω²R = m(2πf)²R
= 4mπ²f²R
मान रखने पर = 4 x 0.1 x (3.14)² x (2)² x 1
= 0.4 x (3.14)² x 4
= 1.6 x (3.14)² = 15.775
अर्थात् 15.8 न्यूटन

प्रश्न 12. 
1.5 मीटर लम्बी डोरी से बँधे एक 500 ग्राम के द्रव्यमान के पिण्ड के प्रति मिनट अधिकतम चक्कर ज्ञात करो, यदि डोरी 40 N के अधिकतम तनाव को वहन कर सकती है।
उत्तर:
पिण्ड का द्रव्यमान = 500g = 0.5 kg
R = वृत्त की त्रिज्या = 1.5m
F = अभिकेन्द्र बल = 40N
Fc = द्रव्यमान x त्वरण
अब
Fc = m ar
= mV²/R = m/R (Rω)²
 ∵ v = Rω
 = mR2ω²/R = mRω²
 = mR(2πf)²
 = 4π²mRf²

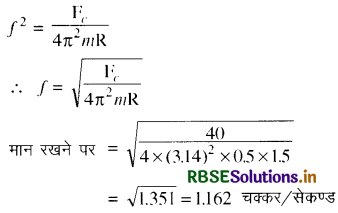
 = 1.162 x 60 = 69.74 चक्कर/मिनट
 अतः डोरी को बिना तोड़े पिण्ड को 69 चक्कर प्रति मिनट दिए जा सकते हैं।

गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न:

प्रश्न 1. 
क्षैतिज घर्षण विहीन टेबिल के केन्द्र पर स्थित खूँटी से l लम्बाई की डोरी का एक सिरा बाँधा गया है तथा दूसरे सिरे पर m द्रव्यमान का एक कण बाँधकर उसे v वेग से वृत्तीय गति करवाई। जाती है, कण पर केन्द्र की ओर लगने वाला बल होगा (T डोरी में तनाव को दर्शाता है):
(a) T
(b) T - mv2/l
(c) T + mv2/l
(d) शून्य
उत्तर:
(a) T

प्रश्न 2. 
एक कण 25 सेमी. त्रिज्या के वृत्त में 2 चक्कर / सेकण्ड की चाल से गति कर रहा है। कण का त्वरण m/s² में होगा:
(a) π²
(b) 8π²
(c) 4π²
(d) 2π²
उत्तर:
(c) 4π²

प्रश्न 3. 
एक कण, 5 cm त्रिज्या के वृत्ताकार पथ में एक स्थिर चाल और सेकण्ड के आवर्तकाल से घूर्णन कर रहा है। कण का 0.2π त्वरण है:
(a) 5m/s² 
(b) 15m/s²
(c) 25m/s²
(d) 36m/s²
उत्तर:
(a) 5m/s² 

प्रश्न 4. 
R त्रिज्या के किसी ऊर्ध्वाधर पाश (लूप) में m द्रव्यमान के किसी पिण्ड को किस निम्नतम वेग से प्रवेश करना चाहिए कि वह पाश को पूर्ण कर सके:

उत्तर:
\(\text { (d) } \sqrt{5 g \mathrm{R}}\)

प्रश्न 5. 
1.0m लम्बी रस्सी का एक सिरा 0.5 kg द्रव्यमान की एक वस्तु से बँधा है। यह 4 rad/s की कोणीय आवृत्ति से ऊर्ध्वय वृत्त में घूम रहा है। जब वस्तु गति करते हुये निम्नतम बिन्दु पर हो तो रस्सी का तनाव होगा (g = 10m/s² लेने पर):
(a) 3N
(b) 5N
(c) 8N
(d) 13N
उत्तर:
(d) 13N

प्रश्न 6. 
विरामावस्था में स्थित 50 सेमी. त्रिज्या की कोई एकसमान वृत्ताकार डिस्क अपने तल के लम्बवत् और केन्द्र से गुजरने वाले अक्ष के परितः घूमने के लिए स्वतंत्र है। इस डिस्क पर कोई बल आघूर्ण कार्य करता है, जो इसमें 2.0 rad s² का नियत कोणीय त्वरण उत्पन्न कर देता है। 2.0s के पश्चात् ms-2 में इसका नेट त्वरण होगा लगभग:
(a) 8.0
(b) 7.0
(c) 6.0
(d) 3.0
उत्तर:
(a) 8.0

प्रश्न 7. 
10g द्रव्यमान का कोई कण 6.4 सेमी. लम्बी त्रिज्या के वृत्त के अनुदिश किसी नियत स्पर्श रेखीय त्वरण से गति करता है। यदि गति आरम्भ करने के पश्चात् दो परिक्रमाएँ पूरी करने पर कण की गतिज ऊर्जा 8 x 10⁴ J हो जाती है, तो इस त्वरण का
परिमाण क्या है:
(a) 0.1m/s²
(b) 0.15m/s²
(c) 0.18 m/s²
(d) 0.2m/s²
उत्तर:
(a) 0.1m/s²

प्रश्न 8. 
चित्रानुसार R = 2.5 m त्रिज्या के वृत्तीय पथ पर दक्षिणावर्त गति करते हुए किसी कण के कुल त्वरण को किसी क्षण a = 15 m/s² से निरूपित किया जाता है। कण की चाल होगी

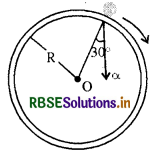
(a) 6.2m/s
(b) 4.5m/s
(c) 5.0m/s
(d) 5.7m/s
उत्तर:
(d) 5.7m/s

प्रश्न 9. 
एक प्रक्षेप्य की अधिकतम ऊँचाई तथा क्षैतिज परास आपस में बराबर हैं तो प्रक्षेप्य का प्रक्षेपण कोण है:
(a) θ = tan^-1 (1/4)
(b) θ = tan^-1
(c) θ = tan^-1 (4)
(d) θ = 45
उत्तर:
(b) θ = tan^-1

प्रश्न 10. 
सभी दिशाओं में वेग से कई गोलियाँ दागी जाती हैं। पृथ्वी तल पर वह अधिकतम क्षेत्रफल क्या होगा जिस पर ये गोलियाँ फैल जायेंगी:
(a) π v²/g
(b) π v⁴/g²
(c) π² v⁴/g²
(d) π² v²/g²
उत्तर:
(b) π v⁴/g²

प्रश्न 11. 
वह प्रक्षेपण कोण जिसके लिए प्रक्षेप्य की क्षैतिज परास तथा अधिकतम ऊँचाई बराबर होगी, है-
(a) 45°
(b) θ = tan^-1 (0.25)
(c) θ = tan^-1 4 अथवा (θ = 76°)
(d) 60°
उत्तर:
(c) θ = tan^-1 4 अथवा (θ = 76°)

प्रश्न 12. 
एक m द्रव्यमान के कण को प्रारम्भिक गति से क्षैतिज से u₀ कोण पर प्रक्षेपित किया जाता है। यह कण प्रक्षेप्य पथ के उच्चतम बिन्दु पर एकसमान द्रव्यमान के कण के साथ पूर्णतः अप्रत्यास्थ संघट्ट करता है, जो कि भूतल से ऊर्ध्वाधर दिशा में समान प्रारम्भिक गति tho ) से फेंका गया था। संयुक्त निकाय संघट्ट के तत्काल बाद क्षैतिज से निम्न कोण बनाएगा:
(a) π/4
(b) π/4 + α
(c) π/4 - α
(d) π/2
उत्तर:
(c) θ = tan^-1 4 अथवा (θ = 76°)

प्रश्न 13. 
किसी प्रक्षेप्य का प्रारम्भिक बिन्दु A पर वेग (\(2 \hat{i}+3 \hat{j}\)) m/s है, तो इसका बिन्दु B पर देग (m/s में) होगा:

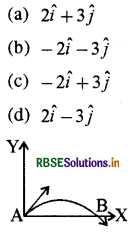
उत्तर:
\(\text { (d) } 2 \hat{i}-3 \hat{j}\)

प्रश्न 14. 
एक वेग \(\vec{v}=\mathrm{K}(y \hat{i}+x \hat{j})\) जहाँ K एक स्थिरांक है। इसके पथ का सामान्य समीकरण है:
(a) y² = x² + स्थिरांक
(b) y = x² + स्थिरांक
(c) y² = x + स्थिरांक
(d) xy = स्थिरांक
उत्तर:
(a) y² = x² + स्थिरांक

प्रश्न 15. 
एक प्रक्षेप्य को पृथ्वी की सतह से 5ms^-1 के वेग से तथा क्षैतिज दिशा से 6 कोण पर छोड़ा जाता है। किसी अन्य ग्रह से 3ms^-1 के वेग तथा इसी कोण (6) पर छोड़े गये एक प्रक्षेप्य का प्रक्षेप पथ पृथ्वी से छोड़े गये एक प्रक्षेप्य पथ के सर्वसम (सर्वथा समान) है। यदि पृथ्वी पर 8 = 9.8ms^-2 है तो इस ग्रह पर गुरुत्वीय त्वरण का मान ms^-2 में होगा:
(a) 16.3
(b) 110.8
(c) 3.5
(d) 5.9
उत्तर:
(c) 3.5

प्रश्न 16. 
यदि किसी समय पर किसी कण के x तथा y निर्देशांक क्रमश: x = 5t - 2t² तथा y = 410t हैं। (जहाँ तथा y मीटर में और t सेकण्ड में है) तो t = 2s पर उस कण का त्वरण होगा:
(a) 0
(b) 5m/s²
(c) - 4m/s²
(d) - 8m/s²
उत्तर:
(c) - 4m/s²

प्रश्न 17. 
एक प्रसारी गोले की तात्क्षणिक त्रिज्या R एवं द्रव्यमान M अचर होते हैं। प्रसार के दौरान इसका तात्क्षणिक घनत्व p पूरे आयतन में एकसमान रहता है एवं आंशिक घनत्व की दर \(\left(\frac{1}{\rho} \frac{d p}{d t}\right)\) अचर है। इस प्रसारी गोले के पृष्ठ पर एक बिन्दु का वेग निम्न के
समानुपाती होगा:
(a) R³
(b) R
(c) R₂/3
(d) 1/R
उत्तर:
(b) R

प्रश्न 18. 
एक त्रिविमीय निर्देशांक निकाय में गतिशील एक कण के स्थिति निर्देशांक निम्न हैं:
x = a cos ωt
y = a sin ωt
तथा
Z = aωt
इस कण की गति का मान होगा:
(a) aω
(b) \(\sqrt{3} a \omega\)
(c) \(\sqrt{2} a \omega\)
(d) 2aω
उत्तर:
 (c) \(\sqrt{2} a \omega\)

प्रश्न 19. 
t = 0 पर क्षैतिज से 60° के कोण पर 10 ms^-1 के वेग से एक पिण्ड को प्रक्षेपित करते हैं। = 1s पर प्रक्षेप पथ की वक्रता त्रिज्या R है। वायु प्रतिरोध को नगण्य मानकर तथा गुरुत्वीय त्वरण g = 10 ms^-2 लेकर R का मान है:
(a) 2.5m 
(b) 10.3m
(c) 2.8m
(d) 5.1m
उत्तर:
(a) 2.5m 

प्रश्न 20. 
एक 60 m लम्बी यात्री गाड़ी 80 km/hr की गति से चल रही है। 120m लम्बाई की एक और मालगाड़ी 30 km/hr से चल रही है। ऐसे समयों का अनुपात जो यात्री गाड़ी को मालगाड़ी को पार करने में लगेंगे जब (i) गाड़ियाँ एक ही दिशा में जा रही हैं, और (ii) गाड़ियाँ विरोधी दिशाओं में जा रही हैं, होगा:
(a) 5/2
(b) 25/11
(c) 3/2
(d) 11/5
उत्तर:
(d) 11/5

प्रश्न 21. 
एक कण एक वृत्ताकार पथ पर 10ms^-1 की नियत गति से चल रहा है। केन्द्र के परितः 60° चलता है जब यह कण वृत्त के इसके वेग में हुए परिवर्तन का तो परिमाण होगा
(a) शून्य
(b) 10m/s
\(\text { (c) } 10 \sqrt{3} \mathrm{~m} / \mathrm{s}\)
\(\text { (d) } 10 \sqrt{2} \mathrm{~m} / \mathrm{s}\)
उत्तर:
(b) 10m/s

प्रश्न 22.
rA और rB त्रिज्याओं के संकेन्द्री वृत्तों पर दो कण A और B क्रमशः VA और VB वेगों से एकसमान वृत्तीय गति कर रहे हैं। इनके घूर्णन का आवर्तकाल समान है। A और B की कोणीय चालों का अनुपात होगा:
(a) rA : rB
(b) vA : vB
(c) rB : rA
(d) 1 : 1
उत्तर:
(d) 1 : 1

प्रश्न 23. 
जब क्षैतिज से 60° कोण पर रखे किसी लम्बे चिकने आनत तल की तली से किसी पिण्ड पर शॉट लगाया जाता है, तो वह तल के अनुदिश X दूरी चल सकता है। परन्तु जब झुकाव को घटाकर 30° कर दिया जाता है तथा इसी पिण्ड पर समान वेग से शॉट लगाया जाता है, तब वह X2 दूरी चल सकता है। तब X1 : X2 होगा

उत्तर:
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)

प्रश्न 24. 
एक गेंद को भूमि (Ground) पर क्षैतिज तल (Horizontal surface) से 45° के कोण पर प्रक्षेपित (Projected) किया जाता है। गेंद 120m की अधिकतम ऊँचाई पर पहुँच कर भूमि पर वापस लौट आती है। भूमि से पहली बार टकराने के उपरान्त गेंद की गतिज ऊर्जा (Kinetic energy ) आधी हो जाती है। टकराने के तुरन्त बाद गेंद का वेग क्षैतिज तल से 30° का कोण बनाता है। टकराने के बाद गेंद मीटर की अधिकतम ऊँचाई पर पहुँचती है।
उत्तर:
30.00

प्रश्न 25. 
समान त्रिज्या R वाली दो एकसमान डिस्क अपनी धुरी पर एकसमान व स्थिर कोणीय चाल ω से विपरीत दिशा में घूम रही हैं। डिस्क एक ही क्षैतिज तल में है। समय t = 0 पर बिन्दु P और Q चित्र में दर्शाये अनुसार आमने-सामने हैं। बिन्दु P और बिन्दु Q की आपेक्षिक चाल V को एक आवर्तनकाल (T) में देखें। तब Vr का समय के साथ परिवर्तन का किस ग्राफ में सर्वोत्तम वर्णन है:

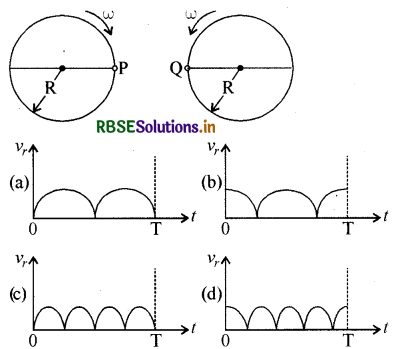
उत्तर:

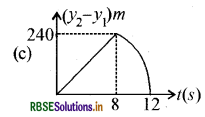
प्रश्न 26. 
किसी 240m ऊँची चोटी के एक किनारे से दो पत्थरों को एक साथ ऊपर की ओर फेंका गया है, इनकी प्रारम्भिक चाल क्रमशः 10 m/s तथा 40 m/s है, तो निम्नांकित में से कौनसा ग्राफ (आलेख) पहले पत्थर के सापेक्ष दूसरे पत्थर की स्थिति के समय विचरण (परिवर्तन) को सर्वाधिक सही दर्शाता है। मान लीजिए कि पत्थर जमीन से टकराने के पश्चात् ऊपर की ओर नहीं उछलते हैं तथा वायु का प्रतिरोध नगण्य है, दिया है g = 10 m/s² (यहाँ ग्राफ केवल व्यवस्था आरेख है और स्केल के अनुसार नहीं है)-

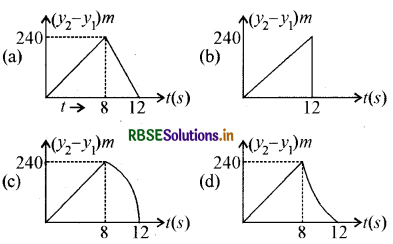
उत्तर: