RBSE Class 11 Physics Important Questions Chapter 3 सरल रेखा में गति

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 3 सरल रेखा में गति Important Questions and Answers.

RBSE Class 11 Physics Chapter 3 Important Questions सरल रेखा में गति

बहुचयनात्मक प्रश्न:

प्रश्न 1. 
एक कण की एकविमीय गति के लिए वेग समय ग्राफ चित्र के अनुसार है। कण का त्वरण है (मी./से. में)

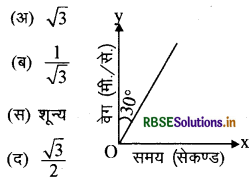
संकेत: त्वरण a = dv/dt = tan θ
यहाँ पर θ, x अक्ष से बनाया गया कोण है।
θ = 90° 30° = 60°
a = tan 60° = \(\sqrt{3}\)
अतः सही विकल्प (अ) है।
उत्तर:
\(\text { (अ) } \sqrt{3}\)

 

प्रश्न 2. 
14 प्रारम्भिक वेग और समान त्वरण a से गतिशील एक कण का वेग- समय ग्राफ है:

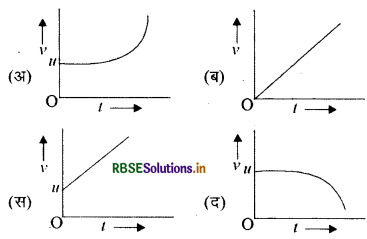
उत्तर:

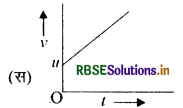
प्रश्न 3. 
एक व्यक्ति सामान्य गति से एक सीधी सड़क पर 500 मीटर, 10 मिनट में चलता है और अगले 5 मिनट में 310 मीटर दूरी पार करता है। इस समय अन्तराल में व्यक्ति की औसत चाल है:
(अ) 0.52 मी./से.
(ब) 0.83 मी./से.
(स) 0.90 मी./से.
(द) 135 मी./से.
संकेत: कुल दूरी = 500+ 310 = 810 मी.
कुल लगा समय = 10 + 5 = 15 मिनट
औसत चाल =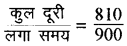
= 0.90 मी./से.
अतः सही विकल्प (स) है।
= 15 × 60 = 900 सेकण्ड
उत्तर:
(स) 0.90 मी./से.

प्रश्न 4. 
एक बस अपनी यात्रा के प्रथम आधे समय 400 किमी/घं. की चाल से और बाकी आधे समय 700 किमी/घं. की चाल से गति करे तब बस की औसत चाल है:
(अ) 6() किमी./घं.
(ब) 55 किमी./घं.
(स) 300 किमी./घं.
(द) 35 किमी./घं.
संकेत माना कुल समय
तो प्रथम समय (1/2) में तय की
गई दूरी = 40 x t/2 = 20 t
अगले 1/2 समय में तय की गई दूरी
= 70 x  t/2 = 35t
कुल दूरी 20t + 35t = 55t

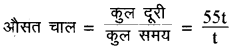
= 55 किमी./ घण्टा
अतः सही विकल्प (ब) है।
उत्तर:
(ब) 55 किमी./घं.

प्रश्न 5. 
V1 वेग से एक कण इसकी आधी दूरी तय करता है तथा शेष आधी दूरी V2 वेग से तय करता है। पूरी यात्रा के दौरान इसकी औसत चाल है:

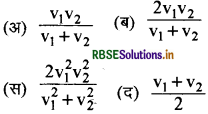
संकेत:
\(v_{a v}=\frac{s+s}{\frac{s}{v_1}+\frac{s}{v_2}}=\frac{2 s}{\frac{s\left(v_2+v_1\right)}{v_1 v_2}}=\frac{2 v_1 v_2}{v_1+v_2}\)
अतः सही विकल्प (ब) है।
उत्तर:
\(\text { (ब) } \frac{2 v_1 v_2}{v_1+v_2}\)
 

प्रश्न 6. 
एक गेंद को ऊर्ध्वाधर ऊपर की ओर 19.6 मी./से. के वेग से फेंका जाता है। गेंद अधिकतम ऊँचाई तक कितने सेकण्ड में पहुँचेगी?
(अ) 1
(ब) 2
(स) 3
(द) 4
संकेत अधिकतम ऊँचाई पर अन्तिम वेग v = (),
g = 9.8 m/s²
गति के प्रथम समीकरण से v = u - gt
\(\mathrm{t}=\frac{\mathrm{u}-\mathrm{v}}{\mathrm{a}}=\frac{19.6-0}{9.8}\)
t = 2 सेकण्ड
अतः सही विकल्प (ब) है।
उत्तर:
(ब) 2

प्रश्न 7. 
प्रारम्भिक वेग तथा त्वरण से चलने वाले कण के द्वारा x वें सेकण्ड में तय की गई दूरी होगी-
(अ) u + 3/2(2x - 1)
(ब) u + a/2(2x + 1)
(स) u + a (2x - 1)
(द) u + a/2(2x - 1)
उत्तर:
(द) u + a/2(2x - 1)

प्रश्न 8. 
किसी पिण्ड का तात्क्षणिक वेग मापा जा सकता है:
(अ) स्पीडोमीटर द्वारा
(ब) ग्राफ द्वारा
(स) वेक्टर विधि द्वारा
(द) इनमें से कोई नहीं
उत्तर:
(अ) स्पीडोमीटर द्वारा

प्रश्न 9. 
किसी गतिमान वस्तु का त्वरण ज्ञात किया जा सकता है:
(अ) दूरी-समय ग्राफ के ढाल द्वारा
(ब) वेग समय ग्राफ के ढाल द्वारा
(स) वेग समय ग्राफ के
(द) दूरी समय ग्राफ के क्षेत्रफल द्वारा
उत्तर:
(ब) वेग समय ग्राफ के ढाल द्वारा

प्रश्न 10. 
यदि दो राशियों का परस्पर ग्राफ सरल रेखा हो तो दोनों राशियाँ:
(अ) अचर होती हैं। 
(ब) बराबर होती हैं। 
(स) अनुक्रमानुपाती होती हैं। 
(द) व्युत्क्रमानुपाती होती हैं। 
उत्तर:
(स) अनुक्रमानुपाती होती हैं। 

प्रश्न 11. 
एक किलोग्राम का एक पत्थर तथा 2 किलोग्राम का एक दूसरा पत्थर, दोनों साथ-साथ एक ही ऊँचाई से स्वतन्त्रतापूर्वक छोड़े जाते हैं। पृथ्वी पर गिरने में लगे पत्थरों के समय का अनुपात क्या होगा ?
(अ) 1 : 1
(ब) 1 : \(\sqrt{2}\)
(स) 1 : 2
(द) 1 : 3
उत्तर:
(अ) 1 : 1

प्रश्न 12. 
स्वतन्त्रतापूर्वक गिर रही एक वस्तु द्वारा अपने प्रथम तथा द्वितीय सेकण्ड में पार की गई दूरियों के अनुपात हैं:
(अ) 1 : 2 
(ब) 1 : 3
(स) 3 : 2
(द) 1 : \(\sqrt{3}\)
संकेत:  n वें सेकण्ड में तय की गई दूरी
Sn = u + 1/2a(2n - 1)
S1 = 0 + 1/2a (n = 1)
S2 = 0 + 3/2a (n = 2)
S1 : S2 = 1 : 3
अतः सही विकल्प (ब) है।
उत्तर:
(ब) 1 : 3

प्रश्न 13. 
एक गेंद को u वेग से ऊर्ध्वाधर ऊपर की ओर फेंकने पर यह h ऊँचाई तक जाती है। यदि इसे 2u वेग से फेंका जाये तब प्राप्त ऊँचाई होगी:
(अ) h
(ब) 2h
(स) 4h
(द) h2
संकेत :
v² = u² - 2gh
0 = u² - 2gh
h = u²/2g
अब u = 2u है।
तब \(h^{\prime}=\frac{(2 u)^2}{2 g}=4 \frac{u^2}{2 g}\)
h' = 4h
अतः सही विकल्प (स) है।
उत्तर:
(स) 4h

प्रश्न 14. 
एकविमीय गति कर रहे एक पिण्ड का विस्थापन x समय t पर
निम्न प्रकार निर्भर करता है:
x = a_o + a₁t + a₂t² + a₃t³
जहाँ a_o, a₁, a₂, a₃ नियत हैं तब सही कथन है:
(अ) कण की स्थिति a₁ है
(ब) कण का प्रारम्भिक वेग 2a₂ है 
(स) कण का त्वरण नियत नहीं है
(द) स्थिति समय वक्र सरल रेखा है।
संकेत:
x = a₀ + a₁t + a₂t² + a₃t³
t = 0 पर स्थिति
= a₀
v = dx/dt = a₁ + 2a²t + 3a₃t²
t = 0 पर वेग
v = a₁
त्वरण a = dv/dt = 2a² + 6a³t
यहाँ पर त्वरण समय पर निर्भर है अतः यह नियत नहीं है।
अतः सही विकल्प (स) है।
उत्तर:
(स) कण का त्वरण नियत नहीं है

प्रश्न 15. 
कोई कण 6.28 मीटर त्रिज्या के वृत्तीय कक्ष में गति करते हुए जब व्यास के एक सिरे से दूसरे सिरे तक पहुँचता है तो तय की गई दूरी एवं विस्थापन में अनुपात होगा:

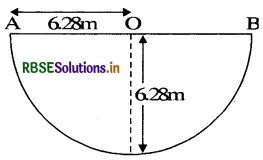
(अ) 2π
(ब) π
(स) π/2
(द) 1
संकेत:

अतः सही विकल्प (स) है।
उत्तर:
(स) π/2

प्रश्न 16. 
किसी वस्तु का विस्थापन समय के वर्ग के अनुक्रमानुपाती होता है तो वस्तु की गति होती है:
(अ) एकसमान त्वरण से
(ब) असमान त्वरण से
(स) एकसमान वेग से
(द) असमान त्वरण परन्तु एकसमान चाल से
उत्तर:
(अ) एकसमान त्वरण से

रिक्त स्थानों की पूर्ति कीजिए:

प्रश्न 1.
दो कारों का समय विस्थापन ग्राफ दो समान्तर रेखाओं से प्रदर्शित होता है। उनके वेगों में .............................. का सम्बन्ध होता है।
उत्तर:
बराबर

प्रश्न 2.
किसी कार का समय वेग ग्राफ समय अक्ष के समान्तर सरल रेखा है। तब इसका त्वरण ................ होगा। 
उत्तर:
शून्य

प्रश्न 3.
दूरी-समय ग्राफ का ढाल .......................... प्रदर्शित करता है।
उत्तर:
चाल

प्रश्न 4.
समय चाल ग्राफ में समय अक्ष तथा ग्राफ के मध्य का क्षेत्रफल .................... प्रदर्शित करता है।
उत्तर:
दूरी

 

प्रश्न 5.
वेग घटने की समय दर ....................... कहलाता है।
उत्तर:
ऋणात्मक त्वरण
 
प्रश्न 6.
समय विस्थापन ग्राफ समय अक्ष के समान्तर सरल रेखा है। वेग तथा त्वरण के मान ........................  होंगे।
उत्तर:
दोनों शून्य

प्रश्न 7.
पृथ्वी तल से ऊर्ध्वाधरतः ऊपर की ओर फेंकी गयी गेंद / मी. ऊँचाई पर जाकर कुछ समय पश्चात् पृथ्वी पर ही लौट आती है, तब उसकी दूरी ................... तथा विस्थापन .............................. होंगे।
उत्तर:
2h, शून्य

प्रश्न 8.
वेग - समय ग्राफ का ढाल ....................... प्रदर्शित करता है।
उत्तर:
त्वरण

प्रश्न 9.
जब दोनों वस्तुएँ विपरीत दिशा में परस्पर सम्पर्क में गतिमान हैं तो A के सापेक्ष B का आपेक्षिक वेग ......................... होता है।
उत्तर:
VBA = VB - VA

प्रश्न 10.
वेग में परिवर्तन की दर को ............................ कहते हैं।
उत्तर:
त्वरण।

नीचे दिये गये वाक्यों में सत्य / असत्य कथन का चयन कीजिए:

प्रश्न 1.
स्थिर अवस्था से नियत त्वरित गति प्रारम्भ करने वाले पिण्ड के लिए दूरी तथा समय के मध्य ग्राफ परवलयाकार होगा।
उत्तर:
सत्य 

प्रश्न 2.
वर्षा की बूँदें एक समान त्वरण से गिरती हैं।
उत्तर:
असत्य

प्रश्न 3.
जब हम किसी वस्तु को ऊपर की ओर फेंकते हैं, उस समय त्वरण, वेग की दिशा में होता है। 
उत्तर:
असत्य

प्रश्न 4.
सीधी पटरी पर रेलगाड़ी की गति एक विमीय गति होती है।
उत्तर:
सत्य

प्रश्न 5.
वृत्ताकार पथ में किसी कण के द्वारा एक चक्कर पूरा करने में विस्थापन शून्य, तय की गई दूरी πr होती है।
उत्तर:
असत्य

प्रश्न 6.
वृत्तीय गति में किसी पिण्ड को बिना चाल बढ़ाये या घटाये त्वरित किया जा सकता है।
उत्तर:
सत्य

प्रश्न 7.
वेग-समय ग्राफ का क्षेत्रफल विस्थापन भौतिक राशि का मान होता है।
उत्तर:
सत्य

प्रश्न 8.
अवंकलन के रूप में त्वरण a = dv/dt तथा a = d2x/dt2 होता है।
उत्तर:
सत्य

प्रश्न 9.
किसी बस का चाल मापक तात्क्षणिक चाल का मापन करता है।
उत्तर:
सत्य

प्रश्न 10.
किसी समान त्वरित वस्तु का तात्क्षणिक वेग शून्य हो सकता है।
उत्तर:
सत्य

कॉलम - A से कॉलम B का सही मिलान कीजिए:

प्रश्न 1. 

1. वृत्ताकार पथ के लिए यदि कोई वस्तुरिथति A से गतिशील होकर पुनः A पर आ जाये विस्थापन का मान होगा?	(A) एक विमीय गति में जब पिण्ड की दिशा नहीं बदले
2. औसत वेग किस तरह की राशि है?	(B) 1 : 3
3. जब पिण्ड एक सरल रेखा में एक ही दिशा में नियत वेग से गतिशील हो, तब पिण्ड कात्वरण का मान कितना होगा?	(C) अनुक्रमानुपाती
4. असमान वेग रिथित में विस्थापन समय आरेख सरल रेखा के अतिंरिक्त करना होगा	(D) वेग-समय ग्राफ के ढल द्वारा
5. वेग-समय ग्राफ में वक्र और समय अका के मध्य का क्षेत्रफल, पिण्ड के कौनसी राशि के बराबर होता है?	(E) tanθ
6. त्वरण a = dv/dt	(F) विस्थापन
7. किसी गतिमान वस्तु का त्वरण किस प्रकार ज्ञात करते हैं?	(G) किसी भी आकृति का
8. यदि दो राशियों का परस्पर ग्राफ सरल रेखा में हो तो दोनों राशियाँ होती हैं?	(H) शून्य
9. स्वतंत्रतापूर्वक गिर रही एक वस्तु द्वारा अपने प्रथम तथा द्वितीय सेकण्ड में पार की गई दूरियों का अनुपात है-	(I) सदिश
10. पिण्ड की कौनसी रिथिति में विस्थापन का मान, पिण्ड द्वारा तय की गई दूरी के बराबर होता है?	(J) शून्य

उत्तर:

1. वृत्ताकार पथ के लिए यदि कोई वस्तुरिथति A से गतिशील होकर पुनः A पर आ जाये विस्थापन का मान होगा?	(J) शून्य
2. औसत वेग किस तरह की राशि है?	(I) सदिश
3. जब पिण्ड एक सरल रेखा में एक ही दिशा में नियत वेग से गतिशील हो, तब पिण्ड कात्वरण का मान कितना होगा?	(H) शून्य
4. असमान वेग रिथित में विस्थापन समय आरेख सरल रेखा के अतिंरिक्त करना होगा	(G) किसी भी आकृति का
5. वेग-समय ग्राफ में वक्र और समय अका के मध्य का क्षेत्रफल, पिण्ड के कौनसी राशि के बराबर होता है?	(F) विस्थापन
6. त्वरण a = dv/dt	(E) tanθ
7. किसी गतिमान वस्तु का त्वरण किस प्रकार ज्ञात करते हैं?	(D) वेग-समय ग्राफ के ढल द्वारा
8. यदि दो राशियों का परस्पर ग्राफ सरल रेखा में हो तो दोनों राशियाँ होती हैं?	(C) अनुक्रमानुपाती
9. स्वतंत्रतापूर्वक गिर रही एक वस्तु द्वारा अपने प्रथम तथा द्वितीय सेकण्ड में पार की गई दूरियों का अनुपात है-	(B) 1 : 3
10. पिण्ड की कौनसी रिथिति में विस्थापन का मान, पिण्ड द्वारा तय की गई दूरी के बराबर होता है?	(A) एक विमीय गति में जब पिण्ड की दिशा नहीं बदले

 

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
औसत वेग व औसत चाल में अन्तर स्पष्ट कीजिए।
उत्तर:

कण के वापस प्रारम्भिक स्थिति में लौट आने पर विस्थापन शून्य होने से औसत वेग का मान शून्य होगा, जबकि औसत चाल का मान शून्य नहीं हो सकता।

प्रश्न 2. 
यदि गेंद A स्वतंत्रतापूर्वक छोड़ी जाये तथा साथ ही साथ गेंद B को क्षैतिज दिशा में u वेग से प्रक्षेपित किया जाये, तो पृथ्वी पर कौनसी गेंद पहले पहुँचेगी?
उत्तर:
दोनों गेंदों के लिए ऊर्ध्वाधर दिशा में प्रारम्भिक वेग (u) शून्य, समान त्वरण तथा ऊर्ध्वाधर दिशा में चली दूरी समान है। अतः h = 1/2gt2 से दोनों गेदों के पृथ्वी तल पर पहुँचने में समान समय लगेगा।

प्रश्न 3. 
किस स्थिति में पिण्ड के विस्थापन का मान, पिण्ड द्वारा तय की गई दूरी के बराबर होता है?
उत्तर:
एकविमीय गति में जब पिण्ड की दिशा नहीं बदले। 

प्रश्न 4. 
क्या विस्थापन समय आरेख में वक्र समय अक्ष के लम्बवत् हो सकता है?
उत्तर:
नहीं। क्योंकि वक्र का ढाल अनन्त नहीं हो सकता है। 

प्रश्न 5. 
एकविमीय गति में पिण्ड के विस्थापन का मान तथा पिण्ड द्वारा तय की गई दूरी में क्या सम्बन्ध है?
उत्तर:
बराबर।

प्रश्न 6. 
वेग- समय ग्राफ का ढाल क्या दर्शाता है?
उत्तर:
त्वरण।

प्रश्न 7. 
वेग समय ग्राफ का क्षेत्रफल किस भौतिक राशि का मान देता है?
उत्तर:
विस्थापन का।

प्रश्न 8. 
तात्क्षणिक वेग के मान तथा तात्क्षणिक चाल के मान में क्या सम्बन्ध है?
उत्तर:
बराबर होते हैं।

प्रश्न 9. 
एकविभीय गति में कोई एक उदाहरण दीजिये। 
उत्तर:
सीधी पटरी पर रेलगाड़ी की गति।

प्रश्न 10. 
क्या किसी समान त्वरित वस्तु का तात्क्षणिक वेग शून्य हो सकता है?
उत्तर:
हाँ चूँकि ऊपर की ओर फेंकी गई वस्तु का उच्चतम बिन्दु पर तात्क्षणिक वेग शून्य होता है जबकि वस्तु (g) से त्वरित है।

प्रश्न 11. 
स्थिर अवस्था से नियत त्वरित गति प्रारम्भ करने वाले पिण्ड के लिये दूरी तथा समय के मध्य ग्राफ कैसा होगा?
उत्तर:
परवलयाकार।

प्रश्न 12. 
किस स्थिति में कण का औसत वेग तथा औसत चाल के मान समान होंगे?
उत्तर:
कण के समान वेग से सीधी रेखा 

प्रश्न 13. 
प्रश्न क्रमांक 11 में पिण्ड की चालकैसा होगा ?
उत्तर:
सरल रेखा।

प्रश्न 14. 
एकविमीय गति का कोई उदाहरण दीजिये जिसमें त्वरण, वेग के विपरीत दिशा में हो।
उत्तर:
जब हम किसी वस्तु को ऊपर की ओर फेंकते हैं उस समय त्वरण, वेग के विपरीत दिशा में होता है।

प्रश्न 15. 
क्या किसी समान त्वरित वस्तु का तात्क्षणिक वेग शून्य हो सकता है ?
उत्तर:
हाँ।

प्रश्न 16. 
स्वतन्त्रतापूर्वक गिर रही वस्तु द्वारा अपने प्रथम तथा द्वितीय सेकण्ड में पार की गई दूरियों का अनुपात क्या है?
उत्तर:
S1 = 0 + 1/2 g (2 x 1 - 1) = 1/2 g
S2 = 0 + 1/2g(2 x 2 - 1) = 3/2 g
S1 : S2 = 1 : 3

प्रश्न 17. 
वर्षा की बूँदें एकसमान वेग से गिरती हैं अथवा एकसमान त्वरण से।
उत्तर:
वर्षा की बूँदें एकसमान वेग से गिरती हैं।

प्रश्न 18. 
किसी कण का वेग नियत होने पर क्या उसकी चाल परिवर्तित हो सकती है?
उत्तर:
नहीं, यहाँ विस्थापन के परिवर्तन की दर व दिशा नहीं बदलने के कारण हर क्षण चाल भी नियत बनी रहेगी।

प्रश्न 19. 
किसी बस का चाल मापक औसत चाल का मापन करता है या तात्क्षणिक चाल का?
उत्तर:
तात्क्षणिक चाल का।

प्रश्न 20. 
वृत्ताकार पथ में किसी कण के द्वारा एक चक्कर पूरा करने में विस्थापन, तय की गई दूरी कितनी होती है? 
उत्तर:
विस्थापन शून्य, तय की गई दूरी = 2πr

प्रश्न 21. 
क्या किसी समय कोई पिण्ड स्थिर एवं गतिशील दोनों हो सकता है?
उत्तर:
हाँ, क्योंकि गति आपेक्षिक होती है।

प्रश्न 22. 
दो स्कूटरों का समय वेग ग्राफ संलग्न चित्रों (अ) व (ब) में प्रदर्शित है। इनके त्वरणों में क्या सम्बन्ध है?

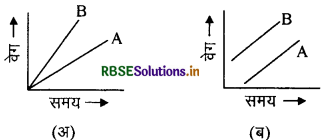
उत्तर:
चित्र (अ) में त्वरण A त्वरण B से कम होगा; चित्र (ब) में दोनों का त्वरण समान होगा, क्योंकि
a = tan θ

प्रश्न 23. 
संलग्न चित्र द्वारा वस्तु के वेग तथा त्वरण के बारे में क्या निष्कर्ष निकलता है?

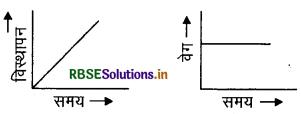
उत्तर:
दोनों में वस्तु एक समान वेग से गतिमान है तथा त्वरण शून्य

प्रश्न 24. 
पेड़ पर बैठे बन्दर के ठीक ओर एक शिकारी निशाना लगाता है। जैसे ही शिकारी गोली छोड़ता है, उसी क्षण बन्दर पेड़ से नीचे ऊर्ध्वाधर गिर पड़ता है क्या गोली बन्दर को लगेगी? क्या बन्दर को गोली लगना अथवा न लगना गोली के प्रारम्भिक वेग पर निर्भर है?
उत्तर:
बन्दर के गिरने पर गोली बन्दर को लगेगी। चाहे गोली का छूटते समय वेग कुछ भी हो।

प्रश्न 25. 
गति के तीनों समीकरणों को लिखिये।
उत्तर:
v = u + at
s = ut + 1/2at²
v² = u² + 2as

प्रश्न 26. 
अवकलन के रूप में त्वरण का मान लिखिये।
उत्तर:
\(-a=\frac{d v}{d t}, \quad a=\frac{d^2 x}{d t^2}\)

प्रश्न 27. 
क्या त्वरण का मान नियते रहते हुए. वेग की दिशा बदल सकती है?
उत्तर:
हाँ, ऊर्ध्वाधर गति में उच्चतम बिन्दु पर वेग की दिशा बदल जाती है, जबकि गुरुत्व जनित त्वरण g सदैव नियत बना रहता है। 

प्रश्न 28. 
कल्पना कीजिये कि कोई पिण्ड समान गति में चलायमान होने पर साम्यावस्था में होता है।
उत्तर:
पिण्ड पर नेट बल शून्य होता है।

प्रश्न 29. 
क्या किसी गतिशील पिण्ड का दूसरे पिण्ड की अपेक्षा सापेक्ष वेग शून्य हो सकता है? उदाहरण दीजिये।
उत्तर:
हाँ, हो सकता है जबकि दो रेलगाड़ियाँ समान्तर पटरियों पर समान चाल से एक ही दिशा में गमन करती हैं।

प्रश्न 30. 
क्या कोई एकविमीय त्वरण के होते हुए द्विविमीय गति हो सकती है?
उत्तर:
हाँ, प्रक्षेपित गति।

प्रश्न 31. 
नीचे दिये गये आरेखों में क्या उभयनिष्ठ है बताइये:

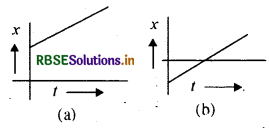
उत्तर:
उपर्युक्त दोनों आरेख धनात्मक वेग दर्शाते हैं। 

प्रश्न 32. 
नीचे दिये गये आरेखों में क्या समानता है:

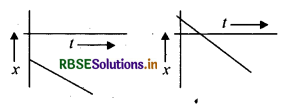
उत्तर:
दोनों ही आरेखों में वेग ऋणात्मक है।

प्रश्न 33. 
किसी पिण्ड को बिना चाल बढ़ाये या घटाये त्वरित किया जा सकता है। उदाहरण दीजिये।
उत्तर:
हाँ, वृत्तीय गति।

प्रश्न 34. 
वेग परिवर्ती होता है तो क्या वेग परिवर्तन की दर दोनों परिमाण एवं दिशा में समान रह सकती है? एक उदाहरण दीजिये। 
उत्तर:
हाँ, प्रक्षेप गति में।

प्रश्न 35. 
एक रेलगाड़ी जिसमें आप सवार हैं, अपने पास वाली रेलगाड़ी के सापेक्ष बिना झटका खाये चल देती है, तो आप देखते हैं कि दूसरी वाली रेलगाड़ी चल रही है। लेकिन जब आप प्लेटफार्म की तरफ देखते हैं, तो पता चलता है कि आपकी गाड़ी चल रही है। ऐसी गति के लिये उत्तरदायी घटना का नाम बताइये।
उत्तर:
आपेक्षिक गति।

प्रश्न 36. 
x = 5 + 10t + 5t² द्वारा विस्थापन दिया है। तात्क्षणिक त्वरण का मान ज्ञात कीजिये।
उत्तर:
तात्क्षणिक त्वरण (a) = d2x/dt²
dx/dt = 0 + 10 × 1 + 5 x 21 
∴ d²x/dt² = 0 + 10 × 1 = 10
अतः तात्क्षणिक त्वरण
(a) = 10

प्रश्न 37 
कोई दो कण A व B एक ही रेखा के अनुदिश गतिमान हैं और B, A के आगे है वेग का मान यदि अपरिवर्तित रहे और A B से आगे हो तो आपेक्षिक वेग के परिमाण पर क्या प्रभाव होगा?
उत्तर:
आपेक्षिक वेग के परिमाण पर कोई प्रभाव नहीं होगा। 

प्रश्न 38. 
एक पत्थर को ऊर्ध्वाधर ऊपर की ओर पृथ्वी तल से फेंका जाता है, जब पत्थर
(a) अपने ऊपरमुखी मार्ग पर अग्रसर है।
(b) अपनी अधोगति में चल रहा है, तो उसके वेग की दिशा तथा त्वरण किस दिशा में कार्य कर रहे हैं?
उत्तर:
(a) ब्रेग ऊपरमुखी तथा त्वरण अधोमुखी होता है। 
(b) दोनों वेग तथा त्वरण अधोमुखी होंगे।

प्रश्न 39. 
क्या किसी तार का त्वरण उस समय अधिक होगा जब त्वरित्र को फर्श की ओर धकेला जाता है या जब ब्रेक पैडल को सख्ती से दबाया जाता है?
उत्तर:
त्वरण की मात्रा उस समय अधिक होगी जब ब्रेक पैडल को सख़्ती से दबाया जाता है, क्योंकि कार वेग की स्थिति से विराम स्थिति में आ जाती है। अतः कार के वेग परिवर्तन की दर (त्वरण) अधिक होती है।

प्रश्न 40. 
विस्थापन - समय आरेख पर दो छात्रों की गति आपस में कटती हुई सरल रेखाओं से दिखायी गयी है। कटाव बिन्दु से गति के विषय में आप क्या सूचना प्राप्त कर सकते हैं?
उत्तर:
कटाव बिन्दु से यह सूचना प्राप्त होती है कि किसी समय दोनों व्यक्ति किस स्थान पर एक-दूसरे को मिलते हैं।

प्रश्न 41. 
यदि किसी कण का औसत वेग इसके तात्क्षणिक वेग के तुल्य हो तो विस्थापन समय आरेख की क्या आकृति होगी? 
उत्तर:
X - 1 आरेख एक सरल रेखा होगा 

प्रश्न 42. 
यदि पृथ्वी की गति सूर्य के परितः उसकी कक्षा में ही ली जाये तो क्या पृथ्वी को बिन्दु पिण्ड माना जा सकता है? क्यों? 
उत्तर:
हाँ, क्योंकि सूर्य के परितः पृथ्वी का अपनी कक्षा पृथ्वी के आकार से बहुत लम्बा होता है।

प्रश्न 43. 
यदि किसी वस्तु का वेग स्थिर हो तो क्या उसकी चाल बदल सकती है? क्यों?
उत्तर:
नहीं बदल सकती। चूँकि चाल वेग का परिमाण होती है। 

प्रश्न 44. 
क्या एक गतिशील वस्तु का दूसरी गतिशील वस्तु की तुलना में आपेक्षिक वेग शून्य हो सकता है? कोई उदाहरण दीजिए। 
उत्तर:
हाँ।
उदाहरण: जब गतिशील दोनों वस्तुएँ (उदाहरणार्थ, कारें) बराबर वेग से एक ही दिशा में गतिशील होती हैं तो उनका आपेक्षिक वेग (उनके वेगों का अन्तर) शून्य होता है।

प्रश्न 45. 
दो वस्तुओं जिनकी आरम्भिक स्थितियाँ भिन्न हैं, परन्तु उनमें आपेक्षिक वेग शून्य है के लिये स्थिति समय का आरेख खींचिये।
उत्तर:

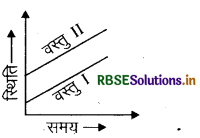
प्रश्न 46.
चित्र में किसी पिण्ड का विस्थापन समय आरेख दिखाया गया है। t < 0 तथा i > 0 के लिये वक्र क्या दिखाता है?

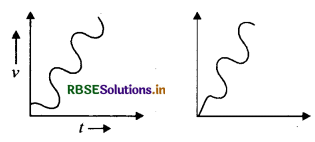
उत्तर:
आरेख से स्पष्ट है कि t < 0 पर पिण्ड विराम t = 0 के लिये भी पिण्ड विराम में है, परन्तु किसी और बिन्दु t > 0 के लिये 0 से भिन्न है।

प्रश्प 47. 
धनात्मक और ऋणात्मक समय से आप क्या समझते हैं? 
उत्तर:
समय का आरम्भ बिन्दु शून्य समय माना जाता है। आरम्भ के बाद लिया समय का क्षण धनात्मक तथा आरम्भ से पहले का क्षण ऋणात्मक समय माना जाता है।

प्रश्न 48. 
नीचे दिये गये दो आरेख एक ही प्रकार की गति को दर्शाते हैं या नहीं? कण की गति का नाम लिखिये।
उत्तर:
हाँ, दोनों आरेख एक ही प्रकार की गति को दर्शाते - असमान गति।

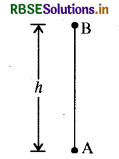
प्रश्न 49.
सामने दिये गये चित्र में कोई वस्तु पृथ्वी पर किसी बिन्दु A से ऊर्ध्वाधर ऊपर की ओर उछाली जाती है जो बिन्दु B पर है ऊँचाई तक जाकर पुनः पृथ्वी पर बिन्दु पर लौट आती है। अन्तिम स्थिति में इसका विस्थापन व तय की गई दूरी क्या होगी?
उत्तर:
वस्तु द्वारा तय की गई दूरी पथ की कुल लम्बाई
= h + h = 2h
कुल विस्थापन = विस्थापन AB + विस्थापन BA

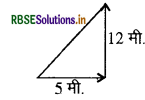
प्रश्न 50, 
कोई पिण्ड 5 मीटर पूर्व की ओर चलता है तत्पश्चात् 12 मीटर उत्तर की ओर 1 पिण्ड की चली हुयी दूरी व विस्थापन की गणना कीजिये।
उत्तर:
पिण्ड द्वारा तय की गई दूरी = 5 + 12
= 17 मीटर
विस्थापन = \(\sqrt{(5)^2+(12)^2}\)
\(=\sqrt{25+144}=\sqrt{169}\)
= 13 मीटर

लघुत्तरात्मक प्रश्न:

प्रश्न 1. 
क्या यह सम्भव है कि किसी वस्तु का औसत वेग शून्य है परन्तु औसत चाल शून्य न हो? यदि हाँ तो उदाहरण देकर स्पष्ट कीजिए। क्या इसका विपरीत भी सम्भव है?
उत्तर:
हाँ, जैसे किसी वस्तु को ऊर्ध्वाधर फेंकने पर वह प्रारम्भिक बिन्दु पर वापस आ जाये, तो उसका औसत वेग शून्य होता है, परन्तु औसत चाल नहीं।

प्रश्न 2. 
किसी नाव को शान्त हवा की स्थिति में तालाब के एक किनारे से दूसरे किनारे पर तथा वापस आने में लगा समय t₁ है। तूफान के आने की स्थिति में नाव को जाने तथा आने में t₂ समय लगता है। t₁ व t₂ में क्या सम्बन्ध है?
उत्तर:
शान्त हवा की स्थिति में जल भी शान्त होता है। यदि तालाब की चौड़ाई x नाव की चाल v तथा जल की चाल ॥ हो तो शान्त जल की स्थिति में

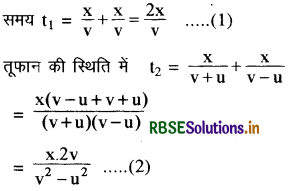
समीकरण (1) तथा (2) से स्पष्ट है कि नाव को तूफान के समय ज्यादा समय लगेगा।
t₂ > t₁

प्रश्न 3. 
जब दो ट्रेनें समान वेग से एक-दूसरे के समान्तर गतिशील होती हैं तो एक ट्रेन में बैठे व्यक्ति को दूसरी ट्रेन स्थिर क्यों प्रतीत होती है?
उत्तर:
ऐसा सापेक्ष वेग के कारण होता है क्योंकि दोनों ट्रेनों का वेग बराबर है अतः उनका एक-दूसरे के सापेक्ष वेग शून्य होगा। 
A ट्रेन का वेग = 100 km/hr, पूर्व की ओर 
B ट्रेन का वेग = 100 km/hr, पूर्व की ओर
A ट्रेन का B ट्रेन के सापेक्ष वेग = 100 - 100 = 0

प्रश्न 4. 
निम्न की परिभाषा देकर अन्तर स्पष्ट कीजिये:
(i) दूरी और विस्थापन
(ii) औसत चाल और औसत वेग
(iii) तात्क्षणिक वेग और तात्क्षणिक त्वरण 
उत्तर:
(i) दूरी एक पिण्ड द्वारा चले गये पथ की वास्तविक लम्बाई को दूरी कहते हैं। 
विस्थापन - पिण्ड की प्रारम्भिक स्थिति से अन्तिम स्थिति को मिलाने वाली रेखा की लम्बाई विस्थापन का मान कहलाती है। पिण्ड की प्रारम्भिक स्थिति से अन्तिम स्थिति को मिलाने वाला सदिश, विस्थापन सदिश कहलाता है।

दूरी और विस्थापन में अन्तर- 

दूरी	विस्थापन
(i) यह एक अदिश राशि है।	जबकि विस्थापन सदिश राशि है।
(ii) दूरी का मान विस्थापन के बराबर या बड़ा होता है।	जबकि विस्थापन का मान दूरी से कम या बराबर हो सकता है।
(iii) एक गतिशील वस्तु के लिये समय में वृद्धि के साथ-साथ दूरी सदैव बढ़ती है।	जबकि विस्थापन का मान ऐसी स्थिति में बढ़ या घट सकता है।

(ii) औसत चाल और औसत वेग:
औसत चाल (Average Speed) किसी समय अन्तराल ∆t में एक पिण्ड द्वारा तय की गई दूरी ∆s और समयान्तराल ∆t का अनुपात पिण्ड की औसत चाल कहलाती है।
औसत चाल Vav = ∆s/∆t
अर्थात् किसी पिण्ड की औसत चाल प्रति एकांक समय में चली गई औसत दूरी के बराबर होती है।

औसत वेग (Average Velocity): किसी समय अन्तराल ∆t में एक पिण्ड का विस्थापन ∆ और समय अन्तराल का अनुपात औसत वेग कहलाता है।
औसत वेग, 
\(\begin{aligned} & \overrightarrow{\mathrm{v}}_{\mathrm{av}}=\frac{\overrightarrow{\Delta \mathrm{x}}}{\Delta \mathrm{t}} \\ & \mathrm{v}_{\mathrm{av}}=\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}=\frac{\mathrm{x}_2-\mathrm{x}_1}{\mathrm{t}_2-\mathrm{t}_1} \end{aligned}\)

औसत चाल और औसत वेग में अन्तर:

1. औसत चाल एक अदिश राशि है जबकि औसत वेग एक सदिश राशि होती है।
2. औसत चाल सदैव धनात्मक होती है जबकि औसत वेग धनात्मक या ऋणात्मक हो सकता है।

(iii) तात्क्षणिक वेग और तात्क्षणिक त्वरण:
तात्क्षणिक वेग (Instantaneous Velocity): किसी दिये हुए क्षण पर वस्तु के वेग को उसका तात्क्षणिक वेग कहते हैं। यह Δx/Δt सीमान्त मान के बराबर होता है जब Δr का मान कम होते-होते शून्य हो जाए। इस प्रकार तात्क्षणिक वेग-
सदिश रूप में
\(v=\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=\frac{d x}{d t}\)
तात्क्षणिक त्वरण: किसी दिये हुए क्षण पर वस्तु के त्वरण को
उसका तात्क्षणिक त्वरण कहते हैं। यह Δν के सीमान्त मान के बराबर होता है जब Δt का मान कम होते-होते शून्य हो जाए इस प्रकार तात्क्षणिक त्वरण

तार्क्षणिक वेग	तात्क्णणिक त्वरण
(i) इसका मात्रक मी./से. है व विमा M0L1T-1 है।	इसका मात्रक मी./ से. 2 है व विमा M0L1T-2 है।
(ii) इसका मान विस्थापन के समय के सापेक्ष प्रथम अवकलन के तुल्य होता है।	इसका मान विस्थापन के समय के सापेक्ष द्वितीय अवकलन के तुल्य होता है।

प्रश्न 5. 
चाल और वेग में क्या अन्तर है? 
उत्तर:

चाल	वेग
(i) कोई पिण्ड इकाई समय में कितनी दूरी तय करता है वह उसकी चाल कहलाती है।	कोई पिण्ड इकाई समय में किसी निश्चित दिशा में जितनी दूरी तय करता है वह उसका वेग कहलाता है।
(ii) यह अदिश राशि है।	यह सदिश राशि है।
(iii) चाल सदैव धनात्मक होती है।	वेग धनात्मक, ऋणात्मक या शून्य कुछ भी हो सकता है।
(vi) इसमें केवल गति के परिमाण का बोध होता है।	इसमें गति के परिमाण के साथ दिशा का भी बोध होता है।

प्रश्न 6. 
एकसमान गति और एकसमान त्वरित गति के लिये वेग-समय आलेखों में क्या भिन्नता होती है?
उत्तर:
नियत वेग से गतिशील पिण्ड की गति एकसमान गति कहलाती है। एकसमान गति में वेग (v) और समय (1) के मध्य ग्राफ, समय अक्ष के समानान्तर एक रेखा प्राप्त होती है। एकसमान त्वरित गति में किसी क्षण पर पिण्ड का तात्क्षणिक त्वरण उस क्षण पर वेग समय ग्राफ पर खींची गई स्पर्श रेखा के ढाल के बराबर होता है।

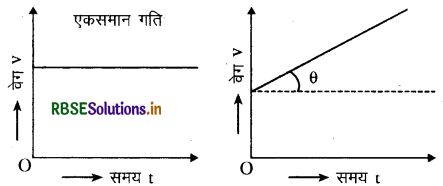
ग्राफ के अनुसार वस्तु का वेग समय के साथ बढ़ेगा। इसके ढाल से त्वरण (a) का मान ज्ञात किया जा सकता है a = tanθ

प्रश्न 7. 
वेग समय आलेख से विस्थापन कैसे ज्ञात करेंगे? समझाइये।
उत्तर:
एकसमान गति में वेग और समय के मध्य खींचे गये ग्राफ (सरल रेखा) व समय अक्ष के बीच बन रहे आयत का क्षेत्रफल, पिण्ड द्वारा तय की गई दूरी (विस्थापन) के बराबर होता है। समय अन्तराल (t2 - t1) में पिण्ड द्वारा तय की गई दूरी ही विस्थापन होगी। चूँकि यहाँ पर एकविमीय में गति हो रही है और दिशा परिवर्तित नहीं हो रही है।
दूरी = वेग x समय
X2 - x1 = V (t2 - t1)

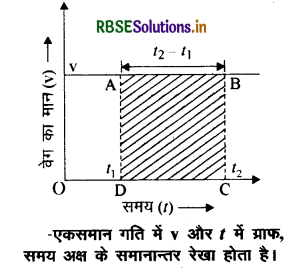
समय अक्ष के समानान्तर रेखा होता है।
व्यापक वेग-समय ग्राफ में भी वक्र और समय अक्ष के मध्य का क्षेत्रफल विस्थापन के बराबर होता है।

प्रश्न 8. 
चित्र में एक काल्पनिक एकविमीय गति के लिये विस्थापन - समय ग्राफ दर्शाया गया है। स्पष्ट कीजिये कि इस प्रकार की गति संभव क्यों नहीं है?

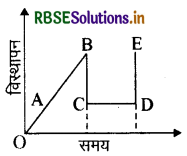
उत्तर:
चित्र में समय- विस्थापन ग्राफ के दो भाग हैं, उनको दो खड़ी रेखाओं द्वारा प्रदर्शित किया गया है। चित्र से स्पष्ट है कि वस्तु का वेग दो शून्य अन्तरालों में अनन्त है। चूँकि किसी वस्तु का वेग प्रकाश के वेग से अधिक नहीं हो सकता है, इसलिये वस्तु का समय - विस्थापन सही नहीं है।

प्रश्न 9. 
एक वस्तु को ऊर्ध्वाधर ऊपर की ओर फेंका जाता है। कुछ समय पश्चात् यह धरती पर लौट आती है। गेंद के लिये चाल- समय ग्राफ खींचिये।
(नोट- यहाँ पर वायुजनित प्रतिरोध नगण्य मानें )।

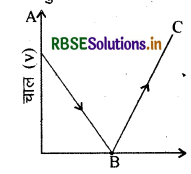
उत्तर:
जब वस्तु को ऊपर की ओर फेंका जाता है तो उसे प्रारम्भिक वेग देकर फेंकते हैं। ऊपर जाने पर वेग में कमी होती है तथा उच्चतम बिन्दु पर वेग शून्य हो जाता है। इसके पश्चात् गेंद नीचे आती है तथा वेग बढ़ता है।

प्रश्न 10. 
कोई पिण्ड समान त्वरण से गति कर रहा है। उसके द्वारा वें सेकण्ड में चली गयी दूरी के लिये व्यंजक स्थापित कीजिये।
उत्तर:
माना पिण्ड का प्रारम्भिक वेग है, समान त्वरण से सेकण्ड में चली गई दूरी ज्ञात करनी गतिमान है। हमको पिण्ड द्वारा है।
पिण्ड द्वारा सेकण्ड में चली दूरी
st = ut + 1/2at²
पिण्ड द्वारा ( t -1) सेकण्ड में चली दूरी
St-1 = u (t - 1) + 1/2a(t - 1)²
∴ t वें सेकण्ड में पिण्ड द्वारा चली गई दूरी- 
S = St - St - 1
S = (ut + 1⁄2at²) - (u(t-1) + 1⁄2a(t-1)²)
S = ut + 1/2at² - (ut - u + 1/2a(t² - 2t + 1)
S = ut + 1/2at² - ut - u - 1/2a(t² - 2t + 1)
S = ut + 1/2at² -  1/2a(t² - 2t + 1)
S = ut + 1/2at² - 1/2at² + at - 1/2a
S = ut + 1/2a(2t - 1)

प्रश्न 11. 
वेग समय ग्राफ के अध्ययन से एकविमीय गति कर रहे कण के लिये क्या महत्वपूर्ण निष्कर्ष प्राप्त किये जा सकते हैं? समझाइये 
उत्तर:
यदि वेग समय ग्राफ समय अक्ष के समानान्तर सरल रेखा है जैसा चित्र (अ) में दिखाया गया है तब यह नियत वेग से गति को दर्शाता है। जहाँ वेग समय ग्राफ का ढाल त्वरण के बराबर होता है।

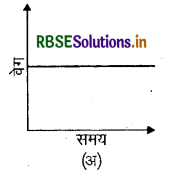
चित्र (ब) में ढाल धनात्मक है अर्थात् त्वरण की दिशा, वेग की दिशा में ही है और वेग में समय के साथ वृद्धि हो रही है।

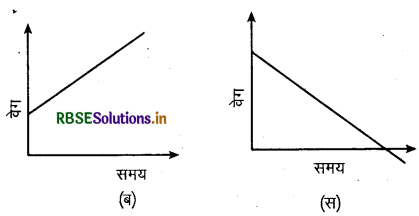
चित्र (स) में ढाल ऋणात्मक है। इसमें कण की गति मंदित है। इसमें त्वरण की दिशा वेग की दिशा के विपरीत है। इस स्थिति में कण का वेग घटकर शून्य हो जायेगा। वेग समय ग्राफ में वक्र और समय अक्ष के मध्य के विभिन्न भागों के क्षेत्रफलों के मानों का योग, कण द्वारा तय की गई दूरी के बराबर होता है, जबकि विभिन्न भागों के क्षेत्रफल का बीजगणितीय योग विस्थापन के बराबर होता है।

आंकिक समीकरण:

प्रश्न 1. 
एक व्यक्ति 15 मीटर उत्तर की ओर फिर 8 मीटर पूर्व की ओर चलता है। उसका प्रारम्भिक स्थिति से विस्थापन ज्ञात कीजिए।
उत्तर:

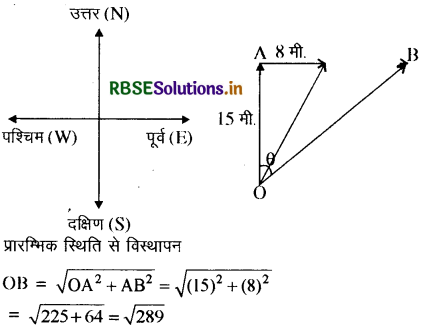
= 17 मीटर
tan θ =
∴ θ = tan^-1(8/15)

प्रश्न 2. 
तीन साइकिल सवार (A, B, C) निम्न चित्रानुसार चलकर P से Q पर एक साथ 10 सेकण्ड में पहुँचते हैं। यदि वृत्त की त्रिज्या 10 मीटर हो तो ज्ञात करो:
(i) तीनों का विस्थापन
(ii) तीनों का औसत वेग तथा
(iii) तीनों की औसत चाल ज्ञात करो। 
उत्तर:
(i) तीनों का विस्थापन

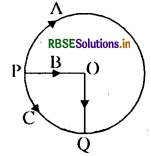
प्रश्न 3. 
एक वाहन चालक किसी स्थान से दूसरे स्थान तक 20 मी./से. गति करते हुए पहुँचकर तुरन्त ही प्रथम स्थान की ओर 30 मी./से. चाल से लौटता है तो इसकी औसत चाल व औसत वेग ज्ञात करो।

उत्तर:
दिया गया है- V₁ = 200 मी./से.
V₂ = 300 मी./से.
तय की गई कुल दूरी s = s₁ + s₂ होगी
यदि A से B तक जाने व B से A तक वापस आने में लगे समय क्रमशः t₁ व t₂ हैं तो
t₁ = s1/20 ............ (1)
t₂ = s²/30 = s1/30 ............ (2)

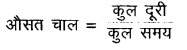
औसत चाल = \(\frac{s_1+s_2}{t_1+t_2}\)
\(=\frac{2 s_1}{\frac{s_1}{20}+\frac{s_1}{30}}=\frac{2 s_1}{\frac{5 s_1}{60}}\)
= 24 मी./से.
क्योंकि कण का कुल विस्थापन शून्य है अतः

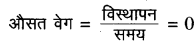
प्रश्न 4. 
दो बसें 150 किमी. की यात्रा पर एक साथ चलती हैं। उनकी चाल क्रमशः 45 किमी./ घण्टा तथा 60 किमी./ घण्टा है। बताओ तेज बस कितने समय पहले पहुँच जायेगी?
उत्तर:

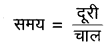
∴ पहली बस का समय t₁ = 150/45 = 10/3 घण्टा
∴ दूसरी बस का समय t₂ = 150/60 = 5/2  घण्टा
∴ दूसरी बस द्वारा कम समय = 10/3 - 5/2
\(=\frac{20-15}{6}=\frac{5}{6}\) घण्टा
= 5/6 x 60 मिनट = 50 मिनट
अतः तेज बस 50 मिनट पहले पहुँचेगी।

प्रश्न 5. 
एक बस की चाल 35 किमी. प्रति घण्टे से बढ़कर 5 सेकण्ड में 80 किमी./ घण्टा हो जाती है। बस का माध्य त्वरण ज्ञात करो।
उत्तर:
माध्य त्वरण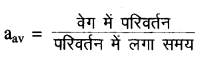
\(=\frac{\mathrm{v}_2-\mathrm{v}_1}{\Delta \mathrm{t}}\)
दिया गया है
V1 = 35 किमी./ घण्टा
\(=\frac{35}{3600}\)किमी./से
V2 = 80 किमी./ घण्टा
\(=\frac{80}{3600}\)किमी./से
इसलिए माध्य त्वरण aav =

प्रश्न 6. 
एक कण एकविमीय गति कर रहा है। इस कण की स्थिति x समय पर निम्न प्रकार निर्भर कर रही है-
x (t) = 8 + 4t
जहाँ दूरी मीटर में और समय सेकण्ड में मापा गया है। कण के (i) समय t = 2 सेकण्ड पर तात्क्षणिक वेग और (ii) समय अन्तराल t = 0 सेकण्ड से t = 2 सेकण्ड के लिए औसत वेग, के मान ज्ञात करो।
उत्तर:
(i) तात्क्षणिक वेग का मान
v = dx/dt = d/dt (8 + 4t - t²)
v = 0 + 4 - 2t = (4 - 2t)
अतः t = 2 सेकण्ड पर
v= 4 - 2 x 2 = 440मी./से.² 
कण का क्षण t = 2 सेकण्ड पर तात्क्षणिक वेग शून्य है।

(ii) औसत वेग का मान
\(\mathrm{v}_{\mathrm{av}}=\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}=\frac{\mathrm{x}(2)-\mathrm{x}(0)}{2-0}\)
दिया है:
x (t) = 8 + 4t - t²
∴ x (2) = 8 + 4 × 2 - (2)² 
= 8 + 8 – 4
= 12 मीटर
x (0) = 8 + 4 x 0 - 0² = 8 मीटर
अतः
\(\mathrm{v}_{\mathrm{av}}=\frac{12-8}{2}=\frac{4}{2}\) = 2 मी./से.

प्रश्न 7. 
किसी वस्तु का विस्थापन समय के साथ s = t³ - 6t² + 3t + 4 के अनुसार परिवर्तित होता है तो जिस क्षण पर वस्तु का त्वरण शून्य है। इसका वेग क्या है?
उत्तर:
दिया गया है: s = t³ - 6t² + 3t + 4
∴ वेग = ds/dt = d/dt (t³ - 6t² + 3t +4)
v = 3t² - 6 x 2t + 3 × 1 + 0
v = 3t² - 12t + 3 ............... (1)
त्वरण a = dv/dt = d/dt (3t² - 12t + 3) 
a = 3 x 2t - 12 x 1 + 0
a = 61 - 12 ................. (2)
जब त्वरण a = 0 तो समीकरण (2) से
6t - 12 = 0
t = 2 सेकण्ड
t = 2 सेकण्ड पर वेग समीकरण (1) से
v = 3(2)² - 12(2) + 3
= 12 - 24 + 3 = 9 मी./से. यहाँ पर ऋणात्मक चिन्ह यह बताता है कि वस्तु का विस्थापन समय के साथ घट रहा है।

प्रश्न 8. 
यदि किसी कण का प्रारम्भिक वेग है तथा इसी दिशा में त्वरण समय के साथ αt अनुसार बदलता है तो कण का किसी क्षण पर वेग क्या होगा?
उत्तर:
यहाँ पर त्वरण परिवर्तित हो रहा है। इस प्रकार न्यूटन के गति के समीकरण का प्रयोग नहीं किया जा सकता है।
∴ त्वरण a = dv/dt  = αt dt
समीकरण (1) का समाकलन करने पर
\(\begin{aligned} \int d v & =\int \alpha t d t \\ v & =\frac{\alpha t^2}{2}+c \end{aligned}\) ............(2)
यहाँ c समाकलन नियतांक है।
t = 0 पर v = u रखने पर
u = 0 + cc = u
∴ समीकरण (2) से
\(\begin{aligned} & v=\frac{\alpha t^2}{2}+u \\ & v=u+\frac{1}{2} \alpha t^2 \end{aligned}\)  ............... (3)

प्रश्न 9. 
एक कार विरामावस्था से चलकर 12 सेकण्ड में 30 मी./से. का वेग प्राप्त करती है तो (i) उस कार का त्वरण (ii) तय की गई कुल दूरी (iii) 7 सेकण्ड के पश्चात् वेग ज्ञात करो। 
उत्तर: 
दिया गया है u = 0 मी./से.
t = 12 सेकण्ड
v = 30 मी./से.
(i) त्वरण (a) = ?
त्वरण (a) = \(\frac{\mathrm{v}-\mathrm{u}}{\mathrm{t}}=\frac{30-0}{12}=\frac{5}{2}\) = 2.5 मी./से. ²

(ii) तय की गई कुल दूरी s = ?
गति के दूसरे समीकरण
S = ut + 1/2at²
= 0 × t² + 2 × 2.5 × (12)²
s = 0 + 1⁄2 × 2.5 × 144
s = 2.5 × 72 = 180 मीटर

(iii) कार का वेग 7 सेकण्ड के पश्चात् = ?
v = u + at से
= 0 + 2.5 × 7 = 17.5 मी./से.

प्रश्न 10. 
एक रेलगाड़ी विरामावस्था से चलना प्रारम्भ करती है और 10 सेकण्ड तक इसकी चाल समान त्वरण से बढ़ती है। 5 सेकण्ड के अन्त में इसकी चाल 54 किमी./ घण्टा हो जाती है। 
(अ) रेलगाड़ी का त्वरण ज्ञात करो।
(ब) 10 सेकण्ड बाद इसकी चाल क्या होगी?
(स) 10 सेकण्ड में रेलगाड़ी कितनी दूरी चलेगी?
(द) सातवें व दसवें सेकण्डों में रेलगाड़ी ने क्रमशः
कितनी कितनी दूरी तय की?
उत्तर:  
(अ) 5 सेकण्ड बाद चाल = 54 किमी./ घण्टा
= 54 x 5/18 मी./से.
= 15 मी./से.
विरामावस्था में u = 0, v = 15 मी./से. t = 5 से, a = ?
गति के प्रथम समीकरण से
v = u + at
∴  \(\mathrm{a}=\frac{\mathrm{v}-\mathrm{u}}{\mathrm{t}}=\frac{15-0}{5}\)
a = 3 मी./से.2

(ब) 10 सेकण्ड बाद वेग
v = u + at
= 0 + 3 × 10 = 30 मी./से.

(स) दूरी s = ut + 1/2at²
= 0 × 10 + x 3 x 10 x 10
= 150 मीटर

(द) n वें सेकण्ड में तय की गई दूरी
Sn = u + 1/2a(2n -1)
इसलिए 7वें सेकण्ड में दूरी
S7 = 0 + 2 × 3 (2 × 7 - 1)
= 39/20
= 19.5 मीटर

10वें सेकण्ड में दूरी
s10 = 0 + 2 × 3 × (2 × 10 - 1)
= 57/2 = 28.5 मीटर

प्रश्न 11. 
एक व्यक्ति किसी गेंद को ऊपर फेंककर 8 सेकण्ड पश्चात् पुनः लपक लेता है तो बतलाइए:
(अ) किस वेग से गेंद को ऊपर फेंका गया था?
(ब) कितनी ऊँचाई पर गेंद का वेग शून्य होगा? 
उत्तर:  
(अ) किसी गेंद को ऊपर जाने व नीचे आने में समान समय लगता है।
∴ केवल ऊपर जाने का समय = 8/2 = 4 से
ऊर्ध्वाधर ऊपर गति के लिए
गति के प्रथम समीकरण से
v = u - gt से
0 = u - 9.8 × 4
u = 39.2 मी./से.
t = 4 से.
u = ?, v = 0 मी./से.
g = 9.8 मी./से.²

(ब) माना कि h ऊँचाई पर वेग शून्य होगा:
v² = u² - 2gh
0 = 39.2 x 39.2 - 2 x 9.8 x h
\(h=\frac{39.2 \times 39.2}{2 \times 9.8}\)
= 78.4 मीटर

प्रश्न 12. 
ऊपर से स्वतन्त्रतापूर्वक गिरती हुई वस्तु उसके अन्तिम सेकण्ड में उसकी कुल ऊँचाई 16/25 का भाग पार करती है तो ज्ञात करो:
(i) कुल ऊँचाई 
(ii) गिरने का समय। 
उत्तर:  
माना कि कुल ऊँचाई = h मीटर
तथा तय करने में लगा समय = 1 सेकण्ड
अन्तिम सेकण्ड में दूरी = 16/25 h
(t - 1) सेकण्ड में दूरी
= h - 16/25h = 9/25h
h = ut + 2gt² से
u = 0 
∵ वस्तु स्वतन्त्रतापूर्वक गिर रही है।
h = 0 + 1/2 x 10 x t²
h = 5t² ............. (1)
इसी प्रकार
9/25h = 5 (t - 1 ⁾² ................ (2)
समीकरण (2) में समीकरण (1) का भाग देने पर
9/25 = (t -1)2/t²
3/5  = t -1/t
⇒ 3t = 5t – 5
⇒ 21 = 5 
⇒ t = 2.5 से.
t का मान समीकरण (1) में रखने पर
h = 5 × (2.5)²
= 5 × 6.25 = 31.25 मीटर

प्रश्न 13. 
एक पिंड एकविमीय गति में कण की स्थिति x (मीटर में) समय (सेकण्ड में) पर निम्न प्रकार निर्भर करती है:
x = t² - 4t + 3
ज्ञात कीजिये (i) समय अन्तराल = 0 से 4 सेकण्ड में पिंड का विस्थापन, (ii) समय अन्तराल t = 2 सेकण्ड से t = 4 सेकण्ड के लिये पिंड का औसत वेग।
उत्तर:  
(i) दिया गया है:
x = t² - 4t + 3
समय अन्तराल t = 0 से t = 4 सेकण्ड में विस्थापन ज्ञात करना
∴  x1 = (0)² - 4 x 0 + 3, 
t = ( ) रखने पर
x1 = 0 - 0 + 3 = 3 मीटर
इसी तरह से x² = (4)² - 4 (4) + 3,
t = 4 रखने पर
= 16 - 16 + 3
x² = 3
∴ विस्थापन = x₂ - x₁ = 3 - 3 = 0 (शून्य)

(ii) x = t² - 4t + 3
t के सापेक्ष अवकलन करने पर
dx/dt = 2t - 4 ............. (1)
t = 2 सेकण्ड पर वेग का मान
V1 = (dx/dt)at = 2 = 2 × 2 - 4
= 8 - 4 = () मीटर/से..
समीकरण (1) का पुनः t 

जो कि अचर राशि है
4 सेकण्ड तक पिण्ड का औसत t के सापेक्ष अवकलन करने पर
d²x/dt = 2 × 1 - 0 = 2
त्वरण अचर है। t = 2 सेकण्ड से =
\(\begin{aligned} & =\frac{v_1+v_2}{2} \\ & =\frac{0+4}{2} \end{aligned} \)
= 2 मी./से. 

प्रश्न 14. 
एकविमीय गति में कण का वेग समय पर निम्न प्रकार निर्भर करता है:
v = (5t + 7) मी./से.
यदि t = 0 पर कण मूल बिन्दु पर है, तो t = 2 सेकण्ड पर कण की स्थिति क्या होगी?
उत्तर:
दिया गया है 
v = 5t + 7
लेकिन
v = dx/dt
∴ dx/dt = 5t + 7
⇒ dx = (5t + 7)dt
⇒ dx = 5tdt + 7dt
समाकलन करने पर
\(\int d x=5 \int t d t+7 \int d t\)
∴ x = 5t²/2 + 7t + c .............. (1)
यहाँ पर c समाकलन नियतांक है।
दिया गया है
t = 0 पर कण मूल बिन्दु पर है 
अर्थात्
t = 0 पर x = () होगा।
0 = 5/2 x 0 + 7 x 0 + c
c = 0
समीकरण (1) में मान रखने पर
x = 5/2t² + 7t + 0
⇒ x = 5/2t² + 7t
t = 2 पर
x = 5/2(2)² + 7 x 2
= 5/2 x 4 + 14
= 5 x 2 + 14
= 10 + 14 = 24 मीटर 

प्रश्न 15. 
एकविमीय गति में कण स्थिति
x = (3 + 4t - t²) मीटर है
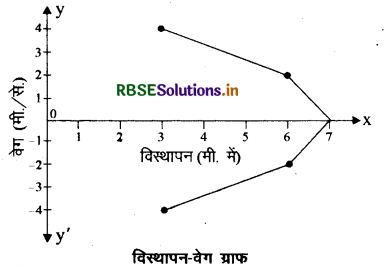
इस गति के लिये समय अन्तराल = 0 सेकण्ड से = 4 सेकण्ड तक विस्थापन वेग आरेख खींचिये।
उत्तर:
दिया गया है:
x = (3 + 4t - t²) मीटर
t के सापेक्ष अवकलन करने पर
dx/dt = 0 + 4 x 1 - 2t
dx/dt = 4 - 2t

समय	t	0	1	2	3	4
विस्थापन	x	3	6	7	6	3
वेग	dx/dt	4	2	0	-2	-4

प्रश्न 16. 
संलग्न चित्र में एकविमीय गति करने वाले कण के लिये वेग समय आरेख दर्शाया गया है। इस कण के लिये
(i) समय t = 1 सेकण्ड पर त्वरण
(ii) समय t = 3 सेकण्ड पर त्वरण तथा
(iii) समय अन्तराल t = 0 सेकण्ड से t = 6 सेकण्ड में कण द्वारा तय की गयी दूरी व कण का विस्थापन ज्ञात करो।

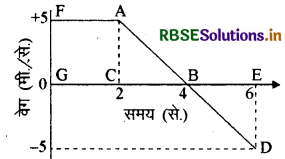
उत्तर: 
(i) वेग (0) से 2 सेकण्ड तक समान रहता
∴ समय t = 1 सेकण्ड पर त्वरण शून्य होगा।
(ii) 2 सेकण्ड पर वेग 5 मी/से है, और 4 सेकण्ड पर वेग का मान शून्य है अतः 2 से 4 सेकण्ड के बीच में होने वाला त्वरण
\(\begin{aligned} & =\frac{0-5}{4-2} \\ & =\frac{-5}{2} \end{aligned}\)
= -2.5 मी./से.² 

(iii) दूरी = आयत GCAF का क्षेत्रफल + त्रिभुज CBA का क्षेत्रफल + त्रिभुज BED का क्षेत्रफल
= 5 × 2 + 1/2(4 - 2) × 5 + 1/2 + (6 - 4) x 5
= 10 + 5 + 5 = 200 मीटर 
विस्थापन = आयत GCAE का क्षेत्रफल + त्रिभुज CBA का क्षेत्रफल + त्रिभुज BED का क्षेत्रफल
= 5 × 2 + 2(4 - 2) × 5 - 2(6 - 4) x 5
= 10 + 5 - 5 = 10 मीटर

प्रश्न 17. 
एकविमीय गति कर रहे एक कण की स्थिति x, समय t पर निम्न प्रकार निर्भर करती हैं:
x = 5 + 5t - t²
(सभी राशियाँ SI मात्रकों में हैं) इस गति के लिये समय अन्तराल t = 0 सेकण्ड से = 6 सेकण्ड तक के लिये (i) विस्थापन समय (ii) वेग- समय और (iii) त्वरण-समय आलेख खींचिये और गति का वर्णन कीजिये।
उत्तर: 
(i) दिये गये समीकरण से
x = 5 + 5t - t²
सारणी तैयार करने पर

t	0	1	2	3	4	5	6
v	5	3	1	-1	-3	-5	-7

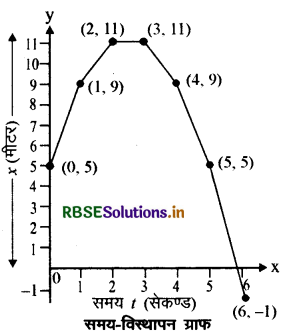
t = 1 रखने पर
समय (सेकण्ड ) समय- विस्थापन ग्राफ
x = 5 + 5 × 1 - ( 1 ) 2 = 9
t = 2 रखने पर
x = 5 + 5 x 2 - (2)²
= 5 + 10 - 4t
t = 3 रखने पर x = 5 + 5 × 3 - (3)²
= 5 + 15  - 9 = 11
t = 4 रखने पर
= 5 + 5 x 4 - (4)² 
= 5 + 20 - 16 =9
t = 5 रखने पर
t = 5 + 5 × 5 - ( 5)² 
= 5 + 25 - 25 = 5
t  = 6 रखने पर
t = 5 + 5 × 6 - (6)²

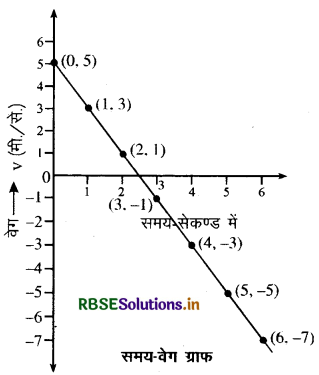
(ii) वेग-समय ग्राफ:
x = 5 + 5t - t²
 dx/dt = 0 + 5 × 1 - 2t
लेकिन
V = dx/dt
= 5 - 2t
v= 5 - 2t
सारणी तैयार करने पर

(iii) त्वरण-समय ग्राफ-
v = 5 - 2t

पुनः के सापेक्ष अवकलन करने पर
dv/dt = 0 - 2
अर्थात्
a = - 2

प्रश्न 18. 
संलग्न चित्र में किसी वाहन के लिये दिये गये समय वेग ग्राफ से समय ग्राफ खींचिये।

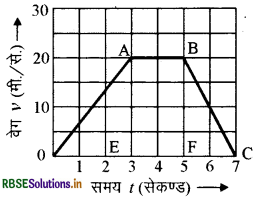
उत्तर:  
(i) O से A तक वाहन का वेग एकसमान रूप से बढ़ता है अर्थात् इसका त्वरण नियत रहता है। अतएव t = 0 से t = 3 सेकण्ड तक
त्वरण a1 = रेखा OA का ढलान
\(=\frac{\mathrm{EA}}{\mathrm{OE}}=\frac{20-0}{3-0}=\frac{20}{3}\)
= 6.7 मी./से.² 

(ii) A से B तक वाहन का वेग नियत रहता है। अतः t = 3 सेकण्ड से t = 5 से तक वाहन का त्वरण a2 = 0 रहता है।

(iii) B से C तक वाहन का वेग एकसमान रूप से घटता है अर्थात् इसका त्वरण नियत रहता है।
अतः t = 5 से. से t = 7 से तक त्वरण a3 = रेखा BC का ढलान

a3 = -20/2 = -10 मी./से.² 
चूँकि यहाँ त्वरण ( a3 ) में मंदन हो रहा है।
मंदन = r = 10 मी./से.²

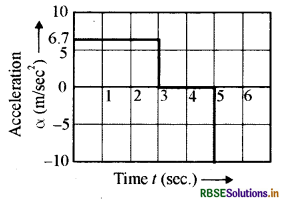
इन आँकड़ों के आधार पर खींचा गया समय त्वरण ग्राफ उपर्युक्त चित्र में दिखाया गया है।

प्रश्न 19. 
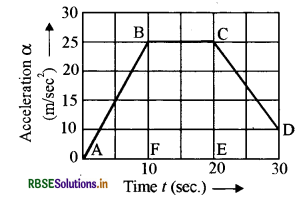
दिये गये चित्र में एक सीधी रेखा में गति करने वाली वस्तु का समय त्वरण ग्राफ दिया गया है ग्राफ से ज्ञात कीजिये:
(i) प्रथम 20 सेकण्ड में औसत त्वरण
(ii) वस्तु पर किस समय से किस समय तक बल अचर रहा?

उत्तर:  
(i) समय त्वरण ग्राफ से वेग परिवर्तन ज्ञात किया जा सकता है। यह समय त्वरण ग्राफ तथा शून्य त्वरण अक्ष के बीच के क्षेत्रफल के बराबर होता है। अतः प्रथम 20 सेकण्ड में
वेग में परिवर्तन = क्षेत्रफल ABCE 
वेग में परिवर्तन = क्षेत्रफल ABF + क्षेत्रफल BCEF
= 1⁄2 x 10 x 20 + 20 x (20 - 10)
= 100 + 200 = 300 मी./से.

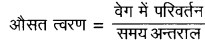
\(=\frac{300}{20}\)
15 मी./से.² 

(ii) बल = द्रव्यमान x त्वरण
अतः त्वरण के अचर रहने पर बल भी अचर रहेगा ग्राफ से स्पष्ट है कि त्वरण 10 सेकण्ड से 20 सेकण्ड तक अचर रहता है अतः वस्तु पर बल 10 से से 20 से तक अचर रहता है।

गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न:

प्रश्न 1. 
एक बिल्ली एकसमान चाल Vu से X से Y तक जाती है और से Y से X पर वापस आती है। इसमें उसकी एकसमान चाल Vd औसत चाल होगी:

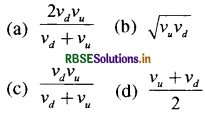
उत्तर:  
\(\text { (a) } \frac{2 v_d v_u}{v_d+v_u}\)

प्रश्न 2. 
एक दिन में मेट्रो स्टेशन पर एस्केलेटर (चलती सीढ़ी) के न चलने पर प्रीति, उसकी सीढ़ियों पर पैदल ऊपर चढ़ती है। इसमें उसे 4 समय लगता है। अन्य दिनों में जब एस्केलेटर चल रहा होता है तब वह उस पर खड़ी रहकर 1⁄2 समय में ऊपर पहुँच जाती है तो उसके द्वारा चलते हुए एस्केलेटर पर चलकर ऊपर चढ़ने में लिया गया समय होगा:

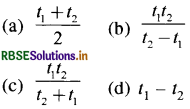
उत्तर:  
\(\text { (c) } \frac{t_1 t_2}{t_2+t_1}\)

प्रश्न 3. 
किसी कण के विस्थापन का समीकरण y = a + bt + ct² - dt⁴ है प्रारम्भिक वेग तथा त्वरण क्रमशः होंगे:
(a) b, - 4d
(b) - b. 2c
(c) b. 2c
(c) 2c - 4d
उत्तर:  
(c) b. 2c

प्रश्न 4. 
एक कण का प्रारम्भिक वेग अ +4j और त्वरण 0.4j + 0.3j है। 10 सेकण्ड के पश्चात् इसकी चाल है:
(a) 10 इकाई
(b) 7√2 इकाई
(c) 7 इकाई
(d) 8.5 इकाई
उत्तर:
(b) 7√2 इकाई

प्रश्न 5. 
एकांक द्रव्यमान का कोई कण एकविमीय गति करता है और इसका वेग निम्नांकित समीकरण के अनुसार परिवर्तित होता है। V(x) = bx - 2n जहाँ b तथा n स्थिरांक हैं तथा x कण की स्थिति है। तो इस कण के त्वरण को, x के फलन के रूप में निरूपित किया जाता है:
(a) - 2nb² x^-4n-1 
(b) -2b²x^-2n+1
(c) - 2nb²e^-4n+1
(d) -2nb²x^-2n-1
उत्तर:
(a) - 2nb² x^-4n-1 

प्रश्न 6. 
एक 10 सेमी मोटाई के गोली का वेग 200 लकड़ी के गुटके को पार करने पर मीटर / सेकण्ड से घटकर 100 मीटर / सेकण्ड रह जाता है। मंदन यदि एकसमान हो, तो इसका मान होगा:
(a) 10 x 10⁴ m/s²
(b) 12 x 10⁴ m/s²
(c) 13.5 x 10⁴ m/s²
(d) 15 x 10⁴ m/s²
उत्तर:
(d) 15 x 10⁴ m/s²

प्रश्न 7. 
यदि किसी कण का वेग V = At + Bt² स्थिरांक हैं, तो इस कण द्वारा 1s और 2s के बीच चली गयी दूरी है:
(a) 3/2A + 4B
(b) 3A + 4B
(c) 3/2A + 7/3B
(d) A/2 + B/3
उत्तर:
(c) 3/2A + 7/3B

प्रश्न 8. 
एक कण समीकरण x = (t + 5)-1 के अनुसार 1 सेकण्ड में x दूरी तय करता है। कण का त्वरण समानुपाती होगा:
(a) (वेग)^31/2
(b) (दूरी)²
(c) (दूरी)²
(d) ( वेग)^2/3
उत्तर:
(a) (वेग)^31/2

प्रश्न 9. 
एक सरल रेखा के अनुदिश किसी कण की गति की समीकरण x = 8 + 12t - t³ के द्वारा प्रदर्शित की जाती है, जहाँ x मीटर में तथा 1 सेकण्ड में है। वेग शून्य होने पर कण का मंदन है।
(a) 24 m/s²
(b) शून्य 
(c) 6m/s²
(d) 12 m/s²
उत्तर:
(d) 12 m/s²

प्रश्न 10. 
दो कारें P तथा Q एक ही समय पर किसी बिन्दु से सरल रेखा चना प्रारम्भ करती हैं और उनकी स्थितियों को क्रमशः Xp (t) = at + bt² तथा XQ(t) = ft - t² किस समय पर इन दोनों का वेग समान होगा:

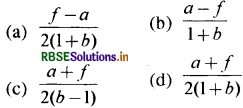
उत्तर:
\(\text { (a) } \frac{f-a}{2(1+b)}\)

प्रश्न 11. 
एक पत्थर मुक्त रूप से गुरुत्वाधीन गिरता है। यह पत्थर पहले पाँच (5) सेकण्डों में h₁, दूरी, उससे अगले 5 सेकण्डों में h₂ दूरी तथा उससे अगले 5 सेकण्डों में h₁,h₂ दूरी तय करता है, तो तथा h₃ में सम्बन्ध है:
(a) h₁ = h₂ = h₃
(b) h₁ = 2h₂ = 3h₃
(c) h₁ = h₂/3 = h₃/5
(d) h₂ = 3h₁ h₃ = 3h₂
उत्तर:
(c) h₁ = h₂/3 = h₃/5

प्रश्न 12. 
एक कण स्थिरावस्था से एक धनात्मक x अक्ष की दिशा में मूल बिन्दु ) से नियत त्वरण से चलता है। वह सभी चित्र ज्ञात कीजिये जो इस कण की गति को गुणात्मक रूप से सही दर्शाते हैं (a = त्वरण, V = वेग x = विस्थापन, t = समय) 

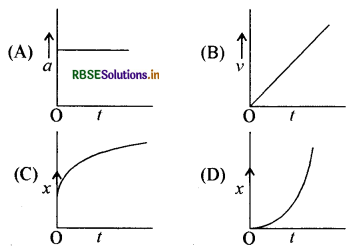
(a) (A), (B), (C)
(b) (A) 
(c) (A), (B), (D)
(d) (B), (C)
उत्तर:
(c) (A), (B), (D)

प्रश्न 13. 
एक कण की स्थिति समय 't' के फलन में निम्न है।
x (t) = at + bt² - ct³
जहाँ a, b तथा नियतांक हैं। जब कण का त्वरण शून्य है, तब उसका वेग होगा:
(a) a + b²/4c
(b) a + b²/c
(c) a + b²/2c
(d) a + b²/3c
उत्तर:
(d) a + b²/3c

प्रश्न 14. 
एक कण का स्थिति सदिश समय के साथ निम्न सूत्र में बदलता है: r(1) = 15t²i + (4 - 20t²)j t = 1 पर कण के त्वरण का परिणाम होगा:
(a) 40
(b) 100
(c) 25
(d) 50
उत्तर:
(d) 50

प्रश्न 15. 
स्थिर जल में किसी तैराक की चाल 20m/s है। नदी के जल की चाल 10m/s है तथा ठीक पूर्व की ओर बह रहा है। यदि वह दक्षिणी किनारे पर खड़ा है और नदी को लघुतम पथ के अनुदिश पार करना चाहता है तो उत्तर के सापेक्ष उसे जिस कोण पर स्ट्रोक लगाने चाहिए वह है-
(a) 30° पश्चिम
(b) 0°
(c) 60° पश्चिम
(d) 45° पश्चिम
उत्तर:
(a) 30° पश्चिम

प्रश्न 16. 
एक गेंद को ऊर्ध्वाधर ऊपर की ओर प्रक्षेपित किया गया है। निम्न ग्राफ में से कौनसा ग्राफ गेंद की हवा में गति के लिये वेगसमय ग्राफ को दर्शाता है। (हवा का प्रतिरोध नगण्य है):

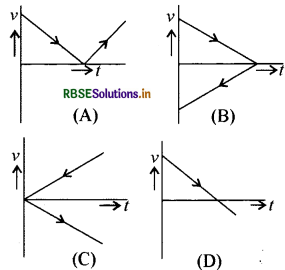
उत्तर:

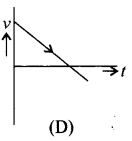
प्रश्न 17. 
दिये गये सारे ग्राफ एक ही गति को दर्शते हैं। कोई एक ग्राफ उस गति को गलत तरीके से दर्शाता है। वह ग्राफ है:

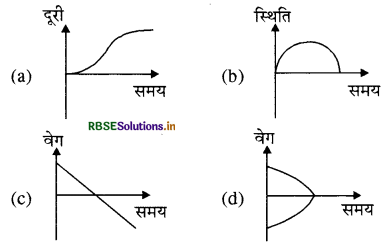
उत्तर: