RBSE Class 11 Physics Important Questions Chapter 3 Motion in a Straight Line

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 3 Motion in a Straight Line Important Questions and Answers.

RBSE Class 11 Physics Chapter 3 Important Questions Motion in a Straight Line

Multiple Choice Questions

Question 1.
Ratio of distance travelled in first and second second by freely falling body is:
(a) 1 : \(\sqrt{3}\)
(b) 1 : 3
(c) 1 : 2
(d) 3 : 2
Answer:
(b) 1 : 3

Question 2.
Slope of graph in retarded motion is:
(a) negative
(b) positive
(c) zero
(d) positive, negative, zero, anything
Answer:
(a) negative

Question 3.
Two bodies of masses m₁ and m₂ fall from heights h₁ and h₂ respectively. The ratio of times taken by the bodies in reaching upto ground is:
(a) \(\sqrt{h_1}\) : \(\sqrt{h_2}\)
(b) h₁ : h₂
(c) \(\sqrt{m_1 h_1}\) : \(\sqrt{m_2 h_2}\)
(d) m₁h₁ : m₂h₂
Answer:
(a) \(\sqrt{h_1}\) : \(\sqrt{h_2}\)

Question 4.
A ball is projected upwards with velocity of 19.6 ms^-1. Within how much time in seconds the ball will reach upto heighest point?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2

Question 5.
The displacement of an object is directly proportional to square of time, then the motion of the object will be:
(a) with uniform acceleration
(b) with uniform velocity
(c) with non-uniform acceleration
(d) with non-uniform acceleration but uniform speed.
Answer:
(a) with uniform acceleration

Question 6.
A particle reaches from point A to B on semicircular path of radius 1.0 m, in 1 second. Magnitude of average velocity is:

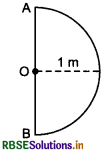
(a) 1.0 ms^-1
(b) 3.14 ms^-1
(c) 2.0 ms^-1
(d) zero
Answer:
(c) 2.0 ms^-1

Question 7.
The displacement of a body is directly proportional to time, magnitude of acceleration of the body will be:
(a) zero
(b) is decreasing with time
(c) is increasing with time
(d) is constant but not zero
Answer:
(a) zero

Question 8.
The velocity of a particle is \(\vec{v}=k(y \hat{i}+x \hat{j})\), where k is a constant. The general equation of its path is:
(a) y² = x + constant
(b) xy = constant
(c) y = x² + constant
(d) y² = x² + constant
Answer:
Given, \(\vec{v}=k(y \hat{i}+x \hat{j})\)
∴ v_x = ky and v_y = kx
or \(\frac{d x}{d t}\) = ky
or dx = ky.dt
or x = kyt ..........................(1)
Now, v_y = kx
or \(\frac{d y}{d t}\) = kx
or dy = kxdt
∴ y = kxt + constant .......................(2)
From equation (1)
t = \(\frac{x}{k y}\)
Substituting the value of t in equation (2)
y = kx x \(\frac{x}{k y}\) + constant

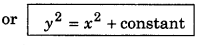
Thus alternative (d)  is correct.

Question 9.
Position (x) of a particle moving in X-direction depends on time (t) according to relation x = at² - t³, where x is in m and t in s, then the position x will be when speed is maximum:
(a) \(\frac{4 a^2}{27}\)m
(b) \(\frac{2 a}{27}\) m
(c) \(\frac{4 a}{27}\) m
(d) \(\frac{2 a^3}{27}\) m
Answer:
[Hint: Given: x = at² - t³
∴ Speed v = \(\frac{d x}{d t}\) = 2at - 3t²
For maximum speed,
\(\frac{d v}{d t}\) = 0
or \(\frac{d }{d t}\) (2at - 3t²) = 2a - 6t = 0
or 6t - 2a ⇒ t = \(\frac{a}{3}\)
∴ x = a x (\(\frac{a}{3}\))² - (\(\frac{a}{3}\))³
= \(\frac{a^3}{9}-\frac{a^3}{27}=\frac{3 a^3-a^3}{27}\)
or x = \(\frac{2a^3}{27}\)
Thus alternative (d) is correct.

Question 10.
A car and a truck are moving with same velocity. After applying breaks:
(a) car will cover less distance
(b) truck will cover less distance
(c) both will cover same distance
(d) none of above
Answer:
(a) car will cover less distance

Fill in the Blanks

Question 1.
The acceleration of body, when its velocity time graph is perpendicular to time axis is ...........................
Answer:
Infinite.

Question 2.
The velocity of a body depends on time according to equation v = 20 + 0.1t². The body is undergoing ...........................
Answer:
Non-uniform acceleration.

Question 3.
The acceleration of a body, when it is velcoity time graph is parallel to time axis is ...........................
Answer:
Zero.

Question 4.
A particle with negative acceleration is speeding up in ...........................
Answer:
simple harmonic motion.

Question 5.
A particle with positive acceleration is slowing down if its ........................... is negative.
Answer:
initial velocity.

Question 6.
If a particle is thrown vertically upwards, then its velocity so that it covers same distance in 5th and 6th seconds would be ...........................
Answer:
49.

Very Short Answer Questions

Question 1.
What is point object?
Answer:
If the size of an object is negligible in comparison to distance travelled by it, then it is treated as point object.

Question 2.
What is speedometer of vehicle?
Answer:
Speedometer measures the instantaneous speed of the vehicle.

Question 3.
What type of quantity is speed and what is its S.I. unit?
Answer:
Speed is scalar quantity and its S.I. unit is ms^-1.

Question 4.
Do the rain-drops fall with uniform velocity or with uniform acceleration?
Answer:
The rain drops fall with uniform speed which is called terminal velocity.

Question 5.
What is called retardation?
Answer:
Negative acceleration i.e. rate of decrease of velocity is called retardation.

Question 6.
What is represented by the slope of velocity time graph?
Answer:
Slope of velocity-time graph represents acceleration.

Question 7.
Can the distance and displacement of a moving body be zero?
Answer:
Displacement canbe zero but distance of moving object can not be zero.

Question 8.
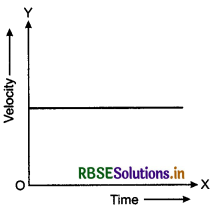
What conclusion is found about velocity and acceleration in following graphs given in figure?

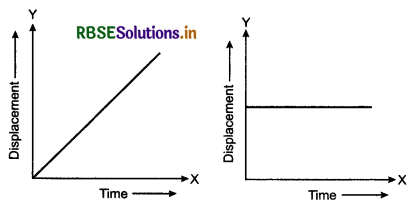
Answer:
In both the graphs,, object is moving with uniform velocity. Hence acceleration is zero.

Question 9.
What will be the ratio of distances covered by a freely falling body in 1st and 2nd second?
Answer:
x₁ = 0 + \(\frac{1}{2}\)g (2 x 1 - 1) = \(\frac{1}{2}\)g
and x₂ = 0 + \(\frac{1}{2}\)g (2 x 2 - 1) = \(\frac{3}{2}\)g
∴ x₁ : x₂ = 1 : 3

Question 10.
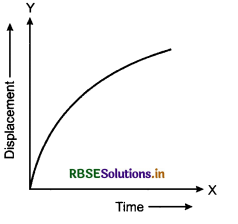
Draw the displacement-time graph for a retarded particle moving in X-direction.
Answer:
For retarded motion of a particles, the displacement time graph will be with decreasing slope as shown in figure.

Question 11.
What is represented by slope of distance-time graph?
Answer:
Speed.

Question 12.
Can the speed of a particle be negative?
Answer:
No, because speed is scalar quantity.

Question 13.
When the relative velocity of two moving objects is zero?
Answer:
When both objects move in same direction with same velcoity then relative velocity is zero.

Question 14.
What does the area of accelaration-time graph represent?
Answer:
Change in velocity (i.e. v - u = a.t).

Question 15.
Velocity-time graph for two cars is shown in figure. Acceleration of which car is greater?
Answer:
Accelation a = tanθ = slope.

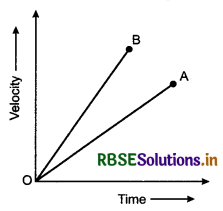
∵ The slope for car B is greater than that of A.
∴ Acceleration of car B will be greater than that of A.

Question 16.
An object is moving on a circular path of radius r, what will be distance and displacement?
Answer:
(i) After half cycle:
Distance = πr
Displacement = 2r

(ii) After full cycle:
Distance = 2πr
Displacement = 0 (zero)

Question 17.
An object is moving with uniform acceleration. Draw the acceleration-time, velocity-time and displacement-time graph for the object.
Answer:

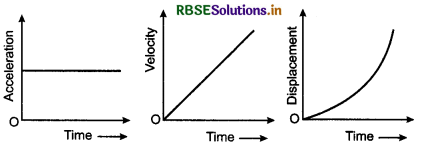
Question 18.
Can the speed of an object be constant and velocity variable?
Answer:
Yes: when object moves on circular path with uniform speed.

Question 19.
Can the average speed and average velocity of an object be zero?
Answer:
Average speed can not be zero while average velocity can be zero.

Question 20.
When average velocity and instantaneous velocity both become the same?
Answer:
When the object moves with uniform velocity.

Question 21.
What will be acceleration of a particle moving with uniform velocity?
Answer:
Zero.

Question 22.
Can there be acceleration in a particle when its velocity is zero?
Answer:
Yes: When vertically upwards projected object reaches its highest point, then its velocity becomes zero but acceleration due to gravity is there.

Question 23.
Can a particle be stationary and in motion simultaneously?
Answer:
Yes; because motion is relative.

Question 24.
Is it possible that the velocity be constant and speed be variable?
Answer:
No; when velocity is constant then the magnitude and direction both will remain unchanged. Therefore speed will also remain unchanged.

Question 25.
Displacement time graph of a moving object is shown in figure. At which point, the instantaneous velocity will be negative?

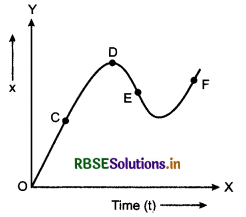
Answer:
At point E.

Question 26.
An object starts moving from rest with constant acceleration and covers distance x in t s. How much distance will it travel in next t s?
Answer:
x₁ = 0 + \(\frac{1}{2}\)at²
and x² = 0 + \(\frac{1}{2}\)a(2t)² = \(\frac{1}{2}\)a(4t²)
∴ Distance travelled in next t s,
∆x = x₂ - x₁ = \(\frac{1}{2}\) a.4t² - \(\frac{1}{2}\) at²
= 3 x \(\frac{1}{2}\) at² or ∆x = 3x

Question 27.
An objejct is allowed to fall from the top of a tower and at the same moment another object is thrown horizontally with some velocity: Will both the object.
(i) Strike the ground at the same time,
(ii) Strike the ground at same place?
Answer:
(i) Yes
(ii) No.

Question 28.
In velocity-time graph, given in figure which part of the graph represents, uniform velocity; retardation?

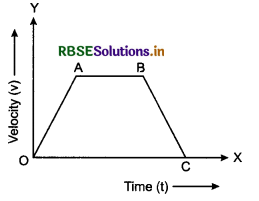
Answer:
In the given velocity-time graph:
(i) Part OA represents uniform acceleration
(ii) Part AB represents uniform velocity.
(iii) Part BC represents uniform retardation.

Question 30.
A body is moving with constant velocity, what is relation between displacement and time?
Answer:
Displacement a time.

Question 31.
Give the situation when Moon revolving around the Earth, can not be treated as point object.
Answer:
At the time of solar eclipe.

Question 32.
A body is running in the grotmd. What type of motion is this?
Answer:
Two dimensional motion.

Question 33.
What do you mean by non-inertial frame of reference?
Answer:
The frame of reference which moves with an acceleration, is called non-inertial frame of reference. For example, rotating frame of reference.

Short Answer Type Question

Question 1.
If instantaneous velocity of an object is zero, then should its instantaneous acceleration also be zero?
Answer:
No, in vertical motion of an obect at highest point its velocity becomes zero i.e. instantaneous velocity becomes zero but instantaneous acceleration still remains equal to acceleration due to gravity (g) which is non zero.

Question 2.
The distance travelled by a moving body is directly proportional to square of time
(i) whether the object is moving with uniform velcoity or with uniform acceleration?
(ii) If the distance travelled is directly proportional to time, then?
Answer:
(i) Given S ∝ t² or S = kt²
Velocity v = \(\frac{d S}{d t}=\frac{d}{d t}\)(kt²) = 2kt
and acceleration a = \(\frac{d v}{d t}=\frac{d}{d t}\)(2kt) = 2k = constant
Hence the object is moving with uniform acceleration.
(ii) When S ∝ t or S = kt
∴ Velocity v = \(\frac{d S}{d t}=\frac{d}{d t}\)(kt) = k = constant
i.e. the object is moving with uniform velocity.

Question 3.
The velocity of a train at the time of passing its first and last compartment from a pole is v and v' respectively. What will be the velocity of its middle compartment?
Answer:
Suppose the length of the train is 2x and the velocity of middle compartment is u. The equation for the engine and middle compartment.
v² - u² = 2ax (using relation v² - u² = 2aS) .........................(1)
Distance between engine and middle compartment = \(\frac{2 x}{2}\) = x
Similarly the equation for middle and last compartment
u² - v'² = 2ax ......................(2)
On subtracting equation (2) from equation (1) we have
2u² - v² - v'² = 0
or 2u² = v² + v'²

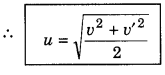
Question 4.
Velocity time graph for a body is shown in figure. What is acceleration of the body? Also draw the displacement-time graph for the body.
Answer:
The given graph shows that velocity is not changing with time. Therefore its acceleration will be zero. The displacement time graph for the body is     
given in figure.

Question 5.
What are differences between distance and displacement?
Answer:
Difference between distance and displacement

Distance	Displacement
1. The length of path actually adopted by a moving body in certain time-interval, is called distance.	1. The minimum distance between initial and final positions is called displacement.
2. It represents magnitude only.	2. It represents magnitude as well as direction also.
3. It is a scalar quantity.	3. It is vector quantity.
4. Distance is always positive.	4. It can be positive, negative and zero also.

Question 6.
Velocity-time graph of a particle is shown in figure. What is represented by shaded area in the graph? 

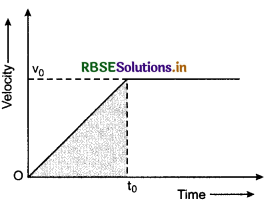
Answer:
The area of shaded part of the graph represents the displacement of the particle in time t₀.
∴ Displacement = Area of the triangle
= \(\frac{1}{2}\)v₀.t₀

Question 7.
Can the given graph be a displacement-time graph of car which goes one place to other place and returns back?

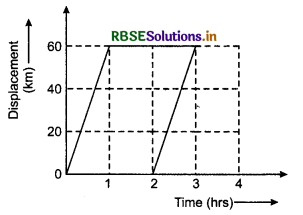
Answer:
No; because according to graph, between 2 and 3 hours, the car is at two places at same time which is not possible.

Question 8.
Acceleration of a particle depends on time according to relation a = bt. If initial velocity of the particle be v₀ then determine its displacement in time t.
Answer:
Given: a = bt or \(\frac{d v}{d t}\) = bt or dv = bt. dt
On integrating both sides, we have
∫ dv = ∫bt.dt
or v = \(\frac{1}{2}\) bt² + c (constant)
when t = 0, then v = v₀
∴ v₀ = 0 x c or c = v₀
∴ v = \(\frac{1}{2}\) bt² + v₀
or \(\frac{d x}{d t}=\frac{1}{2}\)bt² + v₀
or dx = \(\frac{1}{2}\)bt². dt + v₀.dt
Again on integrating the both sides

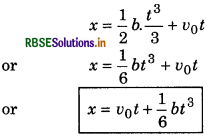
Question 9.
Draw the position-time graph for a uniform linear motion and prove that the slope of the graph is equal to its velocity.
Answer:
Position-time graph for uniform linear motion is straight line making a constant angle with axis of time as shown in fig.

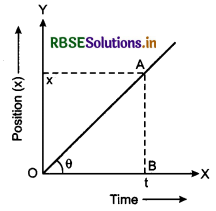
The slope of the graph
tanθ = \(\frac{A B}{O B}=\frac{x}{t}=\frac{\text { displacement }}{\text { time }}\)
or tanθ = velocity

Question 10.
Give the differences between acceleration and retardation.
Answer:
Differences between acceleration and retardation

Acceleration	Retardation
1. Rate of increase of velocity is called accelration.	Rate of decrease of velocity is called retardation
2. Positive value of rate of change of velocity is acceleration.	Negative value of rate of change of velocity is retardation.

Question 11.
Clarify the meaning of following:
(i) Uniform velocity
(ii) Variable velocity
(iii) Uniform acceleration
(iv) Variable acceleration
Answer:
(i) Uniform velocity: If a moving body covers same displacement in same time intervals, then its velocity is said to be uniform velocity.
(ii) Variable velcoity: If the displacements covered in equal time intervals are different, the velocity is said to be variable or non-uniform velocity. Velocity changes due to following two reasons:

• On changing the magnitude
• On changing the direction.

If the speed of the body is constant i.e., uniform, then its velocity will change due to change in direction.
(iii) Uniform acceleration: If the change in velocity in same time intervals is same, then the acceleration is said to be uniform acceleration and the motion of the object is said to be uniformly accelerated motion.
(iv) Variable acceleration: If change in velocity in same time intervals is different, then the acceleration is said to be variable acceleration or non-uniform acceleration.

Question 12.
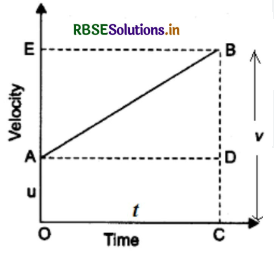
Given the graphical derivation of equation S = ut + \(\frac{1}{2}\)at².
Answer:
Consider the velocity-time graph of a body shown in the figure. The body has an initial velocity u at a point A and then its velocity changes at a uniform rate from A to B in time t. In other words, there is a uniform acceleration a from A to B, and after time t its final velocity becomes v which is equal to BC in the graph. The time t is represented by OC. 

Suppose the body travels a distance s in time t. In the figure, the distance traveled by the body is given by the area of the space between the velocity-time graph AB and the time axis OC, which is equal to the area of the figure OABC. 
Thus: 
Distance traveled = Area of figure OABC
= Area of rectangle OADC + area of triangle ABD
Now, we will find out the area of rectangle OADC and area of triangle ABD. 

(i) Area of rectangle OADC = OA × OC
= u × t
=ut

(ii) Area of triangle ABD = \(\frac{1}{2}\) x Area of rectangle AEBD
= \(\frac{1}{2}\) x AD x BD
= \(\frac{1}{2}\) x t x at
= \(\frac{1}{2}\)at²
Distance travelled, s = Area of rectangle OADC + area of triangle ABD 
s = ut + \(\frac{1}{2}\)at²

Question 13.
Can position-time graph and velocity-time graph be parallel to Y-axis? Given the answer with reason.
Answer:
Important Fact: When graph is plotted between two physical quantities, then a new physical quantity or two physical quantities are obtained, in which one can be obtained by slope of straight graphical line and second is obtained by area of the figure.

Displacement or Distance Time Graph
In distance/displacement-time graph, displacement /distance is taken on Y-axis and time (t) on X-axis.

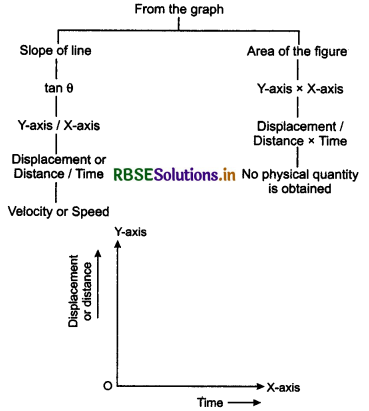
Distance-Time Graph
(i) When the object is at rest
When the object is at rest, then its speed is zero i.e, its distance does not change with time (fig. 3.17).
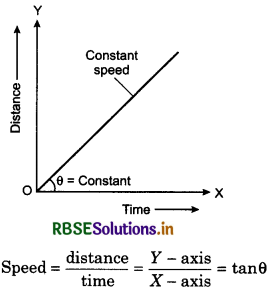
∴ Speed = \(\frac{\text { distance }}{\text { time }}=\frac{y-\text { axis }}{x-\text { axis }}\) = tanθ

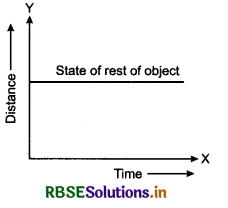
Here θ = 0° ⇒ tanθ = 0
∴ Speed, v = 0
Conclusion: The graphical line, in distance-time graph, which is parallel to axis of time, represent the state of rest of the object.
(ii) When object moves with uniform speed:
When the object moves with uniform speed, then the ratio of change in distance and time interval remains constant and graphical line is a straight line
making some angle (θ) with axis of time i.e. X-axis (fig. 3.18).

Match the Following

Question 1.

Matrix (i)	Matrix (ii)
(a) Speed	(P) m/sec2
(b) Distance	(Q) m/sec
(c) Acceleration	(R) meter

Answer:

Matrix (i)	Matrix (ii)
(a) Speed	(Q) m/sec
(b) Distance	(R) meter
(c) Acceleration	(P) m/sec2

Question 2.

Column (i)	Column (ii)
(a) s = ut + \(\frac{1}{2}\)at2	(P) Ist equation of motion
(b) v = u + at	(Q) IIIrd equation of motion
(c) v2 = u2 - 12 as	(R) IInd equation of motion

Answer:

Column (i)	Column (ii)
(a) s = ut + \(\frac{1}{2}\)at2	(R) IInd equation of motion
(b) v = u + at	(P) Ist equation of motion
(c) v2 = u2 - 12 as	(Q) IIIrd equation of motion

Conceptual Questions

Question 1.
When two trains are running parallel to each other with saine speed, then one train appears to be stationary to a man sitting in other train, why?
Answer:
The experience, given in question, is due to relative velocity. Since the speed of both trains is equal in same direction, therefore relative velocity will be
zero.
Relative velocity of A with respect to B,
v_AB = v_A - v_B = Obecause v_A = v_B.

Question 2.
If the speed of a particle is uniform, then is it possible that its acceleration be zero?
Answer:
Yes: because when the particle moves on circular path with uniform speed, then a centripetal acceleration acts on the particle.

Question 3.
The time taken in operating a boat in still air from one bank of a lake to opposite bank and again back to first bank, is t₁. In the situation of storm, the process takes time t₂. What is relation between t₁ and t₂?
Answer:
In situation of still air, the water is also still. If width of the lake be d, then
t₁ = \(\frac{d}{v}+\frac{d}{v}=\frac{2 d}{v}\) ........................(1)
In situation of storm (velocity u/v),
t₂ =\( \frac{d}{v+u}+\frac{d}{v-u}=d\left[\frac{v-u+v+u}{v^2-u^2}\right]\)
or t₂ = \(\frac{2 d v}{v^2-v^2}\) .......................(2)
From equations (1) and (2) it is clear that t₂ > t₁.

Question 4.
(i) The average velocity of a particle be zero but average speed not zero. Is it opposite also possible?
(ii) Is it possible that the speed of particle be constant but its velocity be variable?
(iii) Is it possible that velocity of a particle be constant but speed be variable?
Answer:
(i) Yes; when an object is projected vertically upwards and it returns back to its initial position, the average velocity becomes zero but average speed is not zero.
(ii) Yes; on circular path, a particle moves with uniform speed, then its velocity remains changing each moment i.e. variable.
(iii) No; on being velocity constant, its magnitude as well as direction both remain unchanged.

Question 5.
The motion of a particle is represented by relation x = ut + \(\frac{1}{2}\) at², where x is position, t is time and u and a₁ are constants. Show that the acceleration of the particle is constant.
Answer:

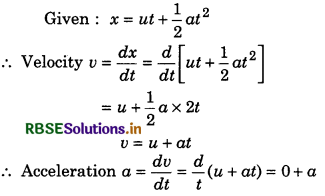
or a = constant
Thus the acceleration of the object is constant.

Question 6.
Wind is blowing west to east along two parallel tracks. Two trains moving with the same speed in opposite directions on these tracks have the stream tracks. If one stream track is double than the other, what the speed of each train?
Answer:
Let v and w be the velocity of each train and wind respectively. As per question
(v + w) = 2(v - w)
or v + w = 2v - 2w
or v = 3w
i.e., velocity of each train is 3 times the velocity of wind.

Question 7.
For ordinary terrestrial experiments, which of the observers below are inertial and which are non-inertial?
(a) A child revolving in a giant wheel.
(b) A driver in a sports ear moving with a constant high speed of 200 km.h^-1 on a straight road.
(c) The pilot of an airplane which is taking off.
(d) A cyclist negotiating a sharp turn.
(e) The guard of a train which is slowing down to stop at a station.
Answer:
An inertial observer is one which is unaccelerated (i.e. a = 0). A non-inertial observer is an accelerated observer.
On this basis we find that:
(a) A child revolving on a giant wheel is a non-inertial.
(b) A driver with a constant speed is an inertial observer.
(c) At take off, airplane has an acceleration. Therefore, the pilot is a non-inertial observer.
(d) A cyclist negotiating a sharp turn has an acceleration. Therefore, he is a non-inertial observer.
(e) The guard of the train is a non-inertial observer, as the train in this case has retardation.

Question 8.
Two straight lines drawn on the same displacement-time graph make angles 30° and 60° with time-axis respectively as shown in figure. Which line represents greater velocity? What is the ratio of these two velocities?

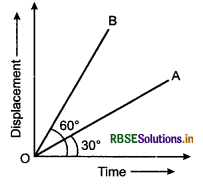
Answer:
The slope of displacement time graph
tanθ = \(\frac{\text { displacement }}{\text { time }}\) = velocity
velocity = tanθ .................(1)
So, the velocity is directly proportional to the angle
∴ v_A > v_A
∴ v_A = tan 30° and v_B = tan 60°
∴ \(\frac{v_A}{v_B}=\frac{\tan 30^{\circ}}{\tan 60^{\circ}}=\frac{1 \sqrt{3}}{\sqrt{3}}=\frac{1}{3}\)

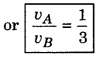
Question 9.
In which situation, the acceleration would be maximum.
(i) Either at the time of pressing accelerator
or
(ii) On applying breaks of the vehicle?
Answer:
At the time of pressing accelerator, the velocity increases gradually but when break is pressed then velocity decreases sharply (retardation). Thus retardation is greater than acceleration in magnitude.

Long Answer Questions

Question 1.
Draw the velocity-time graph of a body moving with uniform acceleration and establish the equations of motion with the help of this graph.
Answer:
1. First Equation: Velocity time graph for uniformly accelerated motion is given in fig. 3.45 The initial velocity of the object is u and after time t it is u.
The angle of graphical line with time-axis is θ.

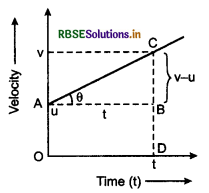
∴ Acceleration,
a = tanθ = \(\frac{C B}{A B}=\frac{v-u}{t}\)
or at = v - u

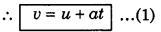
2. Second equation: Distance travelled by the body in time t.
S = Area of trapezium OACD.

3. Third equation: In above part (2) we have seen that
S = \(\frac{u+v}{2}\) x t ..................(3)
From first equation, we get
v - u = at
∴ t = \(\frac{(v-u)}{a}\)
Substituting the value of t n equation (3), we have
S = \(\frac{(v+u)}{2}\) x \(\frac{(v-u)}{a}\) = \(\frac{(v_2-u_2)}{2a}\)
or v² - u² = aS

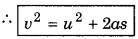
Question 2.
What do mean by relative velocity? Describe the graphs relating relative velocity in different situations.
Answer:
Motion of an object is not absolute as it appears with respect to another object in moving position or rest position. We study motion in terms of velocity. Thus we can say the time rate of change in position of one object with respect to other object is called ‘relative velocity’.
Expression for relative velocity: Relative velocity of A with respect other object B is the rate with which the position of A changes with respect to B.

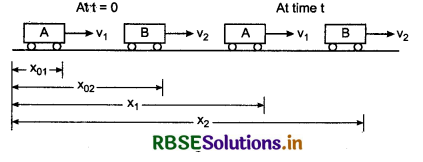
To understand the concept of relative velocity, let us consider two objects A and B moving with uniform velocity u₁ and u₂ respectively.
Suppose, \(\overrightarrow{x_{01}}\) = Displacement of A at t = 0
and \(\overrightarrow{x_{02}}\) = Displacement of B at t = 0
Now let us suppose the displacements of A and B at time t are x₁ and x₂ respectively.

Here, \(\overrightarrow{v_{BA}}\) = Relative velocity of B with respect to A.
Position-time graph of object in relative motion:
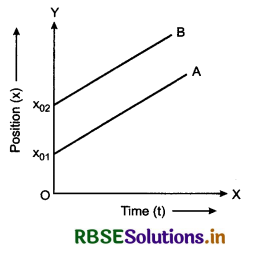
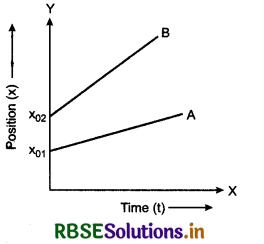
(a) If \(\overrightarrow{v_2}\) - \(\overrightarrow{v_1}\) = 0 or \(\overrightarrow{v_2}\) = \(\overrightarrow{v_1}\) and the objects are seperated by some distance. Since the velocities of both objects A and B are same therefore the slope of both graphical lines will be same (Fig. 3.50).


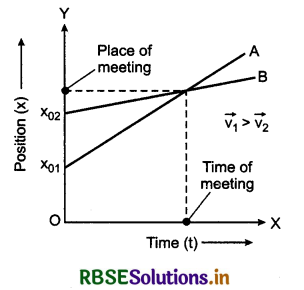
(b) If \(\overrightarrow{v_2}\) - \(\overrightarrow{v_1}\) ≠ 0 or \(\overrightarrow{v_2}\) ≠ \(\overrightarrow{v_1}\) or in this situation, the slopes of both graphs will be different.
(i) If velocity of A is greater than that of B i.e., \(\overrightarrow{v_1}\) > \(\overrightarrow{v_2}\), then slope of graph A will be greater than that of B, as shown in fig. 3.51. After certain time both graphs will intersect each other i.e. the objects will meet each other.

(ii) If \(\overrightarrow{v_2}\) > \(\overrightarrow{v_1}\). In this situation, the slope of graph for B will be greater than that for A. The distance between both objects will go an increasing with time. As a result both object will never meet each other.

(c) If \(\overrightarrow{v_1}\) and \(\overrightarrow{v_2}\) are in opposite directions, then

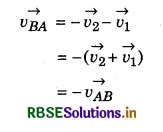
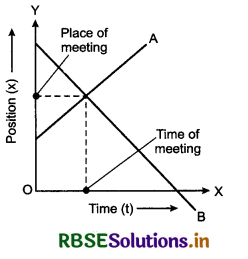
Question 3.
Prove that a uniformly accelerated object covers the distance S = u + \(\frac{1}{2}\) a (2t - 1) in t^th second.
Answer:
Suppose body is moving in straight line with uniform acceleration a. Its initial velocity (i.e. at t = 0) is u and after time t is u. Total distance travelled by the body in this time is S.
First equation: According to definition of instantaneous acceleration
a = \(\frac{d v}{d t}\)
or dv = adt
On integrating both sides,
\(\int_u^v d v=\int_0^t a \cdot d t\)
or [v]_u^v = a [t]₀^t
or v - u = a [t - 0] = at

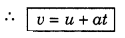
Second equation: According to definition of instantaneous velocity,
v = \(\frac{d S}{d t}\)
or dS = v.dt = (u + at).dt
On integrating both sides,
\(\int_0^S d S=\int_0^t(u+a t) d t=\int_0^t u \cdot d t+\int_0^t a t \cdot d t\)
or [S]₀^S = u[t]₀^K + a[\(\frac{t^2}{2}\)]₀^t
or S - 0 = u(t - 0) + \(\frac{1}{2}\)a(t² - 0)

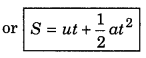
Third equation: According to definitions of instantaneous velocity and acceleration,
We know that the instantaneous acceleration
a = \(\frac{d v}{d t}\) ...............................(1)
We know that the instantaneous velocity
v = \(\frac{d s}{d t}\) .........................(2)
From equation (1) and (2), we have
∴ \(\frac{a}{v}=\frac{d v / d t}{d s / d t}=\frac{d v}{d s}\)
∵ a ds = v dv .......................(3)
On integrating both sides,
\(\int_0^S a d S=\int_u^v v d v\)

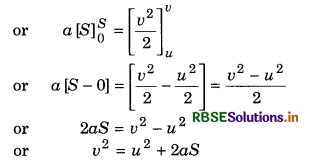
Displacement of body in a particular second:
Suppose an object is moving under uniform acceleration a and we have to find the distance travelled in t^th second.
∵ Distance travelled in t second is obtained by:
S = ut + \(\frac{1}{2}\)at²
∴ Distance travelled in t^th second

Question 4.
What do you understand by reaction time? Explain giving example.
Answer:
We face many situations in daily life when we have to take some time to respond to some event/query/action. “The time taken by a person to observe, think and act is called reaction time”. For instance, if your teacher asks a question to you and you think of the answer and then reply to it, then the time elapsed before you answer the question, is the reaction time.
How can we estimate/measure the reaction time?
To estimate the reaction time, let us consider the following illustrative investigation:
We take a meter scale and release it vertically across the gap, between our thumb and the forefinger. We ask a friend to eatch it. Next, we determine the distance y traversed by the meter scale. If the reaction time is t, then using equation S = ut + \(\frac{1}{2}\)at²

Question 5.
Define velocity and acceleration. Draw velocity-time sketch for uniform acceleration motion and prove that the area covered by graphical line and time-axis provides the displacement of the object.
Answer:
“The distance travelled per unit time in particular direction i.e., rate of change of displacement with time is called the velocity.” It is a vector quantity.
∴ Velocity = speed+ direction
or Velocity = \(\frac{\text { displacement }}{\text { time }}\)

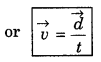
where \vec{d} is displacement in time t.
Unit of velocity in C.G.S. system = cm.s^-1
and that in M.K.S. system = ms^-1
Dimensional formula of u = [M⁰L¹T^-1]

If the velocity of the object is non-uniform i.e., its velocity is different at different points then the mention is non-uniform. If the velocity of the object increases with time, then the motion is said to be ‘accelerated’ and on the other and if the velocity decreases with time, then the motion is said to ‘retarded’ motion. It means.

“The rate of change of velocity of a moving object is called acceleration.” It is denoted by ‘a’ and it is a vector quantity. If the velocity increases with time, then acceleration is positive and on decreasing the velocity, the acceleration is negative i.e., negative acceleration is retardation.
∴ Acceleration = \(\frac{\text { change in velocity }}{\text { time }}\)
If the initial velocity of the object is u and after time t, it becomes v, then
Acceleration = \(\frac{\text { final velocity }-\text { initial velocity }}{\text { time }}\)

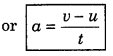
Unit of a in C.G.S. system = cm-s^-2
and that in M.K.S. system = m-s^-2
The dimensional formula of a = \(\frac{\mathrm{L}^1 \mathrm{~T}^{-1}}{\mathrm{~T}^1}\) = L¹T^-2 = [M⁰L¹T^-2]
Types of Acceleration
(a) Uniform acceleration: If the change in velocity in same time intervals is same, then the acceleration is said to be uniform acceleration and the
motion of the object is said to be uniformly accelerated motion.

(b) Variable acceleration: If change in velocity in same time intervals is different, then the acceleration is said to be variable acceleration or non-uniform acceleration.

(c) Average acceleration: If the object is moving with variable acceleration, then the ratio of total change in velocity and total time interval is called average acceleration, i.e.
Average acceleration = \(\frac{\text { Total change in velocity }}{\text { Total time }}\)
If velocity at time t₁ is v₁ and at t₂ is v₂, then

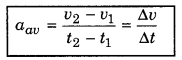
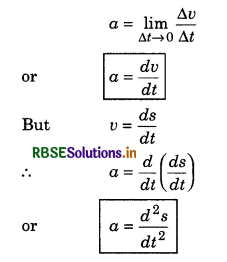
(d) Instantaneous acceleration: In non-uniform accelerated motion, the acceleration at a instantaneous acceleration. For this, the time interval is taken very small i.e. ∆t → 0.
∴ Instantaneous acceleration,

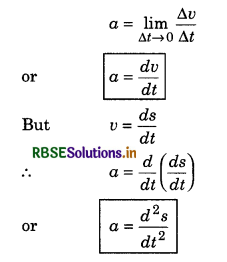
That is, the instantaneous acceleration is second order derivative of its position.
Positive acceleration: When the velocity of the moving object increases with time, then its acceleration is positive. For example, the acceleration of person during race competition. This motion is actually accelerated motion.
Negative acceleration: When the velocity of the moving object decreases with time, then the acceleration said to be negative. For example, the motion of stopping car. This motion is called retarded motion.

1. First Equation: Velocity time graph for uniformly accelerated motion is given in fig. 3.45 The initial velocity of the object is u and after time t it is u.
The angle of graphical line with time-axis is θ.

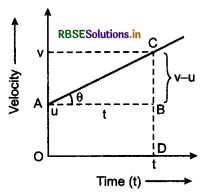
∴ Acceleration,
a = tanθ = \(\frac{C B}{A B}=\frac{v-u}{t}\)
or at = v - u

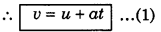
2. Second equation: Distance travelled by the body in time t.
S = Area of trapezium OACD.

3. Third equation: In above part (2) we have seen that
S = \(\frac{u+v}{2}\) x t ..................(3)
From first equation, we get
v - u = at
∴ t = \(\frac{(v-u)}{a}\)
Substituting the value of t n equation (3), we have
S =\( \frac{(v+u)}{2}\) x \(\frac{(v-u)}{a}\) = \(\frac{(v_2-u_2)}{2a}\)
or v² - u² = aS

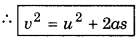
Question 6.
Explain following parameters giving example.
(i) distance
(ii) displacement
(iii) a uniform motion
(iv) non-uniform motion
(v) velocity
(vi) acceleration.
Answer:
Distance: The length of actual path adopted by the body, is called ‘distance’. For example, a person starts moving from point A and reaches point B. Later on he reaches point C (fig. 3.6). The distance covered by the person,

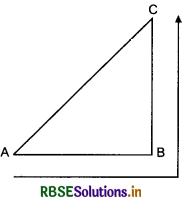
Unit of S in CGS system is centimeter (cm) and in M.K.S. system is metre (m).
Displacement: The minimum distance between initial and final positions is called ‘displacement’.

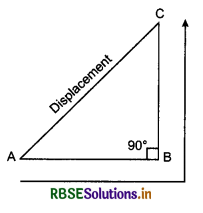
For example, if a person starts moving from point A and ultimately reaches point C through point B, then AC is his displacement (fig. 3.7).
If ∠ABC = 90°,then
AC² = AB² + BC²
or AC = \(\sqrt{A B^2+B C^2}\)
This is the magnitude of displacement AC.
Unit of displacement = Unit of distance
= cm. or m.

When an object moves on straight line with uniform velocity, then this motion is called uniform motion. On the other hand if the velocity of the object
does not remain constant, then its motion is called non-uniform motion.

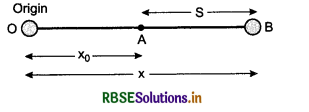
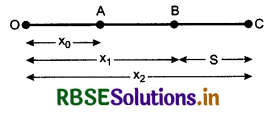
Suppose O is origin and the object is moving with velocity v in X-direction.
At t = 0 i.e. initially the object is at A and after t seconds it reaches to point B which is at a distance S from A Initial distance of the object from origin is x₀.
∴ x = x₀ + S
or x = x₀ + vt ........................(1) [∵ S = vt]
The displacement in tiem t,
x - x₀ = vt .......................(2)

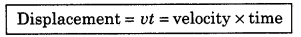
If the object is at a distance of x₁ and x₂ from the origin at times t₁ and t₂ respectively, then
x₁ = x₀ + v x t₁ ........................(3)
and x₂ = x₀ + vt₂ ......................(4)
On subtracting (3) from (4), we have,
x₂ - x₁ = vt₂ - vt₁ = v(t₂ - t₁) ...........................(5)
or Displacement of the object under uniform motion in time interval (t₂ - t₁),
S = (x₂ - x₁) = v(t₂ - t₁) ......................(6)

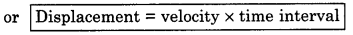
Thus equation (1) represents the position of the object at certain time and equations (2) and (6) represent the displacements of the object under uniform motion.

Some important facts of uniform motion:

1. In uniform motion, the velocity of the particle does not depends on the position of origin.
2. In uniform motion the velocity of the particle does not depend on the freedom of time interval.
3. When in uniform motion, the particle moves on straight line, the displacement of the particle is equal to distance travelled.
4. To maintain uniform motion, there is no need of force.
5. In uniform motion, the instantaneous velocity of the particle is always equal to its average velocity.

“The distance travefled per unit time in particular direction i.e., rate of change of displacement with time is called the velocity.” It is a vector quantity.
∴ Velocity = speed+ direction
or Velocity = \(\frac{\text { displacement }}{\text { time }}\)

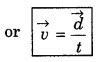
where \(\vec{d}\) is displacement in time t.
Unit of velocity in C.G.S. system = cm.s^-1
and that in M.K.S. system = ms^-1
Dimensional formula of u = [M⁰L¹T^-1]

If the velocity of the object is non-uniform i.e., its velocity is different at different points then the mention is non-uniform. If the velocity of the object increases with time, then the motion is said to be ‘accelerated’ and on the other and if the velocity decreases with time, then the motion is said to ‘retarded’ motion. It means.

“The rate of change of velocity of a moving object is called acceleration.” It is denoted by ‘a’ and it is a vector quantity. If the velocity increases with time, then acceleration is positive and on decreasing the velocity, the acceleration is negative i.e., negative acceleration is retardation.
∴ Acceleration = \(\frac{\text { change in velocity }}{\text { time }}\)
If the initial velocity of the object is u and after time t, it becomes v, then
Acceleration = \(\frac{\text { final velocity }-\text { initial velocity }}{\text { time }}\)

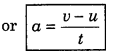
Unit of a in C.G.S. system = cm-s^-2
and that in M.K.S. system = m-s^-2
The dimensional formula of a = \(\frac{\mathrm{L}^1 \mathrm{~T}^{-1}}{\mathrm{~T}^1}\) = L¹T^-2 = [M⁰L¹T^-2]
Types of Acceleration
(a) Uniform acceleration: If the change in velocity in same time intervals is same, then the acceleration is said to be uniform acceleration and the
motion of the object is said to be uniformly accelerated motion.

(b) Variable acceleration: If change in velocity in same time intervals is different, then the acceleration is said to be variable acceleration or non-uniform acceleration.

(c) Average acceleration: If the object is moving with variable acceleration, then the ratio of total change in velocity and total time interval is called average acceleration, i.e.
Average acceleration = \(\frac{\text { Total change in velocity }}{\text { Total time }}\)
If velocity at time t₁ is v₁ and at t₂ is v₂, then

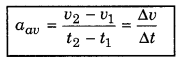
(d) Instantaneous acceleration: In non-uniform accelerated motion, the acceleration at a instantaneous acceleration. For this, the time interval is taken very small i.e. ∆t → 0.
∴ Instantaneous acceleration,

That is, the instantaneous acceleration is second order derivative of its position.
Positive acceleration: When the velocity of the moving object increases with time, then its acceleration is positive. For example, the acceleration of person during race competition. This motion is actually accelerated motion.
Negative acceleration: When the velocity of the moving object decreases with time, then the acceleration said to be negative. For example, the motion of stopping car. This motion is called retarded motion.

Question 7.
What do you understand by acceleration due to gravity? Investigate the equations of motion under gravitational acceleration.
Answer:
When a particle falls freely then Earth attracts this particle with which acceleration, is called acceleration due to gravity and it is denoted by ‘g'. Its value on the surface of Earth is 9.8 ms^-2 or 980 cm-s² or 32 feet ^s-2. The motion under gravity is of following two types:
(a) When acceleration due to gravity acts as accelerations:
When particle falls downward, then gravitational acceleration behaves as acceleration.

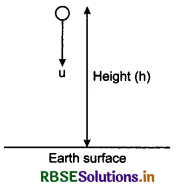
Initiai velocity of the particle = u
Final velocity of the particle = v
Distance travelled by the particle = h
Acceleration of the particle a = +g
First changed equation u = u + gt ........................(1)
Second changed equation
h₂ = ut + \(\frac{1}{2}\)gt² ....................(2)
Third changed equation v² = u² + 2gh ......................(3)
Distance travelled in tth second
h₁^th = u + \(\frac{1}{2}\)g(2t - 1) .......................(4)

Question 8.
What do you understand by average speed. Obtain expressions in different situations.
Answer:
(a) Uniform velocity: If a moving body covers same displacement in same time intervals, then its velocity is said to be uniform velocity.
(b) Variable velocity or non-uniform velocity: If the displacements covered in equal time intervals are different, the velocity is said to be variable or nonuniform velocity. Velocity changes due to following two reasons:
(i) On changing the magnitude
(ii) on changing the direction.
If the speed of the body is constant i.e., uniform, then its velocity will change due to change in direction.
(c) Average velocity: Average velocity of a moving body is the ratio of total displacement and total time taken by the body.
∴ Average velocity = \(\frac{\text { Total displacement }}{\text { Total time }}\)

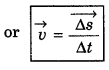
Question 9.
Give the mathematical (calculus method) method for derivation of equations of motion.
Answer:
Suppose body is moving in straight line with uniform acceleration a. Its initial velocity (i.e. at t = 0) is u and after time t is u. Total distance travelled by the body in this time is S.
First equation: According to definition of instantaneous acceleration
a = \(\frac{d v}{d t}\)
or dv = adt
On integrating both sides,
\(\int_u^v d v=\int_0^t a \cdot d t\)
or [v]_u^v = a [t]₀^t
or v - u = a [t - 0] = at

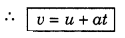
Second equation: According to definition of instantaneous velocity,
v = \(\frac{d S}{d t}\)
or dS = v.dt = (u + at).dt
On integrating both sides,
\(\int_0^S d S=\int_0^t(u+a t) d t=\int_0^t u \cdot d t+\int_0^t a t \cdot d t\)
or [S]₀^S = u[t]₀^K + a[\(\frac{t^2}{2}\)]₀^t
or S - 0 = u(t - 0) + \(\frac{1}{2}\)a(t² - 0)

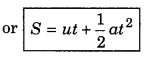
Third equation: According to definitions of instantaneous velocity and acceleration,
We know that the instantaneous acceleration
a = \(\frac{d v}{d t}\) ...............................(1)
We know that the instantaneous velocity
v = \(\frac{d s}{d t}\) .........................(2)
From equation (1) and (2), we have
∴ \(\frac{a}{v}=\frac{d v / d t}{d s / d t}=\frac{d v}{d s}\)
∵ a ds = v dv .......................(3)
On integrating both sides,
\(\int_0^S a d S=\int_u^v v d v\)

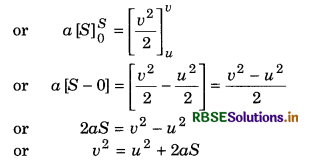
Displacement of body in a particular second:
Suppose an object is moving under uniform acceleration a and we have to find the distance travelled in t^th second.
∵ Distance travelled in t second is obtained by:
S = ut + \(\frac{1}{2}\)at²
∴ Distance travelled in t^th second

Numerical Questions

Based on distance and displacement

Question 1.
A runner is running on a circular path of radius 50 m. The runner and he covers three fourth (i.e. 3/4) path. What will be his distance and displacement?
Answer:
Given: r = 50 m
Distance S = \(\frac{3}{4}\) x 2πr

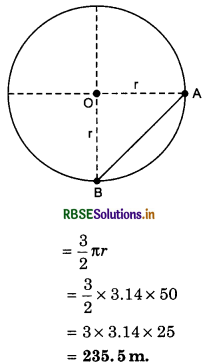
Displacement AB = \(\sqrt{r^2+r^2}=r \sqrt{2}\)
= 50 x 1.414
= 5 x 14.14
= 70.70 m

Question 2.
A particle is projected upwards with velocity' of 20 ms^-1. Calculate its distance travelled and its displacement after 3.0 s. (g = 10ms^-2).
Answer:
Given: u = -20 ms^-1
a = +g = +10 ms^-2
∴ Time taken upto highest point where velocity v = 0.

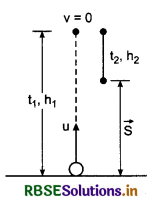
∴ Using equation v = u + at
0 = -20 - gt₁ = -20 - 10t₁
or 10t₁ = 20
∴ t₁ = \(\frac{20}{10}\) = 2 s
∴ t₂ = t - t₁ = 3 - 2 = 1 s
h₁ = ut₁ + \(\frac{1}{2}\)gt₁² = -20 x 2 + \(\frac{1}{2}\) x 10 x 4
= -40 + 20
= -20 m
Now again using S = ut² + \(\frac{1}{2}\)at₂²
h₂ = 0 + \(\frac{1}{2}\) x 10 x 1 = 5 m
∴ Total distance |h₁| + h₂ = 20 + 5 = 25 cm
Displacement |h₁| - h₂ = 20 - 5 = 15 cm

Based on average speed and average velocity

Question 3.
A train of 80 m length is moving with speed of 60 ms^-1 and crosses another train of length 100 m moving with speed of 40 ms^-1. How much time will be taken by first car in crossing the second car?
Answer:
Given: u₁ = 60 ms^-1; u₂ = 40 ms^-1
∴ Relative velocity of first train with respect to second,
v₁² = u₁ - u₂ = 60 - 40 = 20 ms^-1
Total distance for crossing
l = l₁ + l₂ = 80 + 100 = 180 m
∴ Time taken by first train in crossing second train
t = \(\frac{l}{v_{12}}=\frac{180}{20}\)
= 9 s

Question 4.
Nisha starts from her house to her school situated at 50 km with uniform speed of 50 km.h^-1. After becoming over the school time, she returns back to her house with speed of 30 km-h^-1 due to rush on the road. Calculate the average speed during whole journey.
Answer:
Given: v₁ = 50 km-hr^-1; S₁ = 50 km
v² = 30 km-hr^-1, S₂ = 50 km
∴ v_av = \(\frac{S_1+S_2}{\frac{S_1}{v_1}+\frac{S_2}{v_2}}=\frac{50+50}{\frac{50}{50}+\frac{50}{30}}=\frac{50 \times 2}{50\left[\frac{1}{50}+\frac{1}{30}\right]}\)
= \(\frac{2 \times 50 \times 30}{30+50}=\frac{100 \times 30}{80}=\frac{300}{8}\) = 37.5 km.hr^-1
or vav = 37.5 km.hr^-1

Question 5.
An object is moving in x-direction an its displacement is given by x = 30 + 20t², where x is in m and t is in 's'.
(i) Find out the velocity and acceleration of the object and
(ii) initial velocity of the object and its initial position.
Answer:
Given: x = 30 + 20t²
(i) Velocity, v = \(\frac{d x}{d t}=\frac{d}{d t}\)(30 + 20t²) = 0 + 40t
or v = 40 t ms^-1
Acceleration a = \(\frac{d x}{d t}=\frac{d}{d t}\)(40t) = 40 ms^-2
(ii) ∵ v = 40 t ms^-1
∴ Initial velocity i.e. at t = 0
v₀ = 40 x 0 = 0 ms^-1
Initial position i.e. at t = 0
x₀ = 30 + 20 x (0)² = 30 + 0
or x₀ = 30 m

Question 6.
An object starts moving from rest and covers a distance S₁ in time t moving with uniform acceleration. If the object cover a distance S₂ in next t s, then show that S₂ = 3S₁.
Answer:
S₁ = 0 + \(\frac{1}{2}\)at²
or S₁ = \(\frac{1}{2}\)at² ..........................(1)
v = 0 + at

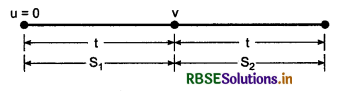
For next t sec, initial velocity = v
∴ S₂ = vt + \(\frac{1}{2}\)at² = at.t + \(\frac{1}{2}\)at²
= at² + \(\frac{1}{2}\)at²
S₂ = \(\frac{3}{2}\)at² ...................(2)
or S₂ = 3 x (\(\frac{1}{2}\)at²)

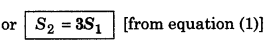
Question 7.
A moving object covers a distance of 200 m in first 2s and 220 m in next 4s. Find the velocity of moving object at the end of 7 s.
Answer:
S₁ = ut₁ + \(\frac{1}{2}\)at₁²
200 = u x 2 + \(\frac{1}{2}\)a x 2 x 2
or 200 = 2u + 2a
or 100 = u + a
or u + a = 100 ..........................(1)

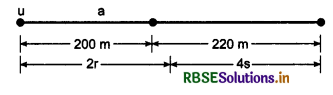
Total distance S₂ = 200 + 220 = 420
Total time t₂ = 2 + 4 = 6 s
∴ S₂ = ut + \(\frac{1}{2}\)at₂²
or 420 = u x 6 + \(\frac{1}{2}\)a x 6 x 6
or 420 = 6u + 18a
or 70 = u + 3a
or u + 3a = 70 .........................(2)
On subtracting equation (2) from (1)

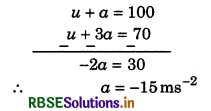
From equation (1)
u - 15 = 100 ⇒ u = 115 ms^-1
∴ Velocity after 7s
v = u + at
= 115 - 15 x 7
= 115 - 105
= 10 ms^-1

Question 8.
A girl reaches railway station situated at 4 km from her house, in 1 hr moving with uniform velocity. She takes rest at railway station for 0.5 hr. Later on moving with uniform speed she returns to her house in 1.5 hrs. Show the distance covered by the girl on displacement-time graph and calculate her average speed.

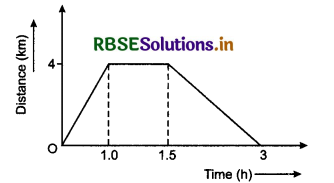
Answer:
Average speed
v_av = \(\frac{\text { Totaldistance }}{\text { Total time }}=\frac{4+4}{3}=\frac{8}{3}\)
= 2.67 km.hr^-1

Question 9.
A car A stops at traffic signal post due to red light. When signal becomes green,then it starts moving. Another car B moving with uniform velocity of 30 km-hr^-1 crosses car A at the same time. The speed of car A becomes 50 km-hr^-1 in 6 min with uniform acceleration. Later on car A stars moving with uniform velocity. Velocity-time graph for both the cars is shown in figure. Answer the following questions on the basis of this graph.

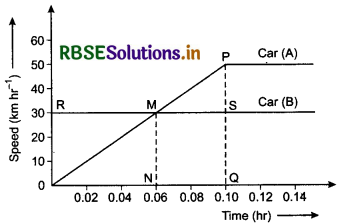
(i) With in how much time the speed of car A becomes equal to that of B?
(ii) How much ahead is car B from car A at this time?
(iii) After first 6 min, by how much distance, car A is behind car B?
(iv) At what time car A will cross the car B?
(v) At this time what will be distance of cars from traffic signal post?
Answer:
(i) Velocity-time graphs of cars A and B cut each other at point M, therefore this point represents common velocity. Hence after time 0.06 hr, the
velocity of car A will be equal to that B.

(ii) The difference of distance between two cars
= Area of ∆OMN
= \(\frac{1}{2}\) x ON x MN
= \(\frac{1}{2}\) x 0.06 x 30
= 0.06 x 15
= 0.90 km

(iii) Time = 6 min = \(\frac{6}{60}\) hr
= 0.10 hr
Distance travelled by car A in 0.10 hr,
S_A = Area of ∆OPQ = \(\frac{1}{2}\) x OQ x PQ
= \(\frac{1}{2}\) x 0.10 x 50
= \(\frac{5}{2}\) = 2.5 km
and that by car B
S_B = Area of \square O R S Q
= OR x OQ
= 30 x 0.10
= 3 km
∴ Distance between them = ∆S = S_B - S_A = 3 - 2.5 = 0.5 km
i.e. ear A is 0.5 km behind car B.

(iv) Suppose after time t hr from 0.10 hr car A will cross the car B.
Relative velocity
v_AB = v_A - v_B = 50 - 30 = 20 km.hr^-1
∴ t = \(\frac{\Delta S}{v_{A B}}=\frac{0.5 \mathrm{~km}}{20 \mathrm{~km} \cdot \mathrm{h}^{-1}}=\frac{0.05}{2}\) = 0.025 hr.
∴ Total time after which car A will cross the car B.
= 0.10 + t
= 0.10 + 0.025
= 0.125 hrs

(v) The distance of cars at this time for signal post
= 30 x 0.125 km
= 3 x 1.25 km
= 3.75 km

Based on uniform accelerated motion

Question 10.
An engine of a car can produce maximum acceleration of 5 ms^-2 and its breaks can produce maximum retardation of 10 ms^-2. How much time will be taken by the car in reaching a point situated at distance of 1.5 km, if the car starts moving from rest?
Answer:
Total distance = 1.5 km
= 1500 m
Maximum acceleration
a_max = +5 ms^-2
Maximum retardation a_max = -10 ms^-2

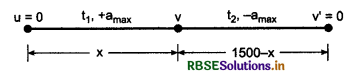
Maximum velocity attained by car during acceleration,
v₂ = 0 + 2a_max.x = 2 x 5 x x
or v =\( \sqrt{10 x}\)
During retardation final velocity v' = 0
∴ Again using the equation v² = u² + 2aS
v'² = v² - 2a_max (1500 - x)
or 0 = 10x - 2 x 10 (1500 - x)
or 10x = 20 (1500 - x)
or x = 3000 - 2x
or 3x = 3000
∴ x = 1000 m
∴ v = \(\sqrt{10 \times 1000}\) = 100 ms^-1
The time taken by car during acceleration is t₁.
∴ From v = u + at
100 = 0 + 5t₁
∴ t₁ = \(\frac{100}{5}\) = 20 s
During retardation if time taken by car is t₂ then again by formula v = u + at
v' = v - a_max.t²
or 0 = 100 - 10 x t²
or 10t₂ = 100
∴ t₂ = \(\frac{100}{10}\) = 10 s
∴ Total time taken by car = t₁ + t₂ = 20 + 10
= 30 s

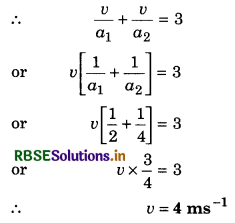
Question 11.
A car starts from rest is uniformly accelerated by 2 ms^-2, later on it retards uniformly by 4 ms^-2 and becomes at rest. It car remains moving for 3 s, then find out the maximum speed of the car.
Answer:
u = 0, a₁ = 2 ms^-2
a₂ = -4 ms^-2
∵ v = u + at

∴ v = 0 + a₁t₁
⇒ t₁ = \(\frac{v}{a_1}\)
During retardation
0 = v - a₂t₂ ⇒ t₂ = \(\frac{v}{a_2}\)
∴ t₁ + t₂ = 3

Question 12.
A car is moving on road with velocity of 15 ms^-1. On aplying breaks, stopping distance is 18 m. If the velocity of the car would is 25 ms^-1 then what will be its stopping distance if retardation produced by the break be the same as previous one?
Answer:
v₁ = 15 ms^-1, stopping distance S₁ = 18 m
u₂ = 25 ms^-1, stopping distance S₂ = ?
∵ Stopping distance

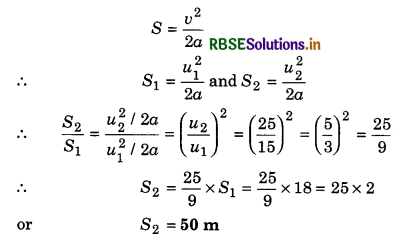
Question 13.
A particle covers a distance of 25 m in 5^th second and 33 m in 7^th second. If the particle accelerates uniformly then what will be distance covered seconds in next 3 seconds?
Answer:
∵ St^th = u + \(\frac{1}{2}\)a(2 x 5 - 1)
∴ 25 = u + \(\frac{9}{2}\)a
or 50 = 2u + 9a
or 2u + 9a = 50 .....................(1)
Similarly 33 = u + \(\frac{1}{2}\)a(2 x 7 - 1)
or 66 = 2u + 13a
or 2u + 13a = 66 .......................(2)
On subtracting equation (1) from (2),

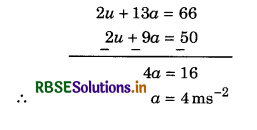
Now from equation (1)
2u + 9 x 4 = 50
or 2u = 50 - 36 = 14
∴ u = 7 ms^-1
Distance travelled in 7 sec,
S₁ = ut + \(\frac{1}{2}\)at²
= 7 x 7 + \(\frac{1}{2}\) x 4 x 49
= 49 + 98
= 147 m
Distance travelled in 10 s
S₂ = 7 x 10 + \(\frac{1}{2}\) x 4 x 10 x 10
= 70 + 200
= 270 m
∴ Distance travelled in next 3 s,
S = S₂ - S₁ = 270 - 147
= 123 m

Based on gravitational acceleration

Question 14.
A freely falling object from some height covers half of total height in its last second. From which height was it droped and for how long it remains in air?
Answer:
Stth = u + \(\frac{1}{2}\) a(2t - 1)
∴ \(\frac{h}{2}\) = 0 + \(\frac{1}{2}\) x 10(2t - 1)
h = 20t - 10 ........................(1)
But h = 0 + \(\frac{1}{2}\)gt² = \(\frac{1}{2}\) x 10 x t² = 5t²
∴ From equation (1),
5t² = 20t - 10
or t² = 4t - 2
or t² - 4t + 2 = 0

Question 15.
A parachute soldier jumps from an air-craft. When he falls freely upto 40 m then his parachute opens. Now he falls with retardation of 2.0 ms^-2 and reaches Earth with velocity of 3.0 ms^-1. What was the height of air-craft and for how long the soldier remained in air?
Answer:
Velocity of soldier after freely falling upto 40 m
v² = 0 + 2gh = 2 x 9.8 x 40

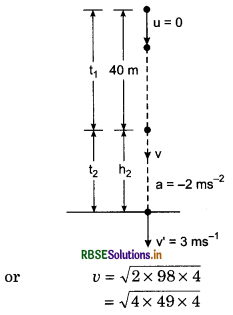
= 4 x 7
= 28 ms^-1
and time taken during distance
v = 0 + gt₁
∴ t₁ = \(\frac{v}{g}=\frac{28}{9.8}=\frac{280}{98}=\frac{20}{7}\)
= 2.857 s
Time taken by soldier during retradation portion
v' = v - at²
3 = 28 - 2 x t²
2t² = 28 - 3 = 25
∴ t² = \(\frac{25}{2}\) = 12.5 s
∴ Total time = t₁ + t₂ = 2.857 + 12.5
= 15.357
= 15.4 s
Distance travelled during retardation peroid,
v'² = u² - 2ah²
or 2ah² = u² - v'² = (28)² - (3)²
or 2 x 2 x h₂ = 784 - 9 = 775
∴ h₂ = \(\frac{775}{4}\) = 194 m
∴ Total height = 194 + 40 = 234 m

Question 16.
A food packet is dropped from a helicopter which is elevating with velocity of 2 ms^-1. After 2s, (i) What is velocity the packet, (ii) What is height of the packet below the helicopter? (g = 9.8 ms^-2).
Answer:
Initial velocity of food packat u = -2 ms^-1
Acceleration a = +g = +9.8 ms^-2
Time t = 2 s
∴ Velocity after 2 s
v = u + at
= -2 + 9.8 x 2
= -2 + 19.6
= 17.6 ms^-1
And height below helicopter.
h = ut + \(\frac{1}{2}\) at² = -2 x 2 + \(\frac{1}{2}\) x 9.8 x 2 x 2 = -4 + 19.6
= 15.6 m

Question 17.
A rocket is launched vertically upwards from the surface of Earth. Air friction etc. are considered negligible. The engine of rocket produced uniform acceleration of 19.6 ms^-2. If the engine of the rocket stops working after 5 s, then what will be maximum height attained by the rocket? After how much time, the rocket will strike the ground and with 'what velocity it will reach the ground?
Answer:
Acceleration of rocket a = 19.6 ms^-2
Time t = 5 s
∴ Maximum velocity attained by the rocket
v = ut + at
= 0 + 19.6 x 5
= 98.0 ms^-1

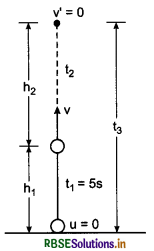
If time t₂ is taken by the rocket upto maximum height, then from relation
v = u + at
Hence v = v' = 0, u = v, a = -g
∴ 0 = v - gt₂
or t₂ = \(\frac{v}{g}=\frac{98}{9.8}\) = 10 s
and height achieved in this period,
v² = u² + 2aS
Here v = v² = 0, u = v
0 = (98)² - 2 x 9.8 x h₂
∴ h₂ = \(\frac{98 \times 98}{2 \times 9.8}=\frac{98 \times 980}{2 \times 98}\) = 490 m
The height in first 5 s
h₁ = 0 + \(\frac{1}{2}\)at² = \(\frac{1}{2}\) x 19.6 x 5 x 5 = 245 m
∴ Maximum height = h₁ + h₂
h = 245 + 490 = 735 m
From maximum height upto ground, the time taken is t₃
∴ h = 0 + \(\frac{1}{2}\)gt₃² ⇒ t₃ = \(\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 735}{9.8}}\)
or t₃ = 12.25 s
∴ Total time = t₁ + t₂ + t₃ = 5 + 10 + 12.25
= 27.25 s
Velocity of rocket on reaching the ground
v'' = u + gt = 0 + 9.8 x 12.25
= 120.05 ms^-1

Question 18.
Four balls are dropped one by one after interval of 1 s each from the top of a tower. First ball reaches the ground after 4s. At this moment, what will be the distances between first and second; second and third; third and fourth balls? (g = 9.8ms^-2)
Answer:
First ball reaches the ground in 4 s.
∴ Distance travelled
h₁ = ut + \(\frac{1}{2}\)gt²
= 0 + \(\frac{1}{2}\) x 9.8 x 4 x 4
= 78.4 m

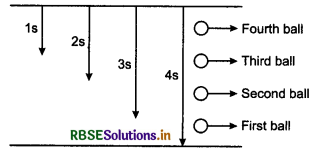
For second ball,
h₂ = 0 + \(\frac{1}{2}\) x 9.8 x 3 x 3
= 44.1 m
For third ball,
h₃ = 0 + \(\frac{1}{2}\) x 9.8 x 2 x 2
= 19.6 m
For fourth ball
h₄ = \(\frac{1}{2}\) x 9.8 x 1 x 1
= 4.9 m
∴ Distance between first and second ball
= h₁ - h₂ = 78.4 - 44.1 = 34.3 m
Distance between second and third ball
= h₂ - h₃ = 44.1 - 19.6 = 24.5 m
and distance between third and fourth ball
= h₃ - h₄ = 19.6 - 4.9 = 14.7 m

Question 19.
A ball is projected vertically upwards. Friction of air has been considered constant. Which time will be greater either time of ascending upto highest point or time of decending from highest point to ground?
Answer:
Suppose the constant force of air friction is f, then for upward motion net retarding force
F = mg + f
If net retardation be a, then force F = ma
∴ mg + f = ma
∴ a = g + \(\frac{f}{m}\) = g + g' where g' = \(\frac{f}{m}\)
If tascent be the time of ascent, then from formula.
v = u + at
0 = v₀ - at_ascent
or t_ascent = \(\frac{v_0}{a}\)
or t_ascent = \(\frac{v_0}{\left(g+g^{\prime}\right)}\)
Now applying equation v² = u² + 2aS
0 = v₀² - 2ah
or v₀² = 2ah = 2 (g + g')h

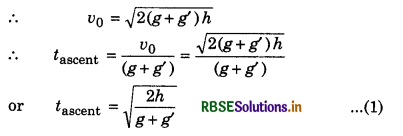
Now for return journey,
a = (g - g')
∴ Applying equation S = ut + \(\frac{1}{2}\)at²
h = 0 + \(\frac{1}{2}\) (g - g')t²_descent
or t_descent = \(\sqrt{\frac{2 h}{\left(g-g^{\prime}\right)}}\) ............................(2)
From equation (1) and (2) it is clear that
t_ascent < t_descent or t_descent > t_ascent

Question 20.
A stone is dropped from the top of a tower of height 50 m. At the same time another stone is thrown vertically upwards from the ground with velocity of 20 ms^-1. At what time both stones will cross each other?
Answer:
Given h = h₁ + h₂
∴ h₁ + h₂ = 50 m

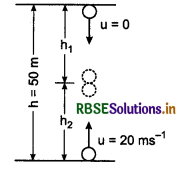
Suppose both the stones cross each other at time 't'
For falling stone
u = 0, a = g
∴ h₁ = 0 + \(\frac{1}{2}\)gt²
h₁ = \(\frac{1}{2}\)gt²
For stone which is thrown vertically upwards,
u = 20 ms^-1, a = -g
∴ h₂ = 20t - \(\frac{1}{2}\)gt²
∴ h₁ + h₂ = \(\frac{1}{2}\)gt² + 20t - \(\frac{1}{2}\)gt²
or 50 = 20t
∴ t = \(\frac{50}{20}\) = 2.5 s

Based on accelerated motion

Question 21.
The displacement of a particle at any instant is given by relation x = -15t² + 20t + 30 where x is in ‘m’ and t is in ‘s’. Find the position, velocity and acceleration of the particle at t = 0.
Answer:
Given x = -15t² + 20t + 30
At t = 0, the position of the particle,
x₀ = 0 + 0 + 30
or x₀ = 30 m
Velocity v = \(\frac{d x}{d t}=\frac{d}{d t}\)[-15t² + 20t + 30]
or v = -30t + 20 + 0
∴ v₀ = -30 x 0 + 20 = 0 + 20
∴ v₀ = 20 ms^-1
Acceleration a = \(\frac{d v}{d t}=\frac{d}{d t}\)(-30t + 20)
or a = -30 + 0
∴ a₀ = -30 ms^-2

Question 22.
Acceleration of a body is a function of time which is shown in figure. If velocity at t = 0 is u = 0, then

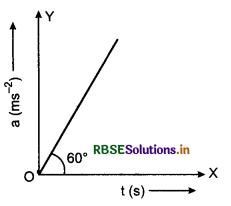
(a) What is velocity of the body at later time?
(b) What is the distance travelled by the body in time t?
Answer:
In this given graph (a - t)graph, the acceleration is not constant. According to figure given in question, slope of the graph,

Based on relative velocity

Question 23.
A century express is moving with speed v. The driver of the express observes that a passenger train is also going on the same track with speed u at the distance of x To avoid the collision of two trains, the driver of express train applies brakes. If a be the retardation of express train, then collision will be avoided if x > \(\frac{(v-u)^2}{2 a} \)
Answer:
Relative velocity of express train w.r.t. passenger train.

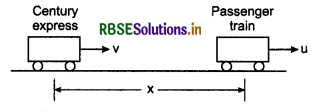
v_ep = (v - u)
∴ Initial velocity = (v - u)
and final velocity = 0
Acceleration = -a
∴ For stopping the express train from formula
v² = u² - 2ax
∴ 0 = (v - u)² - 2ax
or 2ax = (v - u)²
or x = \(\frac{(v-u)^2}{2 a}\)
∴ For avoiding the collision,
x > \(\frac{(v-u)^2}{2 a}\)

Question 24.
In two parallel railway tracks on track a goods train is moving with speed of 72 km-hr^-1 and on other track a passenger train is moving with speed of 108 km.hr^-1. Length of goods train is 150 m and that of passenger train is 90 m. How much time will be taken by the trains in crossing each other if (i) both the trains move in same direction and (ii) in opposite dirction?
Answer:
Speed of passenger train v_p = 72 km.hr^-1
= \(\frac{72 \times 5}{18}\) = 20 ms^-1, length of passenger train
l₁ = 90 m,
Speed of goods-train v_g = 108 km.hr^-1
= \(\frac{108 \times 5}{18}\) = 30 ms^-1
Length of goods-train l₂ = 150 m
(i) When both trains are moving in same direction, then relative velocity of goods train w.r.t. passenger train,
v_gp = v_g - v_p = 30 - 20 = 10 ms^-1
Total length for crossing the trains,
l = l₁ + l₂ = 150 + 90 = 240 m
∴ Required time
t = \(\frac{l}{v_{g p}}=\frac{240}{10}\)
l = 24 s
(ii) When both trains are running in opposite directions, then
v_gp = v_g - v_p
= 30 - (-20)
= 30 + 20
= 50 ms^-1
∴ t = \(\frac{l}{v_{g p}}=\frac{240}{50}\) = 4.8 s

Higher Order Thinking Skills or HOTS 

Question 1.
The speed of a train increases from zero to v at the rate α. Later on for some time it runs with uniform speed. In the last its velocity becomes zero, decreasing at the rate of ß. It total length of journey be l, then prove that the total time of journey = \(\frac{l}{v}+\frac{v}{2}\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)\).
Solution:
Suppose for accelerated motion, the time is t₁ and distance is S₁.
∴ From equation v = u + at
v = 0 + αt₁

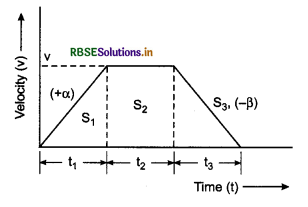
or t₁ = \(\frac{v}{\alpha}\)
Now using formula
v² = u² + 2aS
We have
v² = 0 + 2αS₁
∴ S₁ = \(\frac{v^2}{2 \alpha}\)
Suppose the train moves upto time t₂, with uniform speed.
∴ Distance S = vt₂
∴ t₂ = \(\frac{S_2}{v}\)
Suppose the time for last retarded motion, is t₃ and distance is S₃.
∴ From relation v = u + at
0 = v - ßt₃ ⇒ t₃ = \(\frac{v}{\beta}\)
and from relation v² = u² + 2aS
0 = v₂ - 2 ßS₃ ⇒ S₃ = \(\frac{v^2}{2 \beta}\)
But S₁ + S₂ + S₃ = l

Question 2.
A train starts from station A with uniform accleration ay and after some time it is retarded with retardation a₂ and travels some more distance. Altimately it stops at station B. The distance between A and B is 4 km and train takes a time of 4 min to cover this distance. It unit of acceleration be km/min 2 then prove that \(\frac{1}{a_1}+\frac{1}{a_2}\) = 2
Solution:
Suppose time t₁ and t₂ is taken by train in two parts of journey and their distances are S₁ and S₂ respectively. According to question
S₁ + S₂ = 4 km ...............................(1)
t₁ + t₂ = 4 min ........................(2)

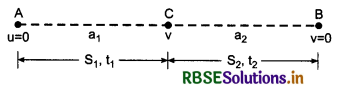
For part AC, distance
S₁ = average velocity x time
= \(\frac{u+v}{2}\) x t₁ = \(\frac{0 \times v}{2}\) x t₁
or S₁ = \(\frac{1}{2}\)vt₁ ..........................(3)
Similarly for part CB,
S₂ = (\(\frac{v+0}{2}\)).t₂
or S₂ = \(\frac{1}{2}\)vt₂ .............................(4)
From equation (1),

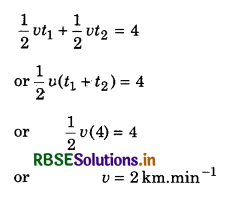
For part AC, from formula v = u + at
v = 0 + a₁t₁ ⇒ t₁ = \(\frac{v}{a_1}=\frac{2}{a_1}\) ..........................(5)
Similarly for part CB,
0 = v - a₂t₂ ⇒ t₂ = \(\frac{v}{a_2}=\frac{2}{a_2}\) .........................(6)
∴ From equation (2),
\(\frac{2}{a_1}+\frac{2}{a_2}\) = 4

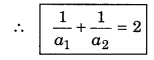
Question 3.
A particle moves between A and B with uniform acceleration. The velocity of the particle at point A of straight line AB is u and that at B is v. Find the velocity of the particle at middle point C of AB and of time from A to C, is double of time from C to B, prove that v = 7 u.
Solution:
Suppose uniform acceleration is a
Let velocity at C is v₁.
Therefore from formula v² = u² + 2aS ............................(1)

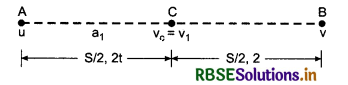
v₁² = u² + 2a(\(\frac{S}{2}\))
or v₁² = u² + aS
or v₁² - u² = aS ............................(2)
Substituting the value of aS from equation (2) in equation (1),
v² = u² + 2(v₁² - u²)
or v² = u² + 2v₁² - 2u²
or v² = 2v₁² - u²
⇒ 2v₁² = v² + u²
∴ v₁ = \(\sqrt{\frac{v^2+u^2}{2}}\) ..........................(3)
Let the time taken by particle from C to B is t,
then time from A to C will be 2t (as given).
∴ Total time from A to B = 3t
∴ Using relation
Distance = average speed x time,

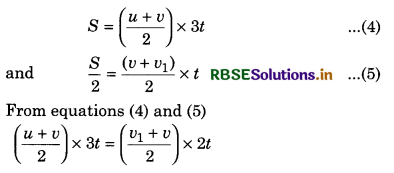
or 3(u + v) = 2(v₁ + v)
or 3u + 3v = 2v₁ + 2v
or 3u + v = 2v₁
Substituting the value of v₁ from equation (3),
3u + v = 2\(\sqrt{\frac{v^2+u^2}{2}}\)
or (3u + v)² = \(\frac{4\left(v^2+u^2\right)}{2}\) = 2v² + 2u²
or 9u² + v² + 6uv = 2v² + 2u²
or 7u² - v² + 6uv = 2v² + 2u²
or 7u² + 6uv - v² = 0
or 7u² + 7uv - uv - v² = 0
or 7u(u + v) - v(u + v) = 0
or (u + v)(7u - v) = 0
If u + v = 0
Then v = -u (Not acceptable)
If 7u - v = 0

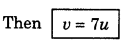
Question 4.
The acceleration of a particle is given by a = 9x. At time t = 0, x = 1m and v = 3ms^-1. Find the velocity of the particle at t = 2s.
Solution:
Given: a = 9x

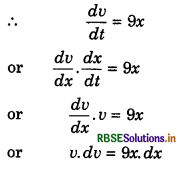
On integrating both sides.
∫vdv = ∫9x.dx
or \(\frac{v^2}{2}=\frac{9 x^2}{2}\) + c₁ Where c₁ = constant of integration,
Given: At x = 1 m, v = 3 ms^-1

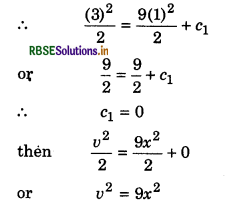
or v = 3x
or \(\frac{d x}{d t}\) = 3x
or \(\frac{d x}{x}\) = 3x
or \(\frac{d x}{x}\) = 3.dt
On integrating both sides,
log_e(x) = 3t + c²
∵ At t = 0, x = 1 m
∴ log_e(1) = 0 + c₂ ⇒ c₂ = 0
∴ log_e(x) = 3t
Taking antilog,
x = e^3t
∴ Velocity v = \(\frac{d x}{d t}=\frac{d}{d t}\)(e^3t)
or v = 3e^3t
∴ At t = 2 s, Velocity v = 3e⁶ ms^-1

Question 5.
Acceleration of a particle is given by relation, a = (3t² + 2t + 2) ms^-2, where t is in seconds. If particle starts motion with velocity of 2 ms^-1 at t = 0 then what will be its velocity after 2s?
Solution:
Given: acceleration,
a = 3t² + 2t + 2
or \(\frac{d v}{d t}\) = 3t² + 2t + 2
or dv = (3t² + 2t + 2)dt
On integrating both sides,
∫ dv = ∫(3t² + 2t + 2) dt
or v = \(\frac{3 t^3}{3}+\frac{2 t^2}{2}\) + 2t + c
or v = t³ + t² + 2t + c where c is integration constant
∵ At t = 0, v = 2 ms^-1
∴ 2 = 0 + 0 + 0 + c
⇒ c = 2
∴ v = t³ + t² + 2t + 2
∴ At t = 2s; v = (2)³ + (2)² + 2 x 2 + 2
= 8 + 4 + 4 + 2
= 18 ms^-1